第9章多元函数微分法及其应用课本基础知识

1 高等数学复习-多元函数微分法及其应用

一、列举二元函数的例子？

二、求多元函数的极限？

三、证明函数的连续性？

四、多元函数的性质？

五、求多元函数再某点的偏导数？

六、求多元函数的偏导数？

七、求多元函数的高阶偏导数？

八、二阶混合偏导数定理？

九、求函数的全微分？

十、全微分的应用?

十一、一元函数与多元函数复合定理?

十二、多元函数与多元函数复合定理?

十三、其它复合定理？

十四、求复合函数的偏导数？

十五、求复合函数的全导数？

十六、利用全微分形式不变形求偏导数？

十七、利用隐函数求导？

十八、利用方程组求偏导数?

十九、求函数的单位切向量？

二十、求曲线的切线及法平面方程？ 2 二十一、求球面的切线及法平面方程？

二十二、求旋转抛物面的切线及法平面方程？

二十三、求某个方向的方向导数？

二十四、求函数在某点的梯度？

函数在某点的梯度是这样一个向量，他的方向是函数再这点方向导数取得最大值的方向，它的模就等于方向导数的最大值。

（1）求出函数在各个自变量上的偏导数

（2）带入点惊醒计算

（3）表示出该向量（记得加上i、j、k）

二十五、求函数再某个方向的变化率？

二十六、举例说明多元函数最值及极值？

二十七、有极值定理?

二十八、求多元函数的极值？

二十九、拉个朗日乘数法求极值？

（3）连续、偏导数存在和可微之间的关系

在点处连续、偏导数存在、可微、存在连续的偏导数之间的关系是：

在点处存在连续的偏导数

在点处可微在点处连续

在点处偏导数存在.

3、多元复合函数求导法

（1）一元函数与多元函数复合的情形

如果函数及都在点可导，函数在对应点具有连续偏导数，则复合函数在点可导，且有

．

（2）多元函数与多元函数复合的情形

如果函数及都在点具有对及对的偏导数．函数在对应点具有连续的偏导数，则复合函数在点的两个偏导数存在，且有

， ．

这里有两个自变量和两个中间变量，随着自变量个数与中间变量个数的变化，链导法公式也因之而异，但如果能搞清楚复合函数结构中哪些是自变量，哪些是中间变量以及它们的个数，则就抓住了复合函数求导的关键.如果自变量只有一个，不论中间变量的个数是多少，所求得的导数就是全导数.

值得注意的是，对自变量兼作中间变量的情形，求导时往往容易弄混.例如下面的情形：

， 则复合函数对，的偏导数为

，．

这里与是不同的，是将复合函数中的看成不变而对的偏导数，是把中的及都看成不变而对的偏导数．与也有类似的区别．读者如能领会此点，就不难正确理解公式中的偏导符号的意义了.

4、隐函数的求导公式

（1）若是由方程所确定的一元隐函数.

则

且 ．

（2）若是由方程所确定的二元隐函数.

则

.

求隐函数的一阶导数或偏导数时，首先要认清公式中或中哪个为自变量，哪个为因变量，然后套用公式，值得注意的是，求二阶偏导数不能用上面的公式.

5、偏导数的应用

（1）偏导数的几何应用

① 设空间曲线方程为 .

则曲线上点处的切线方程为

法平面方程为

.

高等数学（下）知识点

第 1 页 共 18 页 高等数学下册知识点

第七章 空间解析几何与向量代数

一、填空与选择

1、已知点A(,,)321和点B(,,)723，取点M使MBAM2，则向量OM=。

2 已知点A(,,)012和点B(,,)110，则0AB= 。

3、设向量a与三个坐标面的夹角分别为,,，则coscoscos222= 。

4、设向量a的方向角3,为锐角，，且4a，则a= 。

5、向量)5,2,7(a在向量)1,2,2(b上的投影等于。

6、过点121，，P且与直线1432tztytx，，，

垂直的平面方程为_____________________________．

7、已知两直线方程是130211:1zyxL，11122:2zyxL，则过1L且平行2L的平面方程为____________________

8、设直线182511:1zyxL,03206:2zyyxL，则1L与2L的夹角为（ ）

（A）． 6 （B）．4 （C）．3 （D）2．

9、平面AxByCzD0过x轴，则（ ）

（A）AD0 （B）BC00, （C）BC00, （D）BC0

10、平面3510xz（ ）

（A）平行于zox平面 （B）平行于y轴（C）垂直于y轴 （D）垂直于x轴

11、点M(,,)121到平面xyz22100的距离为（ ）

（A）1

（B）1 （C）－1 （D）13

12、与xoy坐标平面垂直的平面的一般方程为

。

13、过点(,,)121与向量kjSkjiS21,32平行的平面方程为 。

14、平面0218419zyx和0428419zyx之间的距离等于 。

基本训练1

1．设函数222),(yxxyyxf，求xyf,1． 答案：222yxxy

2．求下列函数的定义域：

（1）84ln2xyz； 答案：)}2(4|),{(2xyyx；

（2）yxyxz11； 答案：|}||),{(yxyx；

（3）xyzarcsin； 答案：}0|||||),{(xxyyx且

3．求下列极限：

（1）11lim222200yxyxyx； 提示：分母有理化；答案：2

（2）xxyyx)sin(lim00； 答案：0

（3）yxyxyx1cos1sinlim300． 提示：无穷小与有界函数之积仍是无穷小； 答案：0

4．证明极限yxyxyx00lim不存在：

提示：令(x, y) 沿不同的路径kxy趋向于原点，极限等于不同的值.

5．函数yxz1在何处是间断的？

答案：在位于xOy平面的直线y = x上.

6．讨论函数0,00,222222yxyxyxxyz的连续性．

提示：选取直线kxy， 则

2222)0,0(),(l22)0,0(),(1imlimkkkxxkxyxxykxyyxkxyyx

随着k的变化而变化，即22)0,0(),(limyxxyyx不存在，函数在除)0,0(外任一点都连续.

7．求下列函数的偏导数：

(1) 22yxyxz； 第八章

多元函数微分学

第 页 共

18 页

2

答案：221yxxxz，221yxyyz

（2）yxztanln；

答案：yxyxyxzcossin1，yxyxyxyzcossin2

（3）yxzarctan；

答案：)1(22yyxxyxxz，)1(2ln2yyxxxyz

1 第九章 多元函数微分学

§9.1 多元函数的概念、极限与连续性

一、多元函数的概念

1．二元函数的定义及其几何意义

设D是平面上的一个点集，如果对每个点DyxP,，按照某一对应规则f，变量z都有一个值与之对应，则称z是变量x，y的二元函数，记以yxfz,，D称为定义域。 二元函数yxfz,的图形为空间一卦曲面，它在xy平面上的投影区域就是定义域D。

例如 221yxz，1:22yxD， 此二元函数的图形为以原点为球心，半径为1的上半球面，其定义域D就是 xy平面上以原点为圆心，半径为1的闭圆。

2．三元函数与n元函数

zyxfu,, zyx,,空间一个点集称为三元函数

nxxxfu,,21 称为n元函数

它们的几何意义不再讨论，在偏导数和全微分中会用到三元函数。条件极值中，可能会遇到超过三个自变量的多元函数。

二、二元函数的极限

设函数),(yxf在区域D内有定义，),(000yxP是D的聚点，如果存在常数A，对于任意给定的0，总存在0，当),(yxP满足20200)()(0yyxxPP时，恒有Ayxf),(成立。

则记以Ayxfyyxx,lim00或Ayxfyxyx,lim00,,。 称当yx,趋于00,yx时，yxf,的极限存在，极限值A，否则称为极限不存在。

值得注意：这里yx,趋于00,yx是在平面范围内，可以按任何方式沿任意曲线趋于00,yx，所以二元函数的极限比一元函数的极限复杂；但考试大纲只要求知道基本概念和简单的讨论极限存在性和计算极限值，不像一元函数求极限要求掌握各种方法和技巧。

求极限的方法

1、一元函数求极限的方法及运算法则对多元函数依旧成立。如：两个重要极限，等价无穷小法则等等。

第九章 多元函数微分法及其应用

一、填空题

1.若 f ( x, y) x2 y2 xy tan x ,则 f (tx , ty ) t 2 x2 t 2 y 2 t 2 xy tan x

t 2 f ( x, y) .

y y

2.若 f ( x ) x2 y2 1 u2 .

y ( y 0) ,则 f (x)

y

3.函数 z arcsin y 的定义域为 {( x, y) || y | 1且

x 0} .

x x

1

4. lim(1 xy) sin xy e . x 0

y 0

5.若 z exy yx2 ,则 z

xexy x2 .

y

6.若 f ( x, y) 5x2 y3 ,则 f x(0,1) 10xy3 |(0,1) 0 .

7.若 u ln(1 x 2

y 2 2

) ,则 du 2

2 ( xdx ydy zdz) .

z x 2 y 2 z

y y y

8.设 z ex ,则 dz y ex dx 1 ex dy .

x2 x

9.已知 z sin( y ex ) ,而 y x3 ,则 dz (3x2 ex )cos( x3 ex ) .

162 多元函数微分法及其应用（全例题）

一、内容提要

多元函数微分法是一元函数微分法的推广,有许多相似之处,学习时应注意对比,搞清异同.

1．基本概念与定理

设函数)(PfU，点P可以是n,,3,2,1维的.当2n时,称此函数为多元函数.

① 二元函数),(yxfz在几何上表示空间一张曲面.

② 二元函数),(yxfz在点),(000yxP处的极限、连续、偏导数、全微分的定义及关系.

极限 Ayxfyyxx),(lim00：当 ,0,0

成立时，有 |),(| )()(02020Ayxfyyxx

注意 定义中的),(yx是以任意方式趋于点),(00yx.

连续 ),(),(lim0000yxfyxfyyxx

偏导数

);(,),(),(lim),(000000000yyxyxfyxxfyxfxzxxP固定

)(,),(),(lim),(000000000xxyyxfyyxfyxfyzyyP固定 高阶偏导数 一阶偏导数),(),,(yxfyxfyx的偏导数,称为函数),(yxf的二阶偏导数.

xzxyxfxzxx),(22,xzyyxfyxzxy),(2,

yzyyxfyzyy),(22,yzxyxfxyzyx),(2.

类似,可定义三阶以上的偏导数.

可微 若全增量),(),(0000yxfyyxxfz可表示为

)(oyBxAz，其中22)()(yx，

则称),(yxfz在点),(000yxP可微.而yBxA为函数),(yxfz在点),(000yxP的全微分,记作

yBxAzdyx),(00

高等数学（一）教案

期末总复习

- 2 -

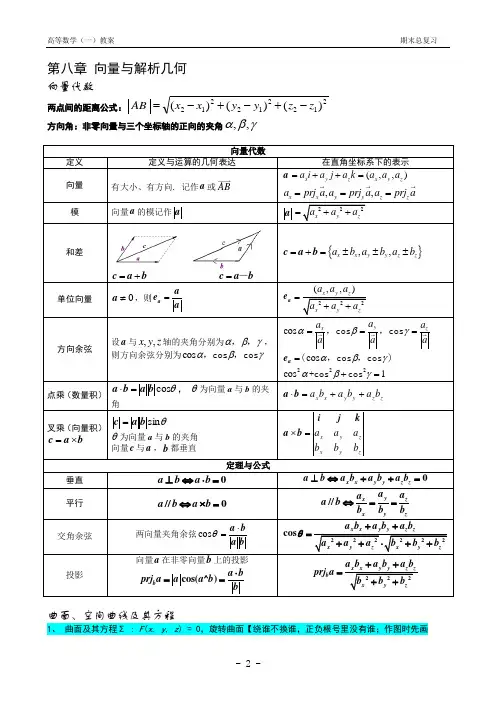
第八章 向量与解析几何

向量代数

两点间的距离公式：212212212)()()(zzyyxxBA

方向角：非零向量与三个坐标轴的正向的夹角,,

向量代数

定义 定义与运算的几何表达 在直角坐标系下的表示

向量 有大小、有方向. 记作a或AB a(,,)xyzxyzaiajakaaa

,,xxyyzzaprjaaprjaaprja

模 向量a的模记作a a222xyzaaa

和差

cab cab－ cab,,xxyyzzababab

单位向量 0a，则aaea ae222(,,)xyzxyzaaaaaa

方向余弦 设a与,,xyz轴的夹角分别为，，，则方向余弦分别为cos，cos，cos cosyxzaaaaaa，cos，cos

cosae(，cos，cos)

222cos1+coscos

点乘（数量积） cosbaba， 为向量a与b的夹角 zzyyxxbabababa

叉乘（向量积）

bac sinbac

为向量a与b的夹角

向量c与a，b都垂直 zyxzyxbbbaaakjiba

定理与公式

垂直 0abab 0xxyyzzabababab

平行 //0abab //yzxxyzaaaabbbb

交角余弦 两向量夹角余弦babacos 222222cosxxyyzzxyzxyzabababaaabbb

投影 向量a在非零向量b上的投影

cos()babprjaaabb 222xxyyzzbxyzabababprjabbb

1 / 41 教 学 内 容 批注

第八章 多元函数微分

第一节 多元函数的基本概念

一、 平面区域

首先我们来了解一下在平面区域内平面点集的知识：

1、 邻域：给定平面内P0（x0，y0）点，和某数>0，以P0点为圆心，为半径作圆，该圆内所有点的全体，即})yy()xx()y,x({22020，称为P0点的邻域，记做：),P(U0，简记)P(U0；

2、 内点：在平面点集，存在P0的一个邻域)P(U0，使得)P(U0，则称P0为的内点；

3、 开集：平面点集内的所有点都是内点，则称点集为开集；

4、 边界点：在平面上，存在某个点P，在P的任何邻域内，都含有点集的点，又含有不是点集的点，则称点P为点集的边界点。

注意：1、点P可以在点集内，也可以不在。2、点集中孤立在外的点，称为孤立点，规定，孤立点为边界点。3、所有边界点组成的集合称为边界。

5、 连通：如果点集内的任意两点都能用全属于的折线连接起来，则称为连通的。

6、 区域：连通的开集称为开区域，简称区域。称区域连同他的边界为闭区域。

7、 有界无界区域：对于平面点集，如果存在一个以原点为圆心的圆盘D，使D，则称为有界区域，否则称为无界区域。 2 / 41 教 学 内 容 批注

8、 聚点：P点的任何一个邻域内都有无限个属于点集的点，称P为点集的聚点。

注意：平面点集中点的关系如图,

其中：

二、 二元函数的极限和连续性

1.二元函数

定义1：设有变量x，y和z，如果当变量x，y在某一固定的范围内，任意取一对值时，变量z按照一定的法则f总有唯一的确定的值与之对应，就称z为x，y的二元函数，记作：)y,x(fz，其中x，y称为自变量，z称为因变量。自变量x，y的取值范围称为二元函数的定义域，一般用大写字母D来表示。 3 / 41 教 学 内 容 批注

注意:1、与定义1相似，我们可以直接定义n元函数（n≥1）；

第9 章测验题（二） 多元函数微分学的应用

一、填空题

1.函数u = x3 − xy2 − z 在点P (1,1, 0 ) 处沿 方向上的函数值增加最快。

0

1 2 2 2

2.函数u = (x + y + z ) 在点P (1,1,1) 处沿 方向上的函数值增加最快。

0

2

1

3.函数 f (x y) = (x + y )在点M (1, 1)处变化率为零的方向是 。

,

2 2

2

4.曲面ez − z + xy = 3 在点(2,1,0)处的单位法向量n= ，法线方程

为 。

5.球面x2 + y2 + z2 = 14 在点(1,2,3)处的单位法向量n= ，法线方程

为 ，切平面方程为 。

6.旋转抛物面z = x2 + y2 −1在点(2,1,4)处的单位法向量n= ，切平面

方程为 。

7.曲线x = acosθ ，y = asinθ ，z = bθ 在点(a,0,0)处的单位切向量T = ，

切线方程为 。

⎛ t ⎞

8.曲线r ( )i ( )j ⎟k

(t) = 在对应于

t − sin t + 1− cost + ⎜4 sin

⎝ 2 ⎠ π

t = 点处的单位切向量

0

2

T ，切线方程为 。

=

9.曲线x = t

1+ t ，y = 1+ ， 在对应于

t

z = t t 1点处的单位切向量T = ，

2 0 =

t

切线方程为 。

⎧ + + =

2 2 2

x z (1,−2,1)处的单位切向量T = ，切线方

y 6

*10.曲线⎨ 在点

x + y + z = 0

⎩

程为 。

11.函数 f (x y) = x + y + x − y 在点(0,0) 处的梯度向量为 gradf (0, 0)= 。

, 2 3 2

2 2

12.函数u = x + 2y + 3z 在点M (1,1, 2)处的梯度向量为 gradu = 。

M

13.函数

高等数学（数三）复习知识点及作业

按照同济大学高等数学第六版制定

第一章 函数与极限 （时间1周，每天2-3小时）

章节 复习知识点及作业 大纲要求

1.1 函数的概念，常见的函数（有界函数、奇函数与偶函数、单调函数、周期函数）、复合函数、反函数、初等函数具体概念和形式.注：一、集合 二、映射

P17-20双曲函数 （不用看）

习题1－1：4，5，8，9，15，16 1．理解函数的概念，掌握函数的表示法，会建立应用问题的函数关系．

2．了解函数的有界性．单调性．周期性和奇偶性．

3．理解复合函数及分段函数的概念，了解反函数及隐函数的概念．

4．掌握基本初等函数的性质及其图形，了解初等函数的概念．

5．了解数列极限和函数极限（包括左极限与右极限）的概念．

6．了解极限的性质与极限存在的两个准则，掌握极限的四则运算法则，掌握利用两个重要极限求极限的方法． 1.2 数列极限的定义，数列极限的性质(唯一性、有界性、保号性 ) 注：用定义证明极限不用看

习题1－2：1，4，5，6注：记住4,5,6的结论，不用证明

1.3 函数极限的定义与基本性质（极限的保号性、极限的唯一性、函数极限的函数局部有界性,函数极限与数列极限的关系等）注：用定义证明极限不用看 习题1－3：1，2，4

1.4 无穷小与无穷大的定义，它们之间的关系，以及与极限的关系

习题1－4：4，6，7

1.5 极限的运算法则(6个定理以及一些推论)

习题1－5：1，2，3，4,5 1.6

重点 两个重要极限（要牢记在心，要注意极限成立的条件，不要混淆，应熟悉等价表达式）,函数极限的存在问题（夹逼定理、单调有界数列必有极限），利用函数极限求数列极限，利用夹逼准则求极限，求递归数列的极限.

习题1－6：1，2，4 7．理解无穷小的概念和基本性质．掌握无穷小量的比较方法．了解无穷大量的概念及其与无穷小量的关系．

8．理解函数连续性的概念（含左连续与右连续），会判别函数间断点的类型．

高等数学（数三）复习知识点及作业

按照同济大学高等数学第六版制定

第一章 函数与极限 （时间1周，每天2-3小时）

章节 复习知识点及作业 大纲要求

1.1 函数的概念，常见的函数（有界函数、奇函数与偶函数、单调函数、周期函数）、复合函数、反函数、初等函数具体概念和形式.注：一、集合 二、映射

P17-20双曲函数 （不用看）

习题1－1：4，5，8，9，15，16 1．理解函数的概念，掌握函数的表示法，会建立应用问题的函数关系．

2．了解函数的有界性．单调性．周期性和奇偶性．

3．理解复合函数及分段函数的概念，了解反函数及隐函数的概念．

4．掌握基本初等函数的性质及其图形，了解初等函数的概念．

5．了解数列极限和函数极限（包括左极限与右极限）的概念．

6．了解极限的性质与极限存在的两个准则，掌握极限的四则运算法则，掌握利用两个重要极限求极限的方法．

7．理解无穷小的概念和基本性质．掌握无穷小量的比较方法．了解无穷大量的概念及其与无穷小量的关系．

8．理解函数连续性的概念（含左连续与右连续），会判别函数间断点的类型． 1.2 数列极限的定义，数列极限的性质(唯一性、有界性、保号性 ) 注：用定义证明极限不用看

习题1－2：1，4，5，6注：记住4,5,6的结论，不用证明

1.3 函数极限的定义与基本性质（极限的保号性、极限的唯一性、函数极限的函数局部有界性,函数极限与数列极限的关系等）注：用定义证明极限不用看 习题1－3：1，2，4

1.4 无穷小与无穷大的定义，它们之间的关系，以及与极限的关系

习题1－4：4，6，7

1.5 极限的运算法则(6个定理以及一些推论)

习题1－5：1，2，3，4,5

1.6

重点 两个重要极限（要牢记在心，要注意极限成立的条件，不要混淆，应熟悉等价表达式）,函数极限的存在问题（夹逼定理、单调有界数列必有极限），利用函数极限求数列极限，利用夹逼准则求极限，求递归数列的极限.

高等数学下册知识点

第八章空间解析几何与向量代数

（一）向量及其线性运算

1、 向量，向量相等，单位向量，零向量，向量平行、共线、共面；

2、 线性运算：加减法、数乘；

3、 空间直角坐标系：坐标轴、坐标面、卦限，向量的坐标分解式；

4、 利用坐标做向量的运算：设a （ax，ay,az），b

（bx,by,bz），

则 a b （ax bx,ay by ,az bz）, a （ ax, ay, az）；

5、 向量的模、方向角、投影：

1） 向量的模：获—y2—z2 ；

2） 两点间的距离公式： AB J（X2 xj2 （y2 yi）2 （Z2 zj2

3） 方向角：非零向量与三个坐标轴的正向的夹角 ,,

5）投影：Prjua a cos ，其中为向量a与u的夹角

（二）数量积，向量积

1、 数量积： a b a ||b cos

1） a a a 2 4）方向余弦: COS x —,cos r —,cos r 2） a b

a b 0

2、 向量积： c a b

大小：|a||b sin ，方向：a, b ,c符合右手规则

1)a a 0

2)a// b a b 0

运算律：反交换律b a a b

(三)曲面及其方程

1、 曲面方程的概念：S:f(x,y,z) 0

2、 旋转曲面：

yoz 面上曲线 C : f (y, z) 0，

绕y轴旋转一周：f(y, Vx2 z2) 0

绕z轴旋转一周：f( \ x2 y2, z) 0

3、 柱面：

F(x,y)

F (x, y) 0表示母线平行于z轴，准线为

z 0 0

的柱面

4、 二次曲面

2 2

x y 2

1)椭圆锥面：Q 2 2 z

a b 2 x

2) 椭球面：亍 b2 2 z

2

c

2 x

旋转椭球面： 2 a 2 y

2 a 2 z

2 c

2 x 2

y 2 z 1 3) 单叶双曲面: 2 a b2 2 c

2 2 2

第八章 多元函数的微分法及其应用

§ 1 多元函数概念

一、设]),,([:,),(,),(22222yyxfyxyxyxyxf求.

二、求下列函数的定义域：

1、2221)1(),(yxyxyxf 222{(,)|(,)R,1};xyxyyx

2、xyzarcsin };0,|),{(xxyyx

三、求下列极限：

1、222)0,0(),(sinlimyxyxyx （0）

2、xyxxy3)2,(),()1(lim (6e)

四、证明极限 242)0,0(),(limyxyxyx不存在.

证明：当沿着x轴趋于（0，0）时，极限为零，当沿着2xy趋于（0，0）时，极限为21,

二者不相等，所以极限不存在

五、证明函数)0,0(),(,0)0,0(),(,1sin),(22yxyxyxxyyxf 在整个xoy面上连续。

证明：当)0,0(),(yx时，为初等函数，连续),(yxf。当)0,0(),(yx时，

)0,0(01sinlim22)0,0(),(fyxxyyx，所以函数在（0，0）也连续。所以函数

在整个xoy面上连续。

六、设)(2yxfyxz且当y=0时2xz，求f(x)及z的表达式.

解：f(x)=xx2，zyxyyx2222

§ 2 偏导数

1、设z=xyxexy ,验证 zxyyzyxzx

高数书题目重点目录整理

2015考研数学高等数学教材导学

【注】 1导学用书：同济大学《高等数学》（上、下册）（第6版）

2 请各位学员认真研读课本内容及完成选择习题，打下一个牢固的基

础。无论是教材上的定理、例题，还是课后的习题，曾作为历年的考

研真题出现过。

第1章函数、极限、连续

1、映射与函数

（一）复习内容

P1-16(表示1至16页，下同)，双曲函数开始之后的不复习。

（二）选做习题

P21-22 第4-12题，第14-16题。

2、数列的极限

（一）复习内容

P23-30

（二）选做习题

P30-31 第1、5、6题。

3、函数的极限

（一）复习内容

P31-37

（二）选做习题

P37-39 第1-4题，第12题。

4、无穷小与无穷大

（一）复习内容

P39-41

（二）选做习题 P42 第4、5、6、7题。

5、极限运算法则

（一）复习内容

P43-49

（二）选做习题

P49 第1-5题。

6、极限存在准则两个重要极限

（一）复习内容

P50-55（除Cauchy极限存在准则）

（二）选做习题

P56-57 第1、2、4题。

7、无穷小的比较

（一）复习内容

P57-59

（二）选做习题

P59-60 第1-4题。

8、函数的连续性与间断点

（一）复习内容

P60-64

（二）选做习题

P64-65 第1-5题，第7-8题。

9、连续函数的运算与初等函数的连续性

（一）复习内容

P66-69

（二）选做习题

P69-70 习题1-9全做

P74 总习题一第1-13题。

第2章函数、极限、连续

1、导数概念

（一）复习内容 P77-86

（二）选做习题

P86-88 习题2-1全做。

2、函数的求导法则

（一）复习内容

P88-96（例17不学）

（二）选做习题

P97-99 第1、5题，第5-11题，第13、14题。

3、高阶导数

（一）复习内容

P99-102

（二）选做习题

高等数学（下）知识点

第 1 页 共 31 页 高等数学下册 （同济大学第七版） 知识点 高等数学（下）知识点

第 2 页 共 31 页 高等数学下册知识点 下册预备知识 第八章 空间解析几何与向量代数 （一） 向量及其线性运算 1、 向量，向量相等，单位向量，零向量，向量平行、共线、共面； 2、 线性运算：加减法、数乘； 3、 空间直角坐标系：坐标轴、坐标面、卦限，向量的坐标分解式； 4、 利用坐标做向量的运算：设),,(zyxaaaa，),,(zyxbbbb， 则 ),,(zzyyxxbabababa, ),,(zyxaaaa； 5、 向量的模、方向角、投影： 1） 向量的模：222zyxr； 2） 两点间的距离公式：212212212)()()(zzyyxxBA 3） 方向角：非零向量与三个坐标轴的正向的夹角,, 4） 方向余弦：rzryrxcos ,cos ,cos 1coscoscos222 5） 投影：cosPraaju，其中为向量a与u的夹角。 （二） 数量积，向量积 1、 数量积：cosbaba 1）2aaa 高等数学（下）知识点

第 3 页 共 31 页 2）ba0ba zzyyxxbabababa 2、 向量积：bac 大小：sinba，方向：cba,,符合右手规则 1）0aa 2）ba//0ba zyxzyxbbbaaakjiba 运算律：反交换律 baab （三） 曲面及其方程 1、 曲面方程的概念：0),,(:zyxfS 2、 旋转曲面： yoz面上曲线0),(:zyfC， 绕y轴旋转一周：0),(22zxyf 绕z轴旋转一周：0),(22zyxf 3、 柱面： 0),(yxF表示母线平行于z轴，准线为00),(zyxF的柱面 4、 二次曲面 高等数学（下）知识点