下载文档原格式
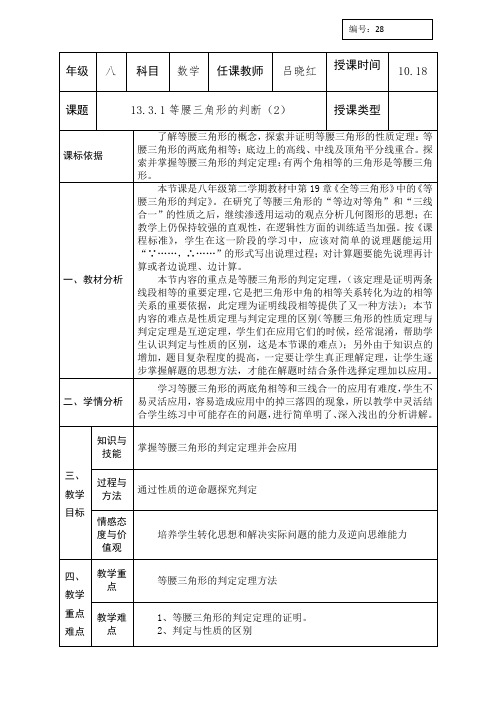
年级八科目数学任课教师吕晓红授课时间10.18课题13.3.1等腰三角形的判断（2）授课类型课标依据了解等腰三角形的概念，探索并证明等腰三角形的性质定理：等腰三角形的两底角相等；底边上的高线、中线及顶角平分线重合。
探索并掌握等腰三角形的判定定理：有两个角相等的三角形是等腰三角形。
一、教材分析本节课是八年级第二学期教材中第19章《全等三角形》中的《等腰三角形的判定》。
在研究了等腰三角形的“等边对等角”和“三线合一”的性质之后，继续渗透用运动的观点分析几何图形的思想；在教学上仍保持较强的直观性，在逻辑性方面的训练适当加强。
按《课程标准》，学生在这一阶段的学习中，应该对简单的说理题能运用“∵……，∴……”的形式写出说理过程；对计算题要能先说理再计算或者边说理、边计算。
本节内容的重点是等腰三角形的判定定理，（该定理是证明两条线段相等的重要定理，它是把三角形中角的相等关系转化为边的相等关系的重要依据，此定理为证明线段相等提供了又一种方法）；本节内容的难点是性质定理与判定定理的区别（等腰三角形的性质定理与判定定理是互逆定理，学生们在应用它们的时候，经常混淆，帮助学生认识判定与性质的区别，这是本节课的难点）；另外由于知识点的增加，题目复杂程度的提高，一定要让学生真正理解定理，让学生逐步掌握解题的思想方法，才能在解题时结合条件选择定理加以应用。
二、学情分析学习等腰三角形的两底角相等和三线合一的应用有难度，学生不易灵活应用，容易造成应用中的掉三落四的现象，所以教学中灵活结合学生练习中可能存在的问题，进行简单明了、深入浅出的分析讲解。
三、教学目标知识与技能掌握等腰三角形的判定定理并会应用过程与方法通过性质的逆命题探究判定情感态度与价值观培养学生转化思想和解决实际问题的能力及逆向思维能力四、教学重点难点教学重点等腰三角形的判定定理方法教学难点1、等腰三角形的判定定理的证明。
2、判定与性质的区别编号：28五、教法学法以学生为主体的讨论探索法。
等边三角形
难点
等边三角形性质和判定方法的应用
五、教学过程设计一、复习巩固
1．叙述等腰三角形的性质，它是怎么得到的?
等腰三角形的两个底角相等，也可以简称“等边对等角”。
把等腰三角形对折，折叠两部分是互相重合的，即AB与AC重合，点B与点 C重合，线段BD与CD也重合，所以∠B＝∠C。
等腰三角形的顶角平分线，底边上的中线和底边上的高线互相重合，简称“三线合一”。
由于AD为等腰三角形的对称轴，所以BD＝ CD，AD为底边上的中线；∠BAD＝∠CAD，AD为顶角平分线，∠ADB＝∠ADC＝90°，AD又为底边上的高，因此“三线合一”。
2．若等腰三角形的两边长为3和4，则其周长为多少?
二、新课
在等腰三角形中，有一种特殊的情况，就是底边与腰相等，这时，三角形三边都相等。
我们把三条边都相等的三角形叫做等边三角形。
等边三角形具有什么性质呢?
1．请同学们画一个等边三角形，用量角器量出各个内角的度数，并提出猜想。
2．你能否用已知的知识，通过推理得到你的猜想是正
确的?
等边三角形是特殊的等腰三角形，由等腰三角形等边对
等角的性质得到∠A＝∠B＝C，又由∠A＋∠B＋∠C＝180°，
从而推出∠A＝∠B＝∠C＝60°。
3．上面的条件和结论如何叙述?
等边三角形的各角都相等，并且每一个角都等于60°。
三个角都相等的三角形是等边三角形
有一个叫是60°的等腰三角形是等边三角形也称为正三角形。
陕西省石泉县八年级数学上册１3《轴对称》同课异构教案(新版）新人教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方,但是任然希望（陕西省石泉县八年级数学上册1３《轴对称》同课异构教案（新版）新人教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉，前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为陕西省石泉县八年级数学上册１3《轴对称》同课异构教案(新版）新人教版的全部内容。
第13章一、教材分析本章的主要内容是从生活中的图形入手，学习轴对称及其基本性质,欣赏、体验轴对称在现实生活中的广泛应用。
在此基础上，利用轴对称,探索等腰三角形的性质,学习它的判定方法，并进一步学习等边三角形。
在本章，轴对称的性质是本章的重点,轴对称的应用，利用轴对称设计图案,用坐标表示轴对称等都是围绕这一性质进行的。
另外，等腰三角形的性质和判定也是本章的重点，它们是证明线段和角相等的重要根据，应用也比较广泛。
二、学情分析本章内容涉及图形的定义、性质和判定方法较多，而多数学生学习主动性不强,不去记忆,理解就更差了。
学生对这部分内容掌握较差。
三、教学目标知识与技能1。
理解轴对称与轴对称图形的概念，掌握轴对称的性质2。
掌握线段的垂直平分线、角的平分线的性质及应用3。
理解等腰三角形的性质并能够简单应用4．理解等边三角形的性质并能够简单应用过程与方法初步体会从对称的角度欣赏设计简单的轴对称图案情感与态度数形结合的思想及方程的思想都应引起广泛的重视和应用四、教学重点难点重点掌握线段的垂直平分线、角的平分线的性质、等腰三角形的性质及应用难点轴对称图形以及关于某条直线成轴对称的概念,等腰三角形的性质应用五、教学过程设计一.知识梳理做轴对称图形的对称轴轴对称做轴对称图形用坐标表示轴对称等腰三角形性质和判定等边三角形二.知识巩固1、以下图形有两条对称轴的是（）A、正六边形Ｂ、矩形C、等腰三角形D、圆2、如图1，在△ABＣ中,ＡＢ＝AC，点D在AC上,且ＢD=BC=AＤ,则∠Ａ为( )ADCB图1BECAD图23、等腰三角形的两边长分别为3cm,7cm，则它的周长为cｍ４、如图2,在△ＡＢC中,DE是边AC的垂直平分线，若BC=8cm，AB=10cm,则△EBC的周长为cm(学生可以合作讨论，互帮互学）5、将一张长方形纸按如图3的方式折叠，BC，ＢD为折痕，则∠ＣＢD为（）Ａ、50°Ｂ、９0°Ｃ、10０°Ｄ、11０°图4６．如图4，A、B、C是三个村庄,现要修建一个自来水厂P,使得自来水厂P到三个村庄的距离相等，请你作出自来水厂的位置7。
陕西省石泉县八年级数学上册13.3.1 等腰三角形（2）同课异构教案1 （新版）新人教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（陕西省石泉县八年级数学上册13.3.1 等腰三角形（2）同课异构教案1 （新版）新人教版）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为陕西省石泉县八年级数学上册13.3.1 等腰三角形（2）同课异构教案1 （新版）新人教版的全部内容。
13。
3。
1等腰三角形一、教材分析等腰三角形的性质它是在认识了轴对称性以及了解了全等三角形的判定的基础上进行的。
主要学习等腰三角形的“等边对等角"和“等腰三角形的三线合一”本节内容既是前面知识的深化和应用,又是今后学习等边三角形的预备知识,还是今后证明角相等、线段相等及两直线互相垂直的依据，因此本节课具有承上启下的重要作用。
二、学情分析学习等腰三角形的两底角相等和三线合一的应用有难度,学生不易灵活应用，容易造成应用中的掉三落四的现象，所以教学中灵活结合学生练习中可能存在的问题,进行简单明了、深入浅出的分析讲解。
三、教学目标知识与技能：掌握等腰三角形的判定定理并会应用过程与方法：通过性质的逆命题探究判定情感态度目标：培养学生转化思想和解决实际问题的能力及逆向思维能力四、教学重点难点重点等腰三角形的判定定理方法难点1、等腰三角形的判定定理的证明。
2、判定与性质的区别五、教学过程设计一．复习1、等腰三角形有什么性质？2、“等腰三角形的两个底角相等”的逆命题是什么？二．探究新知：1、“两个角相等的三角形是等腰三角形”的题设、结论分别是什么？2、引导学生画图并根据图形写出已知、求证。
