2018-2019学年人教A版必修一1.1.2集合间的基本关系学案

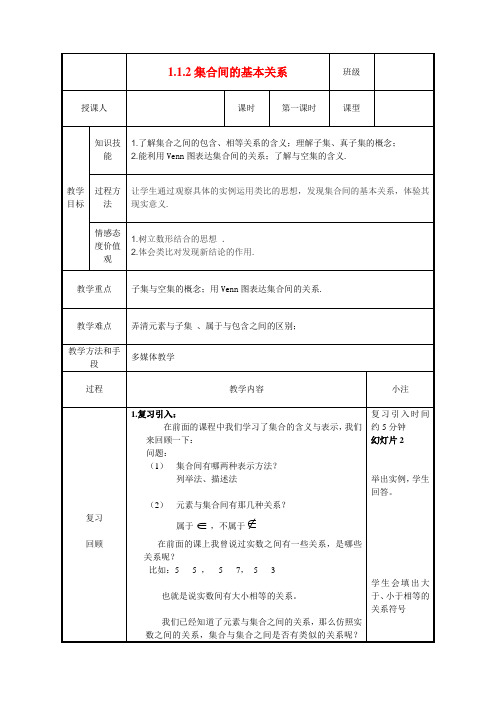
B {0}
例题：写出集合{a,b,c}的所有子集并指出，真子集、非空
1.教师评课：
1）优点：i 教态自然、语言表达较清楚；
ii 讲练结合、课堂、课件思路比较连贯，有条不紊； iii 运用了类比的数学思想。

2）不足：i 老师讲的过多，学生自己思考的少，练习不够；
ii 进度有些慢，对子集真子集强调的不够；
A = B
B A
A B
iii 口头语较多、课件速度有些快，师生互动，让学生多写。

举例应更具体； iv 子集、真子集、非空真子集，让学生说更好，例子引入更好一些； v 有老师一言堂的感觉，多让学生回答问题。

该让学生答的教案中应该有体现，例题不应该让学生答；
vi 学生老师需要磨合，初中学生对课程深度广度理解不够，课堂容量大。

对学生的了解不够，课堂容量大。

⎧⎨⎩A ⊆BA =B ⇔B ⊆A针对练习：A={平面内四边相等的四边形}， B={菱形}，集合A 与B 的关系是探究三 真子集思考：观察以下几组集合，并指出它们元素间的关系：A={1,5}, B={1,3,5}； （2）A={四边形}, B={平行四边形}定义：如果集合A ⊆B,但存在元素x ∈B,且x ∉A ，并且A≠B,称集合A 是集合B 的真子集． 记作： A B （或B A ）读作：“A 真含于B ”（或B 真包含A ）。

韦恩图表示：针对练习：1.已知集合，，则下列关系中正确的是（ ） A. B ． C ． 2.若集合M ={x |x ≤6}，a =2，则下面结论中正确的是（ ）A ．B ．C ．D ． 探究四 空 集 1.我们把不含任何元素的集合叫做空集，记为φ，并规定：空集是任何集合的子集。

空集是任何非空集合的真子集。

即φB ，（B φ≠） 例如:方程x 2+1=0没有实数根,所以方程 x 2+1=0的实数根组成的集合为φ。

问题：你还能举几个空集的例子吗？ 2.深化概念：（1）包含关系{}a A ⊆与属于关系a A ∈有练习巩固集合相等的定义，由具体例子让学生概括出真子集的含义.学生学以致用通过具体的例子巩固空集的含义辨析⊆、∈、 之间的区别，提高学生解决问题的能力。

提高学生分析、 解决问题的能力提高学生分析、 解决问题的能力提高学生抽象思维的能力B A什么区别？答案：前者为集合之间关系，后者为元素与集合之间的关系. （2）集合 A B 与集合B A ⊆有什么区别 ？答案： A = B 或A B.（3）0，{0}与 Φ三者之间有什么关系? 答案：{0}与Φ ：{0}是含有一个元素0的集合， Φ是不含任何元素的集合。

如 Φ{0}不能写成Φ ={0}，Φ ∈{0}3.结论： 由上述集合之间的基本关系,可以得到下列结论： （1）任何一个集合是它本身的子集，即A A ⊆。

（2）对于集合A 、B 、C ，若,,A B B C ⊆⊆则C A ⊆（类比b a ≤，c b ≤则c a ≤）。

1.1.2集合间的基本关系（1课时）一. 教学目标:1．知识与技能(1)了解集合之间包含与相等的含义，能识别给定集合的子集。

(2)理解子集.真子集的概念。

(3)能使用venn 图表达集合间的关系，体会直观图示对理解抽象概念的作用.2. 过程与方法让学生通过观察身边的实例，发现集合间的基本关系，体验其现实意义.3.情感.态度与价值观(1)树立数形结合的思想 ．(2)体会类比对发现新结论的作用.二.教学重点.难点重点：集合间的包含与相等关系，子集与其子集的概念.难点：难点是属于关系与包含关系的区别．三.学法学法：让学生通过观察.类比.思考.交流.讨论，发现集合间的基本关系.四.学习流程（一） 知识连线：1、观察下面几个例子，你能发现两个集合间有什么关系吗？（1）{1,2,3},{1,2,3,4,5}A B ==；(2)设A 为海口二中高一(3)班男生的全体组成的集合，B 为这个班学生的全体组成的集合；(3)设{|},{|};C x x D x x ==是两条边相等的三角形是等腰三角形(4){2,4,6},{6,4,2}E F ==2、两个集合之间的关系:①一般地，对于两个集合A ，B ，如果集合A 中______________________________ ，我们就说这两个集合有包含关系，称集合A 为B 的_______.记作：_______，（或_______），读作：___________，（或___________）用venn 图表示为：②如果两个集合A ，B 所含的元素完全相同，那么我们称集合A 与B_______. 记作：_______。

即: 若A ⊆B ，B ⊆A ，则_______.用venn 图表示为：3、如果A ⊆B ，但存在_____________________________，我们称集合A 是集合B 的真子集 记作：_______，（或_______） 读作：___________。

§1.1.2 集合间的基本关系一、教学目标（1）理解集合间的包含与相等的含义。

（2）会用适当的方法表示集合间的基本关系。

（3）学习类比方法，渗透分类思想，提高数学思维能力。

二、教学重点与难点重点：理解子集、真子集、空集等概念；理解集合间的包含、真包含、相等关系及传递关系。

难点：集合间包含关系的正确表示三、基础知识梳理（1）Venn图的概念用平面___________________的内部代表集合，这种图称为Venn图。

（2）空集的概念_____________________ 的集合叫做空集，记作______________________ 、四、例题分析例1 写出集合{0，1，2}的所有子集，并指出其中哪些是它的真子集。

例2 已知集合M满足{1，2}⊆MØ{1,2,3,4,5},写出集合M例3 已知集合A={2,x,y},B={2x,2,2y},且A=B,求x，y 的值五自我测评1.若A⊆B,A⊆C，且B={0,1,2,3},C={0,2,4,5}，则满足上述条件的集合可以是（ ）(A){0,1} (B) {0,3}(C){2,4} (D) {0,2}2.若集合M={x|x ≤ ）(A){a}ØM (B) a ØM(C){a}∈M (D) a ∉M3.设A={x|-1<x<0},B={x|x <2 或 x >3}, 则（ ）（A ）A ∈B (B) B ∈ A(C) A ØB (D) B ØA4.集合{ａ，ｂ }的子集有（ ）（Ａ）１个 （Ｂ）２个（Ｃ）３个 （Ｄ）４个５.已知Ａ＝｛菱形 ｝，Ｂ＝｛ 正方形 ｝，Ｃ＝｛平行四边形｝，则Ａ、Ｂ、Ｃ 之间的关系是________________。

6．下列六种关系中正确的是__________________.①{}a a ⊆②{}a ∅Ø}{}.{},,{}{a a b a a ⊂∈④③}.,{},,{b a a b a ∈∈∅⑥⑤7．满足条件{}{}11,2,3,4B ⊆Ø的集合B 有___________个8．已知，且p=Q ，},,{},1,,{2x xy x Q y x P ==求ｘ，y 的值．六、能力提升９.数集}ln 12{z n X ∈+=与数集k k Y |14{±=}z ∈之间的关系是( )．=)()()()(XC∉Y∈ØYA X YB X YDX10.已知非空集合P满足：}5,4,3,2,1{①②若,PP⊆-∈，a∈则(6)a P符合上述条件的P的个数是( )．(A)4 (B)5 (C)7 (D)3111已知集合},xxx(|)(1x{2RB∈+=+-3=xx{2Rx|3,04)4x=},0x-+A∈=又A P BØ求：满足条件的集合P．⊆。

集合间的基本关系一、教学目标:知识与技能目标：(1)了解集合之间包含与相等的含义，能识别给定集合的子集。

(2)理解子集.真子集的概念。

(3)能使用Venn图表达集合间的关系，体会直观图示对理解抽象概念的作用.过程与方法目标：让学生通过观察身边的实例，发现集合间的基本关系，体验现实意义.情感态度与价值观：(1)树立数形结合的思想．(2)体会类比对发现新结论的作用.二、教学重点.难点教学重点：集合间的包含与相等关系，子集与其子集的概念.教学难点：难点是属于关系与包含关系的区别．三.教学方法让学生通过观察、类比、思考、交流、讨论，发现集合间的基本关系.四、教学过程：一、复习准备：1.提问：集合的两种表示方法？如何用适当的方法表示下列集合？（1）10以内3的倍数；（2）1000以内3的倍数2.用适当的符号填空： 0______N； -1.5 _____R。

二、情境导入：我们知道，两个实体之间有相等关系、大小关系，如:5=5, 5<7 , 5>3,等等。

两个集合之间是否也有类似的关系呢？三、讲授新课：观察下面几个例子，类比实数之间的相等关系、大小关系，你能发现下面两个集合之间的关系吗？（1）A={1，2，3}，B={1，2，3，4，5}；（2）C为某中学高一（2）班全体女生组成的集合，D为这个班全体学生组成的集合；（3）E={x|x是两条边相等的三角形}，F={x|x是等腰三角形}。

1. 子集、空集等概念的教学：可以发现,在(1)中,集合A的任何一个元素都是集合B的元素.这时我们说集合A包含于集合B,或集合B包含集合A.(2)中的集合C与集合D也有这种关系.一般地,对于两个集合A,B,如果集合A中任意一个元素都是集合B中的元素,就称集合A为集合B的子集,记作A ⊆ B(或B ⊇ A),读作“A包含于B”(或“B包含A”).在数学中,我们经常用平面上封闭曲线的内部代表集合,这种图称为Venn图.这样,上述集合A与集合B的包含关系,可以用图1.2-1表示.图1.2-1在(3)中,由于“两条边相等的三角形”是等腰三角形,因此,集合E,F都是由所有等腰三形组成的集合.即集合E中任何一个元素都是集合F中的元素,同时,集合F中任何一个元素也都是集合E中的元素.这样,集合E的元素与集合F的元素是一样的.一般地,如果集合A的任何一个元素都是集合B的元素,同时集合B的任何一个元素都是集合A的元素,那么集合A与集合B相等,记作A=B. 也就是说,若A⊆ B,且B⊆A,则A=B.如果集合A ⊆ B，但存在元素x∈B，且x∉A，就称集合A是集合B的真子集。

1.2集合间的基本关系【学习目标】素养目标学科素养1. 理解子集、真子集、空集的概念；(重点)2. 能用符号和Venn图表示集合间的关系；(难点)3. 掌握列举有限集的所有子集的方法。

1、逻辑推理2、直观想象3、数形结合【自主学习】一. 子集的相关概念1．Venn图表示：在数学中，经常用平面上___ ___ 的_____代表集合，这种图称为Venn图，这种表示集合的方法叫做图示法．优点：形象直观。

2.子集、真子集、集合相等定义符号表示图形表示子集如果集合A中的元素都是集合B中的元素，就称集合A是集合B的子集A B(或B A)真子集如果集合A⊆B，但存在元素_________，就称集合A是集合B的真子集A B(或B A)集合相等如果集合A的元素都是集合B的元素，同时集合B的元素都是集合A的元素，那么集合A与集合B相等A B3.子集的性质(1)任何一个集合是它本身的，即A⊆A.(2)对于集合A，B，C，如果A⊆B，且B⊆C，那么.二. 空集定义的集合叫做空集符号用符号表示为___规定空集是任何集合的，是任何非空集合的________A【小试牛刀】1.思考辨析(正确的画“√”，错误的画“×”)(1)空集中只有元素0，而无其余元素．()(2)任何一个集合都有子集．()(3)若A＝B，则A⊆B.()(4)空集是任何集合的真子集．()2.已知集合A＝{x|－1－x<0}，则下列各式正确的是()A．0⊆A B．{0}⊆A C．⊆⊆A D．{0}⊆A【经典例题】题型一集合间关系的判断点拨：判断集合间关系的常用方法(1)列举观察法：当集合中元素较少时，可列出集合中的全部元素，通过定义得出集合之间的关系．(2)集合元素特征法：首先确定集合的代表元素是什么，弄清集合元素的特征，再利用集合元素的特征判断关系．(3)数形结合法：利用Venn图、数轴等直观地判断集合间的关系．一般地，判断不等式的解集之间的关系，适合画出数轴．例1 下列各式中，正确的个数是()⊆{0}⊆{0,1,2}；⊆{0,1,2}⊆{2,1,0}；⊆⊆⊆{0,1,2}；⊆⊆＝{0}；⊆{0,1}＝{(0,1)}；⊆0＝{0}．A．1B．2C．3D．4【跟踪训练】1(1)若集合M＝{x|x2－1＝0}，T＝{－1，0,1}，则M与T的关系是()A．M T B．M⊆T C．M＝T D．M ⊆T(2)用Venn图表示下列集合之间的关系：A＝{x|x是平行四边形}，B＝{x|x是菱形}，C＝{x|x是矩形}，D＝{x|x是正方形}．题型二子集、真子集的个数问题点拨：公式法求有限集合的子集个数(1)含n个元素的集合有2n个子集.(2)含n个元素的集合有(2n－1)个真子集.(3)含n个元素的集合有(2n－1)个非空子集.(4)含n个元素的集合有(2n－2)个非空真子集.例2 写出集合{a,b}的所有子集，并指出哪些是它的真子集.例2-变式写出集合{a,b,c}的所有子集? 写出集合{a,b,c,d}的所有子集?【跟踪训练】2 满足{a，b}⊆A{a，b，c，d，e}的集合A的个数是()A．2B．6 C．7D．8题型三根据集合的包含关系求参数点拨：1.分析集合间的关系时，首先要分析、简化每个集合．2.借助数轴，利用数轴分析法，将各个集合在数轴上表示出来，以形定数，还要注意验证端点值，做到准确无误，一般含“＝”用实心点表示，不含“＝”用空心点表示．3.此类问题要注意对空集的讨论．例3 已知集合A＝{x|－3≤x≤4}，B＝{x|2m－1<x<m＋1}，且B⊆A．求实数m的取值范围．【跟踪训练】3 设集合A＝{x|x2－8x＋15＝0}，B＝{x|ax－1＝0}．(1)若a＝15，试判定集合A与B的关系；(2)若B⊆A，求实数a的取值集合．【当堂达标】1.下列说法：⊆空集没有子集；⊆任何集合至少有两个子集；⊆空集是任何集合的真子集；⊆若⊆A，则A≠⊆.其中正确的有()A．0个B．1个C．2个D．3个2.已知集合A＝{－1,0,1}，则含有元素0的A的子集的个数为()A．2 B．4 C．6 D．83.设A＝{x|2<x<3}，B＝{x|x<m}，若A⊆B，则m的取值范围是()A．m>3 B．m≥3 C．m<3 D．m≤34.已知集合A＝{x|x－3>0}，B＝{x|2x－5≥0}，则这两个集合的关系是________．5.已知A＝{x|x2－3x＋2＝0}，B＝{x|ax－2＝0}，且B⊆A，求由实数a的值组成的集合C.6.已知集合A＝{x|x<－1，或x>4}，B＝{x|2a≤x≤a＋3}，若B⊆A，求实数a的取值范围．【课堂小结】1.知识点：(1)子集、真子集、空集、集合相等的概念及集合间关系的判断.(2)求子集、真子集的个数问题.(3)由集合间的关系求参数的值或范围.2.方法归纳：数形结合、分类讨论.3.常见误区：忽略对集合是否为空集的讨论，忽视是否能够取到端点.【参考答案】【自主学习】一．1.封闭曲线内部2.任意一个 ⊆⊇ x ∈B ，且x ∉A 任何一个 任何一个 ＝3.子集 A ⊆C二．不含任何元素 ∅ 子集 真子集 【小试牛刀】1．(1)× (2)√ (3)√ (4)×2. D 解析：集合A ＝{x |－1－x <0}＝{x |x >－1}，所以0∈A ，{0}⊆A ，D 正确． 【经典例题】例1 B 解析：(1)对于①，是集合与集合的关系，应为{0}{0,1,2}；对于②，实际为同一集合，任何一个集合是它本身的子集；对于③，空集是任何集合的子集；对于④，{0}是含有单元素0的集合，空集不含任何元素，并且空集是任何非空集合的真子集，所以∅{0}；对于⑤，{0,1}是含有两个元素0与1的集合，而{(0,1)}是以有序数组(0,1)为元素的单元素集合，所以{0,1}与{(0,1)}不相等；对于⑥，0与{0}是“属于与否”的关系，所以0∈{0}．故②③是正确的，应选B.【跟踪训练】1 (1)A 解析：因为M ＝{x |x 2－1＝0}＝{－1,1}，又T ＝{－1,0,1}，所以M T . (2)根据几何图形的相关知识明确各元素所在集合之间的关系，再画Venn 图．如图例2 解：集合{a,b}的所有子集为∅，{a}，{b}，{a,b}. 真子集为∅，{a}，{b}.例2-变式：集合{a,b,c}的所有子集为∅，{a}，{b}，{c}，{a,b}，{a,c}，{b,c}，{a,b,c}. 集合{a,b,c,d}的所有子集为∅，{a}，{b}，{c}，{d}，{a,b}，{a,c}，{a,d}，{b,c}， {b,d}，{c,d}，{a,b,c}，{a,b,d}，{a,c,d}，{b,c,d}，{a,b,c,d}.【跟踪训练】2 C 解析：由题意知，集合A 可以为{a ，b }，{a ，b ，c }，{a ，b ，d }，{a ，b ，e }，{a ，b ，c ，d }，{a ，b ，c ，e }，{a ，b ，d ，e }．例3 解：(1)因为B ⊆A ，当B ＝⊆时，m ＋1≤2m －1，解得m ≥2.(2)当B ≠⊆时，有⎩⎨⎧－3≤2m －1，m ＋1≤4，2m －1<m ＋1，解得－1≤m <2，综上得m ≥－1.【跟踪训练】3 解：(1)由x 2－8x ＋15＝0得x ＝3或x ＝5，故A ＝{3,5}，当a ＝15时， 由ax －1＝0得x ＝5.所以B ＝{5}，所以BA .(2)当B ＝∅时，满足B ⊆A ，此时a ＝0；当B ≠∅，a ≠0时，集合B ＝⎩⎨⎧⎭⎬⎫1a ，由B ⊆A 得1a ＝3或1a ＝5，所以a ＝13或a ＝15.综上所述，实数a 的取值集合为⎩⎨⎧⎭⎬⎫0，13，15 【当堂达标】1.B 解析：⊆空集是它本身的子集；⊆空集只有一个子集；⊆空集不是它本身的真子集；⊆空集是任何非空集合的真子集．因此，⊆⊆⊆错误，⊆正确．2.B 解析：根据题意，含有元素0的A 的子集为{0}，{0,1}，{0，－1}，{－1,0,1}，共4个．3.B 解析：因为A ＝{x |2<x <3}，B ＝{x |x <m }，A ⊆B ，将集合A ，B 表示在数轴上，如图所示，所以m ≥3.4.A B解析：A ＝{x |x －3>0}＝{x |x >3}，B ＝{x |2x －5≥0}＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≥52. 结合数轴知A B .5.解：由x 2－3x ＋2＝0，得x ＝1或x ＝2. 所以A ＝{1,2}．因为B ⊆A ，所以对B 分类讨论如下：①若B ＝∅，即方程ax －2＝0无解，此时a ＝0； ②若B ≠∅，则B ＝{1}或B ＝{2}． 当B ＝{1}时，有a －2＝0，即a ＝2； 当B ＝{2}时，有2a －2＝0，即a ＝1.综上可知，符合题意的实数a 所组成的集合C ＝{0,1,2}． 6.解：(1)因为B ⊆A ，所以m 2＝2m －1，即(m －1)2＝0，所以m ＝1.当m ＝1时，A ＝{－1,3,1}，B ＝{3,1}，满足B ⊆A ，故m ＝1. (2)当B ＝⊆时，只需2a >a ＋3，即a >3； 当B ≠⊆时，根据题意作出如图所示的数轴，可得⎩⎨⎧ a ＋3≥2a a ＋3<－1或⎩⎨⎧a ＋3≥2a 2a >4，解得a <－4或2<a ≤3.综上可得，实数a 的取值范围为a <－4或a >2.。

1．1.2 集合间的基本关系——题型探究类型一 子集、真子集的概念问题【例1】 已知集合M ＝{x|x ＜2且x ∈N }，N ＝{x|－2＜x ＜2且x ∈Z }．(1)试判断集合M 、N 间的关系．(2)写出集合M 的子集、集合N 的真子集．[思路探索] 把用描述法表示的集合用列举法表示出来，以便于观察集合的关系和写子集与真子集．解 M ＝{x|x ＜2且x ∈N }＝{0,1}，N ＝{x|－2＜x ＜2，且x ∈Z }＝{－1,0,1}．(1)M N.(2)M 的子集为： ，{0}，{1}，{0,1}，N 的真子集为： ，{－1}，{0}，{1}，{－1,0}，{－1,1}，{0,1}．[规律方法] 1.写有限集合的所有子集，首先要注意两个特殊的子集： 和自身；其次按含一个元素的子集，含两个元素的子集…依次写出，以免重复或遗漏．2．若集合A 含n 个元素，那么它子集个数为2n ；真子集个数为2n －1，非空真子集个数为2n －2.【活学活用1】 已知集合A ＝{x|x 2－3x ＋2＝0，x ∈R }．B ＝{x|0＜x ＜5，x ∈N }，则满足条件A C B 的集合C 的个数为( )．A ．1B ．2C ．3D ．4解析 易知A ＝{1,2}，B ＝{1,2,3,4}，又A C B.∴集合C 可以是{1,2}，{1,2,3}，{1,2,4}，{1,2,3,4}．答案 D类型二 集合的相等问题【例2】 集合⎩⎨⎧⎭⎬⎫1，a ，b a ＝{0，a 2，a ＋b}，则a 2 013＋b 2 014的值为( )． A ．0 B ．1 C ．－1 D ．±1[思路探索] 集合相等 集合的元素相同 a ≠0 b ＝0，a 2＝1 a 2013＋b 2014＝－1.解析 ∵⎩⎨⎧⎭⎬⎫1，a ，b a ＝{0，a 2，a ＋b}， 又a ≠0，∴b a＝0，∴b ＝0. ∴a 2＝1，∴a ＝±1.又a ≠1，∴a ＝－1，∴a 2 013＋b 2 014＝(－1)2 013＋02 014＝－1.答案 C[规律方法] 1.本题以“0”为着眼点，b a中a 不为0为突破口． 2．两个集合相等，则所含元素完全相同，与顺序无关，但要注意检验，排除与集合元素互异性或与已知矛盾的情形．例如本题中a ＝1不满足互异性，否则会错选D.【活学活用2】 设集合A ＝{1，－2，a 2－1}，B ＝{1，a 2－3a,0}，若A ＝B ，求实数a 的值．解 由A ＝B 及两集合元素特征，∴⎩⎪⎨⎪⎧ a 2－1＝0，a 2－3a ＝－2， ∴⎩⎪⎨⎪⎧a ＝±1，a ＝1或a ＝2. 因此a ＝1，代入检验满足互异性．∴a ＝1.类型三 由集合间的关系求参数范围问题【例3】 已知集合A ＝{x|－3≤x ≤4}，B ＝{x|2m －1＜x ＜m ＋1}，且B A.求实数m 的取值范围．[思路探索] 借助数轴分析，注意B 是否为空集．解 ∵B A ，(1)当B ＝ 时，m ＋1≤2m －1，解得m ≥2.(2)当B ≠ 时，有⎩⎪⎨⎪⎧ －3≤2m －1，m ＋1≤4，2m －1＜m ＋1，解得－1≤m ＜2，综上得m ≥－1.[规律方法] 1.(1)分析集合间的关系时，首先要分析、简化每个集合．(2)借助数轴，利用数轴分析法，将各个集合在数轴上表示出来，以形定数，还要注意验证端点值，做到准确无误，一般含“＝”用实心点表示，不含“＝”用空心点表示．2．此类问题要注意对空集的讨论．【活学活用3】 已知集合A ＝{x|1≤x ≤2}，B ＝{x|1≤x ≤a ，a ≥1}．(1)若A B ，求a 的取值范围；(2)若B A ，求a 的取值范围．解 (1)若A B ，由图可知a ＞2.(2)若B A ，由图可知1≤a ≤2.方法技巧 分类讨论思想在集合关系中的应用所谓分类讨论，就是当问题所涉及的对象不能统一解决时，就需要对研究对象按某个标准进行分类，然后对每一类分别研究得出每一类结论，最后综合各类结果得到整个问题的答案．在集合包含关系或涉及集合的元素含有参数时，常借助分类讨论思想转化求解．【示例】 (2013·济南高一检测)已知集合A ＝{x|x 2－4x ＋3＝0}，B ＝{x|mx －3＝0}，且B A ，求实数m 的集合．[思路分析]解 由x 2－4x ＋3＝0，得x ＝1或x ＝3.∴集合A ＝{1,3}．(1)当B ＝ 时，此时m ＝0，满足B A.(2)当B ≠ 时，则m ≠0，B ＝{x|mx －3＝0}＝⎩⎨⎧⎭⎬⎫3m . ∵B A ，∴3m ＝1或3m＝3，解之得m ＝3或m ＝1. 综上可知，所求实数m 的集合为{0,1,3}．[题后反思] 1.解答诸如含有集合包含关系的题目时，一定要警惕“ ”这一陷阱，考虑不周而漏掉对空集的讨论，往往造成不应有的失分，初学者要切记．2．在方程或不等式中，当一次项或二次项系数含参数时，在参数取值范围不确定的情况 下要注意分类讨论.作业1．集合{0}与∅的关系是( )．A ．{0}B ．{0}∈C ．{0}＝D ．{0}解析 空集是任何非空集合的真子集，故A 正确．集合与集合之间无属于关系，故B 错；空集不含任何元素，{0}含有一个元素0，故C 、D 均错．答案 A2．已知集合A ＝{x|－1＜x ＜4}，B ＝{x|x ＜a}，若A B ，则实数a 满足( )．A ．a ＜4B ．a ≤4C ．a ＞4D ．a ≥4解析 由A B ，结合数轴，得a ≥4.答案 D3．已知集合A ＝{2,9}，集合B ＝{1－m,9}，且A ＝B ，则实数m ＝________. 解析 ∵A ＝B ，∴1－m ＝2，∴m ＝－1.答案 －14．已知集合A ＝{－1,3,2m －1}，集合B ＝{3，m 2}，若B A ，则实数m ＝________. 解析 ∵B ＝{3，m 2}，A ＝{－1,3,2m －1}，且B A ，∴m 2∈{－1,3,2m －1}，又m 2≠3，∴m 2＝2m －1，解得m ＝1，经检验合题意．答案 15．已知集合A ＝{(x ，y)|x ＋y ＝2，x ，y ∈N }，试写出A 的所有子集．解 ∵A ＝{(x ，y)|x ＋y ＝2，x ，y ∈N }，∴A ＝{(0,2)，(1,1)，(2,0)}．∴A 的子集有： ，{(0,2)}，{(1,1)}，{(2,0)}，{(0,2)，(1,1)}，{(0,2)，(2,0)}，{(1,1)，(2,0)}，{(0,2)，(1,1)，(2,0)}．课堂小结1．子集和真子集(1)A B 包含两种情况：A ＝B 和A B.当A 是B 的子集时，不要漏掉A ＝B 的情况．(2)在真子集的定义中，A B 首先要满足A B ，其次至少有一个x ∈B ，但x A.(3)集合与集合之间的关系有包含关系、相等关系，其中包含关系有：包含于( )、包含( )，真包含于( )、真包含( )等，用这些符号时要注意方向．2．空集(1)空集是任何集合的子集，是任何非空集合的真子集．(2)若利用“A B”或“A B”解题，要讨论A＝ 和A≠ 两种情况．3．涉及字母参数的集合关系时，注意数形结合思想与分类讨论思想的应用.。

1．2 集合间的基本关系学习目标 1.理解子集、真子集、集合相等、空集的概念.2.能用符号和Venn图表达集合间的关系.3.掌握列举有限集的所有子集的方法．知识点一子集、真子集、集合相等1．子集、真子集、集合相等定义符号表示图形表示子集如果集合A中的任意一个元素都是集合B中的元素，就称集合A是集合B的子集A⊆B(或B⊇A)真子集如果集合A⊆B，但存在元素x∈B，且x∉A，就称集合A是集合B的真子集A B(或B A)集合相等如果集合A的任何一个元素都是集合B的元素，同时集合B的任何一个元素都是集合A的元素，那么集合A与集合B相等A＝B2.Venn图用平面上封闭曲线的内部代表集合，这种图称为Venn图．3．子集的性质(1)任何一个集合是它本身的子集，即A⊆A.(2)对于集合A，B，C，如果A⊆B，且B⊆C，那么A⊆C.知识点二空集1．定义：不含任何元素的集合叫做空集，记为∅.2．规定：空集是任何集合的子集．思考{0}与∅相等吗？答案不相等．{0}表示一个集合，且集合中有且仅有一个元素0；而∅表示空集，其不含有任何元素，故{0}≠∅.1．空集中不含任何元素，所以∅不是集合．(×)2．任何一个集合都有子集．(√)3．若A＝B，则A⊆B且B⊆A.(√)4．空集是任何集合的真子集．(×)一、集合间关系的判断例1(1)下列各式中，正确的个数是()①{0}∈{0,1,2}；②{0,1,2}⊆{2,1,0}；③∅⊆{0,1,2}；④∅{0}；⑤{0,1}＝{(0,1)}；⑥0＝{0}．A．1B．2C．3D．4答案 C解析对于①，是集合与集合的关系，应为{0}{0,1,2}；对于②，实际为同一集合，任何一个集合是它本身的子集；对于③，空集是任何集合的子集；对于④，{0}是含有单元素0的集合，空集不含任何元素，并且空集是任何非空集合的真子集，所以∅{0}；对于⑤，{0,1}是含有两个元素0与1的集合，而{(0,1)}是以有序实数对(0,1)为元素的单点集，所以{0,1}与{(0,1)}不相等；对于⑥，0与{0}是“属于与否”的关系，所以0∈{0}．故②③④是正确的．(2)指出下列各组集合之间的关系：①A＝{－1,1}，B＝{(－1，－1)，(－1,1)，(1，－1)，(1,1)}；②M＝{x|x＝2n－1，n∈N*}，N＝{x|x＝2n＋1，n∈N*}．解①集合A的代表元素是数，集合B的代表元素是有序实数对，故A与B之间无包含关系．②方法一两个集合都表示正奇数组成的集合，但由于n∈N*，因此集合M含有元素“1”，而集合N不含元素“1”，故N M.方法二由列举法知M＝{1,3,5,7，…}，N＝{3,5,7,9，…}，所以N M.反思感悟判断集合间关系的方法(1)用定义判断①任意x∈A时，x∈B，则A⊆B.②当A⊆B时，存在x∈B，且x∉A，则A B.③若既有A⊆B，又有B⊆A，则A＝B.(2)数形结合判断对于不等式表示的数集，可在数轴上标出集合，直观地进行判断，但要注意端点值的取舍．跟踪训练1能正确表示集合M＝{x∈R|0≤x≤2}和集合N＝{x∈R|x2－x＝0}关系的Venn图是()答案 B解析x2－x＝0得x＝1或x＝0，故N＝{0,1}，易得N M，其对应的V enn图如选项B所示．二、子集、真子集的个数问题例2已知集合M满足{1,2}M⊆{1,2,3,4,5}，写出集合M所有的可能情况．解由题意可以确定集合M必含有元素1,2，且至少含有元素3,4,5中的一个，因此依据集合M的元素个数分类如下：含有3个元素：{1,2,3}，{1,2,4}，{1,2,5}；含有4个元素：{1,2,3,4}，{1,2,3,5}，{1,2,4,5}；含有5个元素：{1,2,3,4,5}．故满足条件的集合M为{1,2,3}，{1,2,4}，{1,2,5}，{1,2,3,4}，{1,2,3,5}，{1,2,4,5}，{1,2,3,4,5}．反思感悟公式法求有限集合的子集个数(1)含n个元素的集合有2n个子集．(2)含n个元素的集合有(2n－1)个真子集．(3)含n个元素的集合有(2n－1)个非空子集．(4)含n个元素的集合有(2n－2)个非空真子集．跟踪训练2已知集合A＝{x|0≤x<5，且x∈N}，则集合A的子集的个数为()A．15B．16C．31D．32答案 D解析A＝{0,1,2,3,4}，含有5个元素的集合的子集的个数为25＝32.三、集合间关系的应用例3已知集合A＝{x|－2≤x≤5}，B＝{x|m＋1≤x≤2m－1}，若B A，求实数m的取值范围.解(1)当B≠∅时，如图所示．∴⎩⎪⎨⎪⎧m ＋1≥－2，2m －1<5，2m －1≥m ＋1或⎩⎪⎨⎪⎧m ＋1>－2，2m －1≤5，2m －1≥m ＋1，解这两个不等式组，得2≤m ≤3. (2)当B ＝∅时，由m ＋1>2m －1，得m <2.综上可得，m 的取值范围是{m |m ≤3}． 延伸探究1．若本例条件“A ＝{x |－2≤x ≤5}”改为“A ＝{x |－2<x <5}”，其他条件不变，求m 的取值范围．解 (1)当B ＝∅时，由m ＋1>2m －1，得m <2. (2)当B ≠∅时，如图所示．∴⎩⎪⎨⎪⎧m ＋1>－2，2m －1<5，m ＋1≤2m －1，解得⎩⎪⎨⎪⎧m >－3，m <3，m ≥2，即2≤m <3，综上可得，m 的取值范围是{m |m <3}．2．若本例条件“B A ”改为“A ⊆B ”，其他条件不变，求m 的取值范围． 解 当A ⊆B 时，如图所示，此时B ≠∅.∴⎩⎪⎨⎪⎧2m －1>m ＋1，m ＋1≤－2，2m －1≥5，即⎩⎪⎨⎪⎧m >2，m ≤－3，m ≥3，∴m不存在．即不存在实数m使A⊆B.反思感悟(1)利用数轴处理不等式表示的集合间的关系问题时，可化抽象为直观，要注意端点值的取舍，“含”用实心点表示，“不含”用空心点表示．(2)涉及到“A⊆B”或“A B且B≠∅”的问题，一定要分A＝∅和A≠∅两种情况讨论，不要忽视空集的情况．跟踪训练3若集合A＝{x|1<x<2}，B＝{x|x>a}，满足A B，则实数a的取值范围是() A．{a|a≥2} B．{a|a≤1}C．{a|a≥1} D．{a|a≤2}答案 B解析如图所示，A B，所以a≤1.1．下列四个集合中，是空集的是()A．{0} B．{x|x>8，且x<5}C．{x∈N|x2－1＝0} D．{x|x>4}答案 B解析选项A，C，D都含有元素，而选项B中无元素，故选B.2．已知集合A＝{x|－1－x<0}，则下列各式正确的是()A．0⊆A B．{0}∈A C．∅∈A D．{0}⊆A答案 D解析集合A＝{x|－1－x<0}＝{x|x>－1}，所以0∈A，{0}⊆A，∅⊆A，D正确．3．已知A＝{x|x是菱形}，B＝{x|x是正方形}，C＝{x|x是平行四边形}，那么A，B，C之间的关系是()A．A⊆B⊆C B．B⊆A⊆CC．A B⊆C D．A＝B⊆C答案 B解析集合A，B，C关系如图．4．已知集合A＝{－1,3，m}，B＝{3,4}，若B⊆A，则实数m＝________.答案 4解析∵B⊆A，∴元素3,4必为A中元素，∴m＝4.5．已知集合A＝{x|x≥1或x≤－2}，B＝{x|x≥a}，若B A，则实数a的取值范围是________．答案a≥1解析∵B A，∴a≥1.1．知识清单：(1)子集、真子集、空集、集合相等的概念及集合间关系的判断．(2)求子集、真子集的个数问题．(3)由集合间的关系求参数的值或范围．2．方法归纳：数形结合、分类讨论．3．常见误区：忽略对集合是否为空集的讨论，忽视是否能够取到端点．。

§1.2 集合间的基本关系学习目标 1.理解子集、真子集、集合相等、空集的概念.2.能用符号和V enn图表达集合间的关系.3.掌握列举有限集的所有子集的方法．知识点一子集、真子集、集合相等1．子集、真子集、集合相等的相关概念定义符号表示图形表示子集如果集合A中的任意一个元素都是集合B中的元素，就称集合A是集合B的子集A⊆B(或B⊇A)真子集如果集合A⊆B，但存在元素x∈B，且x∉A，就称集合A是集合B的真子集A B(或B A)集合相等如果集合A的任何一个元素都是集合B的元素，同时集合B的任何一个元素都是集合A的元素，那么集合A与集合B相等A＝B2．Venn图用平面上封闭曲线的内部代表集合，这种图称为Venn图．3．子集的性质(1)任何一个集合是它本身的子集，即A⊆A.(2)对于集合A，B，C，如果A⊆B，且B⊆C，那么A⊆C.思考1任何两个集合之间是否有包含关系？答案不一定．如集合A＝{0,1,2}，B＝{－1,0,1}，这两个集合就没有包含关系．思考2符号“∈”与“⊆”有何不同？答案符号“∈”表示元素与集合间的关系；而“⊆”表示集合与集合之间的关系．知识点二空集1．定义：不含任何元素的集合叫做空集，记为∅.2．规定：空集是任何集合的子集．思考{0}与∅相同吗？答案不同．{0}表示一个集合，且集合中有且仅有一个元素0；而∅表示空集，其不含有任何元素，故{0}≠∅.1．已知集合M＝{x|x是菱形}，N＝{x|x是正方形}，则集合M与集合N的关系为________．答案N M解析因为正方形是菱形，所以N M.2．用“⊆”或“∈”填空：{0,2}________{2,1,0},2________{2,1,0}．答案⊆∈3．设a∈R，若集合{2,9}＝{1－a,9}，则a＝________.答案－1解析1－a＝2，解得a＝－1.4．集合{0,1}的子集有________个．答案 4解析集合{0,1}的子集有∅，{0}，{1}，{0,1}，共4个．一、集合间关系的判断例1指出下列各对集合之间的关系：(1)A＝{－1,1}，B＝{(－1，－1)，(－1,1)，(1，－1)，(1,1)}；(2)A＝{x|－1<x<4}，B＝{x|x－5<0}；(3)M＝{x|x＝2n－1，n∈N*}，N＝{x|x＝2n＋1，n∈N*}．解(1)集合A的元素是数，集合B的元素是有序实数对，故A与B之间无包含关系．(2)集合B＝{x|x<5}，用数轴表示集合A，B，如图所示，由图可知A B.(3)由列举法知M＝{1,3,5,7，…}，N＝{3,5,7,9，…}，故N M.反思感悟判断集合关系的方法(1)观察法：一一列举观察．(2)元素特征法：首先确定集合的元素是什么，弄清集合元素的特征，再利用集合元素的特征判断关系．(3)数形结合法：利用数轴或Venn图．跟踪训练1(1)已知集合M＝{x|x2－3x＋2＝0}，N＝{0,1,2}，则集合M与N的关系是() A．M＝N B．N MC．M N D．N⊆M答案 C解析解方程x2－3x＋2＝0得x＝2或x＝1，则M＝{1,2}，因为1∈M且1∈N,2∈M且2∈N，所以M⊆N.又因为0∈N但0∉M，所以M N.(2)已知集合A＝{x|x＝3k，k∈Z}，B＝{x|x＝6k，k∈Z}，则A与B之间的关系是() A．A⊆B B．A＝BC．A B D．B A答案 D解析因为A中元素是3的整数倍，而B中的元素是3的偶数倍，所以集合B是集合A的真子集．二、确定集合的子集、真子集例2设A＝{x|(x2－16)(x2＋5x＋4)＝0}，写出集合A的子集，并指出其中哪些是它的真子集．解由(x2－16)(x2＋5x＋4)＝0，得(x－4)(x＋1)(x＋4)2＝0，解方程得x＝－4或x＝－1或x＝4.故集合A＝{－4，－1,4}．由0个元素构成的子集为∅；由1个元素构成的子集为{－4}，{－1}，{4}；由2个元素构成的子集为{－4，－1}，{－4,4}，{－1,4}；由3个元素构成的子集为{－4，－1,4}．因此集合A的子集为∅，{－4}，{－1}，{4}，{－4，－1}，{－4,4}，{－1,4}，{－4，－1,4}．真子集为∅，{－4}，{－1}，{4}，{－4，－1}，{－4,4}，{－1,4}．(学生)反思感悟求集合子集、真子集的3个步骤跟踪训练2 满足{1,2}M ⊆{1,2,3,4,5}的集合M 有________个． 答案 7解析 由题意可得{1,2}M ⊆{1,2,3,4,5}，可以确定集合M 必含有元素1,2，且含有元素3,4,5中的至少一个，因此依据集合M 的元素个数分类如下： 含有三个元素：{1,2,3}，{1,2,4}，{1,2,5}； 含有四个元素：{1,2,3,4}，{1,2,3,5}，{1,2,4,5}； 含有五个元素：{1,2,3,4,5}． 故满足题意的集合M 共有7个．三、由集合间的关系求参数例3 已知集合A ＝{x |－2≤x ≤5}，B ＝{x |m ＋1≤x ≤2m －1}，若B A ，求实数m 的取值范围.解 (1)当B ≠∅时，如图所示．∴⎩⎪⎨⎪⎧m ＋1≥－2，2m －1<5，2m －1≥m ＋1或⎩⎪⎨⎪⎧m ＋1>－2，2m －1≤5，2m －1≥m ＋1，解这两个不等式组，得2≤m ≤3. (2)当B ＝∅时，由m ＋1>2m －1，得m <2.综上可得，m 的取值范围是{m |m ≤3}． (教师) 延伸探究1．若本例条件“A ＝{x |－2≤x ≤5}”改为“A ＝{x |－2<x <5}”，其他条件不变，求m 的取值范围．解 (1)当B ＝∅时，由m ＋1>2m －1，得m <2. (2)当B ≠∅时，如图所示．∴⎩⎪⎨⎪⎧m ＋1>－2，2m －1<5，m ＋1≤2m －1，解得⎩⎪⎨⎪⎧m >－3，m <3，m ≥2，即2≤m <3，综上可得，m 的取值范围是{m |m <3}．2．若本例条件“B A ”改为“A ⊆B ”，其他条件不变，求m 的取值范围． 解 当A ⊆B 时，如图所示，此时B ≠∅.∴⎩⎪⎨⎪⎧2m －1>m ＋1，m ＋1≤－2，2m －1≥5，即⎩⎪⎨⎪⎧m >2，m ≤－3，m ≥3，∴m 不存在．即不存在实数m 使A ⊆B . (学生)反思感悟 利用集合关系求参数的关注点(1)分析集合关系时，首先要分析、简化每个集合．(2)此类问题通常借助数轴，利用数轴分析法，将各个集合在数轴上表示出来，以形定数，还要注意验证端点值，做到准确无误．一般含“＝”用实心点表示，不含“＝”用空心点表示． (3)此类问题还要注意“空集”的情况，因为空集是任何集合的子集．跟踪训练3 已知集合A ＝{x |x <－1或x >4}，B ＝{x |2a ≤x ≤a ＋3}，若B ⊆A ，求实数a 的取值范围．解 (1)当B ＝∅时，2a >a ＋3，即a >3.显然满足题意．(2)当B ≠∅时，根据题意作出如图所示的数轴，可得⎩⎪⎨⎪⎧ a ＋3≥2a ，a ＋3<－1或⎩⎪⎨⎪⎧a ＋3≥2a ，2a >4，解得a <－4或2<a ≤3.综上可得，实数a 的取值范围为{a |a <－4或a >2}．1．下列六个关系式：①{a ，b }＝{b ，a }；②{a ，b }⊆{b ，a }；③∅＝{∅}；④{0}＝∅；⑤∅{0}；⑥0∈{0}．其中正确的个数是( ) A ．1B ．3C ．4D ．6 答案 C解析 ①正确，集合中元素具有无序性；②正确，任何集合是自身的子集；③错误，∅表示空集，而{∅}表示的是含∅这个元素的集合，是元素与集合的关系，应改为∅∈{∅}；④错误，∅表示空集，而{0}表示含有一个元素0的集合，并非空集，应改为∅{0}；⑤正确，空集是任何非空集合的真子集；⑥正确，是元素与集合的关系． 2．集合{1,2}的子集有( ) A ．4个B ．3个C ．2个D ．1个 答案 A解析 集合{1,2}的子集有∅，{1}，{2}，{1,2}，共4个．3．能正确表示集合M ＝{x ∈R |0≤x ≤2}和集合N ＝{x ∈R |x 2－x ＝0}关系的Venn 图是( )答案 B解析 x 2－x ＝0得x ＝1或x ＝0，故N ＝{0,1}， 易得NM ，其对应的V enn 图如选项B 所示．4．已知集合A ＝{－1,3，m }，B ＝{3,4}，若B ⊆A ，则实数m ＝________. 答案 4解析 ∵B ⊆A ，B ＝{3,4}，A ＝{－1,3，m }，∴4∈A，∴m＝4.5．已知集合A＝{x|x≥1或x≤－2}，B＝{x|x≥a}，若B A，则实数a的取值范围是________．答案a≥1解析∵B A，∴a≥1.1．知识清单：(1)子集、真子集、空集、集合相等的概念及集合间关系的判断．(2)求子集、真子集的个数问题．(3)由集合间的关系求参数的值或范围．2．方法归纳：数形结合、分类讨论．3．常见误区：忽略对集合是否为空集的讨论，忽视是否能够取到端点．。