2019-2020年广东省广州市二模：广州市2019届高三第二次模拟考试文综地理试题-附详细答案

2019年广州市普通高中毕业班综合测试（二）文科综合(政治)2019．4一、选择题：本题共35小题，每小题4分，共140分。

每小题给出的四个选项中，只有一个选项符合题目要求。

24．腾讯公司和360公司因杀毒软件兼容问题而互相封杀，导致亿万电脑用户受到波及。

在国家工信部的干预下，两企业被通报批评并向社会公开道歉。

对此，认识正确的是A．企业应公平竞争，自觉承担社会责任B．维护网民利益是网络公司经营的主要目的C．互联网的健康发展取决于市场规则的制定D．国家工信部不宜用行政手段干预企业的自主经营25．针对日渐扩大的收入差距，我国有关部门正在试点建立低保、最低工资、基本养老金与物价水平相适应的动态调整机制。

这样做的理论依据是①收入是消费的基础和前提②物价变动会影响人们的生活③收入分配的平均化是社会公平的重要体现④实现和维护劳动者合法权益是社会主义制度的本质要求A．①③B．②③C．①②④D．②③④26．存款准备金是指金融机构为保证客户提取存款和资金清算需要而准备的在中央银行的存款，该存款准备金占其存款总额的比例就是存款准备金率。

右图为近期我国存款准备金率的调整情况，这表明①金融机构贷款利率下调，以刺激经济②国家运用货币政策，加强宏观调控③我国严控货币流动性，预防通货膨胀④金融机构支付能力增强，有利于防范风险A．①②④B．①②③C．①③④D．②③④27．“十一五”期间，我国在大力发展国内生产的同时，对外直接投资从211．6亿美元增至565．3亿美元，年均增速38, 8010；对外承包工程完成营业额从300亿美元增至777亿美元，年均增速37．3%；对外劳务合作实现平稳较快增长。

上述材料表明①我国与贸易伙伴的关系进一步改善，贸易摩擦减少②我国发挥资源的比较优势，用好国内国际两个市场③我国坚持对外开放，“走出去”战略取得明显成效④对外投资、工程承包和劳务合作是我国发展对外经济合作的重要形式A．①②④B．①②③C．②③④D．①③④28．我国目前有69万多个行政村，每个村都有一位村长（即村委会主任）。

试卷类型： A2019年广州市普通高中毕业班综合测试（二）语文试题本试卷共10页，22小题，满分150分。

考试用时150分钟。

注意事项：1．答题前，考生先将自已所在县（市、区）、姓名、试室号、座位号和考生号填写清楚，将条形码粘贴在指定区域。

2．选择题每小题选出答案后，用2B铅笔把答题卷上对应题目的答案标号涂黑，如需改动请先用橡皮擦擦干净，再选涂其他答案标号。

主观题请用黑色墨水签字笔在答题卷上作答。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．考试结束，监考人员将试卷、答题卷一并收回。

5．保持答题卷清洁，不要折叠、不要弄破。

一、现代文阅读（36分）（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1～3题。

“天下”是中国传统文化对世界秩序的一种原初想象，“天下主义”是以“天下”理念为核心，由具有普遍性和开放性的世界秩序、价值规范与理想人格构成的思想体系。

在当今全球化语境之下，中国文化理念和文化战略的自觉自信体现的正是“天下主义”的精神内核。

文化自信首先是一种“以天下观天下”的世界观的自信。

《道德经》有云：“修之于天下，其德乃普。

故以身观身，以家观家，以乡观乡，以国观国，以天下观天下。

”“天下”是中国文化特有的思维尺度，是一个最宏大、最完备的分析单位，具有最广阔的容纳力。

面对差异性的多元文化格局，西方文化多以民族国家为基本单位，文化视域限于国家、民族内部，虽然也有关于世界的思考，比如斯多葛学派的“世界主义”等，但其思考方式是“以国家观世界”，与中国文化的立足点和尺度不同。

中国文化的“天下”蕴含了“天下无外”的理想，各个民族的历史文化在世界内部是平等共存的；中国文化依循“修身、齐家、治国、平天下”的进路，从“身-家-国”逻辑同构的角度，最终达到“天下大同”的境界。

与西方文化相较，“天下”的世界观更具有开放性和包容性。

文化自信的核心是“以天下为一家”的价值观的自信。

2019年广东省广州市高考数学二模试卷（文科）一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）已知集合A＝{x∈N|0＜x＜6}，B＝{2，4，6，8}，则A∩B＝（）A．{0，1，3，5}B．{0，2，4，6}C．{1，3，5}D．{2，4}2．（5分）已知复数z＝m（3+i）﹣（2+i）在复平面内对应的点在第三象限，则实数m的取值范围是（）A．（﹣∞，1）B．（﹣∞，）C．（）D．（﹣∞，）∪（1，+∞）3．（5分）某公司生产A，B，C三种不同型号的轿车，产量之比依次为2：3：4，为检验该公司的产品质量，用分层抽样的方法抽取一个容量为n的样本，若样本中A种型号的轿车比B种型号的轿车少8辆，则n＝（）A．96B．72C．48D．364．（5分）执行如图所示的程序框图，则输出z的值是（）A．21B．22C．23D．245．（5分）从某班5名学生（其中男生3人，女生2人）中任选3人参加学校组织的社会实践活动，则所选3人中至少有1名女生的概率为（）A．B．C．D．6．（5分）函数y＝2sin（ωx+φ）（ω＞0，|φ|＜π）的部分图象如图所示，则函数的解析式为（）A．y＝2sin（）B．y＝2sin（）C．y＝2cos（）D．y＝2cos（）7．（5分）设等比数列{a n}的前n项和为S n，则下列等式中一定成立的是（）A．S n+S2n＝S3nB．S22n＝S n S3nC．S22n＝S n+S2n﹣S3nD．S2n+S22n＝S n（S2n+S3n）8．（5分）已知双曲线＝1（a＞0，b＞0）的渐近线方程为5x±3y＝0，则此双曲线的离心率为（）A．B．C．D．9．（5分）一个圆锥的体积为，当这个圆锥的侧面积最小时，其母线与底面所成角的正切值为（）A．B．C．D．10．（5分）设a≥b≥c，且1是一元二次方程ax2+bx+c＝0的一个实根，则的取值范围为（）A．[﹣2，0]B．[﹣，0]C．[﹣2，﹣]D．[﹣1，﹣] 11．（5分）在三棱锥P﹣ABC中，P A＝PB＝PC＝2，AB＝AC＝1，BC＝，则该三棱锥的外接球的表面积为（）A．8πB．C．D．12．（5分）己知函数f（x）＝e x﹣ex+a与g（x）＝lnx+的图象上存在关于x轴对称的点，则实数a的取值范围为（）A．[﹣e，+∞）B．[﹣1，+∞）C．（﹣∞，﹣1]D．（﹣∞，﹣e]二、填空题：本题共4小题，每小题5分，共20分．13．（5分）已知向量＝（1，﹣1），b＝（2，1），向量＝2+，则||＝14．（5分）《莱茵德纸草书》是世界上最古老的数学著作之一．书中有一道这样的题目：把100个面包分给5个人，使每人所得份量成等差数列，且较大的三份之和的是较小的两份之和，则最小一份的量为．15．（5分）若函数f（x）＝x2﹣x+l+alnx在（0，+∞）上单调递增，则实数a的取值范围是．16．（5分）己知点P在直线x+2y﹣l＝0上，点Q在直线x+2y+3＝0，PQ的中点为M（x0，y0），且﹣1≤y0﹣x0≤7，则的取值范围是．三、解答题：共70分，解答应写出文字说明、证明过程和演算步骤，第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17．（12分）△ABC中角A，B，C的对边分别为a，b，c，已知2（tan A+tan B）＝．（1）求的值；（2）若c＝2，C＝，求△ABC的面积．18．（12分）如图，在四棱锥P﹣ABCD中，底面ABCD是边长为2的菱形，∠BAD＝60°，∠APD＝90°，且P A＝PD，AD＝PB．（1）求证：AD⊥PB；（2）求点A到平面PBC的距离．19．（12分）科研人员在对人体脂肪含量和年龄之间关系的研究中，获得了一些年龄和脂肪含量的简单随机样本数据，如表：根据上表的数据得到如下的散点图．（1）根据上表中的样本数据及其散点图： （i ）求；（ii ）计算样本相关系数（精确到0.01），并刻画它们的相关程度． （2）若y 关于x 的线性回归方程为，求的值（精确到0.01），并根据回归方程估计年龄为50岁时人体的脂肪含量． 附：参考数据：＝27，，，＝7759.6，，参考公式：相关系数r ＝＝回归方程中斜率和截距的最小二乘估计公式分别为＝，20．（12分）从抛物线y2＝36x上任意一点P向x轴作垂线段，垂足为Q，点M是线段PQ 上的一点，且满足．（1）求点M的轨迹C的方程；（2）设直线x＝my+1（m∈R）与轨迹c交于A，B两点，T为C上异于A，B的任意一点，直线AT，BT分别与直线x＝﹣1交于D，E两点，以DE为直径的圆是否过x轴上的定点？若过定点，求出符合条件的定点坐标；若不过定点，请说明理由．21．（12分）已知函数f（x）＝（x+2）lnx+ax2﹣4x+7a．（1）若a＝，求函数f（x）的所有零点；（2）若a≥，证明函数f（x）不存在极值．（二）选考题：共10分．请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]22．（10分）在直角坐标系xOy中，倾斜角为α的直线l的参数方程为（t 为参数）．在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，曲线C的极坐标方程为ρ2＝2p cosθ+8．（1）求直线l的普通方程与曲线C的直角坐标方程；（2）若直线l与曲线C交于A，B两点，且|AB|＝4，求直线l的倾斜角．[选修4-5：不等式选讲]23．己知函数f（x）＝|2x﹣l|﹣a．（1）当a＝l时，解不等式f（x）＞x+1；（2）若存在实数x，使得f（x）＜f（x+1）成立，求实数a的取值范围．2019年广东省广州市高考数学二模试卷（文科）参考答案与试题解析一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）已知集合A＝{x∈N|0＜x＜6}，B＝{2，4，6，8}，则A∩B＝（）A．{0，1，3，5}B．{0，2，4，6}C．{1，3，5}D．{2，4}【解答】解：∵A＝{x∈N|0＜x＜6}＝{1，2，3，4，5}，∴A∩B＝{2，4}，故选：D．【点评】本题主要考查集合的基本运算，结合集合交集的定义是解决本题的关键，比较基础．2．（5分）已知复数z＝m（3+i）﹣（2+i）在复平面内对应的点在第三象限，则实数m的取值范围是（）A．（﹣∞，1）B．（﹣∞，）C．（）D．（﹣∞，）∪（1，+∞）【解答】解：z＝m（3+i）﹣（2+i）＝（3m﹣2）+（m﹣1）i，复数对应点的坐标为（3m﹣2，m﹣1），若对应点的坐标在第三象限，则得得m＜，即实数m的取值范围是（﹣∞，），故选：B．【点评】本题主要考查复数的几何意义的应用，结合复数的运算求出复数以及对应点的坐标，结合点在坐标系中的位置建立不等式关系是解决本题的关键．3．（5分）某公司生产A，B，C三种不同型号的轿车，产量之比依次为2：3：4，为检验该公司的产品质量，用分层抽样的方法抽取一个容量为n的样本，若样本中A种型号的轿车比B种型号的轿车少8辆，则n＝（）A．96B．72C．48D．36【解答】解：设样本中A型号车为x辆，则B型号为（x+8）辆，则＝，解得x＝16，即A型号车16辆，则＝，解得n＝72．故选：B．【点评】本题主要考查分层抽样的应用，根据条件建立比例关系是解决本题的关键，是基础题．4．（5分）执行如图所示的程序框图，则输出z的值是（）A．21B．22C．23D．24【解答】解：x＝1，y＝2，则z＝x+y＝1+2＝3，z＜20是，x＝2，y＝3，z＝x+y＝2+3＝5，z＜20是，x＝3，y＝5，z＝x+y＝3+5＝8，z＜20是，x＝5，y＝8，z＝x+y＝5+8＝13，z＜20是，x＝8，y＝13，z＝x+y＝8+13＝21，z＜20否，输出z＝21，故选：A．【点评】本题主要考查程序框图的识别和判断，利用模拟运算法是解决本题的关键．5．（5分）从某班5名学生（其中男生3人，女生2人）中任选3人参加学校组织的社会实践活动，则所选3人中至少有1名女生的概率为（）A．B．C．D．【解答】解：从某班5名学生（其中男生3人，女生2人）中任选3人参加学校组织的社会实践活动，基本事件总数n＝＝10，所选3人中至少有1名女生包含的基本事件个数m＝＝9，∴所选3人中至少有1名女生的概率为p＝．故选：A．【点评】本题考查概率的求法，考查古典概型、排列组合等基础知识，考查运算求解能力，是基础题．6．（5分）函数y＝2sin（ωx+φ）（ω＞0，|φ|＜π）的部分图象如图所示，则函数的解析式为（）A．y＝2sin（）B．y＝2sin（）C．y＝2cos（）D．y＝2cos（）【解答】解：由图象可知，得函数的周期T＝4×（3.5π﹣2π）＝6π，∴T＝6π．则ω＝＝＝．∴函数解析式为f（x）＝2sin（x+φ）．由f（2π）＝2，得2sin（φ+）＝2，∴可得：φ+＝2kπ+，k∈Z，可得：φ＝2kπ﹣，k∈Z，又|φ|＜π，∴当k＝0时，φ＝﹣．则f（x）的解析式是：f（x）＝2sin（x﹣）．故选：B．【点评】本题考查了由函数y＝A sin（ωx+φ）的部分图象求函数解析式，正弦函数的图象和性质，解决此类问题的方法是先由图象看出振幅和周期，由周期求出ω，然后利用五点作图的某一点求φ，属于中档题．7．（5分）设等比数列{a n}的前n项和为S n，则下列等式中一定成立的是（）A．S n+S2n＝S3nB．S22n＝S n S3nC．S22n＝S n+S2n﹣S3nD．S2n+S22n＝S n（S2n+S3n）【解答】解：等比数列{a n}的前n项和为S n，在A中，等比数列{2n}中，S n＝＝2n+1﹣2，S2n＝＝22n﹣2，＝23n﹣2，S n+S2n≠S3n，故A错误；在B中，等比数列{2n}中，S n＝＝2n+1﹣2，S2n＝＝22n﹣2，＝23n﹣2，S22n＝S n S3n，故B错误；在C中，等比数列{2n}中，S n＝＝2n+1﹣2，S2n＝＝22n﹣2，＝23n﹣2，S22n＝S n+S2n﹣S3n，故C错误．在D中，∵S2n+S22n＝+＝（2+2q n+q2n），S n（S2n+S3n）＝[+]＝（2+2q n+q2n），∴S2n+S22n＝S n（S2n+S3n）．故选：D．【点评】本题考查命题真假的判断，考查等差数列的性质等基础知识，考查运算求解能力，是基础题．8．（5分）已知双曲线＝1（a＞0，b＞0）的渐近线方程为5x±3y＝0，则此双曲线的离心率为（）A．B．C．D．【解答】解：双曲线＝1（a＞0，b＞0）的渐近线方程为5x±3y＝0，可得，可得：，即，∵e＝，所以e＝．故选：B．【点评】本题考查双曲线的简单性质的应用，是基本知识的考查．9．（5分）一个圆锥的体积为，当这个圆锥的侧面积最小时，其母线与底面所成角的正切值为（）A．B．C．D．【解答】解：设圆锥的底面半径为r，高为h，则母线长为l＝，则V＝＝，∴r2h＝，即h＝，∴S侧＝πrl＝πr＝π，∵r4+＝r4++≥3＝，当且仅当r4＝即r2＝时取等号，此时，h＝＝1．∴母线与底面所成角的真切值为＝＝．故选：D．【点评】本题考查了圆锥的结构特征，侧面积与体积计算，考查基本不等式的应用，属于中档题．10．（5分）设a≥b≥c，且1是一元二次方程ax2+bx+c＝0的一个实根，则的取值范围为（）A．[﹣2，0]B．[﹣，0]C．[﹣2，﹣]D．[﹣1，﹣]【解答】解：∵1是一元二次方程ax2+bx+c＝0的一个实根，∴a+b+c＝0，得b＝﹣a﹣c，∴a≥b≥c，即a≥﹣a﹣c≥c，即得，若a＞0，则不等式等价为，即得﹣2≤≤﹣，若a＜0，则不等式等价为，即，此时不等式无解，综上的取值范围为﹣2≤≤﹣，故选：C．【点评】本题主要考查不等式的应用，结合根与方程的关系得到b＝﹣a﹣c，然后代入不等式进行求解是解决本题的关键．11．（5分）在三棱锥P﹣ABC中，P A＝PB＝PC＝2，AB＝AC＝1，BC＝，则该三棱锥的外接球的表面积为（）A．8πB．C．D．【解答】解：如图，由P A＝PB＝PC＝2，过P作PG⊥平面ABC，垂足为G，则G为三角形ABC的外心，在△ABC中，由AB＝AC＝1，BC＝，可得∠BAC＝120°，则由正弦定理可得：＝2AG，即AG＝1．∴PG＝＝．取P A中点H，作HO⊥P A交PG于O，则O为该三棱锥外接球的球心．由△PHO∽△PGA，可得，则PO＝＝．即该棱锥外接球半径为．∴该三棱锥外接球的表面积为，故选：B．【点评】本题考查空间中线线、线面、面面间的位置关系等基础知识，考查多面体外接球体积的求法，考查运算求解能力，是中档题．12．（5分）己知函数f（x）＝e x﹣ex+a与g（x）＝lnx+的图象上存在关于x轴对称的点，则实数a的取值范围为（）A．[﹣e，+∞）B．[﹣1，+∞）C．（﹣∞，﹣1]D．（﹣∞，﹣e]【解答】解：g（x）＝lnx+的定义域为（0，+∞），则g（x）关于x对称的曲线为﹣y＝lnx+，即y＝﹣lnx﹣，则条件等价为f（x）＝e x﹣ex+a＝﹣lnx﹣，在（0，+∞）上有解，得a＝﹣lnx﹣﹣e x+ex，设h（x）＝﹣lnx﹣﹣e x+ex，则函数的导数h′（x）＝﹣+﹣e x+e＝﹣（e x﹣e），当x＝1时，h′（x）＝0，当x＞1时，h′（x）＝﹣（e x﹣e）＜0，此时函数为增函数，当0＜x＜1时，h′（x）＝﹣（e x﹣e）＞0，此时函数f（x）为减函数，即当x＝1时，函数h（x）＝﹣lnx﹣﹣e x+ex取得极大值同时也是最大值，最大值为h（1）＝﹣ln1﹣1﹣e+e＝﹣1，作出h（x）＝﹣lnx﹣﹣e x+ex的图象如图：即要使a＝h（x）在（0，+∞）上有解，则a≤﹣1，即实数a的取值范围是（﹣∞，﹣1]，故选：C．【点评】本题主要考查函数与方程的应用，根据对称性求出关于x对称的函数，利用函数与方程之间的关系转化为图象交点问题，利用参数分离法利用数形结合是解决本题的关键．综合性较强，有一定的难度．二、填空题：本题共4小题，每小题5分，共20分．13．（5分）已知向量＝（1，﹣1），b＝（2，1），向量＝2+，则||＝【解答】解：；∴．故答案为：．【点评】考查向量坐标的加法和数乘运算，根据向量的坐标求向量的长度的方法．14．（5分）《莱茵德纸草书》是世界上最古老的数学著作之一．书中有一道这样的题目：把100个面包分给5个人，使每人所得份量成等差数列，且较大的三份之和的是较小的两份之和，则最小一份的量为．【解答】解：设等差数列{a n}的公差是d＞0，首项是a1，由题意得，，则，解得，所以a1＝，所以最小的一份为，故答案为：．【点评】本题考查等差数列的通项公式，等差数列的前n项和公式，以及方程思想，是数列在实际生活中的应用，属于基础题．15．（5分）若函数f（x）＝x2﹣x+l+alnx在（0，+∞）上单调递增，则实数a的取值范围是[）．【解答】解：∵函数f（x）＝x2﹣x+l+alnx在（0，+∞）上单调递增∴f′（x）＝2x﹣1+≥0在（0，+∞）上恒成立，∴a≥x﹣2x2在（0，+∞）上恒成立，令g（x）＝x﹣2x2，x＞0根据二次函数的性质可知，当x＝时，g（x）取得最大值∴故答案为：[）【点评】本题考查了导数与函数单调性的关系，函数恒成立问题，属于中档题．16．（5分）己知点P在直线x+2y﹣l＝0上，点Q在直线x+2y+3＝0，PQ的中点为M（x0，y0），且﹣1≤y0﹣x0≤7，则的取值范围是（﹣∞，﹣2]∪[﹣]∪（0，+∞）．【解答】解：∵直线x+2y﹣1＝0与x+2y+3＝0平行，∴点M的轨迹为与两直线距离相等且平行于两直线的直线，其方程为x+2y+1＝0，即点M（x0，y0）满足x0+2y0+1＝0，而满足不等式﹣1≤y0﹣x0≤7，如图，联立，解得A（，），联立，解得B（﹣5，2），的几何意义为线段AB上的点与原点连线的斜率，∵k AO＝﹣2，，∴的取值范围是（﹣∞，﹣2]∪[﹣]∪（0，+∞）．故答案为：（﹣∞，﹣2]∪[﹣]∪（0，+∞）．【点评】本题考查轨迹方程的求法，考查简单线性规划知识的应用，考查数形结合的解题思想方法，是中档题．三、解答题：共70分，解答应写出文字说明、证明过程和演算步骤，第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17．（12分）△ABC中角A，B，C的对边分别为a，b，c，已知2（tan A+tan B）＝．（1）求的值；（2）若c＝2，C＝，求△ABC的面积．【解答】（本题满分为12分）解：（1）因为2（tan A+tan B）＝，所以2（）＝+．………………………………………………（1分）化简得：2（sin A cos B+cos A sin B）＝sin A+sin B．………………………………………………（2分）即2sin（A+B）＝sin A+sin B．………………………………………………………………………（3分）因在△ABC中，A+B+C＝π，则sin（A+B）＝sin（π﹣C）＝sin C．……………………………（4分）从而sin A+sin B＝2sin C．……………………………………………………………………………（5分）由正弦定理，得a+b＝2c．所以＝2．……………………………………………………………………………………………（6分）（2）由（1）知c＝，且c＝2，所以a+b＝4．……………………………………………………（7分）因为C＝，所以cos C＝＝．……………………………………（9分）即cos＝．所以ab＝4．……………………………………………………………………………………………（10分）所以S△ABC＝ab sin C＝＝．所以△ABC的面积为．……………………………………………………………………………（12分）【点评】本题主要考查了三角函数恒等变换的应用，三角形内角和定理，正弦定理，余弦定理在解三角形中的综合应用，考查了计算能力和转化思想，属于中档题．18．（12分）如图，在四棱锥P﹣ABCD中，底面ABCD是边长为2的菱形，∠BAD＝60°，∠APD＝90°，且P A＝PD，AD＝PB．（1）求证：AD⊥PB；（2）求点A到平面PBC的距离．【解答】（1）证明：取AD的中点O，连结OP，OB，BD，因为底面ABCD为菱形，∠BAD＝60°，所以AD＝AB＝BD．因为O为AD的中点，所以BO⊥AD．在△P AD中，P A＝PD，O为AD的中点，所以PO⊥AD．因为BO∩OP＝O，所以AD⊥平面POB．因为PB⊂平面POB，所以AD⊥PB．（2）在Rt△P AD中，AD＝2，所以PO＝1．因为底面ABCD是边长为2的菱形，∠BAD＝60°，所以OB＝．在△PBO中，PO＝1，OB＝，PB＝BC＝2，因为PO2+OB2＝PB2，所以PO⊥OB．由（1）有PO⊥AD，且AD∩OB＝O，AD⊂平面ABCD，OB⊂平面ABCD，所以OP⊥平面ABCD．在△PBC中，由（1）证得AD⊥PB，且BC∥AD，所以BC⊥PB．因为PB＝BC＝2，所以S△PBC＝2．在△ABC中，AB＝BC＝2，∠ABC＝120°，所以S△ABC＝＝．设点A到平面PBC的距离为h，因为V A﹣PBC＝V P﹣ABC ，即S△PBC•h ＝S△ABC•PO．所以h ＝＝．所以点A到平面PBC 的距离为．【点评】本题考查了线面垂直的判定与性质，考查空间距离的计算，属于中档题．19．（12分）科研人员在对人体脂肪含量和年龄之间关系的研究中，获得了一些年龄和脂肪含量的简单随机样本数据，如表：根据上表的数据得到如下的散点图．（1）根据上表中的样本数据及其散点图：（i）求；（ii）计算样本相关系数（精确到0.01），并刻画它们的相关程度．（2）若y关于x的线性回归方程为，求的值（精确到0.01），并根据回归方程估计年龄为50岁时人体的脂肪含量．附：参考数据：＝27，，，＝7759.6，，参考公式：相关系数r＝＝回归方程中斜率和截距的最小二乘估计公式分别为＝，【解答】解：（1）根据上表中的样本数据及其散点图知，（ⅰ）；………………………………（2分）（ⅱ）回归系数r＝＝…………（3分）＝＝………………………………（4分）＝；……………………………（5分）因为，，所以r≈0.98；…………………………………（6分）由样本相关系数r≈0.98，可以推断人体脂肪含量和年龄的相关程度很强；……………………（7分）（2）因为回归方程为，即，所以；【或利用＝＝】……………………………（10分）所以y关于x的线性回归方程为，将x＝50代入线性回归方程得；………………………………（11分）所以根据回归方程预测年龄为50岁时人的脂肪含量为28.56%．…………………………………（12分）【点评】本题考查了线性回归方程的求法与应用问题，是中档题．20．（12分）从抛物线y2＝36x上任意一点P向x轴作垂线段，垂足为Q，点M是线段PQ 上的一点，且满足．（1）求点M的轨迹C的方程；（2）设直线x＝my+1（m∈R）与轨迹c交于A，B两点，T为C上异于A，B的任意一点，直线AT，BT分别与直线x＝﹣1交于D，E两点，以DE为直径的圆是否过x轴上的定点？若过定点，求出符合条件的定点坐标；若不过定点，请说明理由．【解答】解：（1）设M（x，y），P（x0，y0），则点Q的坐标为（x0，0）．因为足．所以（x﹣x0，y﹣y0）＝2（x0﹣x，﹣y）．即．因为点P在抛物线y2＝36x上．所以y02＝36x0，即（3y）2＝36x．所以点M的轨迹C的方程为y2＝4x．（2）设直线x＝my+1与曲线C的交点坐标为A（，y1），B（，y2），由得y2﹣4my﹣4＝0．由韦达定理得y1+y2＝4m，y1y2＝﹣4．设点T（，y0），则k AT＝＝．所以直线AT的方程为y﹣y0＝（x﹣）．令x＝﹣1，得点D的坐标为（﹣1，）．同理可得点E的坐标为（﹣1，）．如果以DE为直径的圆过x轴某一定点N（n，0），则满足•＝0．因为•＝（﹣1﹣n，）•（﹣1﹣n，）＝（1+n）2+．所以（1+n）2+＝0．即（1+n）2﹣4＝0，解得n＝1或n＝﹣3．故以DE为直径的圆过x轴上的定点（1，0）和（﹣3，0）．【点评】本题考查轨迹方程的求法，直线与抛物线的位置关系的应用，考查转化思想以及计算能力．21．（12分）已知函数f（x）＝（x+2）lnx+ax2﹣4x+7a．（1）若a＝，求函数f（x）的所有零点；（2）若a≥，证明函数f（x）不存在极值．【解答】（1）解：当a＝时，f（x）＝（x+2）lnx+x2﹣4x+，函数f（x）的定义域为（0，+∞），…………………………………………………………………………（1分）且f′（x）＝lnx++x﹣3．……………………………………………………………………………（2分）设g（x）＝lnx++x﹣3，则g′（x）＝﹣+1＝＝，（x＞0）．当0＜x＜1时，g′（x）＜0；当x＞1时，g′（x）＞0，即函数g（x）在（0，1）上单调递减，在（1，+∞）上单调递增，…………………………………………（3分）所以当x＞0时，g（x）≥g（1）＝0（当且仅当x＝1时取等号）．…………………………………（4分）即当x＞0时，f′（x）≥0（当且仅当x＝1时取等号）．所以函数f（x）在（0，+∞）单调递增，至多有一个零点．………………………………………………（5分）因为f（1）＝0，x＝1是函数f（x）唯一的零点．所以若a＝，则函数f（x）的所有零点只有x＝1．…………………………………………………（6分）（2）证法1：因为f（x）＝（x+2）lnx+ax2﹣4x+7a，函数f（x）的定义域为（0，+∞），且f′（x）＝lnx++2ax﹣4．…………………………………（7分）当a≥时，f′（x）≥lnx++x﹣3，………………………………………………………………（9分）由（1）知lnx++x﹣3≥0．………………………………………………………………………（10分）即当x＞0时，f′（x）≥0，所以f（x）在（0，+∞）上单调递增．……………………………………………………………………（11分）所以f（x）不存在极值．…………………………………………………………………………………（12分）证法2：因为f（x）＝（x+2）lnx+ax2﹣4x+7a，函数f（x）的定义域为（0，+∞），且f′（x）＝lnx++2ax﹣4…………………………………（7分）设m（x）＝lnx++2ax﹣4，则m′（x）＝﹣+2a＝，（x＞0）．设h（x）＝2ax2+x﹣2，（x＞0），则m′（x）与h（x）同号．当a≥时，由h（x）＝2ax2+x﹣2＝0，解得x1＝＜0，x2＝＞0．……………………………………………（8分）可知当0＜x＜x2时，h（x）＜0，即m′（x）＜0，当x＞x2时，h（x）＞0，即m′（x）＞0，所以f′（x）在（0，x2）上单调递减，在（x2，+∞）上单调递增．…………………………………………（9分）由（1）知lnx++x﹣3≥0．………………………………………………………………………（10分）则f′（x2）＝lnx2++x2﹣3+（2a﹣1）x2≥（2a﹣1）x2≥0．所以f′（x）≥f′（x2）≥0，即f（x）在定义域上单调递增．…………………………………………（11分）所以f（x）不存在极值．…………………………………………………………………………………（12分）【点评】本题主要考查导数的综合应用，结合函数零点，函数极值与导数之间的关系是解决本题的关键．综合性较强，运算量较大，有一定的难度．（二）选考题：共10分．请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]22．（10分）在直角坐标系xOy中，倾斜角为α的直线l的参数方程为（t 为参数）．在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，曲线C的极坐标方程为ρ2＝2p cosθ+8．（1）求直线l的普通方程与曲线C的直角坐标方程；（2）若直线l与曲线C交于A，B两点，且|AB|＝4，求直线l的倾斜角．【解答】解：（1）因为直线l的参数方程为（t为参数），当α＝时，直线l的直角坐标方程为x＝2．…………………………………………………………（1分）当时，直线l的直角坐标方程为y﹣＝tanα（x﹣2）．……………………………………（3分）因为ρ2＝x2+y2，ρcosθ＝x，…………………………………………………………………………（4分）因为ρ2＝2ρcosθ+8，所以x2+y2＝2x+8．所以C的直角坐标方程为x2+y2﹣2x﹣8＝0．………………………………………………………（5分）（2）曲线C的直角坐标方程为x2+y2﹣2x﹣8＝0，将直线l的参数方程代入曲线C的方程整理，得t2+（2+2cosα）t﹣5＝0．……………（6分）因为△＝（2+2cosα）2+20＞0，可设该方程的两个根为t1，t2，则，t1+t2＝﹣（2+2cosα），t1t2＝﹣5．……………………………………………………（7分）所以|AB|＝|t1﹣t2|＝＝＝4．…………………………………………………………（8分）整理得（+cosα）2＝3，故2sin（α+）＝．…………………………………………………………………………………（9分）因为0＜α＜π，所以＝或，α+＝解得或或π＝综上所述，直线l的倾斜角为或．…………………………………………………………………（10分）【点评】本题考查了简单曲线的极坐标方程，属中档题．[选修4-5：不等式选讲]23．己知函数f（x）＝|2x﹣l|﹣a．（1）当a＝l时，解不等式f（x）＞x+1；（2）若存在实数x，使得f（x）＜f（x+1）成立，求实数a的取值范围．【解答】解（1）当a＝1时，由f（x）＞x，得|2x﹣1|﹣1＞x+1．…………………………………………（1分）当x≥时，2x﹣1﹣1＞x+1，解得x＞3．当x时，1﹣2x﹣1＞x+1，解得x＜﹣．…………………………………………………………（4分）综上可知，不等式f（x）＞x+1的解集为{x|x＞3或x＜﹣}．……………………………………（5分）（2）因为||2x﹣1|﹣|2x+1||≤|（2x﹣1）﹣（2x+1）|，………………………………………………（6分）即﹣2≤|2x﹣1|﹣|2x+1|≤2，则|2x﹣1|﹣|2x+1|≥﹣2．……………………………………………（7分）所以g（x）＝|2x﹣1|﹣|2x+1|+|2x﹣1|≥﹣2+|2x﹣1|≥﹣2，…………………………………………（8分）当且仅当x＝时等号成立．……………………………………………………………………………（9分）所以g（x）min＝﹣2．所以实数a的取值范围为（﹣2，+∞）．…………………………………………………………………（10分）【点评】本题考查了绝对值不等式的解法，属中档题．。

图1俯视图侧视图正视图试卷类型：A2019年广州市普通高中毕业班综合测试（二）数学（文科）2018．4本试卷共4页，21小题， 满分150分.考试用时120分钟.注意事项：1．答卷前，考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型（A ）填涂在答题卡相应位置上.2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上.3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效.4．作答选做题时，请先用2B 铅笔填涂选做题的题号对应的信息点，再作答.漏涂、错涂、多涂的，答案无效.5．考生必须保持答题卡的整洁.考试结束后，将试卷和答题卡一并交回. 参考公式： 锥体的体积公式是13V Sh =,其中S 是锥体的底面积,h 是锥体的高. 一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若复数z 满足 i 2z =，其中i 为虚数单位，则z 等于A ．2-iB ．2iC ．2-D ．2 2．已知集合{}}{20,1,2,3,0A B x x x ==-=，则集合AB 的子集个数为A ．2B ．4C ．6D ．8 3．命题“对任意x ∈R ，都有32x x >”的否定是A ．存在0x ∈R ，使得3200x x >B ．不存在0x ∈R ，使得3200x x >C ．存在0x ∈R ，使得3200x x ≤D ．对任意x ∈R ，都有32x x ≤4. 下列函数中，既是偶函数又在()0,+∞上单调递增的是 A．y =．21y x =-+ C ．cos y x = D ．1y x =+5．有两张卡片，一张的正反面分别写着数字0与1，另一张的正反面分别写着数字2与3， 将两张卡片排在一起组成两位数，则所组成的两位数为奇数的概率是 A ．16 B ．13 C ．12 D ．386．一个几何体的三视图如图1，则该几何体的体积为A ．12πB ．6πC ．4πD ．2π7．设n S 是等差数列{}n a 的前n 项和，公差0d ≠， 若113132,24k S a a =+=，则正整数k 的值为 A ．9 B ．10 C ．11 D ．128．在△ABC 中，60ABC ︒∠=，1AB =，3BC =， 则sin BAC ∠的值为A．14B．14 C．14 D．149．设12,F F 分别是椭圆()2222:10x y C a b a b+=>>的左、右焦点，点P 在椭圆C 上，线段1PF的中点在y 轴上，若1230PF F ︒∠=，则椭圆C 的离心率为A．3 B．6 C ．13 D ． 1610．将正偶数2,4,6,8,按表1的方式进行排列，记ij a 表示第i 行第j 列的数，若2014ij a =，则i j +的值为A ．257B ．256C ．254D ．253表1二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分． （一）必做题（11～13题）11．不等式()()120x x +-<的解集为 .12. 已知四边形ABCD 是边长为3的正方形，若2,2DE EC CF FB ==，则AE AF ⋅的值 为 .13．设,x y 满足约束条件 220,840,0,0.x y x y x y -+≥⎧⎪--≤⎨⎪≥≥⎩若目标函数()0,0z ax by a b =+>>的最大值为8，则ab 的最大值为 .（二）选做题（14～15题，考生从中选做一题）14．（坐标系与参数方程选做题）在平面直角坐标系xOy 中，直线,(x a t t y t=-⎧⎨=⎩为参数)与圆1cos ,(sin x y θθθ=+⎧⎨=⎩为参数)相切，切点在第一象限，则实数a 的值为 .15．（几何证明选讲选做题）在平行四边形ABCD 中，点E 在线段AB 上，且12AE EB =，连接,DE AC ，AC 与DE 相交于点F ，若△AEF 的面积为1 cm 2，则△AFD 的面积为 cm 2.三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本小题满分12分） 已知函数()4f x x π⎛⎫=+ ⎪⎝⎭，x ∈R .(1) 求函数()f x 的最小正周期和值域； （2）若0,2πθ⎛⎫∈ ⎪⎝⎭，且()12f θ=，求sin 2θ的值. 17．（本小题满分12分）某校高三年级一次数学考试之后,为了解学生的数学学习情况, 随机抽取n 名学生的数 学成绩, 制成表2所示的频率分布表. (1) 求a ，b ，n 的值;(2) 若从第三, 四, 五组中用分层抽样方法抽取6名学生，并在这6名学生中随机抽取2 名与张老师面谈，求第三组中至少有1名学生与张老师面谈的概率.H FED C BA表2 18．（本小题满分14分）如图2，在五面体ABCDEF 中，四边形ABCD 是边长为2的正方形，EF ∥平面ABCD ， 1EF =，,90FB FC BFC ︒=∠=，AE =H 是BC 的中点. （1）求证：FH ∥平面BDE ； （2）求证：AB ⊥平面BCF ； （3）求五面体ABCDEF 的体积.图2 19．（本小题满分14分）已知等差数列{}n a 的前n 项和为n S 2(,n pn q p q =++∈R )，且235,,a a a 成等比数列. （1）求,p q 的值；（2）若数列{}n b 满足22log log n n a n b +=，求数列{}n b 的前n 项和n T . 20．（本小题满分14分）已知函数()2ln f x x x ax =++，a ∈R .（1）若函数()f x 在其定义域上为增函数，求a 的取值范围； （2）当1a =时，函数()()1f xg x x x =-+在区间[),t +∞(t ∈N *)上存在极值，求t 的最大 值.( 参考数值: 自然对数的底数e ≈2.71828) 21．（本小题满分14分）已知点()2,1A 在抛物线2:E x ay =上，直线1:1(l y kx k =+∈R ，且0)k ≠与抛物线E相交于,B C 两点，直线,AB AC 分别交直线2:1l y =-于点,S T . （1）求a 的值；（2）若ST =1l 的方程；（3）试判断以线段ST 为直径的圆是否恒过两个定点？若是，求这两个定点的坐标；若 不是，说明理由.2019年广州市普通高中毕业班综合测试（二）数学（文科）试题参考答案及评分标准说明：1．参考答案与评分标准指出了每道题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与参考答案不同，可根据试题主要考查的知识点和能力对照评分标准给以相应的分数．2．对解答题中的计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的得分，但所给分数不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．4．只给整数分数，选择题和填空题不给中间分．一、选择题：本大题共10小题，每小题5分，满分50分．二、填空题：本大题共5小题，每小题5分，满分20分．其中14~15题是选做题，考生只能选做一题．11．()1,2- 12．9 13．4 141+ 15．3三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本小题满分12分）（1）解：∵()4f x x π⎛⎫=+ ⎪⎝⎭，∴ 函数()f x 的最小正周期为2π. ……………2分∵x ∈R ，[]cos 1,14x π⎛⎫+∈- ⎪⎝⎭， ……………3分4x π⎛⎫⎡+∈ ⎪⎣⎝⎭. ……………4分∴ 函数()f x 的值域为⎡⎣. ……………5分 （2）解法1：∵()12f θ=，142πθ⎛⎫+= ⎪⎝⎭. ……………6分∴cos 44πθ⎛⎫+= ⎪⎝⎭. ……………7分 ∴ sin 2cos 22πθθ⎛⎫=-+ ⎪⎝⎭……………9分212cos 4πθ⎛⎫=-+ ⎪⎝⎭ ……………11分2124⎛=-⨯ ⎝⎭34=. ……………12分解法2：∵()12f θ=，142πθ⎛⎫+= ⎪⎝⎭. ……………6分1cos cos sin sin 442ππθθ⎫-=⎪⎭. ……………7分∴1cos sin 2θθ-=. ……………8分两边平方得221cos 2cos sin sin 4θθθθ-+=. ……………10分∴ 3sin 24θ=. ……………12分17．（本小题满分12分）M OH F E D CB A (1) 解：依题意，得5200.05,0.35,a b n n n===， 解得，100n =，35a =，0.2b =. ……………3分(2) 解：因为第三、四、五组共有60名学生，用分层抽样方法抽取6名学生，则第三、四、五组分别抽取306360⨯=名，206260⨯=名，106160⨯=名. …………6分 第三组的3名学生记为123,,a a a ，第四组的2名学生记为12,b b ，第五组的1名学生记为1c ，则从6名学生中随机抽取2名，共有15种不同取法，具体如下：{}12,a a ，{}13,a a ，{}11,a b ，{}12,a b ，{}11,a c ，{}23,a a ，{}21,a b ，{}22,a b ，{}21,a c ，{}31,a b ，{}32,a b ，{}31,a c ，{}12,b b ，{}11,b c ，{}21,b c . ……………8分其中第三组的3名学生123,,a a a 没有一名学生被抽取的情况共有3种，具体如下：{}12,b b ，{}11,b c ，{}21,b c . ……………10分故第三组中至少有1名学生与张老师面谈的概率为310.815-=. ……………12分 18．（本小题满分14分）（1）证明：连接AC ，AC 与BD 相交于点O ，则点O 是AC 的中点，连接,OH EO ， ∵H 是BC 的中点，∴OH ∥AB ，112OH AB ==. ……………1分 ∵EF ∥平面ABCD ，EF ⊂平面ABFE ，平面ABCD 平面ABFE AB =， ∴EF ∥AB . ……………2分 ∵1EF =，∴OH ∥EF ，OH EF =.∴四边形EOHF 是平行四边形. ∴EO ∥FH ，EO =FH . ……………3分∵EO ⊂平面BDE ，FH ⊄平面BDE ， ∴FH ∥平面BDE . ……………4分（2）证法1：取AB 的中点M ，连接EM ，则1AM MB ==，由（1）知，EF ∥MB ，且EF =MB ， ∴四边形EMBF 是平行四边形.∴EM ∥FB ，EM FB =. ……………5分在Rt△BFC 中，2224FB FC BC +==，又FB FC =，得FB =∴EM =……………6分 在△AME中，AE =1AM =，EM =∴2223AM EM AE +==.∴AM EM ⊥. ……………7分 ∴AM FB ⊥，即AB FB ⊥. ∵四边形ABCD 是正方形，∴AB BC ⊥. ……………8分 ∵FB BC B =，FB ⊂平面BCF ，BC ⊂平面BCF ，∴AB ⊥平面BCF . ……………9分 证法2：在Rt △BFC 中，H 为BC 的中点，∴112FH BC ==.在△AEO中，112AE AO AC EO FH =====,∴222AO EO AE +=.∴AO EO ⊥. ……………5分 ∵FH ∥EO ,∴AO FH ⊥. ……………6分OHFE D C B A ∵,FH BC BC ⊥⊂平面ABCD , AO ⊂平面ABCD , AO BC C =,∴FH ⊥平面ABCD .∵AB ⊂平面ABCD ,∴FH ⊥AB . ……………7分 ∵四边形ABCD 是正方形，∴AB BC ⊥. ……………8分∵BC ⊂平面BCF , FH ⊂平面BCF , BC FH H =,∴AB ⊥平面BCF . ……………9分（3）解：连接EC ，在Rt△BFC 中，112FH BC ==， ∴1EO FH ==.由（2）知AB ⊥平面BCF ，且EF ∥AB ，∴EF ⊥平面BCF . ……………10分 ∵FH ⊥平面ABCD , EO ∥FH，∴EO ⊥平面ABCD . ……………11分 ∴四棱锥E ABCD -的体积为113ABCD V EO S =⋅⋅正方形2141233=⨯⨯=. ………12分 ∴三棱锥E BCF -的体积为213BCF V EF S =⋅⋅∆21111323=⨯⨯⨯=. ………13分∴五面体ABCDEF 的体积为1253V V V =+=. ……………14分19．（本小题满分14分）（1）解法1：当1n =时，111a S p q ==++， ……………1分 当2n ≥时，1n n n a S S -=- ……………2分 ()()221121n pn q n p n q n p ⎡⎤=++--+-+=-+⎣⎦. ………3分∵{}n a 是等差数列，∴1211p q p ++=⨯-+，得0q =. ……………4分 又2353,5,9a p a p a p =+=+=+， ……………5分 ∵235,,a a a 成等比数列，∴2325a a a =，即()()()2539p p p +=++， ……………6分解得1p =-. ……………7分 解法2：设等差数列{}n a 的公差为d ，则()2111222n n n d d S na d n a n -⎛⎫=+=+- ⎪⎝⎭. ……………1分 ∵2n S n pn q =++，∴12d =，12da p -=，0q =. ……………4分∴2d =，11p a =-，0q =. ∵235,,a a a 成等比数列，∴2325a a a =， ……………5分即()()()2111428a a a +=++.解得10a =. ……………6分 ∴1p =-. ……………7分 （2）解法1：由（1）得22n a n =-. ……………8分 ∵22log log n n a n b +=， ∴221224na n n nb n n n --=⋅=⋅=⋅. ……………9分∴1231n n n T b b b b b -=+++++()0122142434144n n n n --=+⨯+⨯++-⋅+⋅，①……………10分()1231442434144n n n T n n -=+⨯+⨯++-⋅+⋅，② ……………11分①-②得0121344444n nn T n --=++++-⋅14414n nn -=-⋅-()13413n n -⋅-=.……………13分∴()131419nn T n ⎡⎤=-⋅+⎣⎦. ……………14分 解法2：由（1）得22n a n =-. ……………8分∵22log log n n a n b +=， ∴221224na n n nb n n n --=⋅=⋅=⋅. ……………9分∴1231n n n T b b b b b -=+++++()0122142434144n n n n --=+⨯+⨯++-⋅+⋅.……………10分由()12311n nx x x x x x x x+-++++=≠-， ……………11分两边对x 取导数得，012123n x x x nx -++++=()()12111n n nx n x x +-++-. …………12分 令4x =，得()()0122114243414431419n n nn n n --⎡⎤+⨯+⨯++-⋅+⋅=-⋅+⎣⎦. ∴()131419nn T n ⎡⎤=-⋅+⎣⎦. ……………14分 20．（本小题满分14分）（1）解法1：函数()f x 的定义域为()0,+∞, ……………1分∵()2ln f x x x ax =++， ∴()12f x x a x'=++. ……………2分 ∵ 函数()f x 在()0,+∞上单调递增， ∴ ()0f x '≥, 即120x a x++≥对()0,x ∈+∞都成立. ……………3分 ∴ 12a x x -≤+对()0,x ∈+∞都成立. ……………4分 当0x >时, 12xx +≥=当且仅当12x x=,即2x =时,取等号.……………5分∴a -≤即a ≥-.∴a 的取值范围为)⎡-+∞⎣. ……………6分解法2：函数()f x 的定义域为()0,+∞, ……………1分∵()2ln f x x x ax =++， ∴()21212x ax f x x a x x++'=++=.……………2分方程2210x ax ++=的判别式28a ∆=-.……………3分① 当0∆≤, 即a -≤≤, 2210x ax ++≥,此时, ()0f x '≥对(0,x ∈+∞都成立,故函数()f x 在定义域()0,+∞上是增函数. ……………4分 ②当0∆>, 即a <-或a >时, 要使函数()f x 在定义域()0,+∞上为增函数, 只需2210x ax ++≥对()0,x ∈+∞都成立.设()221h x x ax =++, 则()010,0,4h a ⎧=>⎪⎨-<⎪⎩得0a >.故a >. ……………5分综合①②得a的取值范围为)⎡-+∞⎣. ……………6分（2）解：当1a =时, ()()2ln ln 111f x x x x xg x x x x x x ++=-=-=+++. ()()211ln 1x x g x x +-'=+. ……………7分 ∵ 函数()g x 在[),t +∞(t ∈N *)上存在极值，∴ 方程()0g x '=在[),t +∞(t ∈N *)上有解,即方程11ln 0x x +-=在[),t +∞(t ∈N *)上有解. ……………8分 令()11ln x x x ϕ=+-()0x >, 由于0x >, 则()2110x x xϕ'=--<,∴函数()x ϕ在()0,+∞上单调递减. ……………9分∵()413ln 3ln33ϕ=-=4e 2741 2.5ln 0327>>, ……………10分 ()514ln 4ln44ϕ=-=5e 256513ln 04256<<, ……………11分 ∴函数()x ϕ的零点()03,4x ∈. ……………12分∵方程()0x ϕ=在[),t +∞(t ∈ N *)上有解, t ∈N *∴3t ≤. ……………13分∵t ∈N *，∴t 的最大值为3. ……………14分 21．（本小题满分14分） （1）解：∵点()2,1A 在抛物线2:E x ay =上， ∴4a =. ……………1分第（2）、（3）问提供以下两种解法：解法1：（2）由（1）得抛物线E 的方程为24x y =.设点,B C 的坐标分别为()()1122,,,x y x y ，依题意，2211224,4x y x y ==，由21,4,y kx x y =+⎧⎨=⎩消去y 得2440x kx --=，解得1,2422k x k ±==±. ∴12124,4x x k x x +==-. ……………2分直线AB 的斜率2111111124224AB x y x k x x --+===--， 故直线AB 的方程为()12124x y x +-=-. ……………3分令1y =-，得1822x x =-+，∴点S 的坐标为182,12x ⎛⎫-- ⎪+⎝⎭. ……………4分同理可得点T 的坐标为282,12x ⎛⎫-- ⎪+⎝⎭. ……………5分 ∴()()()121212888222222x x ST x x x x -⎛⎫=---= ⎪++++⎝⎭ ()()()121212121288248x x x x x xx x x x k k---===+++. ……………6分∵ST =，∴12x x -=.由()221212124x x x x x x -=+-，得22201616k k =+，解得2k =, 或2k =-, …………… 7分 ∴直线1l 的方程为21y x =+，或21y x =-+. ……………9分（3）设线段ST 的中点坐标为()0,1x -， 则()()()12012124418822222222x x x x x x x ++⎛⎫=-+-=- ⎪++++⎝⎭ ()()()1212444444222248k k x x x x k k++=-=-=-+++. ……………10分而2ST=()()()2221212122221614k x x x x x x kkk+-+-==， ……………11分∴以线段ST 为直径的圆的方程为()2222114x y ST k ⎛⎫+++= ⎪⎝⎭()2241k k +=. 展开得()()22222414414k x x y k k k++++=-=. ……………12分 令0x =，得()214y +=，解得1y =或3y =-. ……………13分∴以线段ST 为直径的圆恒过两个定点()()0,1,0,3-. ……………14分 解法2：（2）由（1）得抛物线E 的方程为24x y =.设直线AB 的方程为()112y k x -=-，点B 的坐标为()11,x y ，由()112,1,y k x y ⎧-=-⎨=-⎩解得122,1.x k y ⎧=-⎪⎨⎪=-⎩∴点S 的坐标为122,1k ⎛⎫-- ⎪⎝⎭. ……………2分由()1212,4,y k x x y ⎧-=-⎨=⎩消去y ，得2114840x k x k -+-=， 即()()12420x x k --+=，解得2x =或142x k =-.∴1142x k =-，22111114414y x k k ==-+. ∴点B 的坐标为()211142,441k k k --+. ……………3分同理，设直线AC 的方程为()212y k x -=-， 则点T 的坐标为222,1k ⎛⎫-- ⎪⎝⎭，点C 的坐标为()222242,441k k k --+. …………4分 ∵点,B C 在直线1:1l y kx =+上，∴()()()()()()22222211212121214414414242k k k k k k k k k k k k k -+--+---==----121k k =+-.∴121k k k +=+. ……………5分 又()211144142k k k k -+=-1+，得()21111214442412k k kk k k k k k -=-=+--， 化简得122kk k =. ……………6分 ()12121222222k k ST k k k k -⎛⎫⎛⎫=---=⎪ ⎪⎝⎭⎝⎭， ……………7分∵ST = ∴()12122k k k k -=.∴()()2212125k k k k -=.由()()()2221212121212454k k k k k k k k k k +=-+=+， 得()225124k k k +=+， 解得2k =±. ……………8分 ∴直线1l 的方程为21y x =+，或21y x =-+. …………… 9分 （3）设点(),P x y 是以线段ST 为直径的圆上任意一点，则0SP TP ⋅=， ……………10分得()()122222110x x y y k k ⎛⎫⎛⎫-+-++++= ⎪⎪⎝⎭⎝⎭， ……………11分 整理得，()224410x x y k+-++=. ……………12分令0x =，得()214y +=，解得1y =或3y =-. ……………13分∴ 以线段ST 为直径的圆恒过两个定点()()0,1,0,3-. ……………14分。

2019年广州市普通高中毕业班综合测试（二）文科综合第I卷本卷共35个小题，每小题4分，共140分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

蓝洞是地球罕见的自然地理现象，它是地质历史时期在碳酸盐岩地层中发育形成的四壁陡直、敞口朝天的有水洞穴，有的在海洋中，有的在陆地上。

海洋蓝洞（如下图所示）表现出与周边水域不同的深蓝色，仿佛是大海的瞳孔，呈现出深邃、神秘、诡异的自然景观。

据此完成1~3题。

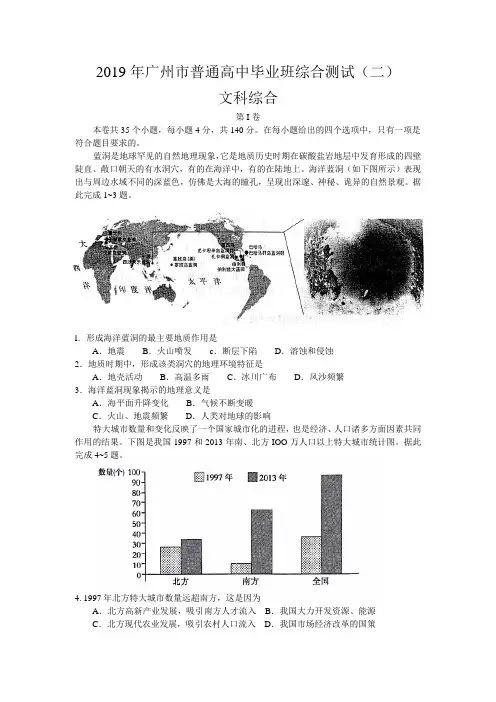
l．形成海洋蓝洞的最主要地质作用是A．地震B．火山喷发c．断层下陷D．溶蚀和侵蚀2．地质时期中，形成该类洞穴的地理环境特征是A．地壳活动B．高温多雨C．冰川广布D．风沙频繁3．海洋蓝洞现象揭示的地理意义是A．海平面升降变化B．气候不断变暖C．火山、地震频繁D．人类对地球的影响特大城市数量和变化反映了一个国家城市化的进程，也是经济、人口诸多方面因素共同作用的结果。

下图是我国1997和2013年南、北方IOO万人口以上特大城市统计图。

据此完成4~5题。

4. 1997年北方特大城市数量远超南方，这是因为A．北方高新产业发展，吸引南方人才流入B．我国大力开发资源、能源C．北方现代农业发展，吸引农村人口流入D．我国市场经济改革的国策5．2013年南、北方特大城市发展差异显著，最主要的原因是A．产业结构差异B．资源和环境状况差异C．自然条件差异D．人口自然增长率差异电动汽车的核心部件是超级锂电池。

世界最大的电动汽车生产商——美国特斯拉，计划兴建世界最大的超级电池工厂。

为此，各国政府都开出极具诱惑力的优惠条件吸引特斯拉，最后特斯拉决定在美国内华达州兴建超级电池厂（如下图所示）。

它制造电池所需的钴、石墨等原料来自世界各地，生产技术来自日本。

从原料到成品整个电池生产、电池回收过程将在一个工厂内完成，厂房顶全部铺设太阳能电池板。

据此完成6~9题。

6．影响特斯拉超级电池厂落户美国的最主要原因是A．接近汽车产地B．共享基础设施C．科学技术先进D．政策税收优惠7．特斯拉在内华达州选址建厂，其考虑的最主要区位因素是A．环境B．交通C．能源D．劳力素质9．特斯拉选择整个电池产业链在一个工厂内完成，而不是全球采购或者全球最优布局各电池部件生产，其最主要原因是A．节省原料和能源，绿色环保B．节省交通运输成本的需要C．规模化生产，提升经济效益D．电池专业生产技术的需要鄱阳湖（如下图所示）是我国最大的淡水湖。

2019年广州市普通高中毕业班综合测试（二）文科数学2019.4本试卷共6页，23小题，满分150分。

考试用时120分钟。

注意事项：1．答卷前，考生务必将自己的姓名和考生号、试室号、座位号填写在答题卡上，用2B 铅笔在答题卡的相应位置填涂考生号，并将试卷类型(B)填涂在答题卡相应位置上。

2．作答选择题时，选出每小题答案后，用2B铅笔在答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保证答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合A={x∈N|0<x<6} , B={2, 4, 6, 8} ,则A∩B=A.{0,1,3,5}B.{0,2,4,6}C. {1,3,5}D.{2,4,6}2．已知复数z=m(3+i)-(2+i)在复平面内对应的点在第三象限，则实数m的取值范围是A． B. C． D.3．某公司生产A，B，C三种不同型号的轿车，产量之比依次为2：3：4，为检验该公司的产品质量，用分层抽样的方法抽取一个容量为n的样本，若样本中A种型号的轿车比B种型号的轿车少8辆，则n=A. 96B. 72C. 48D. 364．执行如图所示的程序框图，则输出z的值是A. 21B. 22C. 23D. 245．从某班5名学生（其中男生3人，女生2人）中任选3人参加学校组织的社会实践活动，则所选3人中至少有1名女生的概率为A. B. C. D.6．函数y=的部分图像如图所示，则函数的解析式为A． B.C. D．7．设等比数列{a n}的前n项和为S n，则下列等式中一定成立的是A. S n+S2n=S3nB. S22n=S n S3nC. S22n=S n+S2n- S3nD. S2n + S22n=S n (S2n+S3n)8．已知双曲线拘渐近线方程为5x±3y=0，则此双曲线的离心率为A. B. C. D.9．一个圆锥的体积为，当这个圆锥的侧面积最小时，其母线与底面所成角的正切值为A． B． C． D．10.设a≥b≥c，且1是一元二次方程ax2+ bx+c=0的一个实根，则的取值范围为A．[-2，0] B．C．D．11．在三棱锥P-ABC中，PA=PB=PC=2，AB=AC=I，BC=，则该三棱锥的外接球的表面积为A． B． C． D．12.己知函数与的图像上存在关于x轴对称的点，则实数a的取值范围为A．B．C．D．二、填空题：本题共4小题，每小题5分，共20分．13.已知向量，向量，则=14. 《莱茵德纸草书》是世界上最古老的数学著作之一．书中有一道这样的题目：把100个面包分给5个人，使每人所得份量成等差数列，且较大的三份之和的是较小的两份之和，则最小一份的量为．15.若函数f(x)=x2 -x+l+ alnx在(0，+∞)上单调递增，则实数a的取值范围是．16.己知点P在直线x+2y-l=0上，点Q在直线x+2y+3=O E，PQ的中点为M(x0，y0)，且-1≤y0-x0≤7，则的取值范围是____．三、解答题：共70分，解答应写出文字说明、证明过程和演算步骤，第17～21题为必考题，每个试题考生都必须做答．第22、23题为选考题，考生根据要求做答．（一）必考题：共60分．17. （本小题满分12分）△ABC中角A，B，C的对边分别为a，b，c，已知(1)求的值；(2)若c=2，求△ABC的面积．18. （本小题满分12分）如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，∠BAD=60°，∠APD=90°，且PA=PD，AD=PB．(1)求证：AD⊥PB；(2)求点A到平面PBC的距离．19. （本小题满分12分）科研人员在对人体脂肪含量和年龄之间关系的研究中，获得了一些年龄和脂肪含量的简单随机样本数据，如下表：根据上表的数据得到如下的散点图．(1)根据上表中的样本数据及其散点图：(i)求;(ii)计算样本相关系数（精确到0.01），并刻画它们的相关程度．(2)若y关于x的线性回归方程为，求的值（精确到0.01），并根据回归方程估计年龄为50岁时人体的脂肪含量．附：参考数据：参考公式：相关系数回归方程中斜率和截距的最小二乘估计公式分别为20. （本小题满分12分）从抛物线y 2 =36x 上任意一点P 向x 轴作垂线段，垂足为Q ，点M 是线段PQ 上的一点，且满足(1)求点M 的轨迹C 的方程；(2)设直线x=my+1(m∈R)与轨迹c 交于A ，B 两点，T 为C 上异于A ，B 的任意一点，直线AT ，BT 分别与直线x=-1交于D ，E 两点，以DE 为直径的圆是否过x 轴上的定点？若过定点，求出符合条件的定点坐标；若不过定点，请说明理由．21. （本小题满分12分）已知函数f(x)=(x+2)lnx+ax 2 - 4x+ 7a ．(1)若a=，求函数f(x)的所有零点；(2)若a≥，证明函数f(x)不存在极值．（二）选考题：共10分．请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分．22．[选修4 -4：坐标系与参数方程]（本小题满分10分）在直角坐标系xOy 中，倾斜角为α的直线l 的参数方程为（t 为参数）．在以坐标原点为⎩⎨⎧+=+=ααsin 3,cos 2t y t x 极点，x 轴正半轴为极轴的极坐标系中，曲线C 的极坐标方程为ρ2= 2p cosθ+8．(1)求直线l 的普通方程与曲线C 的直角坐标方程；(2)若直线l 与曲线C 交于A ，B 两点，且求直线l 的倾斜角．23.[选修4-5：不等式选讲]（本小题满分10分）己知函数f(x) =|2x-l|-a．(1)当a=l时，解不等式f(x)>x+1；(2)若存在实数x，使得f(x)< f(x+1)成立，求实数a的取值范围.绝密 ★ 启用前2019年广州市普通高中毕业班综合测试（二）文科数学试题答案及评分参考评分说明:1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分参考制订相应的评分细则．2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．4．只给整数分数．选择题不给中间分．一、选择题题号123456789101112答案D B B A A B D B D C B C二、填空题13 14． 15． 16．531,8⎡⎫+∞⎪⎢⎣⎭2,05⎡⎤-⎢⎥⎣⎦三、解答题17．解：（1）因为，tan tan 2(tan tan )cos cos A B A B B A+=+所以．………………………………………………1分sin sin sin sinB 2cos cos cos cos cos cos A B A A B A B A B⎛⎫+=+ ⎪⎝⎭化简得．………………………………………………2分()2sin cos cos sin sin sin A B A B A B +=+即．………………………………………………………………………3分()2sin sin sin A B A B +=+因在中，，则．……………………………4分ABC ∆A B C ++=π()()sin sin sin A B C C π+=-=从而．…………………………………………………………………………… 5分sin sin 2sin A B C +=由正弦定理，得．2a b c +=所以．……………………………………………………………………………………………6分=2a b c+（2）由（1）知，且，所以．……………………………………………………7分2a b c +=2c =4a b +=因为，所以．……………………………………9分=3C π()222222cos 22a b ab c a b c C ab ab+--+-==即．122cos 32ab abπ-=所以．……………………………………………………………………………………………10分4ab =所以．11sin 4sin 223ABC S ab C ∆π==⨯⨯=所以△．……………………………………………………………………………12分ABC 18．（1）证明：取的中点，连结，，，AD O OP OB BD 因为底面为菱形，，ABCD 60BAD ∠= DB A P O所以．…………………………………1分AD AB BD ==因为为的中点，所以． ……………2分O AD BO AD ⊥在△中，，为的中点，PAD PA PD =O AD 所以． ………………………………………3分PO AD ⊥因为，所以平面．………4分BO PO O = AD ⊥POB 因为平面，所以．………………………………………………………………5分PB ⊂POB AD PB ⊥（2）解法1：在△ 中，，所以．Rt PAD 2AD =1PO =因为底面是边长为2的菱形，，所以．……………………………6分ABCD 60BAD ∠= BO =在△中，，，，PBO 1PO =BO =2PB BC ==因为，所以．……………………………………………………………7分222PO BO PB +=PO BO ⊥【6-7分段另证：在△中，，为的中点，所以．APD 90APD ∠= O AD 12PO AD AO ==在△ 和△ 中，因为， ，，所以△ △ BOP BOA PO AO =PB AD AB ==BO BO =BOP ≅．BOA 所以．所以．】90BOP BOA ∠=∠= OP OB ⊥由（1）有，且，平面，平面，PO AD ⊥AD BO O = AD ⊂ABCD BO ⊂ABCD 所以平面．…………………………………………………………………………………8分PO ⊥ABCD 在△中，由（1）证得，且，所以．PBC AD PB ⊥//BC AD BC PB ⊥因为，所以．…………………………………………………………………9分2PB BC ==2PBC S ∆=在△中，，，ABC 2AB BC ==120ABC ∠=所以． (10)分1sin 2ABC S AB BC ABC =⨯⨯⨯∠=设点到平面的距离为，A PBC h 因为，即．……………………………………………………11分A PBCP ABC V V --=1133PBC ABC Sh S PO ∆=所以ABC PBC S PO h S ∆===所以点到平面．…………………………………………………………………12分A PBC 解法2：因为，平面，平面，//AD BC BC ⊂PBC AD ⊄PBC 所以平面．//AD PBC 所以点到平面的距离等于点到平面的距离．………………………………………6分A PBC O PBC 过点作于点．…………………………7分O OH PB ⊥H 由（1）证得平面，且，AD ⊥POB //AD BC 所以平面．BC ⊥POB 因为平面，所以．OH ⊂POB BC ⊥OH 因为，平面，平面，PB BC B = PB ⊂PBC BC ⊂PBC 所以平面．…………………………………8分OH ⊥PBC 在△ 中，，所以．Rt PAD 2AD =1PO =H O PABD因为底面是边长为2的菱形，，所以．……………………………9分ABCD 60BAD ∠=BO =在△中，，，，PBO 1PO=BO =2PB BC ==因为，所以．…………………………………………………………10分222PO BO PB +=PO BO ⊥【9-10分段另证：在△中，，为的中点，所以．APD 90APD ∠=O AD 12PO AD AO ==在△和△ 中，因为，，，所以△ △BOP BOA PO AO =PB AD AB ==BO BO =BOP ≅．BOA 所以．所以．】90BOP BOA ∠=∠=OP OB ⊥在△中，根据等面积关系得．…………………………………………11分PBO PB OH PO OB ⨯=⨯所以．PO OB OH PB ⨯===所以点到平面．…………………………………………………………………12分A PBC 19．解：（1）根据上表中的样本数据及其散点图：（ⅰ）．…………………………………2分262739414953565860614710x +++++++++==（ⅱ）…………3分rnnx y==…………………………………4分==…………………………………………………………………………5分=，6.56≈54.18≈所以．……………………………………………………………………………………………6分0.98r ≈由样本相关系数，可以推断人体脂肪含量和年龄的相关程度很强．………………………7分0.98r ≈（2）因为回归方程为，即．ˆˆ 1.56ybx =+ˆ 1.56a =所以．ˆ27 1.56ˆ0.5447y abx--==≈【或利用】……………………………10分()()()121ˆn iii nii x x y y bx x ==--=-∑∑()1221ni ii nii x y nx yxn x==-=-∑∑837.80.541548=≈所以关于的线性回归方程为．y x ˆ0.54 1.56yx =+将代入线性回归方程得．……………………………………11分50x =ˆ0.5450 1.5628.56y=⨯+=所以根据回归方程估计年龄为岁时人体的脂肪含量为%．………………………………12分5028.56 【结论没写%扣1分】28.5620．解：（1）设，，则点的坐标为．(),M x y ()00,P x y Q ()0,0x 因为，2PM MQ =所以，………………………………………………………………………1分()()000,2,x x y y x x y --=--即 ………………………………………………………………………………………………2分00,3.x x y y =⎧⎨=⎩因为点在抛物线上，P 236y x =所以，即．………………………………………………………………………3分20036y x =()2336y x =所以点的轨迹的方程为．…………………………………………………………………4分M C 24y x =（2）解法1：设直线与曲线的交点坐标为，，1x my =+C A 211,4y y ⎛⎫ ⎪⎝⎭222,4y B y ⎛⎫⎪⎝⎭由得．21,4,x my y x =+⎧⎨=⎩2440y my --=由韦达定理得=，=．……………………………………………………………5分+1y 2y 4m 1y 2y 4-设点，则．………………………………………………………6分200,4y T y ⎛⎫ ⎪⎝⎭10220101444AT y y k y y y y -==+-所以直线的方程为．AT 2000144y y y x y y ⎛⎫-=- ⎪+⎝⎭令，得点的坐标为．…………………………………………………………7分1x =-D 010141,y y y y ⎛⎫-- ⎪+⎝⎭同理可得点的坐标为．………………………………………………………………8分E 020241,y y y y ⎛⎫-- ⎪+⎝⎭如果以为直径的圆过轴某一定点，则满足．…………………………9分DE x (),0N n 0ND NE ∙=因为．010********,1,y y y y ND NE n n y y y y ⎛⎫⎛⎫--∙=--∙-- ⎪ ⎪++⎝⎭⎝⎭ ()()()2212001220012124161++y y y y y y n y y y y y y -++=+++所以．………………………………………………………………10分()2200200416161++044y my n y my --+=+-即，解得或．……………………………………………………………11分()2140n +-=1n =3n =-故以为直径的圆过轴上的定点和．………………………………………………12分DE x ()1,0()3,0-解法2：直线与曲线的交点坐标为，，1x =C ()1,2A '()1,2B '-若取，则，与直线的交点坐标为，，()0,0T 'A T ''B T ''1x =-()1,2D '--()1,2E '-所以以为直径的圆的方程为．D E ''()2214x y ++=该圆与轴的交点坐标为和．x ()1,0()3,0-所以符合题意的定点只能是或．…………………………………………………6分()11,0N ()23,0N -设直线与曲线的交点坐标为，，1x my =+C A 211,4y y ⎛⎫ ⎪⎝⎭222,4y B y ⎛⎫⎪⎝⎭由得．21,4,x my y x =+⎧⎨=⎩2440y my --=由韦达定理得=，=．……………………………………………………………7分+1y 2y 4m 1y 2y 4-设点，则．………………………………………………………8分200,4y T y ⎛⎫ ⎪⎝⎭10220101444AT y y k y y y y -==+-所以直线的方程为．AT 2000144y y y x y y ⎛⎫-=- ⎪+⎝⎭令，得点的坐标为．…………………………………………………………9分1x =-D 010141,y y y y ⎛⎫-- ⎪+⎝⎭同理可得点的坐标为．………………………………………………………………10分E 020241,y y y y ⎛⎫-- ⎪+⎝⎭若点满足要求，则满足．()11,0N 110N D N E ∙= 因为0102110102442,2,y y y y N D N E y y y y ⎛⎫⎛⎫--∙=-∙- ⎪ ⎪++⎝⎭⎝⎭．……11分()()212001220012124164+y y y y y y y y y y y y -++=+++20020041616=4+044y my y my --+=+-所以点满足题意．()11,0N 同理可证点也满足题意．()23,0N -故以为直径的圆过轴上的定点和．………………………………………………12分DE x ()1,0()3,0-21．（1）解：当时，，21=a 217()(2)ln 422f x x x x x =++-+函数的定义域为，…………………………………………………………………………1分)(x f ),0(+∞且．……………………………………………………………………………2分()2ln 3f x x x x'=++-设，()2ln 3g x x x x=++-则． ()()222221122()1x x x x g x x x x x+-+-'=-+==()0x >当时，；当时，，01x <<()0g x '<1x >()0g x '>即函数在上单调递减，在上单调递增，…………………………………………3分()g x ()0,1()1,+∞所以当时，（当且仅当时取等号）．…………………………………4分0x >()()10g x g ≥=1=x 即当时，（当且仅当时取等号）．0x >()0f x '≥1=x 所以函数在单调递增，至多有一个零点. ………………………………………………5分()f x ),0(+∞因为，是函数唯一的零点.(1)0f =1=x )(x f所以若，则函数的所有零点只有．…………………………………………………6分21=a ()f x 1=x （2）证法1：因为，2()(2)ln 47f x x x ax x a =++-+函数的定义域为，且．…………………………………7分)(x f ),0(+∞2()ln 24x f x x ax x+'=++-当时，，………………………………………………………………9分12a ≥()2ln 3f x x x x'≥++-由（1）知．………………………………………………………………………10分032ln ≥-++x xx 即当时，0x >()0f x '≥所以在上单调递增．……………………………………………………………………11分()f x ()0,+∞所以不存在极值．…………………………………………………………………………………12分)(x f 证法2：因为，2()(2)ln 47f x x x ax x a =++-+函数的定义域为，且．…………………………………7分)(x f ),0(+∞2()ln 24x f x x ax x+'=++-设，2()ln 24x m x x ax x+=++-则．2221222()2ax x m x a x x x+-'=-+=()0x >设，则与同号．)0( 22)(2>-+=x x ax x h ()m x ')(x h 当时，由，21≥a 2()220h x ax x =+-=解得， ．……………………………………………8分10x =<20x =>可知当时，，即，当时，，即，20x x <<()0h x <()0m x '<2 x x >()0h x >()0m x '>所以在上单调递减，在上单调递增．…………………………………………9分()f x '()20,x ()2,x +∞由（1）知．………………………………………………………………………10分032ln ≥-++x xx 则．2222222()ln 3(21)(21)0f x x x a x a x x '=++-+-≥-≥所以，即在定义域上单调递增．…………………………………………11分2()()0f x f x ''≥≥()f x 所以不存在极值．…………………………………………………………………………………12分)(x f 22．（1）解法1：因为直线的参数方程为（为参数），l ⎩⎨⎧+=+=ααsin 3,cos 2t y t x t 当时，直线的直角坐标方程为．…………………………………………………………1分=2απl 2x =当时，直线的直角坐标方程为．……………………………………3分2απ≠l ()tan 2y x α=-因为，…………………………………………………………………………4分222,cos x y x ρρθ=+=因为，所以．8cos 22+=θρρ2228x y x +=+所以的直角坐标方程为．………………………………………………………5分C 08222=--+x y x 解法2：因为直线的参数方程为（为参数），l ⎩⎨⎧+=+=ααsin 3,cos 2t y t x t 则有 (2)分sin 2sin sin cos ,cos sin cos ,x t y t αααααααα=+⎧⎪⎨=+⎪⎩所以直线的直角坐标方程为 ． (3)分l ()sin cos 2sin 0x y αααα---=因为，…………………………………………………………………………4分222,cos x y x ρρθ=+=因为，所以．8cos 22+=θρρ2228x y x +=+所以的直角坐标方程为．………………………………………………………5分C 08222=--+x y x （2）解法1：曲线的直角坐标方程为，C 08222=--+x y x 将直线的参数方程代入曲线的方程整理，得．……………6分l C 05)cos 2sin 32(2=-++t t αα因为，可设该方程的两个根为，，020)cos 2sin 32(2>++=∆αα1t 2t则，．……………………………………………………7分()122cos t t αα+=-+125t t=-所以12AB t t =-=．…………………………………………………………8分==整理得，)2cos 3αα+=故．…………………………………………………………………………………9分2sin 6απ⎛⎫+= ⎪⎝⎭因为，所以或，0α≤<π63αππ+=263αππ+=解得或6απ=2απ=综上所述，直线的倾斜角为或．…………………………………………………………………10分l 6π2π解法2：直线与圆交于，两点，且，l C A B AB =故圆心到直线的距离．…………………………………………………6分)0,1(C l 1)22(92=-=d ①当时，直线的直角坐标方程为，符合题意．…………………………………………7分2απ=l 2=x ②当时，直线的方程为．0,,22αππ⎡⎫⎛⎫∈π⎪ ⎪⎢⎣⎭⎝⎭l 0tan 23tan =-+-ααy x 所以，………………………………………………………………8分1tan 1|tan 230tan |2=+-+-=αααd．tan α=解得．………………………………………………………………………………………………9分6απ=综上所述，直线的倾斜角为或．…………………………………………………………………10分l 6π2π23．（1）解：当时，由，得．…………………………………………1分1a =()f x x >2111x x -->+当时，， 解得．12x ≥2111x x -->+3x >当时，，解得．…………………………………………………………4分12x <1211x x -->+13x <-综上可知，不等式的解集为 ．……………………………………5分()1f x x >+133x x x ⎧⎫><-⎨⎬⎩⎭或（2）解法1：由，得．1()(1)2f x f x <+1212122a x a x --<+-则．…………………………………………………………………………………6分22121a x x >--+令，()22121g x x x =--+则问题等价于min(())a g x >因为……………………………………………………………………9分123,,211()61,,22123,,2x x g x x x x x ⎧-+<-⎪⎪⎪=-+-≤≤⎨⎪⎪->⎪⎩．min 1()22g x g ⎛⎫==- ⎪⎝⎭所以实数的取值范围为．…………………………………………………………………10分a (2,)-+∞解法2：因为，………………………………………………6分2121(21)(21)x x x x --+≤--+即，则．……………………………………………7分221212x x -≤--+≤21212x x --+≥-所以，…………………………………………8分()2121212212g x x x x x =--++-≥-+-≥-当且仅当时等号成立．……………………………………………………………………………9分12x =所以．min ()2g x =-所以实数的取值范围为．…………………………………………………………………10分a (2,)-+∞。

2019年广州市普通高中毕业班综合测试（二）语文试题阅读下面的文字，完成小题。

“天下”是中国传统文化对世界秩序的一种原初想象，“天下主义”是以“天下”理念为核心，由具有普遍性和开放性的世界秩序、价值规范与理想人格构成的思想体系。

在当今全球化语境之下，中国文化理念和文化战略的自觉自信体现的正是“天下主义”的精神内核。

文化自信首先是一种“以天下观天下”的世界观的自信。

《道德经》有云：“修之于天下，其德乃普。

故以身观身，以家观家，以乡观乡，以国观国，以天下观天下。

”“天下”是中国文化特有的思维尺度，是一个最宏大、最完备的分析单位，具有最广阔的容纳力。

面对差异性的多元文化格局，西方文化多以民族国家为基本单位，文化视域限于国家、民族内部，虽然也有关于世界的思考，比如斯多葛学派的“世界主义”等，但其思考方式是“以国家观世界”，与中国文化的立足点和尺度不同。

中国文化的“天下”蕴含了“天下无外”的理想，各个民族的历史文化在世界内部是平等共存的；中国文化依循“修身、齐家、治国、平天下”的进路，从“身-家-国”逻辑同构的角度，最终达到“天下大同”的境界。

与西方文化相较，“天下”的世界观更具有开放性和包容性。

文化自信的核心是“以天下为一家”的价值观的自信。

中国文化是以儒家文化为代表的伦理型文化，梁漱溟认为“中国伦理始于家庭而不止于家庭”，中国文化重视家庭生活，整个社会关系是依照家庭关系推广发挥的。

“以天下为一家”的价值观实质上是一种关系性伦理，把“自我”和“他者”看成一体共生的关系。

“天下”是一个最大的家，家庭利益的最大化就是个体利益的最大化，共同体的善与个体的善是统一的。

文化自信最终体现为一种人格自信。

无论是“以天下观天下”的世界观，还是“以天下为一家”的价值观，最终都沉淀为个体的精神品格。

中国文化倡导和推崇的理想人格是“君子”，这是由中国人独特的精神气质所决定的。

“君子”是一个自主自足的动态形象，通过“身-家-国-天下”的逐渐扩充延展，人格不断超越并完善。

广东省广州市2019届第二次模拟考试
-历史试题（解析版）
1. 商鞅变法规定，禁止父子兄弟共同住在一间房子里，一家有两个以上成年男子必须分居另立户籍，否则加倍征收赋税。

秦统一后，这一规定推行到全国。

这一规定
A. 瓦解了传统的宗法制度
B. 有利于农业经济的发展
C. 削弱了国家对农民的控制
D. 保障了国家的财政收入
【答案】B
【解析】从材料“禁止父子兄弟共同住在一间房子里”“有两个以上成年男子必须分居另立户籍，否则加倍征收赋税”中可以分析出，这些措施有利于小家庭的推行，也有利于增殖人口、征发徭役和户口税，发展封建经济，故B项正确，D项排除；材料中没有体现出宗法制度的瓦解和对农民的控制，故AC项排除。

点睛：材料“禁止父子兄弟共同住在一间房子里”“有两个以上成年男子必须分居另立户籍，否则加倍征收赋税”表明秦推行小家庭政策；根据所学知识分析出答案。

2. 西汉前期在皇帝陵基旁边设置陵县，专为祭祀陵园之用，该县居民都是强迫迁徙而来的关东豪族和天下富商。

这一举措
A. 解除了豪强势力对中央的威胁
B. 提升了皇帝的独尊地位
C. 使行政区划带有祭祀色彩
D. 有利于巩固国家的统一
【答案】D
【解析】材料“该县居民都是强迫迁徙而来的关东豪族和天下富商”表明，把关东豪族和天下富商集中在皇帝陵基旁边设置的陵县附近，显然便于监视控制，防止叛乱，保证安定，加强中央集权，有利于巩固国家的统一，故D项正确；A项说法错误，错在“解除”；材料强调的是加强中央集权，故B项排除；C项材料中没有体现出。

点睛：材料“该县居民都是强迫迁徙而来的关东豪族和天下富商”的理解是解题的关。