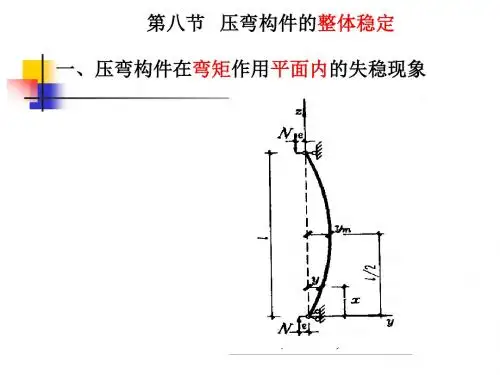
压弯构件的整体稳定

《钢结构》网上辅导材料受弯构件的强度、整体稳定和局部稳定计算钢梁的设计应进行强度、整体稳定、局部稳定和刚度四个方面的计算。

一、强度和刚度计算1．强度计算强度包括抗弯强度、抗剪强度、局部承压强度和折算应力。

（1）抗弯强度荷载不断增加时正应力的发展过程分为三个阶段，以双轴对称工字形截面为例说明如下：图1 梁正应力的分布f，荷载继续增1）弹性工作阶段荷载较小时，截面上各点的弯曲应力均小于屈服点yf（图1b）。

加，直至边缘纤维应力达到y2）弹塑性工作阶段荷载继续增加，截面上、下各有一个高度为a的区域，其应力f。

截面的中间部分区域仍保持弹性（图1c），此时梁处于弹塑性工作阶段。

σ为屈服应力y3）塑性工作阶段当荷载再继续增加，梁截面的塑性区便不断向内发展，弹性核心不断变小。

当弹性核心完全消失（图1d）时，荷载不再增加，而变形却继续发展，形成“塑性铰”，梁的承载能力达到极限。

计算抗弯强度时，需要计算疲劳的梁，常采用弹性设计。

若按截面形成塑性铰进行设计，可能使梁产生的挠度过大。

因此规范规定有限制地利用塑性。

梁的抗弯强度按下列公式计算：单向弯曲时f W M nxx x≤=γσ（1）双向弯曲时f W M W M nyy y nx x x≤+=γγσ（2）式中 M x 、M y —绕x 轴和y 轴的弯矩（对工字形和H 形截面，x 轴为强轴，y 轴为弱轴）；W nx 、W ny —梁对x 轴和y 轴的净截面模量；y x γγ,—截面塑性发展系数，对工字形截面，20.1,05.1==y x γγ；对箱形截面，05.1==y x γγ；f —钢材的抗弯强度设计值。

当梁受压翼缘的外伸宽度b 与其厚度t 之比大于y f /23513 ，但不超过y f /23515时，取0.1=x γ。

需要计算疲劳的梁，宜取0.1==y x γγ。

（2）抗剪强度主平面受弯的实腹梁，以截面上的最大剪应力达到钢材的抗剪屈服点为承载力极限状态。

v wf It VS≤=τ （3）式中 V —计算截面沿腹板平面作用的剪力设计值；S —中和轴以上毛截面对中和轴的面积矩； I —毛截面惯性矩； t w —腹板厚度；f v —钢材的抗剪强度设计值。

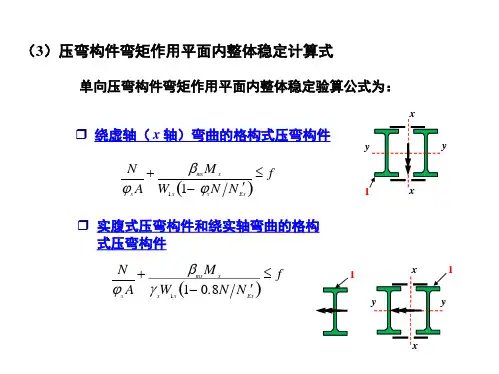
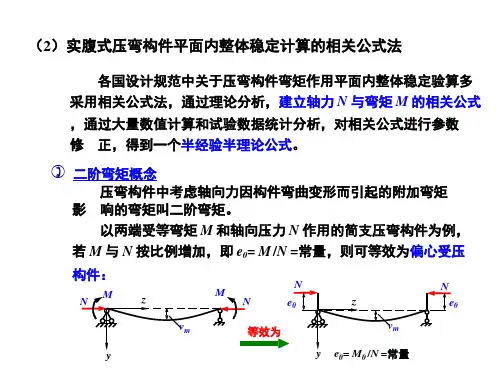
拉弯和压弯构件的强度与稳定计算1．拉弯和压弯构件的强度计算考虑部分截面发展塑性，《规范》规定的拉弯和压弯构件的强度计算式f W M A N nxx x n ≤+γ （6-1）承受双向弯矩的拉弯或压弯构件，《规范》采用了与式（6-1）相衔接的线性公式f W M W M A Nnyy y nx x x n ≤++γγ （6-2）式中：n A ——净截面面积；nx W 、ny W ——对x 轴和y 轴的净截面模量；x γ、y γ——截面塑性发展系数。

当压弯构件受压翼缘的外伸宽度与其厚度之比t b /＞y f /23513，但不超过yf /23515时，应取x γ＝1.0。

对需要计算疲劳的拉弯和压弯构件，宜取x γ＝y γ＝1.0，即不考虑截面塑性发展，按弹性应力状态计算。

2．实腹式压弯构件在弯矩作用平面内的稳定计算目前确定压弯构件弯矩作用平面内极限承载力的方法很多，可分为两大类，一类是边缘屈服准则的计算方法，一类是精度较高的数值计算方法。

按边缘屈服准则推导的相关公式y Ex x x xx f N N W M AN =⎪⎪⎭⎫⎝⎛-+ϕϕ11（6-4）式中：x ϕ——在弯矩作用平面内的轴心受压构件整体稳定系数。

边缘纤维屈服准则认为当构件截面最大受压纤维刚刚屈服时构件即失去承载能力而发生破坏，更适用于格构式构件。

实腹式压弯构件当受压最大边缘刚开始屈服时尚有较大的强度储备，即容许截面塑性深入。

因此若要反映构件的实际受力情况，宜采用最大强度准则，即以具有各种初始缺陷的构件为计算模型，求解其极限承载力。

弯矩沿杆长均匀分布的两端铰支压弯构件，《规范》采用数值计算方法，考虑构件存在l/1000的初弯曲和实测的残余应力分布，算出了近200条压弯构件极限承载力曲线。

然后《规范》借用了弹性压弯构件边缘纤维屈服时计算公式的形式，经过数值运算，得出比较符合实际又能满足工程精度要求的实用相关公式y Ex px xx f N N W M AN=⎪⎪⎭⎫⎝⎛-+8.01ϕ（6-5）式中：px W ——截面塑性模量。

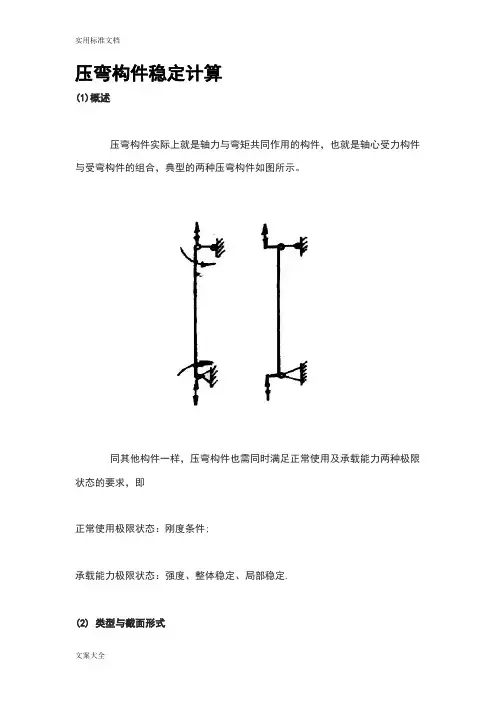
压弯构件稳定计算(1)概述压弯构件实际上就是轴力与弯矩共同作用的构件，也就是轴心受力构件与受弯构件的组合，典型的两种压弯构件如图所示。

同其他构件一样，压弯构件也需同时满足正常使用及承载能力两种极限状态的要求，即正常使用极限状态：刚度条件;承载能力极限状态：强度、整体稳定、局部稳定.(2) 类型与截面形式单向压弯构件: 只绕截面一个形心主轴受弯；双向压弯构件: 绕两个形心主轴均有弯矩作用。

弯矩由偏心轴力引起的压弯构件也称作偏压构件。

截面形式：同轴心受力构件一样，分实腹式截面与格构式截面。

实腹式：型钢截面与组合截面格构式：缀条式与缀板式☻按截面组成方式分为型钢（a、b），钢板焊接组合截面型钢（c、g），组合截面（d、e、f、h、i）☻按截面几何特征分为开口截面，闭口截面（g、h、i、j）☻按截面对称性分为单轴对称截面（d、e、f、n、p），双轴对称截面（其余各图）☻按截面分布连续性分为实腹式截面（a～j）格构式截面（k～p）(3)破坏形式强度破坏、整体失稳破坏和局部失稳破坏。

强度破坏：截面的一部分或全部应力都达到甚至超过钢材屈服点的状况。

整体失稳破坏：单向压弯构件：弯矩平面内失稳：极值失稳，应考虑效应（二阶效应）。

弯矩平面外失稳：弯扭变形，分岔失稳。

双向压弯构件：一定伴随扭转变形，为分岔失稳。

7.2.1 强度计算两个工作阶段，两个特征点。

弹性工作阶段：以边缘屈服为特征点（弹性承载力）；弹塑性工作阶段：以塑性铰弯矩为特征点（极限承载力）。

7.2.2 极限承载力与相关条件联立以上两式，消去η，则有如下相关方程7.2.3 为计算方便，改用线性相关方程, 得《规范》公式 :关于±号的说明：如右图所示对于单对称截面，弯矩绕非对称轴作用时，会出现图示两种控制应力状况。

7.2.4 刚度条件:一般情况，刚度由构件的长细比控制，即：7.3.1 概述实腹式压弯构件在轴力及弯矩作用下，即可能发生弯矩作用平面内的弯曲失稳，也可能发生弯矩作用平面外的弯曲扭转失稳（类似梁）。

第三章压弯构件的失稳轴力偏心作用的构件或同时受轴力和横向荷载作用的构件称为压弯构件。

由于压弯构件兼有受压和受弯的功能，又普遍出现在框架结构中，因此又称为梁柱。

钢结构中的压弯构件多数是截面至少有一个对称轴，且偏心弯矩作用在对称平面的单向偏心情况。

对单向偏心的压弯构件，有可能在弯矩平面内失稳，即发生弯曲失稳；也有可能在弯矩作用平面外失稳，即弯扭失稳。

其弯曲失稳为第二类稳定问题，即极值点失稳；其弯扭失稳对理想的无缺陷的压弯构件属于第一类稳定问题，即分支点失稳，但对实际构件则是极值点失稳。

对理想的两端简支的双轴对称工形截面压弯构件，在两端作用有轴线压力P和使构件产生同向曲率变形的弯矩M，如果在其侧向有足够的支撑(如图3.1（b）)，构件将发生平面内的弯曲失稳，其荷载―挠度曲线如图3.2（a）中曲线a，失稳的极限荷载为P u，属于极值点失稳。

图3.1 两端简支理想压弯构件图3.2 压弯构件荷载变形曲线P时，如果在侧向没有设置支撑（如图3.1（ｃ）），则构件在荷载P未达到平面内极限荷载u可能发生弯扭失稳，即在弯矩作用平面内产生挠度v，在平面外剪心产生位移ｕ，并绕纵轴产生扭转角 （如图3.１（ｄ）），其荷载－变形曲线如图3.2（b）中曲线b，属于分支点失稳，失稳的分荷载为P yw, ，且P yw <P u。

弯曲失稳一般在弹塑性阶段出现，而弯扭失稳可能发生在弹性阶段，也可能出现在弹塑性阶段。

3. 1 压弯构件平面内失稳对压弯构件，当弯矩作用平面外有足够多支撑可以避免发生弯扭失稳时，若失稳则只可能发生平面内弯曲失稳。

当用弹性理论分析理想压弯构件的荷载挠度关系，可以得到图3. 3中的二阶弹性曲线b，它以轴心受压弯构件的分岔点荷载P E 处引出的水平线a为渐近线。

实际压弯构件存在初始缺陷(残余应力﹑几何缺陷)，材料为弹塑性体。

如按弹塑性理论分析，荷载挠度曲线将是图中曲线OABC。

曲线上A点标志着杆件中点截面边缘开始屈服，对应的荷载为P e，随后塑性向截面内部发展，构件变形快速增加，形成OAB上升段，构件处于稳定平衡状态；B点为曲线的极值点，对应的荷载P u为构件在弯矩作用平面内失稳的极限荷载；到达B点以后，由于弹性区缩小到导致构件抵抗力矩的增加小于外力矩的增加程度，出现下降段BC，构件处于不稳定平衡状态。

实腹式压弯构件的整体稳定在轴心压力和弯矩的共同作用下，当压弯构件受力超过它的稳定承载力时，构件就有可能发生屈曲，丧失稳定。

构件有可能在弯矩作用平面内弯曲失稳，也有可能在弯矩作用平面外弯扭失稳。

因此，在设计时，要分别考虑弯矩作用平面内和弯矩作用平面外的稳定性。

一、实腹式压弯构件在弯矩作用平面内的稳定性（一）工作性能如果压弯构件抵抗弯扭变形的能力很强，或者在构件的侧向有足够的支承以阻止其发生弯扭变形，那么，构件在轴心压力和弯矩的共同作用下，可能在弯矩作用平面内发生整体弯曲失稳。

发生这种弯曲失稳的压弯构件，其承载能力可以用图6-11来说明。

图6-11（a ）表示一单向压弯构件，两端铰支，端弯矩M 作用在构件截面的对称轴平面YOZ 内，M 和N 按比例增加。

如其侧向有足够的支承防止其发生弯矩作用平面外的位移，则构件受力后只在弯矩作用平面内发生弯曲变形。

图6-11（b ）ν-N 曲线，υ为构件中点沿y 轴方向的位移。

开始时构件处于弹性工作阶段，ν-N 接近线性变化。

当荷载逐渐加大，曲线在A 点开始偏离直线。

若材料为无限弹性，则此曲线为OAB ，在N 接近于欧拉荷载N cr 时，υ趋向无限大。

事实上因钢材为弹塑性材料，其ν-N 曲线不可能为OAB ，而将遵循OACD 变化。

在曲线上升阶段AC ，挠度v 是随压力的增加而增加的，此时构件内、外力矩平衡，构件处于稳定平衡状态。

当达到曲线的最高点C 时，构件的抵抗能力开始小于外力作用，出现了曲线的下降段CD ，此时的构件截面中，塑性区不断扩展，截面内力矩已不能与外力矩保持稳定的平衡，因而这阶段是不稳定的，并在荷载减小的情况下位移υ不断增加。

图中的C 点是由稳定平衡过渡到不稳定平衡的临界点，也是曲线ACD 的极值点。

相应于C 点的轴力N ux 称为极限荷载、破坏荷载或最大荷载。

荷载达到N ux 后，构件即失去弯矩作用平面内的稳定（以下简称弯矩作用平面内失稳）。

压弯构件失稳时先在受压最大的一侧发展塑性，有时在另一侧的受拉区也会发展塑性，塑性发展的程度取决于截面的形状和尺寸、构件的长度和初始缺陷，其中残余应力的存在会使构件的截面提前屈服，从而降低其稳定承载力。