当前位置：文档之家 › 第四讲 压弯构件

第四讲 压弯构件

  • 格式：ppt
  • 大小：563.00 KB
  • 文档页数：65

下载文档原格式

  / 65

合集下载

6-钢结构基本原理—压弯构件

6-钢结构基本原理—压弯构件

求解过程：p.197
方程解：
(1 −
一、单向压弯构件的平面内失稳
参阅 §7.4.1
不对称实腹式截面，弯矩使较大翼缘受压时的 补充计算公式
N A
−
β mx M x
γ xWx2 (1 − 1.25N
/ NE)
≤
fd
§3 压弯构件的整体稳定
二、单向压弯构件的平面外失稳
平面外失稳的特征
参阅 §7.4.2
Mx
N
y
v
Mx zN
N
x u,θ
zN
与受弯构件整体失稳的相似点：
边缘屈服准则
N A
+
Nv 0m
≤
W x (1 − N / N E )
fy
M max
=
Nv0m 1-N / N E
2阶效应放大因子（弹性范围）
整理为 p.103（5-30）
σ cr
=
fy + (1+ ε0 )σEx 2
−
[
fy
+ (1+ ε0 )σEx 2
]2
−
fyσ Ex
1 1-N / N E
ε0
=
则 N + Mx ≤1 N p M ex
N An
+ Mx Wxn
≤
fd
§2 单向压弯（拉弯）构件截面强度
三、全截面屈服准则
准则描述：
参阅 §4.2
截面各点应力（拉、压）都达到钢材屈服点
截面强度公式
y σ1 = fy
x
记 屈服轴力 N p = Af y 塑性弯矩 M px = Wpx fy
N 经推导可得
Av 0m Wx

第四章压弯构件.ppt

第四章压弯构件.ppt
N
P M 1 P M 1 P /P s s( E)
P M 1 P M 1 P /P s s( E)
钢结构设计规范中压弯构件稳定验算公式就是由上式
而来，只不过规范公式同时还考虑了其它边界条件、 荷载形式和初始缺陷等因素的影响。
§4-3 考虑弹塑性影响的压弯构件整体 稳定验算
其中Mi为内弯矩，与杆件轴向力P和曲率ρ有关：
2 2 u b、由基本假设第二条得到： u sin z m
M f( P , ) i
l
l
c、由基本假设第三条，平衡方程可以表达为：
M Pu f ( P , u ) q m m
dP d、P的最大值可由 0 得到，即为弯矩作用平 du m 面内的稳定承载力。
9.
10.
11.
4）简化计算方法（耶硕克Jezek法）
基本假定：
a、材料理想弹塑性。
b、杆件两端简支，构件变形曲线为正弦半波曲线，即：
v vm sin z l c、只考虑构件中央截面的内外力平衡。
P P um z

y
P
P um
z
y
计算步骤：
内弯矩
a、平衡方程： M Pu M q i 由横向荷载产生 某点的挠度
y
d y i y dx
中和轴以外为
dx
y点处伸长 量为y dθ
拉，以内为压
3）数值积分法（压杆挠曲线法）
具有初弯曲的压弯构件，假设条件最少，可适用于任
意情况。
截面上内弯矩：
－ EIy ' ' 弹性阶段 M ＝ 内 j 弹塑性阶段 A yjdA
有正负 拉＋，压－

压弯构件的整体稳定_图文_图文

压弯构件的整体稳定_图文_图文
1、有侧向支承时，框架平面外的 计算长度等于侧向支承点之间的 距离。 2、无侧向支承时，框架平面外 的计算长度等于柱的全长。
[例题6-8]柱与基础铰接的双跨框架上，沿构件 的轴线作用有轴线压力，边柱为P， 中柱为2P， 沿横梁的水平力为0.2P， 承受弯距如图，框架平 面外有足够支撑。 要求确定柱的承载能力。
Байду номын сангаас
二、腹板的局部稳定
（一） 工字形截面的 腹板
二、腹板的局部稳定 （一） 工字形截面的
腹板
当λ<30时，取λ=30， 当λ>100时，取λ=100，即30≤λ≤100。
二、腹板的局部稳定 （二）箱形截面的腹板
二、腹板的局部稳定 （三）T形截面的腹板
第 五节 压弯构件的计算长度
• 当压弯构件的端部支承条件比较简单，其计算 长度可按照轴心压杆的计算长度系数进行计算；
四、实腹式压弯构件在弯矩作用平面外的稳定计算
四、实腹式压弯构件在弯矩作用平面外的稳定计算
四、实腹式压弯构件在弯矩作用平面外的稳定计算
1、工字形截面 双轴对称时 ：
单轴对称时：
2、Ｔ形截面（弯矩作用在对称轴平面，绕ｘ 轴） （1）弯矩使翼缘受压时：
双角钢Ｔ形截面：
两板组合Ｔ形截面：
（2）弯矩使翼缘受拉时： b=1.0 3、箱形截面： b=1.4 4、 对轧制普通工字钢之压弯构件，可由附表直接查得， 当查得的 b >0.6时，应按表查相应的/ b代替 b
构件看作一个平行桁架，分肢视为弦杆，将压 力和弯矩分配到分肢并按轴心压杆计算。分肢 的轴向力按下式计算：
分肢１
分肢２
压弯构件的整体稳定_图文_图文.ppt
二、压弯构件在弯矩作用平面内的弹性性能 力的平衡方程

钢结构 压弯构件PPT课件

钢结构 压弯构件PPT课件

N
mx M x
f
x A
xW1x
(1
0.8
N NE x
)
式中：
(4 85)
N 压弯构件的轴线压力；
NE x NEx 1.1，NEx 2EA 2x
0.8 修正系数;
x 弯矩作用平面内轴压构件的稳定系数；
M x 计算区段的最大弯矩； W1x 在弯矩作用平面内对较大受压纤维的毛截面模量；
fy
考虑构 件缺陷 的等效 偏心率
(b)
N
mM
x A Wx (1x N
NE)
fy
(4 75)
• 最大强度准则法
考虑构件存在L/1000的初弯曲和实测的残余应力分布， 算出近200条压弯构件极限承载力
N
mx M x
f
x A
xW1x
(1
0.8
N NE x
)
(4 85)
4、实腹式压弯构件在弯距作用平面内稳定计算的适用公式（掌握）
2、悬臂构件: βmx =1.0
补充：*** 单轴对称截面
为此应满足：
N－
mx M x
f
A
xW2x
(1
1.25
N NE x
)
(4 86)
式中：
W2x 对无翼缘端（受拉边缘）的毛截面模量； 其余符号同前。
面内失稳适用公式
N
mx M x
f
x A
xW1x
(1
0.8
N NE x
)
对单轴对称截面，补充：
b 均匀弯矩作用时构件的整体稳定系数，对于一般工字形
截面和T形截面压弯构件均可直接用近似公式(4.63)至
(4.67)计算 注意：

压弯构件原理分析高教知识

压弯构件原理分析高教知识

当
x h0
时，为大偏心受压破坏
b
当
x h0
时，为小偏心受压破坏
b
全面分析
13
N
M
As'
As'
As' 不屈服
受拉破坏
xcb
y
a
' s
界限破坏
受压破坏
h0
全面分析
' y
cu
14
大、小偏压界限状态的进一步讨论 ei与0.3h0
b即x bh0属于大偏心破坏形态
＞ b即x > bh0属于小偏心破坏形态
全面分析
27
全面分析
28
❖ 偏心受压构件
特点：从一开始起，构件即产生侧移（产生弯曲变形）。随 着压力的增加，构件的侧移持续增大，由于弯曲变形逐步增 大，跨中截面可能出现部分塑性区，由于塑性变形的产生， 使侧移的增大也越来越快，当压力达到最大值Pmax时，荷载 必须下降才能维持内外力的平衡，即具有极值点和下降段， 称为极值点失稳，亦称第二类失稳。 极限荷载：极限承载力小于屈曲荷载 Pcr，等于最大荷载 Pmax ，Pmax 称为失稳极限荷载或压溃荷载。
线发生，这是另一个基本的自然规律。面临弯出去还是缩
短的选择，柱子发现在荷载相当小的时候，缩短比较容易
；当荷载相当大时，弯出去比较容易。换句话说，当荷载
达到它的临界值时，用弯曲的办法来降低荷载位置比用缩
短的办法更为容易些。”
《建筑结构》萨瓦多里，穆勒
全面分析
22
三种平衡状态
图1
（1）稳定平衡：偏离平衡位置，总势能增加。
不对称配筋时，将最小配筋率及常用的钢筋和混凝土强度代入
上式得到的e0b大致在0.3h0上下波动，平均值为0.3h0 ，因此设 计时，

钢结构设计原理 拉弯和压弯构件PPT学习教案

钢结构设计原理 拉弯和压弯构件PPT学习教案

修正方法
①相关公式左边第二项的轴压杆稳定系数 x 0.8
②有限度利用截面塑性，引入塑性发展系数 x，并
引入抗力分项系数。
N xA
xW1x
mxM x (1 0.8
RN N Ex
)
f
N 轴向压力设计值
《规范》平面内稳定计算公式 书P203 式(6-14)
Mx 所计算构件段范围内的最大弯矩 x 轴心受压构件绕x轴失稳的整体稳定系数 W1x 受压最大纤维的毛截面抵抗矩
格构式或冷弯薄壁型钢拉弯构件及承受动力荷载的实腹式拉 弯构件—以截面边缘的纤维开始屈服达到承载力的极限（边 缘纤维屈服准则 ：弹性阶段，在构件受力最大截面处，截 面边缘处最大应力达到屈服强度。）
2、稳定破坏: N 较小而M 较大的拉弯构件，与梁一样，出现弯扭失稳的 破坏。
3、刚度破坏：
第1页/共34页
tx 等效弯矩系数，应按下列规定采用：
1）在弯矩作用平面外有支承的构件，应根据两相邻侧向支承点间构件 段内的荷载和内力情况确定：
由平衡微分方程可得
M
(NEy
N )(Nz
N)
(N e)2 i02
0
P204式(6-16)
第18页/共34页
M
(N e)2
(NEy N)(Nz N) i02
N Ey 构件绕y轴弯曲屈曲临界力
0
N Ey
2EIy
l
2 y
Nz 构件绕z轴扭转屈曲临界力
Nz
(GI t
2 EI l2
)
i02
It 截面的扭转常
三、实腹式压弯构件在平面内的稳定承载力计算
从上面分析可知，实腹式压弯构件在平面内失稳时，截面出现塑 性，上述弹性稳定理论已不适用，那么在计算承载力时宜采用塑性 深入截面的最大强度准则，可以采用近似解析法和数值积分法求解 出。

第四讲 压弯构件解析


各种缺陷的等效初弯曲呈跨中挠度为 的正弦v0曲线。任意 横向荷载或端弯矩作用下的计算弯矩为M，则跨中总弯矩应
为
M max
m M Nv0
1 N / NE
构件中点截面边缘纤维达到屈服时
N A
mM
1 N /
Nv0
NE W
fy
令M＝0，即有初始缺陷的轴心压杆边缘屈服时表达式
N0 A
N0v0
1
N0 NE
3 《规范》计算公式 将用数值方法得到的压弯构件的极限承载力与用边缘纤维屈 服准则导出的相关公式中的轴心压力进行比较，对于短粗的 实腹杆，偏于安全；对于细长的实腹杆，偏于不安全。因此 借用了边缘纤维屈服时计算公式的形式，但计算弯曲应力时 考虑了截面的塑性发展和二阶弯矩，初弯曲和残余应力的影 响综合为一个等效偏心距，弯矩为非均匀分布时，用等效弯 矩代替，考虑部分塑性深入截面，并引入抗力分项系数，得 到实腹式压弯构件弯矩作用平面内的稳定计算式
N
mxM x
f
A
xW2 x
1 1.25
N N 'Ex
式中 W2x —受拉侧最外纤维的毛截面模量。 上式第二项分母中的系数1.25也是经过与理论计算结果比
较后引进的修正系数。
二、弯矩作用平面外的稳定计算
开口薄壁截面压弯构件的抗扭刚度及弯矩作用平面外的抗 弯刚度通常较小，当构件在弯矩作用平面外没有足够的支 撑以阻止其产生侧向位移和扭转时，构件可能因弯扭屈曲 而破坏。构件在发生弯扭失稳时，其临界条件为
一类是边缘屈服准则的计算方法 一类是精度较高的数值计算方法
弯矩作用平面外的稳定计算 局部稳定计算 格构式压弯构件的稳定计算
一、弯矩作用平面内的稳定计算
M与N的相关曲线

压弯构件


§7-1 应用和截面形式
钢结构基本原理及设计
钢结构中拉弯构件应用较少， 钢结构中拉弯构件应用较少，桁架的下弦杆有时作 用有非节点荷裁，这种下弦杆就是拉弯构件。 用有非节点荷裁，这种下弦杆就是拉弯构件。
§7-1 应用和截面形式
钢结构基本原理及设计
§7-2 拉弯、压弯构件的强度 拉弯、
7.2.1 拉弯、压弯构件的强度计算 拉弯、
Mx N + =1 N p γ x M ex
§7-2 拉弯、压弯构件的强度 拉弯、
钢结构基本原理及设计
7.2.2 构件强度与刚度计算
1．单向拉弯、压弯构件按下式计算截面强度： ．单向拉弯、压弯构件按下式计算截面强度：
Mx N ± ≤f An γ xWnx
2．双向拉弯、压弯构件计算截面强度： ．双向拉弯、压弯构件计算截面强度： My Mx N ± ± ≤ f An γ xWnx γ yWny 3． ．
§7-3 实腹式构件在弯矩平面内的稳定
钢结构基本原理及设计
数值计算方法可求得单一构件弯矩作用平面内稳定承 载力N 的数值解， 载力 ux的数值解，可以考虑构件的几何缺陷和残余应力影 适用于各种边界条件以及弹塑性工作阶段， 响，适用于各种边界条件以及弹塑性工作阶段，是最常用 N e 的方法。 的方法。 1.0
单向压弯构件的整体失稳分为： 单向压弯构件的整体失稳分为： 弯矩作用平面内和弯矩作用平面外两种情况 弯矩作用平面内失稳为弯曲屈曲 弯矩作用平面外失稳为弯扭屈曲 双向压弯构件则只有弯扭失稳一种可能
§7-3 实腹式构件在弯矩平面内的稳定
钢结构基本原理及设计
N e0 Mx = Ne0 x v v A z e0 N A x x y A-A y Mx y Nux NEx

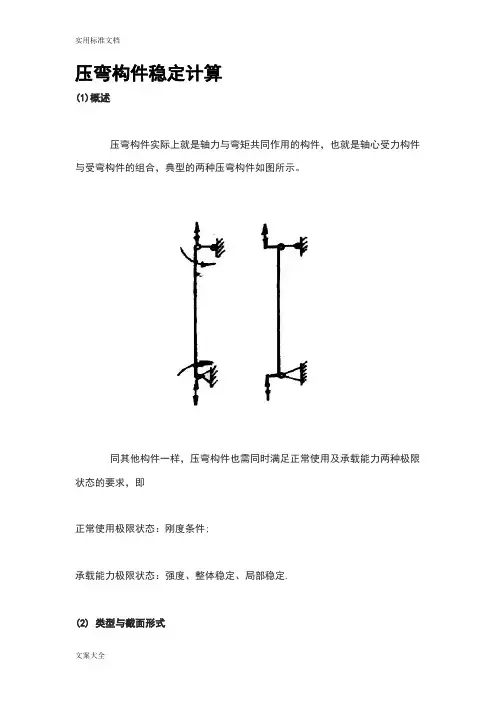
压弯构件稳定计算

压弯构件稳定计算(1)概述压弯构件实际上就是轴力与弯矩共同作用的构件，也就是轴心受力构件与受弯构件的组合，典型的两种压弯构件如图所示。

同其他构件一样，压弯构件也需同时满足正常使用及承载能力两种极限状态的要求，即正常使用极限状态：刚度条件;承载能力极限状态：强度、整体稳定、局部稳定.(2) 类型与截面形式单向压弯构件: 只绕截面一个形心主轴受弯；双向压弯构件: 绕两个形心主轴均有弯矩作用。

弯矩由偏心轴力引起的压弯构件也称作偏压构件。

截面形式：同轴心受力构件一样，分实腹式截面与格构式截面。

实腹式：型钢截面与组合截面格构式：缀条式与缀板式☻按截面组成方式分为型钢（a、b），钢板焊接组合截面型钢（c、g），组合截面（d、e、f、h、i）☻按截面几何特征分为开口截面，闭口截面（g、h、i、j）☻按截面对称性分为单轴对称截面（d、e、f、n、p），双轴对称截面（其余各图）☻按截面分布连续性分为实腹式截面（a～j）格构式截面（k～p）(3)破坏形式强度破坏、整体失稳破坏和局部失稳破坏。

强度破坏：截面的一部分或全部应力都达到甚至超过钢材屈服点的状况。

整体失稳破坏：单向压弯构件：弯矩平面内失稳：极值失稳，应考虑效应（二阶效应）。

弯矩平面外失稳：弯扭变形，分岔失稳。

双向压弯构件：一定伴随扭转变形，为分岔失稳。

7.2.1 强度计算两个工作阶段，两个特征点。

弹性工作阶段：以边缘屈服为特征点（弹性承载力）；弹塑性工作阶段：以塑性铰弯矩为特征点（极限承载力）。

7.2.2 极限承载力与相关条件联立以上两式，消去η，则有如下相关方程7.2.3 为计算方便，改用线性相关方程, 得《规范》公式 :关于±号的说明：如右图所示对于单对称截面，弯矩绕非对称轴作用时，会出现图示两种控制应力状况。

7.2.4 刚度条件:一般情况，刚度由构件的长细比控制，即：7.3.1 概述实腹式压弯构件在轴力及弯矩作用下，即可能发生弯矩作用平面内的弯曲失稳，也可能发生弯矩作用平面外的弯曲扭转失稳（类似梁）。

压弯构件精简版_图文_图文

其中
.6 格构式压弯构件的稳定性计算
.6.2 弯矩绕虚轴作用时 1）弯矩作用平面内的稳定性
采用边缘纤维屈服作为设计准则，不考虑塑性 发展，即x =1.0。
.6 格构式压弯构件的稳定性计算
.6.2 弯矩绕虚轴作用时 1）弯矩作用平面内的稳定性
公式：
式中:
x 和N’Ex均由对虚轴的换算长细比l0x确定。
（c）轴力N=16 kN ，在两端同时作用着弯矩 Mx=10 kN .m，并产生异向屈曲；
[解]：
通过查表确定：A 、Wx、ix 、γx、f
A=14.3cm2, Wx=49cm3 , ix =4.14cm,
γx =1.05, f=215N/mm2
（a） 验算强度和平面内稳定：
强度公式
弯矩作用平面内的稳定性 βmx——等效弯矩系数
分肢２
稳定验算：
分肢的计算长度： 在缀件平面内取缀条相邻节点中心间的距离或 缀板间的净距。 在缀件平面外取侧向支承点之间的距离。
.6 格构式压弯构件的稳定性计算
.6.2 弯矩绕虚轴作用时 3）缀件的计算
与格构式轴心受压构件的缀件计算相同，但所 受剪力取实际剪力和计算剪力两者中的较大值。
其中计算剪力为：
刚度
( b ) 只验算弯矩作用平面内稳定
( c )只验算弯矩作用平面内稳定
3 压弯构件的整体稳定
3.4 实腹式压弯构件在弯矩作用平面外的稳定计算
1） 规范公式
以工字形截面的简化相关关系为基础给出如下 ：
（1）工字形截面 双轴对称时：
单轴对称时：
（2）Ｔ形截面（弯矩作用在对称轴平面，绕x轴 ）弯矩使翼缘受压时：
构件存在初弯曲挠度v0；
M
M引起挠度vm ；
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

构件等效弯矩系数
柱端有相对水平位移时
tx 0.85
tx 1
M2 tx =0.65+0.35 M1

柱端无相对水平位移时

有端弯矩无横向荷载
有横向荷载无端弯矩 二者都有 同向曲率

tx 1
反向曲率
tx 0.85
双向压弯（*）
6.3.3双向弯曲实腹式压弯构件的整体稳定 弯矩作用在两个主轴平面内为双向弯曲压弯构件，工 程中较为少见。《规范》规定了双轴对称截面的计算 方法。 双轴对称的工字形截面(含H型钢)和箱形截面压弯构件 的整体稳定计算
1.边缘屈服准则
横向荷载产生的跨中挠度为vm 。当荷载对称时，假定挠曲 线为正弦曲线。轴心力作用后，挠度增加，在弹性范围，跨 中挠度增加为 vm vmax 1 l／(1－a)称为挠度放大系数。 跨中总弯矩为
M max M N vm M Nv m M 1 1 1 M 1 Nv m mM 1 1 M 1
m —等效弯矩系数。
根据各种荷载和支承情况产生的跨中弯矩M和跨中挠度可以 计算出相应的等效弯矩系数。
弹性压弯构件，可用截面边缘屈服作为稳定计算准则。假定 v0 各种缺陷的等效初弯曲呈跨中挠度为 的正弦曲线。任意 横向荷载或端弯矩作用下的计算弯矩为M，则跨中总弯矩应 为 m M Nv0
M max 1 N / NE
N Ey M x N N 1 1 M N N N Ey Ey z crx 0
2
可以画出相关曲线如图所示。
如偏安全地取 N z / N ＝ Ey 1.0，则上式成为
Mx M crx N 1 N Ey
N x A
m M x
N W1x 1 x N Ex
f
N x A
mx M x xW1x 1 0.8
N ' N Ex
f
mx —等效弯矩系数，按下列情况取值：
(1) 框架柱和两端支承的构件： ① 无横向荷载作用时： mx 0.65 0.35M 2 ， / M1 1和M2 为 端弯矩，使构件产生同向曲率(无反弯点)时取同号，使构件 产生反向曲率(有反弯点时)取异号 ，
N A
经整理得
m M
N W 1 N E
fy
边缘屈服准则导出的相关公式。 规范将上式作为格构式压弯构件绕虚轴平面内稳定计算的相 关公式，引入抗力分项系数
N x A
m M x
N W1x 1 x N Ex
f
2. 最大强度准则 边缘屈服准则当截面最大受压纤维屈服时构件失去承载能力 ，适用于格构式构件。实腹式当受压最大边缘刚屈服时尚有 较大的强度储备，即容许截面塑性深入。因此宜采用最大强 度准则，以具有初始缺陷的构件为计算模型，求解极限承载 力。 采用数值计算方法，考虑l／ 1000的初弯曲和实测的残余应力 ，算出了近200条压弯构件极限承载力曲线。 不同的截面形式或截面形式相同但尺寸不同、残余应力的分 布不同以及失稳方向的不同等，其曲线都将有很大的差异。 200条曲线很难用一统一公式来表达。分析证明采用相关公式 的形式可较好地解决。影响极限承载力的因素很多，要得到 精确的、符合各种不同情况的理论公式是不可能的。因此， 只能根据理论分析的结果，经过数值运算，得出比较符合实 际又能满足工程精度要求的实用相关公式。
2 2
Mx N 1 N Ey M crx
M crx b f yW1x
NEy y f y A 并引入非均匀弯矩作用时的等效
弯矩系数、箱形截面的调整系数以及抗力分项系数后，得到压
弯构件在弯矩作用平面外稳定计算的相关公式为
tx M x N f y A bW1x
M x —所计算构件段范围内(构件侧向支承点间)的最大弯矩；
3 《规范》计算公式 将用数值方法得到的压弯构件的极限承载力与用边缘纤维屈 服准则导出的相关公式中的轴心压力进行比较，对于短粗的 实腹杆，偏于安全；对于细长的实腹杆，偏于不安全。因此 借用了边缘纤维屈服时计算公式的形式，但计算弯曲应力时 考虑了截面的塑性发展和二阶弯矩，初弯曲和残余应力的影 响综合为一个等效偏心距，弯矩为非均匀分布时，用等效弯 矩代替，考虑部分塑性深入截面，并引入抗力分项系数，得 到实腹式压弯构件弯矩作用平面内的稳定计算式

确定，取值方法与弯矩作用平面内的等效弯矩系数相同。 －调整系数，箱形截面0.7，其他截面1.0；
tx —等效弯矩系数，应根据所计算构件段的荷载和内力情况
y －弯矩作用平面外的轴心受压构件稳定系数；
b －均匀弯曲梁的整体稳定系数，可采用近似计算公式
mx

构件等效弯矩系数
柱端有相对水平位移时
构件中点截面边缘纤维达到屈服时
N m M Nv 0 fy A 1 N / N E W
令M＝0，即有初始缺陷的轴心压杆边缘屈服时表达式
N0 N 0v0 fy A N0 1 N W E
N0 A f y
Af y W v0 ( 1) 1 A N E 1
kp为塑性屈曲系数，其值与构件的长细比和应力梯度有关。 取临界应力为235N/mm2，可得到腹板高厚比与应力梯度之间 的关系，此关系可近似地用直线式表示
0 0 1.6
1.6 0 2.0
h0 /t w 16 0 50
h0 /t w 48 0 1
长细比较小的压弯构件，整体失稳时截面的塑性深度实际上 已超过了0.25h0，长细比较大的压弯构件，截面塑性深度则 不到0.25 h0，甚至腹板受压最大的边缘还没有屈服。因此， h0/tw之值宜随长细比的增大而适当放大。 工字形截面压弯构件腹板高厚比限值
0 5 1 0 5 1 1 1 1 2 cr1 2 cr1 cr1
2 2
max min 0 max
0 0 1.6
h0 235 0.8(16 0 0.5 25) tw fy
h0 235 0.8(48 0 0.5 26 .2) tw fy
235 40 fy
压弯构件的整体稳定

弯矩作用平面内的稳定计算.其极限承载力的 方法很多，可分为两大类：


一类是边缘屈服准则的计算方法 一类是精度较高的数值计算方法

弯矩作用平面外的稳定计算 局部稳定计算 格构式压弯构件的稳定计算
一、弯矩作用平面内的稳定计算

M与N的相关曲线
由图可知， 构件长细比 的加大，会 降低构件的 正截面受压 承载力
mx 1.0 ；使构件产生反向曲率时，
M1 M 2
②有端弯矩和横向荷载同时作用时：使构件产生同向曲率时
； mx 0.85
②无端弯矩但有横向荷载作用时： mx 1 。 .0 (2) 悬臂构件和未考虑二阶效应的无支撑纯框架和弱支撑框
架， 。 mx 1.0
对于 T 形截面等单轴对称压弯构件，当弯矩作用于对称轴 平面且使较大翼缘受压时，构件失稳时出现的塑性区除存 在前述受压区屈服和受压、受拉区同时屈服两种情况外， 还可能在受拉区首先出现屈服而导致构件失去承载力，还 应按下式计算
0 1.0
0 1.0
h0 235 15 tw fy
h0 235 18 tw fy
235 fy
(2)弯矩使腹板自由边受拉 热轧剖分T形钢 h 0 (15 0.2 )
tw
焊接T形钢
h0 235 (13 0.17 ) tw fy
3.箱形截面 两腹板受力可能不一致，翼缘对腹板的约束因常为单侧角焊 缝也不如工字形截面，因而箱形截面的宽厚比限值取为工字 形截面腹板的0.8倍。
对压弯构件，腹板中剪应力的影响不大，平均剪应力可取腹板 弯曲应力的0.3倍，腹板弹性屈曲临界应力为
cr 2 E tw ke 2 12(1 ) h0
2
式中，ke为弹性屈曲系数，其值与应力梯度有关。 2 腹板的弹塑性临界应力为 2
cr k p E tw 2 12(1 ) h0
0 0 1.6
h0 235 (16 0 0.5 25) tw fy
h0 235 (48 0 0.5 26.2) tw fy
1.6 0 2.0
2. T形截面 (1)弯矩使腹板自由边受压 当 0 1.0 (弯矩较小)时，T形截面腹板中压应力分布不均的 有利影响不大，宽厚比限值采用与翼缘板相同；当 0 1.0 (弯矩较大)时，有利影响较大，故提高20％
mx 1
mx 1-0.2N/NEX
柱端无相对水平位移时


有端弯矩无横向荷载 mx 有横向荷载无端弯矩 一个集中荷载 多个集中荷载或均布荷载 二者都有 同向曲率 反向曲率 mx
=0.65+0.35M2 /M1
mx 1
mx 1 0.85
tx

压弯构件
content

认识压弯构件 单向压弯构件——实腹式、格构式 双向压弯构件 例题
Z
M N F N
N
e X X N
N
X
N
M
压弯构件主要内容

强度验算 弯矩作用平面内稳定验算 弯矩作用平面外稳定验算 双向受弯稳定验算 格构式压弯构件稳定验算
压弯构件强度验算(应力叠加原理）
为保证压弯构件中板件的局部稳定，限制翼缘和腹板的宽厚 比及高厚比。 1 、受压 翼缘的宽厚比 压弯构件受压翼缘应力情况与梁受压翼缘基本相同，因此自 由外伸宽度与厚度之比以及箱形截面翼缘在腹板之间的宽厚 比均与梁受压翼缘的宽厚比限值相同。 2、 腹板的高厚比 1.工字形截面 平均剪应力和不均匀正应力共同作用下，临界条件