高二数学空间向量数量积的坐标表示

专题三 空间向量及其运算的坐标表示一 知识结构图二.学法指导1．在空间直角坐标系中，确定点的坐标或求对称点坐标时，要记住规律：“在谁的轴上，谁属于R ，其它为零；在谁的平面上，谁属于R ，其它为零．”“关于谁对称谁不变，其余变成相反数．” 2．空间几何体中，要得到有关点的坐标时，先建立适当的坐标系，一般选择两两垂直的三条线段所在直线为坐标轴，然后选择基向量，根据已知条件和图形关系将所求向量用基向量表示，即得所求向量的坐标．3．进行空间向量的数量积坐标运算的技巧利用向量坐标运算解决问题的关键是熟记向量坐标运算的法则，同时掌握下列技巧． (1)在运算中注意相关公式的灵活运用，如(a ＋b )·(a －b )＝a 2－b 2＝|a |2－|b |2，(a ＋b )·(a ＋b )＝(a ＋b )2等．(2)进行向量坐标运算时，可以先代入坐标再运算，也可先进行向量式的化简再代入坐标运算，如计算(2a )·(－b )，既可以利用运算律把它化成－2(a ·b )，也可以求出2a ，－b 后，再求数量积；计算(a ＋b )·(a －b )，既可以求出a ＋b ，a －b 后，求数量积，也可以把(a ＋b )·(a －b )写成a 2－b 2后计算． 4.判断空间向量垂直或平行的步骤(1)向量化：将空间中的垂直与平行转化为向量的垂直与平行； (2)向量关系代数化：写出向量的坐标；(3)对于a ＝(x 1，y 1，z 1)，b ＝(x 2，y 2，z 2)，根据x 1x 2＋y 1y 2＋z 1z 2是否为0判断两向量是否垂直；根据x 1＝λx 2，y 1＝λy 2，z 1＝λz 2(λ∈R )或x 1x 2＝y 1y 2＝z 1z 2(x 2，y 2，z 2都不为0)判断两向量是否平行．5.利用向量数量积的坐标公式求异面直线所成角的步骤(1)根据几何图形的特点建立适当的空间直角坐标系；(2)利用已知条件写出有关点的坐标，进而获得相关向量的坐标；(3)利用向量数量积的坐标公式求得异面直线上有关向量的夹角，并将它转化为异面直线所成的角．6．利用向量坐标求空间中线段的长度的一般步骤(1)建立适当的空间直角坐标系；(2)求出线段端点的坐标；(3)利用两点间的距离公式求出线段的长．三.知识点贯通知识点1 求空间点的坐标例题1.如图，在长方体ABCD ­A 1B 1C 1D 1中，|AB |＝4，|AD |＝3，|AA 1|＝5，N 为棱CC 1的中点，分别以DA ，DC ，DD 1所在的直线为x 轴、y 轴、z 轴，建立空间直角坐标系．(1)求点A ，B ，C ，D ，A 1，B 1，C 1，D 1的坐标； (2)求点N 的坐标． 【解析】(1)显然D (0,0,0)，因为点A 在x 轴的正半轴上，且|AD |＝3， 所以A (3,0,0)．同理，可得C (0,4,0)，D 1(0,0,5)．因为点B 在坐标平面xOy 内，BC ⊥CD ，BA ⊥AD ，所以B (3,4,0)．同理，可得A 1(3,0,5)，C 1(0,4,5)，与B 的坐标相比，点B 1的坐标中只有竖坐标不同，|BB 1|＝|AA 1|＝5，则B 1(3,4,5)．(2)由(1)知C (0,4,0)，C 1(0,4,5)， 则C 1C 的中点N 为⎝⎛⎭⎫0＋02，4＋42，0＋52，即N ⎝⎛⎭⎫0，4，52. 知识点二 求对称点的坐标在空间直角坐标系中，任一点P (a ，b ，c )的几种特殊的对称点的坐标如下：(1)求点P 关于x 轴的对称点的坐标； (2)求点P 关于xOy 平面的对称点的坐标；(3)求点P 关于点M (2，－1，－4)的对称点的坐标【解析】 (1)由于点P 关于x 轴对称后，它在x 轴的分量不变，在y 轴、z 轴的分量变为原来的相反数，所以对称点为P 1(－2，－1，－4)．(2)由于点P 关于xOy 平面对称后，它在x 轴、y 轴的分量不变，在z 轴的分量变为原来的相反数，所以对称点为P 2(－2,1，－4)．(3)设对称点为P 3(x ，y ，z )，则点M 为线段PP 3的中点．由中点坐标公式，可得x ＝2×2－(－2)＝6，y ＝2×(－1)－1＝－3，z ＝2×(－4)－4＝－12，所以P 3(6，－3，－12)． 知识点三 空间向量的坐标表示若),,(),,(2211y x B y x A 则),(1212y y x x --=。

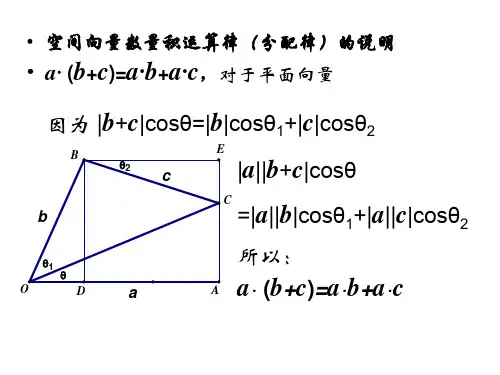
向量数量积的坐标表示公式
向量数量积的坐标表示公式为：
若有两个向量A = (a1, a2, a3)和B = (b1, b2, b3)，它们的数量积（也称为点积）为：
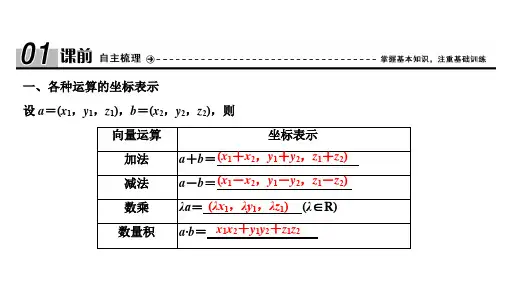
A∙B = a1b1 + a2b2 + a3b3
这个公式表示了两个向量在各个坐标上的对应分量相乘后相加所得到的结果，可以用来计算两个向量的点积。

同时，向量A∙B还可以表示为A·B = |A| |B| cosθ，其中|A|和|B|分别表示A和B的长度，θ表示A和B之间的夹角。

这个公式可以用来计算两个向量之间的夹角，从而得到它们的数量积。

除了上述的坐标表示公式，向量数量积还有几何表示和向量积的定义形式。

向量数量积在几何上表示了向量A在向量B方向上的投影长度与向量B的模长之积，而在向量积中，数量积还可以表示为A∙B = 0，当且仅当向量A和向量B垂直（即夹角为90度）时。

高中数学必修知识点空间向量知识点在高中数学的学习中，空间向量是一个重要的知识点，它为我们解决空间几何问题提供了全新的思路和方法。

接下来，就让我们一起深入了解一下空间向量的相关知识。

一、空间向量的基本概念空间向量是指具有大小和方向的量。

它与平面向量类似，但存在于三维空间中。

一个空间向量可以用有向线段来表示，有向线段的长度表示向量的大小，箭头所指的方向表示向量的方向。

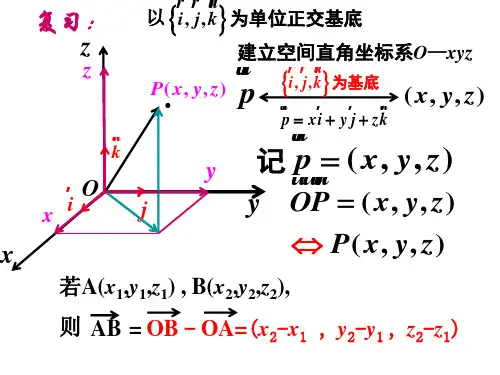
空间向量的坐标表示：在空间直角坐标系中，若向量的起点坐标为\（（x_1,y_1,z_1)＼），终点坐标为\（（x_2,y_2,z_2)＼），则该向量的坐标为\（（x_2 x_1, y_2 y_1, z_2 z_1)＼）。

零向量：长度为\（0\）的向量，其方向任意。

单位向量：长度为\（1\）的向量。

二、空间向量的运算1、加法和减法空间向量的加法和减法运算遵循三角形法则和平行四边形法则。

若\（＼overrightarrow{a} ＝（x_1,y_1,z_1)＼），＼（＼overrightarrow{b} ＝（x_2,y_2,z_2)＼），则\（＼overrightarrow{a} ＋＼overrightarrow{b} ＝（x_1 ＋ x_2, y_1 ＋ y_2, z_1 ＋ z_2)＼），＼（＼overrightarrow{a} ＼overrightarrow{b} ＝（x_1 x_2, y_1 y_2, z_1z_2)＼）2、数乘运算若\（＼lambda\）为实数，＼（＼overrightarrow{a} ＝（x,y,z)＼），则\（＼lambda\overrightarrow{a} ＝（＼lambda x, ＼lambda y, ＼lambda z)＼）数乘运算的规律：＼（＼lambda （＼overrightarrow{a} ＋＼overrightarrow{b}）＝＼lambda\overrightarrow{a} ＋＼lambda\overrightarrow{b}＼）3、数量积空间向量的数量积\（＼overrightarrow{a} ＼cdot ＼overrightarrow{b} ＝｜＼overrightarrow{a}｜｜＼overrightarrow{b}｜＼cos ＜＼overrightarrow{a}，＼overrightarrow{b}＞＼）若\（＼overrightarrow{a} ＝（x_1,y_1,z_1)＼），＼（＼overrightarrow{b} ＝（x_2,y_2,z_2)＼），则\（＼overrightarrow{a} ＼cdot ＼overrightarrow{b} ＝ x_1x_2 ＋ y_1y_2 ＋ z_1z_2\）数量积的性质：＼（＼overrightarrow{a} ＼perp ＼overrightarrow{b} ＼Leftrightarrow ＼overrightarrow{a} ＼cdot ＼overrightarrow{b} ＝ 0\）＼（＼overrightarrow{a} ＼cdot ＼overrightarrow{a} ＝｜＼overrightarrow{a}｜＾2\）4、向量积空间向量的向量积\（＼overrightarrow{a} ＼times ＼overrightarrow{b}＼）是一个向量，其模长为\（｜＼overrightarrow{a}｜｜＼overrightarrow{b}｜＼sin ＜＼overrightarrow{a}，＼overrightarrow{b}＞＼），方向垂直于\（＼overrightarrow{a}＼）和\（＼overrightarrow{b}＼）所确定的平面，遵循右手定则。

1.3.2 空间向量运算的坐标表示教学设计一、内容和内容解析1.内容：空间向量的坐标运算；根据向量坐标判断两向量平行或垂直；向量长度公式；两向量夹角公式、空间两点间距离公式。

2.内容解析本节课是人教A版高中数学选择性必修第一册第一章第三节的第二课时。

引入空间直角坐标系，为学生学习立体几何提供了新的方法，为培养学生思维提供了更广阔的空间。

本节课是在学生学习了空间向量及其运算和基本定理的基础上进一步学习空间向量运算的坐标表示，是平面向量运算的坐标表示在空间的推广，是运用向量坐标运算解决几何问题的基础.二、目标和目标解析1.目标（1）掌握空间向量运算的坐标表示（2）通过向量坐标判断两向量特殊位置关系（3）掌握向量长度公式、两向量夹角公式、空间两点间距离公式（4）培养学生类比思想、转化思想，提升学生“数学运算”和“逻辑推理”学科素养2.目标解析（1）掌握空间向量加减、数乘、数量积的坐标运算（2）会根据向量的坐标，判断两个向量平行或垂直（3）能根据向量的坐标计算出向量的模长，两向量夹角和空间两点距离，并能解决简单的立体几何问题三、教学问题诊断分析1.教学问题诊断：（1）空间向量运算的坐标表示同平面向量运算的坐标表示类似，可以类比平面向量运算的坐标表示进行推广，但怎样推广是学生的困难所在（2）学生难将向量坐标运算的代数结果与几何问题进行转化，利用空间向量运算的坐标表示解决一些立体几何问题是教学中的难点2.教学重点：空间向量的坐标运算，空间向量平行和垂直的条件，距离公式，夹角公式3.教学难点：运用空间向量的坐标运算解决立体几何问题四、教学支持条件：多媒体辅助教学五、教学过程设计(一）知识回顾平面直角坐标系空间直角坐标系空间点和空间向量的坐标表示【设计意图】回顾上节课所学内容，为本节课的学习作铺垫。

(二）类比得到空间向量运算的坐标表示【探究一】有了空间向量的坐标表示，你能类比平面向量的坐标运算，得到空间向量运算的坐标表示并给出证明吗？平面向量运算的坐标表示 空间向量运算的坐标表示{}123123123123111213212223313233,,,,()()10设为空间的一个单位正交基底，则所以因为，所以a a a b b b a a a b b b a b a b a b a b a b a b a b a b a b =++=++=++++=++++++++======i j k a i j k b i j k a b i j k i j k i i i j i k j i j j j k k i k j k k i i j j k k i j j k k i a b 112233.a b a b a b =++其他运算的坐标表示可以类似证明。