当前位置：文档之家 › 工程力学 第三章 一般力系的简化

工程力学 第三章 一般力系的简化

  • 格式：ppt
  • 大小：2.39 MB
  • 文档页数：46

下载文档原格式

  / 46

合集下载

《工程力学》第三章 平面一般力系

《工程力学》第三章 平面一般力系
• 运用解析法：在力系所在平面上取坐标系 O -xy(图3-3(a))，应用合力投影定理， 则由(3-2)式得
• 故主矢R′的模为
• 主矢R′的方向从图3-3(b)中可知
图3-3
• 2.对点O的主矩 • 从图3-3(b)中可知，MO应是该平面一般力偶
系m1，m2，…，mn的合力偶矩。由平面力偶 系的合成定理可知，
• 由于Fd也等于力F对B点的矩，mB(F)=Fd，于 是得
• §3-2 平面一般力系向一点的简化 • 一、平面一般力系向一点的简化 • 在力系的作用平面内，被任选的一点O称为简
化中心。将力系中诸力平移至简化中心，同时 附加一个力偶系的过程，称为力系向给定点的 简化。
图3-2
•经 简 化 后 的 平 面 共 点 力 系 合成为一个合力R′，该合力作用点在简化 中心上；把简化后的附加力偶系m1， m2，…，mn合成得一力偶MO(图32(c))。自然，依据力的平移定理，可将 力R′和MO合成为一个力R(图3-2(d))， 这个力R就是原力系F1，F2，…，Fn的合 力。
• 二、截面法求桁架内力
• 截面法一般采用如下步骤：
• (1)先求出桁架支承约束反力。
• (2)如需求某杆的内力，可通过该杆作一 假想截面，将桁架截为两段(只截杆件， 不能截在节点上)。注意被截杆件一般不 能多于三根。任选半边桁架考虑平衡，在 杆件被截处，画出杆件内力，其指向假定 沿杆件而背离杆件被截处。
图3-5
• 二、平面一般力系向一点简化结果分析
• 1.平面一般力系向一点的简化结果
• 平面一般力系向简化中心简化，其结果可能出现 四种情况：
• (1)R′=0，MO=0
• 主矢和主矩均等于零。它表明简化后的平面汇交 力

工程力学-平面任意力系

工程力学-平面任意力系
即：
R' ( X )2 (Y )2 0
LO mO (Fi ) 0
①一般式 （一矩式）
X 0
平面力系中各力在直角坐标系oxy中
Y 0
各坐标轴上投影的代数和及对任意
点的力矩的代数和均为0。
mO (Fi ) 0
②二矩式
∑X=0 或∑Y=0
mA(Fi ) 0
mB (Fi ) 0
AB O
工程中的桁架结构
桁架的优点：轻，充分发挥材料性能。
桁架的特点：①直杆，不计自重，均为二力杆；②杆端铰接；
力
学 中 的 桁 架 模
基 本 三 角 形
型
③外力作用在节点上。
力
学
中 的 桁 架
简 化 计 算 模
模型
型
力
学
中 的 桁 架
简 化 计 算 模
节点
杆件
模型
型
一、节点法 [例3-3] 已知：如图 P=10kN，求各杆内力？
第三章 平面任意力系
平面任意力系（General coplanar force systems)：各力的作用 线在同一平面内，既不汇交为一点又不相互平行的力系叫∼。
[例]
研究方法：把未知力系（平面任意力系）变成已知 力系（平面汇交力系和平面力偶系）
第三章 平面一般力系
§3–1 力向一点平移 §3–2 平面力系的简化 §3–3 平面力系的平衡条件 §3–4 刚体系统的平衡问题 §3–5 考虑有摩擦时物体的平衡问题
§3-2 平面力系的简化
一、平面力系向作用面内一点简化
O: 简化中心
主矢（Principal vector) R Fi
大小： R' R'x2 R'y2 ( X )2 (Y )2

《工程力学：第三章-力系的平衡条件和平衡方程》解析

《工程力学：第三章-力系的平衡条件和平衡方程》解析

工程力学 1. 选择研究对象。以吊车大梁 AB为研究对象，进行受力分析 （如图所示） 2.建立平衡方程
第三章 力系的平衡条件和平衡方程
FAX FTB cos 0 Fy 0
F
x
0
： （1）
M
FAy FQ FP FTB sin 0
A
(F ) 0
工程力学
第三章 力系的平衡条件和平衡方程
§3.3 考虑摩擦时的平衡问题
3.3.1 滑动摩擦定律
概念：
静摩擦力：F 最大静摩擦力：Fmax 滑动摩擦力： Fd
静摩擦因数：
水平拉力： Fp
Fmax f s FN
fs
工程力学
第三章 力系的平衡条件和平衡方程
3.3.2 考虑摩擦时构件的平衡问题
考虑摩擦力时与不考虑摩擦力时的平衡 解题方法和过程基本相同， 但是要注意摩擦力的方向与运动趋势方向相反；且在滑动之前摩擦 力不是一个定值，而是在一定范围内取值。
l l sin 0
（3）
工程力学
第三章 力系的平衡条件和平衡方程
• 联立方程（1）（2）（3）得：
FAX
FQ FP 3 l x 2
（2）由FTB结果可以看出，当x=L时，即当电动机移动到大梁右 端B点时，钢索所受的拉力最大，最大值为
非静定问题：未知数的数目多于等于独立的平衡方程的数目，不能 解出所有未知量。相应的结构为非静定结构或超静定结构。
会判断静定问题和非静定问题
工程力学
第三章 力系的平衡条件和平衡方程
工程力学
第三章 力系的平衡条件和平衡方程
3.2.2 刚体系统平衡问题的特点与解法
1.整体平衡与局部平衡的概念 系统如果整体是平衡的，则组成系统的每一个局部以及每一个 2.研究对象有多种选择 刚体也必然是平衡的。

工程力学基础第3章 力系的静力等效和简化

工程力学基础第3章 力系的静力等效和简化

二、力系简化的最终结果 根据力系主矢和主矩的性质，力系可最终简化为下列四种情形 1 2 3 4 平衡力系 即与零力系等效。其条件为主矢F′R=0，主矩M 该力偶称为力系的合力偶。力系存在合力 该力称为力系的合力。
O=0 单一等效力偶 单一等效力 力螺旋 偶的条件为主矢F′R≠0，主矩MO≠0。 在最一般的情况下，力系的主矢和主矩不垂直
三、平面力系的简化结果
（1）沿直线路面行驶的汽车，若不考虑由于路面不平引起的
左右摇摆和侧滑，则由汽车所受的重力、空气阻力及地面对车 轮的约束力构成的空间力系将对称于汽车的纵向对称面。将该 力系向汽车的纵向对称面简化，就可得到一个平面一般力系， 如图3-11 （2）工厂车间里的桥式起重机，梁的自重、起重机小车的自 重和起吊物的重量均作用在梁的纵向对称面内。梁两端四个车 轮的约束力也对称于该平面，故该力系可简化为梁纵向对称面 内的一个平面力系，如图3-12所示。
图3-3
力的平移定理
可以把作用于刚体上点A的力F平行移动到任一
点O，同时附加一个力偶，其力偶矩矢M等于力F对点O的力矩
矢，即M=MO（F），则平移后得到的新力系与原力系等效， 如图3-4 力的平移定理可以直接用等效力系定理来证明。反之，作用于 同一刚体的同一平面内的一个力和一个力偶（即力偶矩矢和力 矢垂直时），可以用一个力等效代替。
（一般）力系，这是力系的最一般的形式。当力系中各力的作 用线位于同一平面内时，称为平面（一般）力系，这是工程实 际中常见的重要情形。有些空间力系通过等效转换的方法也可 以变为平面力系。如果力系中各力的作用线交于一点，则称为 汇交力系。如果力系全部由力偶组成，则称为力偶系。汇交力 系和力偶系也有空间和平面两种情形，汇交力系和力偶系是两
图3-4

平面一般力系的简化

平面一般力系的简化
O m2
F1
m1
x
F2
(a)
(b)
1.简化方法
向一点简化
一般力系（任意力系）
（未知力系）
FR（已知力系）
汇交力系合力
4
附加力偶的合力偶矩
2.主矢与主矩
①. 主矢：指原平面一般力系各力的矢量和
。
主矢 的 解析求法
大小： 方向： 注意：因以主它矢与等简于化原中力心系的各位力置的无矢关量。和,所
4、固定端（插入端）约束 在工程中常见的有：
A 雨搭
车刀
固定端（插入端）约束的构造
Fi A
约束反力
①认为Fi这群力在同一 平面内;
7
MA
FA
A
MA A
FA y FA x
② 将Fi向A点简化得一 力和一力偶;
③FA方向不定可用正交 分力FAx, FAy表示;
④ FAx, FAy ,MA为固定端 约束反力; ⑤ FAx, FAy限制物体平动, MA为限制转动。
A (a)
B F
F A (b)
m B A
(c)
2
讨论
①力线平移定理揭示了力与力偶的关系：力 力+力偶
②力线平移定理可考察力对物体的作用效应。
P
e
O
A
P
m
O
A
（刚体、变形体两 种情况）
③力线平移定理是力系简化的理论基础。 3
二、 平面一般力系向一点简化
Fn
An O
A2
F1
A1 F2
y Fn mn
5
②主矩：指原平面一般力系对简化中心之矩的代数和 。
大小：
主矩 MO 正、负规定 ： 转向 +

工程力学第三章-力系的平衡

工程力学第三章-力系的平衡

将上式两边向x、y、z 轴投影，可得平衡方程
F F F
可以求解3个未知量。
x y
z
0 0 0
• 2.平面汇交力系
力系的平衡
• 力偶系的平衡方程 • 1.空间力偶系
平衡的充要条件（几何条件） M Mi 0 将上式两边向x、y、z 轴投影，可得平衡方程
M M M
可以求解3个未知量。
ix iy iz
0 0 0
• 2.平面力偶系
力系的平衡
• 平衡的充要条件:力偶系中各力偶矩的代数和等于零.
m 0
i
• 任意力系的平衡方程 空间任意力系： • 平衡的充要条件:力系的主矢和对任一点的主矩均为零。
FR 0
MO 0
G3 a
e
G 3(a b) FNAb G1e G 2L 0 G 3(a b) G1e G 2L FNA 2 b
由(1)、(2)式 得：
G1 G2 L
G1e G 2L G3 ab
3
A FN A b
B FN B
(2)空载时
不翻倒条件：FNB≥0 (4) 由 mA 0 得：
FAB = 45 kN
600
y B TBC 15 15 30 TBD
0 0 0
x
C
D
150
B
300
TBD=G E
A
E
FAB G
解题技巧及说明：
1、一般地，对于只受三个力作用的物体，且角度特殊时用 几 何法（解力三角形）比较简便。 2、一般对于受多个力作用的物体，且角度不特殊或特殊， 都用解析法。 3、投影轴常选择与未知力垂直，最好使每个方程中只有一 个未知数。

工程力学--平面一般力系解读

工程力学--平面一般力系解读
Fi Fi
作用在简化中心。是各力的矢量和，所以与简化中心位置无关。
主矩 MO m1 m2 m3
mi
mO (F1) mO (F2 ) mO (Fi )
是各力对简化中心的力矩之和，所以与简化中心位置有关。
例题 1 已知平面任意力系如图，F1 100 2N , F2 100N , F3 50N
由于主矢和主矩都不为零，所以最后合成结果是一个合力FR。如图所
示。 合力FR到O点的距离
d
MO FR
0.51
m
例题 3 水平梁AB受三角形分布的载荷作用，如图所示。载荷的最大集
度为q， 梁长l。试求合力作用线的位置。
F
q A
解：在梁上距A端为x的微段dx上，作 q 用力的大小为q’dx，其中q’ 为该处的载 B x 荷集度 ，由相似三角形关系可知
列平衡方程得：
X XA 0 Y YA NB P 0
mA (Fi ) P 2a NB 3a 0
解得： YXAAP30
N
B
2P 3
例题 5 如图所示，支架的横梁AB与斜杆DC彼此以铰链C连接，并各以铰链
A，D连接于铅直墙上。已知AC=CB，杆DC与水平线成45o角；载荷F=10 kN，
(2)当Q=180kN，满载W=200kN时，由平面平行力系的平衡方程可得：
Fi Q P W NA NB 0 mA (F ) Q(6 2) P 2 W (12 2) NB 4 0
解得：
N N
A B
210 870
kN kN
•§3-6 静定与静不定问题的概念
一、静定与静不定问题的概念
作用于B处。设梁和杆的重量忽略不计，求铰链A的约束力和杆DC所受的力。
AA

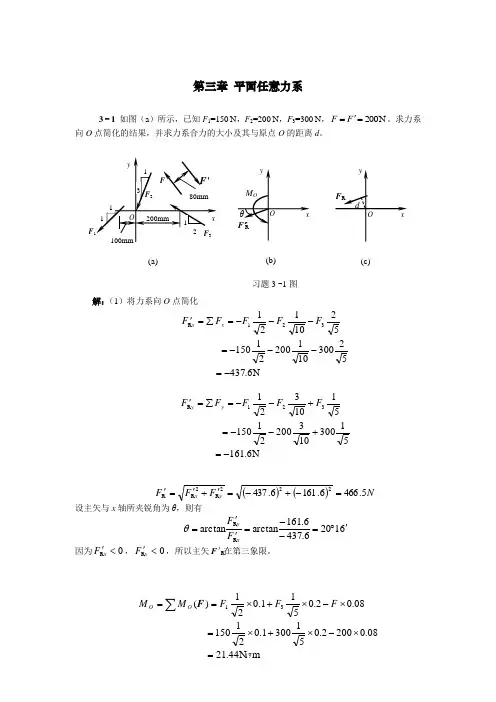
gxt3第三章工程力学课后题答案

gxt3第三章工程力学课后题答案

第三章 平面任意力系3-1 如图（a ）所示，已知F 1=150N ，F 2=200N ，F 3=300N ，N 200='=F F 。

求力系向O 点简化的结果，并求力系合力的大小及其与原点O 的距离d 。

解：（1）将力系向O 点简化N6.43752300101200211505210121321R-=---=---=∑='F F F F F x xN6.16151300103200211505110321321R-=+--=+--=∑='F F F F F y y()()N F F F y x 5.4666.1616.437222R 2R R=-+-='+'='设主矢与x 轴所夹锐角为θ，则有61206.4376.161arctanarctanRR '︒=--=''=x y F F θ因为0R <'x F ，0R <'y F ，所以主矢F ＇R在第三象限。

08.02002.0513001.02115008.02.0511.021)(31⨯-⨯+⨯=⨯-⨯+⨯==∑F F F M M O O F(a)(b) (c)将力系向O 点简化的结果如图（b ）。

(2)因为主矢和主矩都不为零，所以此力系可以简化为一个合力如图（c ），合力的大小mm 96.4504596.05.46644.21N 5.466RR R ====='=m F M d F F o3-2重力坝的横截面形状如图（a ）所示。

为了计算的方便，取坝的长度（垂直于图面）l =1m 。

已知混凝土的密度为2.4×103 kg/m 3，水的密度为1×103 kg/m 3，试求坝体的重力W 1，W 2和水压力P 的合力F R ，并计算F R 的作用线与x 轴交点的坐标x 。

解：（1）求坝体的重力W 1，W 2和水压力P 的大小kNN dy y dy y q P mN y dyy dy y q 5.9922105.9922245108.9)45(108.9)()45(108.9)45(8.91011)(3234534533=⨯=⨯⨯=⋅-⨯=⋅=-⨯=-⨯⨯⨯⨯⨯=⎰⎰（2）将坝体的重力W 1，W 2和水压力P 向O 点简化，则kN 5.9922R==∑='P F F x xkN 3057621168940821R-=--=--=∑='W W F F y y()kN 7.32145305765.9922222R 2R R=-+='+'='y x F F FkN N W kN N W 2116810211688.9104.2136)545(2194081094088.9104.218)545(332331=⨯=⨯⨯⨯⨯⨯+==⨯=⨯⨯⨯⨯⨯+=(a) (b) (c)设主矢与x 轴所夹锐角为θ，则有︒=-=''= 02.725.992230576arctanarctanRR x y F F θ因为0R >'x F ，0R <'y F ，所以主矢F ＇R在第四象限，如图（b ）。

工程力学习题册第三章 答案

工程力学习题册第三章 答案

第三章平面一般力系答案一、填空(将正确的答案填写在横线上)1、作用在物体上的各力的作用线都在同一平面内 ,并呈任意分布的力系,称为平面一般力系。

2、平面一般力系的两个基本问题是平面力系的简化 ,其平面条件的的应用。

3、力的平移定理表明,若将作用在物体某点的力平移到物体上的另一点,而不改变原力对物体的作用效果,则必须附加一力偶,其力偶距等于原来的力对新作用点的距。

4、平面一般力系向已知中心点简化后得到一力和一力偶距。

5平面一般力系的平衡条件为;各力在任意两个相互垂直的坐标轴上的分量的代数和均为零力系中所有的力对平面内任意点的力距的代数和也等零。

6.平面一般力系平衡方程中,两个投影式ΣFix=0 和ΣFiy=0 保证物体不发生移动 ;一个力矩式ΣMo(Fi)=0 保证物体不发生转动。

三个独立的方程,可以求解三个未知量。

7.平面一般力系平衡问题的求解中,固定铰链的约束反力可以分解为相互垂直的两个分力固定端约束反力可以简化为相互垂直的两个分力和一个附加力偶矩。

8.平衡方程ΣMA(Fi)=0、ΣMB(Fi)=0、ΣFiX=0适用于平面一般力系,使其用限制条件为AB连线与X轴不垂直。

9.平衡方程ΣMA(Fi)=0、ΣMB(Fi)=0、ΣMc(Fi)=0的使用限制条约为ABC不在同一直线上。

10.若力系中的各力作用现在同一平面内且相互平行,称为平面平行力系。

它是平面一般力系的特殊情况。

11.平面平行力系有两个独立方程,可以解出两个未知量。

12.平面平行力系的基本平衡方程是：ΣFi X=0，ΣM O(Fi)=0二、判断题（正确的打“√”，错误的打“×”）1.作用于物体上的力,其作用线可在物体上任意平行移动,其作用效果不变。

(×)2.平面一般力系的平衡方程可用于求解各种平面力系的平衡问题。

(√)3.若用平衡方程解出未知力为负值,则表明：(1)该力的真实方向与受力图上假设的方向相反。

(√)(2)该力在坐标轴上的投影一定为负值。

平面一般力系的简化

平面一般力系的简化

（2-14）
平面一般力系的简化
图2-9
于是得合力矩定理：平面任意力系的合力对力系所在平面内任意 点的矩等于力系中各分力对同一点的矩的代数和。根据平面任意力系 与其合力的等效关系，平面任意力系的合力矩定理很容易理解。
平面一般力系的简化
（4）当F′R=0,MO=0时，平面任意力系为 平衡力系。
由上面（2）、（3）可以看出，不论主矩是 否为零，只要主矢不等于零，力系最终简化为一 个合力，且合力的大小、方向与主矢相同，合力 的作用线与主矢间的距离
其中，主矢的大小和方向余弦可按下式求解：
（2-12）
平面一般力系的简化
1.2 平面任意力系简化结果的讨论
（1）当F′R=0,MO≠0时，简化为一个力偶。显见：作用在 简化中心O点的平面汇交力系F′1、F′2、…、F′n是一个平衡力系， 可以减去。原力系等效为平面力偶系M1、M2、…、Mn，此时的 合力偶矩与简化中心的位置无关，主矩MO为原力系的合力偶。
（2-11b）
平面一般力系的简化
结论：平面任意力系向力系所在平面内任意一点简化，得到主 矢和主矩，如图2-8(c)所示，主矢的大小和方向只与原力系中各力 的大小和方向有关，与简化中心的位置无关，其作用线经过简化中 心；而主矩的大小和转向不仅与原力系中各力的大小和方向有关， 一般还和简化中心的位置有关面内任意一点简化：主矢与主矩
设刚体上作用有n个力F1、F2、…、Fn组成平面任意力系，如 图2-8（a）所示。在力系所在平面内任取一点O作为简化中心，根 据力的平移定理，将力系中各力向O点平移，如图2-8（b）所示。
图2-8
平面一般力系的简化
得到一个作用于O点的平面汇交力系F′1、F′2、…、F′n， 和一个附加平面力偶系，其矩分别为M1、M2、…、Mn。显 然，力F′i和Fi大小相等，方向相同，力偶Mi的矩等于力Fi对 简化中心O点的矩为

力系的简化和平衡方程

力系的简化和平衡方程

表示，并 合成为一
个作用在点
O'
的力
v R
如图
3—2
所示。
R΄ O M O΄΄
R′ OR
R″O΄
Od R O΄
（a）
（b） 图 3-2
（c）
这个力
v R
就是原力系的合力，合力矢等于主矢，合力的作用线在
O
的哪一侧，需根
据主矢和主矩的方向确定；合力作用线到点 O 的距离 d，可按下式计算。
d = M0 R
必须指明是力系对哪一点的主矩。
二、简化结果的讨论
由于平面任意力系对刚体的作用决定于力系的主矢和主矩，因此，可由这两个物理
量来研（究一力）系若简主化矢的Rv最′ =后0 ，结主果矩。M 0 ≠ 0 ，则原力系与一力偶等效。此力偶称为平面任意
力系的合力偶，合力偶矩等于
M0
=
n
v
∑ m0 (Fi )
。由力偶的性质可知，力偶对任意点的力
一、平面任意力系向作用面内一点简化、主矢和主矩
设刚体上作用一平面任意力系
v F1 ,
v F2
⋅⋅⋅
⋅
⋅
⋅Fvn
如图(3—1)。根据力的平移定理，将力
矩系Fv1'分中, Fv别诸2' ..等力....F于向vn' 力平,以面MFv及11内,=F相v任2M应⋅ ⋅一0⋅(的⋅F点⋅v1⋅附F)vnO加对点M力O平2偶点=移系M的，0M矩(OF1v,,2M)点即2称:..M..为..3M简=nM化。0这中(Fv些心3 )力。偶这作样用得在到同作一用平于面O内点,它的们力系的
θ
态。取料斗车为研究对象，对料斗车进行受力分析，所
O
受力有：重力

工程力学-平面任意力系的简化教案

工程力学-平面任意力系的简化教案

一、 导入1、平面任意力系引论2、特殊力系二、 新授2.1 平面任意力系的简化2.1.1 平面任意力系向一点简化1.主矢 (平面汇交力系各力的矢量和)：∑∑=+⋅⋅⋅++==+⋅⋅⋅++=F F F F F FF F F nnR21'''2'1'在平面直角坐标系oxy 中，根据合力投影定理∑∑=+⋅⋅⋅++==+⋅⋅⋅++=xnxxx xnxx xRxF F F F F FF F F 21'''2'1'∑∑=+⋅⋅⋅++==+⋅⋅⋅++=ynyyyynyy yRyFF F F F FF F F 21'''2'1')主矢大小：222'2'')(()()(y x Ry Rx R F F F F F +=+=∑主矢方向：∑=Xy F F αtan2.主矩 (附加平面力偶系的合力偶):∑∑==+⋅⋅⋅++=+⋅⋅⋅++=MM M M M MM M M onooono)()()()(2121F F F F 注意：(1)一般情况下主矩与简化中心O 位置的选择有关(2)原力系与主矢和主矩的联合作用等效。

3. 结论：平面力系向一点（简化中心）简化的一般结果是一个力和一个力偶；这个力作用于简化中心，称为原力系的主矢，它等于原力系中所有各力的矢量和；这个力偶称为原力系对简化中心的主矩，它等于原力系中所有各力对于简化中心力矩的代数和。

2.1.2 简化结果的讨论 1．主矢F ，主矩 M (一般情况)合力的大小 F 、方向与主矢 F 相同；合力F 的作用线与简化中心O 点的垂直距离D=M/F2. 主矢F 不等于0，主矩 M=03. 主矢F =0，主矩 M 不等于04. 主矢F =0，主矩 M=0平面任意力系平衡的必要和充分条件为：主矢F =0 主矩M=0例2.1 一端固定于墙内的管线上受力情况及尺寸如图2.3a 所示，已知F 1=600N ，F 2=100N ，F 3=400N 。

工程力学第3节 平面一般力系

工程力学第3节 平面一般力系

• 2）力偶 M 对平面上任意一点的矩为常量。
• 3）应尽量选择各未知力作用线的交点为力矩方 程的矩心，使力矩方程中未知量的个数尽量少。
例2-10 如图所示一可 沿轨道移动的塔式起重 机，机身重G=200kN， 作用线通过塔架中心。 最大起重量FP=80kN。 为防止起重机在满载时 向右倾倒，在离中心线 x 处附加一平衡重FQ， 但又必须防止起重机在 空载时向左边倾倒。试 确定平衡重FQ以及离左 边轨道的距离 x 的值。
i 1 i 1 n i 1 n
n
• 二力矩式：A、B 两点的联线 AB 不能与 x 轴垂直。 • 三力矩式：A、B﹑C 三点不能共线。 • 选用基本式﹑二力矩式还是三力矩式，完全决定于 计算是否方便。不论何种形式，独立的平衡方程只 有三个。
四
平面平行力系的平衡方程
平面平行力系平衡的充分 必要条件是：力系中各力的代 数和等于零，以及各力对任一 点的矩的代数和等于零。 平衡方程 的解析式 （基本式） 注意
Fiy 0 M O ( Fi ) 0
i 1 M A ( Fi ) 0 M B ( Fi ) 0
i 1 i 1 n
n
二力矩式中A、B 两点的联线不能与 x 轴垂直。
例2-7 如图所示，数控车床一齿轮转动轴自重 G = 900N，水平安装在向心轴承A和向心推力轴承B 之间。齿轮受一水平推力F 的作用。已知 a = 0.4m， b = 0.6m，c = 0.25m，F = 160N。当不计轴承的宽度 和摩擦时，试求轴上A、B处所受的约束反力。
Fiy 0 M O ( Fi ) 0
i 1 i 1 n
i 1 n
二 力 矩 式 注意
Fix 0 M A ( Fi ) 0 M B ( Fi ) 0

工程力学-力系的简化

工程力学-力系的简化

A xC
q(x)
xB
FR q(x)dx
Bx
xA
合力作用线：
xB
q(x)xdx
x xA
C
xB
对面分布载荷，积分元改为dA
q(x)dx
xA
32
工程上常见的分布载荷：
qF
xC
l
F
xC l
q1
F
xC l
（1）均布载荷q(x)=q=常数
F=ql , xC=l/2 （2）三角形载荷
F=ql /2 , xC=2l/3
FRx FRy FRz
(力的作用线)方程: x xB y yB z zB
B(xB , yB , zB )
为合力的作用点 15
小结 力系简化的步骤：
（1）任选矩心O，求出力系 的主矢和主矩。
FR Fi MO MO (Fi )
若主矢和主矩全为零
平衡力系(零力系)
若主矢和主矩不全为零，则进一步计算(2)：
FRO
原一般力系简化为一个作用于O点的合力 FR
——最简力系
9
4.
FR 0, MO
MO 0,
FR
FR MO 0
即 FR MO
MO
FR
O
O
原力系简化为过O点的合力
FR
及合力偶，且 FR MO
B (xB,yB,zB) 合力作用线
——不是最简力系
根于据B点力的的合平力移逆FB定 理FR，，二B者点可位进置一为步简OB化为F一R F个R2M 作O 用
简化后的合力作用点B的位置为
OB
F1 M
F12
即将即F1力O平B行于F1其,O作B用线M移, 动OBO距B 离 成MF1为F

理论力学第三章 任意力系的简化与平衡条件

理论力学第三章 任意力系的简化与平衡条件

例3-2 已知：涡轮发动机叶片轴向力F=2kN，力偶矩
M=1kN.M, 斜齿的压力角=20 ,螺旋角 。 =10 ,齿轮节圆半径 r=10cm。不计发动 机自重。 O1O2=L1=50cm, O2A=L2=10cm. 求： FN, O1,O2处的约束力。
。
第三章 力系的简化与平衡条件
§3-5 力系的平衡条件
3
F2 F3
1
F'
F1
1 O 200 1
x
2
1 3 1 FRy F1 F2 F3 = -161.6(N) 2 10 5
第三章 任意力系的简化与平衡条件
§3-4 力系简化计算
解：(1)先将力系向O点简化，求主矢和主矩。 FRx FRy =466.5(N) 2 2 FR
Xi 0 F x F2x Fr 0 1
F y F2y F 0 1
Zi 0
F z Fa F 0 1
第三章 力系的简化与平衡条件
§3-5 力系的平衡条件
例3-2 解： 3、列平衡方程
Mx (F) 0
F2 y L1 F (L1 L2 ) 0
y
100 1
F
80
3
Байду номын сангаас
F2 F3
1
F'
F1
1 O 200 1
x
2
第三章 任意力系的简化与平衡条件
§3-4 力系简化计算
例3-1 (1)先将力系向O点简 解： 化，求主矢和主矩。 1 1 F2 FRx F1 10 2 2 F3 5 = -437 .6（N）
y
100 1
F

工程力学(李卓球) 第3章 力系的简化和平衡

工程力学(李卓球) 第3章 力系的简化和平衡

∑X =0 ∑Y = 0 ∑M = 0
O
3.2
力系的平衡条件和平衡方程 ∑X =0
∑Y = 0 ∑F = 0
z
y
F1 F2
4 5 3
F3
∑M
x
=0
y
O
x
∑M ∑M
平面汇交力系
=0
=0
z
∑ ∑
X = 0
Y = 0
Y = 0
M
O
平面平行力系
∑ ∑
( Fi ) = 0
3.2
力系的平衡条件和平衡方程
四、平面任意力系平衡方程的其他形式 (1)二力矩式 二力矩式
3.2
力系的平衡条件和平衡方程
平面平行力系的平衡方程
∑ ∑ ∑
Fx = 0
∑ M ∑ M
A B
(F i ) = 0 (Fi ) = 0
Fy = 0
M
O
(Fi ) = 0
∑
Fx = 0
A
B
∑Y ∑M
= 0
O
∑ M
(F i ) = 0
(Fi ) = 0
∑
M
(Fi ) = 0
AB连线与力不平行 连线与力不平行 只有两个独立方程，只能求解两个独立的未知数。 只有两个独立方程，只能求解两个独立的未知数。
h h
γy (1 × dy )
dy
= γy
1 2 γh 2
由合力矩定理， 由合力矩定理，有
1 Qd = ∫ yqdy = ∫ γy dy = γh 3 0 0 3
h h 2
d=
2 h 3
3.1
力系向一点简化
y A
2m
在长方形平板的O 例题 3-2 在长方形平板的 、A、 B、C 点上分别作用着有四个力： 点上分别作用着有四个力： F1=1kN，F2=2kN，F3=F4=3kN ， ， 如图）， ），试求以上四个力构成 （如图），试求以上四个力构成 的力系对点O 的简化结果， 的力系对点 的简化结果，以及 该力系的最后的合成结果。 该力系的最后的合成结果。 取坐标系Oxy。 解：取坐标系 。 1、求向 点简化结果： 点简化结果： 、求向O点简化结果 求主矢R′ ①求主矢 ′：

工程力学第三章：平面任意力系

工程力学第三章：平面任意力系

水平尾翼的约束。
车刀
利用平面任意力系的简化讨论固定端约束（以雨搭为例）：
Fi
A
雨搭
雨搭
简化为一个平面任意力系
MA
A
FA
雨搭
FAy
MA
A
FAx
雨搭
向A处简化，简化结果是 一个主矢加一个主矩
主矢方向待定，用两正交分 量表示
例1：已知F1=150N，F2=200N，F3=300N，F=F ́=200N。求此力 系向原点O简化的结果，并求力系的合力。
2
M=0
FR′≠0
3
M=0
合力
合力
合力作用线通过简化中心
合力作用线距离简化中心距离
4
M≠0
d M O / FR
第三种和第四种结果属于同一种情形。是简化中心选择的不同 引起的。
四、合力矩定理
可以证明，M O ( FR ) M O ( Fi )
i 1
n
由于简化中心可任取，因此上式有普遍意义，可描述为：平 面任意力系的合力对作用面内任一点之矩等于力系中各分力 对于同一点之矩的代数和。
4、在列平衡方程时，最好将力矩方程的矩心取为两个未知力的 交点，而对投影方程的投影轴的选取，应尽可能使其与某些未知 力垂直，为什么？ 答：避免解联立方程，使方程尽量简单。
5、在等腰直角三角形上的A、B、C三点分别作用三个力，各力 的大小和方向如图所示。问该力系是否平衡？为什么？
问题引入：平面任意力系研究物体或物系在受到相关力系作用
下的平衡问题。
吊车：工程中吊车的
起重载荷如何进行计
算？
破碎机：鄂式破碎机是矿山机械中常见的机械设备，颚板作用 给矿石的作用力应如何进行计算？

工程力学(天津大学)第3章答案

工程力学(天津大学)第3章答案

习 题3-1 如图（a ）所示，已知F 1=150N ，F 2=200N ，F 3=300N ，N 200='=F F 。

求力系向O 点简化的结果，并求力系合力的大小及其与原点O 的距离d 。

解：（1）将力系向O 点简化N6.43752300101200211505210121321R-=---=---=∑='F F F F F x xN6.16151300103200211505110321321R-=+--=+--=∑='F F F F F y y()()N F F F y x 5.4666.1616.437222R 2R R=-+-='+'='设主矢与x 轴所夹锐角为θ，则有61206.4376.161arctanarctanRR '︒=--=''=x y F F θ因为0R <'x F ，0R <'y F ，所以主矢F ＇R在第三象限。

mN 44.2108.02002.0513001.02115008.02.0511.021)(31⋅=⨯-⨯+⨯=⨯-⨯+⨯==∑F F F M M O O F(a)(b) (c)将力系向O 点简化的结果如图（b ）。

(2)因为主矢和主矩都不为零，所以此力系可以简化为一个合力如图（c ），合力的大小mm 96.4504596.05.46644.21N 5.466RR R ====='=m F M d F F o3-2重力坝的横截面形状如图（a ）所示。

为了计算的方便，取坝的长度（垂直于图面）l =1m 。

已知混凝土的密度为2.4×103 kg/m 3，水的密度为1×103 kg/m 3，试求坝体的重力W 1，W 2和水压力P 的合力F R ，并计算F R 的作用线与x 轴交点的坐标x 。

解：（1）求坝体的重力W 1，W 2和水压力P 的大小kNN dy y dy y q P mN y dyy dy y q 5.9922105.9922245108.9)45(108.9)()45(108.9)45(8.91011)(3234534533=⨯=⨯⨯=⋅-⨯=⋅=-⨯=-⨯⨯⨯⨯⨯=⎰⎰（2）将坝体的重力W 1，W 2和水压力P 向O 点简化，则kN 5.9922R==∑='P F F x xkN 3057621168940821R-=--=--=∑='W W F F y y()kN 7.32145305765.9922222R 2R R=-+='+'='y x F F FkN N W kN N W 2116810211688.9104.2136)545(2194081094088.9104.218)545(332331=⨯=⨯⨯⨯⨯⨯+==⨯=⨯⨯⨯⨯⨯+=(a) (b)(c)设主矢与x 轴所夹锐角为θ，则有︒=-=''=ο02.725.992230576arctanarctanRR x y F F θ因为0R >'x F ，0R <'y F ，所以主矢F ＇R在第四象限，如图（b ）。

力系的简化例题

力系的简化例题

两端用光滑铰链与物体和地面相连，中间不受力（重力
工 忽略不计）的刚杆称为链杆。为二力杆，可受拉或受压，
程 力
通常假设受压，求解后再确定真实方向。
学
第
A
1
章
(a)
B
(b)
力
系 的
FA
简
化
A
r FBy
r
B
FBx
29
版权所有 张强
1.4 约束和约束力
1. 柔索约束
工
程 力
2. 光滑面约束
学
3. 光滑铰链约束
负值 → 假设方向与实际方向相反。
(3) 其作用点应在约束与被约束物体相互接触处。
21
版权所有 张强
主动力
使物体运动或产生运动趋势的力，称为主动力。
工
程 力
主动力与约束力的区别（主动力的特点）
学
(1) 主动力与物体的约束条件无关，
第 1
主动力使物体运动或产生运动趋势。
章
(2) 主动力一般是给定的或可测定的外力，
r
y
F
q(x)
b
a
O Ax
C
dx
Bx
xC
力
分别是图形 ABab 的面积和形心的 x 坐标。
系
r
的 简
xC
F
q
xC
r
F
q
化
18
版权所有 张强
l
F
ql, xC
1l 2
l
F
1 2
ql,
xC
2l 3
§1.4 约束和约束反力
工 1.4.1 约束与约束反力
程
力
自由体
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

（3）、求合力作用线方程
' ' M o M o FR x FRy y FRx x FRy y FRx

即 2355 x 670.1 y 232.9 有： 670.1x 232.9 y 2355 0 求 FR 与x轴的交点 y 0
x 3.514m
§3–4
力对点的矩和力对轴的矩
1、 力对点的矩以矢量表示 ——力矩矢 三要素：
(1）大小:力F与力臂的乘积 (2)方向:转动方向 (3)作用面：力矩作用面。
（3–4）
又 则
（3–5） 力对点O的矩 在 三个坐标轴上的投影为 （3–6)
2.力对轴的矩
（3–7） 力与轴相交或与轴平行（力与轴在同一平面内）， 力对该轴的矩为零。
M O M o ( Fi ) ( xi Fiy yi Fix )
Fy cos( FR, j ) FR
(3 1)
(3 2)
3、简化结果分析
=
其中
MO d FR
o R
M o FRd
O O i
FR FR FR
(3 3)
1、空间力偶矩以矢量表示
空间力偶的三要素 （1） 大小：力与力偶臂的乘积； （2） 方向：转动方向； （3） 作用面：力偶作用面。
力偶矩矢
（3–11）
2、力偶的性质 (1）力偶中两力在任意坐标轴上投影的代数和为零 。 （2）力偶对任意点取矩都等于力偶矩，不因矩心的 改变而改变。
力偶矩
因
（3）只要保持力偶矩不变，力偶可在其作用面内 任意移转，且可以同时改变力偶中力的大小与力偶 臂的长短，对刚体的作用效果不变。
例3-7
已知：F , l , a,
M 求： x F , M y F , M z F
解：把力 F 分解如图
M x F F l a cos
M y F Fl cos
M z F F l sin
§3–5
空间力偶系
力偶矩矢
例4-13 已知：等厚均质偏心块的 R 100mm , r 17mm , b 13mm 求：其重心坐标。 解：用负面积法， 为三部分组成，设大半圆面积为 小半圆（半径为 ）面积为 , 小圆（半径为 ）面积为 ，为负值。 由对称性，有 而 ，
由
A1 y1 A2 y 2 A3 y 3 得 yC A A A 40.01mm 1 2 3
空间汇交力系的合力 称为力系的主矢
空间力偶系的合力偶矩
称为空间力偶系的主矩 由力对点的矩与力对轴的矩的关系，有
式中
分别表示各力
对
，
,
轴的矩。
力系简化的意义
—有效推进力 —有效升力 —侧向力 —滚转力矩 —偏航力矩 —俯仰力矩
飞机向前飞行 飞机上升 飞机侧移 飞机绕x轴滚转 飞机转弯 飞机仰头
2． 空间任意力系的简化结果分析（最后结果） 1） 合力 当 最后结果为一个合力。 合力作用点过简化中心。 当 时，
' Ry
' R
F Fix F1 F2 cos 232.9kN
' Rx
AB ACB arctan 16.7 AC
F 大小 FR'
F F 709.4kN 的方向余弦 cos F , i F 0.3283 F F 向下与x正 F 0.9446 向成70.84度角 cos F , j F
主矢大小 FR ( Fix ) 2 ( Fiy ) 2 方向
Fix cos( FR, i ) FR
作用点
主矩
作用于简化中心上
Fiy cos( FR, j ) FR
M O M O ( Fi ) FR ( Fx ) 2 ( Fy ) 2
Fx cos( FR, i ) FR
2. 计算的简易方法
1）利用对称性 2）分割法 3）负面积法
例4-12 已知：均质等厚Z字型薄板尺寸如图所示。 求：其重心坐标
解:厚度方向重心坐标已确定， 只求重心的x,y坐标即可。 用虚线分割如图， 为三个小矩形， 其面积与坐标分别为 A1 300mm 2 x1 15mm y1 45mm x 2 5mm y 2 30mm A2 400mm 2 A3 300mm 2 x 3 15mm y 3 5mm 则 Ai x i A1 x1 A2 x 2 A3 x 3 xC 2mm A A1 A2 A3 Ai y i A1 y1 A2 y 2 A3 y 3 yC 27mm A A1 A2 A3
例3-9 已知： 两圆盘半径均为200mm， AB =800mm, 圆盘面O1垂直于z轴，圆盘面O2垂直于x轴， 两盘面上作用有力偶，F1=3N，F2=5N，构件自重不计。 求:轴承A,B处的约束力。 解：取整体，受力图如图b所示。 由力偶系平衡方程 M x 0 F2 400mm FAz 800mm 0
(5)力偶没有合力，力偶平衡只能由力偶来平衡。
3．力偶系的合成与平衡条件
=
=
如同右图
有
为合力偶矩矢，等于各分 力偶矩矢的矢量和。
合力偶矩矢的大小和方向余弦
空间力偶系平衡的充分必要条件是 :合力偶矩矢等 于零，即
有 M ix 0 简写为
M iy M ix cos cos M M
最后结果为一合力。合力作用线距简化中心为
合力矩定理：合力对某点之矩等于各分力对同一点 之矩的矢量和。 合力对某轴之矩等于各分力对同一轴之矩的代数和。 （2）合力偶 当 时，最后结果为一个合力偶。此时与简化 中心无关。 当 ∥ 时 （3）力螺旋
力螺旋中心轴过简化中心
当
成角
且
既不平行也不垂直时
力螺旋中心轴距简化中心为
F
' R 2 2 ix iy
' R ix ' R
' R
' R
iy
主矩
M o M o F 3F1 1.5P 3.9P2 2355kN m 1

' R
（2）、求合力及其作用线位置。
Mo 2355 d 3.3197m ' FR 709.4
d x 3.514m 0 0 cos 90 70.84
M iz cos M
M iy 0
M iz 0
（3–12）
称为空间力偶系的平衡方程。
例3-8 已知：在工件四个面上同时钻5个孔，每个孔所受 切削力偶矩均为80N· m。 求：工件所受合力偶矩在 解：把力偶用 力偶矩矢表示， 平行移到点A 。 求力偶的投影 轴上的投影 。
M x M ix M 3 M 4 cos 45 M 5 cos 45 193.1N m M y M iy M 2 80N m M z M iz M 1 M 4 cos 45 M 5 cos 45 193.1N m
4、平面固定端约束
=
=
≠
=
例3-6 P 已知： 1 450kN, F1 300kN,
F2 70kN;
P2 200kN,
求： 力系的合力FR , 合力与OA的交点到点O的距离x， 合力作用线方程。
FR'
解： （1）向O点简化， 求主矢和主矩。
F Fiy P1 P2 F sin 670.1kN
第三章 一般力系的简化
一般力系实例
§3-3 平面一般力系向作用面内一点简化
1、力的平移定理
M B M B ( F ) Fd
2、平面一般力系向作用面内一点简化 ·主矢和主矩
F1 F1
F2 F2 Fn Fn

M1 M 0 ( F1 )
M 2 M 0 ( F2 ) M n M 0 ( Fn )
（4）平衡
当
时，空间力系为平衡力系
§3–7 重 心
1． 计算重心坐标的公式 对y轴用合力矩定理
质 心
有 对x轴用合力矩定理
有
再对x轴用合力矩定理
则计算重心坐标的公式为 （3–13） 对均质物体，均质板状物体，有
xc
V x
i
i
V
yc
V y
i
i
V
zc
V z
V
i i
称为重心或形心公式
3、 力对点的矩与力对过该点的轴的矩的关系
已知：力 ,力 在三根轴上的分力 用点的坐标 x, y, z ， ， ，力 作
求：力
对 x, y, z轴的矩
=
（3-8）
=
+0 -
=
（3-9）
= -
+ 0
=
（3-10）
比较（3-6）、（3-8）、（3-9）、（3-10）式可得
即，力对点的矩矢在过该点的某轴上的投影，等于 力对该轴的矩。
合力矩定理 M ( F ) M M ( F )后结果
合力 合力 合力偶 平衡
说明
合力作用线过简化中心
合力作用线距简化中心M O
FR 0 FR 0
MO 0 MO 0 MO 0 MO 0
FR
与简化中心的位置无关
与简化中心的位置无关
3． 实测法确定重心 如： 悬挂法
图a中左右两部分的重量是否一定相等？
4.质心—质点系的质量中心
rc mi r i m (3 15)
C——即为质点系的质心
投影到坐标系
xc
m x
i
i
yc
mi yi