当前位置：文档之家 › 第十章卡方检验

第十章卡方检验

  • 格式：ppt
  • 大小：759.00 KB
  • 文档页数：37

下载文档原格式

  / 37

合集下载

卡方检验医学统计学

卡方检验医学统计学

卡方检验医学统计学卡方检验是医学统计学中最常用的检验方法之一，它可用于测量两组数据之间的关联性。

在研究中，我们常常需要探究二者之间是否存在某种关联，卡方检验就是我们解决这个问题的利器。

卡方检验的原理卡方检验的原理是基于期望频数和实际频数的差异来检验两个变量之间的关系。

期望频数指的是在假设两个变量独立的情况下，我们可以根据样本量和其他条件，计算出不同组之间的理论值。

而实际频数则是实验中观察到的实际结果。

卡方检验的步骤如下：1.建立零假设和备择假设。

零假设指的是假设两个变量之间不存在任何关系，备择假设则是反之。

2.确定显著性水平 alpha，通常取值为0.05。

3.构建卡方检验统计量。

计算方法为将所有观察值与期望值的差平方后，再除以期望值的总和。

4.根据自由度和显著性水平，查卡方分布表得到 P 值。

5.如果 P 值小于显著性水平，拒绝零假设；否则无法拒绝零假设。

卡方检验的应用卡方检验可以应用于多个领域，其中医学统计学是最为常见的一个。

卡方检验可以用来分析两个疾病之间的相关性或者测量一种治疗方法的效果。

举个例子，某药厂要研发一种新的药物来治疗心脏病。

为了验证该药的疗效，实验组和对照组各50 人。

在 6 个月的治疗后，实验组和对照组中分别有 10 人和 15 人痊愈了。

卡方检验的作用就在于此时可以用来检验两组之间的差异是否具有统计学意义。

除了医学统计学之外，卡方检验在社会学、心理学、市场营销、物理等领域也都有广泛应用。

卡方检验的限制虽然卡方检验被广泛应用于各种实验和研究中，但它也有着自己的限制。

其中比较明显的一点就是对样本量有一定的要求。

当样本量较小的时候，期望频数的计算就会出现一定的误差，进而导致检验结果不准确。

此外，在面对非常态分布数据时，卡方检验也会出现问题。

当数据呈现正态分布时，卡方检验的准确性最高。

然而，实际上，很多数据都呈现出非正态分布，这时需要使用一些修正方法来解决。

卡方检验是医学统计学中最常用的统计方法之一，它可以用来测量两个变量之间的关联性。

第十章卡方检验

第十章卡方检验

2 检验的基本公式，
表，确定其差异是否显著。（常用的方法）
其关键步骤是计算理论次数与确定自由度。 （1）将实际次数分布的统计量代入所选的理论分布函数方程，求各分组 区间的理论频率，然后乘以总数得各分组区间的理论次数；
16 （2）将分组的数目减去计算理论次数时所用统计量的数目即自由度。
[例10-5] 表10-2所列资料是 552 名中学生的身高次数分布，问这些学生的 身高分布是否符合正态分布？
3、去除样本法； 4、使用校正公式。
7
第二节
察次数分布与某理论次数是否有差别。
配合度检验
配合度检验（goodness of fit test）主要用于检验单一变量的实际观
它检验的内容仅涉及一个因素多项分类的计数资料，是一种单因素检验 （one-way test）。
一、配合度检验的问题
（一）统计假设
2、根据各组的理论次数与实际次数计算
2 值，得 2 3.905
3、确定自由度。本题共分 11 组，在计算理论次数时，对最高组和最低
组两极端次数进行了合并，合并后为 9 组。在计算理论次数的过程中共用到
平均数、标准差、总数 3 个统计量，故本题的自由度 df=9-3=6 。 4、查
2 表，得 02.05 12.6， 02.01 16.8
表10-2
身高 分组 169 ~ 166 ~ 163 ~ 160 ~ 157 ~ 154 ~ 151 ~ 148 ~ Xe 170 167 164 161 158 155 152 149 fo 2 7 22 57 110 124 112 80
书中数字错！
552 名学生身高的理论次数分布及卡方检验
x 15.38 12.38 9.38 6.38 3.38 0.38 -2.62 -5.62 Z 3.03 2.44 1.85 1.26 0.67 0.07 -0.52 -1.11 y 0.0040 0.0203 0.0720 0.1840 0.3187 0.3979 0.3484 0.2154 p 0.0023 0.0120 0.0426 0.1088 0.1885 0.2354 0.2061 0.1274 fe 1 7 24 60 104 130 114 70

【实用】卡方检验(2)PPT文档

【实用】卡方检验(2)PPT文档

χ2分布有以下几个特点：
（1）χ2分布呈正偏态，右侧无限延伸， 但永不与基线相交。
（2）自由度越小，χ2分布偏斜度越大； 自由度越大，χ2分布形态越趋于对称。
P172:
从某校随机抽取50个学生，其中男生27人， 女生23人，问该校男女生人数是否相等？
第二节 单向表的卡方检验
把实得的点计数据按一种分类标准编制 成表就是单向表。对于单向表的数据所进行 的卡方检验就是单向表的卡方检验。
第十章 卡方检验
第一节 χ2及其分布
卡方检验是对总体分布是否服从某种理 论分布或某种假设分布所作的假设检验。
某小学历届毕业生汉语拼音测验平均分数 为66分，标标准准差差为1。4，以同样的试题测验应 届毕业生，从中随机抽取18份 ，算得平 均分为69分，问该校应届与历届毕业生汉 语拼音测验成绩是否一样？
第三节 双向表的卡方检验
把实得的点计数据按两种分类标准分类后 所编制成的表就是双向表。对双向表的数据进 行的χ2检验，就是双向表的χ2检验。
在双向表的χ2检验中，如果要判断两种分 类特征，即两个因素之间是否有依从关系，这 种检验称为独立性χ2检验。
例1：P178。
家庭经济状况属于上、中、下的高三毕业 生，对于是否愿意报考师范大学有三种不同 的态度（愿意、不愿意、未定），其人数分 布如下表所示。问学生是否愿意报考师范大 学与家庭经济状况是否有关系？
第四节 四格表的卡方检验
独立样本四格表的χ2检验，就是最简单的双 向表即22表的χ2检验。它既可以用缩减公式来 计算χ2值，又可以用χ2检验的基本公式来计算 χ2值。
第三节
双向表的卡方检验
卡方检验是对总体分布是否服从某种理论分布或某种假设分布所作的假设检验。

卡方检验

卡方检验
1.png
计数资料：又称为定性资料或无序分类变量资料，也称 名义变量资料，是将观察单位按某种属性或类别分组计 数，分别汇总各组观察单位数后而得到的资料，其变量 值是定性的，表现为互不相容的属性或类别。
计量资料：又称定量资料或数值变量资料，为观测每个 观察单位某项指标的大小而获得的资料。其变量值是定 量的，表现为数值大小，一般有度量衡单位（cm、mmhg、 次/分、单位等）。
2
(2 1)(2 1) 1
3. 确定P值，作出统计推断
查2界值表，得2 0.005,1=7.88， 2 > 2 0.005,1，P <0.005，按 = 0.05水准，拒绝H0 ，接受H1，差 异有统计学意义，可以认为两组的显效率不等
四格表资料2检验的条件
例：为比较西药与中药治疗慢性支气管炎的疗效，某医师将符合 研究标准的110例慢性支气管炎患者随机分为两组（两组具有可比 性），西药组86例，中药组24例。服药一个疗程后，观察患者的 疗效，结果见下表。根据显效率，该医师认为中西药治疗慢性支 气管炎的疗效有差别，中药组的疗效好于西药组
表1 中西药治疗慢性支气管炎的显效率
等级资料：将观察单位按某种属性或某个标志分组，然 后清点各观察单位个数得来。具有等级顺序。（-、+、++、 +++；治愈、好转、无效、死亡）
独立样本：一般情况下，比较两个（类）人之间的差异 就是独立样本。（实验组、控制组）
配对样本：1. 一个人的不同部位进行测试。2.前测后测 的情况属于相关样本（同一人先后测试a、b两种药物）。 3. 两个匹配样本的比较。（测试两人智力，控制语文成 绩相等）
组别 西药组 中药组 合 计 治疗人数 86 24 110 显效人数 35 18 53 显效率(%) 40.70 75.00 48.18

第十章统计卡方检验.ppt

第十章统计卡方检验.ppt

二、单因素的2检验(配合度检验)（P297）
赞成 39
反对 21
解： （1）提出假设： H0：fo= fe H1： fo fe
（2）计算检验统计量
2 fo fe 2 (39 30)2 (21 30)2 5.4
fe
30
30
（3）查2分布表，确定临界值：
• 已经统计出小学生识字的优秀率为0.2，及 格率为0.7（不包括优秀在内），不及格率 为0.1，现在进行识字教学的改革实验，实 验后随机抽取了500名学生进行测试，结果 有123人达到优秀水平，有346人达到及格 水平，有31人没有及格。问识字教学的改 革实验是否有显著性效果？
第二节 独立性检验（二因素的2检验）
值表中找到临界值 。
（五）做出接受虚无假设或拒绝虚无假设的统计决策。其原 则是：
• 1．当公式（10.1）所确定的实得 值大于临界 时，可拒绝 虚无假设（H 0），并接受备择假设。
• 2．当公式（8.1）所确定的实得 值小于临界值 时，便没有 充分理由拒绝虚无假设（H 0），故暂认为虚无假设是成立 的，把虚无假设先接受下来。
2 0.05(1)

3.84
2 0.01(1)

6.63
（4）统计决断：02.05(1)

2

2 0.01(1)
0.01 p 0.05
故拒绝虚无假设，接受备择假设，即高中生对文 理分科的意见差异显著。
•
2
检验的假设（p293）
– 分类相互独立，互不包容
– 观测值相互独立
– 期望次数的大小
自学能力
实际观察次数（f0） 15
理论次数（fe又称
18

医学统计学-卡方检验

医学统计学-卡方检验
医学统计学-卡方检验
卡方检验是一种常用的统计方法，用于比较观察值和期望值之间的差异。它 在医学研究中有着广泛的应用，可以帮助我们验证假设、推断总体特征以及 分析类别变量的相关性。
卡方检验的定义和原理
卡方检验是一种基于卡方分布的统计检验方法。它基于观察值与期望值之间 的差异来判断样本数据与理论分布的拟合程度。
卡方检验的局限性和注意事项
• 卡方检验只能验证分类变量之间的关联性，不能验证因果关系。 • 卡方检验对样本足够大和数据分类合理的要求比较严格。 • 卡方检验结果受样本选择和观察误差的影响，需要谨慎解释。 • 在进行卡方检验前，需要对数据进行充分的清洗和准备。
结论和要点
卡方检验是一种常用的统计方法
卡方检验的应用领域
医学研究
卡方检验可以用来分析疾病的发生与某个因素之间的关联性，如吸烟与肺癌。
社会科学
卡方检验可以用来研究不同人群之间的行模式和态度偏好，如性别与政治观点。
市场调研
卡方检验可以用来分析消费者的购买偏好和市场细分，如年龄与产品偏好。
卡方检验的假设和前提条件
1 独立性假设
卡方检验基于观察值和期望值之间的差异来验证两个变量之间是否存在独立性。
它可以帮助我们验证假设、推断总体特征以 及分析类别变量的相关性。
结果解读和意义
卡方检验的结果可以帮助我们了解变量之间 的关系，并为决策提供依据。
应用广泛
卡方检验在医学研究、社会科学和市场调研 等领域都有着重要的应用。
局限性和注意事项
卡方检验有一定的局限性，需要注意样本大 小和数据分类的合理性。
4
比较卡方值和临界值
判断卡方值是否大于临界值，从而做出关于拒绝或接受原假设的决策。
卡方检验的结果解读和意义

《卡方检验》课件


制作交叉表
确定交叉表的行列变量
根据研究目的和内容，选择合适的行列变量，构建交叉表。
制作交叉表
将分组后的数据按照行列变量制作成交叉表，以便于进行卡 方检验。
计算理论频数
确定期望频数
根据交叉表中的数据，结合各组 的概率计算期望频数。
计算理论频数
根据期望频数和实际频数计算理 论频数，为后续的卡方检验提供 依据。
计算卡方值
计算卡方值
使用卡方检验的公式计算卡方值，该 值反映了实际频数与理论频数的差异 程度。
自由度的确定
在计算卡方值时，需要确定自由度， 自由度通常为行数与列数的减一。
显著性水平的确定
选择显著性水平
显著性水平是衡量卡方值是否显著的指标，通常选择0.05或0.01作为显著性水 平。
判断显著性
根据卡方值和自由度，结合显著性水平判断卡方检验的结果是否显著，从而得 出结论。
3.84、6.63等），可以确定观测频数与期望频数之间的差异是否具有统
计学显著性。
02
卡方检验的步骤
收集数据
确定研究目的
制定调查问卷或收集程序
在开始收集数据之前，需要明确研究 的目的和假设，以便有针对性地收集 相关数据。
根据研究目的和内容，制定合适的调 查问卷或建立数据收集程序，确保数 据的完整性和准确性。
详细描述
例如，在市场调研中，我们可以通过卡方检验来分析不同年龄段、性别、职业等 人群对于某产品的态度或购买意愿是否有显著差异，从而为产品定位和营销策略 提供依据。
实际案例二：医学研究中的应用
总结词
在医学研究中，卡方检验常用于病例 对照研究和队列研究中的分类变量关 联性分析。
详细描述
例如，在病例对照研究中，我们可以 通过卡方检验来比较病例组和对照组 在某些基因型、生活方式或暴露因素 上的分布是否有统计学差异，从而探 讨病因或危险因素。

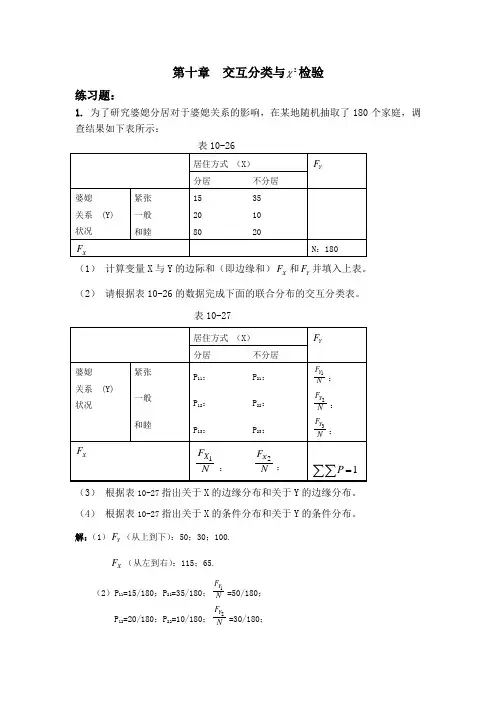
练习题解答：第十章交互分类与卡方检验

第十章 交互分类与2χ检验练习题：1. 为了研究婆媳分居对于婆媳关系的影响，在某地随机抽取了180个家庭，调查结果如下表所示：（1） 计算变量X 与Y 的边际和（即边缘和）X F 和Y F 并填入上表。

（2） 请根据表10-26的数据完成下面的联合分布的交互分类表。

表10-27（3） 根据表10-27指出关于X 的边缘分布和关于Y 的边缘分布。

（4） 根据表10-27指出关于X 的条件分布和关于Y 的条件分布。

解：（1）Y F （从上到下）：50；30；100.X F （从左到右）：115；65.（2）P 11=15/180；P 21=35/180；1Y F N =50/180；P 12=20/180；P 22=10/180；2Y F N =30/180；P 13=80/180；P 23=20/180；3Y F N =100/180；1X F N =115/180；2X F N =65/180.（3）关于X 的边缘分布：x 分居 不分居 P(x)115/18065/180关于Y 的边缘分布： y 紧张 一般 和睦 P(y)50/18030/180100/180（4）关于X 的条件分布有三个：y=“紧张” x 分居 不分居 P(x)15/5035/50y=“一般” x 分居 不分居 P(x)20/3010/30y=“和睦” x 分居 不分居 P(x) 80/10020/100关于y 的条件分布有两个： X=“分居”y紧张 一般 和睦 P(y)15/11520/11580/115X=“不分居”y紧张 一般 和睦 P(y)35/6510/6520/652. 一名社会学家关于“利他主义”的研究中，对被调查者的宗教信仰情况进行 了分析，得到的结果如下表所示：表10-28（1）根据表10-28的观察频次，计算每一个单元格的期望频次并填入表10-29。

表10-29 （2）根据表10-28和表10-29计算2χ，计算公式为2()2o e ef f f χ-=∑。

第十章卡方检验

19
第二节 单向表的卡方(χ2)检验
二、一个自由度的χ2检验
检验的步骤：
（2）计算χ2值
本例df=1，两组的理论频数均为ft=38>5。
2

f0 ft 2
ft
表10.4 喜欢与不喜欢体育人数的χ2值计算表
f0 ft f0-ft (f0-ft)2 (f0-ft)2/ ft
喜欢 50 38 12 144 3.79 不喜欢 26 38 -12 144 3.79
f0 ft 2
求χ2=5.202
ft
29
第二节 单向表的卡方(χ2)检验
三、频数分布正态性的χ2检验 检验的步骤： （3）统计决断 正态性χ2检验的自由度df=K-3。K是合并后保留下来的组数。 df=7-3=4。 自由度df=K-3的原因： 1单向表的χ2检验受到∑(f0-ft)=0一个因子的限制。 2应用Z=(X-X)/ σX的公式计算理论频数时，运用了X和 σX两
12 16 4
3.5
12.25 12.25/16=0.77
非团员 8 4 4
3.5
12.25
12.25/4=3.06
总和 20 20
χ2=3.83
25
第二节 单向表的卡方(χ2)检验
二、一个自由度的χ2检验 2、某组理论频数ft<5的情况 检验的步骤： （3）统计决断 根据df=1，查χ2值表，χ2(1)0.05=3.84， 由于χ2=3.83<3.84=χ2(1)0.05，则P>0.05， 于是保留H0而拒绝H1。 其结论为：该校共青团员的比率与全区没有显著性差异。
4
第一节 卡方(χ2)及其分布
比率和比率之差的假设检验，是对二项分布数据的假设检验。 ——处理一个因素分成两类， ——或者两个因素，每个因素都分为两类的资料。 ——最多只能同时比较两组比率的差异。

卡方检验1011ppt课件

n R nC
多个样本率的比较
例11.3 某研究者欲比较A、B、C 三种方案治疗轻、中度高血压 的疗效，将年龄在50~70岁的240例轻、中度高血压患者随机等 分为3组，分别采用三种方案治疗。一个疗程后观察疗效，结果 见表11.4。问三种方案治疗轻、中度高血压的有效率有无差别？
表11.4 三种方案治疗轻、中度高血压的效果
编号
组别
编号
1
乙药
67
2
甲药
68
3
乙药
69
4
甲药
70
5
乙药
71
6
甲药
72
7
甲药
73
8
乙药
74
9
甲药
75
10
乙药
76
11
甲药
77
组别 甲药 乙药 乙药 甲药 乙药 甲药 甲药 甲药 乙药 乙药 甲药
患儿编号 1 2 3 4 5
.
.
Table. 结果记录表 处理 乙药 甲药 乙药 甲药 乙药
. .
疗效 有效 有效 无效 有效 无效
对子 2
C
随机
T
对子 3
C
配对设计
✓ 自身配对 a. 同一对象给予两种不同处理 b. 同一对象处理前后
例11.6 某研究者欲比较心电图和生化测定 诊断低钾血症的价值，分别采用两种方法 对79名临床确诊的低钾血症患者进行检查 ，结果见表11.9。问两种方法的检测结果是 否不同？
患者编号 1 2 3 4 5
表11.9 两种方法诊断低血钾的结果
心电图
＋ － 合计
生化测定
＋
－
45
25
4
5
49
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
H1：男女学生数学成绩有显著差异；或 者是性别与数学成绩之间有关联。
理论次数的计算
B A
A1
B1
B2
(18)a
(6)b
A2
(10)c
(6)d
边缘小计
(28)
(12)
a+c
b+d
边缘小计
(24)a+b (16)c+d N=a+b+c+d

f
a

(a b)(a c) N
fb

(a b)(b d ) N
第十章 卡方检验
双变量关系的假设检验
变量关系的显著性检验类型
定类 定序 定距
定类
定序
定距
卡方类测量 (卡方检验)
卡方类测量 (卡方检验)
Spearman 相 关系数 (Z 检验)
方差分析 (F 检验)
Spearman 相关 系数
(Z 检验) Pearson 相关
(F 检验) 回归系数 (T 检验)
例如，在教育实证研究中，经常遇到以下 问题：
• 不同文化程度的人对某一政策的态度或工作 业绩是否相关？
• 不同收入程度的家庭对教育政策的态度是否 相关？
• 不同地区的人与不同的价值观是否相关？ • 不同培训方法与培训后的业绩增长是否相关？ • 不同民族学生与某种学习习惯是否相关？
……
上述问题称为品质相关问题，其特征是
独立样本四格表卡方检验
高二40个学生数学测验成绩如下表所示， 问男女学生数学成绩有无本质差异？
男 女 总和
80分以上 a=18
80分以下 b=6
c=10 a+c=28
d=6 b+d=12
总和 a+b=24 c+d=16
N=40
• 统计假设 H0：男女学生数学成绩没有差异；或者
是性别与数学成绩是独立的或无关联的；
• 卡方检验处理的是一个因素分为多种类别，
或多种因素各有多种类别的资料。
卡方检验的假设
• 分类相互排斥，互不包容 • 观测值（或变量）之间相互独立 • 每一单元格中的期望次数应该至少在5
个以上
卡方检验的基本公式
2 f ft 2
ft
f为实际频数；f
为理论频数；
t
卡方检验的类别
55~59 22
59.5
-11.9 -1.02 0.1539 0.0790 25
50~54 18
54.5
-16.9 -1.44 0.0749 0.0442 14
45~49 10
49.5
-21.9 -1.87 0.0307 0.0307 9
∑
314
1.000 314
独立性检验
独立性检验一般多采用列联表的形式记录观察结果，
Z点左 尾面积
比例
当组面 积比例
fe
95~99
4
99.5
28.1
0.0244 7
90~94 12
94.5
23.1 1.97 0.9756 0.0362 11
85~89 18
89.5
18.1 1.55 0.9394 0.0708 22
80~84 28
84.5
13.1 1.12 0.8686 0.1137 36


fc

(a c)(c d ) N
fd

(c d )(b d ) N
卡方统计量
2
N (ad bc)2
(a b)(c d )(a c)(b d )
75~79 44
79.5
8.1 0.69 0.7549 0.1523 48
70~74 72
74.5
3.1 0.26 0.6026 0.1662 52
65~69 46
69.5
-1.9 -0.16 0.4364 0.1638 51
60~64 40
64.5
-6.9 -0.59 0.2776 0.1237 39
故又称为列联表分析。
每一个因素可以分为两个或两个以上的类别， 因分类的数目不同，列联表有多种形式。两个因素 各有两项分类，称为四格表或2×2表。一个因素有 R类另一个因素有C类，则称为R × C表。
四格表的独立性检验
独立样本
相关样本
缩减公式卡方 值的计算
校正卡方 值的计算
缩减公式卡方 值的计算
校正卡方 值的计算
40
46
72
44
28
18
12
4
31 4
X 71.4; S 11.7
• 统计假设：
H0 : 观测数据的次数分布与正态分布没有显著差异； H1 : 观测数据的次数分布与正态分布具有显著差异。
• 确定理论次数 • 计算卡方值 • 确定α水平，并查卡方临界值 • 统计决断
组别
f0
组上限 离差x
标准 分Z
f e差

54
1 4
13.5
• 确定α水平，并查卡方临界值
• 统计决断
• 统计假设：H0 : f0i fei(因f0, fe为多个值)
H1 : f0i fei
• 确定理论次数
f e喜欢

76
1 2

38
• 计算卡方值
f e不喜欢

76
1 2

38
• 确定α水平，并查卡方临界值
• 统计决断
例2：从小学生中随机抽取76人，其中50人喜 欢体育，26人不喜欢体育，问该校学生喜欢 和不喜欢体育的人数是否相等？
• 统计假设：H0 : f0i fei(因f0, fe为多个值)
H1 : f0i fei
•
确定理论次数
f e好

54
1 4

13.5
1 fe中 54 2 27
• 计算卡方值
每个个体至少有两个特征（变量）。每个 特征（变量）的取值，要么是顺序型的， 只能比较大小，不能做加减运算；要么是 名义型的，连大小都不能比较，只是区别 所取的“值”是不同的。解决此类问题一
般采用卡方检验。
• 卡方检验是对样本的频数分布所来自的总
体分布是否服从某种理论分布所作的假设 检验，即根据样本的频数分布来推断总体 的分布。
• 配合度检验：用于检验一个因素多项分类的实
际观察数与理论次数是否接近；又称为无差假说 检验，例正态吻合性检验。
• 独立性检验：用于检验两个或两个以上因素各
种分类之间是否有关联或是否具有独立性。
• 同质性检验：用于检定不同人群母总体在某一 个变量的反应是否具有显著差异。
配合度检验问题实例
例1：大学某系54位老年教师中，健康状况属 于好的有15人，中等的有23人，差的有16人， 问该校老年教师健康状况好、中差的人数比 例是否为1：2：1？
C 卡方分布形状
接受域 拒绝域
频数分布正态性的卡方检验
下表中的314名学生在英语科目上的考试成 绩是否服从一正态分布？
组 别
45 ～
50 ～
55 ～
60 ～
65 ～
70 ～
75 ～
～
∑
49 54 59 64 69 74 79 84 89 94 99
次 数
10
18
22