用牛顿法求解非线性方程教学内容

1. 非线性方程组求解1．分别用牛顿法，及基于牛顿算法下的Steffensen 加速法。

(1) 求ln(sin )x x +的根。

初值0x 分别取0.1，1，1.5，2，4进行计算。

(2) 求sin =0x 的根。

初值0x 分别取1，1.4，1.6，1.8，3进行计算。

分析其中遇到的现象与问题。

（1）牛顿法牛顿法实质上是一种线性化方法，其基本思想是将非线性方程()0f x =逐步归结为某种线性方程来求解。

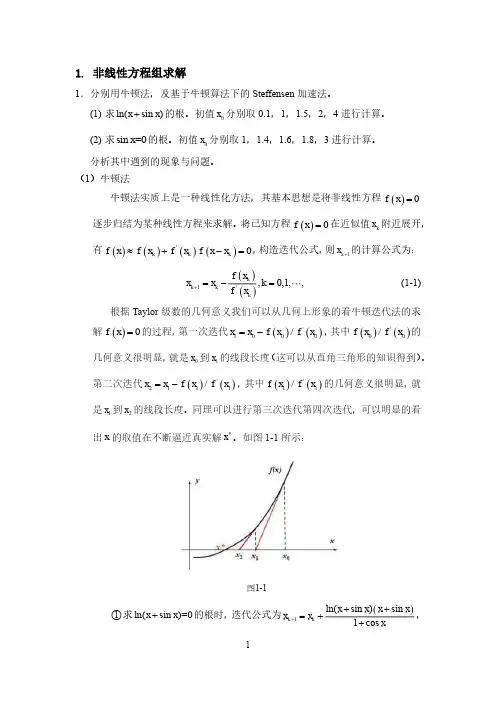
将已知方程()0f x =在近似值k x 附近展开，有()()()()'0k k k f x f x f x f x x ≈+-=，构造迭代公式，则1k x +的计算公式为：()()1',0,1,,k k k k f x x x k f x +=-= (1-1)根据Taylor 级数的几何意义我们可以从几何上形象的看牛顿迭代法的求解()0f x =的过程，第一次迭代()()'1000/x x f x f x =-，其中()()'00/f x f x 的几何意义很明显，就是0x 到1x 的线段长度（这可以从直角三角形的知识得到）。

第二次迭代()()'2111/x x f x f x =-，其中()()'11/f x f x 的几何意义很明显，就是1x 到2x 的线段长度。

同理可以进行第三次迭代第四次迭代，可以明显的看出x 的取值在不断逼近真实解*x 。

如图1-1所示：图1-1○1求ln(sin )=0x x +的根时，迭代公式为()1ln(sin )sin 1cos k k x x x x x x x+++=++，0示。

计算结果见附录1表F.1-1所示。

初值取1.5，2，4进行计算时结果不收敛。

表 1-1 牛顿法计算结果○2求sin =0x 的根时，迭代公式为1cos k k x x x+=+，初值0x 分别取1、1.4、1.6、1.8、3计算时结果收敛，误差小于510-时，近似解如表1-2所示。

求解非线性方程组的非精确牛顿法摘要:在经典牛顿法的基础上,给出了求解非线性方程组的非精确牛顿法。

在一定的条件下,证明了该算法的超线性收敛性,并且这个收敛性是二阶的。

关键词:非线性方程组;非精确牛顿法;收敛性对于无约束问题： minf(x) (1) 其中x∈Rn,f∶Rn→R是一个连续可微函数。

求解无约束优化问题方法大都属于迭代法,这类算法特点是:每一次迭代都要求函数值有所下降,因此人们称这类算法为下降法。

当下降方向取为负梯度时,此时函数值下降量最大,人们称它为最速下降法。

它是无约束最优化问题中最简单的方法,它具有全局收敛性,并且存储最较少,因此它适合于解决大型优化问题。

但它的缺点是收敛速度慢,在最优点处附近容易产生锯齿现象,为了改善收敛速度,人们提出了牛顿法。

牛顿法的基本思想是,在极小点附近用二阶Taylor多项式近似目标函数f(x),进而求出极小点的估计值。

设f(x)是二次可微实函数,x∈Rn。

又设x(k)是f(x)的极小点的一个估计,把f(x)在x(k)展成Taylor级数,并取二阶近似：f(x)≈Φ(x)=f(x(k))+ f(x(k))T(x-x(k))+12(x-x(k))T 2f(x(k))(x-x(k)) (2) 令Φ(x)=0,可得:x(k+1)=x(k)- 2f(x(k))-1 f(x(k)) (3)运用牛顿法时,初点的选择十分重要。

如果初始点靠近极小点,则可能很快收敛;如果初始点远离极小点,迭代产生的点列可能不收敛于极小点。

为了克服这个缺点,可以改进迭代公式(3):x(k+1)=x(k)+λkd(k)(4)其中d(k)=- 2f(x(k))-1 f(x(k))为牛顿方向,λk是由一维搜索得到的步长,即满足：f(x(k)+λkd(k))=minλf(x(k)+λd(k)) 这样修改后的算法称为阻尼牛顿法。

由于阻尼牛顿法含有一维搜索,因此每次迭代目标函数值一般有所下降(绝不会上升)。

解非线性方程的牛顿迭代法及其应用一、本文概述非线性方程是数学领域中的一个重要研究对象，其在实际应用中广泛存在，如物理学、工程学、经济学等领域。

求解非线性方程是一个具有挑战性的问题，因为这类方程往往没有简单的解析解，需要通过数值方法进行求解。

牛顿迭代法作为一种古老而有效的数值求解方法，对于求解非线性方程具有重要的应用价值。

本文旨在介绍牛顿迭代法的基本原理、实现步骤以及在实际问题中的应用。

我们将详细阐述牛顿迭代法的基本思想，包括其历史背景、数学原理以及收敛性分析。

我们将通过具体实例，展示牛顿迭代法的计算步骤和实际操作过程，以便读者能够更好地理解和掌握该方法。

我们将探讨牛顿迭代法在各个领域中的实际应用，包括其在物理学、工程学、经济学等领域中的典型应用案例，以及在实际应用中可能遇到的问题和解决方法。

通过本文的介绍，读者可以深入了解牛顿迭代法的基本原理和应用技巧，掌握其在求解非线性方程中的实际应用方法，为进一步的研究和应用提供有力支持。

二、牛顿迭代法的基本原理牛顿迭代法，又称为牛顿-拉夫森方法，是一种在实数或复数域上近似求解方程的方法。

其基本原理是利用泰勒级数的前几项来寻找方程的根。

如果函数f(x)在x0点的导数f'(x0)不为零，那么函数f(x)在x0点附近可以用一阶泰勒级数来近似表示，即：这就是牛顿迭代法的基本迭代公式。

给定一个初始值x0，我们可以通过不断迭代这个公式来逼近f(x)的根。

每次迭代，我们都用当前的近似值x0来更新x0，即：这个过程一直持续到满足某个停止条件，例如迭代次数达到预设的上限，或者连续两次迭代的结果之间的差小于某个预设的阈值。

牛顿迭代法的收敛速度通常比线性搜索方法快，因为它利用了函数的导数信息。

然而，这种方法也有其局限性。

它要求函数在其迭代点处可导，且导数不为零。

牛顿迭代法可能不收敛，如果初始点选择不当，或者函数有多个根，或者根是重根。

因此，在使用牛顿迭代法时，需要谨慎选择初始点，并对迭代过程进行适当的监控和调整。

《MATLAB 程序设计实践》课程考核１. 编程实现以下科学计算算法，并举一例应用之。

（参考书籍《精通ＭＡT ＬＡＢ科学计算》，王正林等著，电子工业出版社，２００９ 年）“牛顿法非线性方程求解”解：弦截法本质是一种割线法，它从两端向中间逐渐逼近方程的根；牛顿法本质上是一种切线法，它从一端向一个方向逼近方程的根，其递推公式为：-=+n n x x 1)()('n n x f x f初始值可以取)('a f 和)('b f 的较大者，这样可以加快收敛速度。

和牛顿法有关的还有简化牛顿法和牛顿下山法。

在MA TLAB 中编程实现的牛顿法的函数为：NewtonRoot 。

功能：用牛顿法求函数在某个区间上的一个零点。

调用格式：root=NewtonRoot )(```eps b a f 其中，f 为函数名； a 为区间左端点； b 为区间右端点 eps 为根的精度；root 为求出的函数零点。

，牛顿法的matlab程序代码如下：function root=NewtonRoot(f,a,b,eps)%牛顿法求函数f在区间[a,b]上的一个零点%函数名:f%区间左端点:a%区间右端点:b%根的精度:eps%求出的函数零点:rootif(nargin==3)eps=1.0e-4;endf1=subs(sym(f),findsym(sym(f)),a);f2=subs(sym(f),findsym(sym(f)),b);if (f1==0)root=a;endif (f2==0)root=b;endif (f1*f2>0)disp('两端点函数值乘积大于0 ！');return;elsetol=1;fun=diff(sym(f)); %求导数fa=subs(sym(f),findsym(sym(f)),a);fb=subs(sym(f),findsym(sym(f)),b);dfa=subs(sym(fun),findsym(sym(fun)),a);dfb=subs(sym(fun),findsym(sym(fun)),b);if(dfa>dfb) %初始值取两端点导数较大者root=a-fa/dfa;elseroot=b-fb/dfb;endwhile(tol>eps)r1=root;fx=subs(sym(f),findsym(sym(f)),r1);dfx=subs(sym(fun),findsym(sym(fun)),r1); %求该点的导数值 root=r1-fx/dfx; %迭代的核心公式tol=abs(root-r1);endend例：求方程3x^2－exp（x）＝0的一根解：在MATLAB命令窗口输入：>> r=NewtonRoot('3*x^2-exp(x)',3,4)输出结果：X=3.7331流程图：2、编程解决以下科学计算问题1）二自由度可解耦系统的振动模态分析。

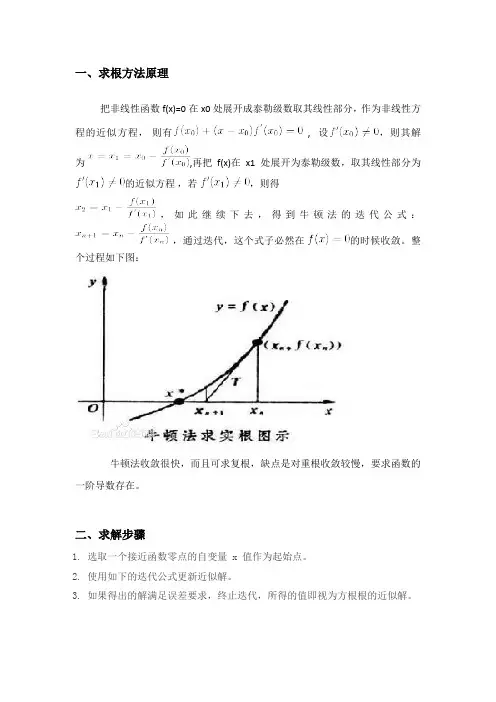
一、求根方法原理把非线性函数f(x)=0在x0处展开成泰勒级数取其线性部分，作为非线性方程的近似方程，则有 , 设，则其解为,再把f(x)在x1处展开为泰勒级数，取其线性部分为的近似方程，若，则得，如此继续下去，得到牛顿法的迭代公式：，通过迭代，这个式子必然在的时候收敛。

整个过程如下图：牛顿法收敛很快，而且可求复根，缺点是对重根收敛较慢，要求函数的一阶导数存在。

二、求解步骤1. 选取一个接近函数零点的自变量 x 值作为起始点。

2. 使用如下的迭代公式更新近似解。

3. 如果得出的解满足误差要求，终止迭代，所得的值即视为方根根的近似解。

三、自定的非线性方程使用牛顿迭代法近似求解如下方程在[-1, 1]之间的根：四、源程序代码clear, close allclcf = @(x) cos(x) -x.^3;f_prime = @(x) -sin(x) -3*x.^2;error = 1; %初始化误差变量iter = 0; %初始化迭代次数变量max_iter = 5000; %定义最大允许迭代次数tol = 1e-8; %定义循环终止误差x0 = 0.5; %初始值while error > tol && iter <= max_iterx = x0 - f(x0)/f_prime(x0); %更新x的值error = abs((x-x0)/x0); %计算相对误差iter = iter +1; %更新迭代次数x0 = x; %计算出的x赋值给x0，继续迭代，直到达到误差条件。

end五、上机运行结果截图六、结论1.迭代法是求解非线性方程组的一种很好的方法，它可以反复校验根的近似值，直到得出符合精度的解。

从几何角度上来解释可以解释为两个函数的无限逼近2.我们为了加快迭代的速度，引入了牛顿法，牛顿法的收敛速度很快，但是其收敛性取决于牛顿法的取值。

3.。

科学计算与数学建模实验报告牛顿法求解非线性方程一、引言非线性方程是数学中的一个重要研究内容，其求解方法有很多，其中之一就是牛顿法。

牛顿法是一种迭代方法，通过不断逼近函数的零点来求解非线性方程。

在本实验中，我们将使用牛顿法来求解给定的非线性方程，并验证其有效性。

二、实验方法1.确定问题：给定非线性方程f(x)=0，需要求解方程的根。

2.初始化：选择一个初始解x_0，并给定停止准则，如迭代次数、函数误差等。

3.迭代计算：a)计算函数f(x)在x_i处的导数f'(x_i)。

b)利用牛顿迭代公式进行迭代计算：x_{i+1}=x_i-f(x_i)/f'(x_i)。

c)检查迭代终止条件，若满足条件则停止迭代，否则返回步骤a)继续迭代。

4.输出结果：输出迭代过程中的迭代次数和解x。

三、实验结果我们选择一个较为简单的非线性方程f(x)=x^2-2来进行牛顿法求解。

初始解选取为x_0=1，停止准则为函数误差小于等于0.0001根据上述计算方法，我们进行迭代计算，并记录迭代次数和解x的变化情况。

具体结果如下表所示：迭代次数解x-----------------11.521.416731.414241.4142(收敛)从表中可以看出，当迭代4次时，解x已经收敛于1.4142，符合停止准则，因此我们可以认为此时已经找到了方程的根。

四、实验讨论通过上述实验可以发现，牛顿法是一种有效的求解非线性方程的方法。

它利用了函数在特定点处的导数的信息来逼近函数的零点，从而实现了迭代计算。

同时，牛顿法的收敛速度比较快，迭代次数较少，可以在较短的时间内找到方程的根。

然而，牛顿法也存在一些不足之处。

首先，它对初始解的选择较为敏感，不同的初始解可能导致迭代结果的差异。

其次，牛顿法可能出现发散现象，即迭代过程无法收敛到方程的根。

因此，对于一些复杂的非线性方程，我们需要选择合适的方法来求解。

五、总结通过本次实验，我们了解了牛顿法求解非线性方程的基本过程，并验证了其有效性。

高斯牛顿方法非线性方程组高斯牛顿法是一类经典的迭代优化方法，也是解决非线性方程组最优化问题的重要工具。

其主要思想是采用线性化和迭代技术，将一个复杂的非线性优化问题转化为一系列的线性或近似的线性优化问题。

1、原理高斯牛顿法假设非线性优化问题存在满足约束的局部最小值。

法以一个初始解为基础，利用其导数的一阶近似逼近求解本质上的一个线性方程组，然后满足函数约束条件的求解最优解。

另外，它还利用了牛顿（Newton）公式来确定迭代步长，有效地加快了收敛速度，并避免了初始解与目标解之间的距离。

2、算法要点（1）选择任意一个解作为初始解；（2）构造一阶导数的线性函数近似；（3）求解一个新的搜索方向；（4）使用牛顿步长法获得新的解；（5）根据函数限制或可行性条件验证新解是否符合要求；（6）如果新解符合，就使用该解作为下一次迭代的出发点；（7）否则，重复上述步骤，直到满足要求或达到最大迭代次数为止。

3、应用高斯牛顿法应用广泛，可以用于处理最小二乘问题、最大似然估计、最小化正则化函数、构建非线性模型等。

首先，它可以用于处理最小二乘问题，例如线性回归问题和非线性回归问题，其理论基础是在最小二乘估计的基础上，利用牛顿迭代方法迭代求解最小二乘估计的系数，最终达到最小二乘估计的解决。

另外，高斯牛顿法还可以用于解决最大似然估计和最小化正则化函数的问题，也可以用于构建参数估计的非线性模型。

这类问题可以转化为最小二乘估计问题，通常可以采用牛顿迭代算法来解决。

4、优点（1）牛顿法法在每一步可以获得与目标函数最佳的近似值；（2）牛顿法具有高效的收敛性；（3）牛顿法的迭代步长几乎总能得到最优结果；（4）牛顿法只需找到局部最优解即可，不需要搜索全局范围；（5）牛顿法可以有效地处理高维问题；（6）牛顿法不需要调整超参数。

5、缺点（1）高斯牛顿法只能有效求解局部最优解；（2）高斯牛顿法需要求解一系列线性方程组，计算量较大；（3）高斯牛顿法由于忽略了其它维度的贡献，如果梯度很大的时候，其发挥的作用就会变小；（4）高斯牛顿法只在局部稳定点有良好的收敛效果，不收敛的情况会发生；（5）高斯牛顿法需要求解函数的一阶导数，在非凸函数中，有可能退化成局部极小值；（6）高斯牛顿法需要通过比较函数值的变化情况来判断是否收敛，容易陷入局部极小点；（7）高斯牛顿法适用于处理有限变量的非线性优化问题，在处理大规模优化问题时，它的表现较差。

数值分析求解非线性方程根的二分法、简单迭代法和牛顿迭代法实验报告一：实验题目 一、 实验目的掌握求解非线性方程根的二分法、简单迭代法和牛顿迭代法，并通过数值实验比较两种方法的收敛速度。

二、 实验内容1、编写二分法、牛顿迭代法程序，并使用这两个程序计算02)(=-+=x e x x f 在[0, 1]区间的解，要求误差小于 410- ，比较两种方法收敛速度。

2、在利率问题中，若贷款额为20万元，月还款额为2160元，还期为10年，则年利率为多少？请使用牛顿迭代法求解。

3、由中子迁移理论，燃料棒的临界长度为下面方程的根，用牛顿迭代法求这个方程的最小正根。

4、用牛顿法求方程的根，精确至8位有效数字。

比较牛顿迭代法算单根和重根的收敛速度，并用改进的牛顿迭代法计算重根。

三、 实验程序第1题：02)(=-+=x e x x f 区间[0,1] 函数画图可得函数零点约为0.5。

画图函数：function Test1()% f(x) 示意图, f(x) = x + exp(x) - 2; f(x) = 0r = 0:0.01:1;y = r + exp(r) - 2plot(r, y);grid on 二分法程序：计算调用函数：[c,num]=bisect(0,1,1e-4)function [c,num]=bisect(a,b,delta)%Input –a,b 是取值区间范围% -delta 是允许误差%Output -c 牛顿迭代法最后计算所得零点值% -num 是迭代次数ya = a + exp(a) - 2;yb = b + exp(b) - 2;if ya * yb>0return;endfor k=1:100c=(a+b)/2;yc= c + exp(c) - 2;if abs(yc)<=deltaa=c;b=c;elseif yb*yc>0b=c;yb=yc;elsea=c;ya=yc;endif abs(b-a)<deltanum=k; %num为迭代次数break;endendc=(a+b)/2;err=abs(b-a);yc = c + exp(c) - 2;牛顿迭代法程序：计算调用函数：[c,num]=newton(@func1,0.5,1e-4) 调用函数：function [y] = func1(x)y = x + exp(x) - 2;end迭代算法：function[c,num]=newton(func,p0,delta)%Input -func是运算公式% -p0是零点值% -delta是允许误差%Output -c牛顿迭代法最后计算所得零点值num=-1;for k=1:1000y0=func(p0);dy0=diff(func([p0 p0+1e-8]))/1e-8;p1=p0-y0/dy0;err=abs(p1-p0);p0=p1;if(err<delta)num=k;%num为迭代次数break;endendc=p0;第2题：由题意得到算式：计算调用函数：[c,num]=newton(@func2,0.02,1e-8)程序：先用画图法估计出大概零点位置在0.02附近。

牛顿法牛顿法作为求解非线性方程的一种经典的迭代方法，它的收敛速度快，有内在函数可以直接使用。

结合着matlab 可以对其进行应用，求解方程。

牛顿迭代法（Newton ’s method ）又称为牛顿-拉夫逊方法（Newton-Raphson method ）,它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法,其基本思想是利用目标函数的二次Taylor 展开，并将其极小化。

牛顿法使用函数()f x 的泰勒级数的前面几项来寻找方程()0f x =的根。

牛顿法是求方程根的重要方法之一，其最大优点是在方程()0f x =的单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根，此时非线性收敛，但是可通过一些方法变成线性收敛。

牛顿法的几何解释：方程()0f x =的根*x 可解释为曲线()y f x =与x 轴的焦点的横坐标。

如下图：设k x 是根*x 的某个近似值，过曲线()y f x =上横坐标为k x 的点k P 引切线，并将该切线与x 轴的交点 的横坐标1k x +作为*x 的新的近似值。

鉴于这种几何背景，牛顿法亦称为切线法。

2 牛顿迭代公式：（1）最速下降法：以负梯度方向作为极小化算法的下降方向，也称为梯度法。

设函数()f x 在k x 附近连续可微，且()0k k g f x =∇≠。

由泰勒展开式： ()()()()()T k k k k fx f x x x f x x x ο=+-∇+- （*）可知，若记为k k x x d α-=，则满足0Tk k d g <的方向k d 是下降方向。

当α取定后，Tk k d g 的值越小，即T kk d g -的值越大，函数下降的越快。

由Cauchy-Schwartz 不等式： T k k kk d g d g ≤，故当且仅当k k d g =-时，Tk k d g 最小，从而称k g -是最速下降方向。

最速下降法的迭代格式为： 1k k k k x x g α+=-。

利⽤⽜顿迭代法求解⾮线性⽅程组最近⼀个哥们，是⽤⽜顿迭代法求解⼀个四变量⽅程组的最优解问题，从⽹上找了代码去改进，但是总会有点不如意的地⽅，迭代的次数过多，但是却没有提⾼精度，真是令⼈揪⼼！经分析，发现是这个⽅程组中存在很多局部的极值点，是⽤⽜顿迭代法不能不免进⼊局部极值的问题，更程序的初始值有关！发现⾃⼰好久没有是⽤Matlab了，顺便从⽹上查了查代码，⾃⼰来修改⼀下！先普及⼀下⽜顿迭代法：(来⾃百度百科)⽜顿（Newton's method）⼜称为⽜顿-拉夫逊（拉弗森）⽅法（Newton-Raphson method），它是在17世纪提出的⼀种在域和域上近似求解⽅程的⽅法。

多数⽅程不存在求根公式，因此求精确根⾮常困难，甚⾄不可能，从⽽寻找⽅程的近似根就显得特别重要。

⽅法使⽤函数f(x）的的前⾯⼏项来寻找⽅程f(x) = 0的根。

⽜顿迭代法是求⽅程根的重要⽅法之⼀，其最⼤优点是在⽅程f(x) = 0的单根附近具有平⽅收敛，⽽且该法还可以⽤来求⽅程的重根、复根，此时线性收敛，但是可通过⼀些⽅法变成超线性收敛。

另外该⽅法⼴泛⽤于计算机编程中。

设r是f(x)=0的根。

选取x0作为r的初始近似值，过点(x0,f(x0))做曲线的切线，求出该切线与x轴的交点，并求出该点的横坐标，称作x1是r 的⼀次近似。

如此就可以推导出⽜顿迭代公式。

已经证明，如果是的，并且待求的零点是孤⽴的，那么在零点周围存在⼀个区域，只要初始值位于这个邻近区域内，那么⽜顿法必定收敛。

并且，如果不为0, 那么⽜顿法将具有平⽅收敛的性能. 粗略的说，这意味着每迭代⼀次，⽜顿法结果的有效数字将增加⼀倍。

在⽹上查了⼀些代码，都是能指定某⼏个函数进⾏求导的，⽽且要是改变函数的个数，却⼜要对原始程序⼤动⼲⼽。

真的是揪⼼。

找到了这个程序，貌似在Matlab上不能很好的运⾏，对于数据的返回值为空没有做处理，后来⼜找了⼀个⽹易朋友的博客，将他的代码拿过来跑跑，还可以，但是对于不同的函数⽅程组，以及变量个数就不同了，真的是揪⼼，这个就是程序设计和编码的问题了！⾃⼰就拿来改了改，可以⽀持多⽅程组和多变量了！下⾯附上我的代码！求⼤家指导！[python]1. function [r,n]=mulNewton(x0,funcMat,var,eps)2. % x0为两个变量的起始值,funcMat是两个⽅程,var为两个⽅程的两个变量,eps控制精度3. % ⽜顿迭代法解⼆元⾮线性⽅程组4. if nargin==05. x0 = [0.2,0.6];6. funcMat=[sym('(15*x1+10*x2)-((40-30*x1-10*x2)^2*(15-15*x1))*5e-4')...7. sym('(15*x1+10*x2)-((40-30*x1-10*x2)*(10-10*x2))*4e-2')];8. var=[sym('x1') sym('x2')];9. eps=1.0e-4;10. end11.12. n_Var = size(var,2);%变量的个数13. n_Func = size(funcMat,2);%函数的个数14. n_X = size(x0,2);%变量的个数15.16. if n_X ~= n_Var && n_X ~= n_Func17. fprintf('Expression Error!\n');18. exit(0);19. end20.21. r=x0-myf(x0, funcMat, var)*inv(dmyf(x0, funcMat, var));22. n=0;23. tol=1;24. while tol>=eps25. x0=r;26. r=x0-myf(x0, funcMat, var)*inv(dmyf(x0, funcMat, var));27. tol=norm(r-x0);28. n=n+1;29. if(n>100000)30. disp('迭代步数太多，⽅程可能不收敛');31. return;32. end33. end34. end % end mulNewton[python]1. function f=myf(x,funcMat, varMat)2. % 输⼊参数x为两个数值,func为1*2符号变量矩阵,var为1*2符号变量矩阵中的变量3. % 返回值为1*2矩阵,内容为数值4.5. n_X = size(x,2);%变量的个数6. f_Val = zeros(1,n_X);7. for i=1:n_X8. tmp_Var = cell(1,n_X);9. tmp_X = cell(1,n_X);10. for j=1:n_X11. tmp_Var{j} = varMat(1,j);12. tmp_X{j} = x(1,j);13. end14. f_Val(i) = subs(funcMat(1, i), tmp_Var, tmp_X);15. end16. f=f_Val;17. end % end myf[python]1. function df_val=dmyf(x, funcMat, varMat)2. % 返回值为2*2矩阵,内容为数值3. %df=[df1/x1, df1/x2;4. % df2/x1. df2/x2];5. n_X = size(x,2);%变量的个数6. df =cell(n_X, n_X);7. for i=1:n_X8. for j=1:n_X9. df{i,j} = diff(funcMat(1, i), varMat(1, j));10. end11. end12.13. df_val=zeros(n_X, n_X);14.15. for i=1:n_X16. for j=1:n_X17. tmp_Var = cell(1,n_X);18. tmp_X = cell(1,n_X);19. for k=1:n_X20. tmp_Var{k} = varMat(1,k);21. tmp_X{k} = x(1,k);22. end23. df_val(i,j) = subs(df{i,j}, tmp_Var, tmp_X);24. end25. end26. end % end dmyf。