第八章 姜启源 层次分析法
- 格式:ppt
- 大小:978.50 KB
- 文档页数:31


姜启源数学建模资料简单的优化模型3.1 3.2 3.3 3.4 存贮模型生猪的出售时机森林救火最优价格3.5 血管分支3.6 消费者均衡3.7 冰山运输<i>姜启源数学建模资料</i>静态优化模型现实世界中普遍存在着优化问题静态优化问题指最优解是数不是函数静态优化问题指最优解是数(不是函数不是函数) 建立静态优化模型的关键之一是根据建模目的确定恰当的目标函数求解静态优化模型一般用微分法<i>姜启源数学建模资料</i>问题3.1存贮模型配件厂为装配线生产若干种产品,配件厂为装配线生产若干种产品,轮换产品时因更换设备要付生产准备费,产量大于需求时要付贮存费。
备要付生产准备费,产量大于需求时要付贮存费。
该厂生产能力非常大,即所需数量可在很短时间内产出。
生产能力非常大,即所需数量可在很短时间内产出。
已知某产品日需求量100件,生产准备费5000元,贮存费件生产准备费已知某产品日需求量元每日每件1元试安排该产品的生产计划,每日每件元。
试安排该产品的生产计划,即多少天生产一次(生产周期),每次产量多少,使总费用最小。
),每次产量多少一次(生产周期),每次产量多少,使总费用最小。
不只是回答问题,而且要建立生产周期、要不只是回答问题,而且要建立生产周期、产量与需求量、准备费、贮存费之间的关系。
求需求量、准备费、贮存费之间的关系。
<i>姜启源数学建模资料</i>问题分析与思考日需求100件,准备费5000元,贮存费每日每件元。
件准备费日需求元贮存费每日每件1元每天生产一次,每次每天生产一次,每次100件,无贮存费,准备费件无贮存费,准备费5000元。
元每天费用5000元元每天费用10天生产一次,每次天生产一次,天生产一次每次1000件,贮存费件贮存费900+800+…+100 =4500 准备费5000元,总计元,准备费元总计9500元。
元平均每天费用950元元平均每天费用50天生产一次,每次天生产一次,天生产一次每次5000件,贮存费件贮存费4900+4800+…+100 =*****元,准备费元准备费5000元,总计元总计*****元。


层次分析法大学生就业选择问题摘要:大学毕业生都面临着就业这个问题,面对着各行各业,应该如何选择适合自己的工作,是迫切需要解决的问题。
针对为大学生对所提供的工作,运用层次分析法来分析大学生对所提供的工作的满意程度,根据所得数据解决问题。
关键词:就业、层次分析法、决策、目标、权向量一.问题的提出对于一个大学毕业生来说,找到适合自己的工作是迫切需要解决的问题。
一个毕业生在找工作时,通过投简历,面试等方法,现有四个单位可以供他选择。
即:C1政府机构,C2化工厂,C3清洁工人,C4销售。
如何从这四个工作岗位中选择他比较满意的工作?这是目前需要解决的。
通过研究,最终确定了六个准则作为参照依据,来判断出最适合且最让他满意的工作。
准则:B1课题研究,B2发展前途,B3待遇,B4同事关系,B5地理位置,B6单位名气;通过这六个标准来评判出最满意的工作。
二.模型的假设一.该毕业生是文科生,但在大学期间也辅修了很多理科方面的学科,文理科兼懂。
二.四个单位对毕业生所具备的客观条件一样。
三.该毕业生对这四个工作岗位的工作都可以胜任。
1.层次结构模型的建立。
第一层:目标层,即对可供选择的工作的满意程度A ;第二层:准则层,即课题研究B1,发展前途B2,待遇B3,同事关系B4,地理位置B5,单位名气B6;第三层:方案层,即政府机构C1,化工厂C2,清洁工人C3,销售C4。
根据以上层次结构模型,我做了一份就业选择满意度的调查表,对100名在校大学生进行抽样调查。
首先让被调查者针对图示的某一层对其上一层某种因素影响的重要性进行打分,再将数据的分值看作服从随机变量的分布,再利用数学期望计算出平均分。
设ξ表示某个问题的分值,根据概率论以及数理统计所学的知识点,得出ξ服从离散型分布如下。
(其中i n 为打分值为i ξξ=的人数,N 为被调查的总人数) 根据数学期望的定义,我们有离散型随机变量ξ的数学期望: 5i i i E P ξξ==∑由调查数据和公式可以得到就业选择的整体评分表(表2,表3)表3就业选择的整体评分表3.构造成对比较矩阵和计算权向量:构造成对比较矩阵A,第二层准则层对第一层目标层的成对矩阵A:即A=111420.5112420.510.51530.5 0.250.250.210.3330.333 0.50.50.333310.333222331⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦运用SAS软件求解得出A的最大特征根及其对应的特征向量,即W13=0.38122380.44265620.40457180.10565730.26943220.6413177⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦归一化0.1700.1970.180?0.0470.1200.286⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦,λ=6.5856436一致性检验:一致性比率0.11712871.24CICRRI===0.0944586<0.1,则一致性检验通过,W13可以作为权向量。

层次分析法应用于城市购房决策中的实例分析濮长飞南京晓庄学院04数本2班摘要:本文针对消费者购房这一具体问题,基于高等代数矩阵内容,立足于数学建模,通过具体实例的分析详细描述了采用层次分析法解决多目标决策问题的方法和步骤,为消费者的购房决策提供科学合理的办法。
关键词:成对比较矩阵;特征根;特征向量;层次分析法随着经济的发展,收入水平的增加,消费者对商品房的要求也在增加。
目前多数消费者购房有的因为工作,有的是为了改善居住环境,还有的是为了投资。
不管是什么原因,由于涉及金额巨大,购房需慎之又慎,以免花钱买后悔。
针对消费者的需求,房地产开发商也在不断地推出新的楼盘。
这些楼盘往往各有各的特点,这使得消费者经常因选房而筋疲力尽,生怕捡了芝麻丢了西瓜。
究其原因,主要是考虑的因素太多,价格、交通、环境等等。
如就价格而言,甲比乙便宜;而就交通而言,乙又不如甲,这就使得购房者难以做出孰优孰劣的判断。
但是,所有的购房者都想买到物美价廉的房子,这是总目标,如果我们能够对备选房源“物美价廉”的程度进行量化,就能通过简单的数值比较做出决策。
运用统计学中的层次分析法就能轻松解决这一决策难题。
一、层次分析法概述1 简介层次分析法是美国运筹学家萨蒂在20世纪70年代提出的一种实用的定性和定量相结合的多准则决策方法。
它是把复杂的决策按照目标层、准则层、子准则层、方案层的顺序表示为一个有序的递阶层次结构,通过人们的比较判断,计算各种决策方案在不同准则及总目标之下的相对重要性权重,从而把难以量化的各种方案定量化,以得到各种方案的相对优劣的排序值,并据此做出最后的决策。
2 层次分析法的基本步骤第一步:根据问题的性质和要求,提出一个总目标。
将目标逐层分解为几个层次,建立层次结构模型。
第二步:对同一层次的各元素关于上一层次某一准则的重要性进行两两比较并赋权值,构造成对比较矩阵。
设某层有n 个因素1{,,}n x X X =,要比较它们对上一层某一准则(或目标)的影响程度,确定在该层中相对于某一准则所占的比重。


层次分析法及其应用摘要在日常生活中我们会遇到许多决策问题,处理决策问题时,要考虑的因素很多。
此文把层次分析法及其应用分为四个部分进行介绍,首先对层次分析的背景、现状、目的,其次对层次分析的原理进行分析,在运用层次分析和评价或决策时,按四个步骤进行描述:建立层次结构模型;构造成对比较矩阵;计算权向量并做一致性检验;计算组合权向量并做组合一致性检验,再次对层次分析的举例分析并行应用,最后进行总结。
关键词:层次分析法基本原理举例分析应用1、绪论层次分析法(The Analytic Hierarchy Pricess,以下简称AHP)是由美国运筹学家、匹兹堡大学萨第(T.L.Saaty)教授于本世纪70年代提出的,他首先于1971年在为美国国防部研究“应急计划”时运用了AHP,又于1977年在国际数学建模会议上发表了“无结构决策问题的建模—层次分析法”一文,此后AHP在决策问题的许多领域得到应用,同时AHP的理论也得到不断深入和发展。
目前每年都有不少AHP的相关论文发表,以AHP为基本方法的决策分析系统—“专家选择系统”软件也已早推向市场,并日益成熟。
AHP于1982年传入我国。
在当年召开的中美能源、资源、环境会议上萨第教授的学生高兰尼柴(H.Gholamnezhad)向中国学者介绍了这一新的决策方法。
随后,许树柏等发表了发表了国内第一篇介绍AHP的文章“层次分析法—决策的一种实用方法”(1982年)。
此后,AHP在我国得到迅速发展,1987年9月我国召开了第一届AHP 学术讨论会,1988年在我国召开了第一届国际AHP学术会议,目前AHP在应用和理论方面得到不断发展与完善。
它的主要特点是定性与定量分析相结合,将人的主观判断用数量形式表达出来并进行科学处理,因此,更能适合复杂的社会科学领域的情况,较准确地反映社会科学领域的问题。
同时,这一方法虽然有深刻的理论基础,但表现形式非常简单,容易被人理解、接受,因此,这一方法得到了较为广泛的应用。


摘要:本文就同学们如何制定旅行方案,以实现费用最少,风景最优美的问题进行研究。
在考虑旅行费用与路线,时间和交通工具的关系之后,我们以实现费用最少为目标,进行了系统建模。
根据此问题,我们用层次分析模型,然后对模型进行求解编程。
把各个方案进行一个全面的分析、比较后,得到一优化方案,由优化方案结果分析表明模型的正确性、实际性和有效性。
最后根据一种更符合实际情况的假设,对模型进一步优化,建立了更加有效、更加节省时间和费用的优化方案,从而达到省钱和享受的目的。
一、问题的重述:同学们相约去旅游,有人想去新疆,有人想去西藏,还有人想去内蒙。
考虑到是学生,费用应占最大的比重,其次是看风景,再者是旅途,至于吃住对年轻人来说不太重要。
如果仅从费用、景色、饮食、居住和旅途等方面考虑,通过建模计算,给出假期旅游地的合理选择方案: 1.按地理位置(经纬度设计最短路旅行方案;2.如果 2011 年 10 月 1 日同学们从太原市出发,可选择航空、铁路(快车卧铺或动车,设计最经济的旅行互联网上订票方案;3.要综合考虑省钱、省时又方便,设定你的评价准则,建立数学模型,修订你的方案;4.对你的算法作复杂性、可行性及误差分析;5.关于旅行商问题提出对你自己所采用的算法的理解及评价。
二、问题的分析: 对于旅游问题,考虑各个景点之间的实际距离即路线距离和交通工具的选择,分析得出一条最短的旅游路径,以达到省时,省钱又方便的目的。
对于调整和改进后得到的几种路线来说,在一个周期开始时,每种可供选择的交通工具的费用已知,且价格在一个周期内相因此一个周期内路线和交通工具已经确定。
我们可以将问题分为两部分:旅行最愉快享受、费用时间最少。
由于各到景点的路线不一,因此存在一个路线问题,由于所乘交通工具的多样性,因此存在考虑费用和时间问题。
评价标准:因为同时要考虑三个方面的问题,各个问题的最优方案很难会一致,所以我们以三个方面问题的最优方案重复的次数来认为是不是最优方案。

层次分析法层次分析法简介层次分析法(Analytic Hierarchy Process简称AHP)是将决策总是有关的元素分解成目标、准则、方案等层次,在此基础之上进行定性和定量分析的决策方法。
该方法是美国运筹学家匹茨堡大学教授萨蒂于本世纪70年代初,在为美国国防部研究"根据各个工业部门对国家福利的贡献大小而进行电力分配"课题时,应用网络系统理论和多目标综合评价方法,提出的一种层次权重决策分析方法。
这种方法的特点是在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上,利用较少的定量信息使决策的思维过程数学化,从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。
尤其适合于对决策结果难于直接准确计量的场合。
在现实世界中,往往会遇到决策的问题,比如如何选择旅游景点的问题,选择升学志愿的问题等等。
在决策者作出最后的决定以前,他必须考虑很多方面的因素或者判断准则,最终通过这些准则作出选择。
比如选择一个旅游景点时,你可以从宁波、普陀山、浙西大峡谷、雁荡山和楠溪江中选择一个作为自己的旅游目的地,在进行选择时,你所考虑的因素有旅游的费用、旅游地的景色、景点的居住条件和饮食状况以及交通状况等等。
这些因素是相互制约、相互影响的。
我们将这样的复杂系统称为一个决策系统。
这些决策系统中很多因素之间的比较往往无法用定量的方式描述,此时需要将半定性、半定量的问题转化为定量计算问题。
层次分析法是解决这类问题的行之有效的方法。
层次分析法将复杂的决策系统层次化,通过逐层比较各种关联因素的重要性来为分析、决策提供定量的依据。
层次分析法的基本步骤1、建立层次结构模型。
在深入分析实际问题的基础上,将有关的各个因素按照不同属性自上而下地分解成若干层次,同一层的诸因素从属于上一层的因素或对上层因素有影响,同时又支配下一层的因素或受到下层因素的作用。
最上层为目标层,通常只有1个因素,最下层通常为方案或对象层,中间可以有一个或几个层次,通常为准则或指标层。
多个成对比较矩阵确定权向量的一种方法_层次分析法论文导读::层次分析法将人们的思维过程层次化,逐层比较其间的相关因素并逐层检验比较结果是否合理,从而为分析决策提供具有说服力的定量依据。
在层次分析法的过程中,成对比较阵的构造是一个非常重要的环节。
但由单个专家构造的成对比较阵中所包含的主观因素对层次分析法得出的决策影响较大,为了减少层次分析法中的主观成分,可请专家群体构造成对比较阵。
本文给出了一种通过对若干个成对比较矩阵求平均值来减少主观影响这种方法确定权向量。
论文关键词:层次分析法,成对比较阵,权向量,主观影响1.引言2.层次分析法的基本步骤层次分析法的基本思路与人对一个复杂问题的思维、判断过程大体上是一样的[4]。
举一个简单的例子:“五一”长假期间你准备去旅游,是去风光秀丽的苏杭二州,还是去迷人的海南三亚,或者是去长春净月旅游村就近一游?假期不过七天,三地均游不可能,因此你必须对此作出选择与决策。
不妨设上面三个旅游方案为P1,P2和P3,你会根据诸如景色、费用、居住和旅途条件等一些准则去反复比较那三个侯选方案。
首先,你会确定这些准则在你的心目中各占多大比重,如果你经济宽绰,醉心旅游层次分析法,便会特别看重景色条件,而平素俭朴或手头拮据的人则会优先考虑费用,中老年旅游者还会对居住、饮食等条件寄以较大关注。
其次,你会就每一个准则将三个方案进行对比,例如,P2景色最好,P1次之;P3费用最低,P1次之;P1居住条件较好,P2次之等等。
最后期刊网。
你要将这几个层次的比较进行综合,在P1、P2、P3中确定哪个作为最佳地点。
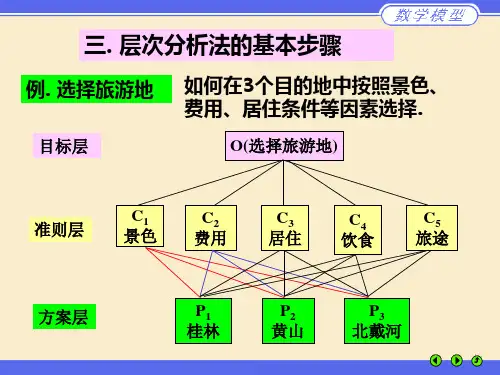
上面的思维过程可以加工整理成以下几个步骤:1.将决策问题分解为三个层次,最上层为总目标层,即选择旅游地;最下层为方案层,分P1、P2、P3三个供选择方案;中间层为准则层,有景色、费用、居住、饮食和旅途五个准则。
各层间的联系用相连的直线段表示(如图1)图12.通过相互比较确定各准则对于目标的权重,各方案对于每个准则的权重。
层次分析法指导老师:梁芬小组成员:1203郭炯荣(22)1203黄健麟(23)1203张伟勇(27)1203庄泳(30)摘要现代大学生毕业之后,首先要做的事便是找到适合自身的工作,而在面对如此多种类的工作岗位之时,该怎么依据自己的条件选择工作岗位成为了大多数毕业生的烦心事。
故我们小组针对这个问题作出了分析。
问题现代大学生就业选择困难问题。
案例介绍某毕业生欲参加毕业生招聘会,但由于意向不是特别明显,现有3个选择方案可供其选择:方案1(s1):高中教师(预期目标--高级教师至少9年)方案2(s2):企业会计(预期目标--管理层至少20年)方案3(s3):自主创业(预期目标--中小企业至少40年)且该毕业生认为,选择工作岗位时,如下几个因素需着重考虑:因素1(p1):发展前景因素2(p2):达到预期所需要时间因素3(p3):达到预期所需作出的努力因素4(p4):个人喜好程度现在需要就以上问题进行决策,需在3个方案(s1-s3)中选用最优方案。
①构建结构层次模型②形成判断矩阵Saaty 九级标度法及其含义标度a(i,j)定义1 因素i 与j 同样重要 3 因素i 与j 稍微重要 5因素i 与j 较强重要就业方向发展前景P1到达预期高度所需时间P2到达预期所需努力程度P3高中教师 企业会计 自主创业个人喜好程度P47 因素i与j强烈重要9 因素i与j绝对重要2,4,6,8 上述相邻判断的中间值1-9的倒数若因素j与i比较,得到判断值为a(j,i)=1/a(i,j),a(i,i)=1随机一致性指标RI的数值n 1 2 3 4 5 6 7 8 9 RI 0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45指标间重要程度判断矩阵指标P1 P2 P3 P4P1 1 7 8 1P2 1/7 1 1/3 1/5P3 1/8 3 1 1/7P4 1 5 7 1发展前景(p1)判断矩阵P1 S1 S2 S3S1 1 1/3 1/9S2 3 1 1/5S3 9 5 1达到预期所需要时间(p2)判断矩阵P2 S1 S2 S3S1 1 3 9S2 1/3 1 7S3 1/9 1/7 1达到预期所需作出的努力(p3)判断矩阵P3 S1 S2 S3S1 1 5 9S2 1/5 1 1/5S3 1/9 5 1个人喜好程度(p4)判断矩阵P4 S1 S2 S3S1 1 2 5S2 1/2 1 3S3 1/5 1/3 1程序代码clc;clear;a=[1,7,8,1;1/7,1,1/3,1/5;1/8,3,1,1/7;1,5,7,1]; [v,d]=eig(a);%求特征值与特征向量e=diag(d);%生成对角阵k=e(1);%k的赋值语句CI1=(k-4)/3;%一致性检验CR1=CI1/0.90w1=v(:,1)/sum(v(:,1));%生成权向量b1=[1,1/3,1/9;3,1,1/5;9,5,1];[v,d]=eig(b1);e=diag(d);k=e(1);CI21=(k-3)/2;CR21=CI21/0.58w21=v(:,1)/sum(v(:,1));b2=[1,3,9;1/3,1,7;1/9,1/7,1];[v,d]=eig(b2);e=diag(d);k=e(1); CI22=(k-3)/2;CR22=CI22/0.58 w22=v(:,1)/sum(v(:,1));b3=[1,2,9;1/2,1,5;1/9,1/5,1]; [v,d]=eig(b3);e=diag(d);k=e(1);CI23=(k-3)/2;CR23=CI23/0.58 w23=v(:,1)/sum(v(:,1));b4=[1,3,8;1/3,1,5;1/8,1/5,1]; [v,d]=eig(b4);e=diag(d);k=e(1);CI24=(k-3)/2;CR24=CI24/0.58 w24=v(:,1)/sum(v(:,1));w_sum=[w21,w22,w23,w24]*w1 CI=[CI21,CI22,CI23,CI24]; CR=CI*w1/sum(0.58*w1)在MATLAB下运行得到结果如下从中可以看出第二层对第一层,第三层对第二层的判断矩阵的一致性比率CR1,CR21,CR22,CR23,CR24都小于0.1,故可以用其特征向量作为权向量。