赏析数学史在高考试题中的渗透

撷英篇数学文化历史悠久，绚丽璀璨，出现了很多优秀的数学论著和数学家，是人类文明精神宝库的重要组成部分。

新课改后国家对数学文化很重视，近年的高考数学试题中也常见对数学文化的考查，特别是2016年教育部考试中心又发布正式文件明确提出要在高考题目中考查数学文化，数学文化在高考试题中的考查已成一种必然趋势。

现以2017年高考试题为分析背景，浅谈数学文化在高考试题中的渗透与考查。

一、数学史在高考试题中的渗透与考查数学史是研究数学科学发生、发展及其规律的科学，简单地说是研究数学的历史。

学习数学史可以很好地培养学生的数学素养。

在高考试题中加入渗透数学史的试题，可以让学生了解数学的发展历程及它的实际意义，激发学生学习数学的兴趣；可以让学生感受数学家进行研究的数学背景和思维方式，更好地培养学生的创新思维能力；可以让学生感受我国古代数学的辉煌成就，增强学生的名族自豪感和爱国主义情感。

例1（2017全国II）我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（）A.1盏B.3盏C.5盏D.9盏本试题是从古代数学名著《算法统宗》引入，然后通过诗歌提出数学问题，考查等比数列的基础知识；考查运算求解能力、应用意识；考查函数与方程思想、化归与转化思想。

中国古代数学的研究大多与实际生活、生产有紧密的联系，都有一定的实际背景，其主要特征是明显的问题式、综合性和算法化，本试题是经典的以“数学史”为背景的试题。

这种以数学史为背景的试题，对学生的数学阅读能力也有较高的要求。

二、数学美在高考试题中的渗透与考查数学美是自然美的客观反映，哪里有数学哪里就有美。

我国著名数学家华罗庚曾说过：“就数学本身而言，是壮丽多彩、千姿百态、引人入胜的……认为数学枯燥乏味的人，只是看到了数学的严谨性，而没有体会出数学的内在美。

•!•GAOKAO YANJIU数学文化在高'真题012透——!2019）*考例◎张畅畅（河南大学数学与统计学院，河南开封475000）【摘要】数学文化体现数学的人文价值和科学价值•渗透数学文化的命题能充分发挥命题的育人功能和积极导向作用•本文从2019年的高考真题入手，以数学美、数学史、数学家三个角度剖析数学文化的高考真题，并提出数学文化渗透教学的【关键词】数学文化；高考真题数学是人类的组分，而数对数学的⑴.2017《数程标准》把数程内容.，高考题对数的考查已明，本2019考题为例，分析数「化在咼考题中的•-#2019年数学文化高考真题统计为分析数在2019考数学真题的，对的数试题统计（见1）,可得岀:数在高考题选择或填空的形式岀现;知识点分布较为广泛，涉及三视图、概率、集合等;涉及的数学为国内外数学巨著、数学家故事等.表12019年高考数学文化试题特征统计省份题号题型口匕旦冃眾出处知识点全国1卷4选择断臂维纳斯黄金分割全国1卷6选择卦《周易》概率全国2卷16填空金石文化正多面体全国3卷3选择四大名著《西游记》集合浙江卷4选择祖眶原理《祖眶原理》三视图北京卷8选择心形线曲线方程二、2019年数学文化高考真题分析过对数考真题归类，从数学美、数学史、数学家三个方面对2019考题赏析•（一）命题渗透数学美数科独特的抽象性、严谨性数学图形的对称美、数的形式美、数公式的简洁美，在试题：透数学美,有助于学生在获得愉悦感.例％（2019•1卷4）期，人为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是5_1252丄，著名的“断臂维纳斯”便是如此•此外，最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是号丄•若某人满足个黄金分割比例，长为105cm，头顶至脖的长度为26cm,高可能是（）•A.165cm9.175cm C.185cm D.190cm赏析通过断臂维纳斯雕塑，引岀古希腊伟大的发现:黄金分割•此题通过给岀的比例条件，让生体会抽象、转与化归的数方法，同时考查学生数的核心，有利于帮助学生将问题简⑵•过数化的，让生发现数的美 值,给学生数学知识美的与•（二）命题渗透数学史一门科有其发展的历史，而数史是研究数学的历史•了解数学史知识，能助学生厘清知识脉络.例2（2019•2卷16）中国有的文化，文化的之一.期的的“体”•图2是一个棱数为48的多体，它的有顶一个体的，且体的棱长为1,体共有________个面,长为________•图1图2赏析在惜字如金的高考试卷中，这道题用百余字介绍金石文化，一方面,为考查学生数学能力实；另一方面，国的金石，背景，数学的对称之美，在生应用素养的同时，提高学生运用数学知识解决实际问题的能力.（三）命题渗透数学家数学广泛的生产与生活，这与数学家的不力，这数家的与会在生的发挥巨大的用.例3（2019•江卷4）期的伟大科学家，他提出的“，积”为,用可以体的体积3体&S.%3体的三视图，体的体积是&）•俯视图图3（下转5页）数学学习与研究2020.8■ZHONGKAO YANJIU(二)加强数学基本定理及模型的巩固初中数学介绍了不少基本定理,在动态问题中最常用的就是“两点之间线段最短” “三角形三边关系”“垂线段最短”等.基于这些基本事实衍生出不少基本模型，在遇到新问题时，首先要确认的是该问题类似于以前熟知的哪一类基本事实或者模型,据此确定相应的解题方法，这也是解决类似问题的基本.因此，在中考复习中基本模型的训练是有必要进行强化训练的，同时加强不同模型之间的组合,提高对基本模型的辨识能力，提升解决动点问题的解题能力％(三)注重举一反三数学问题，特别是难度较大的压轴题是灵活多变的，性质、定理、公式在不同的条件背景下均会产生不同的题型，但是无论问题的形式如何改变，考查的本质是不会改变的％因此，需要对概念、性质、定理及问题从不同切入点，不同背景做出适当变化，从而达到融会贯通、举一反三的学习目的.教师应当引导学生通过一题多解、一题多变、题一的训练,I生的性、性,固和深化学生对所学知识的理解，切实提高课堂教学效果％(四)注重数形结合思想的渗透和培养基础数学中的几何问题中蕴含着一定的数量关系，反之数量关系同时也常常可以通过结合图形做出直观的描述和解决.正如本题一样,几何问题通过代数方法求解是快速而且有效的.因此，数与形之间的相互转化往往是解决问题的利器.当然，在时的练习过程中，教师也要着手培养学生的解题自信，提醒学生应对待每一次考试，沉着冷静地思考才有利于问题的解决％总之，对于压轴题的教学，数学的基础知识和基本技能是“根基”，解题策略和方法是建立在双基之上的“上层建筑”.整个过程不能一味地强调攻坚克难，更要着眼于基础，做好基本题型的复习工作，着重数学方法的渗透和基本解题策略的指导,着眼于学生数学修养的提升，切实提高考数学的效率％【参考文献】[1]钟珍玖.解题教学中存在的问题及应对策略------道中考试题的考后思考[J].中学数学,2018(24)：83-84.[2]刘春艳.理解试题内涵把好教学方向一一从一道北京中考试题说起#J].数学教育学报,2018(3)：35-38.[3]蔡德清.中考数学压轴题的命题研究与反思[J].福建中学数学,2010(11)：11-14.[4]王冰冰，苏圣奎，陈清华.2013—2015年福建省数学中考压轴题分类评析#J].福建中学数学,2018(1):6-9.(上接3页)A.158B.162C.182D.324赏析本题开宗明义地引入我国古代著名数学家祖X，通过他提出的祖X原理阐明试题的数学史背景，激发学生对中华民族优秀传统文化的喜爱，有助于生的几观能力%三、对数学教学的启示数学不仅仅是一门知识,更是一门文化⑶%在数学文化日益受到重视的今天，教师在落实对数：化的，让生感受数科的魅力％(一)追溯知识的起源,激发学生兴趣数学文化知识，其背后的形成与发展经历了一定的背景⑷，通过对知识的，让生深刻地感受数知识蕴的蕴,在数的时,教师可以让学生数系，从自然数、负数、分数、无理数扩的数史,出引数的必性,让生解史一次数，这样做既可以激发学生的兴趣，又可以让学生系统全面地掌握知识％(二)讲述伟人的故事,引起学生共鸣由于数学抽象性强的特点，学生听讲起来会觉得枯燥乏味.在课堂教学中，教师适时为学生讲述数学家名人的故事，会引发学生极大鸣.如，在数列的时候，教师可意大利数学家出的关于的问题,让学生体会到,数学发现并不困难,数学家也是从生活中的问题，由此堂％(三)课堂融入数学文化，培养学生核心素养数学来源于生活并高于生活，顺着生活的可以找到数的脉络.在数堂中，分生活中的数，数与数学知识的，一方面，让生体会数学伟人不求真理的；另一方面，要让生在数发知识的本,对数、数方及数的%【参考文献】[1]齐龙新.高考中的数学文化#M].北京：电子工业出版社,2017.[2]祁平,任子朝，陈昂，等.基于数学文化视角的命题研究#J].数学通报,2018(9)：19-24.[3]阮文婷，孔德鹏.挖掘试题内涵赏析数学文化一一以2018年各省市数学高考题为例[J].高中数学教与学,2018(22)：34-36.[4]陈熙春.立足核心素养，弘扬数学文化一一数学文化在2018年高考试题中的渗透[J].基础教育课程,2018 (Z2)：19-23.数学学习与研究2020.8。

高中数学教学中数学史渗透研究
数学是一门古老的学科，其历史可以追溯到古埃及和古巴比伦文明时期。

数学史渗透教学是指在数学教学中运用数学史的渗透方式，让学生了解数学发展的历史背景、思想方法和成果，从而提高他们的数学认识和兴趣。

数学史渗透教学的目的是使学生认识到数学是一门深厚的学科，具有非凡的发展历程和深远的影响。

同时，数学史渗透教学还能激发学生的好奇心，调动他们的学习积极性，吸引他们对数学的兴趣，使学生拥有对数学的主动学习动力。

在高中数学教学中，数学史渗透教学具体的操作方式可以包括以下三个方面：
首先是讲解历史名人及其成就。

在数学教学中，可以通过讲解各个时期的数学家（如欧几里得、牛顿、莱布尼茨等）及其贡献，引导学生了解数学发展的历史脉络，以及不同时期在数学研究中所发生的历史事件。

其次是引导学生发现数学思想的演进。

在数学教学中，教师可以引导学生在数学思想的发展中，发现数学思想的演进，从而理解数学结论的内在逻辑。

例如，在学习微积分的时候，可以介绍莱布尼茨与牛顿的微积分发展史，这将帮助学生理解微积分的历史背景和思想演进。

最后是帮助学生认识数学在现代生活中的应用。

在高中数学教学中，数学的应用性越来越受到重视。

通过讲解数学在现代工程、科学、经济等领域的应用，可以帮助学生更好地认识数学在现代社会中的重要地位和作用。

总之，数学史渗透教学为学生提供了一个开放、自由的学习环境，在这个环境下，他们可以自由思考、探索、发现，不断提高自己的数学思维和创造力，从而更好地适应现代社会的发展。

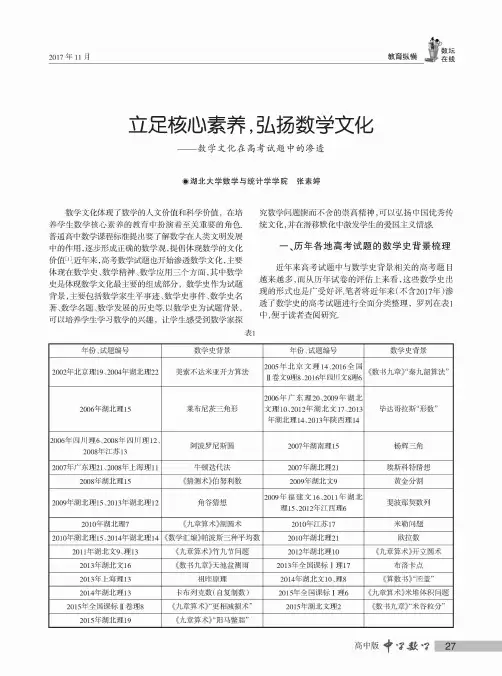
2017年11月教育纵横立足核心素养，弘扬数学文化—数学文化在高考试题中的渗透!湖北大学数学与统计学学院张素婷数学文化体现了数学的人文价值和科学价值，在培 养学生数学核心素养的教育中扮演着至关重要的角色. 普通高中数学课程标准提出要了解数学在人类文明发展 中的作用，逐步形成正确的数学观，提倡体现数学的文化 价值[1].近年来，高考数学试题也开始渗透数学文化，主要 体现在数学史、数学精神、数学应用三个方面，其中数学 史是体现数学文化最主要的组成部分，数学史作为试题 背景，主要包括数学家生平事迹、数学史事件、数学史名著、数学名题、数学发展的历史等.以数学史为试题背景， 可以培养学生学习数学的兴趣，让学生感受到数学家探究数学问题锲而不舍的崇高精神，可以弘扬中国优秀传 统文化，并在潜移默化中激发学生的爱国主义情感.一、历年各地高考试题的数学史背景梳理近年来高考试题中与数学史背景相关的高考题目 越来越多，而从历年试卷的评估上来看，这些数学史出现的形式也是广受好评.笔者将近年来(不含2017年)渗 透了数学史的高考试题进行全面分类整理，罗列在表1 中，便于读者查阅研究.表1年份、试题编号数学史背景年份、试题编号数学史背景2002年北京理19、2004年湖北理22美索不达米亚开方算法2005年北京文理14、2016全国 !卷文9理8、2016年四川文8理6《数书九章》“秦九韶算法”2006年湖北理15莱布尼茨三角形2006年广东理20、2009年湖北文理10、2012年湖北文17、2013 年湖北理14、2013年陕西理14毕达哥拉斯“形数”2006年四川理6、2008年四川理12、2008年江苏13阿波罗尼斯圆2007年湖南理15杨辉三角2007年广东理21、2008年上海理11牛顿迭代法2007年湖北理21埃斯科特猜想2008年湖北理15《猜测术》伯努利数2009年湖北文9黄金分割2009年湖北理15、2013年湖北理12角谷猜想2009年福建文16、2011年湖北理15、2012年江西理6斐波那契数列2010年湖北理7《九章算术》割圆术2010年江苏17米勒问题2010年湖北理15、2014年湖北理14《数学汇编》帕波斯三种平均数2010年湖北理21欧拉数2011年湖北文9、理13《九章算术》竹九节问题2012年湖北理10《九章算术》开立圆术2013年湖北文16《数书九章》天池盆测雨2013年全国课标I 理17布洛卡点2013年上海理13祖眶原理2014年湖北文10、理8《算数书》“囷盖”2014年湖北理13卡布列克数（自复制数）2015年全国课标I 理6《九章算术》米堆体积问题2015年全国课标！卷理8《九章算术》“更相减损术”2015年湖北文理2《数书九章》“米谷粒分”2015年湖北理19《九章算术》“阳马鳖臑”高中版十炎27数坛在线教育纵横2017年11月二、渗透数学文化的2017年高考试题评析根据2017年高考数学考试大纲提出的“加强数学 文化考查”的要求，2017年高考数学通过多种渠道渗透 数学文化，架起试题与学生之间的桥梁，以中华优秀传 统文化为载体，渗透学科思想方法，学生有兴趣、感受 深、易接受，有利于提升学生文化素养，契合学生的成长 发展需求，整体提升了考试的育人效果.例如，通过数学 史展示数学文化的民族性与世界性;通过向考生揭示知 识产生的背景、形成的过程，体现数学既是创造的、发现 的，也是不断发展的；通过对数学思维方法的总结、提 炼，呈现数学的思想性等.2017年高考数学试题加强了 中国古代数学文化的渗透，强调了中国古代数学文化的 传统特色.01(2017年全国！卷第3题)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层，红光点点 倍加增，共灯三百八十一，请问尖头几盏灯？”意思是:一 座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是 上一层灯数的2倍，则塔的顶层共有灯（）.A.1盏B.3盏C.5盏D.9盏评析:试题考查等比数列，从我国古代数学名著《算 法统宗》引人，然后通过诗歌提出数学问题，阐明试题的 数学史背景，激发考生对中华民族优秀传统文化的喜 爱.例2 (2017年全国I卷第2题)如图1，正方形内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是（）.A.丄B.IC.丄4 8 2评析：试题以我国太极图中的阴阳鱼为原型，设计 几何概型及几何概率计算问题.可以使考生了解到中华 民族优秀传统文化的博大精深.例3 (2017年浙江卷第11题)我国古代数学家刘徽创立的“割圆术”可以估算圆周率"理论上能把"的值计算到任意精度，祖冲之继承并发展了“割圆术”，将"的 值精确到小数点后七位，其结果领先世界一千多年，“割 圆术”的第一步是计算单位圆内接正六边形的面积S6, _______.评析:试题以我国古代数学家刘徽创立的割圆术为 背景，设计在圆内计算正六边形的面积问题，使考生深28十.？炎，？高中版刻理解中华民族优秀传统文化.反思：以“割圆术”为背景命题并非史无前例，命题者的意图是通过弘扬数学传统文化，增强学生的民族自豪感，但是本题的落脚点是考查圆内接正六边形的面积，即使没有“割圆术”为背景，学生也完全能解答出来，因此本题的命制似乎有强加数学文化之感，如何能在试题中自然地融人数学传统文化还需再思考推敲.例4 (2017年北京文理卷第8题)根据有关资料，围棋状态空间复杂度的上限）约为3361，而可观测宇宙中普通物质的原子总数*约为1080.则下列各数中与I最接近*的是(参考数据:lg3=0.48)( ).A.1033B.1053C.1073D.1093评析:北京卷文理数学选择题第8题均选择了传统文化中极具代表性的符号一围棋，从数学的视角欣赏和理解优秀传统文化的博大精深.反思：围棋是中国传统文化的精髓，在试题中引人围棋中的数学令人耳目一新，遗憾的是试题没有挖掘出围棋中的数学知识作为考查的知识点.比如，这道题目可改进为：给出围棋状态空间复杂度的概念，然后让学生根据棋盘的特点、围棋的规则，计算出围棋状态空间复杂度的上限.以围棋为载体考查排列组合的知识.这是笔者的一种尝试，读者也可以进行更深人的思考.三、小结高考试题在渗透数学文化时，首先，应当注意数学文化背景与试题所考查的知识点的自然融合，避免为了体现数学文化而勉强套上数学文化的外衣.其次，在渗透数学文化时，应该对古今中外的数学文化都有所覆盖，避免狭隘的民族情结.最后，在渗透数学文化的同时，还应该当心去数学化[2].近年来各省市都有不少高考试题因为渗透数学文化而被奉为经典，这些试题可以使考生感受到中华优秀传统文化的民族性与世界性，深刻地认识到中华民族优秀传统文化的博大精深和源远流长，研究这些优秀试题能对今后的高考命题工作有一定的帮助.在如今人人都谈素养的背景下，如何立足于发展学生的数学核心素养，在高考题中更好地渗透数学文化是值得探究的课题.参考文献：1. 中华人民共和国教育部制订.普通高中数学课程 标准[M].北京：人民教育出版社，2003.2. 张奠宙，赵小平.当心“去数学化”[J].数学教学，2005(6).F。

５２　得出最终的答案。

这样的过程有利于学生锻炼自身的思维能力，还可以对已经学习过的知识进一步的掌握和运用。

教师为学生设置问题的时候，首先需要充分的吸引学生，尤其是让学生不由自主的进入到其中的教学情景当中，更好的增强学生的思维能力。

首先，需要教师充分利用学生在生物学习上存在的疑惑，将其作为主要的中心点，展开相应的教学情景。

通过这样的教学情景，充分吸引学生对问题进行有效的思考，从而更好的提高生物教学效率和教学质量。

比如，教师在讲解关于人体内部的营养物质课程的时候，可以首先向学生抛出一些与生活有关的问题。

例如，你觉得今天和昨天的你有什么大方不一样？同样是牛，为什么公牛和黄牛制成的肉却有着较大的差别呢？等等。

这样可以让学生勾起自身的回忆，对其进行质疑，从而更好对这样的问题进行学习和认识。

有利于教师讲解的课程内容为学生进行更好的引导，并且让学生得到相应的答案，也掌握了大量的知识。

其次，教师还需要在教学的过程当中为学生设置相应的问题，这样不会避免学生得到最初想要的答案之后，则对课堂失去兴趣。

在进行生物教学的过程当中，一个课时很容易穿插大量的知识点，若是学生无法集中精力，则会出现对知识点记忆模糊混乱的情况，这样则无法达到教学的目标。

因此，需要教师在教学的过程当中，通过设立问题情景，充分吸引学生注意力的同时，还能够增强学生的思维能力。

参考文献［１］乔璞．“情景—探究”课堂教学模式在初中生物教学中的应用———以《微生物在生物圈中的作用》为例［Ｊ］．读与写（教育教学刊），２０１８，１５（０７）：１１９．［２］陈明清．初中生物教学创设情景的方法探讨［Ａ］．新教育时代（２０１６年１０月总第１辑）［Ｃ］，２０１６：１．［３］杨晓．基于情境教学法的初中生物学情感教育策略研究［Ｄ］．山东师范大学，２０１７．数学文化在数学高考题中的渗透研究■曹艳芳　（广东省广州市番禺区石鸉中学　５１１４００）【摘　要】加强对高考考题的研究，为学生进行针对性的训练，可以有效的提高学生的数学高考成绩，还可以促进高中数学教育水平的提升，提高数学教师对高考题目的了解，有利于针对性训练的展开。

赏析数学史在高考试题中的渗透从数学文化视角解读2017最新高考考纲变化温馨提示：2016年10月8号，教育部考试中心公布了[2016]第179号文件《关于2017年普通高考考试大纲修订内容的通知》，特别提出要关注数学文化。

前面我连续写了《什么是数学文化？》、《数学文化的四个层次》、《数学文化的人本特性》三篇文章，对数学文化作了一个系统的梳理。

梳理过后，我想大部分老师还是想急切知道数学文化到底如何在考题中体现出来。

事实上，在此之前，各省份的高考试题就已经在这方面有所体现，也出现了一些渗透数学文化的精彩题目。

分析这些高考试题，会发现目前大致出现了以下六种方式:①渗透数学史；②渗透数学名题；③渗透数学精神；④渗透数学美；⑤渗透数学应用；⑥渗透数学语言。

故下一步我将分别从这六个方面进行论述。

本期先谈高考试题中数学史的渗透。

赏析数学史在高考试题中的渗透中国数学文化历史悠久，在长期发展中，形成了“注重归纳”、“强调实用”、“讲究算法”的独特特点。

另外我国数学家的优秀研究品质、研究特点和研究成果对学生影响不可忽视。

把数学史作为数学文化的载体，以数学史为背景进行命题是最近几年高考试题渗透数学文化的一个特色。

例1.（2015年全国卷一卷6题）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。

问:积与为米几何”其意思为:“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有（）赏析：这个问题源于生活中谷物储存，与立体几何体积求解的基础知识结合起来，这样设计可以让学生体会到我们古代数学的优秀传统——数学要关注生产、生活等社会问题，引导学生了解数学文化，体会数学知识在认识世界中的工具作用。

体现了数学文化“以数化人”的功能。

数学史在高中数学课堂中的渗透研究1. 引言1.1 研究背景数学史在高中数学课堂中的渗透研究是近年来教育领域的一个热门话题。

传统上，数学教育主要注重数学方法和技巧的传授，忽视了数学知识的历史渊源和发展过程。

随着数学教育的改革和发展，越来越多的教育学者和教师开始重视数学史教育的重要性，认为通过引入数学史知识可以激发学生的学习兴趣，拓展他们的数学视野，提高他们的学习动力和学习效果。

数学史在高中数学课堂中的渗透研究不仅可以丰富数学教育的内容，还可以帮助学生更好地理解数学知识的本质和意义，培养他们的数学思维和创新能力。

对数学史教育在高中数学课堂中的应用及其效果进行深入研究，对于提高数学教育的质量和水平，促进学生全面发展具有重要意义。

【2000字】1.2 研究意义数要求等。

以下是根据您的要求输出的内容：数学史在高中数学课堂中的渗透研究具有重要的理论和实践意义。

通过深入研究数学史在高中数学课堂中的应用，可以帮助教师更好地把握课程内容，提升教学质量，激发学生学习兴趣。

探讨数学史教育的教学方法有助于发展教学理论，丰富课堂教学形式，提高教学效果。

对数学史在高中数学课堂中的渗透效果进行评价，不仅可以验证其实际应用效果，也可以为今后的教学实践提供参考和借鉴。

研究数学史教育对学生数学学习的影响，有助于促进学生数学素养的全面发展，提高学生的创新能力和解决问题的能力。

探讨数学史教育的挑战与应对策略，可以帮助教师更好地应对教学中遇到的困难和挑战，提升教学水平和教学效果。

数学史在高中数学课堂中的渗透研究不仅具有重要的实践意义，也有重要的理论意义。

2. 正文2.1 数学史教育在高中数学课堂中的应用数学史教育在高中数学课堂中的应用对学生的数学学习起到了重要的促进作用。

通过引入数学史的教学内容，可以使学生更加深入地理解数学知识的来龙去脉，激发他们对数学的兴趣和热情。

在教学实践中，教师可以通过讲解历史事件和数学家的生平事迹，帮助学生了解数学的发展历程，认识到数学的重要性和应用价值。

【原创】【试题研究】以数学史为背景的数学试题赏析1.引言翻开近些年的高考数学试题和全国各地的高考模拟试题，其中有很多以数学史为背景的数学试题.细细品读这些试题可以发现其独具匠心、立意深远、韵味无穷，它们既渗透了数学文化和数学思想，又兼顾考查学生的认知、理解、迁移能力,蕴含着命题人的人文情怀.它们真正体现着以数学史为载体，以考查能力和学生的综合素质为目的的命题趋势. 2.引例2.1 源于数学史料，兼顾现代数学分支——估算与算法例1 （2015年全国新课标I 理）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。

问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆为一个圆锥的四分之一)，米堆底部的弧度为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有A.14斛B.22斛C.36斛D.66斛 解：由1284r l π⨯==得圆锥底面的半径16163r π=≈，所以米堆的体积2111256320=543499V r h π⨯=⨯⨯=，所以堆放的米有3201.62229÷≈斛，故选B赏析：这是一道融入数学史和现代数学估算为一体的新颖试题，将圆锥的体积公式和单位换算结合，既考查学生的基础知识又考查学生的运算能力，同时兼顾考查了学生的理解能力、分析问题能力，属于中等难度试题.变式1（2016年湖北七市联考理）《九章算术》商功章有题：一圆柱形谷仓，高1丈3尺313寸，容纳米2000斛(1丈=10尺，l 尺=10寸，斛为容积单位，l 斛≈1.62立方尺，π≈3)，则圆柱底圆周长约 为A.l 丈3尺B.5丈4尺C.9丈2尺D. 48丈6尺解：设圆柱底圆半径为r ，高为h ，圆柱体积为22000 1.62V r h π==⨯()2313.33r ≈⨯⨯，所以281r ≈，即3r ≈尺，所以圆柱底面圆周长为254r π≈尺，即圆柱底面圆周长约为5丈4尺，故选B.例2（2014年湖北理）《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“囷盖”的术：“置如其周，令相乘也．又以高乘之，三十六成一．”该术相当于给出了由圆锥的底a > ba = a -b b = b - a输出a 结 束开 始 输入a ，b a ≠ b 是是否否 面周长L 与高h ，计算其体积V 的近似公式2136V L h ≈.它实际上是将圆锥体积公式中的圆周率π近似取为3.那么，近似公式2275V L h ≈相当于将圆锥体积公式中的π近似取为( )A.227 B.258C.15750D.157113 解：由题意知2221753L h r h π=，所以2221753L r π=，因为2L r π=，代入得258π=，故选B.赏析：《算数书》是中国现已发现的最古的一部算书，大约比现有传本的《九章算术》还要早近二百年.本题以信息题的形式，考查学生阅读理解能力，属于中等难度题.变式2 （2012年湖北理）我国古代数学名著《九章算术》中“开立圆术”曰：置积尺数，以十六乘之，九而一，所得开立方除之，即立圆径，“开立圆术”相当于给出了已知球的体积V ，求其直径d 的一个近似公式3169d V ≈人们还用过一些类似的近似公式。

数学史融入高考数学试题的现状分析摘要：近年来，随着《高中数学课程标准》中数学文化板块的提出，数学史的价值在教育功能中日益凸显，数学史融入高中数学课堂，为数学教育开辟了一条新的道路。

在推进课程改革和素质教育背景下，数学史融入高中数学教学环节，能提升学生数学核心素养和教学的有效性。

但由于多方面因素影响，目前数学史融入课堂教学存在诸多问题，在教学活动中，应用较少且单一，缺乏完整性，为了更好地体现数学史在数学教学中的文化价值，教师要夯实理论基础，结合现实情况，多方位培养学生的核心素养。

数学史是数学文化的重要组成部分，它是研究数学学科发展的科学，探索数学的演变、发展过程，以及对人类文明的影响，既是史学领域，又属于科学领域，是一门交叉学科。

《高中数学课程标准》中提到，学生要了解数学在人类历史进程中起到的作用，体会数学的科学价值、应用价值、拓展见识，寻找数学发展的足迹，加强数学创造动力，接受出色文化的熏陶，领悟数学的人文价值，进而提升自身的文化素养和创造能力。

一、数学史融入高中数学课堂的必要性分析学习数学史是认识数学、掌握数学的必要途径。

要弄清楚数学观点、数学思维的发展过程，增强对数学的认知，完善数学的整体思想，就必须运用数学史作为补充和引导。

（一）提升学生的学习兴趣高中数学和初中数学相比较有以下特点，第一，知识抽象，数学语言变化大，要求思维要从经验型向理论型过渡。

第二，知识内容的量急剧增加，章节多，时间紧，尤其强调知识的“以旧带新”“融会贯通”“活学活用”。

第三，知识的独立性大，函数、向量、数列、几何、概率等内容相互独立，学生头脑中缺乏整体结构。

由于以上几点原因就会导致部分学生失去对数学学习的兴趣，觉得数学课堂枯燥乏味。

数学课堂融入数学史能够带给学生一些有趣的故事，比如将数学史融入导入部分，能够引人入胜，巧妙的教学设计先声夺人，使学生的兴奋点转移到课堂中，激发学习兴趣，精彩的数学史故事使学生集中精力投入新知识的学习中。