浙江省大学物理试题库302-静电场的高斯定理
- 格式:doc
- 大小:1.61 MB
- 文档页数:18

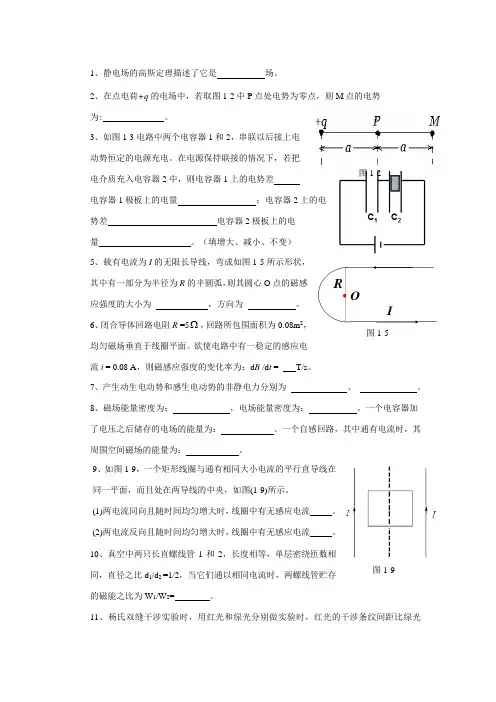
图1-9 1-9(1-121、静电场的高斯定理描述了它是 场。
2、在点电荷+q 的电场中,若取图1-2中P 点处电势为零点,则M 点的电势为: 。
3、如图1-3电路中两个电容器1和2,串联以后接上电动势恒定的电源充电。
在电源保持联接的情况下,若把电介质充入电容器2中,则电容器1上的电势差 电容器1极板上的电量 ;电容器2上的电势差 电容器2极板上的电量 。
(填增大、减小、不变) 5、载有电流为I 的无限长导线,弯成如图1-5所示形状,其中有一部分为半径为R 的半圆弧,则其圆心O 点的磁感应强度的大小为 ,方向为 。
6、闭合导体回路电阻R =5 ,回路所包围面积为0.08m 2,均匀磁场垂直于线圈平面。
欲使电路中有一稳定的感应电流i = 0.08 A ,则磁感应强度的变化率为:d B /d t = T/s 。
7、产生动生电动势和感生电动势的非静电力分别为 、 。
8、磁场能量密度为: ,电场能量密度为: 。
一个电容器加了电压之后储存的电场的能量为: 。
一个自感回路,其中通有电流时,其周围空间磁场的能量为: 。
9、如图1-9,一个矩形线圈与通有相同大小电流的平行直导线在同一平面,而且处在两导线的中央,如图(1-9)所示。
(1)两电流同向且随时间均匀增大时,线圈中有无感应电流 。
(2)两电流反向且随时间均匀增大时,线圈中有无感应电流 。
10、真空中两只长直螺线管1和2,长度相等,单层密绕匝数相同,直径之比d 1/d 2 =1/2,当它们通以相同电流时,两螺线管贮存的磁能之比为W 1/W 2= 。
11、杨氏双缝干涉实验时,用红光和绿光分别做实验时,红光的干涉条纹间距比绿光图1-3图1-5 图1-2的 。
(填:宽 或 窄)。
12、获得相干光常用的方法有两种是: , 。
13、波长为 的单色光垂直照射到宽a 的单缝上,单缝后面放置一个凸透镜, 在凸透镜的焦平面上放置一个屏幕,用以观测衍射条纹,今测得屏幕上中央明条纹两侧第二级暗纹之间的距离为 d ,则透镜的焦距 f 为: 。


四、计算题1、 两个无限大的平行平面都均匀带电,电荷的面密度分别为1σ和2σ,试求空间各处场强. 两面间 , 1σ面外 , 2σ面外 . (填写A 、B 、C 或D ,从下面的选项中选取)A 、n E )(21210σσε-=B 、1201()E n σσε=+C 、n E )(21210σσε+-=D 、n E)(21210σσε+=答案:A ,C ,D解: 如图所示,两带电平面均匀带电,电荷面密度分别为1σ与2σ,两面间, n E)(21210σσε-=1σ面外, n E)(21210σσε+-= 2σ面外, n E)(21210σσε+=n:垂直于两平面由1σ面指为2σ面.2、一无限长带电直线,电荷线密度为λ,傍边有长为a , 宽为b 的一矩形平面, 矩形平面中心线与带电直线组成的平面垂直于矩形平面,带电直线与矩形平面的距离为c ,如图,求通过矩形平面电通量的大小. . (填写A 、B 、C 或DA 、()0arctan 22a b c λπε⎡⎤⎣⎦ B 、()0arctan 2a b c λπε⎡⎤⎣⎦ C 、()0arctan 24a b c λπε⎡⎤⎣⎦ D 、()02arctan 2a b c λπε⎡⎤⎣⎦ 答案:Bλ解:取窄条面元adx ds =,该处电场强度为rE 02πελ=过面元的电通量为()220022cos xc acdxadx r s d E d e +=⨯=⋅=Φπελπεθλ ()⎰⎰-+=Φ=Φ2/2/2202b b e e xc acdxd πελ2/2/0arctan 12b b cxc ac -⋅=πελ()[]02arctan πελc b a =3、 如图所示,在x -y 平面内有与y 轴平行、位于x=a / 2和x =-a / 2处的两条“无限长”平行的均匀带电细线,电荷线密度分别为+λ和-λ.求z 轴上任一点的电场强度.. . (填写A 、B 、C 或D ,从下面的选项中选取)A 、()2204a i a z λπε-+B 、()22024a i a z λπε-+ C 、()22024a i a z λπε-+ D 、()22044a i a z λπε-+ 答案:C解:过z 轴上任一点(0 , 0 , z )分别以两条带电细线为轴作单位长度的圆柱形高斯面,如图所示.按高斯定理求出两带电直线分别在该处产生的场强大小为 ()r E 02/ελπ=± 场强方向如图所示. 按场强叠加原理,该处合场强的大小为r a r E E 2/c o s 20⋅π==+ελθ ()22042z a a +π=ελ方向如图所示. 或用矢量表示 ()iz a a E 22042+π-=ελ4、均匀带电球壳内半径6cm ,外半径10cm ,电荷体密度为2×510-C·m -3求距球心5cm 的场强 ,8cm 的场强 ,12cm 的场强 . (填写A 、B 、C 或D ,从下面的选项中选取).A 、43.4810⨯1C N -⋅, 方向沿半径向外 B 、44.1010⨯1C N -⋅ ,沿半径向外C 、44.1010⨯1C N -⋅,方向沿半径向外D 、 0 答案: D, A ,B解: 高斯定理0d ε∑⎰=⋅qS E s,02π4ε∑=q r E当5=r cm 时,0=∑q ,0=E8=r cm 时,∑q 3π4p=3(r )3内r - ∴ ()2023π43π4rr r E ερ内-=41048.3⨯≈1C N -⋅, 方向沿半径向外. 12=r cm 时,3π4∑=ρq -3(外r )内3r ∴ ()420331010.4π43π4⨯≈-=rr r E ερ内外 1C N -⋅ 沿半径向外.5、有两个半径分别为1R 、2R 的同心球壳,带电分别为1Q 、2Q ,试求空间电场分布。



一、库仑定律和电场力1.关于摩擦一物体后,物体呈现正电性的一种解释是:在摩擦过程中,[ ]A.物体获得了中子。
B.物体获得了质子。
C.物体失去了电子。
D.物体失去了中子。
【答案】:C2.两条平行的无限长直均匀带电线,相距为d,线电荷密度分别为±λ,若已知一无限长均匀带电直线的场强分布为λ2πε0r方向垂直于带电直线,则其中一带电直线上的单位长度电荷受到另一带电直线的静电作用力大小为[ ]A.λ24πε0d2B.λ24πε0dC.λ22πε0d2D.λ22πε0d【答案】:D3.关于电荷与电场,有下列几种说法,其中正确的是[]A.点电荷的附近空间一定存在电场;B.电荷间的相互作用与电场无关;C.若电荷在电场中某点受到的电场力很大,则表明该点的电场强度一定很大;D.在某一点电荷附近的任一点,若没放试验电荷,则该点的电场强度为零。
【答案】:A4. 两个静止不动的点电荷的带电总量为2q,为使它们间的排斥力最大,各自所带的电荷量分别为[]A.q2,3q 2B.q3,5q 3C.q,qD.−q2,5q 2【答案】:C5.关于电场力和电场强度,有下列几种说法,其中正确的是[]A.静电场的库仑力的叠加原理和电场强度的叠加原理彼此独立、没有联系;B.两静止点电荷之间的相互作用力遵守牛顿第三定律;C.在以点电荷为中心的球面上,由该点电荷所产生的电场强度处处相同;D.以上说法都不正确。
【答案】:B6.—点电荷对放在相距d处的另一个点电荷的作用力为F,若两点电荷之间的距离减小一半,此时它们之间的静电力为[ ]A.4FB.2FC.0.5FD.0.25F【答案】:A7.如图所示为一竖直放置的无穷大平板,其上均匀分布着面电荷密度为σ的正电荷,周围激发的电场强度大小为σ2ε0,方向沿水平方向向外且垂直于平板。
在其附近有一水平放置的、长度为l的均匀带电直线,直线与平板垂直,其线电荷密度为λ,则该带电直线所受到的电场力大小为[ ]A.σλ2πε0ln lB.σλ2ε0ln lC.σλl2πε0D.σλl2ε0【答案】:D8.质量为m、电荷为-e的电子以圆轨道绕静止的氢原子核旋转,其轨道半径为r,旋转频率为γ,动能为E,则下列几种关系中正确的是[]A.E=e8πε0rB.γ2=32ε02E3me4C.E=e 24πε0rD.γ2=32ε0E3me2【答案】:B9.电偶极子在非均匀电场中的运动状态[ ]A.只可能有转动运动;B.不可能有转动运动;C.只可能有平动运动;D.既可能有转动运动,也可能有平动运动。

真空中的静电场 一、选择题1、下列关于高斯定理的说法正确的是(A ) A 如果高斯面上E 处处为零,则面内未必无电荷。
B 如果高斯面上E 处处不为零,则面内必有静电荷。
C 如果高斯面内无电荷,则高斯面上E 处处为零。
D 如果高斯面内有净电荷,则高斯面上E 处处不为零。
2、以下说法哪一种是正确的(B )A 电场中某点电场强度的方向,就是试验电荷在该点所受的电场力方向B 电场中某点电场强度的方向可由0q FE 确定,其中0q 为试验电荷的电荷量,0q可正可负,F 为试验电荷所受的电场力C 在以点电荷为中心的球面上,由该点电荷所产生的电场强度处处相同D 以上说法都不正确3、如图所示,有两个电2、 下列说法正确的是(D )A 电场强度为零处,电势一定为零。
电势为零处,电场强度一定为零。
B 电势较高处电场强度一定较大,电场强度较小处电势一定较低。
C 带正电的物体电势一定为正,带负电的物体电势一定为负。
D 静电场中任一导体上电势一定处处相等。
3、点电荷q 位于金属球壳中心,球壳内外半径分别为21,R R ,所带静电荷为零B A ,为球壳内外两点,试判断下列说法的正误(C )A 移去球壳,B 点电场强度变大 B 移去球壳,A 点电场强度变大C 移去球壳,A 点电势升高D 移去球壳,B 点电势升高4、下列说法正确的是(D )A 场强相等的区域,电势也处处相等B 场强为零处,电势也一定为零C 电势为零处,场强也一定为零D 场强大处,电势不一定高5、如图所示,一个点电荷q 位于立方体一顶点A 上,则通过abcd 面上的电通量为(C ) A 06q ε B 012q ε C 024q ε D 036qε6、如图所示,在电场强度E 的均匀电场中,有一半径为R 的半球面,场强E 的方向与半球面的对称抽平行,穿过此半球面的电通量为(C ) A E R 22π B E R 22π C E R 2π DE R 221π7、如图所示两块无限大的铅直平行平面A 和B ,均匀带电,其电荷密度均为)(20-•〉m C σσ,在如图所示的c b a 、、三处的电场强度分别为(D ) A 0,,00,εσ B 0,2,00,εσ C 000,,2εσεσεσ D 00,0,εσεσ8、如图所示为一具有球对称性分布的静电场的E ~r 关系曲线.请指出该静电场是由下列哪种带电体产生的.(B )A 半径为R 的均匀带电球面.B 半径为R 的均匀带电球体.C 半径为R 的、电荷体密度为Ar =ρ(A 为常数)的非均匀带电球体D 半径为R 的、电荷体密度为r A /=ρ(A 为常数)的非均匀带电球体 9、设无穷远处电势为零,则半径为R 的均匀带电球体产生的电场的电势分布规律为(图中的0U 和b 皆为常量):(C)10、如图所示,在半径为R 的“无限长”均匀带电圆筒的静电场中,各点的电场强度E 的大小与距轴线的距离r 关系曲线为(A )da bc qA11、下列说法正确的是( D )(A )闭合曲面上各点电场强度都为零时,曲面内一定没有电荷(B )闭合曲面上各点电场强度都为零时,曲面内电荷的代数和必定为零 (C )闭合曲面的电通量为零时,曲面上各点的电场强度必定为零。

静电场和磁场的高斯定理静电场和磁场是物理学中重要的概念,它们在电磁学中起着至关重要的作用。
本文将介绍静电场和磁场的高斯定理,探讨它们在物理学中的应用。
一、静电场的高斯定理静电场是由电荷引起的,它存在于带电粒子周围的空间中。
静电场的高斯定理描述了电场通过闭合曲面的通量与该闭合曲面内的电荷量之间的关系。
高斯定理表明,闭合曲面内的电场通量等于该闭合曲面内的电荷量除以真空介电常数。
具体而言,如果一个闭合曲面内的电荷量为Q,那么通过该闭合曲面的电场通量Φ等于Q除以真空介电常数ε0。
这个定理对于计算复杂的电场分布非常有用。
我们可以选择适当的闭合曲面来简化计算。
通常选择的闭合曲面是对称的,以便于利用对称性简化计算。
静电场的高斯定理在电场分布对称的情况下特别有用。
例如,当电荷分布具有球对称性、柱对称性或平面对称性时,可以选择相应的闭合曲面来简化计算。
这样,我们就可以通过计算闭合曲面内的电荷量来确定电场的分布情况。
二、磁场的高斯定理磁场是由运动电荷或电流引起的,它是与静电场相对应的一种场。
磁场的高斯定理描述了磁场通过闭合曲面的通量为零。
与静电场不同,磁场的高斯定理表明,闭合曲面内的磁场通量等于零。
这意味着磁场线没有起点和终点,它们是闭合的曲线。
磁场的高斯定理说明了磁单极子不存在。
在物理学中,我们一直没有观察到磁单极子,只有磁偶极子。
这是因为磁场的通量总是形成闭合回路,不存在孤立的磁荷。
磁场的高斯定理对于研究磁场分布非常有用。
通过选择适当的闭合曲面,我们可以计算闭合曲面内的磁场通量,从而确定磁场的分布情况。
三、静电场和磁场的应用静电场和磁场的高斯定理在物理学和工程学中有广泛的应用。
在物理学中,静电场和磁场的高斯定理是研究电场和磁场分布的重要工具。
通过选择适当的闭合曲面,可以简化计算,并确定电场和磁场的分布情况。
在工程学中,静电场和磁场的高斯定理被应用于电场和磁场的建模和仿真。
工程师可以利用高斯定理来计算闭合曲面内的电荷量或磁荷量,从而确定电场和磁场的分布情况,进而设计和优化电子设备和电磁系统。
《大学物理》作业 No .2 静电场中的高斯定理班级 ___________ 学号 ___________ 姓名 ___________ 成绩 ________ 说明:字母为黑体者表示矢量内容提要1.电通量⎰⋅=Φs d S E 电场强度穿过任意曲面的电通量在数值上等于穿过该面的电场线条数;对于封闭曲面,电场线穿出规定电通量为正。
2.真空中高斯定理∑⎰=⋅内q d s 01εS E(1).高斯定理表明穿过封闭曲面的电通量仅与面内电荷有关,面外电荷分布对该通量无贡献;(2).空间任意一点(包括高斯面上各点)的电场由高斯面内外所有场源电荷共同决定;(3).高斯定理是静电学的一条重要基本定理,反映了静电场的有源性,同时该定理又是从库仑定律导出的,反映了库仑平方反比律的正确性;(4).运用高斯定理可以方便地求解具有某些对称性分布的电场,根据电场的对称性分布特点,选取恰当的高斯面,从而简化积分,求出电场。
基本要求1.理解电通量概念,掌握电通量计算2.理解并掌握真空中高斯定理3.会用高斯定理计算几种典型对称电荷分布的电场一、 选择题1. 将一个点电荷(忽略重力)无初速地放入静电场中,关于电荷的运动情况,正确的是:[ ] (A )电荷一定顺着电场线加速运动;(B )电荷一定逆着电场线加速运动;(C )到底是顺着还是逆着电场线运动,由电荷的正负决定;(D )以上说法均不正确。
2.关于电场线,以下说法正确的是[ ] (A) 电场线上各点的电场强度大小相等;(B) 电场线是一条曲线,曲线上的每一点的切线方向都与该点的电场强度方向平行;(C) 电场线是电场空间实际存在的系列曲线;(D) 在无电荷的电场空间,电场线可以相交.3.如图2.1,一半球面的底面圆所在的平面与均强电场E 的夹角为30° ,球面的半径为R ,球面的法线向外,则通过此半球面的电通量为 [ ] (A) π R 2E/2 . (B) -π R 2E/2.(C) π R 2E .(D) -π R 2E .4.关于高斯定理的理解有下面几种说法,其中正确的是[ ] (A) 如高斯面上E 处处为零,则该面内必无电荷;(B) 如高斯面内无电荷,则高斯面上E 处处为零;(C) 如高斯面上E 处处不为零,则高斯面内必有电荷;(D) 如高斯面内有净电荷,则通过高斯面的电通量必不为零;(E) 高斯定理仅适用于具有高度对称的电场5. 两个同心均匀带电球面,半径分别为a R 和b R (b a R R <) , 所带电量分别为a Q 和b Q ,设某点与球心相距r , 当b a R r R <<时, 该点的电场强度的大小为:[ ] (A) 2b a 041r Q Q +⋅πε (B) 2b a 041r Q Q -⋅πε (C))(412bb 2a 0R Q r Q +⋅πε (D) 2a 041r Q ⋅πε 6. 如图2.2所示,两个“无限长”的、半径分别为R 1和R 2的共轴圆柱面均匀带电,轴线方向单位长度上的带电量分别为1λ 和2λ, 则在内圆柱面里面、距离轴线为r 处的P 点的电场强度大小 [ ] (A) r0212πελλ+ (B) 20210122R R πελπελ+ (C) 1014R πελ (D) 0 二、 填空题1.将一电量为q 的点电荷置于一正方体盒子的中心,则穿过盒子六个面的电通量是多少 ,如果将点电荷置于盒子的一个顶点处,穿过盒子各个面的电通量又是多少 .2.如图2.3所示,真空中两个正点电荷,带电量都为Q ,相距2R ,若以其中一点电荷所在处O 点为中心,以R 为半径作高斯球面S ,则通过该球面的电场强度通量Φ= ;若以r 0表示高斯面外法线方向的单位矢量,则高斯面上a 、b 两点的电场强度的矢量式分别为 , .三、计算题 1. 一半径为R 的带电球体,其电荷体密度分布为⎩⎨⎧><=)(0)(R r R r Ar ρ , 其中A 为一常数,试求球体内、外的场强分布。
- 选择题题号:30212001 分值:3分难度系数等级:2如图所示,任一闭合曲面S 内有一点电荷q ,O 为S 面上任一点,若将q 由闭合曲面内的P 点移到T 点,且OP=OT ,那么()A 穿过S 面的电通量改变,O 点的场强大小不变;()B 穿过S 面的电通量改变,O 点的场强大小改变;()C 穿过S 面的电通量不变,O 点的场强大小改变;()D 穿过S 面的电通量不变,O 点的场强大小不变。
〔 〕答案:()C题号:30213002 分值:3分难度系数等级:3关于高斯定理的理解有下面几种说法,其中正确的是:()A 如果高斯面上E处处为零,则该面内必无电荷;()B 如果高斯面内无电荷,则高斯面上E处处为零;()C 如果高斯面上E处处不为零,则高斯面内必有电荷;()D 如果高斯面内有净电荷,则通过高斯面的电场强度通量必不为零。
〔 〕 答案:()D题号:30213003 分值:3分难度系数等级:3如在边长为a 的正立方体中心有一个电量为q 的点电荷,则通过该立方体任一面的电场强度通量为()A 0/q ε ; ()B 0/2q ε; ()C 0/4q ε; ()D 0/6q ε。
〔 〕答案:()D题号:30212004 分值:3分难度系数等级:2 如图所示,闭合面S 内有一点电荷Q ,P 为S 面上一点,在S 面外A 点有一点电荷'Q ,若将电荷'Q 移至B 点,则;()A S 面的总通量改变,P 点场强不变;()B S 面的总通量不变,P 点场强改变; ()C S 面的总通量和P 点场强都不变;()D S 面的总通量和P 点场强都改变。
〔 〕 答案:()B题号:30214005 分值:3分难度系数等级:4在电场强度为E Ej =的匀强电场中,有一如图所示的三棱柱,取表面的法线向外,设过面AA'CO ,面B'BOC ,面ABB'A'的电通量为1φ,2φ,3φ,则()A 1230E b c E bc φφφ===; ()B 1230Eac Eac φφφ=-==;()C123Eac Ebc φφφ=-=-=-;()D123Eac Ebc φφφ===。
静电场的高斯定理
《静电场的高斯定理》
一、概述
静电场是一种重要的物理场,它是电学系统中最基本的物理量。
其中,高斯定理可以很好地描述静电场的行为,它是物理学中最重要的数学定理之一。
二、高斯定理的定义
高斯定理(Gauss’s law)是一个关于电压、电势和电场强度之间关系的定理,它可以用来求解电场强度和电势。
它可以用如下公式表示:
负电荷面密度和电势的总和*电场强度的积分= n电荷的电量/εo
其中,n是电荷数,εo是真空电介质中的介电常数。
三、高斯定理的应用
高斯定理可用于研究电荷在各种形状的电容器中的分布情况。
在分析电势和电能场时,也会用到高斯定理。
它同时也可以用来在不完全对称情况下分析和计算电场强度。
四、总结
高斯定理是物理学中一个重要的数学定理,它可以用来求解电场强度和电势,并可用于研究电荷在各种形状的电容器中的分布情况。
它可以用来解决电势和电能场的分析问题,也可以用来解决不完全对称情况下的电场强度计算问题。
大学物理(下)试题库第九章 静电场知识点1:电场、电场强度的概念 1、、【 】下列说法不正确的是:A : 只要有电荷存在,电荷周围就一定存在电场;B :电场是一种物质;C :电荷间的相互作用是通过电场而产生的;D :电荷间的相互作用是一种超距作用。
2、【 】 电场中有一点P ,下列说法中正确的是:A : 若放在P 点的检验电荷的电量减半,则P 点的场强减半;B :若P 点没有试探电荷,则P 点场强为零;C : P 点的场强越大,则同一电荷在P 点受到的电场力越大;D : P 点的场强方向为就是放在该点的电荷受电场力的方向 3、【 】关于电场线的说法,不正确的是: A : 沿着电场线的方向电场强度越来越小; B : 在没有电荷的地方,电场线不会中止;C : 电场线是人们假设的,用以形象表示电场的强弱和方向,客观上并不存在:D :电场线是始于正电荷或无穷远,止于负电荷或无穷远。
4、【 】下列性质中不属于静电场的是: A :物质性; B :叠加性;C :涡旋性;D :对其中的电荷有力的作用。
5、【 】在坐标原点放一正电荷Q ,它在P 点(x=+1, y=0)产生的电场强度为E.现在,另外有一个负电荷-2Q ,试问应将它放在什么位置才能使P 点的电场强度等于零? (A) x 轴上x>1. (B) x 轴上0<x<1.(C) x 轴上x<0. (D) y 轴上y>06、真空中一点电荷的场强分布函数为:E= ___________________。
7、半径为R ,电量为Q 的均匀带电圆环,其圆心O 点的电场强度E=_____ 。
8、【 】两个点电荷21q q 和固定在一条直线上。
相距为d ,把第三个点电荷3q 放在21,q q 的延长线上,与2q 相距为d ,故使3q 保持静止,则(A )212q q = (B )212q q -=(C )214q q -= (D )2122q q -=9、如图一半径为R 的带有一缺口的细圆环,缺口长度为d (d<<R), 环上均匀带有正电,电荷为q ,则圆心O 处的场强大小E =__________,场强方向为___________ 。
- 选择题题号:30212001 分值:3分难度系数等级:2如图所示,任一闭合曲面S 内有一点电荷q ,O 为S 面上任一点,若将q 由闭合曲面内的P 点移到T 点,且OP=OT ,那么()A 穿过S 面的电通量改变,O 点的场强大小不变;()B 穿过S 面的电通量改变,O 点的场强大小改变;()C 穿过S 面的电通量不变,O 点的场强大小改变;()D 穿过S 面的电通量不变,O 点的场强大小不变。
〔 〕答案:()C题号:30213002 分值:3分难度系数等级:3关于高斯定理的理解有下面几种说法,其中正确的是:()A 如果高斯面上E处处为零,则该面内必无电荷;()B 如果高斯面内无电荷,则高斯面上E处处为零;()C 如果高斯面上E处处不为零,则高斯面内必有电荷;()D 如果高斯面内有净电荷,则通过高斯面的电场强度通量必不为零。
〔 〕 答案:()D题号:30213003 分值:3分难度系数等级:3如在边长为a 的正立方体中心有一个电量为q 的点电荷,则通过该立方体任一面的电场强度通量为()A 0/q ; ()B 0/2q ; ()C 0/4q ; ()D 0/6q 。
〔 〕 答案:()D题号:30212004 分值:3分难度系数等级:2 如图所示,闭合面S 内有一点电荷Q ,P 为S 面上一点,在S 面外A 点有一点电荷'Q ,若将电荷'Q 移至B 点,则;()A S 面的总通量改变,P 点场强不变;()B S 面的总通量不变,P 点场强改变;()C S 面的总通量和P 点场强都不变; ()D S 面的总通量和P 点场强都改变。
〔 〕 答案:()B题号:30214005 分值:3分难度系数等级:4在电场强度为E Ej v v的匀强电场中,有一如图所示的三棱柱,取表面的法线向外,设过面AA'CO ,面B'BOC ,面ABB'A'的电通量为1 ,2 ,3 ,则x yza bcEOAABBCQ ’ A PSQB()A 1230Ebc Ebc ; ()B 1230EacEac ; ()C 22123Eac Ec a b Ebc ;()D 22123Eac Ec a b Ebc 。
〔 〕答案:()B题号:30212006 分值:3分难度系数等级:2已知一高斯面所包围的体积内电荷代数和0iq,则可肯定:()A 高斯面上各点场强均为零。
()B 穿过高斯面上每一面元的电通量均为零。
()C 穿过整个高斯面的电通量为零。
()D 以上说法都不对。
〔 〕 答案:()C题号:30214007 分值:3分难度系数等级:4有两个点电荷电量都是q ,相距为2a ,今以左边的点电荷所在处为球心,以a 为半径作一球形高斯面。
在球面上取两块相等的小面积1S 和2S ,其位置如图所示。
设通过1S 和2S 的电场强度通量分别为1 和2 ,通过整个球面的电场强度通量为 ,则()A 120,/q ; ()B 120,2/q ;()C 120,/q ;()D 120,/q 。
〔 〕 答案:()D题号:30212008 分值:3分难度系数等级:2如图所示,一球对称性静电场的~E r 关系曲线,请指出该电场是由下列哪种带电体产生的(E 表示电场强度的大小,r 表示离对称中心的距离) ()A 点电荷; ()B 半径为R 的均匀带电球体;()C 半径为R 的均匀带电球面;()D 内外半径分别为r 和R 的同心均匀带球壳。
〔 〕 答案:()C题号:30212009 分值:3分难度系数等级:2半径为R 的均匀带电球体的静电场中各点的电场强度的大小E 与距球心的距离r 的关系曲线为:xOqq a2aS 1 S 2E1/r 2ORrE()A ()B ()C ()D〔 〕 答案:()B题号:30213010 分值:3分难度系数等级:3 如图所示,两个“无限长”的共轴圆柱面,半径分别为1R 和2R ,其上均匀带电,沿轴线方向单位长度上的带电量分别为1 和2 ,则在两圆柱面之间、距离轴线为r 的P 点处的场强大小E 为:()A102r ; ()B 1202r ; ()C 2022()R r ; ()D 1012()r R 。
〔 〕 答案:()A题号:30211011 分值:3分难度系数等级:1一点电荷,放在球形高斯面的中心处。
下列哪一种情况,通过高斯面的电场强度通量发生变化: ()A 将另一点电荷放在高斯面外; ()B 将另一点电荷放进高斯面内; ()C 将球心处的点电荷移开,但仍在高斯面内; ()D 将高斯面半径缩小。
答案:()B题号:30212012 分值:3分 难度系数等级:2A 和B 为两个均匀带电球体,A 带电荷q ,B 带电荷q ,作一与A 同心的球面S 为高斯面,如图所示。
则 ()A 通过S 面的电场强度通量为零,S 面上各点的场强为零;()B 通过S 面的电场强度通量为0/q ,S 面上场强的大小为20π4rq E;()C 通过S 面的电场强度通量为 0()/q ,S 面上场强的大小为20π4r q E;()D 通过S 面的电场强度通量为0/q ,但S 面上各点的场强不能直接由高斯定理求出。
〔 〕 答案:()D题号:30212013 分值:3分难度系数等级:2若穿过球形高斯面的电场强度通量为零,则()A 高斯面内一定无电荷; ()B 高斯面内无电荷或正负电荷的代数和为零;()C 高斯面上场强一定处处为零; ()D 以上说法均不正确。
〔 〕 答案:()B题号:30214014 分值:3分难度系数等级:4如果把一点电荷Q 放在某一立方体的一个顶点,则()A 穿过每一表面的电通量都等于Q6; ()B 穿过每一表面的电通量都等于Q 60()C 穿过每一表面的电通量都等于Q 30 ;()D 穿过每一表面的电通量都等于024Q〔 〕答案:()D题号:30214015 分值:3分难度系数等级:4 高斯定理nti dqS E S()A 适用于任何静电场。
()B 只适用于真空中的静电场。
()C 只适用于具有球对称性、轴对称性和平面对称性的静电场。
()D 只适用于虽然不具有()C 中所述的对称性,但可以找到合适的高斯面的静电场。
〔 〕 答案:()A题号:30213016 分值:3分难度系数等级:3半径为R 的均匀带电球面,若其电荷面密度为 ,则在距离球面R 处的电场强度大小为: ()A0 ; ()B 02 ; ()C 04 ; ()D 08 。
〔 〕答案:()C题号:30214017 分值:3分难度系数等级:4一电偶极子的偶极矩为p v,两个点电荷之间的距离是l 。
以偶极子的中心为球心,半径为l 作一高斯球面,当球面中心沿p v方向移动时,则穿过高斯球面的电通量的变化顺序是: ()A 00,,0pl ; ()B 00,,0p l; ()C 0,0,0; ()D 条件不充分。
〔 〕答案:()A题号:30215018 分值:3分难度系数等级:5空间有一非均匀电场,其电场线如图所示。
若在电场中取一半径为R 的球面,已知通过球面上S 面的电通量为e ,则通过其余部分球面的电通量为:()A e ; ()B 24/e R S ; ()C 2(4)/e R S S ; ()D 0 〔 〕 答案:()A题号:30212019 分值:3分难度系数等级:2同一束电场线穿过大小不等的两个平面,如图所示。
则两个平面的E 通量和场强关系是:S R()A 12 21E E ; ()B 12 21E E ;()C 12 21E E ; ()D 12 21E E 。
〔 〕答案:()D题号:30212020 分值:3分难度系数等级:2下述带电体系的场强分布可以用高斯定理来计算的是:()A 均匀带电圆板; ()B 均匀带电的导体球; ()C 电偶极子; ()D 有限长均匀带电棒 〔 〕 答案:()B题号:30213021 分值:3分难度系数等级:3在静电场中,一闭合曲面外的电荷的代数和为q ,则下列等式不成立的是:()A0dSS E()B0dLl E()C 0d q S E S()Dd ql E L〔 〕答案:()C二 判断题题号:30223001 分值:2分难度系数等级:3电荷1q 、2q 、3q 和4q 在真空中的分布如图所示, 其中2q 是半径为R 的均匀带电球体,S 为闭合曲面,由于通过闭合曲面S 的电通量SS E d 与1q ,4q 有关,所以电场强度E 是1q ,4q 电荷产生的。
答案:错题号:30222002 分值:2分 难度系数等级2高斯定理说明静电场是保守的。
答案:错题号:30224003 分值:2分 难度系数等级4一点电荷q 处在球形高斯面的中心,当将另一个点电荷置于高斯球面外附近,此高斯面上任意点的电场强度是发生变化,但通过此高斯面的电通量不变化。
答案:对题号:30222004 分值:2分难度系数等级:2• q 1• q 3• q 4Sq 2对于两个相距较近的均匀带电球体所产生的电场,可以用高斯定律求出它的场强分布。
答案:错题号:30221005 分值:2分难度系数等级:1点电荷q 位于一边长为a 的立方体中心,若以该立方体作为高斯面,可以求出该立方体表面上任一点的电场强度。
答案:错题号:30225006 分值:2分难度系数等级:5应用高斯定理求得的场强仅仅是由高斯面内的电荷激发的。
答案:错题号:30223007 分值:2分难度系数等级:3如果高斯面上E处处为零,则该面内必无电荷。
答案:错题号:30222008 分值:2分 难度系数等级2通过闭合曲面的电通量仅由面内的电荷决定。
答案:对题号:30223009 分值:2分难度系数等级:3凡是对称分布的均匀带电系统都可以通过高斯定理求它的电场强度。
答案:错题号:30223010 分值:2分难度系数等级:3闭合曲面内的电荷的代数和为零,闭合曲面上任一点的场强一定为零。
答案:错三 填空题题号:30232001 分值:2分难度系数等级:2如图所示,在场强为E 的均匀电场中取一半球面,其半径为R ,电场强度的方向与半球面的对称轴平行。
则通过这个半球面的电通量为 。
答案:2E R题号:30231002 分值:2分难度系数等级:1E Oxy如图所示,在场强为E 的均匀电场中取一半球面,其半径为R ,电场强度的方向与半球面的对称轴垂直。
则通过这个半球面的电通量为 。
答案:0题号:30231003 分值:2分难度系数等级:1反映静电场性质的高斯定理表明静电场是___ ___场。
答案:有源场题号:30232004 分值:2分 难度系数等级:2 如图所示, 真空中有两个点电荷, 带电量分别为Q 和Q , 相距2R 。