下载文档原格式
高考数学一轮复习讲义导言本讲义旨在为高考考生提供一轮全面复数学的指导。
根据往年考试情况以及高考数学的考点分布，此讲义涵盖了高考数学的各个重要知识点，帮助考生对数学知识进行系统复和巩固。
第一章：代数与函数1.1 一元一次方程- 方程的定义和基本性质- 一元一次方程的解法- 应用题：利用一元一次方程解决实际问题1.2 一元二次方程- 方程的定义和基本性质- 一元二次方程的解法- 应用题：利用一元二次方程解决实际问题1.3 指数与对数- 指数与对数的基本知识- 指数与对数的运算- 应用题：利用指数与对数解决实际问题第二章：几何与图形2.1 直线与曲线- 直线与曲线的基本概念- 直线与曲线的性质与判定方法- 应用题：利用直线与曲线解决实际问题2.2 三角形- 三角形的基本概念和性质- 三角形的判定方法- 三角形的相似与全等- 应用题：利用三角形解决实际问题2.3 圆与圆周角- 圆的基本概念和性质- 圆周角的性质和计算- 应用题：利用圆和圆周角解决实际问题第三章：概率与统计3.1 概率- 概率的基本概念和性质- 概率计算方法- 应用题：利用概率解决实际问题3.2 统计- 统计的基本概念和方法- 统计图表的制作和分析- 水果调查统计案例总结通过全面复习以上各个单元的知识，考生可以更好地应对高考数学题目，提高解题能力和应变能力。
在复习过程中，建议考生多做习题并及时查找解答，加强对知识点的理解和掌握。
祝愿所有考生在高考中取得优异成绩！。
答案与解析二 配套精练第一章 集合与常用逻辑用语、不等式第1讲 集合及其运算1. D 解析： M ＝{x |0≤x <16}，N ＝{x ⎪⎪⎪⎭⎬⎫x ≥13，则M ∩N ＝{x ⎪⎪⎪⎭⎬⎫13≤x <16. 2. A 解析： 因为U ＝{x ∈N |x ≤4}＝{0,1,2,3,4}，∁U (A ∩B )＝{0,2,3}，所以A ∩B ＝{1,4}，即1∈A 且4∈A .又A ＝{1，m }，所以m ＝4.3. C 解析： 由题意，非空且互不相等的集合A ，B ，C 满足A ∪B ＝A ，可得B ⊆A .又因为B ∩C ＝C ，可得C ⊆B ，所以C ⊆A ，所以A ∩C ＝C .4. C 解析： 由题可知A ＝{－1,0,1}，所以A ∩B ＝{0,1}，所以其子集分别是∅，{1}，{0}，{0,1}，共有4个子集．5. C 解析： 因为集合M ＝{x |x ＝2k ＋1，k ∈Z }，集合N ＝{y |y ＝4k ＋3，k ∈Z }＝{y |y ＝2(2k ＋1)＋1，k ∈Z }，且x ∈N 时，x ∈M 成立，所以M ∪N ＝{x |x ＝2k ＋1，k ∈Z }．6. ABC 解析： 当B ＝∅时，m ＋1>2m －1，即m <2，此时∁U B ＝R ，符合题意；当B ≠∅时，m ＋1≤2m －1，即m ≥2，由B ＝{x |m ＋1≤x ≤2m －1}，得∁U B ＝{x |x <m ＋1或x >2m －1}．因为A ⊆∁U B ，所以m ＋1>7或2m －1<－2，可得m >6或m <－12.因为m ≥2，所以m >6.综上，实数m 的取值范围为{m |m <2或m >6}．7. BD 解析： 因为N ∩(∁R M )＝∅，所以N ⊆M .若N 是M 的真子集，则M ∩(∁R N )≠∅，故A 错误；由N ⊆M ，得M ∪(∁R N )＝R ，故B 正确；由N ⊆M ，得∁R N ⊇∁R M ，故C 错误，D 正确．8. BD 解析： 对于A ，由B －A ＝{x |x ∈B 且x ∉A }，知B －A ＝{3,8}，A 错误；对于B ，由A －B ＝{x |x ∈A 且x ∉B }，A －B ＝∅，知A ⊆B ，B 正确；对于C ，由韦恩图知B －A 如图中阴影部分所示，则B －A ＝B ∩(∁U A )，C 错误；对于D ，∁U B ＝{x |x <－2或x ≥4}，则A －B ＝A ∩(∁U B )＝{x |x <－2或x ≥4}，D 正确．(第8题)9. (－∞，1] 解析： 由x －a ≥0，得x ≥a ，所以B ＝[a ，＋∞)．因为A＝[1,6]，且A ⊆B ，所以a ≤1，所以实数a 的取值范围是(－∞，1]．10. (－∞，－1]∪[1，＋∞)∪{0} 解析： 由题意，原问题转化为方程ax 2－2x ＋a ＝0至多只有一个根．当a ＝0时，方程为－2x ＝0，解得x ＝0，此时方程只有一个实数根，符合题意；当a ≠0时，方程ax 2－2x ＋a ＝0为一元二次方程，所以Δ＝4－4a 2≤0，解得a ≤－1或a ≥1.综上，实数a 的取值范围为(－∞，－1]∪[1，＋∞)∪{0}．11. 15 解析： 因为1∈A ，11＝1∈A ；－1∈A ，1－1＝－1∈A ；2∈A ，12∈A ；3∈A ，13∈A ，所以所求集合即为由1，－1，“3和13”，“2和12”这“四大”元素所组成的集合的非空子集，所以满足条件的集合的个数为24－1＝15.12. 【解答】 (1) 当a ＝0时，A ＝{x |－1<x <1}，所以∁R A ＝{x |x ≤－1或x ≥1}，所以(∁R A )∩B ＝{x |1≤x <4}．(2) 因为A ⊆B ，所以集合A 可以分为A ＝∅和A ≠∅两种情况讨论．当A ＝∅时，2a －1≥3a ＋1，即a ≤－2；当A ≠∅时，得⎩⎨⎧ 2a －1≥－1，3a ＋1≤4，2a －1<3a ＋1，即0≤a ≤1.综上，a ∈(－∞，－2]∪[0,1]．13. 【解答】 集合A ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x |0<x －13≤1＝{x |1＜x ≤4}，B ＝⎩⎨⎧⎭⎬⎫x |y ＝1－x 2＋10x －16＝{x |2＜x ＜8}． (1) 因为集合C ＝{x |x ≤a }满足A ∩C ＝A ，所以A ⊆C ，所以a ≥4，所以实数a 的取值范围是[4，＋∞)．(2) 因为A ∩B ＝{x |2＜x ≤4}，A ∪B ＝{x |1＜x ＜8}，所以集合D ＝{x |1＜x ≤2或4＜x ＜8}．14. 【解答】 (1) 因为集合A ＝{x |x 2－ax ＋a 2－19＝0}，B ＝{x |x 2－5x ＋6＝0}＝{2,3}，且A ∩B ＝{2}，所以2∈A ，所以4－2a ＋a 2－19＝0，即a 2－2a －15＝0，解得a ＝－3或a ＝5.当a ＝－3时，A ＝{x |x 2＋3x －10＝0}＝{－5,2}，A ∩B ＝{2}，符合题意；当a ＝5时，A ＝{x |x 2－5x ＋6＝0}＝{2,3}，A ∩B ＝{2,3}，不符合题意．综上，实数a 的值为－3.(2) 因为A ＝{x |x 2－ax ＋a 2－19＝0}，B ＝{2,3}，C ＝{x |x 2＋2x －8＝0}＝{－4,2}，且A ∩B ≠∅，A ∩C ＝∅，所以3∈A ，所以9－3a ＋a 2－19＝0，即a 2－3a －10＝0，解得a ＝－2或a ＝5.当a ＝－2时，A ＝{x |x 2＋2x －15＝0}＝{－5,3}，满足题意；当a ＝5时，A ＝{x |x 2－5x ＋6＝0}＝{2,3}，不满足题意．综上，实数a 的值为－2.第2讲 充分条件、必要条件、充要条件1. B 解析： 若x <0，y ＝0满足x <y ，则(x －y )·y 2＝0，即(x －y )·y 2<0不成立；若(x －y )·y 2<0，则有y ≠0，必有y 2>0，从而得x －y <0，即x <y 成立．所以“x <y ”是“(x －y )·y 2<0”成立的必要不充分条件．2. D 解析： 非有志者不能至，是必要条件；但“有志”也不一定“能至”，不是充分条件．3. B4. A 解析： 因为x <z ，y <z ，所以x ＋y <2z ，故充分性成立；当x ＝3，y ＝1，z ＝2.5时，满足x ＋y <2z ，但不满足x <y <z ，故必要性不成立．5. C 解析： x －1x >0⇒x 2－1x >0⇒x (x ＋1)(x －1)>0⇒x >1或－1<x <0.因为{x |－1<x <0}{x |x >1或－1<x <0}，所以不等式x －1x >0成立的一个充分条件是－1<x <0.6. BC 解析： x 2>x 的解集为(－∞，0)∪(1，＋∞)．对于A ，因为(1，＋∞)为(－∞，0)∪(1，＋∞)的真子集，故A 不符合；对于B ，因为2x 2>2x 等价于x 2>x ，解集也是(－∞，0)∪(1，＋∞)，故B 符合；对于C ，1x <1即为x (x －1)>0，解集为(－∞，0)∪(1，＋∞)，故C 符合；对于D ，|x (x －1)|＝x (x －1)即为x (x －1)≥0，解集为(－∞，0]∪[1，＋∞)，(－∞，0)∪(1，＋∞)为(－∞，0]∪[1，＋∞)的真子集，故D 不符合．7. AC 解析： 对于p ：|2x －1|<3，解得x ∈A ＝{x |－1<x <2}．对于q ：2x 2－ax －a 2≤0，得(2x ＋a )(x －a )≤0，当a ≥0时，解得x ∈B ＝{x ⎪⎪⎪⎭⎬⎫－a 2≤x ≤a ；当a <0时，解得x ∈B ＝{x ⎪⎪⎪⎭⎬⎫a ≤x ≤－a 2.因为p 是q 的一个必要不充分条件，所以B A .当a ≥0时，⎩⎪⎨⎪⎧ －a 2>－1，a <2，解得0≤a <2.当a <0时，⎩⎪⎨⎪⎧ a >－1，－a 2<2，解得－1<a <0.综上，可得－1<a <2.故只要实数a 的取值集合是集合{a |－1<a <2}的真子集即可．8. BCD 解析： 对于A ，方程为x 2＋3＝0，方程没有实数根，所以A 错误；对于B ，如果方程没有实数根，则Δ＝(m －3)2－4m ＝m 2－10m ＋9<0，所以1<m <9，m >1是1<m <9的必要条件，所以B 正确；对于C ，因为方程有两个正根，所以⎩⎨⎧ Δ＝m 2－10m ＋9≥0，－(m －3)>0，m >0，所以0<m ≤1，所以方程有两个正根的充要条件是0<m ≤1，所以C 正确；对于D ，如果方程有一个正根和一个负根，则⎩⎨⎧Δ＝m 2－10m ＋9>0，m <0，所以m <0，所以方程有一个正根和一个负根的充要条件是m <0，所以D 正确．9. [1，＋∞) 解析： 由不等式|x ＋1|>2，可得x >1或x <－3，所以綈p ：－3≤x ≤1.又由綈q ：x ≤a ，且綈p 是綈q 的充分不必要条件，可知a ≥1，所以实数a 的取值范围为[1，＋∞)．10. m ＝1(答案不唯一) 解析： 当x ∈(2,3)时，易知x 2－x ＝⎝ ⎛⎭⎪⎫x －122－14∈(2,6)．又∃x ∈(2,3)，mx 2－mx －3>0⇔∃x ∈(2,3)，m >3x 2－x ⇔m >⎝ ⎛⎭⎪⎫3x 2－x min ，x ∈(2,3)⇔m ≥12.显然m ＝1⇒m ≥12，m ≥12D ⇒/m ＝1，故“m ＝1”是命题“∃x ∈(2,3)，mx 2－mx －3>0”成立的充分不必要条件．11. [1,2] 解析： 由(x －a )2<1得a －1<x <a ＋1.因为1<x <2是不等式(x －a )2<1成立的充分不必要条件，所以满足⎩⎨⎧a －1≤1，a ＋1≥2且等号不能同时取得，即⎩⎨⎧a ≤2，a ≥1，解得1≤a ≤2. 12. 【解答】 (1) 当m ＝2时，A ＝{x |1<x <5}，B ＝{x |－2<x <2}，所以A ∪B ＝{x |－2<x <5}，A ∩B ＝{x |1<x <2}．(2) 由“x ∈A ”是“x ∈B ”成立的充分不必要条件，得A B .当A ＝∅，即m－1≥m 2＋1时，m 无解，所以A ≠∅，所以⎩⎨⎧m －1≥－2，m 2＋1≤2且等号不能同时取得，解得－1≤m ≤1.当m ＝－1时，A ＝B ＝(－2,2)，不成立．故实数m 的取值范围为{m |－1<m ≤1}．13. 【解答】 (1) 不存在，理由如下：由|4x －3|≤1，得－1≤4x －3≤1，故12≤x ≤1，即p ：12≤x ≤1.假设存在a ，使得p 是q 的充要条件，则不等式x 2－4ax ＋3a －1≤0的解集为{x ⎪⎪⎪⎭⎬⎫12≤x ≤1，所以x 1＝12，x 2＝1是方程x 2－4ax ＋3a －1＝0的两个根，故⎩⎪⎨⎪⎧ 12＋1＝4a ，12×1＝3a －1，此方程组无解，故假设不成立，所以不存在实数a ，使得p 是q 的充要条件．(2) 若p 是q 的充分不必要条件，则集合{x ⎪⎪⎪⎭⎬⎫12≤x ≤1为不等式x 2－4ax ＋3a －1≤0的解集的真子集．令f (x )＝x 2－4ax ＋3a －1，则由二次函数的图象性质可得⎩⎪⎨⎪⎧ f ⎝ ⎛⎭⎪⎫12≤0，f (1)≤0，即⎩⎪⎨⎪⎧ ⎝ ⎛⎭⎪⎫122－4a ×12＋3a －1≤0，1－4a ＋3a －1≤0，解得⎩⎪⎨⎪⎧ a ≤34，a ≥0，故0≤a ≤34.当a ＝0时，x 2－4ax ＋3a －1≤0⇒x 2－1≤0，解得－1≤x ≤1，满足题意；当a ＝34时，x 2－4ax ＋3a －1≤0⇒x 2－3x ＋54≤0，解得12≤x ≤52，满足题意．所以实数a 的取值范围为⎣⎢⎡⎦⎥⎤0，34. 14. 【解答】 必要性：若方程ax 2＋2x ＋1＝0有且只有一个负数根，当a ＝0时，方程为2x ＋1＝0，解得x ＝－12，符合题意；当a <0时，Δ＝4－4a >0，设方程ax 2＋2x ＋1＝0的两根分别为x 1，x 2，则x 1x 2＝1a <0，此时方程ax 2＋2x ＋1＝0有且只有一个负数根；当a >0时，由Δ＝4－4a ≥0，可得0<a ≤1，设方程ax 2＋2x ＋1＝0的两根分别为x 1，x 2，则⎩⎪⎨⎪⎧ x 1x 2＝1a >0，x 1＋x 2＝－2a <0，则x 1，x 2均为负数．由题意可知Δ＝0，可得a ＝1，符合题意．所以“方程ax 2＋2x ＋1＝0有且只有一个负数根”⇒“a ≤0或a ＝1”．充分性：当a ＝0时，原方程变为2x ＋1＝0，解得x ＝－12，原方程只有一个负数根；当a ＝1时，方程为x 2＋2x ＋1＝0，解得x ＝－1，原方程只有一个负数根；当a <0时，对于原方程，Δ＝4－4a >0，此时方程ax 2＋2x ＋1＝0有两根，设为x 1，x 2，则x 1x 2＝1a <0，此时方程ax 2＋2x ＋1＝0有且只有一个负数根．所以“方程ax 2＋2x ＋1＝0有且只有一个负数根”⇐“a ≤0或a ＝1”．综上所述，方程ax 2＋2x ＋1＝0有且只有一个负数根的充要条件为a ≤0或a ＝1.第3讲 全称量词和存在量词1. C 解析： 因为集合M ，N 满足M ∩N ≠∅，所以根据交集的定义可得∃x ∈M ，x ∈N .2. A 解析： 命题“∀x ∈R,2x >0”为全称量词命题，该命题的否定为“∃x ∈R,2x ≤0”．3. A 解析： 由题意，①若甲说的是真话，则甲不会证明，乙会证明，丙不会证明，丁不会证明，此时丁说的也是真话，与题意矛盾；②若乙说的是真话，则丙会证明，甲和丁均会证明，与题意矛盾；③若丙说的是真话，则丁会证明，甲和丁均会证明，与题意矛盾；④若丁说的是真话，则丁不会证明，甲会证明，丙不会证明，满足题意．4. A 解析： 若p 为真，则Δ1＝4－4a ≤0，解得a ≥1.若q 为真，则Δ2＝4a 2－4(2－a )<0，解得－2<a <1.若p 真q 假，则a ≥1；若p 假q 真，则－2<a <1.综上所述，若p ，q 一真一假，则实数a 的取值范围为(－2，＋∞)．5. A 解析： 若不等式(m ＋1)x 2＋(m ＋1)x ＋1>0对任意x ∈R 恒成立，则有①当m ＋1＝0，即m ＝－1时，不等式显然成立；②当m ＋1>0时，Δ＝(m ＋1)2－4(m ＋1)<0，解得－1<m <3；③当m ＋1<0时，不等式(m ＋1)x 2＋(m ＋1)x ＋1>0对任意x ∈R 显然不恒成立，舍去．综上①②③可知，不等式(m ＋1)x 2＋(m＋1)x ＋1>0对任意x ∈R 恒成立，则－1≤m <3，所以当“∀x ∈R ，(m ＋1)x 2＋(m ＋1)x ＋1>0”是假命题时，m ∈(－∞，－1)∪[3，＋∞)．6. AB 解析： 由条件可知∀x ∈⎣⎢⎡⎦⎥⎤12，2，2x 2－λx ＋1≥0是真命题，即λ≤2x 2＋1x ＝2x ＋1x ，即λ≤⎝ ⎛⎭⎪⎫2x ＋1x min ，x ∈⎣⎢⎡⎦⎥⎤12，2.设f (x )＝2x ＋1x ≥22x ·1x ＝22，x ∈⎣⎢⎡⎦⎥⎤12，2，等号成立的条件是2x ＝1x ⇒x ＝22∈⎣⎢⎡⎦⎥⎤12，2，所以f (x )的最小值是22，即λ≤22，满足条件的是AB.7. BC 解析： 当x ＝0时，1x 2＋1＝1，A 错误．当x ＝－1时，1x <x ＋1，B 正确．命题“∃n ∈N ，n 2>2n ”的否定是命题“∀n ∈N ，n 2≤2n ”，C 正确．命题“∀n >4,2n >n 2”的否定是命题“∃n >4,2n ≤n 2”，D 错误．8. AD 解析： 函数f (x )＝x ＋4x 在[1,2]上单调递减，在[2,6]上单调递增，f (x )min＝f (2)＝4，f (x )max ＝f (6)＝203.对任意a ，b ，c ∈[1,6]，不妨令f (a )≥f (b )≥f (c )，则f (b )＋f (c )≥2f (c )≥2f (x )min >f (x )max ≥f (a )，即f (a )，f (b )，f (c )均能作为一个三角形的三条边长，A 正确，B 错误；取a ＝b ＝2，c ＝22＋2，满足a ，b ，c ∈[1,6]，则f (a )＝f (b )＝4，f (c )＝42，显然有[f (a )]2＋[f (b )]2＝[f (c )]2，即以f (a )，f (b )，f (c )为边的三角形是直角三角形，C 错误，D 正确．9. ⎣⎢⎡⎭⎪⎫52，＋∞ 解析： 因为∀x ∈[1,2]，x 2－ax ＋1≤0为真命题，所以a ≥⎝ ⎛⎭⎪⎫x ＋1x max ，x ∈[1,2]．因为y ＝x ＋1x 在区间[1,2]上单调递增，所以⎝ ⎛⎭⎪⎫x ＋1x max ＝2＋12＝52，即a ≥52，所以实数a 的取值范围为⎣⎢⎡⎭⎪⎫52，＋∞. 10. (－∞，2] 解析： 设x 1，x 2是方程的两个负实数根，则⎩⎨⎧ Δ＞0，x 1＋x 2＝－m ＜0，x 1x 2＝1＞0，即⎩⎨⎧m 2－4＞0，m ＞0，解得m ＞2，所以当綈p 是真命题时，m 的取值范围是(－∞，2]．11. ∀x ∈[1,2]，x 2＋2ax ＋2－a ≤0 (－3，＋∞)解析： 綈p ：∀x ∈[1,2]，x 2＋2ax ＋2－a ≤0.若綈p 是真命题，令f (x )＝x 2＋2ax ＋2－a ，则 ⎩⎨⎧ f (1)≤0，f (2)≤0，即⎩⎨⎧1＋2a ＋2－a ≤0，4＋4a ＋2－a ≤0，解得a ≤－3，故满足题意的实数a 的取值范围为(－3，＋∞)．12. 【解答】 (1) 因为命题p ：∀x ∈R ，x 2＋ax ＋2≥0为真命题，所以Δ＝a 2－4×1×2≤0，解得－22≤a ≤22，所以实数a 的取值范围为[－22，22]．(2) 因为命题q ：∃x ∈⎣⎢⎡⎦⎥⎤－3，－12，x 2－ax ＋1＝0为真命题，所以a ＝x 2＋1x ＝x ＋1x ，又y ＝x ＋1x 在[－3，－1]上单调递增，在⎣⎢⎡⎦⎥⎤－1，－12上单调递减，所以当x ＝－1时，a 取最大值－2.当x ＝－3时，a ＝－103；当x ＝－12时，a ＝－52.所以实数a 的取值范围为⎣⎢⎡⎦⎥⎤－103，－2. 13. 【解答】 若命题p 为真命题，则Δ＝(m －2)2－4≥0，解得m ≤0或m ≥4.若命题q 为真命题，由a ，b ∈(0，＋∞)，知b ＝2a a －1>0，所以a －1>0，则a (b －1)＝a ⎝ ⎛⎭⎪⎫2a a －1－1＝a ·a ＋1a －1＝(a －1＋1)⎝⎛⎭⎪⎫1＋2a －1＝a －1＋2a －1＋3≥3＋22，m ＋22≤22＋3⇒m ≤3.当命题p 为真，命题q 为假时，⎩⎨⎧ m ≤0或m ≥4，m >3，解得m ≥4；当命题p 为假，命题q 为真时，⎩⎨⎧0<m <4，m ≤3，解得0<m ≤3.综上所述，实数m 的取值范围为{m |0<m ≤3或m ≥4}．14. 【解答】 (1) 由题设知f ′(x )＝x 2＋2x ＋a ≥0在[1，＋∞)上恒成立，即a ≥－(x ＋1)2＋1在[1，＋∞)上恒成立，而函数y ＝－(x ＋1)2＋1在[1，＋∞)上单调递减，则y max ＝－3，所以a ≥－3，所以a 的最小值为－3.(2) 由题可知，当x ∈⎣⎢⎡⎦⎥⎤12，2时，f ′(x )max ≤g (x )max .因为f ′(x )＝x 2＋2x ＋a ＝(x ＋1)2＋a －1在⎣⎢⎡⎦⎥⎤12，2上单调递增，所以f ′(x )max ＝f ′(2)＝8＋a .而g ′(x )＝1－xe x ，由g ′(x )＞0，得x ＜1，由g ′(x )＜0，得x ＞1，所以g (x )在(－∞，1)上单调递增，在(1，＋∞)上单调递减，所以当x ∈⎣⎢⎡⎦⎥⎤12，2时，g (x )max ＝g (1)＝1e .由8＋a ≤1e ，得a ≤1e －8，所以实数a 的取值范围为⎝ ⎛⎦⎥⎤－∞，1e －8. 第4讲 不等式的性质、基本不等式1. D 解析： 对于A ，取a ＝－1，b ＝1，则1a <1b ，A 错误；对于B ，取a＝－1，b ＝1，则a 2＝b 2，B 错误；对于C ，取a ＝－1，b ＝1，则1a 2＝1b 2，C 错误；对于D ，由a <b ，可得b 3－a 3＝(b －a )·(b 2＋ab ＋a 2)＝(b －a )⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫b ＋12a 2＋34a 2>0，所以a 3<b 3，D 正确．2. D 解析： 对于A ，当c ＝0时，显然不成立，故A 为假命题；对于B ，当a ＝－3，b ＝－2时，满足a <b <0，但a 2<ab <b 2不满足，故B 为假命题；对于C ，当c ＝3，a ＝2，b ＝1时，a c －a ＝23－2>b c －b＝12，不满足，故C 为假命题；对于D ，因为a >b >c >0，所以a b －a ＋c b ＋c ＝a (b ＋c )－b (a ＋c )b (b ＋c )＝ac －bc b (b ＋c )＝(a －b )c b (b ＋c )>0，即a b >a ＋c b ＋c，故D 为真命题． 3. B 解析： 由题知4b ＋1a ＝12⎝ ⎛⎭⎪⎫4b ＋1a (a ＋b )＝12⎝ ⎛⎭⎪⎫4a b ＋b a ＋5≥12(4＋5)＝92，当且仅当4a b ＝b a 时等号成立．4. C 解析： 7＝(a ＋2b )2－ab ＝(a ＋2b )2－12a ·2b ≥(a ＋2b )2－12⎝ ⎛⎭⎪⎫a ＋2b 22＝7(a ＋2b )28，则(a ＋2b )2≤8，当且仅当a ＝2b ＝2时等号成立，又a ，b ∈(0，＋∞)，所以0<a ＋2b ≤22，当且仅当a ＝2b ＝2时等号成立，所以a ＋2b 的最大值为2 2.5. BCD 解析： 对于A ，当c ＝0时，ac ＝bc ，故A 错误；对于B ，若ac 2>bc 2，则a >b ，故B 正确；对于C ，若a <b <0，则|a |>|b |，故C 正确；对于D ，若c >a >b >0，则0<c －a <c －b ，从而1c －a >1c －b，故D 正确． 6. AB 解析： 对于A ，ab ≤⎝ ⎛⎭⎪⎫a ＋b 22＝⎝ ⎛⎭⎪⎫122＝14，当且仅当a ＝b ＝12时取等号，故A 正确．对于B ，(a ＋b )2＝a ＋b ＋2ab ≤a ＋b ＋a ＋b ＝2，故a ＋b ≤2，当且仅当a ＝b ＝12时取等号，故B 正确．对于C ，1a ＋1b ＝⎝ ⎛⎭⎪⎫1a ＋1b (a ＋b )＝2＋b a ＋a b ≥2＋2b a ·a b ＝4，当且仅当a ＝b ＝12时取等号，所以1a ＋1b 有最小值4，故C 错误．对于D ，(a ＋b )2＝1⇒a 2＋2ab ＋b 2＝1≤a 2＋(a 2＋b 2)＋b 2，即a 2＋b 2≥12，故a 2＋b 2有最小值12，故D 错误．7. －1，－2，－3(答案不唯一) 解析： －1>－2>－3，(－1)＋(－2)＝－3>－3，矛盾，所以－1，－2，－3可验证该命题是假命题．8. 9 解析： 因为0<x <1，所以0<1－x <1，则1x ＋41－x ＝⎝ ⎛⎭⎪⎫1x ＋41－x [(1－x )＋x ]＝1＋4＋1－x x ＋4x 1－x ≥5＋21－x x ·4x 1－x ＝9，当且仅当1－x x ＝4x 1－x，即x ＝13时，等号成立，故1x ＋41－x的最小值为9. 9. 6 解析： 设矩形空地的长为x m ，则宽为32x m ．由题意，试验区的总面积S ＝(x －0.5×4)⎝ ⎛⎭⎪⎫32x －0.5×2＝34－x －64x ≤34－2x ·64x ＝18，当且仅当x＝64x ，即x ＝8时，等号成立，所以每块试验区的面积的最大值为183＝6(m 2)．10. 【解答】 (1) 由不等式4a 2＋b 2≥4ab ，解得ab ≤12，当且仅当2a ＝b ＝1时取等号，所以ab 的最大值为12，此时a ＝12，b ＝1.(2) 由4a 2＋b 2＝2，得4a 2＋(1＋b 2)＝3.由4a 2＋(1＋b 2)≥24a 2·(1＋b 2)＝4a 1＋b 2，解得a 1＋b 2≤34，当且仅当4a 2＝1＋b 2，即a ＝64，b ＝22时取等号，所以a 1＋b 2的最大值为34，此时a ＝64，b ＝22.11. 【解答】 (1) 因为a >1，b >2，所以a －1>0，b －2>0，所以1a －1＋1b －2＝14⎝ ⎛⎭⎪⎫1a －1＋1b －2(a －1)(b －2)＝14[(b －2)＋(a －1)]≥14×2(b －2)(a －1)＝1，当且仅当⎩⎨⎧b －2＝a －1，(a －1)(b －2)＝4时，等号成立，解得a ＝3，b ＝4，所以1a －1＋1b －2的最小值为1，此时a ＝3，b ＝4.(2) 由2a ＋b ＝6，得2(a －1)＋(b －2)＝2，所以(a －1)＋b －22＝1，所以1a －1＋1b －2＝⎝ ⎛⎭⎪⎫1a －1＋1b －2×1＝⎝ ⎛⎭⎪⎫1a －1＋1b －2×⎣⎢⎡⎦⎥⎤(a －1)＋b －22＝32＋a －1b －2＋b －22(a －1)≥3＋222，当且仅当⎩⎨⎧b －2＝2(a －1)，2(a －1)＋(b －2)＝2时，等号成立，解得a ＝3－2，b ＝22，所以1a －1＋1b －2的最小值为3＋222，此时a ＝3－2，b ＝2 2.(3) 因为b >2，由1a ＋1b ＝1，可得a ＝b b －1，所以a －1＝1b －1，所以1a －1＋1b －2＝b －2＋1b －2＋1≥3，当且仅当a ＝32，b ＝3时，等号成立，所以1a －1＋1b －2的最小值为3，此时a ＝32，b ＝3.12. D 解析： 因为A ＝{1,2,3}，B ＝{0,1,2}，所以A ∩B ＝{1,2}，A ∪B ＝{0,1,2,3}，所以当x ∈A ∩B ，y ∈A ∪B 时，z ＝0,1,2,3,4,6，所以A *B ＝{0,1,2,3,4,6}，所以∁(A *B )A ＝{0,4,6}．13. BC 解析： A 错误，当a <0时，显然有P <0.B 正确，当a >1时，P ＝a ＋2a ≥2a ·2a ＝22，故充分性成立，而P ≥22只需a >0即可．C 正确，P ＝a＋2a >3可得0<a <1或a >2，当a >2时，P >3成立．D 错误，当a >3时，a ＋2a >3＋23>3.14. 【解答】 (1) 当m ＝1时，B ＝{x |2<x <3}．因为A ＝{x |－1≤x ≤2}，所以∁R A ＝{x |x <－1或x >2}，所以A ∪B ＝{x |－1≤x <3}，(∁R A )∩B ＝{x |2<x <3}．(2) 因为∅是A ∩B 的真子集，所以A ∩B ≠∅.因为A ＝{x |－1≤x ≤2}，B ＝{x |2m <x <3}，所以⎩⎨⎧2m <3，2m <2，解得m <1，即实数m 的取值范围为(－∞，1)．(3) 因为B ∩(∁R A )中只有一个整数，∁R A ＝{x |x <－1或x >2}，B ＝{x |2m <x <3}，所以B ≠∅，且－3≤2m <－2，解得－32≤m <－1，所以实数m 的取值范围是{m ⎪⎪⎪⎭⎬⎫－32≤m <－1. 第5讲 一元二次不等式1. A 解析： 因为不等式x 2＋kx ＋1<0的解集为空集，所以Δ＝k 2－4≤0，解得－2≤k ≤2.2. D 解析： 当a ＝1时，不等式为－4<0恒成立，故满足题意；当a ≠1时，要满足⎩⎨⎧a －1<0，Δ<0，解得－3<a <1.综上，实数a 的取值范围是(－3,1]．3. C 解析： 由x ＋a x －b ＝(1－b )x ＋ax ≥0，可知⎩⎨⎧x [(b －1)x －a ]≤0，x ≠0的解集为[－1,0)，所以⎩⎪⎨⎪⎧b －1>0，ab －1＝－1，则b >1且a ＋b ＝1.4. C 解析： 因为关于x 的一元二次不等式ax 2＋bx ＋c >0的解集为{x |1<x <3}，所以1,3为方程ax 2＋bx ＋c ＝0的两个根，由韦达定理得⎩⎪⎨⎪⎧1＋3＝－ba ，1×3＝c a ，所以⎩⎨⎧c ＝3a ，b ＝－4a ，且a <0，则ax ＋b cx ＋a >0等价于x －43x ＋1>0，即(3x ＋1)(x －4)>0，故原不等式的解集为⎝ ⎛⎭⎪⎫－∞，－13∪(4，＋∞)．5. ACD 解析： 对于A ，ax 2>0(a >0)的解集为{x |x ≠0}，A 错误；对于B ，因为Δ＝1－4＝－3<0，所以x 2＋x ＋1<0的解集为∅，B 正确；对于C ，若a <0，Δ＝0，则ax 2＋bx ＋c ≥0的解集为{x ⎪⎪⎪⎭⎬⎫x ＝－b 2a ，C 错误；对于D ，x 2＋3x －4>0的解集为(－∞，－4)∪(1，＋∞)，不等式组⎩⎨⎧x －1>0，x ＋4>0的解集为(1，＋∞)，D错误．6. BD 解析： 设x 小时后蓄水池中的水量为y t ，则y ＝400＋60x －1206x .设6x ＝u ，则u 2＝6x (u ∈[0,12])，所以y ＝400＋10u 2－120u ＝10(u －6)2＋40.因为u ∈[0,12]，故当u ＝6，即x ＝6时，y min ＝40，即从供水开始到第6个小时时，蓄水池中的存水量最少，为40t ，所以A 错误，B 正确．令400＋10u 2－120u >80，即u 2－12u ＋32>0，解得u <4或u >8，所以0≤x <83或323<x ≤24，所以C 错误．由400＋10u 2－120u <80，得83<x <323，又323－83＝8，所以每天约有8小时蓄水池中水量少于80t ，所以D 正确．7. [1，＋∞) 解析： x －1x >0⇒x (x －1)>0⇒x >1或x <0，则当x >a 时，x －1x >0成立，所以a ≥1.8. (－1,2) 解析： 由表中二次函数y ＝ax 2＋bx ＋c (x ∈R )的部分对应值，得⎩⎨⎧c ＝2，a ＋b ＋c ＝2，a －b ＋c ＝0，解得⎩⎨⎧a ＝－1，b ＝1，c ＝2，所以y ＝－x 2＋x ＋2.不等式ax 2＋bx ＋c ＞0化为－x 2＋x ＋2＞0，即x 2－x －2＜0，解得－1＜x ＜2，所以该不等式的解集为(－1,2)．9. ⎝ ⎛⎭⎪⎫－12，32 解析： 由题意可知，不等式(x －a )(x ＋a )<1对任意实数x 都成立，又由(x －a )(x ＋a )＝(x －a )(1－x －a )，即x 2－x －a 2＋a ＋1>0对任意实数x 都成立，所以Δ＝1－4(－a 2＋a ＋1)<0，即4a 2－4a －3<0，解得－12<a <32.10. 【解答】 (1) 因为不等式ax 2＋bx －1>0的解集是{x |1<x <2}，所以a <0，且1和2是方程ax 2＋bx －1＝0的两个根，所以⎩⎨⎧a ＋b －1＝0，4a ＋2b －1＝0，解得⎩⎪⎨⎪⎧a ＝－12，b ＝32.(2) 由(1)知不等式ax ＋1bx －1≥0即为－12x ＋132x －1≥0⇔x －23x －2≤0⇔⎩⎨⎧3x －2≠0，(x －2)(3x －2)≤0，解得23<x ≤2，所以不等式的解集是{x ⎪⎪⎪⎭⎬⎫23<x ≤2.11. 【解答】 (1) 由已知易得y ≥4＋2a 即为x 2－(a －2)x －2a ≥0.令x 2－(a －2)x －2a ＝0，可得x ＝－2或x ＝a ，所以，当a <－2时，原不等式的解集为{x |x ≤a 或x ≥－2}；当a ＝－2时，原不等式的解集为R ；当a >－2时，原不等式的解集为{x |x ≤－2或x ≥a }．(2) 由y －2a ＋14≥0，可得a (x ＋2)≤x 2＋2x ＋18.由1≤x ≤6，得x ＋2>0，所以a ≤x 2＋2x ＋18x ＋2.因为x 2＋2x ＋18x ＋2＝x ＋18x ＋2＝(x ＋2)＋18x ＋2－2≥218－2＝62－2，当且仅当x ＋2＝18x ＋2，即x ＝32－2时等号成立，所以a ≤62－2，所以a 的取值范围是{a |a ≤62－2}．12. C 解析： 因为B ＝{x ∈N *|x 2－x －2≤0}＝{x ∈N *|(x －2)(x ＋1)≤0}＝{1,2}，A ＝{－2，－1}，所以A ∪B ＝{－2，－1,1,2}．13. C 解析： 命题“∀x ∈R ，cos x ≤1”的否定是“∃x 0∈R ，cos x 0>1”，A 正确．在△ABC 中，因为sin A ≥sin B ，所以由正弦定理可得a 2R ≥b2R (R 为△ABC 外接圆的半径)，所以a ≥b ，则由大边对大角可得A ≥B ；反之，由A ≥B 可得a ≥b ，所以由正弦定理可得sin A ≥sin B .即为充要条件，B 正确．当a ＝b ＝0，c ≥0时，满足ax 2＋bx ＋c ≥0，但是得不到“a >0，且b 2－4ac ≤0”，即不是充要条件，C 错误．“若sin α≠12，则α≠π6”是真命题，D 正确．14. 【解答】 (1) 当a ＝1时，B ＝{x ⎪⎪⎪⎭⎪⎬⎪⎫x －51－x >0，因为x －51－x >0⇔(x －1)(x －5)<0⇒1<x <5，所以B ＝{x |1<x <5}．(2) 因为|x －1|<3⇒－3<x －1<3⇒－2<x <4，所以A ＝{x |－2<x <4}．因为A ∩B ＝B ，所以B ⊆A .①当B ＝∅时，3a ＋2＝1，解得a ＝－13，满足题意；②当B ≠∅时，若3a ＋2>1，即a >－13，则B ＝{x ⎪⎪⎪⎭⎪⎬⎪⎫x －3a －21－x >0＝{x |1<x <3a ＋2}，故3a ＋2≤4，所以－13<a ≤23.若3a ＋2<1，即a <－13，则B ＝{x ⎪⎪⎪⎭⎪⎬⎪⎫x －3a －21－x >0＝{x |3a ＋2<x <1}，43≤a<－13.综上所述，a的取值范围为⎣⎢⎡⎦⎥⎤－43，23.故3a＋2≥－2，所以－。
§1.3 等式性质与不等式性质考试要求 1.掌握等式性质.2.会比较两个数的大小.3.理解不等式的性质，并能简单应用．知识梳理1．两个实数比较大小的方法作差法Error! (a ，b ∈R )2．等式的性质性质1 对称性：如果a ＝b ，那么b ＝a ；性质2 传递性：如果a ＝b ，b ＝c ，那么a ＝c ；性质3 可加(减)性：如果a ＝b ，那么a ±c ＝b ±c ；性质4 可乘性：如果a ＝b ，那么ac ＝bc ；性质5 可除性：如果a ＝b ，c ≠0，那么a c ＝b c .3．不等式的性质性质1 对称性：a >b ⇔b <a ；性质2 传递性：a >b ，b >c ⇒a >c ；性质3 可加性：a >b ⇔a ＋c >b ＋c ；性质4 可乘性：a >b ，c >0⇒ac >bc ；a >b ，c <0⇒ac <bc ；性质5 同向可加性：a >b ，c >d ⇒a ＋c >b ＋d ；性质6 同向同正可乘性：a >b >0，c >d >0⇒ac >bd ；性质7 同正可乘方性：a >b >0⇒a n >b n (n ∈N ，n ≥2)．常用结论1．若ab >0，且a >b ⇔1a <1b .2．若a >b >0，m >0⇒b a <b ＋ma ＋m ；若b >a >0，m >0⇒b a >b ＋ma ＋m .思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)两个实数a ，b 之间，有且只有a >b ，a ＝b ，a <b 三种关系中的一种．( √ )(2)若b a>1，则b >a .( × )(3)若x >y ，则x 2>y 2.( × )(4)若1a >1b，则b <a .( × )教材改编题1．(多选)设b >a >0，c ∈R ，则下列不等式中正确的是( )A ．1122a b ＜B.1a >1bC.a ＋2b ＋2>a bD ．ac 3<bc 3答案 ABC解析 因为y ＝12x 在(0，＋∞)上单调递增，所以1122a b ＜，A 正确；因为y ＝1x在(0，＋∞)上单调递减，所以1a >1b，B 正确；因为a ＋2b ＋2－a b ＝2(b －a )(b ＋2)b >0，所以a ＋2b ＋2>a b ，C 正确；当c ＝0时，ac 3＝bc 3，所以D 不正确．2．已知M ＝x 2－3x ，N ＝－3x 2＋x －3，则M ，N 的大小关系是________．答案 M >N解析 M －N ＝(x 2－3x )－(－3x 2＋x －3)＝4x 2－4x ＋3＝(2x －1)2＋2>0，∴M >N .3．已知－1<a <2，－3<b <5，则a ＋2b 的取值范围是______．答案 (－7,12)解析 ∵－3<b <5，∴－6<2b <10，又－1<a <2，∴－7<a ＋2b <12.题型一 比较两个数(式)的大小例1 (1)若a <0，b <0，则p ＝b 2a ＋a 2b 与q ＝a ＋b 的大小关系为( )A ．p <qB ．p ≤qC ．p >qD ．p ≥q答案 B解析 p －q ＝b 2a ＋a 2b －a －b＝b 2－a 2a ＋a 2－b 2b ＝(b 2－a 2)·(1a －1b )＝(b 2－a 2)(b －a )ab ＝(b －a )2(b ＋a )ab ，因为a <0，b <0，所以a ＋b <0，ab >0.若a ＝b ，则p －q ＝0，故p ＝q ；若a ≠b ，则p －q <0，故p <q .综上，p ≤q .(2)(2022·菏泽模拟)已知a ，b ，c ∈(0,3)，且a 5＝5a ，b 4＝4b ，c 3＝3c ，下列不等式正确的是( )A ．a >b >cB ．c >a >bC ．c >b >aD ．a >c >b答案 C解析 a 5＝5a ，即ln a a ＝ln 55，b 4＝4b ，即ln b b ＝ln 44，c 3＝3c ，即ln c c ＝ln 33，设f (x )＝ln x x ，则f (a )＝f (5)，f (b )＝f (4)，f (c )＝f (3)，f ′(x )＝1－ln xx 2(x >0)，当x >e 时，f ′(x )<0，f (x )＝ln x x 单调递减，当0<x <e 时，f ′(x )>0，f (x )＝ln x x 单调递增，因为a ，b ，c ∈(0,3)，f (a )＝f (5)，f (b )＝f (4)，f (c )＝f (3)，所以a，b，c∈(0，e)，因为f(5)<f(4)<f(3)，所以f(a)<f(b)<f(c)，a<b<c.教师备选已知M＝e2 021＋1e2 022＋1，N＝e2 022＋1e2 023＋1，则M，N的大小关系为________．答案 M>N解析 方法一 M－N＝e2 021＋1e2 022＋1－e2 022＋1e2 023＋1＝(e2 021＋1)(e2 023＋1)－(e2 022＋1)2 (e2 022＋1)(e2 023＋1)＝e2 021＋e2 023－2e2 022 (e2 022＋1)(e2 023＋1)＝e2 021(e－1)2(e2 022＋1)(e2 023＋1)>0.∴M>N.方法二 令f(x)＝e x＋1e x＋1＋1＝1e(e x＋1＋1)＋1－1ee x＋1＋1＝1e＋1－1ee x＋1＋1，显然f(x)是R上的减函数，∴f(2 021)>f(2 022)，即M>N.思维升华 比较大小的常用方法(1)作差法：①作差；②变形；③定号；④得出结论．(2)作商法：①作商；②变形；③判断商与1的大小关系；④得出结论．(3)构造函数，利用函数的单调性比较大小．跟踪训练1 (1)已知0<a<1b，且M＝11＋a＋11＋b，N＝a1＋a＋b1＋b，则M，N的大小关系是( )A．M>N B．M<N C．M＝N D．不能确定答案 A解析 ∵0<a<1 b ，∴1＋a>0,1＋b>0,1－ab>0.∴M －N ＝1－a 1＋a ＋1－b 1＋b ＝2(1－ab )(1＋a )(1＋b )>0，∴M >N .(2)e π·πe 与e e ·ππ的大小关系为________．答案 e π·πe <e e ·ππ解析 e π·πe e e ·ππ＝e π－eππ－e ＝(e π)π－e ，又0<e π<1,0<π－e<1，∴(e π)π－e <1，即e π·πee e ·ππ<1，即e π·πe <e e ·ππ.题型二 不等式的性质例2 (1)(2022·滨州模拟)下列命题为真命题的是( )A ．若a >b ，则ac 2>bc 2B ．若a <b <0，则a 2<ab <b 2C ．若c >a >b >0，则a c －a <b c －bD ．若a >b >c >0，则a b >a ＋c b ＋c答案 D解析 对于A 选项，当c ＝0时，显然不成立，故A 选项为假命题；对于B 选项，当a ＝－3，b ＝－2时，满足a <b <0，但不满足a 2<ab <b 2，故B 选项为假命题；对于C 选项，当c ＝3，a ＝2，b ＝1时，a c －a ＝23－2>b c －b ＝12，故C 选项为假命题；对于D 选项，由于a >b >c >0，所以a b －a ＋c b ＋c ＝a (b ＋c )－b (a ＋c )b (b ＋c )＝ac －bc b (b ＋c )＝(a －b )c b (b ＋c )>0，即a b >a ＋c b ＋c ，故D 选项为真命题．(2)(多选)若1a <1b<0，则下列不等式正确的是( )A.1a ＋b <1ab B ．|a |＋b >0C ．a －1a >b －1bD ．ln a 2>ln b 2答案 AC解析 由1a <1b<0，可知b <a <0.A 中，因为a ＋b <0，ab >0，所以1a ＋b <0，1ab >0.故有1a ＋b <1ab ，即A 正确；B 中，因为b <a <0，所以－b >－a >0.故－b >|a |，即|a |＋b <0，故B 错误；C 中，因为b <a <0，又1a <1b <0，则－1a >－1b >0，所以a －1a >b －1b，故C 正确；D 中，因为b <a <0，根据y ＝x 2在(－∞，0)上单调递减，可得b 2>a 2>0，而y ＝ln x 在定义域(0，＋∞)上单调递增，所以ln b 2>ln a 2，故D 错误．教师备选若a ，b ，c ∈R ，a >b ，则下列不等式恒成立的是( )A.1a <1b B ．a 2>b 2C ．a |c |>b |c | D.a c 2＋1>bc 2＋1答案 D解析 对于A ，若a >0>b ，则1a >1b ，故A 错误；对于B ，取a ＝1，b ＝－2，则a 2<b 2，故B 错误；对于C ，若c ＝0，a |c |＝b |c |，故C 错误；对于D ，因为c 2＋1≥1，所以1c 2＋1>0，又a >b ，所以a c 2＋1>bc 2＋1，故D 正确．思维升华 判断不等式的常用方法(1)利用不等式的性质逐个验证．(2)利用特殊值法排除错误选项．(3)作差法．(4)构造函数，利用函数的单调性．跟踪训练2 (1)(2022·珠海模拟)已知a ，b ∈R ，满足ab <0，a ＋b >0，a >b ，则( )A.1a <1b B.b a ＋a b >0C ．a 2>b 2D ．a <|b |答案 C解析 因为ab <0，a >b ，则a >0，b <0，1a >0，1b <0，A 不正确；b a <0，a b <0，则b a ＋a b<0，B 不正确；又a ＋b >0，即a >－b >0，则a 2>(－b )2，a 2>b 2，C 正确；由a >－b >0得a >|b |，D 不正确．(2)(多选)设a >b >1>c >0，下列四个结论正确的是( )A.1ac >1bcB ．ba c >ab cC ．(1－c )a <(1－c )bD ．log b (a ＋c )>log a (b ＋c )答案 CD解析 由题意知，a >b >1>c >0，所以对于A ，ac >bc >0，故1ac <1bc，所以A 错误；对于B ，取a ＝3，b ＝2，c ＝12，则ba c ＝23，ab c ＝32，所以ba c <ab c ，故B 错误；对于C ，因为0<1－c <1，且a >b ，所以(1－c )a <(1－c )b ，故C 正确；对于D ，a ＋c >b ＋c >1，所以log b (a ＋c )>log b (b ＋c )>log a (b ＋c )，故D 正确．题型三 不等式性质的综合应用例3 (1)已知－1<x <4,2<y <3，则x －y 的取值范围是______，3x ＋2y 的取值范围是______．答案 (－4,2) (1,18)解析 ∵－1<x <4,2<y <3，∴－3<－y <－2，∴－4<x －y <2.由－1<x <4,2<y <3，得－3<3x <12,4<2y <6，∴1<3x ＋2y <18.延伸探究 若将本例(1)中条件改为－1<x ＋y <4,2<x －y <3，求3x ＋2y 的取值范围．解 设3x ＋2y ＝m (x ＋y )＋n (x －y )，则Error!∴Error!即3x ＋2y ＝52(x ＋y )＋12(x －y )，又∵－1<x ＋y <4,2<x －y <3，∴－52<52(x ＋y )<10,1<12(x －y )<32，∴－32<52(x ＋y )＋12(x －y )<232，即－32<3x ＋2y <232，∴3x ＋2y 的取值范围为(－32，232).(2)已知3<a <8,4<b <9，则a b的取值范围是________．答案 (13，2)解析 ∵4<b <9，∴19<1b <14，又3<a <8，∴19×3<a b <14×8，即13<a b<2.教师备选已知0<β<α<π2，则α－β的取值范围是________．答案 (0，π2)解析 ∵0<β<π2，∴－π2<－β<0，又0<α<π2，∴－π2<α－β<π2，又β<α，∴α－β>0，即0<α－β<π2.思维升华 求代数式的取值范围，一般是利用整体思想，通过“一次性”不等关系的运算求得整体范围．跟踪训练3 (1)已知a >b >c ,2a ＋b ＋c ＝0，则c a的取值范围是( )A ．－3<c a<－1 B ．－1<c a <－13C ．－2<c a<－1 D ．－1<c a <－12答案 A解析 因为a >b >c ,2a ＋b ＋c ＝0，所以a >0，c <0，b ＝－2a －c ，因为a >b >c ，所以－2a －c <a ，即3a >－c ，解得c a>－3，将b ＝－2a －c 代入b >c 中，得－2a －c >c ，即a <－c ，得c a <－1，所以－3<c a<－1.(2)已知1<a <b <3，则a －b 的取值范围是________，a b的取值范围是________．答案 (－2,0) (13，1)解析 ∵1<b <3，∴－3<－b <－1，又1<a <3，∴－2<a －b <2，又a <b ，∴a －b <0，∴－2<a －b <0，又13<1b <1a，∴a 3<a b <1，又a 3>13，∴13<a b<1.综上所述，a －b 的取值范围为(－2,0)；a b 的取值范围为(13，1).课时精练1．(2022·长春模拟)已知a >0，b >0，M ＝a ＋b ，N ＝a ＋b ，则M 与N 的大小关系为( )A ．M >NB ．M <NC ．M ≤ND ．M ，N 大小关系不确定答案 B解析 M 2－N 2＝(a ＋b )－(a ＋b ＋2ab )＝－2ab <0，∴M <N .2．已知非零实数a ，b 满足a <b ，则下列命题成立的是( )A ．a 2<b 2B ．ab 2<a 2bC.1ab 2<1a 2b D.b a <a b答案 C解析 若a <b <0，则a 2>b 2，故A 不成立；若Error!则a 2b <ab 2，故B 不成立；若a ＝1，b ＝2，则b a ＝2，a b ＝12，b a >a b ，故D 不成立，由不等式的性质知，C 正确．3．已知－3<a <－2,3<b <4，则a 2b 的取值范围为( )A ．(1,3) B.(43，94)C.(23，34)D.(12，1)答案 A解析 因为－3<a <－2，所以a 2∈(4,9)，而3<b <4，故a 2b 的取值范围为(1,3)．4．若a >1，m ＝log a (a 2＋1)，n ＝log a (a ＋1)，p ＝log a (2a )，则m ，n ，p 的大小关系是( )A ．n >m >p B ．m >p >nC ．m >n >pD ．p >m >n答案 B解析 由a >1知，a 2＋1－2a ＝(a －1)2>0，即a 2＋1>2a ，而2a －(a ＋1)＝a －1>0，即2a >a ＋1，∴a 2＋1>2a >a ＋1，而y ＝log a x 在定义域上单调递增，∴m >p >n .5．(2022·杭州模拟)若(13)a <(13)b<1，则下列各式中一定成立的是( )A ．ln(a －b )>0B ．2b －a >1C ．－1a >－1bD ．log c a >log c b (c >0且c ≠1)答案 C解析 指数函数y ＝(13)x在(－∞，＋∞)上单调递减，由(13)a <(13)b<1可知，a >b >0.所以1a <1b ，则－1a >－1b ，故C 正确；a －b >0，但不一定有a －b >1，则不一定有ln(a －b )>0，故A 错误；函数y ＝2x 在(－∞，＋∞)上单调递增，b －a <0.则2b －a <20＝1，故B 错误；当0<c <1时，函数y ＝log c x 在(0，＋∞)上单调递减，则log c a <log c b ，故D 错误．6．(多选)(2022·济宁模拟)已知x >y >z ，x ＋y ＋z ＝0，则下列不等式不成立的是( )A ．xy >yz B ．xy >xzC ．xz >yzD ．x |y |>|y |z答案 ACD解析 因为x >y >z ，x ＋y ＋z ＝0，所以x >0，z <0，y 的符号无法确定，对于A ，因为x >0>z ，若y <0，则xy <0<yz ，故A 错误；对于B ，因为y >z ，x >0，所以xy >xz ，故B 正确；对于C ，因为x >y ，z <0，所以xz <yz ，故C 错误；对于D ，因为x >z ，当|y |＝0时，x |y |＝|y |z ，故D 错误．7．(多选)设a ，b ，c ，d 为实数，且a ＞b ＞0＞c ＞d ，则下列不等式正确的有( )A．c2＜cd B．a－c＜b－dC．ac＜bd D.ca－db＞0答案 AD解析 因为a＞b＞0＞c＞d，所以a>b>0,0>c>d，对于A，因为0>c>d，由不等式的性质可得c2<cd，故选项A正确；对于B，取a＝2，b＝1，c＝－1，d＝－2，则a－c＝3，b－d＝3，所以a－c＝b－d，故选项B错误；对于C，取a＝2，b＝1，c＝－1，d＝－2，则ac＝－2，bd＝－2，所以ac＝bd，故选项C错误；对于D，因为a>b>0，d<c<0，则ad<bc，所以ca>d b，故ca－db＞0，故选项D正确．8．(多选)若0<a<1，b>c>1，则( )A.(b c)a>1B.c－a b－a>c b C．c a－1<b a－1D．log c a<log b a 答案 AD解析 对于A，∵b>c>1，∴bc>1.∵0<a<1，则(b c)a>(b c)0＝1，故选项A正确；对于B，若c－ab－a>cb，则bc－ab>bc－ac，即a(c－b)>0，这与0<a<1，b>c>1矛盾，故选项B错误；对于C，∵0<a<1，∴a－1<0.∵b>c>1，∴c a－1>b a－1，故选项C错误；对于D，∵0<a<1，b>c>1，∴log c a<log b a，故选项D正确．9．已知M＝x2＋y2＋z2，N＝2x＋2y＋2z－π，则M________N．(填“>”“<”或“＝”)答案 >解析 M －N ＝x 2＋y 2＋z 2－2x －2y －2z ＋π＝(x －1)2＋(y －1)2＋(z －1)2＋π－3≥π－3>0，故M >N .10．(2022·烟台模拟)若1a <1b <0，已知下列不等式：①a ＋b <ab ；②|a |>|b |；③a <b ；④b a ＋a b>2.其中正确的不等式的序号为________．答案 ①④解析 因为1a <1b<0，所以b <a <0，故③错误；所以a ＋b <0<ab ，故①正确；所以|a |<|b |，故②错误；所以b a >0，a b >0且均不为1，b a ＋a b ≥2b a ·a b＝2，当且仅当b a ＝a b ＝1时，等号成立，所以b a ＋a b>2，故④正确．11．若0<a <b ，且a ＋b ＝1，则将a ，b ，12，2ab ，a 2＋b 2从小到大排列为________________．答案 a <2ab <12<a 2＋b 2<b 解析 方法一 令a ＝13，b ＝23，则2ab ＝49，a 2＋b 2＝19＋49＝59，故a <2ab <12<a 2＋b 2<b .方法二 ∵0<a <b 且a ＋b ＝1，∴a <12<b <1，∴2b >1且2a <1，∴a <2b ·a ＝2a (1－a )＝－2a 2＋2a ＝－2(a －12)2＋12<12，即a <2ab <12.又a 2＋b 2＝(a ＋b )2－2ab ＝1－2ab >1－12＝12，即a 2＋b 2>12.∵12<b <1，∴(a 2＋b 2)－b ＝[(1－b )2＋b 2]－b ＝2b 2－3b ＋1＝(2b －1)(b －1)<0，即a 2＋b 2<b ，综上可知a <2ab <12<a 2＋b 2<b .12．(2022·上海模拟)设实数x ，y 满足3≤xy 2≤8,4≤x 2y ≤9，则x 3y 4的最大值是________．答案 27解析 x 3y 4＝x 4y 2·1xy 2＝(x 2y )2·1xy 2≤81×13＝27，当且仅当x 2y＝9，xy 2＝3，即x ＝3，y ＝1时等号成立．13．(多选)(2022·长沙模拟)设实数a ，b ，c 满足b ＋c ＝6－4a ＋3a 2，c －b ＝4－4a ＋a 2，则下列不等式成立的是( )A ．c <bB ．b ≥1C ．b ≤aD ．a <c 答案 BD解析 ∵Error!两式相减得2b ＝2a 2＋2，即b ＝a 2＋1，∴b ≥1.又b －a ＝a 2＋1－a ＝(a －12)2＋34>0，∴b >a .而c －b ＝4－4a ＋a 2＝(a －2)2≥0，∴c ≥b ，从而c ≥b >a .14．实数a ，b ，c ，d 满足下列三个条件：①d >c ；②a ＋b ＝c ＋d ；③a ＋d <b ＋c .那么a ，b ，c ，d 的大小关系是________．答案 b >d >c >a解析 由题意知d >c ①，②＋③得2a ＋b ＋d <2c ＋b ＋d ，化简得a <c ④，由②式a ＋b ＝c ＋d 及a <c 可得到，要使②成立，必须b >d ⑤成立，综合①④⑤式得到b >d >c >a .15．已知函数f(x)＝ax2＋bx＋c满足f(1)＝0，且a>b>c，则ca的取值范围是________．答案 (－2，－12)解析 因为f(1)＝0，所以a＋b＋c＝0，所以b＝－(a＋c)．又a>b>c，所以a>－(a＋c)>c，且a>0，c<0，所以1>－a＋ca>ca，即1>－1－ca>ca.所以Error!解得－2<ca<－12.即ca的取值范围为(－2，－12).16．某学习小组由学生和教师组成，人员构成同时满足以下三个条件：(1)男学生人数多于女学生人数；(2)女学生人数多于教师人数；(3)教师人数的两倍多于男学生人数．①若教师人数为4，则女学生人数的最大值为________．②该小组人数的最小值为________．答案 ①6 ②12解析 设男学生人数为x，女学生人数为y，教师人数为z，由已知得Error!且x，y，z均为正整数．①当z＝4时，8>x>y>4，∴x的最大值为7，y的最大值为6，故女学生人数的最大值为6.②x>y>z>x2，当x＝3时，条件不成立，当x＝4时，条件不成立，当x＝5时，5>y>z>52，此时z＝3，y＝4.∴该小组人数的最小值为12.。
§6.3等比数列课标要求1.通过生活中的实例，理解等比数列的概念和通项公式的意义.2.掌握等比数列前n 项和公式，理解等比数列的通项公式与前n 项和公式的关系.3.能在具体问题情境中，发现数列的等比关系，并解决相应的问题.4.体会等比数列与指数函数的关系．知识梳理1．等比数列有关的概念(1)如果一个数列从第2项起，每一项与它的前一项的比值都是同一个常数，那么称这样的数列为等比数列，称这个常数为等比数列的公比，通常用字母q 表示(q ≠0)．(2)等比中项：如果在a 与b 之间插入一个数G ，使a ，G ，b 成等比数列，那么称G 为a 与b 的等比中项，此时，G 2＝ab .2．等比数列的有关公式(1)通项公式：a n ＝a 1q n －1(a 1≠0，q ≠0)．(2)前n 项和公式：S n ，＝a 1－a n q 1－q，q ≠1且q ≠0.3．等比数列的常用性质(1)若m ＋n ＝p ＋q ，则a m a n ＝a p a q ，其中m ，n ，p ，q ∈N ＋.特别地，若2w ＝m ＋n ，则a m a n ＝a 2w ，其中m ，n ，w ∈N ＋.(2)a k ，a k ＋m ，a k ＋2m ，…仍是等比数列，公比为q m (k ，m ∈N ＋)．(3)若数列{a n }，{b n }是两个项数相同的等比数列，则数列{ba n }，{pa n ·qb n }数列(b ，p ，q ≠0)．(4)1>0，>11<0，q <1，则等比数列{a n }递增．1>0，q <11<0，>1，则等比数列{a n }递减．4．等比数列前n 项和的常用性质若等比数列{a n }的公比q ≠－1,前n 项和为S n ，则S n ，S 2n －S n ，S 3n －S 2n 仍成等比数列，其公比为q n .常用结论1．等比数列{a n }的通项公式可以写成a n ＝cq n ，这里c ≠0，q ≠0.2．等比数列{a n }的前n 项和S n 可以写成S n ＝Aq n －A (A ≠0，q ≠1,0)．3．设数列{a n }是等比数列，S n 是其前n 项和．(1)S m ＋n ＝S n ＋q n S m ＝S m ＋q m S n .(2)若a 1·a 2·…·a n ＝T n ，则T n ，T 2n T n ，T3n T 2n ，…成等比数列．(3)若数列{a n }的项数为2n ，则S 偶S 奇＝q ；若项数为2n ＋1，则S 奇－a 1S 偶＝q .自主诊断1．判断下列结论是否正确．(请在括号中打“√”或“×”)(1)等比数列的公比q 是一个常数，它可以是任意实数．(×)(2)三个数a ，b ，c 成等比数列的充要条件是b 2＝ac .(×)(3)数列{a n }为等比数列，则S 4，S 8－S 4，S 12－S 8成等比数列．(×)(4)对有穷等比数列，与首末两项“等距离”的两项之积等于首末两项的积．(√)2．设a ，b ，c ，d 是非零实数，则“ad ＝bc ”是“a ，b ，c ，d 成等比数列”的()A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件答案B解析若a ，b ，c ，d 成等比数列，则ad ＝bc ，数列－1，－1,1,1满足－1×1＝－1×1，但数列－1，－1，1,1不是等比数列，即“ad ＝bc ”是“a ，b ，c ，d 成等比数列”的必要不充分条件．3．在等比数列{a n }中，若a 3＝32，S 3＝92，则a 2的值为()A ．32B ．－3C ．－32D ．－3或32答案D解析由S 3＝a 1＋a 2＋a 3＝a 3(q －2＋q －1＋1)，得q －2＋q －1＋1＝3，即2q 2－q －1＝0，解得q ＝1或q ＝－12，∴a 2＝a 3q ＝32或－3.4．数列{a n }的通项公式是a n ＝a n (a ≠0)，则其前n 项和为S n ＝________.答案a ≠0，a ≠1解析因为a ≠0，a n ＝a n ，所以{a n }是以a 为首项，a 为公比的等比数列．当a ＝1时，S n ＝n ；当a ≠1时，Sn ＝a (1－a n )1－a.题型一等比数列基本量的运算例1(1)(2023·全国甲卷)设等比数列{a n }的各项均为正数，前n 项和为S n ，若a 1＝1，S 5＝5S 3－4，则S 4等于()A.158B.658C ．15D ．40答案C 解析方法一若该数列的公比q ＝1，代入S 5＝5S 3－4中，有5＝5×3－4，不成立，所以q ≠1.由1－q 51－q ＝5×1－q 31－q －4，化简得q 4－5q 2＋4＝0，所以q 2＝1或q 2＝4，因为此数列各项均为正数，所以q ＝2，所以S 4＝1－q 41－q ＝15.方法二由题知1＋q ＋q 2＋q 3＋q 4＝5(1＋q ＋q 2)－4，即q 3＋q 4＝4q ＋4q 2，即q 3＋q 2－4q －4＝0，即(q －2)(q ＋1)(q ＋2)＝0.由题知q >0，所以q ＝2.所以S 4＝1＋2＋4＋8＝15.(2)记S n 为等比数列{a n }的前n 项和．若a 5－a 3＝12，a 6－a 4＝24，则Sn a n 等于()A ．2n －1B ．2－21－nC ．2－2n －1D ．21－n －1答案B 解析方法一设等比数列{a n }的公比为q ，易知q ≠1，1q 4－a 1q 2＝12，1q 5－a 1q 3＝24，1＝1，＝2，所以S n ＝a 1(1－q n )1－q ＝2n －1，a n ＝a 1q n －1＝2n －1，所以S n a n ＝2n －12n －1＝2－21－n .方法二设等比数列{a n }的公比为q ，易知q ≠1，因为a 6－a 4a 5－a 3＝a 4(q 2－1)a 3(q 2－1)＝a 4a 3＝2412＝2，所以q ＝2，所以S na n ＝a 1(1－q n )1－q a 1q n －1＝2n －12n －1＝2－21－n .思维升华等比数列基本量的运算的解题策略(1)等比数列中有五个量a 1，n ，q ，a n ，S n ，一般可以“知三求二”，通过列方程(组)求解．(2)解方程组时常常利用“作商”消元法．(3)运用等比数列的前n 项和公式时，一定要讨论公比q ＝1的情形，否则会漏解或增解．跟踪训练1(1)(2023·天津)已知{a n }为等比数列，S n 为数列{a n }的前n 项和，a n ＋1＝2S n ＋2，则a 4的值为()A ．3B ．18C ．54D ．152答案C解析由题意可得，当n ＝1时，a 2＝2a 1＋2，即a 1q ＝2a 1＋2，①当n ＝2时，a 3＝2(a 1＋a 2)＋2，即a 1q 2＝2(a 1＋a 1q )＋2，②联立①②1＝2，＝3，则a 4＝a 1q 3＝54.(2)(2023·青岛模拟)云冈石窟，古称为武州山大石窟寺，是世界文化遗产．若某一石窟的某处“浮雕像”共7层，每一层的“浮雕像”个数是其下一层的2倍，共有1016个“浮雕像”，这些“浮雕像”构成一幅优美的图案，若从最下层往上每一层的“浮雕像”的个数构成数列{a n }，则log 2(a 3a 5)的值为()A ．8B ．10C ．12D ．16答案C解析从最下层往上每一层的“浮雕像”的个数构成数列{a n }，则{a n }是以2为公比的等比数列，∴S 7＝a 1(1－27)1－2＝1016，即127a 1＝1016，解得a 1＝8，∴a n ＝8×2n －1，∴log 2(a 3a 5)＝log 2(8×22×8×24)＝12.题型二等比数列的判定与证明例2(2023·长沙模拟)记S n 为数列{a n }的前n 项和，已知a 1＝2，a 2＝－1，且a n ＋2＋a n ＋1－6a n ＝0(n ∈N ＋)．(1)证明：{a n ＋1＋3a n }为等比数列；(2)求数列{a n }的通项公式a n 及前n 项和S n .(1)证明由a n ＋2＋a n ＋1－6a n ＝0，可得a n ＋2＋3a n ＋1＝2(a n ＋1＋3a n )，即a n ＋2＋3a n ＋1a n ＋1＋3a n＝2(n ∈N ＋)，∴{a n ＋1＋3a n }是以a 2＋3a 1＝5为首项，2为公比的等比数列．(2)解由(1)可知a n ＋1＋3a n ＝5·2n －1(n ∈N ＋)，∴a n ＋1－2n ＝－3(a n －2n －1)，∴a n ＋1－2n a n －2n －1＝－3，∴{a n －2n －1}是以a 1－20＝1为首项，－3为公比的等比数列，∴a n －2n －1＝1×(－3)n －1，∴a n ＝2n －1＋(－3)n －1，S n ＝1－2n 1－2＋1－(－3)n 1－(－3)＝2n －34－(－3)n 4.思维升华等比数列的四种常用判定方法(1)定义法：若a na n －1＝q (q 为非零常数，且n ≥2，n ∈N ＋)，则{a n }是等比数列．(2)等比中项法：若在数列{a n }中，a n ≠0且a 2n ＋1＝a n a n ＋2(n ∈N ＋)，则{a n }是等比数列．(3)通项公式法：若数列{a n }的通项公式可写成a n ＝cq n －1(c ，q 均为非零常数，n ∈N ＋)，则{a n }是等比数列．(4)前n 项和公式法：若数列{a n }的前n 项和S n ＝kq n －k (k 为常数，且k ≠0，q ≠0,1)，则{a n }是等比数列．跟踪训练2(2024·潍坊模拟)已知数列{a n }和{b n }满足a 1＝3，b 1＝2，a n ＋1＝a n ＋2b n ，b n ＋1＝2a n ＋b n .(1)证明：{a n ＋b n }和{a n －b n }都是等比数列；(2)求{a n b n }的前n 项和S n .(1)证明因为a n ＋1＝a n ＋2b n ，b n ＋1＝2a n ＋b n ，所以a n ＋1＋b n ＋1＝3(a n ＋b n )，a n ＋1－b n ＋1＝－(a n －b n )，又由a 1＝3，b 1＝2得a 1－b 1＝1，a 1＋b 1＝5，所以数列{a n ＋b n }是首项为5，公比为3的等比数列，数列{a n －b n }是首项为1，公比为－1的等比数列．(2)解由(1)得a n ＋b n ＝5×3n －1，a n －b n ＝(－1)n －1，所以a n ＝5×3n －1＋(－1)n －12，b n ＝5×3n －1－(－1)n －12，所以a n b n ＝5×3n －1＋(－1)n －12×5×3n －1－(－1)n －12＝25×32n －2－14＝254×9n －1－14，所以S n ＝254×1－9n 1－9－n 4＝25×(9n －1)－8n32.题型三等比数列的性质命题点1项的性质例3(1)(2023·全国乙卷)已知{a n }为等比数列，a 2a 4a 5＝a 3a 6，a 9a 10＝－8，则a 7＝________.答案－2解析方法一{a n }为等比数列，∴a 4a 5＝a 3a 6，∴a 2＝1，又a 2a 9a 10＝a 7a 7a 7，∴1×(－8)＝(a 7)3，∴a 7＝－2.方法二设{a n }的公比为q (q ≠0)，则a 2a 4a 5＝a 3a 6＝a 2q ·a 5q ，显然a n ≠0，则a 4＝q 2，即a 1q 3＝q 2，则a 1q ＝1，∵a 9a 10＝－8，则a 1q 8·a 1q 9＝－8，则q 15＝(q 5)3＝－8＝(－2)3，则q 5＝－2，则a 7＝a 1q ·q 5＝q 5＝－2.下标和相等的等差(比)性质的推广(1)若数列{a n }为等比数列，且m 1＋m 2＋…＋m n ＝k 1＋k 2＋…＋k n ，则12m m a a ·…·n m a ＝12k k a a ·…·n k a .(2)若数列{a n }为等差数列，且m 1＋m 2＋…＋m n ＝k 1＋k 2＋…＋k n ，则1m a ＋2m a ＋…＋n m a ＝1k a ＋2k a ＋…＋n k a .典例已知等差数列{a n }，S n 为前n 项和，且a 9＝5，S 8＝16，则S 11＝________.答案33解析S 8＝8(a 1＋a 8)2＝16，∴a 1＋a 8＝4，又∵a 9＋a 1＋a 8＝3a 6，∴a 6＝3，故S 11＝11a 6＝33.(2)已知数列{a n }满足log 2a n ＋1＝1＋log 2a n (n ∈N ＋)，且a 1＋a 2＋a 3＋…＋a 10＝1，则log 2(a 101＋a 102＋…＋a 110)＝________.答案100解析因为log 2a n ＋1＝1＋log 2a n ，可得log 2a n ＋1＝log 2(2a n )，所以a n ＋1＝2a n ，所以数列{a n }是以a 1为首项，2为公比的等比数列，又a 1＋a 2＋…＋a 10＝1，所以a 101＋a 102＋…＋a 110＝(a 1＋a 2＋…＋a 10)×2100＝2100，所以log 2(a 101＋a 102＋…＋a 110)＝log 22100＝100.命题点2和的性质例4(1)已知等比数列{a n }共有2n 项，其和为－240，且奇数项的和比偶数项的和大80，则公比q ＝________.答案2解析奇＋S 偶＝－240，奇－S 偶＝80，奇＝－80，偶＝－160，所以q ＝S 偶S 奇＝－160－80＝2.(2)已知S n 是正项等比数列{a n }的前n 项和，S 10＝20，则S 30－2S 20＋S 10的最小值为________．答案－5解析依题意，S 10，S 20－S 10，S 30－S 20成等比数列，且S 10＝20，不妨令其公比为q (q >0)，则S 20－S 10＝20q ，S 30－S 20＝20q 2，∴S 30－2S 20＋S 10＝(S 30－S 20)－(S 20－S 10)＝20q 2－20q ＝－5，故当q ＝12时，S 30－2S 20＋S 10的最小值为－5.思维升华(1)在解决与等比数列有关的问题时，要注意挖掘隐含条件，利用性质，特别是“若m ＋n ＝p ＋q ，则a m a n ＝a p a q ”，可以减少运算量，提高解题速度．(2)在应用等比数列的性质解题时，要注意性质成立的前提条件，有时需要进行适当变形．此外，解题时注意设而不求思想的运用．跟踪训练3(1)(2024·南昌模拟)已知等比数列{a n }满足a 2＋a 4＋a 6＋a 8＝20，a 2a 8＝2，则1a 2＋1a 4＋1a 6＋1a 8＝________.答案10解析1a 2＋1a 4＋1a 6＋1a 8＝＝a 2＋a 8a 2a 8＋a 4＋a 6a 4a 6＝a 2＋a 8＋a 4＋a 6a 2a 8＝202＝10.(2)(2023·长春统考)在等比数列{a n }中，q ＝12，S 100＝150，则a 2＋a 4＋a 6＋…＋a 100的值是________．答案50解析设T 1＝a 1＋a 3＋a 5＋…＋a 99，T 2＝a 2＋a 4＋a 6＋…＋a 100，所以T 2T 1＝a 2＋a 4＋a 6＋…＋a 100a 1＋a 3＋a 5＋…＋a 99＝12，所以S 100＝T 1＋T 2＝2T 2＋T 2＝3T 2＝150，所以T 2＝a 2＋a 4＋a 6＋…＋a 100＝50.课时精练一、单项选择题1．(2023·本溪模拟)已知等比数列{a n }的各项均为正数，公比q ＝12，且a 3a 4＝132，则a 6等于()A.18 B.116C.132D.164答案C解析由a 3a 4＝132，得a 1q 2·a 1q 3＝132，即a 21＝132，所以a 21＝1.又a n >0，所以a 1＝1，a 6＝a 1q 5＝1＝132.2．若1，a 2，a 3,4成等差数列；1，b 2，b 3，b 4,4成等比数列，则a 2－a 3b 3等于()A.12B ．－12C ．±12D.14答案B解析由题意得a 3－a 2＝4－13＝1，设1，b 2，b 3，b 4，4的公比为q ，则b 3＝q 2>0，b 23＝1×4＝4，解得b 3＝2，a 2－a 3b 3＝－12＝－12.3．(2023·济宁模拟)在数列{a n }中，a 1＝2，a n ＋1＝2a n ，S n 为{a n }的前n 项和．若S n ＝126，则n 等于()A ．5B ．6C ．7D ．8答案B解析∵a 1＝2，a n ＋1＝2a n ，∴数列{a n }是首项为2，公比为2的等比数列．又S n ＝126，∴2(1－2n )1－2＝126，解得n ＝6.4．已知等比数列{a n }为递减数列，若a 2a 6＝6，a 3＋a 5＝5，则a5a 7等于()A.32B.23C.16D ．6答案A解析由{a n }为等比数列，得a 2a 6＝a 3a 5＝6，又a 3＋a 5＝5，∴a 3，a 5为方程x 2－5x ＋6＝0的两个根，解得a 3＝2，a 5＝3或a 3＝3，a 5＝2，由{a n }为递减数列得a n >a n ＋1，∴a 3＝3，a 5＝2，∴q 2＝a 5a 3＝23，则a 5a 7＝1q 2＝32.5．(2024·揭阳模拟)在《增减算法统宗》中有这样一则故事：“三百七十八里关，初行健步不为难；次日脚痛减一半，如此六日过其关”．其大意是有人要去某关口，路程为378里，第一天健步行走，从第二天起由于脚痛，每天走的路程都为前一天的一半，一共走了六天，才到目的地．则此人后三天所走的里程数为()A ．6B ．12C ．18D ．42答案D解析设第n (n ∈N ＋)天走a n 里，其中1≤n ≤6，由题意可知，数列{a n }是公比为12的等比数列，1－12＝6332a 1＝378，解得a 1＝192，所以此人后三天所走的里程数为a 4＋a5＋a 6＝192×18×1－12＝42.6．(2023·新高考全国Ⅱ)记S n 为等比数列{a n }的前n 项和，若S 4＝－5，S 6＝21S 2，则S 8等于()A ．120B ．85C ．－85D ．－120答案C解析方法一设等比数列{a n }的公比为q ，首项为a 1，若q ＝1，则S 6＝6a 1＝3×2a 1＝3S 2，不符合题意，所以q ≠1.由S 4＝－5，S 6＝21S 2，可得a 1(1－q 4)1－q ＝－5，a 1(1－q 6)1－q ＝21×a 1(1－q 2)1－q ，①由①可得，1＋q 2＋q 4＝21，解得q 2＝4，所以S 8＝a 1(1－q 8)1－q ＝a 1(1－q 4)1－q ·(1＋q 4)＝－5×(1＋16)＝－85.方法二设等比数列{a n }的公比为q ，因为S 4＝－5，S 6＝21S 2，所以q ≠－1，否则S 4＝0，从而S 2，S 4－S 2，S 6－S 4，S 8－S 6成等比数列，所以(－5－S 2)2＝S 2(21S 2＋5)，解得S 2＝－1或S 2＝54，当S 2＝－1时，S 2，S 4－S 2，S 6－S 4，S 8－S 6，即为－1，－4，－16，S 8＋21，易知S 8＋21＝－64，即S 8＝－85；当S 2＝54时，S 4＝a 1＋a 2＋a 3＋a 4＝(a 1＋a 2)(1＋q 2)＝(1＋q 2)S 2>0，与S 4＝－5矛盾，舍去．综上，S 8＝－85.二、多项选择题7．(2023·太原模拟)已知数列{a n }是等比数列，以下结论正确的是()A ．{a 2n }是等比数列B ．若a 3＝2,a 7＝32，则a 5＝±8C ．若a 1<a 2<a 3，则数列{a n }是递增数列D ．若数列{a n }的前n 项和S n ＝3n ＋r ，则r ＝－1答案ACD 解析令等比数列{a n }的公比为q ，则a n ＝a 1q n －1，对于A ，a 2n ＋1a 2n ＝＝q 2，且a 21≠0，则{a 2n }是等比数列，故A 正确；对于B ，由a 3＝2，a 7＝32，得q 4＝16，即q 2＝4，所以a 5＝a 3q 2＝2×4＝8，故B 错误；对于C ，由a 1<a 2<a 31(q －1)>0，1q (q －1)>0，>0，1(q －1)>0，a n ＋1－a n ＝q n －1·a 1(q －1)>0，即∀n ∈N ＋，a n ＋1>a n ，所以数列{a n }是递增数列，故C 正确；对于D ，显然q ≠1，则S n ＝a 1(1－q n )1－q ＝a 1q －1·q n －a 1q －1，而S n ＝3n ＋r ，因此q ＝3，a 1q －1＝1，r ＝－a 1q －1＝－1，故D 正确．8．记等比数列{a n }的前n 项和为S n ，前n 项积为T n ，且满足a 1>1，a 2022>1，a 2023<1，则()A ．a 2022a 2024－1<0B ．S 2022＋1<S 2023C ．T 2022是数列{T n }中的最大项D ．T 4045>1答案AC 解析设数列{a n }的公比为q .∵a 1>1，a 2023<1，∴0<a 2023<1，又a 2022>1，∴0<q <1.∵a 2022a 2024＝a 22023<1，∴a 2022a 2024－1<0，故A 正确；∵a 2023<1，∴a 2023＝S 2023－S 2022<1，即S 2022＋1>S 2023，故B 错误；∵0<q <1，a 1>1，∴数列{a n }是递减数列，∵a 2022>1，a 2023<1，∴T 2022是数列{T n }中的最大项，故C 正确；T4045＝a1a2a3·…·a4045＝a1(a1q)(a1q2)·…·(a1q4044)＝a40451q1＋2＋3＋…＋4044＝a40451q2022×4045＝(a1q2022)4045＝a40452023，∵0<a2023<1，∴a40452023<1，即T4045<1，故D错误．三、填空题9．(2023·全国甲卷)记S n为等比数列{a n}的前n项和．若8S6＝7S3，则{a n}的公比为________．答案－1 2解析若q＝1，则由8S6＝7S3得8·6a1＝7·3a1，则a1＝0，不符合题意．所以q≠1.当q≠1时，因为8S6＝7S3，所以8·a1(1－q6)1－q＝7·a1(1－q3)1－q，即8(1－q6)＝7(1－q3)，即8(1＋q3)(1－q3)＝7(1－q3)，即8(1＋q3)＝7，解得q＝－1 2 .10．设等比数列{a n}共有3n项，它的前2n项的和为100，后2n项的和为200，则该等比数列中间n项的和等于________．答案200 3解析设数列{a n}的前n项和、中间n项和、后n项和依次为a，b，c.由题意知a＋b＝100，b＋c＝200，b2＝ac，∴b2＝(100－b)(200－b)，∴b＝200 3.11．在等比数列{a n}中，若a9＋a10＝4，a19＋a20＝24，则a59＋a60＝______.答案31104解析设等比数列{a n}的公比为q，则a n＝a1q n－1.因为a 9＋a 10＝4，a 19＋a 20＝24，所以a 19＋a 20＝(a 9＋a 10)q 10＝24，解得q 10＝6，所以a 59＋a 60＝(a 9＋a 10)q 50＝4×65＝31104.12．记S n 为数列{a n }的前n 项和，S n ＝1－a n ，记T n ＝a 1a 3＋a 3a 5＋…＋a 2n －1a 2n ＋1，则a n ＝________，T n ＝________.答案12n解析由题意得a 1＝1－a 1，故a 1＝12.当n ≥2n ＝1－a n ，n －1＝1－a n －1，得a n ＝S n －S n －1＝－a n ＋a n －1，则a n a n －1＝12，故数列{a n }是以12为首项，12为公比的等比数列，故数列{a n }的通项公式为a n ＝12n .由等比数列的性质可得a 1a 3＝a 22，a 3a 5＝a 24，…，a 2n －1a 2n ＋1＝a 22n ，所以数列{a 2n －1a 2n ＋1}是以a 22＝116为首项，116为公比的等比数列，则T n ＝a 22＋a 24＋…＋a 22n ＝161－116＝四、解答题13．已知数列{a n }满足a 1＝1，a n ＋1＝2a n ＋2.(1)证明数列{a n ＋2}是等比数列，并求数列{a n }的通项公式；(2)求数列{a n }落入区间(10,2023)的所有项的和．解(1)由a n ＋1＝2a n ＋2，得a n ＋1＋2＝2(a n ＋2)，又a 1＋2＝3，所以a n ＋1＋2a n ＋2＝2，所以{a n ＋2}是首项为3，公比为2的等比数列，所以a n ＋2＝3×2n －1，a n ＝3×2n －1－2.(2)由10<a n <2023，得10<3×2n －1－2<2023，即4<2n －1<675，即4≤n ≤10，故{a n }落入区间(10,2023)的项为a 4，a 5，a 6，a 7，a 8，a 9，a 10，所以其和S ＝a 4＋a 5＋a 6＋a 7＋a 8＋a 9＋a 10＝3×(23＋24＋…＋29)－2×7＝3×8－10241－2－14＝3034.14．(2024·邯郸模拟)已知数列{a n }的前n 项和为S n ，且a 1＝1，a n ＋1＝3S n ＋1，n ∈N ＋.(1)求{a n }通项公式；(2)设b n ＝a n n ＋1，在数列{b n }中是否存在三项b m ，b k ，b p (其中2k ＝m ＋p )成等比数列？若存在，求出这三项；若不存在，说明理由．解(1)由题意知，在数列{a n }中，a n ＋1＝3S n ＋1，a n ＝3S n －1＋1，n ≥2，两式相减可得，a n ＋1－a n ＝3a n ，a n ＋1＝4a n ，n ≥2，由条件知，a 2＝3a 1＋1＝4a 1，符合上式，故a n ＋1＝4a n ，n ∈N ＋.∴{a n }是以1为首项，4为公比的等比数列．∴a n ＝4n －1，n ∈N ＋.(2)由题意及(1)得，在数列{a n }中，a n ＝4n －1，n ∈N ＋，在数列{b n }中，b n ＝4n －1n ＋1，如果满足条件的b m ，b k ，b p 存在，则b 2k ＝b m b p ，其中2k ＝m ＋p ，∴(4k －1)2(k ＋1)2＝4m －1m ＋1·4p －1p ＋1，∵2k ＝m ＋p ，∴(k ＋1)2＝(m ＋1)(p ＋1)，解得k 2＝mp ，∴k ＝m ＝p ，与已知矛盾，∴不存在满足条件的三项．15．(2023·杭州模拟)已知数列{a n }的前n 项和为S n .若p ：数列{a n }是等比数列；q ：(S n ＋1－a 1)2＝S n (S n ＋2－S 2)，则p 是q 的()A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件答案A 解析若{a n }是等比数列，设公比为k ，则a 2＋a 3＋…＋a n ＋1＝k (a 1＋a 2＋…＋a n )，a 3＋a 4＋…＋a n ＋2＝k (a 2＋a 3＋…＋a n ＋1)，于是(a 2＋a 3＋…＋a n ＋1)2＝k 2(a 1＋a 2＋…＋a n )2＝(a 3＋a 4＋…＋a n ＋2)(a 1＋a 2＋…＋a n )，即q ：(S n ＋1－a 1)2＝S n (S n ＋2－S 2)成立；若(S n ＋1－a 1)2＝S n (S n ＋2－S 2)，取a n ＝0，n ∈N ＋，显然{a n }不是等比数列，故p 是q 的充分不必要条件．16．(2023·泰安模拟)若m ，n 是函数f (x )＝x 2－px ＋q (p >0，q >0)的两个不同零点，且m ，n ，－2这三个数可适当排序后成等差数列，也可适当排序后成等比数列，则pq ＝________.答案20解析＋n ＝p >0，＝q >0>0，>0，则m ，－2，n 或n ，－2，m 成等比数列，得mn ＝(－2)2＝4.不妨设m <n ，则－2，m ，n 成等差数列，得2m ＝n －2.结合mn ＝4，可得(2m ＋2)m ＝4⇒m (m ＋1)＝2，解得m ＝1或m ＝－2(舍去)，＝1，＝4＝5，＝4⇒pq ＝20.。
随机事件的概率进门测判断下列结论是否正确(请在括号中打“√”或“×”)(1)事件发生频率与概率是相同的．()(2)随机事件和随机试验是一回事．()(3)在大量重复试验中，概率是频率的稳定值．()(4)两个事件的和事件是指两个事件都得发生．()(5)对立事件一定是互斥事件，互斥事件不一定是对立事件．()(6)两互斥事件的概率和为1. ( )阶段训练题型一事件关系的判断例1(1)从1,2,3，…，7这7个数中任取两个数，其中：①恰有一个是偶数和恰有一个是奇数；②至少有一个是奇数和两个都是奇数；③至少有一个是奇数和两个都是偶数；④至少有一个是奇数和至少有一个是偶数．上述事件中，是对立事件的是()A．①B．②④C．③D．①③(2)设条件甲：“事件A与事件B是对立事件”，结论乙：“概率满足P(A)＋P(B)＝1”，则甲是乙的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件(3)在5张电话卡中，有3张移动卡和2张联通卡，从中任取2张，若事件“2张全是移动卡”的概率是310，那么概率是710的事件是()A．至多有一张移动卡B．恰有一张移动卡C．都不是移动卡D．至少有一张移动卡从装有两个白球和两个黄球的口袋中任取2个球，以下给出了四组事件：①至少有1个白球与至少有1个黄球；②至少有1个黄球与都是黄球；③恰有1个白球与恰有1个黄球；④恰有1个白球与都是黄球．其中互斥而不对立的事件共有()A．0组B．1组C．2组D．3组题型二随机事件的频率与概率例2某险种的基本保费为a(单位：元)，继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：(1)记A为事件：“一续保人本年度的保费不高于基本保费”，求P(A)的估计值；(2)记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160%”，求P(B)的估计值；(3)求续保人本年度的平均保费的估计值．某超市随机选取1 000位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“√”表示购买，“×”表示未购买.(1)估计顾客同时购买乙和丙的概率；(2)估计顾客在甲、乙、丙、丁中同时购买3种商品的概率；(3)如果顾客购买了甲，则该顾客同时购买乙、丙、丁中哪种商品的可能性最大？题型三互斥事件、对立事件的概率命题点1 互斥事件的概率例3 袋中有12个小球，分别为红球、黑球、黄球、绿球，从中任取一球，得到红球的概率是13，得到黑球或黄球的概率是512，得到黄球或绿球的概率也是512，试求得到黑球、黄球和绿球的概率各是多少？命题点2 对立事件的概率例4 某商场有奖销售中，购满100元商品得1张奖券，多购多得.1 000张奖券为一个开奖单位，设特等奖1个，一等奖10个，二等奖50个．设1张奖券中特等奖，一等奖，二等奖的事件分别为A ，B ，C ，求：(1)P (A )，P (B )，P (C )； (2)1张奖券的中奖概率；(3)1张奖券不中特等奖且不中一等奖的概率．经统计，在某储蓄所一个营业窗口等候的人数相应的概率如下：求：(1)至多2人排队等候的概率；(2)至少3人排队等候的概率．1．概率和频率(1)在相同的条件S 下重复n 次试验，观察某一事件A 是否出现，称n 次试验中事件A 出现的次数n A 为事件A 出现的频数，称事件A 出现的比例f n (A )＝n An为事件A 出现的频率．(2)对于给定的随机事件A ，在相同条件下，随着试验次数的增加，事件A 发生的频率会在某个常数附近摆动并趋于稳定，我们可以用这个常数来刻画随机事件A 发生的可能性大小，并把这个常数称为随机事件A 的概率，记作P (A )． 2．事件的关系与运算定义符号表示包含关系如果事件A 发生，则事件B 一定发生，这时称事件B 包含事件A (或称事件A 包含于事件B )B ⊇A (或A ⊆B ) 相等关系若B ⊇A 且A ⊇BA ＝B 并事件(和事件)若某事件发生当且仅当事件A 发生或事件B 发生，称此事件为事件A 与事件B 的并事件(或和事件)A ∪B (或A ＋B )交事件 若某事件发生当且仅当事件A 发生且事件B 发生，则称此事件为事件A 与事件B 的交事件(或A ∩B (或AB )阶段重难点梳理(积事件)积事件)若A∩B为不可能事件(A∩B＝∅)，那么称事件A互斥事件A∩B＝∅与事件B互斥若A∩B为不可能事件，A∪B为必然事件，那P(A)＋P(B)＝1 对立事件么称事件A与事件B互为对立事件3.概率的几个基本性质(1)概率的取值范围：0≤P(A)≤1.(2)必然事件的概率P(E)＝1.(3)不可能事件的概率P(F)＝0.(4)概率的加法公式如果事件A与事件B互斥，则P(A∪B)＝P(A)＋P(B)．(5)对立事件的概率若事件A与事件B互为对立事件，则P(A)＝1－P(B)．【知识拓展】互斥事件与对立事件的区别与联系互斥事件与对立事件都是两个事件的关系，互斥事件是不可能同时发生的两个事件，而对立事件除要求这两个事件不同时发生外，还要求二者之一必须有一个发生，因此，对立事件是互斥事件的特殊情况，而互斥事件未必是对立事件．重点题型训练典例 某超市为了了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如下表所示.已知这100位顾客中一次购物量超过8件的顾客占55%. (1)确定x ，y 的值，并估计顾客一次购物的结算时间的平均值；(2)求一位顾客一次购物的结算时间不超过．．．2分钟的概率．(将频率视为概率)1．从{1,2,3,4,5}中随机选取一个数a ，从{1,2,3}中随机选取一个数b ，则b >a 的概率是( ) A.45 B.35 C.25 D.152．将一枚硬币向上抛掷10次，其中“正面向上恰有5次”是( ) A ．必然事件B ．随机事件C ．不可能事件D ．无法确定3．某射手在一次射击中，射中10环，9环，8环的概率分别为0.2,0.3,0.1，则此射手在一次射击中不超过8环的概率为( ) A ．0.5 B ．0.3 C ．0.6 D ．0.94．袋中装有9个白球，2个红球，从中任取3个球，则①恰有1个红球和全是白球；②至少有1个红球和全是白球；③至少有1个红球和至少有2个白球；④至少有1个白球和至少有1个红球．在上述事件中，是对立事件的为________．1．甲、乙两人下棋，两人下成和棋的概率是12，甲获胜的概率是13，则甲不输的概率为( )A.56 B.25 C.16D.132．袋中装有3个白球，4个黑球，从中任取3个球，则①恰有1个白球和全是白球；②至少有1个白球和全是黑球；③至少有1个白球和至少有2个白球；④至少有1个白球和至少有1个黑球． 在上述事件中，是对立事件的为( ) A ．① B ．② C ．③ D ．④3．从一箱产品中随机地抽取一件，设事件A ＝{抽到一等品}，事件B ＝{抽到二等品}，事件C ＝{抽到三等品}，且已知P (A )＝0.65，P (B )＝0.2，P (C )＝0.1，则事件“抽到的产品不是一等品”的概率作业布置为()A．0.7 B．0.65 C．0.35 D．0.54．有一个游戏，其规则是甲、乙、丙、丁四个人从同一地点随机地向东、南、西、北四个方向前进，每人一个方向．事件“甲向南”与事件“乙向南”是()A．互斥但非对立事件B．对立事件C．相互独立事件D．以上都不对5．从一篮子鸡蛋中任取1个，如果其重量小于30克的概率为0.3，重量在[30,40]克的概率为0.5，那么重量不小于30克的概率为()A．0.8 B．0.5 C．0.7 D．0.36．从存放的号码分别为1,2,3，…，10的卡片的盒子中，有放回地取100次，每次取一张卡片并记下号码，统计结果如下：则取到号码为奇数的卡片的频率是()A．0.53 B．0.5 C．0.47 D．0.377．在200件产品中，有192件一级品，8件二级品，则下列事件：①在这200件产品中任意选出9件，全部是一级品；②在这200件产品中任意选出9件，全部是二级品；③在这200件产品中任意选出9件，不全是二级品．其中________是必然事件；________是不可能事件；________是随机事件．8．若随机事件A，B互斥，A，B发生的概率均不等于0，且P(A)＝2－a，P(B)＝4a－5，则实数a 的取值范围是________________．9．在5张卡片上分别写有数字1,2,3,4,5，然后将它们混合，再任意排列成一行，则得到的数能被2或5整除的概率是________．10．一个口袋内装有大小相同的红球，白球和黑球，从中摸出一个球，摸出红球或白球的概率为0.58，摸出红球或黑球的概率为0.62，那么摸出红球的概率为________．11．某保险公司利用简单随机抽样方法，对投保车辆进行抽样，样本车辆中每辆车的赔付结果统计如下：(1)若每辆车的投保金额均为2 800元，估计赔付金额大于投保金额的概率；(2)在样本车辆中，车主是新司机的占10%，在赔付金额为4 000元的样本车辆中，车主是新司机的占20%，估计在已投保车辆中，新司机获赔金额为4 000元的概率．12．国家射击队的队员为在射击世锦赛上取得优异成绩，正在加紧备战，经过近期训练，某队员射击一次命中7～10环的概率如下表所示：求该射击队员射击一次：(1)射中9环或10环的概率；(2)命中不足8环的概率．*13.一盒中装有12个球，其中5个红球，4个黑球，2个白球，1个绿球．从中随机取出1球，求：(1)取出1球是红球或黑球的概率；(2)取出1球是红球或黑球或白球的概率．随机事件的概率进门测判断下列结论是否正确(请在括号中打“√”或“×”)(1)事件发生频率与概率是相同的．(×)(2)随机事件和随机试验是一回事．(×)(3)在大量重复试验中，概率是频率的稳定值．(√)(4)两个事件的和事件是指两个事件都得发生．(×)(5)对立事件一定是互斥事件，互斥事件不一定是对立事件．(√)(6)两互斥事件的概率和为1.(×)阶段训练题型一事件关系的判断例1(1)从1,2,3，…，7这7个数中任取两个数，其中：①恰有一个是偶数和恰有一个是奇数；②至少有一个是奇数和两个都是奇数； ③至少有一个是奇数和两个都是偶数； ④至少有一个是奇数和至少有一个是偶数． 上述事件中，是对立事件的是( ) A ．① B ．②④ C ．③ D ．①③(2)设条件甲：“事件A 与事件B 是对立事件”，结论乙：“概率满足P (A )＋P (B )＝1”，则甲是乙的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件(3)在5张电话卡中，有3张移动卡和2张联通卡，从中任取2张，若事件“2张全是移动卡”的概率是310，那么概率是710的事件是( )A ．至多有一张移动卡B ．恰有一张移动卡C ．都不是移动卡D ．至少有一张移动卡答案 (1)C (2)A (3)A解析 (1)③中“至少有一个是奇数”即“两个奇数或一奇一偶”，而从1～7中任取两个数根据取到数的奇偶性可认为共有三个事件：“两个都是奇数”、“一奇一偶”、“两个都是偶数”，故“至少有一个是奇数”与“两个都是偶数”是对立事件，易知其余都不是对立事件．(2)若事件A 与事件B 是对立事件，则A ∪B 为必然事件，再由概率的加法公式得P (A )＋P (B )＝1.设掷一枚硬币3次，事件A ：“至少出现一次正面”，事件B ：“3次出现正面”，则P (A )＝78，P (B )＝18，满足P (A )＋P (B )＝1，但A ，B 不是对立事件． (3)至多有一张移动卡包含“一张移动卡，一张联通卡”，“两张全是联通卡”两个事件，它是“2张全是移动卡”的对立事件．思维升华(1)准确把握互斥事件与对立事件的概念①互斥事件是不可能同时发生的事件，但可以同时不发生．②对立事件是特殊的互斥事件，特殊在对立的两个事件不可能都不发生，即有且仅有一个发生．(2)判别互斥、对立事件的方法判别互斥事件、对立事件一般用定义判断，不可能同时发生的两个事件为互斥事件；两个事件，若有且仅有一个发生，则这两事件为对立事件，对立事件一定是互斥事件．从装有两个白球和两个黄球的口袋中任取2个球，以下给出了四组事件：①至少有1个白球与至少有1个黄球；②至少有1个黄球与都是黄球；③恰有1个白球与恰有1个黄球；④恰有1个白球与都是黄球．其中互斥而不对立的事件共有()A．0组B．1组C．2组D．3组答案 B解析①中“至少有1个白球”与“至少有1个黄球”可以同时发生，如恰好1个白球和1个黄球，①中的两个事件不是互斥事件．②中“至少有1个黄球”说明可以是1个白球和1个黄球或2个黄球，则两个事件不互斥．③中“恰有1个白球”与“恰有1个黄球”，都是指有1个白球和1个黄球，因此两个事件是同一事件．④中两事件不能同时发生，也可能都不发生，因此两事件是互斥事件，但不是对立事件，故选B.题型二随机事件的频率与概率例2 某险种的基本保费为a (单位：元)，继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：(1)记A 为事件：“一续保人本年度的保费不高于基本保费”，求P (A )的估计值；(2)记B 为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160%”，求P (B )的估计值；(3)求续保人本年度的平均保费的估计值．解 (1)事件A 发生当且仅当一年内出险次数小于2.由所给数据知，一年内出险次数小于2的频率为60＋50200＝0.55，故P (A )的估计值为0.55. (2)事件B 发生当且仅当一年内出险次数大于1且小于4.由所给数据知，一年内出险次数大于1且小于4的频率为30＋30200＝0.3，故P (B )的估计值为0.3.(3)由所给数据得调查的200名续保人的平均保费为0.85a×0.30＋a×0.25＋1.25a×0.15＋1.5a×0.15＋1.75a×0.10＋2a×0.05＝1.192 5a.因此，续保人本年度平均保费的估计值为1.192 5a.思维升华(1)概率与频率的关系频率反映了一个随机事件出现的频繁程度，频率是随机的，而概率是一个确定的值，通常用概率来反映随机事件发生的可能性的大小，有时也用频率作为随机事件概率的估计值．(2)随机事件概率的求法利用概率的统计定义求事件的概率，即通过大量的重复试验，事件发生的频率会逐渐趋近于某一个常数，这个常数就是概率．某超市随机选取1 000位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“√”表示购买，“×”表示未购买.(1)估计顾客同时购买乙和丙的概率；(2)估计顾客在甲、乙、丙、丁中同时购买3种商品的概率；(3)如果顾客购买了甲，则该顾客同时购买乙、丙、丁中哪种商品的可能性最大？ 解 (1)从统计表可以看出，在这1 000位顾客中有200位顾客同时购买了乙和丙， 所以顾客同时购买乙和丙的概率可以估计为2001 000＝0.2.(2)从统计表可以看出，在这1 000位顾客中，有100位顾客同时购买了甲、丙、丁，另有200位顾客同时购买了甲、乙、丙，其他顾客最多购买了2种商品．所以顾客在甲、乙、丙、丁中同时购买3种商品的概率可以估计为100＋2001 000＝0.3.(3)与(1)同理，可得：顾客同时购买甲和乙的概率可以估计为2001 000＝0.2，顾客同时购买甲和丙的概率可以估计为100＋200＋3001 000＝0.6，顾客同时购买甲和丁的概率可以估计为1001 000＝0.1.所以，如果顾客购买了甲，则该顾客同时购买丙的可能性最大． 题型三 互斥事件、对立事件的概率 命题点1 互斥事件的概率例3 袋中有12个小球，分别为红球、黑球、黄球、绿球，从中任取一球，得到红球的概率是13，得到黑球或黄球的概率是512，得到黄球或绿球的概率也是512，试求得到黑球、黄球和绿球的概率各是多少？解 方法一 从袋中选取一个球，记事件“摸到红球”“摸到黑球”“摸到黄球”“摸到绿球”分别为A ，B ，C ，D ，则有P (A )＝13，P (B ∪C )＝P (B )＋P (C )＝512，P (C ∪D )＝P (C )＋P (D )＝512，P (B ∪C ∪D )＝P (B )＋P (C )＋P (D )＝1－P (A )＝1－13＝23，解得P (B )＝14，P (C )＝16，P (D )＝14，因此得到黑球、黄球、绿球的概率分别是14，16，14.方法二 设红球有n 个，则n 12＝13，所以n ＝4，即红球有4个． 又得到黑球或黄球的概率是512，所以黑球和黄球共5个． 又总球数是12，所以绿球有12－4－5＝3(个)．又得到黄球或绿球的概率也是512，所以黄球和绿球共5个，而绿球有3个，所以黄球有5－3＝2(个)．所以黑球有12－4－3－2＝3(个)． 因此得到黑球、黄球、绿球的概率分别是 312＝14，212＝16，312＝14. 命题点2 对立事件的概率例4 某商场有奖销售中，购满100元商品得1张奖券，多购多得.1 000张奖券为一个开奖单位，设特等奖1个，一等奖10个，二等奖50个．设1张奖券中特等奖，一等奖，二等奖的事件分别为A ，B ，C ，求：(1)P (A )，P (B )，P (C )；(2)1张奖券的中奖概率；(3)1张奖券不中特等奖且不中一等奖的概率． 解 (1)P (A )＝11 000，P (B )＝101 000＝1100， P (C )＝501 000＝120.故事件A ，B ，C 的概率分别为11 000，1100，120. (2)1张奖券中奖包含中特等奖，一等奖，二等奖． 设“1张奖券中奖”这个事件为M ，则M ＝A ∪B ∪C . ∵A ，B ，C 两两互斥，∴P (M )＝P (A ∪B ∪C )＝P (A )＋P (B )＋P (C ) ＝1＋10＋501 000＝611 000.故1张奖券的中奖概率为611 000.(3)设“1张奖券不中特等奖且不中一等奖”为事件N ，则事件N 与“1张奖券中特等奖或中一等奖”为对立事件，∴P (N )＝1－P (A ∪B )＝1－⎝⎛⎭⎫11 000＋1100＝9891 000. 故1张奖券不中特等奖且不中一等奖的概率为9891 000.思维升华 求复杂事件的概率的两种方法求概率的关键是分清所求事件是由哪些事件组成的，求解时通常有两种方法： (1)将所求事件转化成几个彼此互斥的事件的和事件，利用概率加法公式求解概率；(2)若将一个较复杂的事件转化为几个互斥事件的和事件时，需要分类太多，而其对立面的分类较少，可考虑利用对立事件的概率公式，即“正难则反”．它常用来求“至少”或“至多”型事件的概率．经统计，在某储蓄所一个营业窗口等候的人数相应的概率如下：排队人数012345人及5人以上概率0.10.160.30.30.10.04求：(1)至多2人排队等候的概率；(2)至少3人排队等候的概率．解记“无人排队等候”为事件A，“1人排队等候”为事件B，“2人排队等候”为事件C，“3人排队等候”为事件D，“4人排队等候”为事件E，“5人及5人以上排队等候”为事件F，则事件A、B、C、D、E、F彼此互斥．(1)记“至多2人排队等候”为事件G，则G＝A＋B＋C，所以P(G)＝P(A＋B＋C)＝P(A)＋P(B)＋P(C)＝0.1＋0.16＋0.3＝0.56.(2)方法一记“至少3人排队等候”为事件H，则H＝D＋E＋F，所以P(H)＝P(D＋E＋F)＝P(D)＋P(E)＋P(F)＝0.3＋0.1＋0.04＝0.44.方法二记“至少3人排队等候”为事件H，则其对立事件为事件G，所以P(H)＝1－P(G)＝0.44.1．概率和频率(1)在相同的条件S 下重复n 次试验，观察某一事件A 是否出现，称n 次试验中事件A 出现的次数n A 为事件A 出现的频数，称事件A 出现的比例f n (A )＝n An为事件A 出现的频率．(2)对于给定的随机事件A ，在相同条件下，随着试验次数的增加，事件A 发生的频率会在某个常数附近摆动并趋于稳定，我们可以用这个常数来刻画随机事件A 发生的可能性大小，并把这个常数称为随机事件A 的概率，记作P (A )． 2．事件的关系与运算若A∩B为不可能事件，A∪B为必然事件，那对立事件P(A)＋P(B)＝1么称事件A与事件B互为对立事件3.概率的几个基本性质(1)概率的取值范围：0≤P(A)≤1.(2)必然事件的概率P(E)＝1.(3)不可能事件的概率P(F)＝0.(4)概率的加法公式如果事件A与事件B互斥，则P(A∪B)＝P(A)＋P(B)．(5)对立事件的概率若事件A与事件B互为对立事件，则P(A)＝1－P(B)．【知识拓展】互斥事件与对立事件的区别与联系互斥事件与对立事件都是两个事件的关系，互斥事件是不可能同时发生的两个事件，而对立事件除要求这两个事件不同时发生外，还要求二者之一必须有一个发生，因此，对立事件是互斥事件的特殊情况，而互斥事件未必是对立事件．重点题型训练典例某超市为了了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如下表所示.已知这100位顾客中一次购物量超过8件的顾客占55%.(1)确定x，y的值，并估计顾客一次购物的结算时间的平均值；(2)求一位顾客一次购物的结算时间不超过．．．2分钟的概率．(将频率视为概率)思想方法指导若某一事件包含的基本事件多，而它的对立事件包含的基本事件少，则可用“正难则反”思想求解．规范解答解(1)由已知得25＋y＋10＝55，x＋30＝45，所以x＝15，y＝20.[2分]该超市所有顾客一次购物的结算时间组成一个总体，所收集的100位顾客一次购物的结算时间可视为总体的一个容量为100的简单随机样本，顾客一次购物的结算时间的平均值可用样本平均数估计，其估计值为1×15＋1.5×30＋2×25＋2.5×20＋3×10100＝1.9(分钟)．[7分](2)记A为事件“一位顾客一次购物的结算时间不超过2分钟”，A1，A2分别表示事件“该顾客一次购物的结算时间为2.5分钟”，“该顾客一次购物的结算时间为3分钟”，将频率视为概率得P(A1)＝20100＝15，P(A2)＝10100＝110.[10分]P(A)＝1－P(A1)－P(A2)＝1－15－110＝710.[12分]故一位顾客一次购物的结算时间不超过2分钟的概率为710.[15分]1．从{1,2,3,4,5}中随机选取一个数a ，从{1,2,3}中随机选取一个数b ，则b >a 的概率是( ) A.45 B.35 C.25 D.15 答案 D解析 基本事件的个数有5×3＝15，其中满足b >a 的有3种，所以b >a 的概率为315＝15.2．将一枚硬币向上抛掷10次，其中“正面向上恰有5次”是( ) A ．必然事件 B ．随机事件 C ．不可能事件 D ．无法确定答案 B解析 抛掷10次硬币正面向上的次数可能为0～10，都有可能发生，正面向上5次是随机事件． 3．某射手在一次射击中，射中10环，9环，8环的概率分别为0.2,0.3,0.1，则此射手在一次射击中不超过8环的概率为( ) A ．0.5 B ．0.3 C ．0.6 D ．0.9 答案 A解析 依题设知，此射手在一次射击中不超过8环的概率为1－(0.2＋0.3)＝0.5.4．袋中装有9个白球，2个红球，从中任取3个球，则①恰有1个红球和全是白球；②至少有1个红球和全是白球；③至少有1个红球和至少有2个白球；④至少有1个白球和至少有1个红球．在上述事件中，是对立事件的为________． 答案 ②解析 ①是互斥不对立的事件，②是对立事件，③④不是互斥事件.1．甲、乙两人下棋，两人下成和棋的概率是12，甲获胜的概率是13，则甲不输的概率为( )A.56 B.25 C.16 D.13答案 A解析 事件“甲不输”包含“和棋”和“甲获胜”这两个互斥事件，所以甲不输的概率为12＋13＝56.2．袋中装有3个白球，4个黑球，从中任取3个球，则①恰有1个白球和全是白球；②至少有1个白球和全是黑球；③至少有1个白球和至少有2个白球；④至少有1个白球和至少有1个黑球． 在上述事件中，是对立事件的为( ) A ．① B ．② C ．③ D ．④ 答案 B解析 至少有1个白球和全是黑球不同时发生，且一定有一个发生． ∴②中两事件是对立事件．3．从一箱产品中随机地抽取一件，设事件A ＝{抽到一等品}，事件B ＝{抽到二等品}，事件C ＝{抽到三等品}，且已知P (A )＝0.65，P (B )＝0.2，P (C )＝0.1，则事件“抽到的产品不是一等品”的概率为( )A ．0.7B ．0.65C ．0.35D ．0.5作业布置答案 C解析∵“抽到的产品不是一等品”与事件A是对立事件，∴所求概率P＝1－P(A)＝0.35.4．有一个游戏，其规则是甲、乙、丙、丁四个人从同一地点随机地向东、南、西、北四个方向前进，每人一个方向．事件“甲向南”与事件“乙向南”是()A．互斥但非对立事件B．对立事件C．相互独立事件D．以上都不对答案 A解析由于每人一个方向，故“甲向南”意味着“乙向南”是不可能的，故是互斥事件，但不是对立事件，故选A.5．从一篮子鸡蛋中任取1个，如果其重量小于30克的概率为0.3，重量在[30,40]克的概率为0.5，那么重量不小于30克的概率为()A．0.8 B．0.5 C．0.7 D．0.3答案 C解析由互斥事件概率公式知重量大于40克的概率为1－0.3－0.5＝0.2，又∵0.5＋0.2＝0.7，∴重量不小于30克的概率为0.7.6．从存放的号码分别为1,2,3，…，10的卡片的盒子中，有放回地取100次，每次取一张卡片并记下号码，统计结果如下：则取到号码为奇数的卡片的频率是( ) A ．0.53 B ．0.5 C ．0.47 D ．0.37 答案 A解析 取到号码为奇数的卡片的次数为13＋5＋6＋18＋11＝53，则所求的频率为53100＝0.53.故选A.7．在200件产品中，有192件一级品，8件二级品，则下列事件： ①在这200件产品中任意选出9件，全部是一级品； ②在这200件产品中任意选出9件，全部是二级品； ③在这200件产品中任意选出9件，不全是二级品．其中________是必然事件；________是不可能事件；________是随机事件． 答案 ③ ② ①8．若随机事件A ，B 互斥，A ，B 发生的概率均不等于0，且P (A )＝2－a ，P (B )＝4a －5，则实数a 的取值范围是________________． 答案 (54，43]解析 由题意可知⎩⎪⎨⎪⎧0<P (A )<1，0<P (B )<1，P (A )＋P (B )≤1⇒⎩⎪⎨⎪⎧0<2－a <1，0<4a －5<13a －3≤1，⇒⎩⎪⎨⎪⎧1<a <2，54<a <32，a ≤43⇒54<a ≤43. 9．在5张卡片上分别写有数字1,2,3,4,5，然后将它们混合，再任意排列成一行，则得到的数能被2或5整除的概率是________． 答案 35解析个位数字共有5种情况，只有当个位数字取2,4,5时，得到的数才能被2或5整除，所以概率为3 5.10．一个口袋内装有大小相同的红球，白球和黑球，从中摸出一个球，摸出红球或白球的概率为0.58，摸出红球或黑球的概率为0.62，那么摸出红球的概率为________．答案0.2解析记事件A，B，C分别是摸出红球，白球和黑球，则A，B，C互为互斥事件且P(A＋B)＝0.58，P(A＋C)＝0.62，所以P(C)＝1－P(A＋B)＝0.42，P(B)＝1－P(A＋C)＝0.38，P(A)＝1－P(C)－P(B)＝1－0.38－0.42＝0.2.11．某保险公司利用简单随机抽样方法，对投保车辆进行抽样，样本车辆中每辆车的赔付结果统计如下：(1)若每辆车的投保金额均为2 800元，估计赔付金额大于投保金额的概率；(2)在样本车辆中，车主是新司机的占10%，在赔付金额为4 000元的样本车辆中，车主是新司机的占20%，估计在已投保车辆中，新司机获赔金额为4 000元的概率．解(1)设A表示事件“赔付金额为3 000元”，B表示事件“赔付金额为4 000元”，以频率估计概率得P(A)＝1501 000＝0.15，P(B)＝1201 000＝0.12.由于投保金额为2 800元，赔付金额大于投保金额对应的情形是赔付金额为3 000元和4 000元，所以其概率为P(A)＋P(B)＝0.15＋0.12＝0.27.。
高中数学一轮专题讲义
一、集合与函数
1. 集合的基本概念和性质
2. 集合的运算
3. 函数的定义和性质
4. 函数的图像和变换
5. 函数的导数和极值
二、三角函数与解三角形
1. 三角函数的定义和性质
2. 三角函数的图像和变换
3. 三角函数的解法和应用
4. 三角形的解法和平行四边形的性质
三、数列与不等式
1. 数列的定义和性质
2. 等差数列和等比数列的通项公式和求和公式
3. 数列的极限和数学归纳法
4. 不等式的性质和证明方法
5. 不等式的求解和应用
四、平面几何与立体几何
1. 点、直线、平面的性质和关系
2. 平面图形的性质和证明方法
3. 立体几何的基本概念和性质
4. 空间几何体的表面积和体积计算
5. 空间几何体的位置关系和证明方法
五、解析几何与向量
1. 直线的方程和性质
2. 圆的方程和性质
3. 圆锥曲线的方程和性质
4. 向量的基本概念和运算规则
5. 向量的应用和证明方法。
高三数学第一轮复习讲义一、函数与方程1. 函数的定义与性质函数是数学中非常重要的概念之一。
在高中数学中，我们常常遇到各种各样的函数问题，理解函数的定义与性质对于解决这些问题至关重要。
1.1 函数的定义函数是一个集合与集合之间的映射关系，它可以将一个自变量的值映射到一个唯一的因变量的值上。
通常表示为：f(x)，其中f表示函数名，x表示自变量，f(x)表示函数的值。
1.2 函数的性质•定义域：函数的自变量所能取到的值的集合。
•值域：函数的因变量所能取到的值的集合。
•单调性：函数在整个定义域内的增减关系。
•奇偶性：函数的对称性质。
2. 一元二次方程一元二次方程是高中数学中常见的一种方程类型，它的一般形式为ax2+bx+c=0。
解一元二次方程的方法有因式分解、配方法、求根公式等。
2.1 因式分解法当一元二次方程可以因式分解为两个一次因式的乘积时，我们可以通过解两个一次方程来求解原方程。
例如：x2−5x+6=0可以分解为(x−2)(x−3)=0，解方程得x=2或x=3。
2.2 配方法当一元二次方程的一次项系数为 2 或 -2 时，可以采用配方法来求解方程。
例如：2x2−7x−3=0。
我们可以通过将2x2−7x−3=0看作(ax+b)x+ c=0的形式，其中a、b、c分别表示方程的系数。
然后，我们将x的系数−7分解为两个数，使得这两个数相乘等于ac，即2∗(−3)=−6，并且这两个数的和等于b，即−7。
在这个例子中，可以写成−3和2。
然后将方程改写为(2x−3)(x+ 1)=0，解得 $x=\\frac{3}{2}$ 或x=−1。
2.3 求根公式当一元二次方程无法通过因式分解或配方法来求解时，我们可以使用求根公式来求解方程。
一元二次方程的求根公式为：$x=\\frac{-b\\pm\\sqrt{b^2-4ac}}{2a}$。
通过代入方程的系数a、b、c到公式中，就可以得到方程的解。
3. 三角函数三角函数是解决与角相关问题的数学工具，广泛应用于物理、工程、计算机图形学等领域。
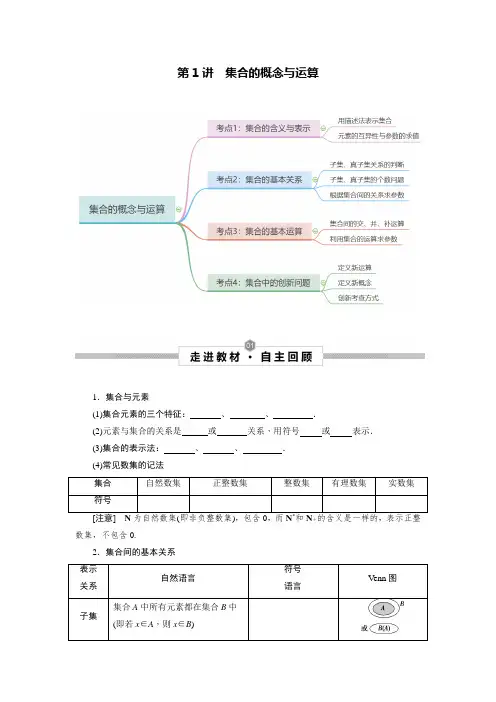
第1讲集合的概念与运算1．集合与元素(1)集合元素的三个特征：、、．(2)元素与集合的关系是或关系，用符号或表示．(3)集合的表示法：、、．(4)常见数集的记法集合自然数集正整数集整数集有理数集实数集符号[注意]N为自然数集(即非负整数集)，包含0，而N*和N＋的含义是一样的，表示正整数集，不包含0.2．集合间的基本关系表示关系自然语言符号语言Venn图子集集合A中所有元素都在集合B中(即若x∈A，则x∈B)真子集 集合A 是集合B 的子集，且集合B 中至少有一个元素不在集合A 中集合 相等集合A ，B 中元素相同A ＝B3.集合的基本运算集合的并集集合的交集集合的补集图形 语言符号 语言A ∪B ＝A ∩B ＝∁U A ＝➢考点1 集合的含义与表示[名师点睛]与集合元素有关问题的解题策略(1)研究集合问题时，首先要明确构成集合的元素是什么，即弄清该集合是数集、点集，还是其他集合；然后再看集合的构成元素满足的限制条件是什么，从而准确把握集合的含义． (2)利用集合元素的限制条件求参数的值或确定集合中元素的个数时，要注意检验集合是否满足元素的互异性．2＋y 2≤3，x ∈Z ，y ∈Z }，则A 中元素的个数为( )A ．9B ．8C ．5D ．4(2)设A ＝⎩⎨⎧⎭⎬⎫2，3，a 2－3a ，a ＋2a ＋7，B ＝{|a －2|,3}，已知4∈A 且4∉B ，则a 的取值集合为________．[举一反三]1．（2022·江西·新余四中模拟预测（理））已知集合()(){}20A x a x x a =--<，若2A ∉，则实数a 的取值范围为（ ）A ．()(),12,-∞+∞ B ．[)1,2 C ．()1,2D ．[]1,22．（2022·菏泽模拟）设a ，b ∈R ，集合{1，a ＋b ，a }＝⎩⎨⎧⎭⎬⎫0，b a ，b ，则b －a ＝( ) A ．1 B ．－1 C ．2D ．－23．(多选)（2022· 广州一调）已知集合{x |mx 2－2x ＋1＝0}＝{n }，则m ＋n 的值可能为( )A ．0B ．12C ．1D ．24．（2022·福建·模拟预测）设集合{2,1,1,2,3}A =--，{}2|log ||,B y y x x A ==∈ ，则集合B 元素的个数为（ ）A ．2B ．3C ．4D ．55．（2022·武汉校级月考）已知集合A ＝{m ＋2，2m 2＋m }，若3∈A ，则m 的值为________．➢考点2 集合的基本关系R N )＝( )A ．∅B ．MC ．ND ．R(2)[2022·广东阳江月考]已知集合A ＝{x |y ＝4－x 2}，B ＝{x |a ≤x ≤a ＋1}，若B ⊆A ，则实数a 的取值范围为( )A ．(－∞，－3]∪[2，＋∞)B ．[－1，2]C ．[－2，1]D ．[2，＋∞)[举一反三]1.（2022·广东广州·一模）已知集合{}11A x x =∈-≤≤Z ，{}02B x x =≤≤，则A B 的子集个数为（ ）A ．2B ．3C ．4D ．62．[2022·湖北武汉摸底]已知集合A ＝{x |x 2－3x ＋2＝0，x ∈R }，B ＝{x |0<x <5，x ∈N }，则满足条件A ⊆C ⊆B 的集合C 的个数为( ) A ．1 B ．2 C ．3D ．43．（2022·山东·潍坊一中模拟预测）已知集合M ，N 是全集U 的两个非空子集，且()U M N ⊆，则（ ）A ．M N ⋂=∅B ．M N ⊆C ．N M ⊆D ．()U N M U ⋃=4.[2021·湖南长沙长郡中学适应性考试]已知集合A ＝{x ∈Z |x ≥a }，集合B ＝{x ∈Z |2x ≤4}．若A ∩B 只有4个子集，则实数a 的取值范围是( )A ．(－2，－1]B ．[－2，－1]C ．[0,1]D ．(0,1]5．[2022·吉林辽源五校期末联考]已知集合M ＝{x |x －a ＝0}，N ＝{x |ax －1＝0}，若M ∩N ＝N ，则实数a 的值是________．➢考点3 集合的基本运算[典例]1.(1)（2021·全国·高考真题）设集合{1,2,3,4,5,6},{1,3,6},{2,3,4}U A B ===，则()UAB =（ ）A ．{3}B ．{1,6}C ．{5,6}D ．{1,3}(2)(多选)[2022·湖南长沙模拟]已知全集U ＝R ，集合M ＝{x |－3≤x <4}，N ＝{x |x 2－2x －8≤0}，则( )A ．M ∪N ＝{x |－3≤x <4}B ．M ∩N ＝{x |－2≤x <4}C ．(∁U M )∪N ＝(－∞，－3)∪[－2，＋∞)D ．M ∩(∁U N )＝(－3，－2)2.(1)(2020·高考全国卷Ⅰ)设集合A ＝{x |x 2－4≤0}，B ＝{x |2x ＋a ≤0}，且A ∩B ＝{x |－2≤x ≤1}，则a ＝( )A ．－4B ．－2C ．2D ．4(2)[2022·湖南六校联考]集合A ＝{0，2，a }，B ＝{1，a 2}，若A ∪B ＝{0，1，2，4，16}，则a 的值为( )A ．0B ．1C ．2D ．4[举一反三]1．（2022·河北石家庄·二模）已知集合{3,2,1,0,1}A =---，301x B x Zx +⎧⎫=∈<⎨⎬-⎩⎭，则A B =（ ）A ．[3,1)-B ．[3,1]-C ．{3,2,1,0,1}---D ．{2,1,0}--2．[2022·华南师范大学附属中学月考]已知集合A ＝{x |x <3}，B ＝{x |x >a }，若A ∩B ≠∅，则实数a 的取值范围为( )A ．[3，＋∞)B ．(3，＋∞)C ．(－∞，3)D ．(－∞，3]3．(2020·高考全国卷Ⅲ)已知集合A ＝{(x ，y )|x ，y ∈N *，y ≥x }，B ＝{(x ，y )|x ＋y ＝8}，则A ∩B 中元素的个数为( )A ．2B ．3C ．4D ．64．（2022·重庆·二模）已知集合{}{}21,3,5,6,7,8,9,14480A B xx x ==-+∣，则下图中阴影部分表示的集合为（ ）A ．{}1,3,5,7,9B ．{}1,3,5,9C ．{}1,3,5D ．{}1,3,95．（2021·全国·高考真题（理））已知集合{}21,S s s n n ==+∈Z ，{}41,T t t n n ==+∈Z ，则S T （ ）A ．∅B ．SC ．TD ．Z6.[2021·豫北名校联考]设集合A ＝{x |x 2＋2x －3>0}，集合B ＝{x |x 2－2ax －1≤0，a >0}，若A ∩B 中恰含有一个整数，则实数a 的取值范围是( )A ．⎝⎛⎭⎫0，34 B ．⎣⎡⎭⎫34，43 C ．⎣⎡⎭⎫34，＋∞ D ．(1，＋∞)7.（2020·浙江·高考真题）设集合S ，T ，S ⊆N *，T ⊆N *，S ，T 中至少有两个元素，且S ，T 满足：①对于任意x ，y ∈S ，若x ≠y ，都有xy ∈T ②对于任意x ，y ∈T ，若x <y ，则yx∈S ； 下列命题正确的是（ ）A ．若S 有4个元素，则S ∪T 有7个元素B ．若S 有4个元素，则S ∪T 有6个元素C ．若S 有3个元素，则S ∪T 有5个元素D ．若S 有3个元素，则S ∪T 有4个元素➢考点4 集合中的创新问题[典例] 1.（2022·北京房山·一模）已知U 是非实数集，若非空集合A 1，A 2满足以下三个条件，则称（A 1，A 2）为集合U 的一种真分拆，并规定（A 1，A 2）与（A 2，A 1）为集合U 的同一种真分拆 ①A 1∩A 2=0 ②A 1A 2=U③(1,2)i A i =的元素个数不是i A 中的元素.则集合U ={1，2，3，4，5，6}的真分拆的种数是（ ） A ．5B ．6C ．10D ．152.[2022·广东六校联考]已知集合A 0＝{x |0<x <1}．给定一个函数y ＝f (x )，定义集合A n＝{y |y ＝f (x )，x ∈A n －1}，若A n ∩A n －1＝∅对任意的x ∈N *成立，则称该函数具有性质 “∅”． (1)具有性质“∅”的一个一次函数的解析式可以是________．(2)给出下列函数：①y ＝1x ；②y ＝x 2＋1；③y ＝cos π2x ＋2.其中具有性质“∅”的函数的序号是________．3.[2022·河北保定质检]现有100名携带药品出国的旅游者，其中75人带有感冒药，80人带有胃药，那么对既带感冒药又带胃药的人数统计中，下列说法正确的是( ) A ．最多人数是55 B ．最少人数是55 C ．最少人数是75 D ．最多人数是80[举一反三]1．（2022·湖南·雅礼中学一模）已知集合{}22(,)|1,,A x y x y x y Z =+≤∈，{}(,)|2,2,,B x y x y x y Z =≤≤∈，定义集合{}12121122(,)|(,),(,)A B x x y y x y A x y B ⊕=++∈∈，则A B ⊕中元素的个数为A ．77B ．49C ．45D ．302．[2021·四川成都联考]已知集合A ＝{1,2,3,4,5,6}的所有三个元素的子集记为B 1，B 2，B 3，…，B k ，k ∈N *.记b i 为集合B i (i ＝1,2,3，…，k )中的最大元素，则b 1＋b 2＋b 3＋…＋b k ＝( )A ．45B ．105C ．150D ．2103．[多选][2022·湘赣皖十五校第一次联考]已知集合M ，N 都是非空集合U 的子集，令集合S ＝{x |x 恰好属于M ，N 中的一个}，下列说法正确的是( )A ．若S ＝N ，则M ＝∅B ．若S ＝∅，则M ＝NC ．若S ⊆M ，则M ⊆ND ．∃M ，N ，使得S ＝(∁U M )∪(∁U N )4．[2022·湖北华大新联盟考试]中国古代重要的数学著作《孙子算经》下卷有题：今有物，不知其数．三三数之，剩二；五五数之，剩三；七七数之，剩二．问：物几何？现有如下表示：已知A ＝{x |x ＝3n ＋2，n ∈N *}，B ＝{x |x ＝5n ＋3，n ∈N *}，C ＝{x |x ＝7n ＋2，n ∈N *}，若x ∈(A ∩B ∩C )，则整数x 的最小值为( ) A ．128 B ．127 C ．37D ．235．[2022·山东省实验中学第二次诊断]若集合{a ，b ，c ，d }＝{1,2,3,4}，且下列四个关系：①a ＝1；②b ≠1；③c ＝2；④d ≠4有且只有一个是正确的．请写出满足上述条件的一个有序数组(a ，b ，c ，d )＝________，符合条件的全部有序数组(a ，b ，c ，d )的个数是________．6．[2022·山东潍坊重点高中联考]已知U ＝{a 1，a 2，a 3，a 4}，集合A 是集合U 中的两个元素所组成的集合，且同时满足下列三个条件：①若a 1∈A ，则a 2∈A ；②若a 3∉A ，则a 2∉A ；③若a 3∈A ，则a 4∉A .求集合A .第1讲 集合的概念与运算1．集合与元素(1)集合元素的三个特征：确定性、互异性、无序性．(2)元素与集合的关系是属于或不属于关系，用符号∈或∉表示．(3)集合的表示法：列举法、描述法、图示法．(4)常见数集的记法集合自然数集正整数集整数集有理数集实数集符号N N*(或N＋)Z Q R [注意]N为自然数集(即非负整数集)，包含0，而N*和N＋的含义是一样的，表示正整数集，不包含0.2．集合间的基本关系表示关系自然语言符号语言Venn图子集集合A中所有元素都在集合B中(即若x∈A，则x∈B)A⊆B(或B⊇A)真子集集合A是集合B的子集，且集合B中至少有一个元素不在集合A中A⫋B(或B⫌A)集合 相等集合A ，B 中元素相同 A ＝B3.集合的基本运算集合的并集集合的交集集合的补集图形 语言符号 语言A ∪B ＝ {x |x ∈A 或x∈B }A ∩B ＝ {x |x ∈A 且x ∈B }∁U A ＝ {x |x ∈U 且 x ∉A }➢考点1 集合的含义与表示[名师点睛]与集合元素有关问题的解题策略(1)研究集合问题时，首先要明确构成集合的元素是什么，即弄清该集合是数集、点集，还是其他集合；然后再看集合的构成元素满足的限制条件是什么，从而准确把握集合的含义． (2)利用集合元素的限制条件求参数的值或确定集合中元素的个数时，要注意检验集合是否满足元素的互异性．2＋y 2≤3，x ∈Z ，y ∈Z }，则A 中元素的个数为( )A ．9B ．8C ．5D ．4(2)设A ＝⎩⎨⎧⎭⎬⎫2，3，a 2－3a ，a ＋2a ＋7，B ＝{|a －2|,3}，已知4∈A 且4∉B ，则a 的取值集合为________．[解析] (1)将满足x 2＋y 2≤3的整数x ，y 全部列举出来，即(－1，－1)，(－1,0)，(－1,1)，(0，－1)，(0,0)，(0,1)，(1，－1)，(1,0)，(1,1)，共有9个．故选A.(2)因为4∈A ，即4∈⎩⎨⎧⎭⎬⎫2，3，a 2－3a ，a ＋2a ＋7，所以a 2－3a ＝4或a ＋2a ＋7＝4.若a 2－3a ＝4，则a ＝－1或a ＝4；若a ＋2a ＋7＝4，即a 2＋3a ＋2＝0，则a ＝－1或a ＝－2.由a 2－3a 与a ＋2a ＋7互异，得a ≠－1.故a ＝－2或a ＝4.又4∉B ，即4∉{|a －2|,3}， 所以|a －2|≠4，解得a ≠－2且a ≠6. 综上所述，a 的取值集合为{4}． [答案] (1)A (2){4} [举一反三]1．（2022·江西·新余四中模拟预测（理））已知集合()(){}20A x a x x a =--<，若2A ∉，则实数a 的取值范围为（ ）A ．()(),12,-∞+∞B ．[)1,2C ．()1,2D ．[]1,2【答案】D【解析】因为2A ∉，所以()()2220a a --≥，解得12a ≤≤．故选：D ．2．（2022·菏泽模拟）设a ，b ∈R ，集合{1，a ＋b ，a }＝⎩⎨⎧⎭⎬⎫0，b a ，b ，则b －a ＝( )A ．1B ．－1C ．2D ．－2解析：选C.因为{1，a ＋b ，a }＝⎩⎨⎧⎭⎬⎫0，b a ，b ，a ≠0，所以a ＋b ＝0，则ba ＝－1，所以a＝－1，b ＝1.所以b －a ＝2.3．(多选)（2022· 广州一调）已知集合{x |mx 2－2x ＋1＝0}＝{n }，则m ＋n 的值可能为( )A ．0B ．12C ．1D ．2解析：选BD.因为集合{x |mx 2－2x ＋1＝0}＝{n }，所以⎩⎪⎨⎪⎧m ＝0，－2n ＋1＝0或⎩⎪⎨⎪⎧m ≠0，Δ＝4－4m ＝0，n ＝－－22m ，解得⎩⎪⎨⎪⎧m ＝0，n ＝12或⎩⎨⎧m ＝1，n ＝1，所以m ＋n ＝12或m ＋n ＝2.故选BD.4．（2022·福建·模拟预测）设集合{2,1,1,2,3}A =--，{}2|log ||,B y y x x A ==∈ ，则集合B 元素的个数为（ ）A ．2B ．3C ．4D ．5【答案】B 【解析】当2x =±时，y ＝1；当1x =±时，y ＝0；当x ＝3时，2log 3y =．故集合B 共有3个元素．故选：B.5．（2022·武汉校级月考）已知集合A ＝{m ＋2，2m 2＋m }，若3∈A ，则m 的值为________． 解析：由题意得m ＋2＝3或2m 2＋m ＝3， 则m ＝1或m ＝－32.当m ＝1时，m ＋2＝3且2m 2＋m ＝3，根据集合中元素的互异性可知不满足题意； 当m ＝－32时，m ＋2＝12，而2m 2＋m ＝3，符合题意，故m ＝－32.答案：－32➢考点2 集合的基本关系R N )＝( )A ．∅B ．MC ．ND ．R(2)[2022·广东阳江月考]已知集合A ＝{x |y ＝4－x 2}，B ＝{x |a ≤x ≤a ＋1}，若B ⊆A ，则实数a 的取值范围为( )A ．(－∞，－3]∪[2，＋∞)B ．[－1，2]C ．[－2，1]D ．[2，＋∞)【解析】 (1)因为M ，N 均为R 的子集，且∁R M ⊆N ，所以N ＝∁R M ，所以M ∪(∁R N )＝M .故选B.(2)集合A ＝{x |y ＝4－x 2}＝{x |－2≤x ≤2}，因为B ⊆A ，所以有⎩⎨⎧a ≥－2，a ＋1≤2，所以－2≤a ≤1. 【答案】 (1)B (2)C [举一反三]1.（2022·广东广州·一模）已知集合{}11A x x =∈-≤≤Z ，{}02B x x =≤≤，则A B 的子集个数为（ ）A ．2B ．3C ．4D ．6【答案】C【解析】由题可知{}1,0,1A =-，所有{}0,1A B =，所有其子集分别是{}{}{},1,0,0,1∅，所有共有4个子集，故选：C2．[2022·湖北武汉摸底]已知集合A ＝{x |x 2－3x ＋2＝0，x ∈R }，B ＝{x |0<x <5，x ∈N }，则满足条件A ⊆C ⊆B 的集合C 的个数为( ) A ．1 B ．2 C ．3D ．4解析：选D 求解一元二次方程，得A ＝{x |x 2－3x ＋2＝0，x ∈R }＝{x |(x －1)(x －2)＝0，x ∈R }＝{1,2}，易知B ＝{x |0<x <5，x ∈N }＝{1,2,3,4}．因为A ⊆C ⊆B ，所以根据子集的定义，集合C 必须含有元素1,2，且可能含有元素3,4，原题即求集合{3,4}的子集个数，即有22＝4个，故选D.3．（2022·山东·潍坊一中模拟预测）已知集合M ，N 是全集U 的两个非空子集，且()U M N ⊆，则（ ）A ．M N ⋂=∅B ．M N ⊆C ．N M ⊆D ．()U N M U ⋃=【答案】A 【解析】UN 表示集合N 的补集，因为()U M N ⊆，所以M N ⋂=∅．故选：A4.[2021·湖南长沙长郡中学适应性考试]已知集合A ＝{x ∈Z |x ≥a }，集合B ＝{x ∈Z |2x ≤4}．若A ∩B 只有4个子集，则实数a 的取值范围是( )A ．(－2，－1]B ．[－2，－1]C ．[0,1]D ．(0,1][答案] D [解析] 本题考查根据集合的子集个数求参数的取值．集合A ＝{x ∈Z |x ≥a }，集合B ＝{x ∈Z |2x ≤4}＝{x ∈Z |x ≤2}，故A ∩B ＝{x ∈Z |a ≤x ≤2}．因为A ∩B 只有4个子集，所以A ∩B 中元素只能有2个，即A ∩B ＝{1,2}，所以0<a ≤1，故选D.5．[2022·吉林辽源五校期末联考]已知集合M ＝{x |x －a ＝0}，N ＝{x |ax －1＝0}，若M ∩N ＝N ，则实数a 的值是________．解析：由题易得M ＝{a }．因为M ∩N ＝N ， 所以N ⊆M ， 所以N ＝∅或N ＝M ， 所以a ＝0或a ＝±1. 答案：0或1或－1➢考点3 集合的基本运算[典例]1.(1)（2021·全国·高考真题）设集合{1,2,3,4,5,6},{1,3,6},{2,3,4}U A B ===，则()UAB =（ ）A ．{3}B ．{1,6}C ．{5,6}D ．{1,3}【答案】B【解析】由题设可得{}U1,5,6B =，故(){}U 1,6A B ⋂=，故选：B.(2)(多选)[2022·湖南长沙模拟]已知全集U ＝R ，集合M ＝{x |－3≤x <4}，N ＝{x |x 2－2x －8≤0}，则( )A ．M ∪N ＝{x |－3≤x <4}B ．M ∩N ＝{x |－2≤x <4}C ．(∁U M )∪N ＝(－∞，－3)∪[－2，＋∞)D ．M ∩(∁U N )＝(－3，－2)【解析】 (1)方法一：由题意，得A ∪B ＝{－1，0，1，2}，所以∁U (A ∪B )＝{－2，3}，故选A.方法二：因为2∈B ，所以2∈A ∪B ，所以2∉∁U (A ∪B )，故排除B ，D ；又0∈A ，所以0∈A ∪B ，所以0∉∁U (A ∪B )，故排除C ，故选A.(2)由x 2－2x －8≤0，得－2≤x ≤4，所以N ＝{x |－2≤x ≤4}，则M ∪N ＝{x |－3≤x ≤4}，A 错误；M ∩N ＝{x |－2≤x <4}，B 正确；由于∁U M ＝(－∞，－3)∪[4，＋∞)，故(∁U M )∪N ＝(－∞，－3)∪[－2，＋∞)，C 正确；由于∁U N ＝(－∞，－2)∪(4，＋∞)，故M ∩(∁U N )＝[－3，－2)，D 错误．故选BC.【答案】 (1)A (2)BC2.(1)(2020·高考全国卷Ⅰ)设集合A ＝{x |x 2－4≤0}，B ＝{x |2x ＋a ≤0}，且A ∩B ＝{x |－2≤x ≤1}，则a ＝( )A ．－4B ．－2C ．2D ．4(2)[2022·湖南六校联考]集合A ＝{0，2，a }，B ＝{1，a 2}，若A ∪B ＝{0，1，2，4，16}，则a 的值为( )A ．0B ．1C ．2D ．4【解析】 (1)方法一：易知A ＝{x |－2≤x ≤2}，B ＝{x |x ≤－a2}，因为A ∩B ＝{x |－2≤x ≤1}，所以－a2＝1，解得a ＝－2.故选B.方法二：由题意得A ＝{x |－2≤x ≤2}．若a ＝－4，则B ＝{x |x ≤2}，又A ＝{x |－2≤x ≤2}，所以A ∩B ＝{x |－2≤x ≤2}，不满足题意，排除A ；若a ＝－2，则B ＝{x |x ≤1}，又A ＝{x |－2≤x ≤2}，所以A ∩B ＝{x |－2≤x ≤1}，满足题意；若a ＝2，则B ＝{x |x ≤－1}，又A ＝{x |－2≤x ≤2}，所以A ∩B ＝{x |－2≤x ≤－1}，不满足题意，排除C ；若a ＝4，则B ＝{x |x ≤－2}，又A ＝{x |－2≤x ≤2}，所以A ∩B ＝{x |x ＝－2}，不满足题意．故选B.(2)根据集合并集的概念，可知{a ，a 2}＝{4，16}，故a ＝4. 【答案】 (1)B (2)D [举一反三]1．（2022·河北石家庄·二模）已知集合{3,2,1,0,1}A =---，301x B x Zx +⎧⎫=∈<⎨⎬-⎩⎭，则A B =（ ）A ．[3,1)-B ．[3,1]-C ．{3,2,1,0,1}---D ．{2,1,0}--【答案】D 【解析】因为30311x x x +<⇒-<<-，所以{}2,1,0B =--，而{3,2,1,0,1}A =---， 所以A B ={2,1,0}--，故选：D2．[2022·华南师范大学附属中学月考]已知集合A ＝{x |x <3}，B ＝{x |x >a }，若A ∩B ≠∅，则实数a 的取值范围为( )A ．[3，＋∞)B ．(3，＋∞)C ．(－∞，3)D ．(－∞，3]解析：选C 因为A ∩B ≠∅，所以结合数轴可知实数a 的取值范围是a <3，故选C. 3．(2020·高考全国卷Ⅲ)已知集合A ＝{(x ，y )|x ，y ∈N *，y ≥x }，B ＝{(x ，y )|x ＋y ＝8}，则A ∩B 中元素的个数为( )A ．2B ．3C ．4D ．6解析：选C.由题意得，A ∩B ＝{(1，7)，(2，6)，(3，5)，(4，4)}，所以A ∩B 中元素的个数为4，选C.4．（2022·重庆·二模）已知集合{}{}21,3,5,6,7,8,9,14480A B xx x ==-+∣，则下图中阴影部分表示的集合为（ ）A ．{}1,3,5,7,9B ．{}1,3,5,9C ．{}1,3,5D ．{}1,3,9【答案】B【解析】由图可知，图中阴影部分表示()R A B ⋂，由214480x x -+≤，得68x ≤≤， 所以{}68B x x =≤≤，所以{R 6B x x =<或}8x >，因为{}1,3,5,6,7,8,9A =， 所以(){}R1,3,5,9AB =，故选：B5．（2021·全国·高考真题（理））已知集合{}21,S s s n n ==+∈Z ，{}41,T t t n n ==+∈Z ，则S T （ ）A ．∅B ．SC ．TD ．Z【答案】C【解析】任取t T ∈，则()41221t n n =+=⋅+，其中n Z ∈，所以，t S ∈，故T S ⊆， 因此，S T T =.故选：C.6.[2021·豫北名校联考]设集合A ＝{x |x 2＋2x －3>0}，集合B ＝{x |x 2－2ax －1≤0，a >0}，若A ∩B 中恰含有一个整数，则实数a 的取值范围是( )A ．⎝⎛⎭⎫0，34 B ．⎣⎡⎭⎫34，43 C ．⎣⎡⎭⎫34，＋∞D ．(1，＋∞)[答案] B [解析] A ＝{x |x 2＋2x －3>0}＝{x |x >1或x <－3}，设函数f (x )＝x 2－2ax －1，因为函数f (x )＝x 2－2ax －1图象的对称轴为直线x ＝a (a >0)，f (0)＝－1<0，根据对称性可知，若A ∩B 中恰有一个整数，则这个整数为2，所以有⎩⎪⎨⎪⎧ f (2)≤0，f (3)>0，即⎩⎪⎨⎪⎧4－4a －1≤0，9－6a －1>0，所以⎩⎨⎧a ≥34，a <43，即34≤a <43.故选B. 7.（2020·浙江·高考真题）设集合S ，T ，S ⊆N *，T ⊆N *，S ，T 中至少有两个元素，且S ，T 满足：①对于任意x ，y ∈S ，若x ≠y ，都有xy ∈T ②对于任意x ，y ∈T ，若x <y ，则yx∈S ； 下列命题正确的是（ ）A ．若S 有4个元素，则S ∪T 有7个元素B ．若S 有4个元素，则S ∪T 有6个元素C ．若S 有3个元素，则S ∪T 有5个元素D ．若S 有3个元素，则S ∪T 有4个元素 【答案】A 【解析】 首先利用排除法：若取{}1,2,4S =，则{}2,4,8T =，此时{}1,2,4,8S T =，包含4个元素，排除选项 C ； 若取{}2,4,8S =，则{}8,16,32T =，此时{}2,4,8,16,32S T =，包含5个元素，排除选项D ； 若取{}2,4,8,16S =，则{}8,16,32,64,128T =，此时{}2,4,8,16,32,64,128S T =，包含7个元素，排除选项B ；下面来说明选项A 的正确性：设集合{}1234,,,S p p p p =，且1234p p p p <<<，*1234,,,p p p p N ∈，则1224p p p p <，且1224,p p p p T ∈，则41p S p ∈， 同理42p S p ∈，43p S p ∈，32p S p ∈，31p S p ∈，21p S p ∈，若11p =，则22p ≥，则332p p p <，故322p p p =即232p p =，又444231p p p p p >>>，故442232p p p p p ==，所以342p p =， 故{}232221,,,S p p p =，此时522,p T p T ∈∈，故42p S ∈，矛盾，舍.若12p ≥，则32311p p p p p <<，故322111,p pp p p p ==即323121,p p p p ==， 又44441231p p p p p p p >>>>，故441331p p p p p ==，所以441p p =， 故{}2341111,,,S p p p p =，此时{}3456711111,,,,p p p p p T ⊆.若q T ∈， 则31q S p ∈，故131,1,2,3,4i qp i p ==，故31,1,2,3,4i q p i +==，即{}3456711111,,,,q p p p p p ∈，故{}3456711111,,,,p p p p p T =，此时{}234456711111111,,,,,,,S T p p p p p p p p ⋃=即S T 中有7个元素.故A 正确. 故选：A .➢考点4 集合中的创新问题[典例] 1.（2022·北京房山·一模）已知U 是非实数集，若非空集合A 1，A 2满足以下三个条件，则称（A 1，A 2）为集合U 的一种真分拆，并规定（A 1，A 2）与（A 2，A 1）为集合U 的同一种真分拆 ①A 1∩A 2=0 ②A 1A 2=U③(1,2)i A i =的元素个数不是i A 中的元素.则集合U ={1，2，3，4，5，6}的真分拆的种数是（ ） A ．5 B ．6C ．10D ．15【答案】A 【解析】解：由题意，集合U ={1，2，3，4，5，6}的真分拆有{}{}125,1,2,3,4,6A A ==；{}{}121,4,2,3,5,6A A ==；{}{}123,4,1,2,5,6A A ==；{}{}124,5,1,2,3,6A A ==；{}{}124,6,1,2,3,5A A ==，共5种，故选：A.2.[2022·广东六校联考]已知集合A 0＝{x |0<x <1}．给定一个函数y ＝f (x )，定义集合A n＝{y |y ＝f (x )，x ∈A n －1}，若A n ∩A n －1＝∅对任意的x ∈N *成立，则称该函数具有性质 “∅”． (1)具有性质“∅”的一个一次函数的解析式可以是________．(2)给出下列函数：①y ＝1x ；②y ＝x 2＋1；③y ＝cos π2x ＋2.其中具有性质“∅”的函数的序号是________．[解析] (1)答案不唯一，合理即可．示例： 对于解析式y ＝x ＋1，因为A 0＝{x |0<x <1}，所以A 1＝{x |1<x <2}， A 2＝{x |2<x <3}，…，显然符合A n ∩A n －1＝∅.故具有性质“∅”的一个一次函数的解析式可以是y ＝x ＋1. (2)对于①，A 0＝{x |0<x <1}，A 1＝{x |x >1}，A 2＝{x |0<x <1}，…， 依次循环下去，符合A n ∩A n －1＝∅.对于②，A 0＝{x |0<x <1}，A 1＝{x |1<x <2}，A 2＝{x |2<x <5}，A 3＝{x |5<x <26}，…，根据函数y ＝x 2＋1的单调性得相邻两个集合不会有交集，符合A n ∩A n －1＝∅.对于③，A 0＝{x |0<x <1}，A 1＝{x |2<x <3}，A 2＝{x |1<x <2}，A 3＝{x |1<x <2}， 不符合A n ∩A n －1＝∅.所以具有性质“∅”的函数的序号是①②. [答案] (1)y ＝x ＋1 (2)①②3.[2022·河北保定质检]现有100名携带药品出国的旅游者，其中75人带有感冒药，80人带有胃药，那么对既带感冒药又带胃药的人数统计中，下列说法正确的是( ) A ．最多人数是55 B ．最少人数是55 C ．最少人数是75D ．最多人数是80解析：选B 设100名携带药品出国的旅游者组成全集I ，其中带感冒药的人组成集合A ，带胃药的人组成集合B .设所携带药品既非感冒药又非胃药的人数为x ，则0≤x ≤20.设以上两种药都带的人数为y .由图可知，x ＋card(A )＋card(B )－y ＝100.∴x ＋75＋80－y ＝100，∴y ＝55＋x .∵0≤x ≤20，∴55≤y ≤75，故最少人数是55. [举一反三]1．（2022·湖南·雅礼中学一模）已知集合{}22(,)|1,,A x y x y x y Z =+≤∈，{}(,)|2,2,,B x y x y x y Z =≤≤∈，定义集合{}12121122(,)|(,),(,)A B x x y y x y A x y B ⊕=++∈∈，中元素的个数为则A BA．77 B．49 C．45 D．30【答案】C【解析】因为集合，所以集合中有5个元素（即5个点），即图中圆中的整点，集合中有25个元素（即25个点）：即图中正方形中的整点，集合的元素可看作正方形中的整点（除去四个顶点），即个．2．[2021·四川成都联考]已知集合A＝{1,2,3,4,5,6}的所有三个元素的子集记为B1，B2，B3，…，B k，k∈N*.记b i为集合B i(i＝1,2,3，…，k)中的最大元素，则b1＋b2＋b3＋…＋b k＝()A．45 B．105C．150 D．210[答案]B[解析]本题考查集合的新定义问题．集合A的含有3个元素的子集共有C36＝20个，所以k＝20.在集合B i(i＝1,2,3，…，k)中，最大元素为3的集合有C22＝1个；最大元素为4的集合有C23＝3个；最大元素为5的集合有C24＝6个；最大元素为6的集合有C25＝10个，所以b1＋b2＋b3＋…＋b k＝3×1＋4×3＋5×6＋6×10＝105.故选B.3．[多选][2022·湘赣皖十五校第一次联考]已知集合M，N都是非空集合U的子集，令集合S＝{x|x恰好属于M，N中的一个}，下列说法正确的是()A．若S＝N，则M＝∅B．若S＝∅，则M＝NC．若S⊆M，则M⊆ND．∃M，N，使得S＝(∁U M)∪(∁U N)[答案] ABD [解析]本题考查Venn 图．用Venn 图表示，集合S 为如图1中的阴影部分，对于A 选项，若S ＝N ，利用S 的Venn 图观察，则有M ∩N ＝∅，M ＝∅，故A 选项正确；对于B 选项，若S ＝∅，则M ＝N ，故B 选项正确；对于C 选项，反例：如图集合S 为如图2中的阴影部分，N ⊆M ，故C 选项错误；对于D 选项，例如U ＝{1,2,3,4}，M ＝{1,2,3}，N ＝{4}，S ＝{x |x 恰好属于M ，N 中的一个}＝{1,2,3,4}＝U ，而(∁U M )∪(∁U N )＝{4}∪{1,2，3}＝{1,2,3,4}＝S ，故D 选项正确，故选ABD.图1 图24．[2022·湖北华大新联盟考试]中国古代重要的数学著作《孙子算经》下卷有题：今有物，不知其数．三三数之，剩二；五五数之，剩三；七七数之，剩二．问：物几何？现有如下表示：已知A ＝{x |x ＝3n ＋2，n ∈N *}，B ＝{x |x ＝5n ＋3，n ∈N *}，C ＝{x |x ＝7n ＋2，n ∈N *}，若x ∈(A ∩B ∩C )，则整数x 的最小值为( ) A ．128 B ．127 C ．37D ．23解析：选D ∵求整数的最小值，∴先将23代入检验，满足A ，B ，C 三个集合，故选D.5．[2022·山东省实验中学第二次诊断]若集合{a ，b ，c ，d }＝{1,2,3,4}，且下列四个关系：①a ＝1；②b ≠1；③c ＝2；④d ≠4有且只有一个是正确的．请写出满足上述条件的一个有序数组(a ，b ，c ，d )＝________，符合条件的全部有序数组(a ，b ，c ，d )的个数是________． 解析：显然①不可能正确，否则①②都正确；若②正确，则⎩⎪⎨⎪⎧ a ＝2，b ＝3，c ＝1，d ＝4或⎩⎪⎨⎪⎧ a ＝3，b ＝2，c ＝1，d ＝4.若③正确，则⎩⎪⎨⎪⎧ a ＝3，b ＝1，c ＝2，d ＝4.若④正确，则⎩⎪⎨⎪⎧ a ＝2，b ＝1，c ＝4，d ＝3或⎩⎪⎨⎪⎧ a ＝3，b ＝1，c ＝4，d ＝2或⎩⎪⎨⎪⎧a ＝4，b ＝1，c ＝3，d ＝2.所以符合条件的数组共6个． 答案：(3,2,1,4)(填一个正确的即可) 66．[2022·山东潍坊重点高中联考]已知U ＝{a 1，a 2，a 3，a 4}，集合A 是集合U 中的两个元素所组成的集合，且同时满足下列三个条件：①若a1∈A，则a2∈A；②若a3∉A，则a2∉A；③若a3∈A，则a4∉A.求集合A.解：假设a1∈A，则a2∈A.又若a3∉A，则a2∉A，∴a3∈A，与集合A中有且仅有两个元素不符，∴假设不成立，∴a1∉A.假设a4∈A，则a3∉A，则a2∉A，且a1∉A，与集合A中有且仅有两个元素不符，∴假设不成立，∴a4∉A.故集合A＝{a2，a3}，经检验知符合题意．。
