当前位置：文档之家 › 圆的参数方程(公开课)(最新整理).ppt

圆的参数方程(公开课)(最新整理).ppt

  • 格式：ppt
  • 大小：957.00 KB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

圆的参数方程讲课文档

圆的参数方程讲课文档

(2)把圆x 方 2y程 22x4y10化为参数方程为
x 12cos y 22sin
第10页，共30页。
例2. 如图,已知点P是圆x2+y2=16上的一个动点, 点A是x轴上的定点,坐标为(12,0).当点P在圆 上运动时,线段PA中点M的轨迹是什么?
第11页，共30页。
例2. 如图,已知点P是圆x2+y2=16上的一个动点,
所以椭圆 x 2 y 2 1的参数方程是 94
{ x 3 cos ( 为参数 ) y 2 sin
第26页，共30页。
（2）把y 2t代入椭圆方程，得 x2 4t 2 1 94
于是x2 9(1 t 2 ), x 3 1 t 2
所以，椭圆 x2 y2 1的参数方程是 94
x 3
（1）写出定义域（x的范围） （2）消去参数(代入消元，三角变换消元） 注意：在参数方程与普通方程的互化中，必须使x,y
前后的取值范围保持一致。
2、普通方程化为参数方程的步骤
把含有参数等式代入即可
第30页，共30页。
y
(1,-1)
o
x
代入消元法
第21页，共30页。
(2)x sin cos 2 sin( ),
4 所以x[ 2, 2],
把x sin cos平方后减去y 1 sin2
得到x2 y, x[ 2, 2]. 这是抛物线的一部分。 y
三角变换 消元法
第22页，共30页。
2 o
2
参数方程化为普通方程的步骤
步骤：
1、写出定义域（x的范围）
2、消去参数(代入消元，三角变换消元)
注意：
在参数方程与普通方程的互化中，必 须使x,y前后的取值范围保持一致。

2.1.2.圆的参数方程 课件(人教A选修4-4)

2.1.2.圆的参数方程 课件(人教A选修4-4)
x＝2cos θ＋1，y＝2sin θ－2， 故 2x＋y＝4cos θ＋2＋2sin θ－2. ＝4cos θ＋2sin θ＝2 5sin(θ＋φ)． ∴－2 5≤2x＋y≤2 5. 即 2x＋y 的最大值为 2 5，最小值为－2 5.
返回
圆的参数方程突出了工具性作用，应用时，把圆 上的点的坐标设为参数方程形式，将问题转化为三角
返回
点击下图进入
返回
x＝cos θ 是圆 y＝sin θ
上一动点，求 PQ 中
点的轨迹方程，并说明轨迹是什么曲线．
解：设中点 M(x，y)．则 x＝2＋cos θ， 2 0＋sin θ ， y＝ 2 1 x＝1＋2cos θ， 即 y＝1sin θ， 2
(θ 为参数)
返回
返回
圆的参数方程 (1)在 t 时刻，圆周上某点 M 转过的角度是 θ，点 M 的坐 标是(x，y)，那么 θ＝ωt(ω 为角速度)．设|OM|＝r，那么由三
x y 角函数定义，有 cos ωt＝ r ，sin ωt＝ r ，即圆心在原点 O，
x＝rcosωt 的圆的参数方程为 (t y＝rsinωt
函数问题，利用三角函数知识解决问题．
返回
3． 求原点到曲线
x＝3＋2sin θ， C： y＝－2＋2cos θ
(θ 为参数)的最短距离．
解：原点到曲线 C 的距离为： x－02＋y－02＝ 3＋2sin θ2＋－2＋2cos θ2 ＝ 17＋43sin θ－2cos θ ＝ 3 2 17＋4 13 sin θ－ cos θ 13 13
＝ 17＋4 13sinθ＋φ≥ 17－4 13＝ 13－22＝ 13－2. ∴原点到曲线 C 的最短距离为 13－2.

圆的参数方程精选教学PPT课件

圆的参数方程精选教学PPT课件

P
M
由线段中点坐标公式得点M的轨迹

的参数方程为xy

6 2c
2 sin
os
O
4B
10 A(12,0)
解法2(动点转移法或代入法) : 设点M的坐标是(x, y),点P的坐标为
(x1, y1).因为点P在圆x2 y2 16上,所以有x12 y12 16.1
由线段中点坐标公式得x
x f (t)

y

g(t)
并且对于t的每一个允许值，由上述方程组所 确定的点M（x,y）都在这条曲线上，那么上述 方程组就叫做这条曲线的参数方程 ，联系x、 y之间关系的变数叫做参变数，简称参数。参 数方程的参数可以是有物理、几何意义的变数， 也可以是没有明显意义的变数。
相对于参数方程来说，前面学过的直接给 出曲线上点的坐标关系的方程，叫做曲线的普 通方程。
生死教会她锐利果敢。所以她说，那一刻，没有一个母亲，会如苏珊般高贵沉着。 九天九夜的追捕，孩子们找到了。不在暗夜不在森林，而沉在冰冷的湖底。苏珊，终于向警方自首，的确是她，因为一点情欲的贪念，亲手杀了自己的孩子。
1994年的事了。偶尔在一本书里，读到前因后果，和那陌生女子的信。我低一低头，其实并没有泪。我想我懂。 我尚不及为人母，也不曾遭逢死亡，我却曾站在高处林下，看着爱人轻快远去，仿佛有鹳雀在他鞋底翻飞，他是急着赶另一个女子的约会吧?真相凄厉地直逼眼前。不是不知道，在泪落之前应该说再见，我却做不到。因为我爱他。
x a r cos y b r sin
课件制作：湘潭县一中 李小清
1．参数方程的概念
（1）圆心在原点
2．圆的参数方程 的圆参数方程 （2）圆心不在原 点的圆的参数方程

圆的参数方程 课件

圆的参数方程 课件

1．已知(x，y)在曲线 F(x，y)＝0 上，求 φ(x，y)的最值，常用曲线 F(x，y)＝0 的
参数方程：xy＝＝gftt， 化目标函数 φ(x，y)＝φ(t)的形式，然后用求函数最值的方法 求解．
2．注意化 F(x，y)＝0 为xy＝＝gftt， 要等价转化才能正确地求出最值，例如：(x－
则xy′′＝＝ccooss
θ＋sin θ，① θsin θ，②
①2－2×②，得 x′2－2y′＝1，即 x′2＝2y′＋12， ∴所求点 P 的轨迹为抛物线 x2＝2y＋12的一部分|x|≤ 2，|y|≤12.
探究三 圆的参数方程的应用
[例 3] 已知点 P(x，y)是圆 x2＋y2－6x－4y＋12＝0 上的动点，求： (1)x2＋y2 的最值； (2)x＋y 的最值． [解析] 由 x2＋y2－6x－4y＋12＝0， 得(x－3)2＋(y－2)2＝1，
3)2＋(y－2)2＝1(x≥3)⇔xy＝＝23＋＋scions
t， t
(－π2≤t≤π2)．
3．在直x＝3－ 的参数方程为
22t，
y＝ 5＋ 22t
(t 为参数)．在极坐标
系(与直角坐标系 xOy 取相同的长度单位，且以原点 O 为极点，以 x 轴正半轴为极轴)
中，圆 C 的方程为 ρ＝2 5sin θ. (1)求圆 C 的直角坐标方程；
即
x＝2＋5cos α， y＝1＋5sin α
(α∈R，α 为参数)．
怎样把普通方程化为参数方程 (1)普通方程化为参数方程的关键是选参数，并且利用三角等式 sin2α＋cos2α ＝1. (2)把普通方程转化为参数方程时，必须指明参数的取值范围，取值范围不同， 所表示的曲线也可能会有所不同．

圆的参数方程(PPT)3-1

圆的参数方程(PPT)3-1
2 如果圆心不在原点，而是（a，b）， 半径仍为r，那么圆的参数方程又该如
何求？
x a r cos

y

b

r
sin
海王星的光环十分暗淡，但它们的内部结构仍是未知数。人们已命名了海王星的光环：最外面的是Adams（它包括三段明显的圆弧，今已分别命名为自由 Liberty，平等Equality和友爱Fraternity），其次是一个未命名的包有Galatea卫星的弧然后是Leverrier（它向外延伸的部分叫作Lassell和Arago），最里面暗淡 但很宽阔的叫Galle。这颗蓝色行星有着暗淡的天蓝色圆环，但与土星比起来相去甚远。当这些环由以爱德华·奎南为首的团队发现时曾被认为也许是不完整的。 然而，“旅行者号”的发现表明并非如此。这些行星环有一个特别的“堆状”结构其起因如今不明但也许可以归结于附近轨道上的小卫星的引力相互作用。 认为海王星环不完整的证据首次出现在8年代中期，当时观测到海王星在掩星前后出现了偶尔的额外“闪光”旅行者号在989年拍摄的图像发现了这个包含几 个微弱圆环的行星环系统，从而解决了这个问题。最外层的圆环，亚当斯，包含三段显著的弧，如今名为“Liberté”，“Egalité”和“Fraternité”（自由、 平等、博爱）。弧的存在非常难于理解，因为；镀锌方管 / 镀锌方管 ；运动定律预示弧应在不长的时间内变成分布一致的圆环。如 今认为环内侧的卫星海卫六的引力作用束缚了弧的运动。“旅行者”的照相机发现了其他几个环。除了狭窄的、距海王星中心,千米的亚当斯环之外，勒维耶 环距中心,米，更宽、更暗的伽勒环距中心,千米。勒维耶环外侧的暗淡圆环被命名为拉塞尔;再往外是距中心7,千米的Arago环。年新发表的在地球上观察的 结果表明，海王星的环比原先以为的更不稳定。凯克天文台在年和年拍摄的图像显示，与"旅行者号"拍摄时相比，海王星环发生了显著的退化，特别是“自 由弧”，也许在一个世纪左右就会消失。光环数据[9]光环距离（千米）宽度（千米）另称Diffuse9989NR,GalleInner989NR,勒威耶 Plateau8989NR,Lassell,AragoMain9<989NR,Adams（距离是海王星中心到光环的内端）卫星海王星有颗已知的天然卫星。其中最大的、也是唯一拥有足够质 量成为球体的海卫一在海王星被发现7天以后就被威廉·拉塞尔发现了。与其他大型卫星不同，海卫一运行于逆行轨道，说明它是被海王星俘获的，大概曾经 是一个柯伊伯带天体。它与海王星的距离足够近使它被锁定在同步轨道上，它将缓慢地经螺旋轨道接近海王星，当它到达洛希极限时最终将被海王星的引力 撕开。海卫

2.1.2.圆的参数方程 课件(人教A选修4-4)

2.1.2.圆的参数方程 课件(人教A选修4-4)

返回
点击下图进入
返回
x＝2cos θ＋1，y＝2sin θ－2， 故 2x＋y＝4cos θ＋2＋2sin θ－2. ＝4cos θ＋2sin θ＝2 5sin(θ＋φ)． ∴－2 5≤2x＋y≤2 5. 即 2x＋y 的最大值为 2 5，最小值为－2 5.
返回
圆的参数方程突出了工具性作用，应用时，把圆 上的点的坐标设为参数方程形式，将问题转化为三角
[解]
根据圆的特点，结合参数方程概念求解．
如图所示，
设圆心为 O′，连 O′M，∵O′为圆心， ∴∠MO′x＝2φ.
x＝r＋rcos ∴ y＝rsin 2φ.
2φ，
返回
(1)确定圆的参数方程，必须根据题目所给条件， 否则，就会出现错误，如本题容易把参数方程写成
x＝r＋rcos y＝rsin φ.
＝ 17＋4 13sinθ＋φ≥ 17－4 13＝ 13－22＝ 13－2. ∴原点到曲线 C 的最短距离为 13－2.
返回
4．已知圆
x＝cos θ， C y＝－1＋sin
θ
与直线 x＋y＋a＝0 有公共点，
求实数 a 的取值范围．
x＝cos θ， 解：法一：∵ y＝－1＋sin
半径为 r
为参数)．其中参数
t 的物理意义是： 质点做匀速圆周运动的时间 ．
返回
(2)若取 θ 为参数，因为 θ＝ωt，于是圆心在原点 O，半 径为 r
x＝rcos θ 的圆的参数方程为y＝rsin θ (θ
为参数)．其中参数 θ
的几何意义是：OM0(M0 为 t＝0 时的位置)绕点 O 转到
逆 时针旋
OM
的位置时，OM0 转过的角度．

2.1.2.圆的参数方程 课件(人教A选修4-4)


逆 时针旋
OM
的位置时，OM0 转过的角度．
(3)若圆心在点 M0(x0，y0)，半径为 R，则圆的参数方程 为
x＝x ＋Rcos θ 0 y＝y0＋Rsin θ
(0≤θ＜2π) ．
返回
返回
[例1]
圆(x－r)2＋y2＝r2(r＞0)，点M在圆上，O为原点，
以∠MOx＝φ为参数，求圆的参数方程． [思路点拨]
这就是所求的轨迹方程． 1 它是以(1,0)为圆心，以 为半径的圆. 2
返回
[例2]
若x，y满足(x－1)2＋(y＋2)2＝4，求2x＋y的最值． (x－1)2＋(y＋2)2＝4表示圆，可考虑利用圆的
[思路点拨]
参数方程将求2x＋y的最值转化为求三角函数最值问题． [解] 令 x－1＝2cos θ，y＋2＝2sin θ，则有
＝ 17＋4 13sinθ＋φ≥ 17－4 13＝ 13－22＝ 13－2. ∴原点到曲线 C 的最短距离为 13－2.
返回
4．已知圆
x＝cos θ， C y＝－1＋sin
θ
与直线 x＋y＋a＝0 有公共点，
求实数 a 的取值范围．
x＝cos θ， 解：法一：∵ y＝－1＋sin
φ，
(2)由于选取的参数不同，圆有不同的参数方程．
返回
1．已知圆的方程为x2＋y2＝2x，写出它的参数方程．
解：x2＋y2＝2x 的标准方程为(x－1)2＋y2＝1， 设 x－1＝cos θ，y＝sin θ，则
x＝1＋cos 参数方程为 y＝sin θ
θ，
(0≤θ＜2π)．
返回
2．图进入
返回
x＝2cos θ＋1，y＝2sin θ－2， 故 2x＋y＝4cos θ＋2＋2sin θ－2. ＝4cos θ＋2sin θ＝2 5sin(θ＋φ)． ∴－2 5≤2x＋y≤2 5. 即 2x＋y 的最大值为 2 5，最小值为－2 5.

圆的参数方程 课件


(2013·安徽高考)在极坐标系中，圆 ρ＝2cos θ 的垂直于极轴的两条切线方程分别为( )
A．θ＝0(ρ∈R)和 ρcos θ＝2 B．θ＝π2(ρ∈R)和 ρcos θ＝2 C．θ＝π2(ρ∈R)和 ρcos θ＝1 D．θ＝0(ρ∈R)和 ρcos θ＝1
【命题意图】 考查极坐标方程与直角坐标方程之间的 转化，圆的方程及其切线的求解．通过极坐标方程和直角坐 标方程之间的转化考查了知识的转化能力、运算求解能力和 转化应用意识．
∴满足条件的圆的极坐标方程为 ρ＝－4sin θ. ∵sin56π＝12， ∴ρ＝－4sin θ＝－4sin56π＝－2， ∴点(－2，sin56π)在此圆上．
1．求曲线的极坐标方程通常有以下五个步骤：①建立适 当的极坐标系(本题无需建)；②在曲线上任取一点 M(ρ，θ)； ③根据曲线上的点所满足的条件写出等式；④用极坐标(ρ，θ) 表示上述等式，并化简得曲线的极坐标方程；⑤证明所得的 方程是曲线的极坐标方程．(一般只要对特殊点加以检验即 可)．
圆心为(r，π2)，半 径为 r 的圆
极坐标方程 ρ＝r (0≤θ<2π)
ρ＝2rcos θ (－π2≤θ≤π2) ρ＝2rsin θ
(0≤θ<π)
曲线 过极点，倾斜角 为 α 的直线
过点(a,0)，与极轴 垂直的直线
过点(a，π2)，与极 轴平行的直线
图形
极坐标方程 θ＝α或θ＝α＋π
ρcos θ＝a (－π2<θ<π2)
θ)＝0，
即 ρsin θ－ρcos θ＝0，∴x－y＝0.
由于圆(x－2)2＋(y－1)2＝5 的半径为 r＝ 5，圆心(2,1)到
直线
x－y＝0
的距离为

2.1.2.圆的参数方程 课件(人教A选修4-4)


逆 时针旋
OM
的位置时，OM0 转过的角度．
(3)若圆心在点 M0(x0，y0)，半径为 R，则圆的参数方程 为
x＝x ＋Rcos θ 0 y＝y0＋Rsin θ
(0≤θ＜2π) ．
返回
ห้องสมุดไป่ตู้
返回
[例1]
圆(x－r)2＋y2＝r2(r＞0)，点M在圆上，O为原点，
以∠MOx＝φ为参数，求圆的参数方程． [思路点拨]
φ，
(2)由于选取的参数不同，圆有不同的参数方程．
返回
1．已知圆的方程为x2＋y2＝2x，写出它的参数方程．
解：x2＋y2＝2x 的标准方程为(x－1)2＋y2＝1， 设 x－1＝cos θ，y＝sin θ，则
x＝1＋cos 参数方程为 y＝sin θ
θ，
(0≤θ＜2π)．
返回
2．已知点 P(2,0)，点 Q
函数问题，利用三角函数知识解决问题．
返回
3． 求原点到曲线
x＝3＋2sin θ， C： y＝－2＋2cos θ
(θ 为参数)的最短距离．
解：原点到曲线 C 的距离为： x－02＋y－02＝ 3＋2sin θ2＋－2＋2cos θ2 ＝ 17＋43sin θ－2cos θ ＝ 3 2 17＋4 13 sin θ－ cos θ 13 13
＝ 17＋4 13sinθ＋φ≥ 17－4 13＝ 13－22＝ 13－2. ∴原点到曲线 C 的最短距离为 13－2.
返回
4．已知圆
x＝cos θ， C y＝－1＋sin
θ
与直线 x＋y＋a＝0 有公共点，
求实数 a 的取值范围．
x＝cos θ， 解：法一：∵ y＝－1＋sin

《2.2.2 圆的参数方程》课件2-优质公开课-人教B版选修4-4精品


当 堂 双 基 达 标
且平行于极轴的直线；(2)过
课 堂 互 动 探 究
π 3π A 3，3 且和极轴成 4 的直线．
菜
单
【自主解答】 (1)如图 1 所示，在所求直线上任意取点 M(ρ，θ)，过 M 作 MH⊥Ox 于 H，连 OM.
课 前 自 主 导 学 当 堂 双 基 达 标
菜
单
【自主解答】
课 前 自 主 导 学
∵ρ＝2cos θ，∴ρ2＝2ρcos θ，
课 堂 互 动 探 究
π π ∵A2，4，∴MH＝2· sin ＝ 4
2，在 Rt△OMH 中，MH
π A2，4平行于极轴的
＝OMsin θ，即 ρsin θ＝ 2，所以，过 直线方程为 ρsin θ＝ 2.
菜 单
课 前 自 主 导 学
(2)如图 2 所示，在所求直线上任取一点 M(ρ，θ)，
当 堂 双 基 达 标
表示成ρ和θ之间的关系式．这一过程需要用到解三角形的知
课 堂 互 动 探 究
识．用极角和极径表示三角形的内角和边是解决这个问题的 一个难点．直线和圆的极坐标方程也可以用直角坐标方程转 化而来．
菜
单
课 前 自 主 导 学
2．直角坐标与极坐标互化时有哪些注意事项？
【提示】
(1)由直角坐标求极坐标时，理论上不是惟一
当 堂 双 基 达 标
的，但一般约定只在规定范围内求值； (2)由直角坐标方程化为极坐标方程，最后要化简；
课 堂 互 动 探 究
(3)由极坐标方程化为直角坐标方程时要注意变形的等价 性，通常总要用ρ去乘方程的两端.
菜
单
课 前 自 主 导 学
求直线的极坐标方程
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4
)=1时,d
max
2
2 1
小组讨论 例2后实战演练1、2、3、4
例2. 如图,已知点P是圆x2+y2=16上的一个动点,点A是x 轴上的定点,坐标为(12,0).当点P在圆上运动时,线段PA 中点M的轨迹是什么?
解:设M的坐标为(x,y), 圆x2+y2=16
y P M
的参数方程为 x =4cosθ
中点M的轨迹是什么?
解:设M的坐标为(x,y),
y P M
由中点坐标公式得:
O
Ax
点P的坐标为(2x-12,2y)
∵点P在圆x2+y2=16上
∴(2x-12)2+(2y)2=16
即 M的轨迹方程为(x-6)2+y2=4 ∴点M的轨迹是以(6,0)为圆心、2为半径的圆.
例2、已知点P(x，y)是圆x2 y2 6x 4y 12 0上动点， 求（2）点P到x y 1 0的距离的最大值;
p r
d
O
解：圆心（3, 2）到l：x+y-1=0的距离 d= |3+2-1| =2 2
2 p到l的最大距离为d+r=2 2 +1
例2、已知点P(x，y)是圆x2 y2 6x 4y 12 0上动点，
O
Ax
y =4sinθ
∴可设点P坐标为(4cosθ,4sinθ)
由中点公式得:点M的轨迹方程为
x =6+2cosθ y =2sinθ
∴点M的轨迹是以(6,0)为圆心、2为半径的圆.
例2. 如图,已知点P是圆x2+y2=16上的一个动点,点A是x
轴上的定点,坐标为(12,0).当点P在圆上运动时,线段PA
引例:如图，设圆O的半径是r， 点M从初始位置M0（t=0时的 位置）出发，按逆时针方向在 圆O上作匀速圆周运动.点M绕 点O转动的角速度为w.经过t秒， M的位置在何处?
圆x2+ y2=r2对应的参数方程：
ห้องสมุดไป่ตู้
x
y
r r
cos sin
wt wt
(t为参数）
x
y
r r
cos sin
( 为参数）
y
M(x,y)
r
o
M0 x
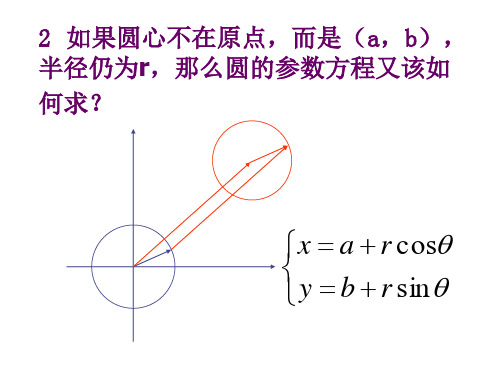
思考 :圆心为O1(a,b)、半径为r的圆的标准方程 为(x a)2 ( y b)2 r2,那么参数方程是什么呢?
圆心为O1 (a, b)、半径为r的圆可以 看作由圆心为原点O、半径为r的圆
平移得到,设圆O1上任意一点P(x, y) 是圆O上的点P1 (x1, y1)平移得到的, 由平移公式, 有
(x 2)2 ( y 2)2 1
半径为 1 的圆，化为标准方程为
( 2 )把圆方程 x 2 y 2 2 x 4 y 1 0 化为参数方程为
x
y
1 2cosθ 2 2sinθ
(θ
为参数）
自查自改：探究一1、2、3、4 同桌研讨解决5
探究二 应用圆的参数方程求最值
例3、已知点P(x，y)是圆x2 y2 6x 4 y 12 0上动点， 求（1）x y的最值;
求（2）点P到x y 1 0的距离的最大值;
解：
P(x,
y）是圆上一动点设 xy
3 cos 2 sin
(为参数）
p到l的距离为d= |x+y-1| | (3 cos) (2 sin) 1|
2
2
| (sin cos ) 4 | |
2 sin( ) 4 | 4
2
2
当sin(
x
y
5 cosθ 5 sin θ
(0
θ
2π )
⑴如果圆上点P所对应的参数θ 5π 则点P的坐标是 _______
3
2
如果圆上点Q所对应的坐标是
2
5 2
,
5
3 2
,
则点Q对应
的参数 等于____3___
3、填空题 :
(1)参数方程
x
y
2 cosθ 2 sinθ
表示圆心为（2，-2）
)=1时,(x
4
y ) max
2 5
当sin(
)=-1时,(x
4
y ) max
2 5
yP
O
Ax
解：z=x y, z的几何意义为直线y x z在y轴上的截距；
P(x,y)是圆上的点直线与圆有公共点
圆心（3,2）到直线的距离d r
d= | 3 2 z | 1 2
zmin 5 2, zmax 5 2,
x
y
x1 y1
a b
(a,b)
r P1(x1, y1)
又
x1 r cosθ
y1
r
sinθ
所以
x
y
a b
r r
cos sin
(为参数）
例1、已知圆的方程为x2 y2 2x 6y 9 0, 将它化为参数方程.
∴参数方程为 练习：
x 1 cos y 3 sin
(θ为参数)
1.填空：已知圆O的参数方程是
解：x2 y2 6x 4 y 12 0化为标准方程为
（ x 3）2 +(y 2)2 1
P(
x,
y）是圆上一动点设
x
y
3 cos 2 sin
( 为参数）
x y (3 cos ) (2 sin ) sin cos 5
2 sin( ) 5 4
当sin(
圆的参数方程及其应用
目标引领：
本节教学目标
（1）掌握圆的参数方程；
（2）理解圆参数方程中参数的几何意义；
（3）应用圆的参数方程解决与圆有关的最值问题
探究一 圆的参数方程
阅读教材P23页 （1）试推导以（0,0）为圆心， r为半径 的圆x2 y2 r2的参数方程
（2）指出参数的几何意义。
求参数方程的步骤: (1)建立直角坐标系, 设曲线上任一点P坐标(x,y) (2)选取适当的参数 (3)建立点P坐标与参数的函数式