2010-2011第二学期高一数学答案A卷

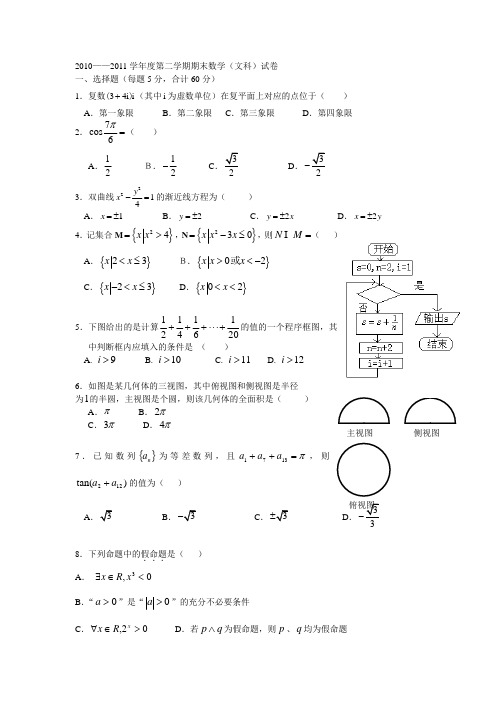
主视图侧视图2010——2011学年度第二学期期末数学（文科）试卷 一、选择题（每题5分，合计60分）1．复数34i i +()（其中i 为虚数单位）在复平面上对应的点位于（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限2．7cos6π=（ ）A ．12Ｂ．12-C ．2D ．2-3．双曲线2214yx -=的渐近线方程为（ ）A ．1x =±B ．2y =±C ．2y x =±D ．2x y =±4．记集合M {}24x x =>，N {}230x x x =-≤，则=M N （ ） A ．{}23x x <≤ Ｂ．{}02x x x ><-或 C ．{}23x x -<≤ D ．{}02x x <<5．下图给出的是计算201614121+⋅⋅⋅+++的值的一个程序框图，其中判断框内应填入的条件是 （ ）A. 9i >B. 10i >C. 11i >D. 12i >6．如图是某几何体的三视图，其中俯视图和侧视图是半径 为1的半圆，主视图是个圆，则该几何体的全面积是（ ） A ．π B ．π2 C ．π3 D ．π47．已知数列{}n a 为等差数列，且π=++1371a a a ，则)t a n (122a a +的值为（ ）A ．B ．C ．D ．3-8．下列命题中的假命题．．．是（ ） A ． 0,3<∈∃x R xB ．“0>a ”是“0>a ”的充分不必要条件C ．02,>∈∀x R xD ．若q p ∧为假命题，则p 、q 均为假命题0.00040.00030.00020.00019．已知两个不同的平面α，β和两条不重合的直线m ，n ，在下列四个命题中错误．．的是 （ ）A ．若m ∥α，n =βα ，则m ∥n Ｂ．若m ⊥α，m ⊥β，则α∥β C ．若m ∥n ，m ⊥α ，则n ⊥α D ．若m ⊥α，m ∥n ，β⊂n ，则α⊥β10．若方程()20f x -=在(,0)-∞内有解，则()y f x =的图象是（ ）11．在区间()0,1内任取两个实数，则这两个实数的和大于13的概率为A ．1718B ．79C ．29D ．11812．对任意实数,x y ，定义运算x y ax by cxy *=++，其中,,a b c 是常数，等式右边的运算是通常的加法和乘法运算。

太原市2010-2011学年高一年级第三学段测评（必修3）数学试卷一、选择题：（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合1．二进制数110011(2)在十进制数中是(A) 32 (B) 48 (C) 50 (D) 512．算法有三种基本逻辑结构，任何一个算法都离不开的基本结构是(A)顺序结构 (B)条件结构 (C)循环结构 (D)三种都有3．用简单随机抽样方法从含有64个个体的总体中，抽取一个容量为m 的样本，已知某一个体a 在整个抽样过程中被抽到的概率是81，则m = (A)2 (B)4 (C)8 (D) 164．现有60个机器零件，编号从1到60，若从中抽取6个进行检验，用系统抽样的方法确定所抽的编号可以是(A)3,13, 23, 33, 43, 53 (B)2,14, 26. 38, 40. 52 (C)5,8,31, 36, 48, 54 (D)5,10, 15, 20, 25, 30 5．在右图所示的“茎叶图”表示的数据中，众数和中位数分别是 (A) 23与26 (B) 31与26 (C) 24与30 (D) 26与306．在右图所示的程序中，执行循环的次数是 (A) 998 (B) 999 (C) 1000 (D) 10017．袋中装有除颜色外完全相同的2个红球和2个白球，若从袋内任取2个球，则事件A ：“至少有1个白球”的对立事件是(A)恰有1个白球(B)至少有1个红球 (C)都是红球 (D)都是白球 8．阅读右图的程序框图，若输出的S=57，则在判断框内应填入 (A)k >4？ (B)k >5？ (C)k >6？ (D)k >7？9．用秦九韶算法求多项式3.02345)(2345+++++=x x x x x x f 在x=5的值时，所做加法和乘法的次数和等于 (A) 11 (B) 10 (C) 12 (D) 1310．已知某运动员每次投篮的命中率约为40%．现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率，先由计算器产生0到9之间取整数值的随机数，指定1，2，3，4表示命中，5，6，7，8，9，0表示不命中，再以每三个隧机数为一组代表三次投篮的结果，经随机模 拟产生了如下20组随机数： 907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989 据此估计，该运动员三次投篮恰有两次命中的概率为 (A) 0.25 (B) 0.35 (C) 0.2011．某同学在5次上学途中所花的时间（单位：分钟）分别为x ,10,y ,11,9已知这组数据的平均数为10，方差为2，则y x -的值为（A ）1 （B ）2 （C ）3 （D ）412．函数2)(2--=x x x f ，]5,5[-∈x ，在定义域内随机取一个数0x ，使0)(0≤x f 的概率是（A ）101 （B ）52 （C ）103 （D ）54 二、填空题（本大题共4小题，每小题3分，共12分，请将答案填在题中横线上）13．某校高中生共有900人，其中高一年级300人，高二年级200人，高三年级400人，现采用分层抽样法抽取一个容量为45的样本，那么从高一年级的人数为 人14．下图是200辆汽车通过某一段公路时，时速的频率分布直方图，则时速在[50，70）的汽车大约有 （14题）15．阅读15题的程序框图，若输入的n 的值是10，则输出的变量S 与T 的和等于16．有4位顾客将各自的帽子随意放在衣帽架上，然后每人取走一顶帽子，则4人拿到都是自己帽子的概率为三、解答题（本大题共5小题，共52分，解答应写出必要的文字说明，过程或演算步骤） 17．（本小题满分10分）用辗转相除法或者更相减损术求98与63的最大公约数80 40 时速50 60 70 0组距频率18．（本小题满分10分）一个包装箱内有6件产品，其中4件正品，2件次品，随机抽出两件产品 （1）求恰好有一件次品的概率 （2）求都是正品的概率19．（本小题满分10分）某连锁经营公司所属的5个零售店某月的销售额和利润额的有关数据如下表：商店名称 A B C D E 销售额x (千万元) 3 5 6 7 9 利润额y (百万元)23345（1）请画出上表数据的散点图；（2）请根据上表提供的数据，用最小二乘法求出y 关于x 的线性回归方程；（3）当销售额为4千万元时，估计利润额的大小。

2010-2011学年度第二学期期末教学质量检查高一数学（A ）答案二、填空题（本大题共4小题，每小题5分，共20分．） 11． 60 12. 552-13. 4.27.3ˆ-=x y14． ①④三、解答题（本大题共6小题，共80分..） 15. （本小题满分12分）解：（1） 150cos 210tan)30cos (30tan-= ………………2分)23(33-⨯=………………3分21-=． ………………4分（2）①∵2tan =α，∴tan tan 4tan()41tan tan 4παπαπα++=-⋅ ………………6分tan 12131tan 12αα++===---． ………………8分②22222211sin sin 2sin 2sin cos 22cos sin cos sin ααααααααα++⨯=-- sin (sin cos )(cos sin )(cos sin )ααααααα+=-+sin cos sin ααα=- ………………10分tan 221tan 12αα===---． ………………12分16. （本小题满分12分） 解：（1）∵a AB =，b AD =， ∴BD AD AB b a =-=-． ……………2分又 ∵M为BO 中点， ∴11()44B M B D b a ==-， ……………4分 ∴131()444A M AB B M a b a a b =+=+-=+． ………………6分（2）∵2()AB BD a b a a b a ⋅=⋅-=⋅- ………………8分B DO C M又 ∵1A B =，2A D =，060=∠BAD ，∴12cos 601a b ⋅=⨯⨯︒= ，1||22==a a ． ………………10分∴2110AB BD a b a ⋅=⋅-=-= ． ………………11分即AB BD ⊥． ………………12分17.（本小题满分14分）解：（1）小张5次的平均成绩89818280984308655x ++++===； ………………2分 小李5次的平均成绩86543058687908483==++++=x . ………………4分（2）将小张这5次的成绩输入，按程序框图进行运算，输出的S 是小张的数学成绩的方差，222221[(8986)(8186)(8286)(8086)(9886)]5S =-+-+-+-+- ………………5分 11(9251636144)2304655=++++=⨯=.即此时输出的S 是46. ………………7分将小李这5次的成绩输入，按程序框图进行运算，输出的S 是小李的数学成绩的方差，222221[(8386)(8486)(9086)(8786)(8686)]5S =-+-+-+-+- ………………8分 1(941610)65=++++=.即此时输出的S 是6. ………………10分 （3）由（1）、（2）的结果可知，小张和小李的数学平均成绩相等， ………………12分但由于小李的数学成绩的方差比小张的小，所以小李的数学成绩较小张的稳定. …………14分 18．（本小题满分14分） 解：（1）依题意知，圆C 的圆心为(0,0)C ，半径为12r =， ………………1分∴圆心C 到直线l 的距离2131k d k =+. ………………2分∵圆C 和直线l 有两个不同的公共点A 、B ，∴r d <，即213121k k <+， ………………4分∴ 225144k <， 解得： 121255k -<<， ………………6分所以实数k 的取值范围为1212(,)55-. ………………7分 (2) 直线l 被圆C 截得的弦长125144211691222||2222222+-=+-=-=kk kk dr AB ……………8分由r AB >||得，12125144222>+-kk ， ………………9分解得210861k <，即1081086161k << ………………10分又∵Z k ∈，且1081261<<，∴1,0,1k =-. ………………11分设“直线l 被圆C 截得的弦长大于半径”为事件A ，则事件A 包含的基本事件有3个，即k 取1,0,1-. ………………12分又由（1）知121255k -<<，且Z k ∈，∴2,1,0,1,2k =--，即总事件Ω包含的基本事件共有5个，即k 取2,1,0,1,2--. ………………13分 所以，直线l 被圆C 截得的弦长大于半径的概率为53)(=A P . ………………14分19.（本小题满分14分）解: (1) 由2T πω=得: 4ω=. ………………1分所以()sin(4)4f x x π=+. ………………2分(2) ()sin[4()]sin[(4)]cos(4)884424y f x x x x ππππππ=+=++=++=+………………3分将函数c o s (2)3y x π=+的图像上所有点的纵坐标不变,横坐标缩短到原来的12倍，可得函数c o s (4)3y x π=+的图像； ………………5分再将函数cos(4)3y x π=+的图像向右平移48π个单位，可得函数()8y f x π=+的图像. …… 7分(3) 由308x π<≤得74444x πππ<+≤. ………………8分 设44t x π=+,有7()sin ,(,]44f x t t ππ=∈,其图象如下:………………9分因为44t x π=+，所以要使得方程m x f =)(（830π≤<x ）有两个不同的实数根，即m t =sin ])47,4((ππ∈t 有两个不同的实数根，也即曲线t y sin =与m y =两个不同的交点. ………………10分 因此，由上图可知，1-122m m <<<≤-或时，曲线t y sin =与m y =两个不同的交点，即方程m t =sin ])47,4((ππ∈t 有两个不同的实数根. ………………11分当12m <<时，1222t t ππ+=⨯=，即124444x x πππ+++=，所以128x x π+=； ………………12分当-12m <≤-时，123232t t ππ+=⨯=，即1244344x x πππ+++=，所以1258x x π+=. ………………13分所以，实数m的取值范围是(-1,22⋃-.12m <<时，这两个根的和为8π；当-12m <≤-时，这两个根的和为58π. ………………14分20．（本小题满分14分）解：（1）由0=⋅OB OA ，得22300x y ⨯+⨯=，解得20x =. …………………1分把20x =代入圆方程得到2y =……………2分 所以B 的坐标为)3,0(或)3,0(-. ……………3分 （2）如图，设圆心2C 的坐标为),(00y x ，由AO B ∆是直角三角形可得：|,|21||2AB OC =即221221220)()(21y y x x y x -+-=+，亦即])()[(412212212020y y x x y x -+-=+， …………………5分展开得：)(2)(42121222122212020y y x x y y x x y x +-+++=+. …………………6分 由0=⋅OB OA 得到02121=+y y x x ， …………………7分 所以有222122212020)(4y y x x y x +++=+ ①又B A ,是圆1C 上的两动点，所以有⎪⎩⎪⎨⎧=+-=+-4)1(4)1(22222121y x y x ； 两式相加得到：8)(222122212221=+-++++x x y y x x ， …………………8分 又因为0212x x x =+，代入上式得到02221222146x y y x x +=+++ ② ……………9分由①与②式得到圆心2C 的方程为：02302020=--+x y x ，所以，圆心2C 的轨迹方程为02322=--+x y x . …………………10分（3）由圆心2C 的方程02302020=--+x y x ，得0x 的取值范围是]2127,2127[++-，………11分设圆2C 的半径为R .因为0OA OB ⋅=，即AOB ∆为以AB 边为斜边的直角三角形，所以圆2C 的半径为20202||y x OCR +==，即=+=20202y x R 230+x ， …………………12分所以=max 2)(R （max 0)23+x =227+， …………………13分所以圆2C 的面积的最大值是π)227(+. …………………14分。

2010—2011学年度第二学期期末考试高一数学参考答案及评分标准命题人：齐力一、选择题：DBACB BCDCA CA 二、填空题：（13）85，1.6; (14)221- (15) 2; (16) 12三、解答题：（本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤；字迹工整、清楚。

） （17）(本小题满分1０分)已知△ABC 三个顶点的坐标分别为(1,0)A -，(4,0)B ，(0,)C c ．（I ）若AC BC ⊥，求c 的值；（II ）若3c =，求ACB ∠的余弦值. 解：（I ）(1,)AC c =，(4,)BC c =-，由AC BC ⊥，得0AC BC ⋅=，所以，240c -=，所以，2c =±. …………5分 （II ）当3c =时，10CA =5CB =，(1,3)CA =--，(4,3)CB =- 因此，10cos CA CB ACB CA CB⋅∠==. ……………………………1０分 （18）(本小题满分12分)已知函数()sin f x x ω=（0ω>）.(I ) 当1ω=时，函数()y f x =经过怎样的变换得到函数sin 26y x π⎛⎫=+ ⎪⎝⎭，请写出变化过程；(II )若()y f x =图象过2(,0)3π点，且在区间(0,)3π上是增函数，求ω的值. 解：（I ）方法1 保持每点纵坐标不变，横坐标缩短为原来的一半，再向左平移12π个单位。

方法2 向左平移6π个单位，再保持每点纵坐标不变，横坐标缩短为原来的一半。

………………………4分（II ）由()y f x =的图象过2(,0)3π点，得2sin 03πω=，所以23k πωπ=，k ∈Z .即32k ω=，k ∈Z .又0ω>，所以*k ∈N . 当1k =时，32ω=，3()sin 2f x x =，其周期为43π，此时()f x 在0,3π⎛⎫⎪⎝⎭上是增函数； 当k ≥2时，ω≥3，()sin f x x ω=的周期为2πω≤2433ππ<， 此时()f x 在0,3π⎛⎫⎪⎝⎭上不是增函数. 所以，32ω=. ……………………12分 （19）（本小题满分12分）某工厂有工人1000名， 其中250名工人参加过短期培训（称为A 类工人），另外750名工人参加过长期培训(称为B 类工人），现用分层抽样方法（按A 类、B 类分二层）从该工厂的工人中共抽查100名工人，调查他们的生产能力（此处生产能力指一天加工的零件数）.从A 类工人中的抽查结果和从B 类工人中的抽查结果分别如表1和表2.（I ）先确定x ，y ，再在下图中完成表1和表2的频率分布直方图.就生产能力而言，A 类工人中个体间的差异程度与B 类工人中个体间的差异程度哪个更小？（不用计算，可通过观察直方图直接回答结论）（II ）分别估计A 类工人和B 类工人生产能力的平均数，并估计该工厂工人的生产能力的平均数.（同一组中的数据用该组区间的中点值作代表） 解：（I ）由题意知A 类工人中应抽查25名，B 类工人中应抽查75名.故485325x ++++=，得5x =， …………………………………………1分 6361875y +++=，得15y = . …………………………………………2分 频率分布直方图如下……………5分从直方图可以判断：B 类工人中个体间的差异程度更小 . ……………7分 （II ）485531051151251351451232525252525A x =⨯+⨯+⨯+⨯+⨯=， 6153618115125135145133.875757575B x =⨯+⨯+⨯+⨯=，2575123133.8131.1100100x =⨯+⨯= ……………………………………11分A 类工人生产能力的平均数，B 类工人生产能力的平均数以及全工厂工人生产能力的平均数的估计值分别为123，133.8和131.1 . …………………………………12分（20）(本小题满分12分)某商场实行优惠措施，若购物金额x 在800元以上(含800元)打8折；若购物金额在500元以上(含500元)打9折，否则不打折．请设计一个算法程序框图，要求输入购物金额x ，能输出实际交款额，并写出程序．【解析】 程序框图程序：…………………12分（21）(本小题满分12分)甲、乙二人用4张扑克牌(分别是红桃2、红桃3、红桃4、方片4)玩游戏，他们将扑克牌洗匀后，背面朝上放在桌面上，甲先抽，乙后抽，抽出的牌不放回，各抽一张．（Ⅰ）设(i，j)分别表示甲、乙抽到的牌的牌面数字，写出甲、乙二人抽到的牌的所有情况；（Ⅱ）若甲抽到红桃3，则乙抽到的牌的牌面数字比3大的概率是多少？（Ⅲ）甲、乙约定：若甲抽到的牌的牌面数字比乙大，则甲胜，反之，则乙胜．你认为此游戏是否公平，说明你的理由．【解析】 (1)甲、乙二人抽到的牌的所有情况(方片4用4’表示，其他用相应的数字表示)为(2,3)，(2,4)，(2,4’)，(3,2)，(3,4)，(3,4’)，(4,2)，(4,3)，(4,4’)，(4’，2)，(4’，3)，(4’4)，共12种不同情况．(2)甲抽到红桃3，乙抽到的牌的牌的牌面数字只能是2,4,4’，因此乙抽到的牌的牌面数字比3大的概率为23.(3)甲抽到的牌的牌面数字比乙大的情况有(3,2)，(4,2)，(4,3)，(4’，2)，(4’，3)，共5种，故甲胜的概率P 1＝512，同理乙胜的概率P 2＝512.因为P 1＝P 2，所以此游戏公平．（22）(本小题满分12分)已知向量],2,0[),2sin ,2(cos ),23sin ,23(cosπ∈-==x x x x x 且 （Ⅰ）求a b ⋅与a b +；（Ⅱ）求函数()2f x a b a b =⋅-+的最小值； （Ⅲ）若()f x a b a b λ=⋅-+的最小值是23-，求实数λ的值. 解：xx x xx x x xx x x b a x xx x x cos 2cos 22cos 22)2sin 23(sin )2cos 23(cos )2sin 23sin ,2cos 23(cos 2cos 2sin 23sin 2cos 23cos)1(22==+=-++=+-+=+=-=⋅ 3)1(cos 21cos 4cos 2cos 42cos )()2(22--=--=-=+-⋅=x x x x x x f 3)(,1cos 0]1,0[cos ]2,0[min -===∴∈∴∈x f x x x x 时，当π.11232121)(201)(0(45232121122)(221)2(cos 21cos 2cos 2cos 22cos )()3(22min min min 222=±=-=----=<<-=≤=-=--=--=≥---=--=-=λλλλλλλλλλλλλλλ综上，，得由时，当（舍去）时，当舍去），得由时，当x f x f x f x x x x x x f。

第5题7 8 9 9 8 2 79 11 2 5 6 甲 乙安徽省马鞍山市2010-2011学年度高一第二学期期末素质测试数学必修③试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，满分l00分.考生注意事项：1.答题前，务必在试题卷、答题卡规定的地方填写自己的姓名、座位号，并认真核对答题卡上所粘贴的条形码中姓名、座位号与本人姓名、座位号是否一致.2.答第Ⅰ卷时，每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.3.答第Ⅱ卷时，必须使用0.5毫米的黑色墨水签字笔在答题卡上．．．．书写，要求字体工整、笔迹清晰.作图题可先用铅笔在答题卡．．．规定的位置绘出，确认后再用0.5毫米的黑色墨水签字笔描清楚.必须在题号所指示的答题区域作答，超出答题区域书写的答案无效．．．．．．．．．．．．．，在试题卷．．．．、草．稿纸上答题无效．．．．．．．. 4.考试结束，务必将试题卷和答题卡一并上交.第Ⅰ卷（选择题，共36分）一、选择题（本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的，请在答题卡相应位置将正确结论的代号用2B 铅笔涂黑.）1．算法的三种基本结构是A. 顺序结构、模块结构、条件结构B. 顺序结构、循环结构、模块结构C. 顺序结构、条件结构、循环结构D. 模块结构、条件结构、循环结构2．从容量为160的总体中用随机数表法抽取一个容量为10的样本.下面对总体的编号正确的是A. 1,2,…,160B. 0,1,…,159C. 00,01,…,159 D. 000,001,…,1593．运行右面的算法程序输出的结果应是A.2B.4C.8D.16 4．已知，之间的一组数据： 则y 与x 的线性回归方程a bx y +=ˆ必过点A ．(20,16)B ．(16,20)C ．(4,5)D ．(5,4)5．将甲、乙两名同学5次物理测验的成绩用茎叶图表示如图，若甲、乙两人成绩的中位数分别为乙甲、x x ，则下列说法正确的是 A ．乙甲x x <；乙比甲成绩稳定B ．乙甲x x >；甲比乙成绩稳定C ．乙甲x x >；乙比甲成绩稳定D ．乙甲x x <；甲比乙成绩稳定6．某人在打靶练习中，连续射击2次，则事件“至少有1次中靶”的互斥事件是A ．至多中靶一次B ．2次都不中靶C ．2次都中靶D ．只有一次中靶x=4 y=2x=y PRINT x^y END 第3题7．有五组变量：①汽车的重量和汽车每消耗1升汽油所行驶的平均路程；②平均日学习时间和平均学习成绩；③某人每日吸烟量和其身体健康情况；④正方形的边长和面积；⑤汽车的重量和百公里耗油量；其中两个变量成正相关关系的是A ．①③B ．②④C ．②⑤D ．④⑤ 8．若将[]1,0内的随机数a 均匀地转化到[]6,2-内的随机数b ，则可实施的变换为A ．6*=a bB ．28-*=a bC ．8*=a bD ．28+*=a b9．若()1033=a ，()652=b ，()211111=c ，则三个数的大小关系是A ．a b c >>B ． a c b >>C ．b a c >>D ．c b a >>10．一枚质地均匀的硬币，如果连续抛掷1000次，那么第999次出现正面朝上的概率是A ．9991B ．10001 C ．1000999 D ．21 11．甲、乙两人做“石头、剪刀、布”游戏，两人平局的概率为 A ．91 B ．92 C ．31 D ．94 12．将参加夏令营的600名学生编号为：001,002，…，600．采用系统抽样方法抽取一个容量为50的样本，且在第一段中随机抽得的号码是003．这600名学生分别住在三个营区，从001到300在第一营区，从301到495在第二营区，从496到600在第三营区．则三个营区被抽到的人数分别为A ．25，17，8B ．25，16，9C ．26，16，8D ．24，17，9第Ⅱ卷（非选择题，共64分）二、填空题（本大题共5个小题，每小题4分，共20分．请在答题卡上答题．）13．频率分布直方图中各小长方形的面积总和为____________．14．口袋内装有100个大小相同的红球、白球和黑球，其中有45个红球；从中摸出1个球，若摸出白球的概率为0.23，则摸出黑球的概率为____________．15. 经统计，某小店卖出的饮料杯数y 杯与当天气温x ℃的回归方程为767.147352.2ˆ+-=x y ．若天气预报说“明天气温为2℃”，则该小店明天大约可卖出饮料 杯．16．下面程序表示的函数解析式是 ．第17题第16题17．如上图，四边形ABCD 为矩形，3 AB ，BC=1，以A 为圆心，1为半径画圆，交线段AB 于E ，在圆弧DE 上任取一点P ，则直线AP 与线段BC 有公共点的概率为____________．三、解答题（本大题共5个小题，满分44分.解答应写出必要的文字说明、证明过程或演算步骤. 请在答题卡上规定区域内答题．）18．（本小题满分8分）某网站欲调查网民对当前网页的满意程度，在登录的所有网民中，收回有效帖子共50000份，其中持各种态度的份数如下表所示．为了调查网民的具体想法和意见，以便决定如何更改才能使网页更完美，打算从中抽选500份，为使样本更具有代表性，每类帖子中各应抽选出多少份？19．（本小题满分8分）一个口袋内装有大小相同的5 个球，其中3个白球分别记为A 1、A 2、A 3；2个黑球分别记为B 1、B 2，从中一次摸出2个球．（Ⅰ）写出所有的基本事件；（Ⅱ）求摸出2球均为白球的概率．20．（本小题满分8分）一个容量为M 的样本数据，其频率分布表如下．（Ⅰ）表中a= ，b = ；（Ⅱ）画出频率分布直方图；（Ⅲ）用频率分布直方图，求出总体的众数及平均数的估计值．频率分布表 频率分布直方图21．（本小题满分10分）执行如图所示的程序框图．（Ⅰ）当输入n=5时，写出输出的a 的值； （Ⅱ）当输入n=100时，写出输出的T 的值．22．（本小题满分10分）如图，在长为52宽为42的大矩形内有一个边长为18的小正方形，现向大矩形内随机投掷一枚半径为1的圆片，求： （Ⅰ）圆片落在大矩形内部时，其圆心形成的图形面积；（Ⅱ）圆片与小正方形及内部有公共点的概率．马鞍山市2010―2011学年度第二学期期末素质测试数学必修③参考解答A. 顺序结构、模块结构、条件结构B. 顺序结构、循环结构、模块结构A B C D EF G H第5题7 8 9 9 8 2 7 9 1 1 2 5 6 甲 乙C. 顺序结构、条件结构、循环结构D. 模块结构、条件结构、循环结构 本题考查：算法的三种基本逻辑结构名称，简单题．选C ．1.从容量为160的总体中用随机数表法抽取一个容量为10的样本.下面对总体的编号正确的是 A. 1,2,…,160 B. 0,1,…,159 C . 00,01,…,159 D. 000,001,…,159本题考查：系统抽样对总体的编号，简单题．选D ．2.运行右面的算法程序输出的结果应是( ) A.2 B.4 C.8 D.16本题考查：识别程序的运算意义，简单题．选B ． 3.已知，之间的一组数据： A ．(20,16) B ．(16,20) C ．(4,5) D ．(5,4)本题考查：回归直线的性质，简单题．选D ．4.将甲、乙两名同学5次物理测验的成绩用茎叶图表示如图，若甲、乙两人成绩的中位数分别为乙甲、x x ，则下列说法正确的是 A ．乙甲x x <；乙比甲成绩稳定B ．乙甲x x >；甲比乙成绩稳定C ．乙甲x x >；乙比甲成绩稳定D ．乙甲x x <；甲比乙成绩稳定本题考查：茎叶图及其应用，简单题．选A ． 5.某人在打靶练习中，连续射击2次，则事件“至少有1次中靶”的互斥事件是 ( )A ．至多中靶一次B ．2次都不中靶C ．2次都中靶D ．只有一次中靶 本题考查：事件与事件之间的关系，简单题．选B ．6.有五组变量：①汽车的重量和汽车每消耗1升汽油所行驶的平均路程；②平均日学习时间和平均学习成绩；③某人每日吸烟量和其身体健康情况；④正方形的边长和面积；⑤汽车的重量和百公里耗油量；其中两个变量成正相关关系的是 ( )A ．①③B ．②④C ．②⑤D ．④⑤本题考查：相关关系的正负性，简单题．选C ．8．若将[]1,0内的随机数a 均匀地转化到[]6,2-内的随机数b ，则可实施的变换为 ( )A ．6*=a bB ．28-*=a bC ．8*=a bD ．28+*=a b本题考查：均匀随机数的变换，中等题．选B ．9．若()1033=a ，()652=b ，()211111=c ，则三个数的大小关系是( )A ．a b c >>B ． a c b >>C ．b a c >>D ．c b a >>本题考查：数的进制及其大小比较，中等题．选D ．10．一枚质地均匀的硬币，如果连续抛掷1000次，那么第999次出现正面朝上的概率是A ．9991B ．10001C ．1000999D ．21 本题考查：古典概型中的等可能性，中等题．选D ． 11．甲、乙两人做“石头、剪刀、布”游戏，两人平局的概率为( ) x=4 y=2 x=y PRINT x^yEND 第3题第16题 A ．91 B ．92 C ．31D ．94 本题考查：古典概型的概率计算，中等题．选C ．12．将参加夏令营的600名学生编号为：001,002，…，600.采用系统抽样方法抽取一个容量为50的样本，且在第一段中随机抽得的号码是003．这600名学生分别住在三个营区，从001到300在第一营区，从301到495在第二营区，从496到600在第三营区.则三个营区被抽到的人数分别为( )A ．25，17，8B ．25，16，9C ．26，16，8D ．24，17，9本题考查：系统抽样与数列综合，较难题．选A ．二、填空题（本大题共5个小题，每小题4分，共20分．请在答题卡上答题．）13．频率分布直方图中各小长方形的面积总和为____________．本题考查：频率分布直方图的意义，简单题．【答案】114．口袋内装有100个大小相同的红球、白球和黑球，其中有45个红球，从中摸出1个球，若摸出白球的概率为0.23，则摸出黑球的概率为____________．本题考查：互斥事件的概率加法公式，简单题．【答案】0.32．15. 经统计，某小店卖出的饮料杯数y 杯与当天气温x ℃的回归方程为767.147352.2ˆ+-=x y ．若天气预报说“明天气温为2℃”，则该小店明天大约可卖出17．如上图，四边形ABCD 为矩形，3=AB ，BC=1，以A 为圆心，1为半径画圆，交线段AB 于E ，在圆弧DE 上任取一点P ，则直线AP 与线段BC 有公共点的概率为骤. 请在答题卡上规定区域内答题．）18．（本小题满分8分）某网站欲调查网民对当前网页的满意程度，在登录的所有网民中， 500份，为使样本更具有代表性，每类帖子中各应抽选出多少份？【解】首先确定抽取比例，然后再根据各层份数确定各层要抽取的份数.∵50000500=1001，--------------------------------------------------------------------------------2分∴10010800=108，10012400=124，10015600=156，10011200=112.--------------------------------4分 故四种态度应分别抽取108、124、156、112份进行调查.--------------------------------8分 本题考查：分层抽样方法，简单题．19．（本小题满分8分）一个口袋内装有大小相同的5 个球，其中3个白球分别记为：A 1、A 2、A 3；2个黑球分别记为B 1、B 2，从中一次摸出2个球.（Ⅰ）写出所有的基本事件；（Ⅱ）求摸出2球均为白球的概率．【解】（Ⅰ）从中一次摸出2个球,有如下基本事件:(A 1,A 2),(A 1,A 3), (A 1,B 1),(A 1,B 2),(A 2,A 3), (A 2,B 1),(A 2,B 2),(A 3,B 1),(A 3,B 2),(B 1,B 2),共有10个基本事件. ---------------------------------------------------------------------4分 （Ⅱ）从袋中的5个球中任取2个,所取的2球均为白球的方法有:(A 1,A 2),(A 1,A 3), (A 2,A 3),共3种, 故所求事件的概率P =103．--------------------8分 本题考查：古典概型中基本事件及其概率的求法，简单题．20．（本小题满分8分）一个容量为M 的样本数据，其频率分布表如下.（Ⅰ）表中a= ，b = ； （Ⅱ）画出频率分布直方图； （Ⅲ）用频率分布直方图，求总体的众数及平均数的估计值． 频率分布表频率分布直方图【解】（Ⅰ）a=5，b =0.25--------------------------2分 （Ⅱ）频率分布直方图，如图右所示：-----------4分 （Ⅲ）众数为：4525040=+------------------------6分平均数：411.0270602.02605025.0250402.02403015.0230201.022010=⨯++⨯++⨯++⨯++⨯++⨯+ -------------------------------8分本题考查：利用样本的频率分布直方图估计总体的特征数，中等题．21．（本小题满分10分）执行如图所示的程序框图.（Ⅰ）当输入n=5时，写出输出的a 的值；（Ⅱ）当输入n=100时，写出输出的T 的值．【解】（Ⅰ）输出的a 分别是：1，2，3，4，5；-------------------5分（Ⅱ）1003211321121111+++++++++++= T ------7分 ⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+=10111001241312312121 10120010112121=⎪⎭⎫ ⎝⎛-⨯+=--------------------------------------10分 故输出的T 的值为101200． 本题考查：程序框图与数列求和，较难题．22．（本小题满分10分）如图，在长为52宽为42的大矩形内有一个边长为18的小正方形，现向大矩形内随机投掷一枚半径为1的圆片，求： （Ⅰ）圆片落在大矩形内部时，其圆心形成的图形面积；（Ⅱ）圆片与小正方形及内部有公共点的概率. 【解】（Ⅰ）当小圆片落在大矩形内部时，其圆心形成的图形为一个长为50，宽为40的矩形，故其面积为：20004050=⨯=S ；-------------------------------------------------4分（Ⅱ）当小圆片与小正方形及内部有公共点时，其圆心形成的图形面积为：ππ+=⨯⨯+⨯⨯-+⨯+='3961414114)218()218(2S ，-------------------8分 故小圆片与小正方形及内部有公共点的概率为2000396π+=P ．------------------10分 本题考查：几何概型的应用，较难题．A B C D E F G H。

2010-2011第二学期第一次月考-高一数学试题DC. 5D. 2 5. 在等差数列{}nb 中，若284,10bb ==，则该等差数列的公差d = ( ) A. 1 B. 2C. 3D. 4 6. 已知数列{}na 是等差数列，若468212aa a ++=，那么111a a +=( )A. 6B. 3C. 33D. 66 7. 设nS 为等差数列{}na 的前n 项和，若20112011S=，那么1006a = ( )A. 1006B. 1005C. 1D. 2 8. 若等差数列{}na 的通项公式,n a kn b n N +=+∈，. 那么，下列说法错误．．的是 ( ) A. 0k <，{}na 是递减数列 B. 不论k 是何值，na 都是n 的一次函数C.k >，{}na 是递增数列 D. 只有k ≠时，na 才是n 的一次函数9. 在数学中，任意相邻的两个正整数通常用,1,(1)n n n +≥或者1,,(1)n n n ->表示，所以在数列{}na 中，1,,(1)n n a a n +≥或者1,,(1)nn a an ->表示的是{}na 中任意相邻的两项.若在某数列{}nb 中，满足112,2,(1)nn bb n b -==>，则{}nb 的通项公式nb = ( )A.2nB.22n -C.12n -D. 2n10. 设等差数列{}na 的前n 项和为nS ，且102010,30SS ==，那么30S=( )A. 50B. 80C. 60D.4511. 在各项均为负数的等比数列{}na 中，若200920132011201220102014216a a a a a a ++=，那么20112012a a +=( )A. 4B.4±C.4-D. 8 12. 设数列{}na 的前n 项和1,2nSn N n+=∈，则{}na 的通项公式为 ( )A.1(1)n a n n =--B.12(1)nan n =--C.112112(1)n n a n n n ⎧=⎪⎪=⎨⎪->-⎪⎩D.11211(1)n n a n n n ⎧=⎪⎪=⎨⎪->-⎪⎩第Ⅱ卷非选择题(共90分)二、填空题(本大题共4小题，每小题5分，满分20分) 13. 在ABC中，若32sin b a B=，则角A=__________________.14. 记数列3，33，333，3333，的一个通项公式为nb ，则nb =__________________.15. 在等比数列{}n a 中，3711a a a =+，则公比4q =__________________.16. 在等差数列{}nb 中，我们知道：若1212,,,m m n n 都是正整数，且1212m mn n +=+，则1212m m n n bb b b +=+；实际上，在等差数列{}nb 中还有：若123123,,,,,m m m n n n 都是正整数，且123123m m m n n n ++=++则123123m m m n n n bb b b b b ++=++.由此可以得出：一般地，在等差数列{}nb 中,若1212,,,;,,,()s s m m m n n n s N +∈都是正整数,且1212s sm m m n n n +++=+++,则___________________________________________.三、解答题(本大题共6小题,共70分，解答应写出必要的文字说明、证明过程和演算步骤) 17. (本题满分l0分)在ABC中，角,,A B C 所对应的边分别为,,a b c ，且4cos ,2,35ABCA b S === (1).求c 与a (2).求cos C.18. (本题满分l2分)已知等差数列{}na 的前n 项和为n S ，且45104,aS S ==(1).求通项公式na (2).求nS 的最小值并说明理由.19. (本题满分l2分) 在等比数列{}na 中，163466,128a aa a +==(1).求通项公式na (2).求{}na 的前n 项和为nS .20. (本题满分l2分)设数列{}na 的通项公式1,n nanx n N -+=∈，求该数列的前n 项和为nS .21. (本题满分l2分) 在数列{}na 中，已知11a=，且121(1,)n n aa n n N ++=+≥∈(1).设1nn ba =+，求证：{}nb 是等比数列(2).求数列{}na 的通项公式(3).设数列{}na 的前n 项和为n S ，求nS .22. (本题满分l2分)在数列{}na 中，13a=，且12(1)1nn an n a n -+=>+，数列{}nb 满足11(1)nn n bn a a +=≥，设数列{}nb 的前n 项和为nT(1).求na (2).求nT(3).若实数a 于任意的n N +∈，有1na T >恒成立，求a 的取值范围.高一数学试题参考答案及评分参考一、选择题.共12小题，每小题5分，共60分 题号1 2 3 4 5 6 7 8 9 10 11 12 答案C AD A A A C B D C C C 二、填空题.共4小题，每小题5分，共20分13. 3π或23π(60或120) 14. 13n （10-1)(写成39n（10-1)也给全分)15.152-+ 16.1212s sm m m n n n b b b b b b +++=+++三、解答题.本题共6小题，满分70分，解答应写出必要的文字说明、证明过程和演算步骤 17. (本题满分10分)(本题主要考查三角形的面积公式和余弦定理，考查公式的基本运用和学生的计算能力) (1). 解：在ABC中，4cos 05A =>∴A为锐角 ……1分 ∴3sin 5A =……2分 又3ABCS= ∴1sin 32bc A = ∴5c = ……4分∵2222cos a b c bc A=+- ∴24425225135a =+-⨯⨯⨯=∴13a =……7分 (2). 解：∵2222cos c a b ab A=+- ∴251342132cos C=+-∴4138C -=∴2cos 131313C ==……10分18.(本题满分12分)(本题主要考查等差数列的通项公式，前n 项和公式及其最值，考查公式的基本运用及运用二次函数思想来求最值) (1) 解：设等差数列{}n a 的通项公式为1(1)n a a n dn N +=+-∈ ……1分则444510678910844400a a a S S a a a a a a ===⎧⎧⎧⇒⇒⎨⎨⎨=++++==⎩⎩⎩……3分111347701a d a a d d +==⎧⎧⇒⎨⎨+==-⎩⎩……5分1(1)7(1)8,n a a n d n n n N +=+-=--=-+∈……6分 (2)解法一：由(1)得221()151(15)222n n n a a n n S n n +-+===-- ……7分2115225()228n =--+……9分∵n N +∈ ∴7n = 或8n = (10)分nS的最大值为7828S S ==……12分 解法二：∵17010a d =>=-< ∴nS 必有最大值 ……7分令108078070n n a n n a n +≥-+≥⎧⎧⇒⇒≤≤⎨⎨≤-+≤⎩⎩……9分 ∵n N +∈ ∴7n = 或8n = (10)分nS的最大值为7828S S ==……12分19.(本题满分12分)(本题主要考查等比数列通项公式及通项性质的应用，考查学生的计算能力和分类意识) (1)解：∵{}n a 是等比数列 ∴设11()n n a a q n N -+=∈ ……1分则161634166666128128a a a a a a a a +=+=⎧⎧⇒⎨⎨==⎩⎩ 164a⇒=或12a = ……3分 (ⅰ)当164a =时，62a =……4分 ∴51122a q q =⇒=……5分 ∴1712,n n n a a q n N --+==∈……6分 (ⅱ)当12a=时，664a=∴ 51642a q q =⇒=……7分 ∴112,n n n a a q n N -+==∈……8分(2)解：(ⅰ)当12q =时1164[1()](1)21112n nn a q S q --==-- 1128(1)2n=-或者(71282n-－) ……10分(ⅱ)当2q =时1(1)2[12]112n n n a q S q --==--122n +=-……12分 20. (本题满分12分)(本题主要考查学生的细心分类能力，错位相减的求和思想以及严密的计算能力) 解：∵当1n =时 011a x =⨯ ∴11a=且0x ≠(无此步必须扣2分) ……2分∴(ⅰ)当1x =时n a nn N +=∈ ……3分12n nS a a a =+++(1)2n n +=……5分(ⅱ)当0x ≠且1x ≠时221123(1)n n n S x x n x nx --=+++-+ ――――①23123(1)n nn xS x x x n x nx -=+++-+ ――――② ……8分 ①-②得21(1)1n nnx S x xx nx --=++++-11n nx nx x-=--……11分 ∴21(1)1n nn x nx S x x-=--- (其他等价形式也给相同分值) ……12分 21. (本题满分12分)(本题主要考查数学中最重要的整体思维能力，等比数列的通项公式以及数列分组求和的方法) (1)证明：∵121n n a a +=+ ∴11222(1)n n n a a a ++=+=+ ……2分又∵1n n b a =+ ∴111n n b a ++=+ (3)分 ∴1122n n nnb b b b ++=⇒=……4分 又1112b a =+=∴{}nb 是以12b =为首项，2q =为公比的等比数列 ……6分 (2) 解：由(1)得112n nn b b q -==……7分 又1n n b a =+∴1221nn n n a a n N ++=⇒=-∈ ……9分(3)解：12nnS a a a =+++ 2(21)(21)(21)n =-+-++-2(222)n n=++-……11分12(12)2212n n n n +-=-=---……12分 22. (本题满分12分)(本题主要考查累乘法求数列通项，列项相消求数列前n 项以及不等式的简单知识) (1)解：∵12(1)1nn an n a n -+=>+∴121n n an an--+=2143aa=由叠乘法得12142(1)133n a n n n n a n n+++=⨯⨯=>+∴2(1)n a n n =+>……2分 当1n =时，1a 也满足na……3分 ∴2()n a n n N +=+∈……4分 (2)解：11111(2)(3)23n n n b a a n n n n +===-++++……6分 12nnT b b b =+++111111()()()344523n n =-+-++-++1133n N n +=-∈+……8分(3)解法一：由(2)得 11123nT≤<∴1312nT <≤……10分又任意的n N +∈ 有1na T >∴3a ≤……12分 解法二：由(2)得11333(3)n n T n n =-=++……9分∴ 13(3)93nn a Tn n+==+> (于任意的n N +∈都成立) ……11分∴a3……12分。

高一数学试题 第1页(共6页)2011年南山区高一下学期期末统一考试数 学2010.07.04本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分，考试时间120分钟.第Ⅰ卷(选择题共50分)注意事项：1、答卷前，考生首先检查答题卡是否整洁无缺损.之后务必用黑色签字笔在答题卡指定位置填写自己的学校、班级、姓名及座位号，在右上角的信息栏填写自己的考号，并用2B 铅笔填涂相应的信息点.2、选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，答案不能答在试卷上.不按要求填涂的，答案无效.3、非选择题必须用黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上，请注意每题答题空间，预先合理安排.如需改动，先划掉原来的答案，然后再写上新的答案.不准使用铅笔和涂改液.不按以上要求作答的答案无效.4、考生必须保持答题卡的整洁，不折叠，不破损.考试结束后，将答题卡交回.5、考试可以使用计器.一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确答案的编号用铅笔涂在．．．．．．．．．．．．．．答题卡上．．．．. 1、已知角α的终边上一点P(－3，4)，则cos α的值为A 、45 B 、35 C 、45- D 、35- 2、在四边形ABCD 中，若AB (61)= ，，BC (x y)= ，，CD (23)=--，，且BC//DA，则x+2y 的值为A 、0B 、2C 、0.5D 、－23、已知3tan()5α+β=，1tan()44πβ-=，那么tan()4πα+为 A 、1318 B 、1323 C 、318 D 、7234、若向量00a (cos23cos67)= ，，00b (cos53cos37)= ， ，则a b ⋅=高一数学试题 第2页(共6页)A 、32-B 、12C 、32D 、12-5、将两个数a=8，b=17交换，使a=17，b=8，下面语句正确一组是6、为了得到函数πy =sin(2x )3-的图象，只需将函数y=sin2x 的图象单A 、向右平移π3 B 、向左平移π3C 、向右平移π6D 、向左平移π67、右边框图的功能是计算220111 (222)+++ 的值，那么在①②两处应填入A 、n=0或和n ≤10B 、n=1或和n ≤10C 、n=0或和n<10D 、n=1或和n<108、若f(tanx)=sin2x ，则f(－1)的值是A 、1B 、－1C 、0.5D 、09、一块各面均涂有油漆的正方体被锯成1000个同样大小的小正方体，若将这些小正方体均匀地搅混在一起，则任意取出一个正方体其两面涂有油漆的概率是A 、12125 B 、325 C 、110D 、11210、定义在R 上的偶函数f(x)，满足f(x+2)= f(x)，且f(x)在[－3，－2]上是减函数，又α，β是锐角三角形的两个内角，则A 、f(sin α)<f(cos β)B 、f(cos α)<f(cos β)C 、f(sin α)>f(cos β)D 、f(sin α)<f(sin β) 一、选择题答案表：题 号 1 2 3 4 5 6 7 8 9 10 答 案a=b b=a A Bc=b b=aa=c C b=a a=b D a=c c=b b=a 否是 输出s结束开始第7题图 ②S=0， ①n=n=1 n1s s 2=+高一数学试题 第3页(共6页)第Ⅱ卷(非选择题共100分)二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题．．．．．．．卷上．．. 11、已知一扇形所在圆的半径为10cm ，扇形的周长是45cm ，那么这个扇形的圆心角为 ____ 弧度.12、如图是某单位200名职工的 年龄分布情况，现要从中抽取40 名职工样本，用系统抽样法，将全 体职工随机按1～200编号，并按编号顺序0平均分为40组(1～5号， 6～10号，…，196～200号)，若第五组抽出的号码为22，则第8组抽出的号码是_____，若用分层抽样方法， 则50岁以上年龄段在40名名样本中应抽取____人.13、不等式13tan x 0+≥的解集是 ________ . 14、下列结论中正确的是 ___________ .(写出所有正确结论的序号)①若a b 0⋅= ，则a 0= 或b 0=；②若|a b ||a ||b |⋅=⋅，则a //b ；③若a b 0⋅= ，则|a b ||a b |+=- ；④在△ABC 中，点M 满足MA MB MC 0++=，若存在实数λ使得 AB AC AM +=λ⋅成立，则λ=3.三、解答题：本大题共6小题，共80分，解答应写出文字说明或演算步骤.15、(本小题满分12分)设集合A={1，2，3，4，5}，集合B={1，2，3}，在集合A 中任取一个数为x ，在集合B 中任取一个数为y ，组成点(x ，y). (Ⅰ)写出所有的基本事件；(Ⅱ)求事件“x+y 为偶数”的概率； (Ⅲ) 求事件“xy 为奇数”的概率；50%20% 30%40岁以下50岁以上40～50岁第12题图高一数学试题 第4页(共6页)16、(本小题满分12分)已知A(5，0)，B(0，5)，C(cos α，sin α)，α∈(0，π)点O 是坐标原点.(Ⅰ)若AC BC ⊥，求sin2α；(Ⅱ)若|OA+OC|31=，求OB 和OC 的夹角.17、(本小题满分14分)某校参加高一年级期中考试的学生中随机抽取60名学生，将其数学成绩(均为整数)分成六段[40，50)，[50，60)，…，[90，100)后得到如下部分频率分布直方图. 观察图形的信息，回答下列问题：(Ⅰ)求分数在[70，80)内的频率；并补全频率分布直方图； (Ⅱ)求在[60，70)，[70，80)分数段上各有多少人？(Ⅲ)用分层抽样方法在分数段[60，80)的学生中抽取一个容量为6的样本.将该样本看成一个总体，从中任取2人，求至多有一人在分数段[60，80)的概率.第17题图分数频率/组距10040 50 60 7080 0.015 0.010 0.0050.020 0.025 0.030 0.035 90高一数学试题 第5页(共6页)18、(本小题满分14分)已知点P(0，5)及圆C ：x 2+y 2+4x －12y+24=0.(Ⅰ)若直线l 过点P 且被圆C 截得的线段长为43，求直线l 的方程； (Ⅱ)过点P 作圆C 的弦，求该弦的中点的轨迹方程.19、(本小题满分14分)如图是函数 f(x)=Asin(ωx+φ) (A>0，ω>0，||2πφ<)在一个周期的图象. (Ⅰ)求函数f(x)的表达式； (Ⅱ)求函数f(x)的单调区间；(Ⅲ)设0<α<π，若方程f(x)=m 有两个不同的实数根，求实数m 的取值范围和这两个根的和.20、(本小题满分14分)若向量33a (cos x sin x)22= ，，x x b (cos sin )22=- ，，且x []44ππ∈-，. (Ⅰ)求|a b |+ ；(Ⅱ)若f (x)a b =⋅，求函数f(x)关于x 的解析式和值域；(Ⅲ)设t=2f(x)+a 的值域为D ，且函数21g(t)=t t 22+-在D 上的最小值为2，求实数a 的值.(命题人：华侨城中学 王宏 审题人：区教研室 罗诚)xyO－22 11π12第19题图1高一数学试题 第6页(共6页)高一数学参考答案及评分标准2010.7.4 一、选择题：(10×5＇=50＇) 题 号 1 2 3 4 5 6 7 8 9 10 答 案DADCBCCBAC二、填空题：(4×5＇=20＇)11、_2. 5_； 12、_37__ ，__8_(前空2分，后空3分)； 13、ππ{x |+k πx <+k πk Z}62-≤∈，； 14、②③④. 三、解答题：(80＇)15、(本小题满分12分)解：解：设(x ，y)表示一个基本事件，则所有基本事件包括：(1，1)，(1，2)，(1，3)，(2，1)，(2，2)，(2，3)，(3，1)，(3，2)，(3，3)， (4，1)，(4，2)，(4，3)，(5，1)，(5，2)，(5，3)，共15个基本事件.……3分 (Ⅰ) 事件“x+y 为偶数” 记为A ，事件A 包括: (1，1)，(1，3)，(2，2)， (3，1)，(3，3)，(4，2)，(5，1)，(5，3)，共8个基本事件， ……5分 且是等可能的，故所求的事件A 概率为8P(A)15=； ……7分 (Ⅱ)设事件“xy 为奇数”记为B ，则事件B 包括: (1，1)，(1，3)，(3，1)，(3，3)，(5，1)，(5，3)共6个基本事件， ……9分且是等可能的，故所求的事件A 概率为62155= .……11分 答：事件“x+y 为偶数”的概率为815；事件“xy 为奇数”的概率为25……12分16、(本小题满分12分)解：(Ⅰ)由A(5，0)，B(0，5)，C(cosα，sinα)，得A C (c o s 5s i n )=α-α，， BC (cos sin 5)=αα-，， .……1分 若AC BC ⊥ ，则AC BC=0⋅，即cosα(cosα－5)+sinα(sinα－5)=0，.……3分 ∴5(si nα+cosα)=sin 2α+cos 2α=1， ……4分高一数学试题 第7页(共6页)∴25(1+sin2α)=1，∴224sin 225α=-. .……5分 (Ⅱ)OA =(50) ，，OB =(05) ，，OC (cos sin )=αα ，，∴OA+OC =(5+cos αsin α)，， …… 6分22|OA+OC|(5+cos )+sin =31=αα， …… 7分∵α∈(0，π)，∴1cos =2α，3sin =2α， …… 9分 即 13OC ()22= ，，|OC|=1 ，又|OB|=5 ，1353OB OC (05)()=222⋅=⋅ ，，， …… 10分设OB 和OC 的夹角为θ，则53OB OC 32cos 152|OB ||OC |⋅θ===⨯⋅，…… 11分故OB 和OC的夹角为300. …… 12分17、(本小题满分14分)解：(Ⅰ)分数在[70，80)内的频率为:高一数学试题 第8页(共6页)1－(0.010+0.015+0.015+0.025+0.005)×10=0.3，故0.3=0.0310. ……2分 如图所示： ……4分 如图所示：(求频率2分，作图2分) (Ⅱ)由题意，[60，70)分数段的人数为：0.15×60=9人； …… 6分 [70，80)分数段的人数为：0.3×60=18人； …… 8分 (Ⅲ)∵在[60，80)的学生中抽取一个容量为6的样本，∴[60，70)分数段抽取2人，分别记为m ，n ；[70，80)分数段抽取4人，分别记为a ，b ，c ，d ； …… 10分 设从样本中任取2人，则此基本事件空间包含的基本事件有：(m ，n)，(m ，a)，(m ，b)，(m ，c)，(m ，d)，(n ，a)，(n ，b)，(n ，c)， (n ，d)，(a ，b)，(a ，c)，(a ，d)，(b ，c)，(b ，d)，(c ，d)共15种基本事件， ……11分 若至多有1人在分数段[70，80)为事件A ，则事件A 包含的基本事件有： (m ，n)，(m ，a)，(m ，b)，(m ，c)，(m ，d)， (n ，a)，(n ，b)，(n ，c)， (n ，d)，共9种基本事件， …… 12分且是等可能的，∴93P(A)155==. …… 13分 答：至多有1人在分数段[70，80)的概率为35. …… 14分18、（本小题满分14分）解：(Ⅰ)圆的方程可化为(x+2)2+(y －6)2=16，…… 1分高一数学试题 第9页(共6页)xO yC A BD P圆心C(－2，6)]，半径r=4，如图所示，AB 43=，D 是AB 的中点， …… 2分 CD ⊥AB ，AD =23，AC=4，在直角△ACD 中，可得CD=2. ……3分 设所求直线的斜率为k ，则直线的方程为y －5=kx ， 即kx －y+5=0. …… 4分 由点C 到直线AB 的距离公式得：22|2k 6+5|=2k +(1)---， ……5分解之得3k 4=. ……6分当3k 4=时，直线l 的方程为3x －4y+20=0； ……7分又直线l 的斜率不存在时，也满足题意，此时方程为x=0. ……8分 所以所求直线方程为3x －4y+20=0或x=0. ……9分 (Ⅱ)设过P 点的圆C 的弦的中点为D(x ，y)，则CD ⊥PD ，即CD PD =0⋅， ……11分则(x+2，y －6)· (x ，y －5)=0，即(x+2)x+(y －6)(y －5)=0， ……12分 经化简得所求轨迹方程为x 2+y 2+2x －11y+30=0. ……14分 19、(本小题满分14分)解：(Ⅰ)显然A=2， ……1分 又图象过(0，1)点，∴f(0)=1，∴ 1sin 2φ=，∵π||<2φ，∴π=6φ； ……2分 由图象结合“五点法”可知，11(0)12π，对应函数y=sinx 图象的点(2π，0)， ∴11ππω+=2π126⨯，ω=2. ……4分 所以所求的函数的解析式为：πf (x)=2sin(2x +)6. ……5分高一数学试题 第10页(共6页)(Ⅱ)当πππ2k π2x +2k π+ (k z)262-≤≤∈，时，函数πf (x)=2sin(2x +)6单调递增，即2ππ2k π2x 2k π+ (k z)33-≤≤∈，. ……7分 解得ππk πx k π(k z)36-≤≤+∈. ……8分故函数πf (x)=2sin(2x +)6单调递增区间为ππ[k πk π](k z)36-+∈，.……9分(Ⅲ)如图所示，在同一坐标系中画出πy =2sin(2x +)6和y=m(m ∈R) 的图象，由图可知，当－2<m<1或1<m<2时，直线y=m 与曲线有两个不同的交点，即原方程有两个不同的实数根. ……10分 ∴m 的取值范围为：－2<m<1或1<m<2； ……12分 当－2<m<1时，两根和为3π；当1<m<2时，两根和为43π. ……14分 20、(本小题满分14分)解：3x 3xa +b =(cos x +cos sin x sin )2222- ，， ……1分223x 3x |a +b |(cos x +cos )(sin x sin )2222=+-高一数学试题 第11页(共6页) 3x 3x =2+2(cos x cos sin x sin )2222⋅-⋅ ……2分 2=2(1+cos2x)=22cos x =2cosx ⨯(由x 44ππ∈-[，]知cosx>0). ……3分(Ⅱ) 3x 3x f(x)=a b =cos x cos sin x sin =cos2x 2222⋅⋅-⋅ . ……4分 由题意，2x 22ππ∈-[，]，从而[]1,02cos ∈x ，即f(x)的值域为[0，1]. ……6分 (Ⅲ)由(Ⅱ)得D=[a ，a+2] ……7分 可以求出22115g(t)=t +t 2=(t +1)222--可知其对称轴为t=－1. ……8分 下面分情况讨论：①当a≤－1≤a+2时，即－3≤a≤－1时，min 5g(t)=g(1)=2--， 不成立； ……9分 ②当a+2<－1时，即a<－3时，2min 1g(t)=g(a +2)=a +3a +22. ……10分 由21a +3a +2=22，得a=－6 (a=0舍去). ……11分 ③ 当a>－1时，2min 1g(t)=g(a)=a +a 2=22-， ……12分 解得a=2 (a=－4舍去)， ……13分 综上知，a=－6或a=2. ……14分。

2011年普通高等学校招生全国统一考试文科数学注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．2．回答第Ⅰ卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．写在本试卷上无效． 3．回答第Ⅱ卷时，将答案写在答题卡上，写在本试卷上无效． 4．考试结束后，将本试卷和答题卡一并交回．第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合M={0，1，2，3，4}，N={1，3，5}，P=M N ，则P 的子集共有A ．2个B ．4个C ．6个D ．8个2．复数512ii=-A ．2i -B ．12i -C ． 2i -+D ．12i -+3．下列函数中，既是偶函数又在(0,)+∞单调递增的函数是A ．3y x =B ．||1y x =+C ．21y x =-+D ．||2x y -=4．椭圆221168x y +=的离心率为A ．13B ．12C D ．25．执行右面的程序框图，如果输入的N 是6，那么输出的p 是 A ．120 B ． 720 C ． 1440 D ． 50406．有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为 A ．13 B ．12C ．23D ．347．已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos 2θ=A ． 45-B ．35-C ．35D ．458．在一个几何体的三视图中，正视图与俯视图如右图所示，则相应的侧 视图可以为9．已知直线l 过抛物线C 的焦点，且与C 的对称轴垂直，l 与C 交于A ，B 两点，||12AB =，P为C 的准线上一点，则ABP ∆的面积为 A ．18 B ．24 C ． 36D ． 4810．在下列区间中，函数()43x f x e x =+-的零点所在的区间为A ．1(,0)4-B ．1(0,)4C ．11(,)42D ．13(,)2411．设函数()sin(2)cos(2)44f x x x ππ=+++，则 A ．()y f x =在(0,)2π单调递增，其图象关于直线4x π=对称 B ．()y f x =在(0,)2π单调递增，其图象关于直线2x π=对称 C ．()y f x =在(0,)2π单调递减，其图象关于直线4x π=对称D ．()y f x =在(0,)2π单调递减，其图象关于直线2x π=对称12．已知函数()y f x =的周期为2，当[1,1]x ∈-时2()f x x =，那么函数()y f x =的图象与函数|lg |y x =的图象的交点共有 A ．10个B ．9个C ．8个D ．1个第Ⅱ卷本卷包括必考题和选考题两部分．第13题-第21题为必考题，每个试题考生都必须做答．第22题-第24题为选考题，考生根据要求做答． 二、填空题：本大题共4小题，每小题5分．13．已知a 与b 为两个不共线的单位向量，k 为实数，若向量a+b 与向量ka-b 垂直，则k=_____________． 14．若变量x ，y 满足约束条件32969x y x y ≤+≤⎧⎨≤-≤⎩，则2z x y =+的最小值是_________．15．ABC ∆中，120,7,5B AC AB =︒==，则ABC ∆的面积为_________．16．已知两个圆锥有公共底面，且两圆锥的顶点和底面的圆周都在同一个球面上．若圆锥底面面积是这个球面面积的316，则这两个圆锥中，体积较小者的高与体积较大者的高的比值为______________．三、解答题：解答应写文字说明，证明过程或演算步骤． 17．（本小题满分12分） 已知等比数列{}n a 中，113a =，公比13q =．（I ）n S 为{}n a 的前n 项和，证明：12nn a S -=（II ）设31323log log log n n b a a a =+++ ，求数列{}n b 的通项公式．18．（本小题满分12分）如图，四棱锥P ABCD -中，底面ABCD 为平行四边形，60DAB ∠=︒，2AB AD =，PD ⊥底面ABCD ．（I ）证明：PA BD ⊥； （II ）设PD=AD=1，求棱锥D-PBC 的高．19．（本小题满分12分） 某种产品的质量以其质量指标值衡量，质量指标越大表明质量越好，且质量指标值大于或等于102的产品为优质品．现用两种新配方（分别称为A 配方和B 配方）做试验，各生产了100件这种产品，并测量了每产品的质量指标值，得到时下面试验结果：A 配方的频数分布表指标值分组 [90，94） [94，98） [98，102） [102，106） [106，110]频数8 20 42 22 8 B 配方的频数分布表指标值分组 [90，94） [94，98） [98，102） [102，106） [106，110]频数4 12 42 32 10 （I ）分别估计用A 配方，B 配方生产的产品的优质品率；（II ）已知用B 配方生产的一种产品利润y （单位：元）与其质量指标值t 的关系式为2,942,941024,102t y t t -<⎧⎪=≤<⎨⎪≥⎩估计用B 配方生产的一件产品的利润大于0的概率，并求用B 配方生产的上述100件产品平均一件的利润．20．（本小题满分12分） 在平面直角坐标系xOy 中，曲线261y x x =-+与坐标轴的交点都在圆C 上． （I ）求圆C 的方程；（II ）若圆C 与直线0x y a -+=交于A ，B 两点，且,OA OB ⊥求a 的值．21．（本小题满分12分） 已知函数ln ()1a x bf x x x=++，曲线()y f x =在点(1,(1))f 处的切线方程为230x y +-=． （I ）求a ，b 的值；（II ）证明：当x>0，且1x ≠时，ln ()1xf x x >-． 请考生在第22、23、24三题中任选一题做答，如果多做，则按所做的第一题计分．做答是用2B 铅笔在答题卡上把所选题目对应题号下方的方框涂黑． 22．（本小题满分10分）选修4-1：几何证明选讲如图，D ，E 分别为ABC ∆的边AB ，AC 上的点，且不与ABC ∆的顶点重合．已知AE 的长为m ，AC 的长为n ，AD ，AB 的长是关于x 的方程2140x x mn -+=的两个根． （I ）证明：C ，B ，D ，E 四点共圆；（II ）若90A ∠=︒，且4,6,m n ==求C ，B ，D ，E 所在圆的半径．23．（本小题满分10分）选修4-4：坐标系与参数方程在直角坐标系xOy 中，曲线1C 的参数方程为2cos (22sin x y ααα=⎧⎨=+⎩为参数），M 为1C 上的动点，P 点满足2OP OM =，点P 的轨迹为曲线2C ．（I ）求2C 的方程；（II ）在以O 为极点，x 轴的正半轴为极轴的极坐标系中，射线3πθ=与1C 的异于极点的交点为A ，与2C 的异于极点的交点为B ，求|AB|．24．（本小题满分10分）选修4-5：不等式选讲 设函数()||3f x x a x =-+，其中0a >． （I ）当a=1时，求不等式()32f x x ≥+的解集．（II ）若不等式()0f x ≤的解集为｛x|1}x ≤-，求a 的值．参考答案一、选择题（1）B （2）C （3）B （4）D （5）B （6）A （7）B （8）D （9）C （10）C （11）D （12）A 二、填空题（13）1 （14）-6 （15）4315 （16）31三、解答题 （17）解：（Ⅰ）因为.31)31(311n n n a =⨯=- ,2311311)311(31nn n S -=--= 所以,21nn a S --（Ⅱ）n n a a a b 32313log log log +++= )21(n +++-= 2)1(+-=n n所以}{n b 的通项公式为.2)1(+-=n n b n (18)解：（Ⅰ）因为60,2DAB AB AD ∠=︒=，由余弦定理得BD = 从而BD 2+AD 2= AB 2，故BD ⊥AD 又PD ⊥底面ABCD ，可得BD ⊥PD 所以BD ⊥平面PAD. 故 PA ⊥BD（Ⅱ）如图，作DE ⊥PB ，垂足为E 。

(第6题图)郑州市2010-2011学年下期期末试题高一数学第Ⅰ卷 （选择题 共60分）一．选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的） 1．18与30的最大公约数是A ．2B ．15C ．6D ．92．某单位有职工52人，现将所有职工随机编号，用系统抽样的方法抽取一个容量为4的样本，已知6号、32号、45号职工在样本中，则样本中还有一个职工的编号是A ．19B ．20C ．18D ．213．某学习小组在一次数学测验中，得100分的有1人，95分的有1人，90分的有2人，85分的有4人，80分和75分的各有1人，则该小组成绩的平均数、众数、中位数分别是A ．85、85、85B ．87、85、86C ．87、85、85D ．87、85、904．函数)32sin(π-=x y 在区间],2[ππ-上的简图是5．若5sin cos 4αα-=-，则sin 2α的值为 A ．2 B ．98- C ．916 D ．916- 6．右面的程序框图，如果输入三个实数a 、b 、cA ．x c >B ．c x >C ．c b >D ．b c >7．为得到函数cos(2)3y x π=+的图象，只需将函数sin 2y x =的图象A ．向左平移56π个长度单位 B ．向右平移56π个长度单位 C ．向左平移512π个长度单位 D ．向右平移512π个长度单位8．一个扇形的面积为1，周长为4，则该扇形圆心角的弧度数为A ．23πB ．2C ．πD ．3π9．已知sin 5α=，则44sin cos αα-的值为A ．35-B ．35C ．5D ．510．已知sin 3cos αα=，则sin cos αα的值为A BC ．310-D ．31011．P 是ABC ∆所在平面上一点，若PA PB PB PC PC PA ⋅=⋅=⋅，则P 是ABC ∆的A ．内心B ．外心C ．垂心D ．重心12．点M 、N 分别在ABC ∆的边AB 、AC 上，且13AM AB =，14AN AC =，BN 与CM 交与点P ，设AB a =，AC b =，若(,)AP xa yb x y R =+∈，则x y +=A ．712-B ．712C ．511-D ．511第Ⅱ卷（非选择题 共90分）二、填空题（本大题共4小题，每小题5分，共20分．把答案填在题中横线上）13．1tan151tan15-=+ ． 14．已知4||=，e 是单位向量，当a 、e 之间的夹角是23π时，向量a 在e 方向上的投影为 ．15．若正ABC ∆的内切圆为圆O ，则ABC ∆内的一点落在圆O 外部的概率为 ． 16．给出下列命题：①长度等于半径长的弦所对的圆心角是1弧度的角；②函数5sin 2y πθ⎛⎫=- ⎪⎝⎭是偶函数；③正弦函数在第一象限是增函数；④关于函数()4sin 2()3f x x x R π⎛⎫=+∈ ⎪⎝⎭，由12()()0f x f x ==可得12x x -是π的整数倍；⑤正切函数是周期函数，最小正周期是2π．其中正确命题的序号是 ． 三．解答题（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）17．（本小题满分10分）已知α为第二象限角，且1sin 2α=，求sin 4sin2cos21πααα⎛⎫+ ⎪⎝⎭++的值．18．（本小题满分12分）已知奇函数sin()(0,||)2y A x πωϕωϕ=+><的图象的最近两条对称轴之间的距离为π，且过点,22π⎛⎫⎪⎝⎭，求函数的解析式．19．（本小题满分12分）已知向量(sin ,1)a θ=，(1,cos )b θ=． （I ）若a b ⊥，求角θ；（II ）是否存在角θ使得//a b ？若存在，求出θ的值，若不存在，请说明理由．O 1 2 3 4 5 620．（本小题满分12分）某同学大学毕业后在一家公司上班，工作年限x 和年收入y （万元），有以下的统计数据：（I ）请画出上表数据的散点图；（II ）请根据上表提供的数据，用最小二乘法求出y 关于x 的线型回归方程y bx a =+；（III ）请你估计该同学第8年的年收入是多少？（参考公式：1122211()()()n niii ii i nniii i x x y y x y nx yb x x xnx====---==--∑∑∑∑，a y bx =-．）21．（本小题满分12分）某校高一（1）班有男同学45名，女同学15名，老师按照分层抽样的方法抽取4人组建了一个课外兴趣小组． （I ）求课外兴趣小组中男、女同学的人数；（II ）经过一个月的学习、讨论，这个兴趣小组决定选出两名同学做某项实验，方法是先从小组里选出一名同学做实验，该同学做完后，再从小组内剩下的同学中选出一名同学做实验，求选出的两名同学中恰有一名女同学的概率；（III ）在（II ）的条件下，第一次做实验的同学A 得到的实验数据为38,40,41,42,44，第二次做实验的同学B 得到的实验数据为39,40,40,42,44，请问哪位同学的实验更稳定？并说明理由．22．（本小题满分12分）已知向量(cos3,sin 3)a x x =，(cos ,sin )b x x =-，且0,4x π⎡⎤∈⎢⎥⎣⎦，求()||sin 2(0)f x a b a b x λλλ=⋅-+≠的单调区间．2010~2011学年度下期期末考试高中一年级 数学 参考答案一、C A C A D BC B A D C D 二、1314．-2 15．1- 16．② 三、解答题（本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤）. 17.解：1sin 2α=,α为第二象限角, cos 2α∴=- ……………………2分 2sin()44sin 2cos 21sin cos cos sin4462sin cos 2cos παααππααααα+∴+++=+分分)()sin cos 22cos sin cos ααααα+=+ (8)分 22cos α=62==-⎝⎭…………………10分 18．解：()sin (0,||)2y A x πωϕωϕ=+><的图象的最近两条对称轴之间的距离为π，22T ππω∴==，…………2分1.ω∴= …………4分 又因为它是奇函数，所以()k k ϕπ=∈Z ，…………6分 由||2πϕ<得0.ϕ=sin .y A x ∴= …………………8分sin y A x =的图象过点,22π⎛⎫⎪⎝⎭，2sin , 2.2A A π∴=∴= ………………… 11分故所求函数的解析式为2sin y x =. ………………… 12分19．解：（Ⅰ）因为⊥a b ，所以0,⋅=a b …………………2分即sin cos 0θθ+=,sin cos ,θθ=-tan 1.θ=- …………………4分 所以,.4k k πθπ=-∈Z （或者3,.4k k πθπ=+∈Z ） …………………6分 （Ⅱ）因为//a b ，所以sin cos 10,θθ-= …………………9分sin 22θ∴=，这是不可能的.所以θ不存在. …………………12分20．解: （Ⅰ） 散点图略． ……………………4分（Ⅱ）4166.5i i i x y ==∑，4222221345686ii x==+++=∑ ，4.5x = ， 3.5y =，…………………6分266.54 4.5 3.566.563ˆ0.7864 4.58681b-⨯⨯-===-⨯-; …………………8分 ˆˆ 3.50.7 4.50.35,ay bx =-=-⨯=所求的回归方程为0.70.35y x =+． ……………………10分（Ⅲ） 当x =8时, 0.780.35 5.95y =⨯+=．∴该同学第8年的年收入是5.95万元． ………………12分21．解：（Ⅰ）设课外兴趣小组中有x 名男同学，则45,45154x=+解得x =3，所以男同学的人数为3、女同学的人数分别为1. ……………3分（Ⅱ）把三名男同学和一名女同学分别记为123,,,,a a a b 则选取两名同学先后做实验的基本事件有：()()()()()()1213121232,,,,,,,,,,,,a a a a a b a a a a a b ()1,,b a()()()31323,,,,,,a a a a a b ()()23,,,,b a b a 共12种， …………………5分其中有一名女同学的情况有6种， …………………6分所以选出的两名同学中恰有一名女同学的概率为61.122P ==…………7分（Ⅲ）由题知，138********41,5x ++++==2394040424441,5x ++++==…………………9分()()()()()22222213841404141414241444145s -+-+-+-+-==，()()()()()222222239414041404142414441 3.2.5s -+-+-+-+-==……11分 221221,.x x s s ∴=<故同学B 的实验更稳定. …………………12分22．解：0,4x π⎡⎤∈⎢⎥⎣⎦，20,2x π⎡⎤∴∈⎢⎥⎣⎦，[]cos20,1.x ∈ ………………… 2分cos3cos sin3sin cos(3)cos 4x x x x x x x ⋅=-=+=a b ，2cos 2x +===a b ， (4)分()()sin 2cos42sin 2cos2cos4sin 4cos 44f x x x x xx x x λλλλπλ∴=⋅-+=-⎛⎫=-=+ ⎪⎝⎭a b a b …………………6分0,4x π⎡⎤∈⎢⎥⎣⎦，[]40,x π∴∈，54,,444x πππ⎡⎤∴+∈⎢⎥⎣⎦由444x πππ≤+≤，得30;16x π≤≤由5444x πππ≤+≤，得3.164x ππ≤≤ ………8分 所以当0λ>时，()f x 的单调减区间为30,16π⎡⎤⎢⎥⎣⎦，单调增区间为3,164ππ⎡⎤⎢⎥⎣⎦； (10)分当0λ<时，()f x 的单调增区间为30,16π⎡⎤⎢⎥⎣⎦，单调减区间为3,164ππ⎡⎤⎢⎥⎣⎦. ……12分。