2019-2020学年八年级数学下册 1.1 等腰三角形(第1课时)学案(新版)北师大版.doc
- 格式:doc
- 大小:111.50 KB
- 文档页数:3

八年级数学下册1.1 等腰三角形导学案1(新版)北师大版1、理解等边三角形的判别条件及其证明;2、理解含有30角的直角三角形性质及其证明;3、利用以上两个定理解决一些简单的问题。
重点:等腰三角形的性质定理难点:等腰三角形的性质定理的应用、导学过程导学过程导学后反思1、回忆一下:1、等腰三角形性质定理及判定方法;2、等边三角形性质定理。
2、自主学习:阅读教材P10-12。
并尝试解决课后问题。
1、如何确定一个三角形是等边三角形呢?如何确定一个等腰三角形是等边三角形呢?ABC定理:三个角都相等的三角形是等边三角形;(结合题设与结论写出已知与求证)已知:在ΔABC 中,求证:证明:推理格式:∵ ∴ 定理:有一个角是60的等腰三角形是等边三角形;(结合题设与结论写出已知与求证)已知:在ΔABC中,求证:证明:推理格式:∵ ∴2、用含30角的两个相同的三角尺,能拼成一个三角形定理:在直角三角形中,如果一个锐角等于30,那么它所对的等于的一半、推理格式:∵ ∴3、简单运用巩固新知1、Rt△ABC中,∠C=90,如图下左图,若b=5,c=13,则a=__________;若a=8,b=6,则c=__________、2、等边△ABC,AD为它的高线,下中图所示,若它的边长为2,则它的周长为__________,AD=__________,BD∶AD∶AB=__________∶__________∶__________、3、上右图所示,正方形ABCD,AC为它的一条对角线,若AB=2,则AC=__________;若AC=2,则AB=__________;AC∶AB=__________∶__________、4、如右图,△ABC中,∠A+∠C=2∠B,∠A=30,则∠C=__________;若AB=6,则BC=__________、5、、如图所示,△ABC中,∠ACB=90,CD⊥AB,垂足是D,∠A=60、求证:BD=3AD、6、如图,DE∥BC,CG=GB,∠1=∠2,求证:△DGE是等腰三角形、、四:教学反思。

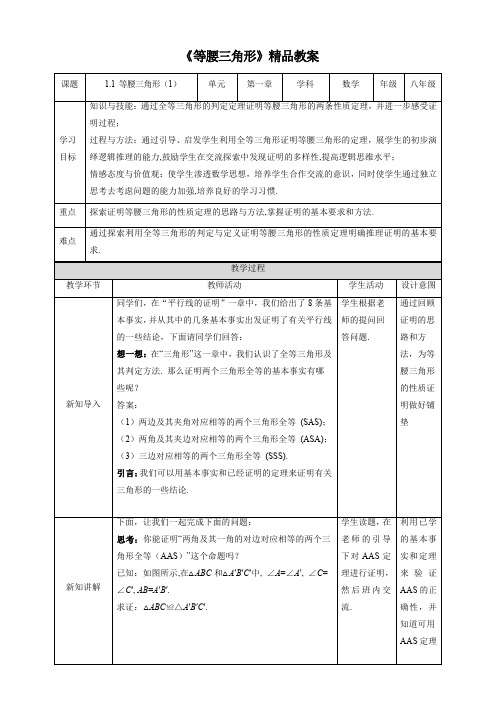
《等腰三角形》精品教案证明:∵∠A =∠A ′,∠C =∠C ′(已知)∴∠B =∠B ′(三角形内角和定理)在△ABC 与△A ′B ′C ′中A AAB A B B B ∠=∠'⎧⎪=''⎨⎪∠=∠'⎩Θ(已知)(已知)(已证)∴△ABC ≌△A ′B ′C ′(ASA ).归纳:全等三角形判定定理:两角分别相等且其中一组等角的对边相等的两个三角形全等(AAS ).符号语言:在△ABC 与△A ′B ′C ′中A A C C AB A B ∠=∠'⎧⎪∠=∠'⎨⎪=''⎩Θ∴△ABC ≌△A ′B ′C ′(AAS ).指出:根据全等三角形的定义,我们可以得到全等三角形的性质:全等三角形的对应边相等、对应角相等.符号语言:∵△ABC ≌△A ′B ′C ′∴∠A =∠A ′,∠B =∠B ′,∠C =∠C ′AB =A ′B ′,AC =A ′C ′,BC =B ′C ′.议一议:你还记得我们探索过的等腰三角形的性质吗?答案:定理:等腰三角形的两个底角相等.跟老师一起学习AAS 定理的符号语言表达形式.学生回答全等三角形的定义并得出全等三角形的性质.在老师的引判定两个三角形全等.认识AAS 的几何语言表达语言.体会全等三角形性质的几何语言表达形式.推论:等腰三角形顶角的平分线,底边上的中线底边上的高互相重合(三线合一).引问:你能利用已有的公理和定理证明这些结论吗?介绍:我们曾经利用折叠的方法说明了这两个底角相等.实际上,折痕将等腰三角形分成了两个全等三角形.这启发我们,可以作一条辅助线把原三角形分成两个全等的三角形,从而证明这两个底角相等.想一想:如何证明“等腰三角形的两个底角相等.”这个定理呢?已知:如图所示,在△ABC 中,AB =AC 求证:∠B =C·证明:如图所示,取BC 的中点D ,连接AD .∵AB =AC ,BD =CD ,AD =AD ,∴△ABD ≌△ACD (SSS).∴∠B =∠C (全等三角形的对应角相等).追问:你还有其他证明的方法吗?归纳:定理:等腰三角形的两底角相等.这一定理可以简述为:等边对等角.导下对等腰三角形的性质进行证明,然后小组交流,并真听老师的讲解.跟老师一起学习“等边对等角”的符号语言表达形式.对等腰三角形的性质定理进行证明.体会等腰三角形性质定理的几何语言表达形式.几何语言:∵AB =AC (已知)∴∠B =∠C (等边对角)例1:如图所示,在△ABC 中,AB =AC ,若∠A =50°,求∠B 的度数.解:∵AB =AC ,∴∠B =∠C .∵∠A +∠B +∠C =180°,∴50°+2∠B =180°,∴∠B =65°.想一想:在前面的证明中,线段AD 还具有怎样的性质呢?·答案:线段AD 即是这个等腰三角形底边上的中线,也是顶角的平分线,同时也是底边上的高.即:三线合一追问:你能证明它们吗?已知:如图所示,在△ABC 中,AB =AC ,线段AD 是△ABC 的中线.求证:AD ⊥BC ,∠BAD =∠CAD .学生读题后认真进行求解,然后班内交流.学生认真观察并思考,然后小组讨论、班内交流,然后对所发现的:三线合一的性质进行证明.交流后仔细听老师讲评.体会等腰三角形性质的应用.对等腰三角形的性质定理的推论进行证明.归纳:推论:等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合(三线合一).符号语言:∵AB =AC ,∠BAD =∠CAD .∴BD =CD .AD ⊥BC .或∵AB =AC ,BD =CD .∴∠BAD =∠CAD .AD ⊥BC .或∵AB =AC ,AD ⊥BC .∴BD =CD .∠BAD =∠CAD .例2:如图,在△ABC 中,AB =AC ,AD 是BC 边上的中线,∠ABC 的平分线BG 交AC 于点G ,交AD 于点E ,EF ⊥AB ,垂足为F .求证:EF =ED .跟老师一起学习“三线合一”的符号语言表达形式.学生独立完成例2,并小组交流,然后老师点评.体会等腰三角形性质定理的推论的几何语言表达形式.对等腰三角形的性质定理的推论进行应用,并进一步体会证明的方法和步骤.证明:∵AB =AC ,AD 是BC 边上的中线,∴ED ⊥BC .又∵BG 平分∠ABC ,EF ⊥AB ,∴EF =ED .课堂练习1.下列各图中a ,b ,c 为三角形的边长,则甲、乙、丙三个三角形和△ABC 全等的是()A .甲和乙B .乙和丙C .甲和丙D .只有丙答案:B2.等腰三角形的一个角是80°,则它的顶角度数是()A.80°B.80°或20°C.80°或50°D.20°答案:B3.如图,在△ABC 中,AB =AC ,D 为BC 的中点,则下列结论中不一定正确的是()A .∠BAD =∠CADB .AD ⊥BC C .∠B =∠CD .∠BAC =∠B答案:D学生自主完成课堂练习,做完之后班级内交流.借助练习,检测学生的知识掌握程度,同时便于学生巩固知识.拓展提高我们一起完成下面的问题:如图,在△ABC 中,AB =AC ,点D 在AC ,且BD =BC =AD ,求△ABC 各角的度数.在师的引导下完成问题.提高学生对知识的应用能力解:∵AB =AC ,AD =BD =BC ,∴∠ABC =∠C =∠BDC ,∠A =∠ABD (等边对等角),设∠A =x ,则∠BDC =∠A +∠ABD =2x ,∴∠ABC =∠C =∠BDC =2x ,在△ABC 中,有∠A +∠ABC +∠C =x +2x +2x =180°,解得x =36°,∴△ABC 中,∠A =36°,∠ABC =∠C =72°.中考链接下面让我们一起赏析一道中考题:(2018·镇江)如图,△ABC 中,AB =AC ,点E ,F 在边BC 上,BE =CF ,点D 在AF 的延长线上,AD =AC .(1)求证:△ABE ≌△ACF ;(2)若∠BAE =30°,则∠ADC =°.证明:(1)∵AB =AC ,∴∠B =∠ACF ,在△ABE 和△ACF 中,AB AC B ACF BE CF =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△ACF (SAS ).解:(2)∵△ABE ≌△ACF ,∠BAE =30°,∴∠CAF =∠BAE =30°,∵AD =AC ,∴∠ADC =∠ACD ,在师的引导下完成中考题.体会所学知识在中考试题运用.。


1.1等腰三角形(第一课时)教学设计一、教材的地位和作用“等腰三角形(第一课时)”选自《义务教育课程标准实验教科书(北师大版)·数学》八年级下册第一章第一节。
现实生活中,等腰三角形的应用比比皆是,利用“轴对称”的知识,进一步研究等腰三角形的特殊性质,不仅是现实生活的需要,而且从思想方法和知识储备上,为学生今后研究“四边形”和“圆”的性质打下坚实的基础。
本节课主要研究的是等腰三角形的重要性质,这是在已经学习过三角形的有关概念及性质、全等三角形、轴对称变换等知识的基础上进行的,它既是前面所学知识的深化和应用,又为两个角相等、两条线段相等、两条直线互相垂直这类问题的证明提供了新的依据,所以它在教材中处于非常重要的位置。
另外研究和学习本节课不仅让学生体会到数学图形的美及应用价值,而且对培养学生的思维能力、分析能力,使学生学会在等腰三角形中添加适当的辅助线,以及向学生渗透转化、类比思想都有很大作用。
二、学情分析就其知识掌握而言,学生虽然在学习三角形全等时已经具备初步的演绎推理能力,但是对规范的、需要经过缜密思维推理过程的表达,还需要教师在课堂上加以规范和引导。
就其生理、心理特点而言,八年级学生思维正处于活跃期,在课堂上能积极思考,敢于发表自己的见解,演绎推理能力已初步形成,动手能力较强,注意力比较集中,对直观生动的事物很容易产生浓厚兴趣。
因而,一方面教师要运用直观生动的形象激发学生的学习兴趣,使他们的注意力始终集中在课堂上;另一方面教师要给学生创造更多发表见解的条件和机会,发挥学生在知识探究中的主体作用,让他们真正理解知识的形成过程。
三、教学目标1.掌握等腰三角形的性质定理及其推论,并能运用它们进行有关的证明和计算。
2.培养学生多角度思考问题的习惯,提高学生分析问题和解决问题的能力;使学生进一步了解探究——猜想——归纳——论证的发现真理的方法。
3.通过对等腰三角形的观察、试验、归纳,体验数学活动充满着探索性和创造性。

北师大版数学八年级下册
《1.1 等腰三角形(第1课时)》教学设计
同一平面内,过一点有且只有________直线与已知直线垂直. ___________相等,两直线平行.
过直线外一点有且只有________直线与这条直线平行.
____________分别相等的两个三角形全等.(SAS)
____________分别相等的两个三角形全等.(ASA)
_________分别相等的两个三角形全等.(SSS)
二、探究新知
独立思考、自主探究:如何证明AAS定理?
定理:__________分别相等且其中一组等角的________边相等的两个三角形全等.( AAS )
提示:
已知:如图,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
三、学以致用
1.开放式探究:等腰三角形有哪些性质?
2.尝试证明,等边对等角定理.
提示:
已知:在△ABC中,AB=AC.。
2019-2020学年八年级数学下册 1.1 等腰三角形教案北师大版1.1等腰三角形【教学内容】等腰三角形的两腰相等,两底角相等,三线合一。
【教学目标】知识与技能让学生在轴对称的基础上,认识等腰三角形;掌握运用等腰三角形的重要特征——两腰相等,两底角相等,三线合一,并能学以致用。
过程与方法让学生通过亲自动手操作,利用轴对称的变换,得出等腰三角形区别于一般三角形的重要特征。
情感、态度与价值观通过折叠观察归纳等方法,探索和发现等腰三角形的特征,并用适当的方式进行说理,让学生体现数学说理的必要性和应用性。
【教学重难点】重点:掌握等腰三角形三线合一的特征。
难点:运用等腰三角形的有关知识解决实际问题。
【导学过程】【知识回顾】三角形全等判定公理:1.三边对应相等的两个三角形全等(SSS)。
2.两边及其夹角对应相等的两个三角形全等(SAS)。
3.两角及其夹边对应相等的两个三角形全等(ASA)。
性质公理:全等三角形的对应边、对应角相等。
【情景导入】多媒体展示生活中的等腰三角形,继而复习等腰三角形的定义及引出各部分的名称。
即:两条边相等的三角形叫做等腰三角形。
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
【新知探究】探究一、(出示导纲,学生自学)学生自学教材后完成填空:在△ABC中,AB、AC叫做这个三角形的(),BC叫做这个三角形的(),∠A是这个三角形的(),∠B、∠C是这个三角形的()。
探究二、做一张等腰三角形的纸片,每个人的等腰三角形的大小和形状可以不一样,把纸片对折,让两腰AB、AC重叠在一起,折痕为AD.通过动手操作,你能发现什么现象吗?(利用动画片演示对折前后的变化)折叠的两个部分是互相重合的,所以等腰三角形是一个轴对称图形,折痕所在的直线就是它的对称轴.由于AB与AC重合,因此点B与点C重合,这样线段BD与CD也重合,所以∠B =∠C.结论:等腰三角形的两个底角相等.(简写成“等边对等角”)(多媒体展示)用数学语言表示:∵AB=AC∴∠B=∠C(等边对等角)探究三、例1:已知:在△ABC中,AB=AC,∠B=80°.求∠C和∠A的度数.(学生合作交流后,教师在板书解题过程)(1).若把已知条件∠B=80°改为∠C =80°,求另外两个角的度数呢?(2).那么改为∠A =80°,又怎样呢?(3)如果改为“有一个角等于80°”,应该怎么解答呢?回忆并操作:请画出等腰三角形底边上的中线、高线、角平分线,这三条线并比一比,能发现什么特征。
课题:1.1等腰三角形(第一课时)一、学习目标理解作为证明基础的几条公理的内容,应用这些公理证明等腰三角形的性质定理;二、自学指导与检测自学指导自学检测及课堂展示回顾旧知导出公理;1.请回忆并整理已经学过的8条基本事实:2.我们已知全等三角形的另一判别条件是AAS,请你利用前面所提到的公理进行证明?已知:如图,∠A=∠D,∠B=∠E,BC=EF.求证:△ABC≌△DEF.3.回忆全等三角形的性质:。
探索新知:等腰三角形的性质.自学课本2-3页关于“等腰三角形”的相关内容,完成下面的问题。
1.等腰三角形的性质定理有:(1)定理:。
(2)推论:。
2.你还有除了课本所提供的其他证明“等角对等边”的方法吗?3.如何证明“等腰三角形的三线合一”?三、练习:CBAFEDCBAA 层1.判定三角形全等的方法有: 。
2.全等三角形的性质 。
3.等腰三角形的性质是: 。
4.已知等腰三角形的顶角是40° ,那么它的两个底角分别是 。
5.已知等腰三角形的一个底角是60°,那么它的顶角是 。
6.(2009·宁波中考)等腰直角三角形的一个底角的度数是( )A .30°B .45°C .60°D .90°B 层7.如图(图略),在△ABD 中,C 是BD 上的一点,且AC ⊥BD ,AC=BC=CD ,(1)求证:△ABD 是等腰三角形;(2)求∠BAD 的度数。
C 层8.(2009·黔东南中考)如图,在△ABC 中,AB=AC ,点D 在AC 上,且BD=BC=AD ,则∠A 等于( )A 、30oB 、40oC 、45oD 、36o9.(2009·威海中考)如图,AB AC BD BC ==,,若40A ∠= ,则ABD ∠的度数是( )A .20B .30C .35D .40D C B A。