河北省武邑中学2019年新高一入学分班考试数学试题-含答案

第 1 页，共 9 页河北省武邑中学 2018-2019 学年高一上学期第一次月考数 学试题（解析版）一、选择题（本大题共 10小题，共 50.0 分） 1. 已知集合0， ， ，则A. B. C. D.【答案】 B【解析】解：由 B 中方程变形得： ，解得： 或 ，即 ，0， ，故选： B ．求出B 中方程的解确定出 B ,找出A 与B 的交集即可. 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．的图象必过定点 的图象必过定点 ，的图象必过定点 ，由此可得函数的图象必过的定点.本题主要考查对数函数的单调性和特殊点，利用了函数的图象必过定点 ，属于中档题.3. 设， ， ，则 a ， b ， c 的大小关系是A.B. C. D.答案】 B 解析】解：故选： B . 利用指数函数和对数函数的性质求解. 本题考查三个数的大小的比较，是基础题，解题时要认真审题，注意指数函数和对数函2. 函数A.的图象必过定点B.C. D【答案】 C 【解析】解：由于函数 故函数 故选： C . 根据函数数的性质的合理运用.4. 垂直于同一条直线的两条直线一定A.平行B.相交C.异面D.以上都有可能【答案】D【解析】解：分两种情况：在同一平面内，垂直于同一条直线的两条直线平行；在空间内垂直于同一条直线的两条直线可以平行、相交或异面. 故选：D .根据在同一平面内两直线平行或相交，在空间内两直线平行、相交或异面判断.本题主要考查在空间内两条直线的位置关系.【答案】C，故函数是奇函数，故 为偶函数，故B 错误， 是奇函数，故C 正确. 为偶函数，故D 错误，故选：C .根据函数奇偶性的性质即可得到结论.本题主要考查函数奇偶性的判断，根据函数奇偶性的定义是解决本题的关键.A. -B. -C. -D. -【答案】B 【解析】解： 函数的图象是方向朝上，以直线--- 为对称轴的抛物线 又 函数在区间 上是减函数，故 ——解得 - 故选：B .由已知中函数的解析式，结合二次函数的图象和性质，可以判断出函数第2页，共9页5. 设函数正确的是的定义域都为R ,且是奇函数,是偶函数，则下列结论A. 是偶函数B. 是奇函数C.是奇函数D.是奇函数【解析】解: 是奇函数, 是偶函数,A 错误,6.若函数 在区间第3页，共9页图象的形状，分析区间端点与函数图象对称轴的关键，即可得到答案.本题考查的知识点是函数单调性的性质， 其中熟练掌握二次函数的图象和性质是解答本题的关键.7. 已知 , ，则 用a , b 表小为A.B. -C.-D.-【答案】C【解析】解：故选：C .利用幕的对数的运算法则由 ，求出-；将75写出；利用积的对数的运算法则将用a , b .本题考查对数的运算法则、将一个对数由其它对数表示关键是将真数由其它真数表示.【答案】C【解析】解：由上表可知, 令，则 ,求出选项中的端点函数值， 从而由根的存在性定理判断根的位置.的一个根所在的区间是 A.B.C.D.故选：C . 令考查了二分法求方程近似解的步骤，属于基础题.9. 下面四个命题：若直线a, b异面，b, c异面，则a, c异面；若直线a，b相交，b，c相交，则a，c相交；若，则a，b与c所成的角相等；若，，则其中真命题的个数为A. 4B. 3C. 2D. 1【答案】D【解析】解：在长方体中，i若直线记为直线a，直线BC记为直线b，直线直线c，则满足a和b是异面直线，b和c是异面直线，而a和c相交；ii若直线记为直线a，直线BC记为直线b，直线此时a和c平行；iii若直线记为直线a，直线BC记为直线b，直线记为直线c，此时a和c异面.故若直线a，b异面，b，c异面，则a，c相交、平行或异面，故错误；若直线a，b相交，b，c相交，则a，c相交、平行或异面，故错误；若，则由异面直线所成的角的定义知a，b与c所成的角相等，故正确;若，，则a与c相交、平行或异面，故错误.故选：D.若直线a，b异面，b，c异面，则a，c相交、平行或异面；若直线a，b相交，b，c相交，则a, c相交、平行或异面；由异面直线所成的角的定义知正确；若，，则a与c相交、平行或异面.本题考查命题的真假判断，是基础题解题时要认真审题，解题时要认真审题，注意空间想象能力的培养.10.已知函数，对任意的两个不相等的实数，，都有成立，且，则的值是A. 0B. 1C.!D.!【答案】B【解析】解：令，则，所以令，，则，所以故选：B.本题为抽象函数问题，可用赋值法求解令，则，所以，则结果可求.第4页，共9页令，，则第5页，共9页。

2019-2020河北省武邑中学高三上学期开学考试数学（文）试题一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项符合题目要求的。

1.若集合，，则（）A. B. C. D.2.设命题：，，则为（）A. ，B. ，C. ，D. ，3.已知等差数列的前项和，若，则等差数列的公差是（）A. 2B. -2C.D.4.已知，则（）A. B. C. D.5.若满足约束条件，则的最大值是（）A. -8B. 0C. -3D. 16.在中，，是的中点，则（）A. B. C. D.7.已知向量，，且，则（）A. B. C. D.8.函数在上的图象为（）A. B.C. D.9.要得到函数的图像，只需将函数的图像（）A. 向右平移个单位长度B. 向左平移个单位长度C. 向右平移个单位长度D. 向左平移个单位长度10.已知且，函数，则“”是“在上单调递减”的（）A. 充要条件B. 必要不充分条件C. 充分不必要条件D. 既不充分也不必要条件11.已知函数在上的值域为，若的最小值与最大值分别为，则（）A. B. C. D.12.已知函数，，若两曲线，有公共点，且在该点处它们的切线相同，则当时，的最大值为（）A. B. C. D.二、填空题：本题共4小题，每小题5分，共20分.13.设函数，则___________.14.已知，满足，则的最大值为__________.15.已知的两个单位向量，且，则__________.16.的垂心在其内部，，，则的取值范围是________.三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题，每个试题考生都必须作答.第（22）、（23）题为选考题，考生根据要求作答.17.已知数列是公差不为0的等差数列，，成等比数列.（1）求；（2）设，数列的前项和为，求.18.某厂分别用甲、乙两种工艺生产同一种零件，尺寸在[223,228]内（单位：mm）的零件为一等品，其余为二等品.在两种工艺生产的零件中，各随机抽取10个，其尺寸的茎叶图如图所示：（1）分别计算抽取的两种工艺生产的零件尺寸的平均数；（2）已知甲工艺每天可生产300个零件，乙工艺每天可生产280个零件，一等品利润为30元/个，二等品利润为20元/个.视频率为概率，试根据抽样数据判断采用哪种工艺生产该零件每天获得的利润更高？19.在直角三角形中，，为的中点，以为折痕将折起，使点到达点的位置且.（1）求证：；（2）求点到平面的距离.20.斜率为的直线与抛物线交于两点，且的中点恰好在直线上.（1）求的值；（2）直线与圆交于两点，若，求直线的方程.21.设（1）求的最小值；（2）证明：.22.在极坐标系中，曲线方程为.以极点为原点，极轴为轴正半轴建立直角坐标系，直线：，（t为参数，）.（1）求曲线的直角坐标方程；（2）设直线与曲线相交于两点，求的取值范围.23.已知.（1）求不等式解集；（2）若时，不等式恒成立，求的取值范围.2019-2020河北省武邑中学高三上学期开学考试数学（文）试题一、选择题：本题共12小题，每小题5分，共60分。

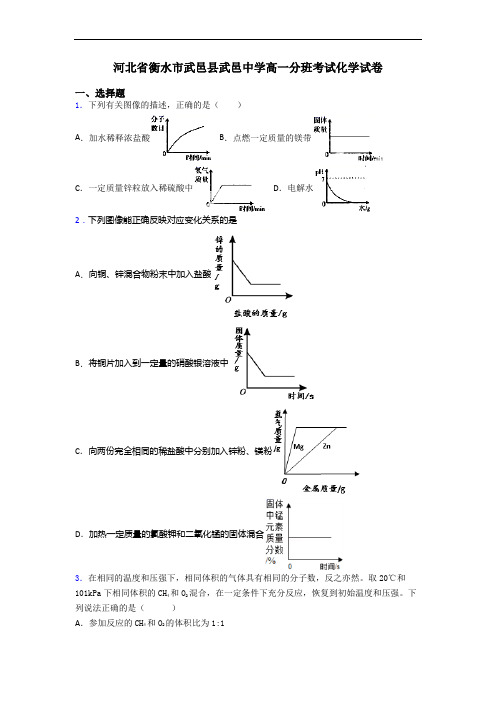
河北省衡水市武邑县武邑中学高一分班考试化学试卷一、选择题1．下列有关图像的描述，正确的是（）A．加水稀释浓盐酸 B．点燃一定质量的镁带C．一定质量锌粒放入稀硫酸中 D．电解水2．下列图像能正确反映对应变化关系的是A．向铜、锌混合物粉末中加入盐酸B．将铜片加入到一定量的硝酸银溶液中C．向两份完全相同的稀盐酸中分别加入锌粉、镁粉D．加热一定质量的氯酸钾和二氧化锰的固体混合3．在相同的温度和压强下，相同体积的气体具有相同的分子数，反之亦然。

取20℃和101kPa下相同体积的CH4和O2混合，在一定条件下充分反应，恢复到初始温度和压强。

下列说法正确的是（）A．参加反应的CH4和O2的体积比为1:1B．生成的CO2分子个数为原来气体分子数的三分之一C．反应后气体的体积为原来的二分之一D．反应后的气体中C、O原子的个数比为1:24．甲、乙两种固体物质（不含结晶水）的溶解度曲线如图所示。

下列说法正确的是A．t1℃时，甲溶液中溶质的质量分数一定等于乙溶液B．降低温度，可使甲的饱和溶液变为不饱和溶液C．t2℃时，分别在100 g水中加入50 g 甲、乙，同时降温至t1℃，甲、乙溶液均为饱和溶液D．将t2℃时甲的饱和溶液降温至t1℃，溶液质量不变5．下列归纳和总结完全正确的一组是A．化学与生活B．化学与安全①用甲醛可保鲜海产品②用熟石灰改良酸性土壤③用生石灰作食品干燥剂①点燃氢气前一定要检验纯度②进行化学实验时配戴护目镜③发现厨房中天然气泄漏马上拨打119报警C．化学与资源D．化学与发现①塑料的使用一定程度上保护了金属资源②稀土是宝贵的不可再生资源③海洋中蕴藏着丰富的化学资源①卢瑟福确定了原子的核式结构②拉瓦锡第一个发现并提出了质量守恒定律③门捷列夫发现元素周期律并编制元素周期表A．A B．B C．C D．D6．向硫酸亚铁、硫酸铜的混合溶液中加入一些锌粉，充分反应后，过滤，得到滤渣A和滤液。

将滤渣A加入少量稀硫酸中，有气泡产生。

2018-2019学年河北省武邑中学高一上学期第一次月考数学试题本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分，考试时间120分钟．第Ⅰ卷(选择题 共60分)注意事项：1．答第1卷前，考生务必将自己的姓名、学号、考试科目涂写在答题卡上． 2．每题选出答案后，用2B 铅笔把答题卡对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再改涂在其它答案标号.一、选择题：(本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求)1.已知集合A ＝{－2,0,2}，B ＝{x |x 2－x －2＝0}，则A ∩B ＝( )A ．∅B ．{2}C ．{0}D ．{－2}2 函数()11log +-=x y a 的图象必过定点 ( )A.()2,1B.()2,2C.()0,1D.()1,23、设0.3777,log 0.3,0.3a b c ===，则c b a ,,的大小关系是 （ ）A ．c b a <<B ．a c b <<C ．b a c <<D ． a b c << 4 垂直于同一条直线的两条直线位置关系是（ ）A.平行B.相交C .异面D.以上都有可能5 设函数()x f ，()x g 的定义域都为R ，且()x f 是奇函数，()x g 是偶函数，则下列结论中正确的是（ ）A. ()x f ()x g 是偶函数B. ()x f ()x g 是奇函数C.()()x g x f 是奇函数D.()()x g x f 是奇函数6．若函数()2211y x a x =+-+在区间(],2-∞上是减函数，则实数a 的取值范围是（ ）A. 3,2⎡⎫-+∞⎪⎢⎣⎭ B. 3,2⎛⎤-∞- ⎥⎝⎦ C. 3,2⎡⎫+∞⎪⎢⎣⎭ D. 3,2⎛⎤-∞ ⎥⎝⎦7．某同学在用描点法画二次函数y ＝ax 2＋bx ＋c 的图象时，列出了下面的表格：x … －2 －1 0 1 2 … y…－11－21－2－5…由于粗心，他算错了其中一个y 值，则这个错误的数值是( ) A ．－11 B ．－2 C ．1 D ．－58. 据报道，北京市今年开工及建设启动的8条轨道交通线路，总投资约82 000 000 000元．将82 000 000000 用科学计数法表示为( )A ．110.8210⨯B ．108.210⨯C ．98.210⨯D ．98210⨯ 9. 已知a =9log 2,b =5log 2,则75log 2用b a ,表示为( )A.b a 22+B. b a 212+C. b a 221+D. )(21b a + 10. 根据表格中的数据，可以断定方程20xe x --=的一个根所在的区间是（ ）x－1 0 1 2 3 x e0．37 1 2．72 7．39 20．09 2x +12345A ． （－1，0）B ．（0，1）C ．（1，2）D ． （2，3） 11 下面四个命题：1)直线a ，b 异面，b ，c 异面，则a ，c 异面； 2)若直线a ，b 相交，b ，c 相交，则a ，c 相交； 3) 若a ∥b ，则a ，b 与c 所成的角相等； 4)若a ⊥b ，b ⊥c ，则a ∥c .其中真命题的个数为( )A ．4B ．3C ．2D ．112. 已知函数)(x f ，对任意的两个实数21,x x ，都有)()()(2121x f x f x x f =+成立，且0)0(≠f ，则(2006)(2005)f f -⋅-(2005)(2006)f f ⋅的值是( )A. 0B. 1C. 2006D. 20062第Ⅱ卷 (非选择题 共90分)二、填空题：（本大题共4小题，每小题5分，满分20分） 13 已知等差数列{}n a 中， 1210112019a a a a π+++=，则()6cos a -=__________________14. 函数()log (2)1a f x x =-+(0,1)a a >≠的图象恒过定点P ,则P 点的坐标是 。

2018-2019学年河北省衡水市武邑中学高一上学期第三次月考数学试题一、单选题1．设集合{}{}22,,10x A y y x R B x x ==∈=-<，则A B ⋃=（ ） A ． ()1,1- B ． ()0,1 C ． ()1,-+∞ D ． ()0,+∞ 【答案】C【解析】∵A={y|y=2x ，x ∈R}=（0，+∞），B={x|x 2-1＜0}=（-1，1）， ∴A ∪B=（0，+∞）∪（-1，1）=（-1，+∞）． 故选C 2．已知集合则（ ）A ．B ．C ．D ．【答案】B【解析】先求出集合A ，在根据集合补集的运算，即可得到答案. 【详解】 由题意，集合或，所以，故选B.【点睛】本题主要考查了集合的求解及集合的运算，着重考查了正确求解集合A ，熟记集合的补集的运算方法是解答的关键，属于基础题. 3．若函数f(x)＝()1,0{2,0x x f x x +≥+<,则f(－3)的值为( )A ． 5B ． －1C ． －7D ． 2 【答案】D【解析】试题分析： ()()()311112f f f -=-==+=. 【考点】分段函数求值．4．已知，，下列对应不表示从到的映射是( )A ．B ．C ．D ．【答案】A【解析】直接利用映射的定义对选项中的对应逐一判断即可. 【详解】对，时，中没有元素与之对应，不表示从到的映射；对、，集合中每一个元素在集合中都有唯一的元素与之对应，都表示从到的映射，故选A.【点睛】本题主要考查映射的定义，意在考查对基本概念的掌握与应用，属于简单题. 5．已知23x y a ==，则112x y+=，则a 值为（ ） A ． 36 B ． 6 C ． 6 D ． 6【答案】D【解析】∵23x y a ==， ∴23log ,log x a y a ==， ∴231111log 2log 3log 62log log a a a x y a a+=+=+==， ∴26a =，解得6a =又0a >， ∴6a =D 。

河北武邑中学2018—2019学年上学期高三开学摸底考试理 科 数 学本试卷共5页，23题(含选考题)．全卷满分150分．考试用时120分钟．★祝考试顺利★注意事项：1．答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置．2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑．写在试卷、草稿纸和答题卡上的非答题区域均无效．3．非选择题的作答：用黑色签字笔直接答在答题卡对应的答题区域内．写在试卷、草稿纸和答题卡上的非答题区域均无效．4．选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑．答案写在答题卡上对应的答题区域内，写在试卷、草稿纸和答题卡上的非答题区域均无效． 5．考试结束后，请将本试卷和答题卡一并上交．一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知全集{}6,5,4,3,2,1=U ，集合{}3,5,1=A ，集合{}Z x x x x B ∈≤--=,0)4)(2(|，则()U C A B =A ．{}1,6 B ．{}6 C ．{}63，D ．{}1,3 2．欧拉公式cos sin ix e x i x =+ (i 为虚数单位)是由瑞士著名数学家欧拉发明的，他将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位，被誉为“数学中的天桥”．根据欧拉公式可知，3i e 表示的复数在复平面中位于 (A)第一象限(B)第二象限(C)第三象限(D)第四象限3．对任意非零实数b a ,，若b a ⊗的运算原理如图所示，则41log )21(22⊗-的值为（ ） A ．2 B ．2- C ．3 D ．3- 4．2018年3月7日《科学网》刊登“动物可以自我驯化”的文章表明：关于野生小鼠的最新研究，它们在几乎没有任何人类影响的情况下也能表现出进化的迹象——皮毛上白色的斑块以及短鼻子．为了观察野生小鼠的这种表征，从有2对不同表征的小鼠（白色斑块和短鼻子野生小鼠各一对）的实验箱中每次拿出一只，不放回地拿出2只，则拿出的野生小鼠不是同一表征的概率为（ ） A ．14B ．13C ．23D ．345．()()6221x x -+的展开式中4x 的系数为（ ）A ．-160B ．320C ．480D ．6406．某几何体的三视图如图所示，其侧视图为等边三角形，则该几何体的体积为A ．3263+π B ．43+π C ．32123+π D ．432+π 7．()61211x x ⎛⎫+- ⎪⎝⎭的展开式中的常数项是（ ）A ．-5B ．7C ．-11D ．138．《九章算术》卷5《商功》记载一个问题“今有圆堡瑽，周四丈八尺，高一丈一尺．问积几何？答曰：二千一百一十二尺．术曰：周自相乘，以高乘之，十二而一”．这里所说的圆堡瑽就是圆柱体，它的体积为“周自相乘，以高乘之，十二而一”．就是说：圆堡瑽（圆柱体）的体积为112V =⨯（底面圆的周长的平方⨯高），则由此可推得圆周率π的取值为（ ） A ．3B ．3.1C ．3.14D ．3.29．已知向量,5=-=++的取值范围是A ．]5,0[B ．]25,5[C ．]7,25[D ．]10,5[10．如图，网格纸上小正方形的边长为2，粗实线及粗虚线画出的是某四棱锥的三视图，则该四棱锥的外接球的表面积为（ ）A BC ．41πD ．31π11．已知圆22:1C x y +=，点P 为直线240x y +-=上一动点，过点P 向圆C 引两条切线,,,PA PB A B 为切点，则直线AB 经过定点.（ ）A. 11,24⎛⎫ ⎪⎝⎭B. 11,42⎛⎫⎪⎝⎭C. 4⎛⎫⎪ ⎪⎝⎭D. 0,4⎛ ⎝⎭12．已知定义在R 上的可导函数()f x 的导函数为()f x '，对任意实数x 均有()()()10x f x xf x '-+>成立，且()1e y f x =+-是奇函数，则不等式()e 0xxf x ->的解集是（ ）A ．(),e -∞B ．()e,+∞C ．(),1-∞D ．()1,+∞二、填空题：本题共4小题，每小题5分，共20分。

河北武邑中学2018-2019学年上学期高一入学考试数 学 试 题注意事项：1．本试卷分试题卷和答题卡两部分，请将答案写在答题卡上每题对应的答题区域内，写在试题卷上无效．2．考试结束，请将本试题卷和答题卡一并上交． 3．参考公式：二次函数2y ax bx c =++图象的顶点坐标是（2ba-，244ac b a -）．一、选择题（下列各小题中，只有一个选项是符合题目要求的，请在答题卡上指定的位置填涂符合要求的选项前面的字母代号. 每小题3分，计45分.） 1.下列计算正确的是（ ）A ．3|3|-=--B ．030=C ．13-＝－3D ．9＝3±2. 若sin 0α<，且tan 0α>，则α是（ ）A. 第一象限角B. 第二象限角C. 第三象限角D. 第四象限角 3. 若右图是某几何体的三视图，则这个几何体是（ ）A.圆柱B.正方体C.球D.圆锥4. 已知点P （a －1，a ＋2）在平面直角坐标系的第二象限内，则a 的取 值范围在数轴上可表示为（阴影部分）( )5. 某同学在用描点法画二次函数y ＝ax 2＋bx ＋c 的图象时，列出了下面的表格：x … －2 －1 0 1 2 …y…－11－21－2－5…由于粗心，他算错了其中一个y 值，则这个错误的数值是( ) A ．－11 B ．－2 C ．1 D ．－56.如图，均匀地向此容器注水，直到把容器注满．在注水的过程中，下列图象能大致反映水面高度h 随时间t 变化规律的是（ ）1－2 －3 －1 02 A ．1－2 －3 －1 02B ．C ．1－2 －3 －1 02D ．1－2 －3 －1 02A ．B ．C ．D ．7. 实数a ，b 在数轴上的位置如图所示，则下列结论正确的是（ ）A ．a +b ＞0B ．a ﹣b ＞0C ．a•b ＞0D ．＞08. 如图，A ．B 是边长为1的小正方形组成的网格上的两个格点，在格点中任意放置点C ， 恰好能使△ABC 的面积为1的概率是（ ） A ．256 B ．51 C ．254 D ．2579.若等腰三角形中有两边长分别为2和5，则这个三角形的周长为（ ） A ．9 B ．12 C ． 7或9 D ．9或1210. 设函数()x f ，()x g 的定义域都为R ，且()x f 是奇函数，()x g 是偶函数，则下列结论中正确的是（ ） A. ()x f ()x g 是偶函数 B. ()x f ()x g 是奇函数 C.()()x g x f 是奇函数 D.()()x g x f 是奇函数11.如图，正方形ABCD 中，E 是BC 边上一点，以E 为圆心，EC 为半径的半圆与以A 为圆心，AB 为半径的圆弧外切，则sin ∠EAB 的值为（ ）． A ．74 B ．53 C ．107 D ．7312. 下列命题：①三角形的内心到三角形三个顶点的距离相等；②如果，那么；③若关于的方程的解是负数，则m 的取值范围为m<-4；④相等的圆周角所对的弧相等；⑤对于反比例函数，当﹥-1时，y 随着x 的增大而增大其中假命题有 A ．1个 B ．2个 C ．3个 D ．4个13. 设62,0,1=+≥≥y x y x 则y x y xy x u 363422--++=的最大值是（ ）A.227B ．18C ．20D ．不存在 14. 在下列四个图案中，不是中心对称图形的是 （ ）A ．B ．C ．D ．15. 出售某种文具盒，若每个可获利x 元，一天可售出(6－x )个．当一天出售该种文具盒的总利润y 最大时，x 的值为()009045<α<α>αcos sin x 223=+-x mx xy 2-=xA ．1B ．2C ．3D ．4二、解答题（将解答过程写在答题卡上指定的位置．本大题共有9小题，计75分．）16.（6分）先化简，再求值：235(2)362m m m m m -÷+--- ，其中m 是方程x 2＋3x －1＝0的根。

河北武邑中学2018-2019学年下学期高一年级开学考试数学试题本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分。

总分150分。

考试时间120分钟。

第Ⅰ卷（选择题，满分60分）一．选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求）1．已知集合，集合，则下列结论正确的是 }0|{2=-=x x x A {|13}B x N x +=∈-≤< A ． B ． C ． D ．)(1B A ⊆)(1B A ∈A B =∅ BB A = 2.已知扇形的面积为，半径为1，则扇形的圆心角为（ ）83πA.B.C.D.163π83π43π23π3.函数是R 上的偶函数，则的值是（　）））（πϕϕ≤≤+=02sin(x y ϕ B.C.D.04π2ππ4．若函数()()20.3log 54f x x x =+-在区间()1,1a a -+上单调递减，且，，则（1.0log 2=b 2.02=c ）A ．c b a <<B ．b c a <<C ．a b c <<D ．b a c<<5．设函数是R 上的减函数，则的取值范围是（）　⎩⎨⎧≥-<--=0,30,1)(x a a x ax x f x ），且（10≠>a a a A ．B ．C ．D ．2[,13（2,13（（]320，（203（（（6. 复利是一种计算利息的方法.即把前一期的利息和本金加在一起算作本金，再计算下一期的利息.某同学有压岁钱1000元，存入银行，年利率为 2.25%；若放入微信零钱通或者支付宝的余额宝，年利率可达 4.01%.如果将这1000元选择合适方式存满5年，可以多获利息(▲)元.（参考数据：）217.10401.1,170.10401.1,117.10225.1,093.10225.15454====A.176 B.100 C.77 D.887. 函数在区间上为减函数，则的取值范围为2)1(2)(2+-+=x a ax x f ]4,(-∞a A.B. C. D.105a <≤105a≤≤105a <≤51>a 8. 已知中，，则的形状为ABC △0=+⋅（ABC △A.正三角形B.直角三角形C.等腰三角形D.等腰直角三角形9.设偶函数的部分图象如图所示,△KMN 为等腰直角三角形,()cos()(0,0,0)f x A x A ωϕωϕπ=+>>≤<∠KMN=90°,则的值为1()3fA. BC 1412-10.先把函数-的图象上各点的横坐标变为原来的2倍(纵坐标不变),再把新得到的图象向()sin(23f x x π=-左平移个单位,得到y =g(x )的图象当时,函数g(x )的值域为6π5(,)66x ππ∈-A B. C. D. ](1(,1]2-([1,0)-11．若实数满足,x y ，则1|1|ln0x y--=关于的函数图象的y x 大致形状是12.定义域为R 的偶函数满足对任意的，有且当时，)(x f R x ∈),1()()2(f x f x f +=+[]3,2∈x ，若函数在上恰有六个零点，则实数的取值范围是18122)(2-+-=x x x f )1(log )(+-=x x f y a R a A. B. C. D.)55,0()1,55()33,55()1,33(第Ⅱ卷（非选择题 共90分）二．填空题：本大题共4小题，每小题5分，共20分.13. 函数的最大值为 .()12sin f x x =+14. 已知函数在区间上是单调函数，则实数的取值范围为 .()221f x x kx =-+[]1,3k 15.如图,已知平面⊥平面,且AB=4,AC=3,BD=12,则αβ,,,,,,,l BD l AC BD AC l B l A l ⊥⊥⊂⊂∈∈=βαβαCD= .三.解答题：本大题共6小题，共70分．解答应写出文字说明，演算步骤或证明过程．17．（本小题满分10分）已知全集.2,{|230},{|0}U R A x x x B x x a ==--≤=->（1）若，求；2a =,U A B A B U I ð（2）若，求实数的取值范围．A B A = a 18．(本题满分12分) 某地区某农产品近几年的产量统计如表：年份201220132014201520162017年份代码t 123456年产量（万吨）y 6.6 6.777.17.27. 4（1）根据表中数据，建立关于的线性回归方程；y t ∧∧+=a t b y （2）根据线性回归方程预测2019年该地区该农产品的年产量．附：，.参考数据:∑==∧---∑=ni ii i ni tty y t t b 121)())((t b y a ∧∧-=8.2))((61=--∑=i i iy y t t19.（本题满分12分）已知圆C ：x 2+y 2+x ﹣6y+m=0与直线l ：x+2y ﹣3=0．（1）若直线l 与圆C 没有公共点，求m 的取值范围；（2）若直线l 与圆C 相交于P 、Q 两点，O 为原点，且OP ⊥OQ ，求实数m 的值．20.（本小题满分12分）据市场调查发现，某种产品在投放市场的30天中，其销售价格P （元）和时间t ()（天）的关系如图∈t N 所示.（I ） 求销售价格P （元）和时间t （天）的函数关系式；（II ）若日销售量Q (件)与时间t （天）的函数关系式是)，问该产品投放市场40(030,=-+≤≤Q t t ∈t N 第几天时，日销售额（元）最高，且最高为多少元？y 20.(15分) 已知函数为偶函数，()()()21x x t f x x +-=(Ⅰ) 求实数的值；t (Ⅱ) 是否存在实数，使得当时，函数的值域为？0b a >>],[b a x ∈()f x 222,2a b ⎡⎤--⎢⎥⎣⎦若存在请求出实数的值，若不存在，请说明理由.,a b 21.本小题满分12分）已知，若在上的最大值为，最小值为，令113a ≤≤()221f x ax x =-+[]1,3()M a ()N a.()()()g a M a N a =- ( I ) 求的函数表达式；()g a (II) 判断函数的单调性，并求出的最小值.()g a ()g a 22.(本小题满分12分）已知函数是定义在上的奇函数.a a x f x +-=241)()10(≠>a a 且()∞+∞，- (1)求的值;a (2)证明: 函数在定义域内是增函数;)(x f ()∞+∞，- (3)当时,恒成立,求实数的取值范围.]1,0(∈x 22)(-≥xx f t t 试题答案1. B2. C3. C4. D5. A6. B7. B8. C9. B 10. A 11. B 12. C13. 10, 14. 15. 13 16.112a -≤<17.解：，……2分2{|230}{|13}A x x x x x =--≤=-≤≤{|}B x x a =>（1）当时，，2a ={|2}B x x =>{|2}U B x x =≤ð所以， ……4分{|1}A B x x =≥-U 所以 ……6分{|12}U A B x x =-≤≤ðI （2）因为，所以， ……8分A B A ⋂=A B ⊆所以 ……10分1a <-18.解（1）由题意可知：，，5.3=t 7=y ，()5.175.25.15.0)5.0()5.1(5.2)(222222261=+++-+-+-=-∑=i it t，所以16.05.178.2)())((26161==---=∴∑∑==∧i ii i it ty y t tb 44.65.316.07=⨯-=-=∧∧t b y a ∴关于的线性回归方程为.y t 44.616.0+=∧t y （2）由（1)可得，当年份为2019年时，年份代码，此时，所以，可预测8=t 72.744.6816.0=+⨯=∧y 2019年该地区该农产品的年产量约为7.72万吨.19.（1）将圆的方程化为标准方程得：（x+）2+（y ﹣3）2=9﹣m ，∴圆心C （﹣，3），半径r 2=9﹣m ＞0，即m ＜，∵圆心C 到直线l 的距离d 2=，直线l 与圆C 没有公共点∴9﹣m ＜，即m ＞8，则m 的范围为（8，）；（2）根据题意得：△OQP 为直角三角形，即OP ⊥OQ ，5x 2+10x+4m ﹣27=0，设P （x 1，y 1），Q （x 2，y 2），∴x 1+x 2=﹣2，x 1x 2=，y 1y 2=•==，∵x 1x 2+y 1y 2=0，∴+=1，解得：m=3．20.（本小题满分12分）解：（Ⅰ）函数为偶函数，()()()21x x t f x x+-=()()fx f x -=， 5分()()()()2211x x t x x t x x -+--+-∴=1t ∴=(Ⅱ) ，在上是增函数 8分()()()221111x x f x x x +-==-()f x ∴[], a b若的值域为()f x 222,2a b ⎡⎤--⎢⎥⎣⎦则 11分()()2212121212f a a a f b b b ⎧=-=-⎪⎪⎨⎪=-=-⎪⎩解得 13分1a b ==，所以不存在满足要求的实数 15分b a > 又,a b 21.解：（Ⅰ）因为，又，所以.211()(1f x a x a a =-+-113a ≤≤113a≤≤当即时，，112a ≤≤112a ≤≤()(3)95M a f a ==-，；1()1N a a =-1()()()96g a M a N a a a=-=+-当，即时，，123a <≤1132a ≤<()(1)1M a f a ==-，.1()1N a a =-1()()()2g a M a N a a a=-=+-所以.1196,12()1112,32a a a g a a a a ⎧+-≤≤⎪⎪=⎨⎪+-≤<⎪⎩（Ⅱ）设，则12112a a ≤<≤12111()()96g a g a a a -=+--21221(96)9()a a a a +-=-，所以在上为增函数；1212190a a a a -<()g a 1[,1]2设，则，121132a a ≤<≤12111()()g a g a a a -=+2212(2)a a --+-=12()a a -121210a a a a ->所以在上为减函数.所以当时，.()g a 11[,]3212a =min 11()()22g x g ==22.解：（1）∵函数)10(≠>a a 且是定义在()∞+∞，-上的奇函数，a a x f x +-=241)(∴，解得：………………………………………2分0241)0(=+-=a f 2=a （2）设为定义域上的任意两个实数，且，21,x x ()∞+∞，-21x x <则…………………………4分()()1212)22(21221222224122241)()(2121122121+⋅+-=+-+=+⋅+-+⋅-=-x x x x x x x x x f x f 21x x <12,012,0222121>+>+<-∴x x x x …………………………………………………5分)()(0)()(2121x f x f x f x f <<-∴即∴函数在定义域()∞+∞，-内是增函数。

2018-2019学年河北省衡水市武邑中学高一（下）开学数学试卷（2月份）一、选择题（本大题共12小题，共60.0分）1.已知集合A={x|x2-x=0}，集合B={x∈N+|-1≤x＜3}，则下列结论正确的是（）A. B. ∈ C. D.2.已知扇形面积为，半径是1，则扇形的圆心角是（）A. B. C. D.3.函数y=sin（2x+φ）（0≤φ≤π）是R上的偶函数，则φ的值是（）A. 0B.C.D.4.若函数f（x）=log0.3（5+4x-x2）在区间（a-1，a+1）上单调递减，且b=log20.1，c=20.2，则（）A. B. C. D.5.设函数（a＞0，且a≠1）是R上的减函数，则a的取值范围是（）A. B. C. D.6.复利是一种计算利息的方法．即把前一期的利息和本金加在一起算作本金，再计算下一期的利息．某同学有压岁钱1000元，存入银行，年利率为2.25%；若放入微信零钱通或者支付宝的余额宝，年利率可达4.01%．如果将这1000元选择合适方式存满5年，可以多获利息（）元．（参考数据：1.02254=1.093，1，02255=1.170，1.04015=1.217）（）A. 176B. ．C. 77D. 887.函数f（x）=ax2+2（a-1）x+2在区间（-∞，4]上为减函数，则a的取值范围为（）A. B. C. D.8.已知△ABC中，•（+）=0，则△ABC的形状为（）A. 正三角形B. 直角三角形C. 等腰三角形D. 等腰直角三角形9.设偶函数f（x）=A cos（ωx+φ）（A＞0，ω＞0，0≤φ＜π）的部分图象如图所示，△KMN为等腰直角三角形，∠KMN=90°，则f（）的值为（）A. B. C. D.10.先把函数f（x）=sin（2x-）的图象上各点的横坐标变为原来的2倍（纵坐标不变），再把新得到的图象向左平移个单位，得到y=g（x）的图象．当x∈（-，）时，函数g（x）的值域为（）A. B. C. D.11.若实数x，y满足|x-1|-ln=0，则y关于x的函数图象的大致形状是（）A.B.C.D.12.定义域为R的偶函数f（x）满足对任意的x∈R，有f（x+2）=f（x）+f（1），且当x∈[2，3]时，f（x）=-2x2+12x-18，若函数y=f（x）-log a（|x|+1）在R上恰有六个零点，则实数a的取值范围是（）A. B. C. D.二、填空题（本大题共4小题，共20.0分）13.函数f（x）=1+2sin x的最大值为______．14.已知函数f（x）=2x2-kx+1在区间[1，3]上是单调函数，则实数k的取值范围为______．15.如图，已知平面α⊥平面β，α∩β=l，A∈l，B∈l，AC⊂α，BD⊂β，AC⊥l，BD⊥l，且AB=4，AC=3，BD=12，则CD=______．16.已知在区间，上是增函数，则实数a的取值范围是______．三、解答题（本大题共7小题，共85.0分）17.已知全集U=R，A={x|x2-2x-3≤0}，B={x|x-a＞0}．（1）若a=2，求A∪B，A∩∁U B；（2）若A∩B=A，求实数a的取值范围．18.某地区某农产品近几年的产量统计如表：（1）根据表中数据，建立y关于t的线性回归方程；（2）根据线性回归方程预测2019年该地区该农产品的年产量．附：，．参考数据：19.已知圆C：x2+y2+x-6y+m=0与直线l：x+2y-3=0．（1）若直线l与圆C没有公共点，求m的取值范围；（2）若直线l与圆C相交于P、Q两点，O为原点，且OP⊥OQ，求实数m的值．20.据市场调查发现，某种产品在投放市场的30天中，其销售价格P（元）和时间t（t∈N）（天）的关系如图所示．（Ⅰ）求销售价格P（元）和时间t（天）的函数关系式；（Ⅱ）若日销售量Q（件）与时间t（天）的函数关系式是Q=-t+40（0≤t≤30，t∈N），问该产品投放市场第几天时，日销售额y（元）最高，且最高为多少元？21.已知函数为偶函数，（Ⅰ）求实数t的值；（Ⅱ）是否存在实数b＞a＞0，使得当x∈[a，b]时，函数f（x）的值域为，？若存在请求出实数a，b的值，若不存在，请说明理由．22.已知≤a≤1，若f（x）=ax2-2x+1在区间[1，3]上的最大值M（a），最小值N（a），设g（a）=M（a）-N（a）．（1）求g（a）的解析式；（2）判断g（a）单调性，求g（a）的最小值．23.已知函数f（x）=1-（a＞0且a≠1）是定义在（-∞，+∞）上的奇函数．（1）求a的值；（2）证明：函数f（x）在定义域（-∞，+∞）内是增函数；（3）当x∈（0，1]时，tf（x）≥2x-2恒成立，求实数t的取值范围．答案和解析1.【答案】B【解析】解：集合A={x|x2-x=0}={0，1}，集合B={x∈N+|-1≤x＜3}={1，2}，则A∩B={1}，则1∈（A∩B），显然A，C，D不对，B正确．故选：B．运用列举法，化简集合A，B，求得交集，即可判断正确结论．本题考查集合的化简和运算，主要是交集的求法，以及元素与集合的关系和集合与集合的关系，属于基础题．2.【答案】C【解析】解：因为扇形面积为，半径是1，所以扇形的弧长为：，所以扇形的圆心角为：．故选：C．直接利用扇形面积公式，求出扇形的弧长，然后求出扇形的圆心角．本题是基础题，考查扇形的面积公式的应用，圆心角的求法，考查计算能力，常考题型．3.【答案】C【解析】解：函数y=sin（2x+φ）是R上的偶函数，就是x=0时函数取得最值，所以f（0）=±1即sinφ=±1所以φ=kπ+（k∈Z），当且仅当取k=0时，得φ=，符合0≤φ≤π 故选：C．根据函数y=sin（2x+φ）的图象特征，若它是偶函数，只需要x=0时，函数能取得最值．本题考查了正弦型函数的奇偶性，正弦函数的最值，是基础题．4.【答案】D【解析】解：由5+4x-x2＞0，得-1＜x＜5，又函数t=5+4x-x2的对称轴方程为x=2，∴复合函数f（x）=log0.3（5+4x-x2）的减区间为（-1，2），∵函数f（x）=log0.3（5+4x-x2）在区间（a-1，a+1）上递减，∴，则0≤a≤1．而b=log20.1＜0，c=20.2＞1，∴b＜a＜c．故选：D．利用复合函数的单调性求出函数f（x）=log0.3（5+4x-x2）减区间，再由函数f（x）=log0.3（5+4x-x2）在区间（a-1，a+1）上递减求出a的范围，然后利用指数函数与对数函数的性质比较b，c与0和1的大小，则答案可求．本题主要考查了复合函数的单调性以及单调区间的求法．对应复合函数的单调性，一要注意先确定函数的定义域，二要利用复合函数与内层函数和外层函数单调性之间的关系进行判断，判断的依据是“同增异减”，是中档题．5.【答案】A【解析】解：∵函数f（x）（a＞0且a≠1）是R上的减函数，∴0＜a＜1，且-1≥a0-3a，∴≤a＜1．故选：A．根据函数的单调性得到关于a的不等式组，从而可解得a的取值范围．本题考查函数单调性的性质，由题意得到-1≤a0-3a是关键，也是难点所在，属于中档题．6.【答案】B【解析】解：将1000元钱存入微信零钱通或者支付宝的余额宝，选择复利的计算方法，则存满5年后的本息和为1000•1.04015=1217，故而共得利息1217-1000=217元．将1000元存入银行，不选择复利的计算方法，则存满5年后的利息为1000•0.0225×5=112.5，故可以多获利息217-112.5=104.5．故选：B．计算两种情况下的利息，得出结论．本体考查了函数模型的选择与应用，属于基础题．7.【答案】B【解析】解：当a=0时，f（x）=-2x+2，符合题意当a≠0时，要使函数f（x）=ax2+2（a-1）x+2在区间（-∞，4]上为减函数∴⇒0＜a≤综上所述0≤a≤故选：B．根据a取值讨论是否为二次函数，然后根据二次函数的性质建立不等关系，最后将符合条件的求并集．本题主要考查了已知函数再某区间上的单调性求参数a的范围的问题，以及分类讨论的数学思想，属于基础题．8.【答案】C【解析】解：∵•（+）=0，∴（-）•（+）=0，∴2-2=0，可得：2=2，∴||=||，可得：△ABC的形状为等腰三角形．故选：C．由于=-，根据已知可求2=2，进而可得||=||，可求△ABC的形状为等腰三角形．本题主要考查了平面向量的运算在三角形的形状判定中的应用，属于基础题．9.【答案】B【解析】解：由题图知函数的周期T=2（-）=2，由=2，得ω=π．由△KMN为等腰直角三角形，∠KMN=90°，知点M到x轴的距离是，则f（x）=cos（πx+φ），由f（x）是偶函数，所以π×0+φ=0，∴φ=0，f（x）=cos πx，故f （）=cos =．故选：B．根据图象得到周期，代入公式得到ω，根据△KMN为等腰直角三角形得到振幅A=，根据对称轴可得φ，得到解析式后，代入即可．本题考查了由y=Asin（ωx+φ）的部分图象确定其解析式．属中档题．10.【答案】A【解析】解：先把函数f（x）=sin（2x-）的图象上各点的横坐标变为原来的2倍（纵坐标不变），可得y=sin（x-）的图象；再把新得到的图象向左平移个单位，得到y=g（x）=sin（x-）的图象．当x∈（-，）时，x-∈（-，），sin（x-）∈（-，1]，故函数g（x）的值域为（-，1]，故选：A．根据函数y=Asin（ωx+φ）的图象变换规律求得g（x）的解析式，再利用正弦函数的定义域和值域，求得函数g（x）的值域．本题主要考查函数y=Asin（ωx+φ）的图象变换规律，正弦函数的定义域和值域，属于基础题．11.【答案】B【解析】解：∵|x-1|-ln=0，∴f（x）=（）|x-1|其定义域为R，当x≥1时，f（x）=（）x-1，因为0＜＜1，故为减函数，又因为f（x）的图象关于x=1轴对称，对照选项，只有B正确．故选：B．先化简函数的解析式，函数中含有绝对值，故可先去绝对值讨论，结合指数函数的单调性及定义域、对称性，即可选出答案．本题考查指数函数的图象问题、考查识图能力，属于基础题．12.【答案】C【解析】解：令x=-1得，f（1）=f（-1）+f（1）；又f（x）是偶函数，可得f（-1）=f（1），即有f（1）=0，故f（x+2）=f（x），即f（x）的最小正周期为2，又当x∈[2，3]时，f（x）=-2x2+12x-18，函数y=f（x）-log a（|x|+1）的零点的个数即y=f（x）与y=log a（|x|+1）的交点的个数；作函数y=f（x）与y=log a（|x|+1）的图象，易知0＜a＜1，故log a3＞-2，且log a5＜-2，解得＜a ＜．故选：C．令x=-1得，f（1）=f（-1）+f（1）可得f（x+2）=f（x），而函数y=f（x）-log a（|x|+1）的零点的个数即y=f（x）与y=log a（|x|+1）的交点的个数；作两个函数的图象求解．本题考查了函数的零点与函数的图象的交点的应用，属于中档题．13.【答案】3【解析】解：因为sinx∈[-1，1]，所以函数f（x）=1+2sinx的最大值为3；故答案为：3．利用正弦函数的有界性解答即可．本题考查了正弦函数的有界性；x∈R，则sinx∈[-1，1]．14.【答案】（-∞，4]∪[12，+∞）【解析】解：∵函数f（x）=2x2-kx+1∴对称轴为x=，∵函数f（x）=2x2-kx+1在区间[1，3]上是单调函数，∴≤1或≥3，即k≤4或k≥12，故答案为：（-∞，4]∪[12，+∞）．对称轴为x=，函数f（x）=2x2-kx+1在区间[1，3]上是单调函数，得≤1，或≥3求解即可本题考查了二次函数的单调性，对称性，难度不大，属于容易题，关键是确定对称轴．15.【答案】13【解析】解：连接BC．因为AC⊥l，AC=3，AB=4，所以BC=5．因为BD⊥l，α⊥β，α∩β=l，BD⊂β，所以BD⊥α．所以BD⊥BC．在Rt△BDC中，CD==13．故答案为：13连接BC，得△ACB为直角三角形，BC=5，由BD⊥l，得BD⊥BC．由此以求出CD．本题考查线段长的求法，考查了转化思想、空想思维能力，属于中档题．16.【答案】-1≤a＜【解析】解：令g（x）=x2-ax-a．∵f（x）=log g（x）在（-∞，-）上为增函数，∴g（x）应在（-∞，-）上为减函数且g（x）＞0在（-∞，-）上恒成立．因此，．解得-1≤a ＜，故实数a的取值范围是-1≤a ＜．用复合函数的单调性来求解，令g（x）=x2-ax-a．由“f（x）=log g（x）在（-∞，-）上为增函数”，可知g（x）应在（-∞，-）上为减函数且g（x）＞0在（-∞，-）上恒成立．再用“对称轴在区间的右侧，且最小值大于零”求解可得结果．本题主要考查复合函数的单调性，要注意函数的定义域及复合函数单调性的结论：同增异减的应用．17.【答案】解：A={x|x2-2x-3≤0}={x|-1≤x≤3}，B={x|x＞a}；（1）当a=2时，B={x|x＞2}，A∪B={x|x≥-1}，∁U B={x|x≤2}；∴A∩∁U B={x|-1≤x≤2}；（2）∵A∩B=A；∴A B；∴a＜-1；∴实数a的取值范围为（-∞，-1）．【解析】（1）可解出A={x|-1≤x≤3}，B={x|x＞a}，当a=2时，得出B={x|x＞2}，然后进行并集、交集和补集的运算即可；（2）根据A∩B=A即可得出A B，从而得出a＜-1，即得出实数a的取值范围．考查描述法的定义，交集、并集和补集的运算，以及子集的定义．18.【答案】解（1）由题意可知：=（1+2+3+4+5+6）=3.5，=（6.6+6.7+7+7.1+7.2+7.4）=7，（t i-）2=2.52+1.52+0.52+0.52+1.52+2.52=17.5，则==0.16，又=7-0.16×3.5=6.44，所以y关于t 的线性回归方程为=0.16t+6.44．（2）由（1）可得，当年份为2019年时，年份代码t=8，此时=0.16×8+6.44=7.72，所以可预测2019年该地区该农产品的年产量约为7.72万吨．【解析】（1）根据数据求出，，以及，的值即可求出线性回归方程．（2）当t=8时，求出对应的值，即可预测2019年该地区该农产品的年产量．本题主要考查线性回归方程的应用，以及利用回归方程进行预测，考查学生的运算能力．19.【答案】解：（1）将圆的方程化为标准方程得：（x+）2+（y-3）2=9-m，∴圆心C（-，3），半径r2=9-m＞0，即m＜，∵圆心C到直线l的距离d2=，直线l与圆C没有公共点∴9-m＜，即m＞8，则m的范围为（8，）；（2）根据题意得：△OQP为直角三角形，即OP⊥OQ，将直线l与圆方程联立消去y得到：5x2+10x+4m-27=0，设P（x1，y1），Q（x2，y2），∴x1+x2=-2，x1x2=，y1y2=•==，∵x1x2+y1y2=0，∴+=1，解得：m=3．【解析】（1）找出圆心坐标与半径r ，利用点到直线的距离公式求出圆心到直线l 的距离d ，根据直线l 与圆没有公共点得到直线l 与圆外离，即d 大于r 列出关于m 的不等式，求出不等式的解集即可得到m 的范围；（2）根据题意得出直线OP 与直线OQ 垂直，即斜率乘积为-1，设P （x 1，y 1），Q （x 2，y 2），将直线l 方程与圆方程联立，消去y 得到关于x 的一元二次方程，利用根与系数的关系表示出两根之和与两根之积，根据斜率乘积为-1列出关于m 的方程，求出方程的解即可得到m 的值． 此题考查了直线与圆的位置关系，涉及的知识有：根与系数的关系，两直线垂直时斜率的乘积为-1，圆的标准方程，以及点到直线的距离公式，直线与圆的位置关系有d 与r 的大小关系来判断：当d ＞r 时，直线与圆相离；当d=r 时，直线与圆相切；当d ＜r 时，直线与圆相交（d 为圆心到直线的距离，r 为圆的半径）．20.【答案】解：（I ）①当0≤t ＜20，t ∈N 时，设P =at +b ，将（0，20），（20，40）代入，得 解得所以P =t +20（0≤t ＜20，t ∈N ）．…．（3分） ②当20≤t ≤30，t ∈N 时，设P =at +b ，将（20，40），（30，30）代入，解得所以 P =-t +60（20≤t ≤30，t ∈N ），…．（6分）综上所述 ∈ ∈…．（7分） （II ）依题意，有y =P •Q ，得 ∈ ∈…．（9分）化简得 ∈ ∈整理得 ∈∈…．（11分） ①当0≤t ＜20，t ∈N 时，由y =-（t -10）2+900可得，当t =10时，y 有最大值900元．…（12分）②当20≤t ≤30，t ∈N 时，由y =（t -50）2-100可得，当t =20时，y 有最大值800元．…．（13分） 因为 900＞800，所以在第10天时，日销售额最大，最大值为900元．…．（14分） 【解析】（Ⅰ）通过讨论t 的范围，求出函数的表达式即可；（Ⅱ）先求出函数的表达式，通过讨论t 的范围，求出函数的最大值即可．本题考查了求函数的表达式问题，考查分段函数，函数的最值问题，是一道中档题．21.【答案】解：（Ⅰ）根据题意，若函数为偶函数，则f （-x ）=f （x ），即，解得：t =1；（Ⅱ）由（Ⅰ）的结论，，则f （x ）在[a ，b ]上是增函数，若当x ∈[a ，b ]时，函数f （x ）的值域为，则，解得a =b =1；又由b ＞a ，所以不存在满足要求的实数a ，b ． 【解析】（Ⅰ）根据题意，由函数奇偶性的定义可得，据此分析可得t 的值；（Ⅱ）根据题意，由函数的解析式分析可得f （x ）在[a ，b]上是增函数，结合题意分析可得，解可得a 、b 的值，结合a 、b 的关系分析可得答案．本题考查函数的奇偶性与单调性的综合应用，涉及函数的定义域与值域问题，属于基础题． 22.【答案】解：（1）当≤a ≤时N （a ）=f （），M （a ）=f （1），此时g （a ）=f （1）-f （）=a +-2；当＜a ≤1时N （a ）=f （ ），M （a ）=f （3）， 此时g （a ）=f （3）-f （）=9a +-6； ∴g （a ）=＜…（6分） （2）当≤a ≤时，∵g （a ）=a +-2，∴g ′（a ）=1-＜0， ∴g （a ）在[，]上单调递减．同理可知g（a）在（，1]上单调递增∴g（a）min=g（）=．…（12分）【解析】（1）根据已知条件a＞0，知函数是二次函数，其图象是开口向上的抛物线．因此讨论对称轴：x=与区间[1，3]的关系，得到函数的单调性后再找出相应的最值，即可得g（a）的解析式；（2）通过求导数，讨论其正负，可得到函数g（a）在区间[，]上单调减，而在（，1]上单调增，因此不难得出g（a）的最小值为g（）=．本题考查了二次函数在闭区间上的最值问题，属于基础题．研究二次函数的最值的关键是用其图象，或用导数研究它的单调性．23.【答案】解：（1）函数f（x）=1-（a＞0且a≠1）是定义在（-∞，+∞）上的奇函数，∴f（0）=1-=0，解得：a=2；……………………（2分）（2）证明：设x1、x2为定义域（-∞，+∞）上的任意两个实数，且x1＜x2，则f（x1）-f（x2）=（1-）-（1-）=-：=；……………………（4分）又x1＜x2，∴ -＜0，+1＞0，+1＞0；∴f（x1）-f（x2）＜0，即f（x1）＜f（x2）；…………………………（5分）∴函数f（x）在定义域（-∞，+∞）内是增函数；………………………………（6分）（3）由（1）得f（x）=，当0＜x≤1时，f（x）＞0；…………………………（7分）∴当0＜x≤1时，tf（x）≥2x-2恒成立，等价于t≥=对任意的x∈（0，1]恒成立，……………………（8分）令m=2x-1，即t≥m-+1；当0＜m≤1时成立，即t≥m-+1在（0，1]上的最大值，…………………………（10分）易知y=m-+1在（0，1]上单增∴当m=1时y=m-+1有最大值0，……………………………（11分）所以实数t的取值范围是[0，+∞）．……………………………（12分）【解析】（1）根据函数f（x）为定义域R上的奇函数，利用f（0）=0求得a的值；（2）根据单调性的定义证明函数f（x）在定义域R上增函数；（3）由题意把问题转化为t≥对任意的x∈（0，1]恒成立，构造函数求函数的最大值即可得出实数t的取值范围．本题考查了函数的单调性与奇偶性的应用问题，也考查了不等式恒成立问题，是中档题．。

河北省武邑中学2018-2019学年上学期高一入学考试数学试题注意事项：1．本试卷分试题卷和答题卡两部分，请将答案写在答题卡上每题对应的答题区域内，写在试题卷上无效．2．考试结束，请将本试题卷和答题卡一并上交．3．参考公式：二次函数图象的顶点坐标是（，）．一、选择题（下列各小题中，只有一个选项是符合题目要求的，请在答题卡上指定的位置填涂符合要求的选项前面的字母代号.）1.下列计算正确的是（）A. B. C. D. ＝2.若，且，则是（）A. 第一象限角B. 第二象限角C. 第三象限角D. 第四象限角3. 如图是某几何体的三视图，则这个几何体是（）A. 圆柱B. 球C. 圆锥D. 棱柱4.已知点）在平面直角坐标系的第二象限内，则的取值范围在数轴上可表示为（阴影部分）( )A. B.C. D.5.某同学在用描点法画二次函数的图象时，列出了下面的表格：x …－2 －1 0 1 2 …y …－11 －2 1 －2 －5 …由于粗心，他算错了其中一个值，则这个错误的数值是( )A. －11B. －2C. 1D. －56.如图，均匀地向此容器注水，直到把容器注满．在注水的过程中，下列图象能大致反映水面高度随时间变化规律的是（）A. B. C. D.7.实数在数轴上的位置如图所示，则下列结论正确的是（）A. a+b＞0B. a﹣b＞0C. a•b＞0D. ＞08.如图，是边长为1的小正方形组成的网格上的两个格点，在格点中任意放置点，恰好能使△ABC的面积为1的概率是（）A. B. C. D.9.若等腰三角形中有两边长分别为2和5，则这个三角形的周长为（）A. 9B. 12C. 7或9D. 9或1210.设函数，的定义域为，且是奇函数，是偶函数，则下列结论中一定正确的是（）A. 是偶函数B. 是奇函数C. 是奇函数D. 是奇函数11.如图，正方形ABCD中，E是BC边上一点，以E为圆心，EC为半径的半圆与以A为圆心，AB为半径的圆弧外切，则sin∠EAB的值为（）．A. B. C. D.12.下列命题：①三角形的内心到三角形三个顶点的距离相等；②如果，那么；③若关于x的方程的解是负数，则m的取值范围为m<-4；④相等的圆周角所对的弧相等；⑤对于反比例函数，当﹥-1时，y随着x的增大而增大其中假命题有A. 1个B. 2个C. 3个D. 4个13.设则的最大值是（）A. B. 18 C. 20 D. 不存在14.在下列四个图案中，不是中心对称图形的是（）A. B. C. D.15.出售某种文具盒，若每个可获利元，一天可售出（）个．当一天出售该种文具盒的总利润最大时，的值为( )A. 1B. 2C. 3D. 4二、解答题（将解答过程写在答题卡上指定的位置．本大题共有9小题，计75分．）16.先化简，再求值：，其中是方程的根。