映射导学案

映射的概念一、学习目标：1.了解映射的概念，能够判定一些简单的对应是不是映射2.通过对映射特殊化的分析，揭示出映射与函数之间的内在联系二、课前预习：1.一般地，设A 、B 是两个非空集合.如果按某种对应法则f .对于A 中的每一个元素，在B 中都有 的元素与之对应，那么，这样的单值对应叫做集合A 到B 的映射，记作 。

2.由映射的概念可以看出，映射是 概念的推广，特殊地，在函数概念中，A 、B 为两个 。

3.一般地，在没有任何限制的条件下，将一个含n 个元素的集合映射到一个含m 个元素的集合的映射共有 个（+∈N n m ,）。

三、典型例题：例1．设f ：A →B 是从集合A 到集合B 的映射，则下面说法正确的是________．(填序号)①A 中的每一个元素在B 中必有元素与之对应； ②B 中每一个元素在A 中必有元素与之对应；③A 中的一个元素在B 中可以有多个元素与之对应 ④A 中不同元素在B 中对应的元素可能相同．例2．下列集合A 到集合B 的对应中，不能构成映射的是________．(填序号)例3．给出下列两个集合之间的对应法则，回答问题：①A ＝{你们班的同学}，B ＝{体重}，f ：每个同学对应自己的体重；②M ＝{1,2,3,4}，N ＝{2,4,6,8}，f ：n ＝2m ，n ∈N ，m ∈M ；③M ＝R ，N ＝{x |x ≥0}，f ：y ＝x 4；④A ＝{中国，日本，美国，英国}，B ＝{北京，东京，华盛顿，伦敦}，f ：对于集合A 中的每一个国家，在集合B 中都有一个首都与它对应．上述四个对应中映射的个数为______，函数的个数为______．例4．集合A ＝{1,2,3}，B ＝{3,4}，从A 到B 的映射f 满足f (3)＝3，则这样的映射共有________个．四、检测反馈1．已知集合P ＝{x |0≤x ≤4}，Q ＝{y |0≤y ≤2}，则下列能表示从P 到Q 的映射的是________．(填序号)①f ：x →y ＝12x ；②f ：x →y ＝13x ；③f ：x →y ＝23x ；④f ：x →y ＝x .2．下列集合A ，B 及对应法则能构成函数的是______．(填序号)①A ＝B ＝R ，f (x )＝|x |； ②A ＝B ＝R ，f (x )＝1x ；③A ＝{1,2,3}，B ＝{4,5,6,7}，f (x )＝x ＋3； ④A ＝{x |x >0}，B ＝{1}，f (x )＝x 0.3．设f ：A →B 是集合A 到集合B 的映射，其中A ＝{正实数}，B ＝R ，f ：x →x 2－2x －1，求A 中元素1＋2在B 中的对应元素和B 中元素－1在A 中的对应元素．4．已知集合A ＝R ，B ＝{(x ，y )|x ，y ∈R }，f ：A →B 是从A 到B 的映射，f ：x →(x＋1，x 2＋1)，求A 中元素2在B 中的对应元素和B 中元素⎝ ⎛⎭⎪⎫32，54在A 中的对应元素．。

赣马高级中学2010级高一数学导学案20 映射的概念知识网络映射⎪⎩⎪⎨⎧映射与函数的关系映射的概念对应的概念学习目标1、了解映射的概念，能够判定一些简单的对应是不是映射。

2、通过对映射特殊化的分析，揭示出映射与函数之间的内在联系。

1、对应是两个集合元素之间的一种关系，对应关系可用图示或文字描述来表示。

2、一般地设A 、B 两个集合，如果按__________，对于A 中的_____元素，在B 中都有____的元素与之对应，那么，这样的____对应叫做集合A 到集合B 的映射，记作：________.3、由映射的概念可以看出，映射是函数概念的推广，特殊在函数概念中，A 、B 为两个___________。

一、 判断对应是否为映射例1、下列集合M 到P 的对应f 是映射的是( )A.M={－2，0，2}，P={－1，0，4},f ：M 中数的平方B.M={0，1}，P={－1，0，1}，f:M 中数的平方根C.M=Z ，P=Q ，f:M 中数的倒数。

D.M=R ，P=R +，f:M 中数的平方二、映射概念的应用例2、已知集合A=R ，B={(x,y)|x,y ∈R}，f:A →B 是从A 到B 的映射，f:x →(x+1,x 2+1)，求A 中的元素2在B 中的象和B 中元素(23,45)在A 中的原象。

三、映射与函数的关系例3、给出下列四个对应的关系①A=N*,B=Z,f:x →y=2x －3；②A={1，2，3，4，5，6}，B={y|y ∈N*,y ≤5}，f:x →y=|x －1|；③A={x|x ≥2}，B={y|y=x 2－4x+3}，f:x →y=x －3；④A=N,B={y ∈N*|y=2x －1，x ∈N*}，f:x →y=2x －1。

上述四个对应中是函数的有( )A.①B.①③C.②③D.③④1、下列对应是A 到B 上的映射的是( )A.A=N*,B=N*,f:x →|x －3|B.A=N*，B={－1,1, －2}，f:x →(－1)xC.A=Z,B=Q,f:x →x3 D.A=N*，B=R ，f:x →x 的平方根2、设f:A →B 是集合A 到B 的映射，下列命题中是真命题的是( )A.A 中不同元素必有不同的象B.B 中每一个元素在A 中必有原象C.A 中每一个元素在B 中必有象D.B 中每一个元素在A 中的原象唯一3、已知映射f: A →B,下面命题(1)A 中的每一个元素在B 中有且仅有一个象；(2)A 中不同的元素在B 中的象必不相同；(3)B 中的元素在A 中都有原象(4)B 中的元素在A 中可以有两个以上的原象也可以没有原象。

2017年8月4日高一数学映射导学案一． 学习本节知识点：1. 映射概念：一般地，设A 、B 是两个______，如果按照某种对应法则f ，对于集合A 中的_______元素，在集合B 中都有_________元素和它______，那么这样对应(包括集合A 、B 以及A 到B 对应法则f )叫做_____________记作A B f →：。

2.象与原象：如果A 中元素a 对应的B 中的元素b ，则b 是a ____，而a 叫做b _____3.一一映射：对于A B f →：映射，①A 中每一个元素在 B 中都有________象与之对应②A 中不同元素象也不同 ③B 中的每一个元素都有原象，满足以上条件映射叫做A 到B 一一映射。

4.对应，映射，一一映射的关系：5.映射与函数的关系：二．本节知识点涉及题型举例：（Ⅰ）概念理解：1.在映射f :A→B 中,下列判断正确的是( )A 中任一元素在B 中都有象,但不一定唯一B 中某些元素在A 中可能有多个原象,也可能没有原象 C.集合A 和B 一定是数集D f :A→B 与f : B→A 含义是一样2.给出下列四个对应：① ② ③ ④构成映射是（ ）A 只有①② B 只有①④ C 只有①③④ D 只有③④3.已知集合{04}P x x =≤≤，{02}Q y y =≤≤，下列不表示从P 到Q 映射是（ ）1:2A f x y x →= 1:3B f x y x →= 2:3C f x y x →=:D f x y → 4.设A={x|0≤x ≤2},B={y|1≤y ≤2},如下图,能表示从集合A 到集合B 的映射是（ ）5．设f ：x →x 2是集合A 到集合B 的映射，如果B={1，2}，则A ∩B 等于( )A ．{1}B ．ΦC ．Φ或{1}D ．Φ或{2}6.从集合A 到B 的映射中，下列说法正确是（ ）① B 中某一元素的原象可能不只一个 ② A 中某一元素的象可能不只一个 ③A 中两个不同元素的象必不相同 ④ B 中两个不同元素的原象可能相同 ⑤若集合A 是无限集,集合B 是有限集,则一定不能建立一个从集合A 到集合B 的映射⑥若集合A={a},B={1,2},则从集合A 到集合B 只能建立一个映射⑦若集合A={1，2}，B={a},则从集合A 到集合B 只能建立一个映5．点),(b a(Ⅱ)映射个数求法：1. 从集合A={a,b}到集合B={x,y}的映射有多少个.？2. 集合A={3,4},B={5,6,7},则A 到B 的映射个数与从B 到A 的映射个数各是多少？3．从集合M={0，1，2}到集合N={1，2，3，4}的不同映射的个数是（ ）A.81B.64C.24D.12(Ⅲ)象与原象1若x 在映射f :R→R 下象是x 2-1,则3在f 下原象是( ) A.2 B.-2 C.2和-2 D.83. 给定从A 到B 映射f :{(x,y)}→{(x 2+y 2,xy)},则象(5,2)的原象是4.已知（x ，y ）在映射f 下象是，那么（﹣5，2）在f 下原象是（ ）A ． （-10，4）B ．（-6，-4）C ．（-3，-7）D ．（-23，-27） 5.若点（x ，y ）在映射f 下的象是点（x+y ，x ﹣y ），则在映射f 下点（2，1）的象是（ ）A ．（3，1）B ．（23，21） C ．（23，-21） D ．（1， 3） 三．课后作业：1．下列对应是从集合A 到集合B 的映射是（ ）A ．A =R ，B ={x |x ＞0且x ∈R}，x ∈A ，f ：x →|x | B ．A =N ，B =N ＋，x ∈A ，f ：x →|x －1|C ．A ={x |x ＞0且x ∈R}，B =R ，x ∈A ，f ：x →x 2D ．A =Q ，B =Q ，f ：x →x 12，已知映射f:A →B ，其中A =B =R ，对应法则f:x →y =−x 2+2x ，对于实数k ∈B 在集合A 中存在不同的两个原象，则k 的取值范围是（ ） A ．k >1 B ．k ≤1 C ．k ≥1 D ．k <14．已知函数①；②y=x 2﹣4x+1（x ≤0）；③y=3x+1；④。

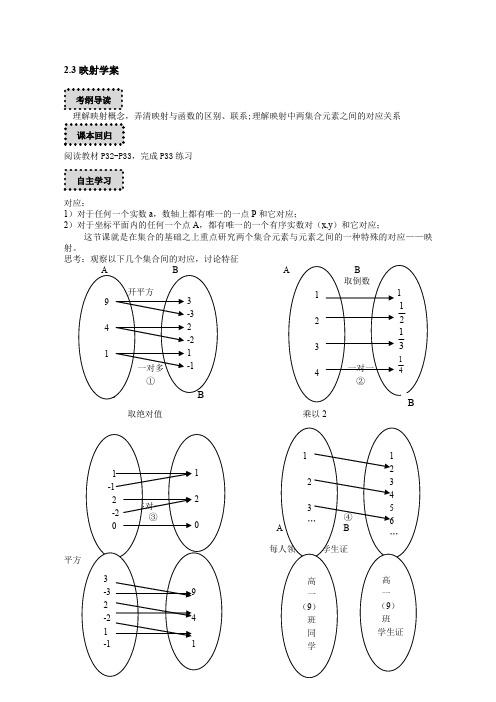
映射【学习目标】1．了解映射的概念及表示方法．2．会利用映射的概念来判断“对应关系”是否是映射．3．感受对应关系在刻画函数和映射概念中的作用．【重点突破】1．利用映射的概念判断“对应关系”是否是映射(重点)．2．映射与函数的关系(易混点)．【预习导学】一、基础梳理1、映射(1)映射的概念两个集合A与B间存在着对应关系，，而且对于A中的元素x，B中总有的一个元素y与它对应，就称这种对应为从A到B的映射，记作．(2)像与原像的概念在映射f：A→B中，称为原像，称为x的像．记作．2．一一映射一一映射是一种特殊的映射，它满足：①A中每一个元素在B中都有与之对应；②A中的元素的像也不同；③B中的每一个元素都有．3．函数与映射设A、B是两个非空数集，厂是A到B的一个，那么映射就叫作A 到B的函数．即函数是一种特殊的映射，是从到的映射．二、思考探究1．如何题解映射的概念？【探究】对映射的理解，应注意以下五点：(1)非空性：集合A、B不能为空集．(2)方向性：f：A→B是由A到B的映射，与f：B→A一般是不同的．(3)存在性：A中的每一个元素在B中都存在像．(4)唯一性：A中每个元素在B中必有唯一的像．(5)特殊性：对于A中的不同元素，在B中可以有相同的像，可以是一对一，多对一，但不能是一对多．允许B中的元素没有原像．2．如何理解一一映射的概念?【探究】一对一：一一映射f：A→B中，要求原像不同，像也不同，A、B中元素都不剩余．(2)集合A中不同的元素在集合B中有不同的像，集合B中的元素都有不同的原像．(3)可逆性：若映射f：A→B是一一映射，则集合B到集合A的映射一定是一一映射'f：B→A．【达标训练】1．给出下列4个对应，是映射的是( )．A．③④B．①②C．②③D．①④2．D．对集合A中的数立方3．4．5．6．【拓展延伸】4．５．。

线性映射及其运算导学案
概述
本文档将介绍线性映射的概念以及与其相关的运算。

线性映射的定义
线性映射是指一个向量空间到另一个向量空间的映射，同时满
足以下两个条件：
1. 对于任意向量a和b，映射对向量的加法运算是封闭的。

即，映射(a+b)的结果等于映射a和映射b的结果之和。

2. 对于任意向量a和标量k，映射对标量的乘法运算是封闭的。

即，映射(k*a)的结果等于k乘以映射a的结果。

线性映射的性质
线性映射具有以下性质：
1. 线性映射保持向量空间中的零向量。

即，映射(0)的结果等于0。

2. 线性映射对向量的减法运算也是封闭的。

即，映射(a-b)的结
果等于映射a减去映射b的结果。

3. 线性映射对向量的线性组合运算也是封闭的。

即，映射(k*a + l*b)的结果等于k乘以映射a的结果加上l乘以映射b的结果，其中k和l为标量。

线性映射的运算
线性映射之间的运算包括加法运算和标量乘法运算：
1. 加法运算：对于两个线性映射，其加法运算的结果是将两个映射对应的向量分别相加得到的新映射。

2. 标量乘法运算：对于一个线性映射和一个标量，其标量乘法运算的结果是将映射对应的向量乘以该标量得到的新映射。

注意：线性映射的运算仍然满足线性映射的定义和性质。

总结
线性映射是满足特定条件的向量空间之间的映射，具有保持向量空间运算封闭性的特性。

线性映射之间可以进行加法运算和标量乘法运算，仍然满足线性映射的定义和性质。

参考资料：
- 张宇《高等数学》
- 朱彦斌《线性代数》。

户县第四中高效课堂导学案(高一数学）课题：映射（导学案10）课型：新授课班级：学生姓名：组名：主备人：吴春娥备课组长：蔡亚荣日期：一、学习目标:1.通过实例了解映射的含义，体会像与原像关系。

2.理解函数与映射的区别和联系。

重点：映射的概念。

难点：函数与映射的区别和联系。

二、课堂实施步骤：1.自主学习:(1).复习内容:求出下列函数的定义域：835yx=+；2143yx x=-+；43y x=-+已知1()1f xx=-，求(2)f，((3))f f，(())f f x.(2)背写出函数的定义：（2）.独学环节:（15分钟）认真阅读教材 P32—33页。

深入理解本节的学习目标及重难点，认真独立完成本节的题目理解映射的概念: 一般地，集合A与B间存在着，而且对于A中的每一个元素x， B中都有唯一的元素y和它对应，那么就称对应为从A到B的映射。

记作。

称为原像，称为x的像，记作下列哪些对应是从集合A到集合B的映射？（1）A={P|P是数轴上的点}，B=R, f:数轴上的点与它所代表的实数对应（2）A={P|P是平面直角坐标系上的点}，B={(x, y)|x∈R, y∈R}, f: 平面直角坐标系上的点与它的坐标对应（3）A={三角形}，B={x|x是圆}，f:每一个三角形都对应它的内切圆（4）A ={x|x是人英中学的班级}，B={x|x是人英中学的学生}，f:每个班级都对应班里的学生点拨：©映射有三个要素：两个集合，一种对应关系，缺一不可；© A ，B 可以是数集，也可以是点集或其它集合。

这两个集合具有先后顺序：符号“f ：A →B ”表示A 到B 的映射，符号“f ：B →A ”表示B 到A 的映射，两者是不同的；© 集合A 中的元素在集合B 中一定有元素和它对应，并且是唯一的；但集合B 中的元素在A 中可以没有元素和它对应，即使有也可以不唯一。

2.对学、群学、组内展示环节问题1计算：. 如果(x , y )在映射f 的作用下的像为(x +y , x y )，其中x , y ∈R ，则（1,2）的像是（2，—3）的原像是 。

课题 映射的概念编制人:陈忠明 审核人:张志勇 使用时间:例1 探究下列从集合A 到集合B 的对应法则，哪些是映射？（1）A ={P | P 是数轴上的点}，B =R ； 对应法则：数轴上的点与它所代表的实数对应；（2）A ={三角形}，B ={圆}；对应法则：每一个三角形都对应它的外接圆；（3）A ={ P | P 是平面直角体系中的点}，{(,)|,}B x y x R y R =∈∈； 对应法则：平面直角坐标系中的点与它的坐标对应；（4） A ={高一学生}，B = {高一班级}. 对应法则：每一个班级都对应班里的学生。

变式：若是从集合B 到集合A 呢？例2 设A={1，2，3，4，5}，B={1，3，7，15，31，33}，下列对应f ：A →B 是从A 到B 的映射的是（ ）A ．f ：x →12+-x x B. f: x →2)1(-+x x C. f ：x →121--x D. f ：x →12-x※ 学习小结判定某对应关系是否是映射主要看两条：一条是A 集合中的元素都要有对应，但B 中元素未必要有对应；二条是A 中元素与B 中元素只能出现“一对一”或“多对一”的对应形式．※ 当堂检测（时量：5分钟 满分：10分）计分：1. 已知下列四个对应，其中是从A 到B 的映射的是（ ）A B A B A B A Ba m a m a a mb n b m nc n b p c b p (1) (2) (3) (4) A. (3)(4) B. (1)(2)C. (2)(3)D. (1)(4) 2. 下列对应:f A B →： ① {},0,:;A R B x R x f x x ==∈>→②*,,:1;A N B N f x x ==→-③{}20,,:.A x R x B R f x x =∈>=→不是从集合A 到B 映射的有（ ）.A. ①②③B. ①②C. ②③D. ①③3.已知A={x ∣40≤≤x }, B={ y ∣20≤≤y },下列对应中不表示从A 到B 的映射的是( )A.f:x →y=41x,B.f: x →y=3231+xC.f:x →y=x 43, D.f: x →x y =课后作业1. 下列对应是否是集合A 到集合B 的映射？（1）A ={1，2，3，4}，B={3，4，5，6，7，8，9}，对应法则:21f x x →+；（2）*,{0,1}A N B ==，对应法则:f x x →除以2得的余数；（3）A N =，{0,1,2}B =，:f x x →被3除所得的余数；（4）设111{1,2,3,4},{1,,,}234X Y ==1:f x x→；（5）{|2,},A x x x N B N =>∈=，:f x →小于x 的最大质数. 2. 设集合A 和集合B 都是正整数集合, 映射f: A →B 把集合A 中的元素x 映射到集合B 中的元素x x +2,则在映射f 下,与集合B 中的20对应的元素是A 中的( )A. 2,B. 3,C. 4,D. 5。

第10课时映射的概念教学过程一、问题情境函数是建立在两个非空数集之间的单值对应,而对于某班级全体同学组成的集合与其体重数组成的集合之间的对应,又该如何定义呢?二、数学建构(一)生成概念问题1对应是什么?函数是什么?(对应是两个集合元素之间的一种关系,对应关系可用图示或文字描述来表示)问题2讨论“即时体验”中两个例子的区别与联系.(引导学生发现与函数概念的区别,总结出不同之处的关键词)通过讨论,结合函数的概念,给出映射的定义.一般地,设A,B是两个非空集合,如果按某种对应法则f,对于A中的每一个元素,在B中都有唯一的元素与之对应,那么这样的单值对应叫做从集合A到集合B的映射,记作f:A→B.(二)理解概念1.函数是映射,但映射不一定是函数.映射是函数概念的推广,特殊之处是在函数的概念中,A,B为两个非空数集.2.单值对应的理解:对于A中的每一个元素,在B中都有唯一的元素与之对应.三、数学运用【例1】(教材P46例1)下图所示的对应中,哪些是从A到B的映射?(1)(2)(3)(4)(见学生用书课堂本P29) [处理建议]引导学生比较、分析、归纳,从而使他们更好地理解映射的概念.[规范板书]解根据映射的定义,可以知道,(4)的对应是从A到B的映射,(1)、(2)、(3)的对应不是从A到B的映射.[题后反思]映射中的对应可以是一对一或多对一,但不能一对多.变式下列从集合M到集合P的对应f中,是映射的是①.(填序号)①M={-2, 0, 2},P={-1, 0, 4},f:M中的数的平方;②M={0, 1},P={-1, 0, 1},f:M中的数的平方根;③M=Z,P=Q,f:M中的数的倒数;④M=R,P={正实数},f:M中的数的平方.[处理建议]判定对应f:M→P是否是映射,关键是看是否符合映射的定义,即集合A中的每一个元素在集合B中是否有象并且唯一,若不是映射只要举一反例即可.【例2】设集合A=B={(x,y)|x∈R,y∈R},f:A→B是从集合A到集合B的映射,且f:(x,y)→(x+y,x-y).求:(1)在B中与A的元素(2, 3)对应的元素;(2)在A中与B的元素(2, 3)对应的元素.(见学生用书课堂本P29)[处理建议]指导学生分清集合A,B中x与y之间的对应关系.[规范板书]解(1)A中的元素(2, 3),对应B中的元素为(2+3, 2-3),即为(5,-1).(2)设B中的元素(2, 3)对应A中的元素为(x,y),则根据题意得错误！未找到引用源。