平面齿轮机构设计(甲类精制)
- 格式:doc
- 大小:182.00 KB
- 文档页数:27



齿轮机构及其设计齿轮机构是现代机械中应用最广泛的一种传动机构。
与其它传动机构相比,齿轮机构的优点是结构紧凑,工作可靠,效率高,寿命长,能保证恒定的传动比,而且其传动的功率与适用的速度范围达。
但是,其制造安装费用较高,及精度齿轮传动的振动噪声较大。
齿轮机构根据实现传动比的情况,分为定传动比和变传动比齿轮机构。
定传动比的圆形齿轮机构根据两传动轴线的相对位置,可分三类:平行轴齿轮机构(两齿轮的传动轴线平行)、相交轴齿轮机构(两齿轮的传动轴线相较于一点)、交错轴齿轮机构(两齿轮的传动轴线为空间任意交错位置)。
1.瞬时传动比两齿轮的传动比总等于齿数的反比,即n1/n2=z2/z1,但其瞬时传动比却与齿廓的形状有关。
按三心定理,公法线n-n与二齿轮连心线的交点C为二齿轮的相对速度瞬心,即二齿轮在C点的线速度应相等:ω1 O1C=ω2 O2C,由此得瞬时传动比і12:і12= ω1/ω2= O2C/ O1C=r2/r1该式说明,具有任意齿廓的二齿轮啮合时,其瞬时角速度的比值等于齿廓接触点公法线将其中心距分成两段长度的反比。
这就是齿廓啮合基本定律。
满足齿廓啮合基本定律的传动比为常数或按一定规律变化的一对齿廓称为共轭齿廓。
在齿轮机构中,相对速度瞬心C称为啮合节点,简称节点。
为实现定传动比传动,要求两齿廓在任何位置啮合时,其节点C都为中心线上的一个固定点,分别以O1、O2为圆心、以O1C 和O2C为半径的圆C1和C2,称为齿轮的节圆(注意非分度圆)。
故节圆是齿轮的相对瞬心线,齿轮的啮合传动相当于其两节圆作无滑动的纯滚动。
2.渐开线圆柱齿轮及其基本齿廓1)齿轮的各部分名称•齿顶圆(直径d a)•齿根圆(直径d f)•齿厚(分度圆处s,任意圆周处sі)•齿槽宽(分度圆处e,任意圆周处eі)•齿距(分度圆处p,任意圆周处pі=sі+eі)•分度圆(直径d,规定标准齿轮分度圆上的齿厚s与齿槽宽e相等,即s=e=1/2 p)•齿顶高(齿顶部分的径向高度h a)•齿根高(齿根部分的径向高度h f)•全齿高(齿顶圆与齿根圆之间的径向距离,h=h a+h f)。


平面齿轮机构设计一、特点:1)功率和速度范围↑。
2)η↑。
3)寿命长。
4)保证精确角速比,传动比i。
5)制造设备要求↑(专门机构,刀具),成本↑,装配要求↑。
二、分类1、按两齿轮轴相对位置分:平行,相交,交叉。
平行(外啮合,内啮合):直齿,斜齿,人字齿,图8-1(a,b,c);相交:直齿圆锥,斜齿圆锥,曲齿圆锥,图8-4(a,b,c);交错:螺旋(图8-5),蜗轮蜗杆(图8-7),双曲线体(图8-6)。
2、按两齿轮相对运动:a).平面运动机构(平行轴);b).空间运动机构(其他:相交,交叉)。
3、按齿廓曲线分:渐开线,摆线,圆弧。
§7-2 齿廓啮合基本定理与渐开线齿廓(图8-8)一、齿廓啮合基本定理(齿廓曲线与齿轮传动比关系)一对齿轮啮合传动是靠主动轮的齿廓推动从动轮的齿廓来实现的,所以当主动轮按一定角速度转动时,从动轮转动角速度显然与两轮齿廓的形状有关,也就是说:两齿轮传动时,其传动比变化规律与两轮齿廓曲线有关。
两轮角速比称传动比:i=ω1/ω2=常数。
如图:为一对互相啮合的齿轮:主动轮1,ω1方向从动轮2,ω2 方向两轮齿齿廓C1,C2在K点接触,两轮在K点的线速度分别为V k1,V k2,过点k 作两齿廓公法线n-n,要一对齿廓能连续地接触传动,它们沿接触点的公法线方向是不能有相对运动的。
否则,两齿廓将不是彼此分离就是互相嵌入,因而不能达到正常传动目的。
这就是说,要使两齿廓能够接触传动,则V k1和V k2在公法线n-n方向的分速度应相等,所以两齿廓接触点间的相对速度V k2k1只能沿两齿廓接触点的公切线方向,设以η表示两齿廓在接触点的公法矢量,则有:V k2k1 xη=0。
这就是齿廓的啮合基本要求,上式为齿廓啮合基本方程式,由于V k1和V k2在公法线方向分速度应相等。
故:故由图得:P--啮合点齿廓公法线(n-n)和连心线交点上式表明:互相啮合传动的一对齿轮,在任一位置时的传动比,都与其连心线O1O2被其啮俣合齿廓在接触点处的公法线所分成的两段成反比---齿廓啮合基本定理。

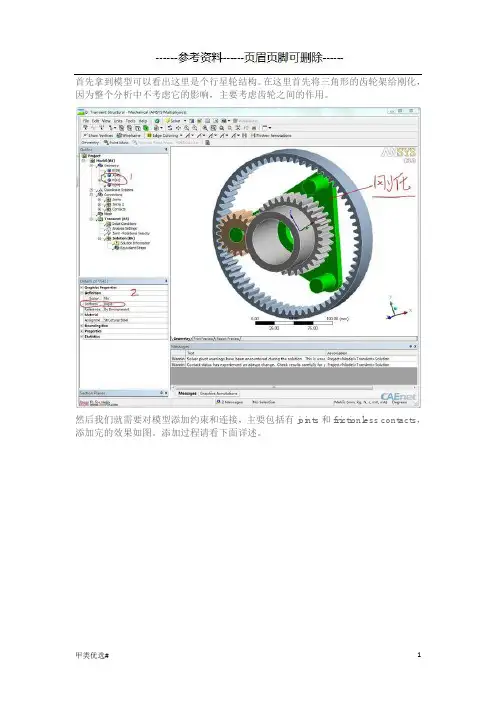
摘要平面齿轮连杆组合机构的分析与仿真学科名称: 机械设计及理论论文作者: 王有飞 签名:指导教授: 刘凯(教授) 签名:答辩时间:摘 要本文主要研究对象是功能丰富的平面齿轮连杆组合机构,借助运动学原理作者详细地分析了传动比对机构特征曲线的影响,得到各类型机构的特征曲线,并利用VC 软件开发出相应的运动仿真软件,再现该机构的三维实体运动过程。
该方法大大节约设计者在机构的实现和检验上所花费的时间,减少重复性劳动,同时通过虚拟模拟机构的运动,也锻炼了设计者的创新能力。
本文主要工作如下:首先,利用闭合矢量方程法,推导出9种组合机构各自的数学模型,建立运动学参数计算所需要的方程。
其次,利用MatLab软件和数值分析的方法求解该方程,得到各类型机构的运动参数值,同时也为以后的三维实体运动仿真提供了可靠的数据。
通过深入地分析输出结果,得到各类型机构的特征曲线与传动比的关系图。
再次,通过两种参数化建模方法创建了构件的三维模型库。
利用连杆机构和齿轮机构参数间的固有约束关系开发出Fourbar_gear验证软件,用该软件检查已建立的零件尺寸值是否满足指定类型的机构,改变零件的尺寸值直到满足了指定类型,然后再输出结果,这样做的目的是避免运动干涉。
最后,开发出的运动仿真软件通过加载动态链接库到SolidWorks软件中,再现了机构的运动轨迹,所开发的软件具有界面友好、操作简单等优点。
【关键词】:特征曲线 运动仿真 API 二次开发iAbstractThe Analysis and Simulation of Planar Gear-Linkage MechanismSPECIALTY: Mechanical Design & TheoryCANDIDATE: Wang.Youfei SIGNATURE: SUPERVISOR: Liu.Kai (professor)SIGNATURE:ABSTRACTThis paper is mainly focus on the planar gear-linkage mechanism (GLM), which canbe applied in various ways. The author use the basic kinematics theory to analysis the influences of transmission ratios to the characterized curve of the GLM, put the curve on the computer screen, develop corresponding software by VC and reappear the whole process of the GLM. In virtue of the method mentioned above, a lot of time people spendon the mechanism inspection and actualization can be saved, and the innovation capability of researchers can be improved by the virtual simulation of the movement of the GLM.Firstly, based on close-vector-equation method, the mathematic models of nine kindsof the GLM are established. Secondly, the equations are resolved by numerical computing method, as a result, the values of kinematics parameters are gained, which can offer realized data for immediately simulation. The relational graph between transmission ratios and characterized curve can be obtained, after the serious analysis of the output. Thirdly, the 3D part library is developed by two ways of parameter driving, and the problems of collision among models are avoided by “Fourbar-gear” software. Lastly, the author develops the simulation software by loading DLL in SolidWorks to reappear the 3D movement of the GLM.Key Words: characterized curve movement simulation API the second developmentii目录目录1前言 (1)1.1 选题背景 (1)1.2 国内外研究现状 (2)1.3 本文的主要工作 (4)1.3.1 平面齿轮组合机构的运动分析 (4)1.3.2 运动学参数求解和运动曲线的输出 (4)1.3.3三维零件库的创建和Fourbar_gear验证软件 (4)1.3.4 机构的组装和运动动画仿真的实现 (4)2 平面齿轮连杆组合机构的运动分析 (6)2.1 平面齿轮连杆组合机构的组成规则 (6)2.2 平面齿轮连杆组合机构的分类 (6)2.3 平面齿轮连杆组合机构的运动分析 (7)2.3.1 简单型回归式齿轮曲柄摇杆机构 (7)2.3.2 最简型回归式齿轮曲柄摇杆机构 (8)2.3.3 简单型非回归式齿轮曲柄摇杆机构 (9)2.3.4 最简型非回归式齿轮曲柄摇杆机构 (9)2.3.5 最简型回归式齿轮曲柄滑块机构 (10)2.3.6 最简型非回归式齿轮曲柄滑块机构 (10)2.3.7 最简型回归式齿轮导杆、摇块组合机构 (11)3平面齿轮连杆组合机构中构件的参数化建模和零件库的建立 (13)3.1 程序驱动参数化建模实例(齿轮构件) (13)3.1.1 系统界面设计模块 (13)3.1.2 齿形计算与生成模块 (13)3.1.3 轮毂生成模块 (14)3.1.4三维实体模型生成模块 (14)3.1.5 渐开线齿廓的数学模型建立 (14)3.2 尺寸驱动参数化建模实例(杆构件) (16)3.3 三维零件库的建立 (17)3.3.1 零件库的用途 (17)3.3.2 零件库的开发要求 (18)3.4 Fourbar_gear软件介绍 (19)4 平面齿轮连杆组合机构运动参数的求解 (23)4.1 机构运动参数的求解 (23)4.1.1 最简型回归式齿轮曲柄滑块机构 (24)4.1.2最简型非回归式齿轮曲柄滑块机构 (27)4.1.3 简单型非回归式齿轮曲柄摇杆机构 (28)4.1.4 最简型非回归式齿轮曲柄摇杆机构 (31)4.1.5 最简型回归式齿轮曲柄摇杆机构 (31)4.1.6 最简型非回归式齿轮双曲柄机构 (31)4.1.7 最简型回归式齿轮双曲柄机构 (32)4.1.8 最简型回归式齿轮导杆机构 (32)5 三维实体动画仿真的制作 (35)5.1机构的装配 (35)iii目录iv5.1.1 三维平移变换 (35)5.1.2 绕坐标轴的三维旋转变换 (36)5.1.3 混合变换 (36)5.1.4 装配体中实体零件的添加 (37)5.1.5 零件的位置设置 (37)5.2 动画仿真设计的核心技术 (37)5.2.1 Mat文件中数据的输出 (38)5.2.2 构件的运动控制 (39)5.3 SolidWorks二次开发 (39)5.3.1 SolidWorks二次开发的方法 (40)5.3.2 向软件中添加用户自定义的各类资源 (42)a. 用户菜单的添加 (42)b. 用户工具栏的添加 (42)c. 对话框资源的添加 (43)5.4 平面齿轮连杆组合机构中相关类的设计 (44)5.5 平面齿轮组合机构的界面设计 (45)6 结论 (49)致谢 (50)参考文献 (51)附录 Ⅰ (55)附录Ⅱ (56)附录Ⅲ (57)1 前言1前言1.1 选题背景在对«机械原理»的学习过程中,机构由于其本身概念的抽象性和类型的多样性,使得在对它的理解和掌握上存在着一定的困难;为了实际问题的解决,有时我们不得不对已有的机构进行改进甚至直接设计出新的机构,而设计出的机构可行与否,还需要进行检验和校核。

平面齿轮机构设计一、特点:1)功率和速度范围↑。
2)η↑。
3)寿命长。
4)保证精确角速比,传动比i。
5)制造设备要求↑(专门机构,刀具),成本↑,装配要求↑。
二、分类1、按两齿轮轴相对位置分:平行,相交,交叉。
平行(外啮合,内啮合):直齿,斜齿,人字齿,图8-1(a,b,c);相交:直齿圆锥,斜齿圆锥,曲齿圆锥,图8-4(a,b,c);交错:螺旋(图8-5),蜗轮蜗杆(图8-7),双曲线体(图8-6)。
2、按两齿轮相对运动:a).平面运动机构(平行轴);b).空间运动机构(其他:相交,交叉)。
3、按齿廓曲线分:渐开线,摆线,圆弧。
§7-2 齿廓啮合基本定理与渐开线齿廓(图8-8)一、齿廓啮合基本定理(齿廓曲线与齿轮传动比关系)一对齿轮啮合传动是靠主动轮的齿廓推动从动轮的齿廓来实现的,所以当主动轮按一定角速度转动时,从动轮转动角速度显然与两轮齿廓的形状有关,也就是说:两齿轮传动时,其传动比变化规律与两轮齿廓曲线有关。
两轮角速比称传动比:i=ω1/ω2=常数。
如图:为一对互相啮合的齿轮:主动轮1,ω1方向从动轮2,ω2 方向两轮齿齿廓C1,C2在K点接触,两轮在K点的线速度分别为V k1,V k2,过点k作两齿廓公法线n-n,要一对齿廓能连续地接触传动,它们沿接触点的公法线方向是不能有相对运动的。
否则,两齿廓将不是彼此分离就是互相嵌入,因而不能达到正常传动目的。
这就是说,要使两齿廓能够接触传动,则V k1和V k2在公法线n-n方向的分速度应相等,所以两齿廓接触点间的相对速度V k2k1只能沿两齿廓接触点的公切线方向,设以η表示两齿廓在接触点的公法矢量,则有:V k2k1 xη=0。
这就是齿廓的啮合基本要求,上式为齿廓啮合基本方程式,由于V k1和V k2在公法线方向分速度应相等。
故:故由图得:P--啮合点齿廓公法线(n-n)和连心线交点上式表明:互相啮合传动的一对齿轮,在任一位置时的传动比,都与其连心线O1O2被其啮俣合齿廓在接触点处的公法线所分成的两段成反比---齿廓啮合基本定理。


平面齿轮机构设计
一、特点:
1)功率和速度范围↑。
2)η↑。
3)寿命长。
4)保证精确角速比,传动比i。
5)制造设备要求↑(专门机构,刀具),成本↑,装配要求↑。
二、分类
1、按两齿轮轴相对位置分:平行,相交,交叉。
平行(外啮合,内啮合):直齿,斜齿,人字齿,图8-1(a,b,c);相交:直齿圆锥,斜齿圆锥,曲齿圆锥,图8-4(a,b,c);交错:螺旋(图8-5),蜗轮蜗杆(图8-7),双曲线体(图8-6)。
2、按两齿轮相对运动:a).平面运动机构(平行轴);b).空间运动机构(其他:相交,交叉)。
3、按齿廓曲线分:渐开线,摆线,圆弧。
§7-2 齿廓啮合基本定理与渐开线齿廓(图8-8)
一、齿廓啮合基本定理(齿廓曲线与齿轮传动比关系)
一对齿轮啮合传动是靠主动轮的齿廓推动从动轮的齿廓来实现的,所以
当主动轮按一定角速度转动时,从动轮转动角速度显然与两轮齿廓的形状有关,也就是说:两齿轮传动时,其传动比变化规律与两轮齿廓曲线有关。
两轮角速比称传动比:i=ω1/ω2=常数。
如图:为一对互相啮合的齿轮:
主动轮1,ω1方向
从动轮2,ω2 方向
两轮齿齿廓C1,C2在K点接触,两轮在K点的线速度分别为V k1,V k2,过点k作两齿廓公法线n-n,要一对齿廓能连续地接触传动,它们沿接触点的公法线方向是不能有相对运动的。
否则,两齿廓将不是彼此分离就是互相嵌入,因而不能达到正常传动目的。
这就是说,要使两齿廓能够接触传动,则V k1和V k2在公法线n-n方向的分速度应相等,所以两齿廓接触点间的相对速度V k2k1只能沿两齿廓接触点的公切线方向,设以η表示两齿廓在接触点的公法矢量,则有:V k2k1 xη=0。
这就是齿廓的啮合基本要求,上式为齿廓啮合基本方程式,由于V k1和V k2在公法线方向分速度应相等。
故:
故由图得:
P--啮合点齿廓公法线(n-n)和连心线交点
上式表明:互相啮合传动的一对齿轮,在任一位置时的传动比,都与其连心线O1O2被其啮俣合齿廓在接触点处的公法线所分成的两段成反比---齿廓啮合基本定理。
由齿廓啮合基本定理知:如两齿轮齿廓在不同位置啮合时,过其接触点的公法线与两齿轮连心线交点的位置不同,则两齿轮传动比也不同。
两齿廓在接触点公法线方向如何,则决定于两齿廓曲线形状,所以根据齿廓啮合基本定理,即得齿廓曲线与齿轮传动林关系。
(下面就讨论此关系)
由:i12=ω1/ω2 =O1P/O2P,知:欲使i12为常数,则O1P/O2P应为一常数,由于轴心O1,O2均为(即O102为定长)所以欲使O1P/O2P为常数,则点P
在连心线上为一定点,由此得出结论:要使两齿轮作定传动比传动,则其齿廓曲线必须满足下述条件:
即:不论两齿廓在任何位置接触,过其接触点所作的齿廓公法线必须与两齿轮的连心线相交于一固定点p(节点),由于点P为定点,故在轮1上的轨迹为以O1为圆心,O1P半径圆。
由于点P为定点,故在轮2上的轨迹为以02为圆心,O2P为半径圆。
O1P、O2P---节圆。
由此可知:轮1与轮2节圆在P点相切,而且在P点两轮线速度相等:ω1O1P =ω2O2P,故两齿轮的啮合传动可以视为两节圆作无滑动的滚动。
二、渐开线性质
1、形成及其性质(如图)
形成:当一直线ll沿一圆周作纯滚动,直线上任意点K的轨迹AK,就是该圆的渐开线,这个圆称基圆。
如果发生线沿相反方向在基圆上滚动,亦可得到方向相反的同样的渐开线。
性质:(图8-10)1)发生线沿基圆滚过的长度,等于基圆滚过的圆弧长度BK=BA,KK1=AA1。
2)因发生线L-L沿基圆作纯滚动,故它与基圆的切点B即为速度瞬心,所以发生线e-e即为渐开线在点K法线,又因发生恒切于基圆,故可得结论:渐开线上任意点的法线恒为基圆的切线。
即K点的法线(e-e)=r b的切线。
3)发生线与基圆的切点B也是渐开线在点K的曲率中心,而线段BK是渐开线在点K的曲率半径,即P k=BK, P k(k 点的曲率半径)。
由图可知:渐开线愈接近于基圆的部分,其曲率半径愈小,即曲率愈大,曲线愈弯曲,反之则曲线愈平直。
4)渐开线形状。