正弦交流电的相量图表示法
- 格式:ppt
- 大小:458.50 KB
- 文档页数:6

三相电压的相量表示是将时间上连续变化的三相正弦交流电压以复数形式表达,这种方法可以直观地描述各相电压在幅值、频率以及相位上的关系。
在电力系统分析中,通常采用极坐标或直角坐标(也称作笛卡尔坐标)来表示。
极坐标表示:
对于星形连接(Y接法)的三相电源或负载,其相电压相对于同一基准(例如A相)的相量表示为:
- A相:UA = V∠0°
- B相:UB = V∠-120°
- C相:UC = V∠120°
这里的V代表每相的有效电压幅值,角度表示的是相对于A 相的相位差,按照逆时针方向,B相滞后A相120度,C相超前A相120度。
直角坐标表示:
在静止对称坐标系(如αβγ坐标系或dq0坐标系)中,也可以转换成直角坐标形式表示,但此处不涉及具体的坐标变换过程。
对于三角形连接(Δ接法)的三相电压,线电压与相电压之间的关系如下:
- 线电压UAB = UA - UB = 380∠30° (假设有效线电压为380V)
- 线电压UBC = UB - UC = 380∠-90°
- 线电压UCA = UC - UA = 380∠150°
相量图中,三个电压相量按照120度均匀分布,且同时绕着同一个轴以相同的角速度逆时针旋转,这个角速度对应的就是系统的角频率ω(对于50Hz的交流电,ω=2π×50 rad/s)。
通过相量图和相量计算,能够简化复杂电路的分析和计算。

学时:2学时教学目的:1.运用相量图分析交流电路; 2.相量图与波形图的关系。
重点:相量图的注意事项;难点:运用相量图分析交流电路。
导入新课:相量图是学习正弦交流电的基本工具,在计算相应的问题时是可以起到很好的作用的。
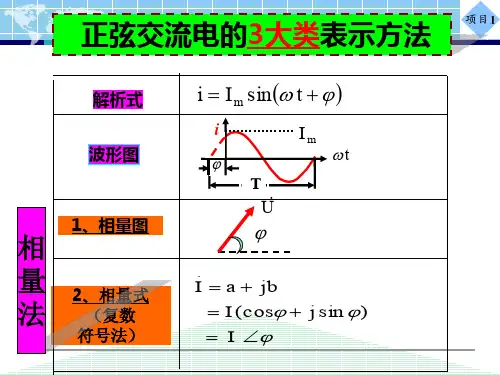
§ 5—2正弦交流电的相量图表示法一、表示正弦交流电的方法1.解析式。
例如 V t U u u m )sin(ϕω+=2.波形图。
例如下图1所示3.相量图。
例如下图2所示二、相量图(矢量图) 1.旋转矢量与波形图的关系怎样用相量图来表示正弦交流电呢?现在以正弦电动势V t E e m )sin(ϕω+=为例说明如下:如图2所示,在直角坐标系内,作一条有向线段OA ,其长度为正弦电动势e 的最大值m E ,它的起始位置与x 轴正方向的夹角等于初相0ϕ,并以正弦电动势的角频率ω为角速度逆时针匀速旋转,则在任一瞬间旋转相量与x 轴的夹角即为正弦电动势的相位)(0φω+t ,它在y 轴的投影)(Oa 即为该正弦电动势的瞬时值。
正弦交流电的相量用“m E 、m U 、mI ”表示。
但实际应用更多的是有效值相量(如图3所示),即将有向线段OA 的长度定为正弦量的有效值,相应符号则为“E 、U 、I ”。
例如,当0=t 时,旋转相量在y 轴的投影为e图12.应用相量图时应注意以下几点:①同一相量图中,各正弦交流电的频率应相同。
②同一相量图中,相同单位的相量应按相同比例画出。
③一般取直角坐标轴的水平正方向为参考方向,逆时针转动的角度为正,顺时针转动的角度为负。
有时为了方便起见,也可在几个相量中任选其一作为参考相量,并取消直角坐标轴。
④用相量表示正弦交流电后,它们的加、减运算可按平行四边形法则进行。
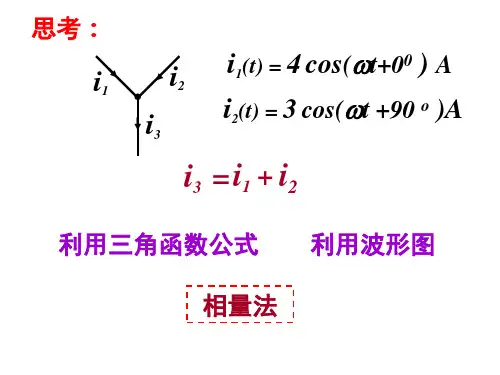
3.举例已知V t u )30314sin(2301+=,V t u )60314sin(2402-=,利用相量图求21u u u +=和21u u u -='的瞬时值表达式。






正弦交流电的表示法2.1.2 正弦量的相量表示法如前所述,一个正弦量由幅值、角频率和初相位三个要素确定,而正弦量的这些特征,可以用正弦波和三角函数表示出来。
除此之外,还可以用相量表示,复数是相量的基础。
(1)复数如图2-6所示,一复数A,a1为其实部,a2为其虚部,a为其长度,则复数A可用四种形式来表示:图2-6 复平面上表示复数A①代数式A=a1+j a2(2-8)为虚单位。
②三角函数式令复数A的模|A|=a,φ角是复数A的辐角,有A=|A|(cosφ+jsinφ)=a(cosφ+jsinφ)(2-9)式中,,,③指数式根据欧拉公式e jφ=cosφ+jsinφA=a e jφ(2-10)④极坐标式极坐标式是复数指数式的简写,这四种复数的表示形式,可以相互转换。
复数的指数形式(或极坐标形式)与复数的三角函数式之间可以通过欧拉公式进行转换,指数形式(或极坐标形式)要变换成代数式可以通过欧拉公式进行转换;代数式变换成指数形式(或极坐标形式)可以通过式(2-9)进行转换。
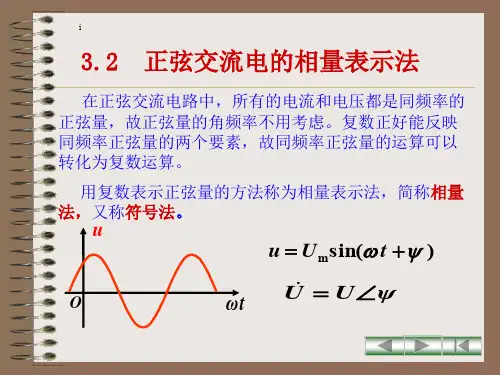
(2)正弦量的相量表示用复数来表示正弦量的方法称为正弦量的相量表示法,即用复数的模来表示正弦量的幅值(最大值或有效值),用复数的辐角来表示正弦量的初相位。
只有同频率的正弦量用相量进行分析计算才有意义,它使得正弦交流电路的分析和计算变得更为简单。
在线性正弦交流电路中,各部分的电流和电压都是同频率的正弦量。
因为频率不变,所以可以用相量来表示正弦量。
正弦量的相量形式是用大写字母上面加小圆点表示。
例如,“”“”“”等。
同理,可自行写出和相量。
相量、、称为有效值相量,、、称为最大值相量或幅值相量。
相量在复平面上的几何图形叫做相量图,如图2-7所示。
图2-7 正弦量的相量图同频率的正弦量,由于它们之间相位的相对位置不变,即相位差不变,因此可以将它们的相量画在同一个坐标上。
不同频率的正弦量,用相量表示时,不能画在同一相量图上。
(3)相量运算相量的运算规则符合复数运算中的交换律、结合律和分配律等。