四点共圆判定定理ppt课件

四点共圆的判定和性质
如果同一平面内的四个点在同一个圆上，则称这四个点共圆，一般简称为“四点共圆”。

四点共圆有三个性质：共圆的四个点所连成同侧共底的两个三角形的顶角相等；圆内接四边形的对角互补；圆内接四边形的外角等于内对角。

以上性质可以根据圆周角等于它所对弧的度数的一半进行证明。

托勒密定理：
若ABCD四点共圆（ABCD按顺序都在同一个圆上），那么AB*DC+BC*AD=AC*BD。

例题：证明对于任意正整数n都存在n个点使得所有点间两两距离为整数。

解答：归纳法。

我们用归纳法证明一个更强的定理：对于任意n 都存在n个点使得所有点间两两距离为整数，且这n个点共圆，并且有两点是一条直径的两端。

n=1，n=2很轻松。

当n=3时，一个边长为整数的勾股三角形即可：比如说边长为3，4，5的三角形。

我们发现这样的三个点共圆，边长最长的边是一条直径。

假设对于n大于等于3成立，我们来证明n+1。

假设直径为r（整数）。

四点共圆在二维几何中，我们经常遇到一些有趣的现象和形状。

其中之一便是四点共圆。

当四个点都在同一个圆周上时，我们称它们是共圆的。

下面，我们将详细介绍四点共圆的性质和证明。

性质1：共圆定义四点共圆指的是四个点A、B、C、D可以构成一个圆，即这四个点都在同一个圆周上。

记这个圆为O，我们可以用如下方式表示四点共圆的条件：AB + CD = AC + BD共圆示意图共圆示意图性质2：共圆的判定判断四个点是否共圆的一种方法是通过计算它们的距离来判断。

具体而言，有如下定理：若四个点A、B、C、D的任意三点不共线，则ABCD四个点共圆的充要条件为：AC^2 * BD^2 = AD^2 * BC^2 + AB^2 * CD^2 - 2 * AB * AD * BC * CD * cos(∠ADC - ∠BAC)性质3：四边形共圆四边形ABCD是共圆的充要条件是，它的对角线交点E满足AB EC + BC EA =AC*EB。

这说明，当四个点A、B、C、D能够构成一个四边形，且满足这个等式时，它们就是共圆的。

性质4：垂直弦交点当ABCD四点共圆时，圆心为O，连接两点的弦AD和BC垂直，交点为M。

那么，我们可以得出以下结论：AM * MC = BM * MD证明接下来，我们将对性质2进行证明。

假设四个点A、B、C、D的任意三点不共线。

首先，我们构造三角形ADC，以及四边形ABCD的两条对角线，连接点A和C，以及点B和D。

根据余弦定理，我们可以得到：AC^2 = AD^2 + CD^2 - 2 * AD * CD * cos(∠ADC)同理，我们可以得到：BD^2 = AB^2 + CD^2 - 2 * AB * CD * cos(∠BAC)进一步地，我们可以得到：AC^2 * BD^2 = (AD^2 + CD^2 - 2 * AD * CD * cos(∠ADC)) * (AB^2 + CD^2 - 2 * AB * CD * cos(∠BAC))展开上式，我们可以得到：AC^2 * BD^2 = AD^2 * AB^2 + AD^2 * CD^2 + CD^2 * AB^2 + CD^4 - 2 * AD * AB * CD^2 * cos(∠BAC) - 2 * AD^2 * CD * cos(∠ADC) - 2 * AB^2 * CD * cos(∠BAC) + 4 * AB * AD * CD^2 * cos(∠BAC) * cos(∠ADC) - 2 * AB * AD * CD^2 * cos(∠ADC) *cos(∠BAC)我们可以观察到一些项可以进行合并和简化，最终得到：AC^2 * BD^2 = AD^2 * BC^2 + AB^2 * CD^2 - 2 * AB * AD * BC * CD * cos(∠ADC - ∠BAC)由此可见，当AC^2 * BD^2 = AD^2 * BC^2 + AB^2 * CD^2 - 2 * AB * AD * BC * CD * cos(∠ADC - ∠BAC)成立时，四个点A、B、C、D共圆。

四点共圆性质
四点共圆的性质是共圆的四个点所连成同侧共底的两个三角形的顶角相等、圆内接四边形的对角互补、圆内接四边形的外角等于内对角。

以上性质可以根据圆周角等于它所对弧的度数的一半进行证明。

如果同一个平面上的四个点在同一个圆上，则称之为圆，一般称为“四点圆”。

由一个圆的四个点连接的两个三角形的顶角相等。

如果同一个平面上的四个点在同一个圆上，则称之为圆，一般称为“四点圆”。

由一个圆的四个点连接的两个三角形的顶角相等。

四点共圆的判定
将四个被证明是共圆的点连接成两个有公共底边的三角形，两个三角形都在底边的同一侧。

如果能证明它们的顶角相等(同一个圆弧相对的圆角相等)，就可以确认这四个点是共圆的。

被证明是共圆的四个点被连接成两条相交的线段。

如果能证明由交点划分的两条线段的乘积相等，则四点可确认为共圆(相交弦定理的逆定理)。

或者将证明共圆的四个点成对连接起来，延伸相交的两条线段。

如果能证明两个线段从交点到一个线段的两个端点的积等于两个线段从交点到另一个线段的两个端点的积，则可以确认这四个点也是共圆的。

四点共圆(一)第二十四讲四点共圆（一）知识要点】四点共圆的判定方法：1.若四个点到一定点的距离相等，则这四个点在同一个圆上（即这四点共圆）。

2.若一个四边形的一组对角的和等于180度，则这个四边形的四个顶点共圆。

3.若一个四边形的一个外角等于它的内对角，则这个四边形的四个顶点共圆。

4.若两个点在一条线段的同旁，并且和这条线段的两端连线所夹的角相等，那么这两个点和这条线的两个端点共圆。

5.若线段AB和CD相交于点P，且PA×PB=PC×PD，则A、B、C、D四点共圆。

6.若线段AB和CD延长后相交于点P，且PA×PB=PC×PD，则A、B、C、D四点共圆。

7.若四边形两组对边乘积的和等于对角线的乘积，则四边形的四个顶点共圆。

典例精讲】例1、锐角三角形ABC的三条高AD、BE、CF交于H，在A、B、C、D、E、F、H七个点中，能组成四点共圆的组数是（）A。

4组 B。

5组 C。

6组 D。

7组解析：由于锐角三角形的三条高交于同一点，所以ABCH、BDHF、CEHF、AEHD四个四边形的四个顶点都共圆，共4组。

例2、如图，A、B、C、D四点在同一圆上，AD的延长线与BC的延长线交于E点，且EC=ED。

（1）证明：CD//AB；（2）延长CD到F，延长DC到G，使得EF=EG，证明：A、B、G、F四点共圆。

DEFACGB解析：（1）连接AC、BD，由于ABCD四点共圆，所以∠ACB=∠ADB，又∠AEC=∠BED=90°，所以AE=EB，DE=EC，所以三角形AED和BEC全等，所以∠ADE=∠BEC，又∠ADE+∠BEC=180°，所以CD//AB。

2）连接CF、BG，由于CD//AB，所以∠DCB=∠DAB，所以∠ECB=∠EAB，所以三角形ECF和EAB全等，所以∠XXX∠EBA=∠EDA，所以EF=ED，同理EG=EC，所以EF=EG，又∠XXX∠CAB，所以∠EFG=∠EAB，所以四边形ABGF的四个顶点共圆。

第十五讲 四点共圆“四点共圆”问题在数学竞赛中经常出现，这类问题一般有两种形式：一是以“四点共圆”作为证题的目的，二是以“四点共圆”作为解题的手段，为解决其他问题铺平道路. 一、四点共圆如果同一平面内的四个点在同一个圆上，则称这四个点共圆，一般简称为“四点共圆”。

1、四点共圆的性质：（1）共圆的四个点所连成同侧共底的两个三角形的顶角相等； （2）圆内接四边形的对角互补；（3）圆内接四边形的一个外角等于它的内对角。

以上性质可以根据圆周角等于它所对弧的度数的一半进行证明。

2、四点共圆的判定方法：（1）从被证共圆的四点中先选出三点作一圆，然后证另一点也在这个圆上，若能证明这一点，即可肯定这四点共圆．（2）把被证共圆的四点连成四边形，若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时，即可肯定这四点共圆。

（可以说成：若平面上四点连成四边形的对角互补或一个外角等于其内对角，那么这四点共圆。

）（3）把被证共圆的四个点连成共底边的两个三角形，且两三角形都在这底边的同侧，若能证明其顶角相等(同弧所对的圆周角相等），从而即可肯定这四点共圆．（若能证明其两顶角为直角，即可肯定这四个点共圆，且斜边上两点连线为该圆直径。

）（4）把被证共圆的四点两两连成相交的两条线段，若能证明它们各自被交点分成的两线段之积相等，即可肯定这四点共圆（相交弦定理的逆定理）；或把被证共圆的四点两两连结并延长相交的两线段，若能证明自交点至一线段两个端点所成的两线段之积等于自交点至另一线段两端点所成的两线段之积，即可肯定这四点也共圆．（割线定理逆定理） （5）证被证共圆的点到某一定点的距离都相等，从而确定它们共圆．既连成的四边形三边中垂线有共同交点，即可肯定这四点共圆．（6）同斜边的两个直角三角形的四个顶点共圆，其斜边为圆的直径。

二、托勒密定理及其逆定理托勒密定理是平面几何中的一个重要定理，它揭示了圆内接四边形的对角线与边的关系。

1．托勒密定理：圆内接四边形两组对边乘积之和，等于两条对角线的乘积。

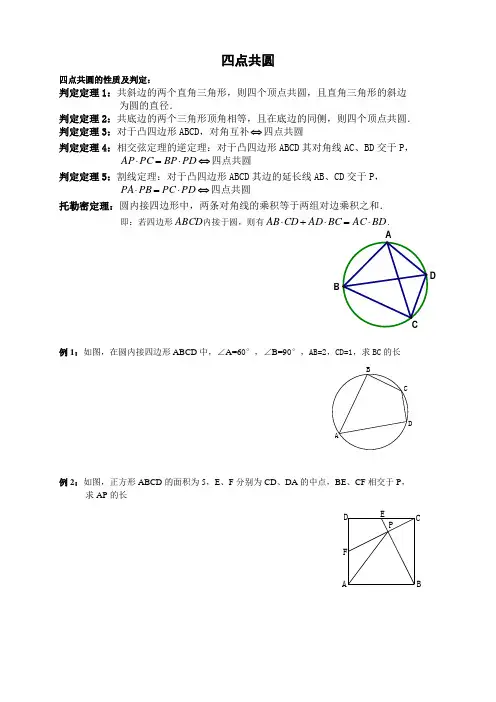
四点共圆四点共圆的性质及判定：判定定理1：共斜边的两个直角三角形，则四个顶点共圆，且直角三角形的斜边为圆的直径．判定定理2：共底边的两个三角形顶角相等，且在底边的同侧，则四个顶点共圆． 判定定理3：对于凸四边形ABCD ，对角互补⇔四点共圆判定定理4：相交弦定理的逆定理：对于凸四边形ABCD 其对角线AC 、BD 交于P ，PD BP PC AP ⋅=⋅⇔四点共圆判定定理5：割线定理：对于凸四边形ABCD 其边的延长线AB 、CD 交于P ，PD PC PB PA ⋅=⋅⇔四点共圆托勒密定理：圆内接四边形中，两条对角线的乘积等于两组对边乘积之和． 即：若四边形ABCD 内接于圆，则有BD AC BC AD CD AB ⋅=⋅+⋅.例1：如图，在圆内接四边形ABCD 中，∠A=60°，∠B=90°，AB=2，CD=1，求BC 的长例2：如图，正方形ABCD 的面积为5，E 、F 分别为CD 、DA 的中点，BE 、CF 相交于P ，求AP 的长P F E D C B A D C BAD B例3：如图，四边形ABCD 内接于⊙O ，CB=CD=4，AC 与BD 相交于E ，AE=6，线段BE 和DE 的长都是正整数，求BD 的长例4：如图，OQ ⊥AB ，O 为△ABC 外接圆的圆心，F 为直线OQ 与AB 的交点，BC 与OQ 交于P点，A 、C 、Q 三点共线，求证：2OA OP OQ =⋅E A BC D例5：如图，P 是⊙O 外一点，PA 与⊙O 切于点A ，PBC 是⊙O 的割线，AD ⊥PO 于D ，求证： ::.PB BD PC CD例6：如图，直线AB 、AC 与⊙O 分别相切于B 、C 两点，P 为圆上一点，P 到AB 、AC 的距离分别为6cm 、4cm ，求P 到BC 的距离例7：在半⊙O中，AB为直径，一直线交半圆周于C、D，交AB延长线与M（MB<MA，AC<MD），设K是△AOC与△DOB的外接圆除点O外的另一个交点，求证：∠MKO=90°例8：如图，在圆内接四边形ABCD中，AB=AD，∠BAD=60°，AC=a，求：四边形ABCD的面积（用a表示）。

四边形四点共圆的判定话说啊，四边形四点共圆这事儿，听起来挺玄乎，其实啊，它就像是咱们生活中的小秘密，一旦你掌握了它的规律，嘿，那简直就是“手到擒来”，轻松搞定！想象一下，你手里有四张纸片，每张纸片上都标着一个点，这四个点要是能在同一个圆上，那得多有趣呢？就像是四个小伙伴手拉手，围成一个完美的圆圈，玩起了“丢手绢”的游戏。

不过啊，这可不是随便四个点就能做到的，得满足一些条件才行。

首先呢，咱们得说说这个“对角互补”。

听起来挺高大上的，其实啊，就是四边形里头的两个对角加起来得是个直角，也就是180度。

就像是咱们平时说的“互补互助”，两个角得互相帮忙，才能凑成个完整的圆。

比如说啊，你有个四边形，其中一个角是钝角，那它的对角就得是个锐角，这样它们两个加起来才能是180度。

要是四个角都乱糟糟的，那它们可就没法手拉手围成个圆啦！再来说说这个“外角等于内对角”。

这又是什么鬼？别急，听我慢慢道来。

就是四边形的一个外角，它得等于它不相邻的那个内对角。

就像是咱们平时交朋友，你得找个能聊得来的，才能成为好朋友。

这个外角啊，它就得找个能“对上眼”的内对角，才能一起围成个圆。

比如说啊，你有个四边形，其中一个外角是60度，那它不相邻的那个内对角也得是60度，这样它们才能“心心相印”，一起组成个完美的圆。

当然了，除了这两个条件，还有一个更简单的，就是“相交弦定理”。

这个啊，就像是咱们平时玩的“找朋友”游戏。

你得先找出两条相交的弦，然后看看它们被交点分成的四段，要是其中两段乘积等于另外两段乘积，那这四个点就能围成个圆啦！就像是四个小伙伴找到了彼此的“另一半”，一起手拉手跳起了圆圈舞。

不过啊，说归说，做归做。

要想真正掌握四边形四点共圆的判定方法，还得靠咱们自己动手实践。

你得拿出纸笔，画出一个个四边形，然后试着用这些方法去验证。

就像是咱们平时学做饭，光看菜谱可不行，还得自己动手炒几个菜，才能真正掌握厨艺。

当然了，学习这事儿啊，也得有个度。