理论课教案教案编号
编写教师编写日期
审核教师审核日期年月日教学班级
教学日期
课程名称流体力学泵与风机
课题：第四章流动形态与能量损失
4-5紊流沿程损失的计算4-6非圆管内沿程损失4-7局部水头损失
教学目标：1．能进行紊流沿程损失的计算。
2.掌握水力半径、当量直径的计算方法
教学重点：利用伯努利方程对实际管道进行计算；
教学难点：阻力系数的确定
教学方法：讲授法、练习法
其它说明：
时间分配教学组织1分钟小结与作业5分钟引入新课4分钟分钟讲解新课80分钟分钟
课后记事
教学内容
教学方法 [复习引入]
略。 [讲解新课]
第四章 流动形态与能量损失 §4-5紊流的沿程损失计算
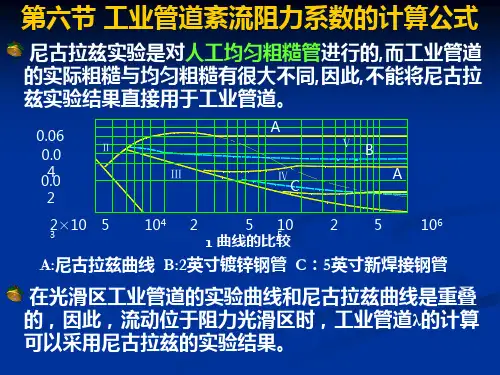
一、紊流形成的过程分析 二、紊流沿程阻力系数的确定方法 1.尼古拉斯实验
2.实际管道试验曲线-莫迪图
3.各种沿程阻力系数的计算公式
§4-6非缘管内的沿程阻力损失
一、当量直径de
1、湿周χ：过流断面上流体与固体壁面接触的周界(长度)
2、水力半径R ：过流断面面积与湿周之比
圆管的水力半径 3. 当量直径
de ： 把水力半径相等的圆管直
径定义为非圆管 的当量直径，即4倍水力半径
二、几种非圆管水力半径计算
§4-7局部水头损失
一、产生原因
主流脱离边壁，漩涡区的形成是造成局部水头损失的主要原因。旋涡
区越大，旋涡强度越大，局部水头损失越大。 二、变管径的局部损失 三、弯管的局部损失 四、减小局部阻力损失的措施 [小结与作业]
1．紊流沿程阻力损失计算及阻力系数的确定；
2．非圆管当量直径的计算方法及减小局部阻力损失的方法。
讲授 讲授 举例
χ
A
R =
4
412d d d A R =
==ππχχ
A
R d e 44=
=
3.作业：4-10、4-13、4-14。
冷热水管道系统的压力损失 无论在供暖、制冷或生活冷热水系统，管道是传送流量和热量必不可少的部分。计算管道系统的压力损失有助于： （1） 设选择正确的管径。 （2） 设选择相应的循环泵和末端设备。也就是让系统水循环起来并且达到热能传送目的 的设备。 如果不进行准确的管道选型，会导致系统出现噪音、腐蚀（比如管道阀门口径偏小）、严重的能耗及设备的浪费（比如管道阀门水泵等偏大）等。 管道系统的水在流动时遇到阻力而造成其压力下降，通常将之简称为压降或压损。 压力损失分为延程压力损失和局部压力损失： — 延程压力损失指在管道中连续的、一致的压力损失。 — 局部压力损失指管道系统内特殊的部件，由于其改变了水流的方向，或者使局部水流通道变窄（比如缩径、三通、接头、阀门、过滤器等）所造成的非连续性的压力损失。 以下我们将探讨如何计算这两种压力损失值。在本章节内我们只讨论流动介质为水的管道系统。 一、 延程压力损失的计算方式 对于每一米管道，其水流的压力损失可按以下公式计算 其中：r=延程压力损失 Pa/m Fa=摩擦阻力系数 ρ=水的密度 kg/m 3 v=水平均流速 m/s D=管道内径 m 公式（1） 延程压力损失 局部压力损失
管径、流速及密度容易确定，而摩擦阻力系数的则取决于以下两个方面： （1）水流方式，（2）管道内壁粗糙程度 表1：水密度与温度对应值 水温°C10 20 30 40 50 60 70 80 90 密度 kg/m3999.6 998 995.4 992 987.7 982.8 977.2 971.1 964.6 1．1 水流方式 水在管道内的流动方式分为3种： —分层式，指水粒子流动轨迹平行有序（流动方式平缓有规律） —湍流式，指水粒子无序运动及随时变化（流动方式紊乱、不稳定） —过渡式，指介于分层式和湍流式之间的流动方式。 流动方式通过雷诺数（Reynolds Number）予以确定： 其中： Re=雷诺数 v=流速m/s D=管道内径m。 ?=水温及水流动力粘度，m2/s 表2：水温及相关水流动力粘度 水温m2/s cSt °E 10°C 1.30×10-6 1.30 1.022 20°C 1.02×10-6 1.02 1.000 30°C 0.80×10-6 0.80 0.985 40°C 0.65×10-6 0.65 0.974 50°C 0.54×10-6 0.54 0.966 60°C 0.47×10-6 0.47 0.961 70°C 0.43×10-6 0.43 0.958 80°C 0.39×10-6 0.39 0.956 90°C 0.35×10-6 0.35 0.953 通过公式2计算出雷诺数就可判断水流方式： Re<2,000：分层式流动 Re：2,000-2,500：过渡式流动
除尘系统中的管道压力损失计算 管道的压力损失就是含尘空气在管道中流动的压力损失.它等于管道沿程（摩擦）压力损失和局部损失之和 ，在实际计算中以最长沿程一条管道进行计算，其计算结果作为风机造型的参考依据. 一：管道的沿程压力损失 1. a △P m =△P m λR S P -----湿周，既管道的周长（m ） 左管道系统计算中，一般先计算出单位长度的摩擦损失，通常也称比摩阻（Pa/m ）: △P m =λ 比摩阻力可通过查阅图表14-1得出，我公司的管道主要应用于除尘系统中，考虑到含尘空气中粉尘沉降的问题，除尘管道内的风速选择为25～28m/s. 4R S 1 2 V 2e
根据计算图标得出的以下数据： 局部阻力引起的能量损失，称之为局部压力损失或局部损失。 局部损失可按下列公式计算： △P J =δ △P J ----局部压力损失（Pa ） δ------局部阻力系数 2 V 2e
局部阻力系数δ可根据不同管道组件：如进出风口、弯头、三通等的不同尺寸比例，在相关资料中可查得，然后再根据上式计算出局部损失的大小。 例如：整体压制900圆弯头：当r/D=1.5时 δ=0.15 当r/D=2.0时 δ=0.13 当r/D=2.5时 δ=0.12 0总之，△P 为数。 F---Pq---风机全压（Pa ） Q---风机风量（m 3/s ） η----风机效率（一般为0.8～0.86） K---安全系统（1.0～1.2） 上式所得结果即为风机数电机功率，实际使用功率为：
Fs= Fs/F 即为风机的实际使用负载率 Pq*Q 1000* η
水泵的管道压力损失计算,水泵管道压力损失计算公式 点击次数：7953 发布时间：2011-10-28 管道压力损失,管道压力损失计算公式 为了方便广大用户在水泵选型时确定管道压力损失博禹公司技术工程师特意在此发布管道压力损 失计算公式供大家选型参考。通过水泵性能曲线可以看出每台水泵在一定转速下，都有自己的性能曲线，性能曲线反映了水泵本身潜在的工作能力，这种潜在的工作能力，在泵站的实际运行中，就表现为在某一特定条件下的实际工作能力。水泵的工况点不仅取决于水泵本身所具有的性能，还取决于进、出水位与进、出水管道的管道系统性能。因此，工况点是由水泵和管路系统性能共同决定的。 水泵的管道系统，包括管路及其附件。由水力学知，管路水头损失包括管道沿程水头 损失与局部损失。 Σh=Σhf+Σhj=Σλι/d v2/2g+Σζv2/2g （3-1） 式中Σh—管道水头损失，m； Σhf--管道沿程水头损失，m； Σhj--管道局部水头损失，m； λ--沿程阻力系数； ζ--局部水头损失系数； ι--管道长度，m； d--管道直径，m； v --管道中水流的平均流速，m/s。 对于圆管v=4Q/πd2,则式（3-1）可写成下列形式
Σh=（Σλι/12.1d5+Σζ/12.1d4）Q2=（ΣS沿+ΣS局）Q2=SQ2 （3-2） 式中S沿--管道沿程阻力系数，S2/m5,当管材、管长和管径确定后，ΣS沿值为一常数；S局--管道局部阻力系数，S2/m5,当管径和局部水头损失类型确定后，ΣS局值为一常数； S--管路沿程和局部阻力系数之和，S2/m5。 由式（3-2）可以看出，管路的水头损失与流量的平方成正比，式（3-2）可用一条顶点在原点的二次抛物线表示，该曲线反映了管路水头损失与管路通过流量之间的规律，称为管路水头损失特性曲线。如图3-1所示。 在泵站设计和运行管理中，为了确定水泵装置的工况点，可利用管路水头损失特性曲线，并将它与水泵工作的外界条件联系起来。这样，单位重力液体通过管路系统时所需要的能 量H需为 H需=H st+v2出-v2进/2g+Σh （3-3） 式中H需--水泵装置的需要扬程，m； H st--水泵运行时的净扬程，m； v2出-v2进/2g --进、出水的流速水头差，m; Σh--管路水头损失，m。 若进、出水池的流速水头差较小可忽略不计，则式（3-3）可简化为 H需=H st+Σh=H st=SQ2 （3-4） 利用式（3-4）可以画出如图3-2所示的二次抛物线，该曲线上任意一点表示水泵输送某一流量并将其提升H st高度时，管道中每位重力的液体所消耗的能量。因此，称该曲线为水泵装置的需要扬程或管路系统特性曲线。 本文档部分内容来源于网络，如有内容侵权请告知删除，感谢您的配合！
管道的阻力计算 风管内空气流动的阻力有两种，一种是由于空气本身的粘滞性及其与管壁间的摩擦而产生的沿程能量损失，称为摩擦阻力或沿程阻力；另一种是空气流经风管中的管件及设备时，由于流速的大小和方向变化以及产生涡流造成比较集中的能量损失，称为局部阻力。通常直管中以摩擦阻力为主，而弯管以局部阻力阻力为主（图6-1-1）。 图6-1-1 直管与弯管 （一）摩擦阻力 1．圆形管道摩擦阻力的计算 根据流体力学原理，空气在横断面形状不变的管道内流动时的摩擦阻力按下式计算： （6-1-1） 对于圆形风管，摩擦阻力计算公式可改为： （6-1-2） 圆形风管单位长度的摩擦阻力（又称比摩阻）为： （6-1-3） 以上各式中 λ——摩擦阻力系数；
v——风秘内空气的平均流速，m/s； ρ——空气的密度，kg/m3； l——风管长度，m； Rs——风管的水力半径，m； f——管道中充满流体部分的横断面积，m2； P——湿周，在通风、空调系统中即为风管的周长，m； D——圆形风管直径，m。 摩擦阻力系数λ与空气在风管内的流动状态和风管管壁的粗糙度有关。在通风和空调系统中，薄钢板风管的空气流动状态大多数属于紊流光滑区到粗糙区之间的过渡区。通常，高速风管的流动状态也处于过渡区。只有流速很高、表面粗糙的砖、混凝土风管流动状态才属于粗糙区。计算过渡区摩擦阻力系数的公式很多，下面列出的公式适用范围较大，在目前得到较广泛的采用： （6-1-4） 式中K——风管内壁粗糙度，mm； D——风管直径，mm。 进行通风管道的设计时，为了避免烦琐的计算，可根据公式（6-1-3）和（6-1-4）制成各种形式的计算表或线解图，供计算管道阻力时使用。只要已知流量、管径、流速、阻力四个参数中的任意两个，即可利用线解图求得其余的两个参数。线解图是按过渡区的λ值，在压力B0=101.3kPa、温度t0=20℃、宽气密度ρ0=1.204kg/m3、运动粘度 v0=15.06×10－6m2/s、管壁粗糙度K=0.15mm、圆形风管等条件下得出的。当实际使用条件下上述条件不相符时，应进行修正。 （1）密度和粘度的修正 （6-1-5） 式中Rm——实际的单位长度摩擦阻力，Pa/m； Rmo——图上查出的单位长度摩擦阻力，Pa/m； ρ——实际的空气密度，kg/m3； v——实际的空气运动粘度，m2/s。
DN8DN10DN15DN20DN25DN32DN40DN50DN65DN80 DN100DN125DN150DN200DN250DN300DN350DN400DN500DN600DN700DN800DN900DN100 912.515.7521.252735.7541536880.5106131156207259311363410513614702800898998 0.10.82240.53660.39730.26920.19720.13690.11460.0820.05930.04770.03330.02530.02020.0140.01040.00820.00670.00570.00430.00340.00290.00240.00210.00180.2 2.7522 1.7956 1.32960.90080.65980.45810.38330.27460.19860.15950.11150.08470.06750.04670.03490.02750.02250.01920.01440.01140.00950.00810.00690.0060.3 5.6326 3.6748 2.7212 1.8436 1.35040.93750.78450.56190.40640.3264 0.22820.17330.13810.09560.07140.05630.04610.0393 0.02940.02330.01950.01650.01420.01240.49.4149 6.1425 4.5485 3.0815 2.2571 1.567 1.31130.93920.67930.54550.38140.28970.23080.15980.11940.09410.0770.06570.04910.03890.03270.02760.02370.02070.514.0759.1831 6.8 4.6069 3.3744 2.3427 1.9604 1.4042 1.01560.81550.57030.4330.34510.23890.17850.14070.11510.09830.07340.05810.04880.04120.03550.03090.619.612.7889.4693 6.4153 4.699 3.2623 2.73 1.9553 1.4142 1.1357 0.79410.6030.48050.33270.24860.1960.16030.1368 0.1022 0.08090.0680.05740.04940.043 0.725.98216.95112.5528.5038 6.2289 4.3244 3.6188 2.5919 1.8747 1.5054 1.05270.79930.6370.4410.32950.25980.21250.18140.13550.10730.09010.07610.06550.05710.833.21321.66916.04610.8717.9626 5.528 4.626 3.3134 2.3964 1.9244 1.3456 1.02180.81430.56370.42120.33210.27160.23190.17330.13720.11520.09720.08370.07290.941.29226.9419.94913.5159.8993 6.8726 5.7512 4.1193 2.9793 2.3925 1.6729 1.2704 1.01230.70080.52370.41280.33770.28820.21540.17050.14330.12090.1040.0907150.21432.76124.25916.43512.0388.3576 6.9939 5.0093 3.6231 2.9094 2.0344 1.5448 1.23110.85230.63690.50210.41060.35050.26190.20740.17420.1470.12650.11031.159.97839.13128.97619.63114.3799.98268.3538 5.9834 4.3276 3.4751 2.43 1.8452 1.4704 1.0180.76070.59970.49050.41870.31290.24770.20810.17560.15110.13171.270.34545.89533.98523.02416.86411.7089.79787.0176 5.0756 4.0758 2.85 2.1642 1.7246 1.19390.89220.70330.57530.49110.36690.29050.24410.20590.17720.15451.382.55753.86339.88527.02119.79213.74111.4998.2359 5.9567 4.7834 3.3448 2.5399 2.024 1.4012 1.04710.82540.67510.57630.43060.34090.28640.24170.2080.18131.495.74762.46846.25731.33822.95415.93613.3369.5517 6.9084 5.5476 3.8792 2.9457 2.3474 1.6251 1.21440.95730.7830.66840.49940.39540.33220.28030.24120.21031.5109.9171.71153.10135.97526.35118.29415.30910.9657.9306 6.3684 4.4532 3.3815 2.6947 1.8655 1.394 1.09890.89890.76730.57330.45390.38140.32180.27690.24141.6125.0681.59160.41740.93129.98120.81417.41812.4769.02327.2458 5.0667 3.8474 3.0659 2.1226 1.5861 1.2504 1.02270.8730.65230.51640.43390.36610.3150.27461.7141.1892.10868.20546.20833.84623.49819.66414.08410.1868.1799 5.7198 4.3434 3.4611 2.3962 1.7906 1.4115 1.15450.98550.73640.5830.48980.41330.35560.311.8158.28103.2676.46551.80437.94526.34322.04515.7911.429.1705 6.4126 4.8694 3.8803 2.6864 2.0074 1.5825 1.2943 1.10490.82560.65360.54910.46340.39870.34761.9176.35115.0685.19757.7242.27829.35224.56217.59312.72410.2187.1449 5.4255 4.3234 2.9932 2.2367 1.7632 1.4422 1.2310.91990.72820.61190.51630.44430.38732 195.4 127.49 94.402 63.955 46.846 32.523 27.216 19.493 14.099 11.322 7.9167 6.0116 4.7905 3.3165 2.4783 1.9537 1.598 1.364 1.01930.8069 0.678 0.572 0.4922 0.4291 2.1215.43140.55104.0870.51151.64835.85630.00621.49115.54412.4828.7282 6.6278 5.2815 3.6565 2.7323 2.1539 1.7617 1.5038 1.12380.88960.74750.63070.54270.47312.2236.4415 4.26114.2377.38656.68339.35232.93123.58717.0613.6999.57937.2741 5.7965 4.013 2.9987 2.364 1.9335 1.6505 1.23330.97640.82030.69220.59560.51922.3258.42168.6124.8584.58161.95443.01135.99325.7818.64614.97310.477.9504 6.3355 4.3861 3.2776 2.5838 2.1133 1.8039 1.348 1.06710.89660.75650.6510.56752.4281.38183.58135.9492.0966 7.45846.83339.1912 8.0720.30216.30311.48.6567 6.8983 4.7758 3.5688 2.8133 2.3011 1.9642 1.4678 1.16190.97630.82370.70880.61792.5305.3219 9.2147.599.9373.19750.81742.52530.45822.02917.6912.379.39317.4852 5.1821 3.8723 3.0526 2.4968 2.1313 1.5926 1.2608 1.05930.89380.76910.6705 2.6 330.23215.45159.54108.0879.16954.96345.99532.94423.82719.13413.379 10.16 8.096 5.6049 4.1883 3.3017 2.7005 2.3052 1.7226 1.3637 1.14580.96670.83190.7252 2.7356.12232.34172.05116.5685.37759.27249.60135.52725.69520.63414.42810.9568.7307 6.0444 4.5167 3.5606 2.9123 2.4859 1.8576 1.4706 1.2356 1.04250.89710.78212.8382.99249.87185.03125.3591.81863.74453.34338.20727.63422.1915.51711.7839.3894 6.5004 4.8575 3.8292 3.132 2.6735 1.9978 1.5815 1.3288 1.12120.96480.84112.9410.83268.04198.48134.4798.49368.37957.22240.98529.64323.80416.64512.63910.072 6.973 5.2106 4.1076 3.3597 2.8679 2.143 1.6965 1.4254 1.2027 1.0350.90223439.6528 6.84212.4143.9105.473.17661.23643.8631.72225.4741 7.81313.52610.7797.4622 5.5762 4.3958 3.5954 3.0691 2.2934 1.8155 1.5254 1.2871 1.10760.96553.1469.45306.28226.8153.65112.557 8.13565.38746.83333.87227.21 9.0214.44311.5097.9679 5.9541 4.6937 3.8391 3.2771 2.4488 1.9386 1.6288 1.3743 1.1826 1.03093.2500.23326.36241.67163.73119.9383.25869.67349.90336.09328.98320.26715.3912.2648.4903 6.3445 5.0014 4.0908 3.4919 2.6093 2.0657 1.7356 1.4644 1.2602 1.09853.3531.98347.08257.01174.12127.5488.54374.09653.0738.38430.82321.55316.36713.0429.0292 6.7472 5.3189 4.3504 3.7136 2.775 2.1968 1.8458 1.5574 1.3401 1.16833.4564.71368.43272.82184.83135.3893.9978.65456.33640.74632.7222.87917.37413.8459.58477.1623 5.6462 4.6181 3.9421 2.9457 2.332 1.9593 1.6532 1.4226 1.24013.5598.42390.42289.1195.86143.4799.683.34959.69843.17834.67324.24518.41114.67110.1577.5898 5.9832 4.8937 4.1773 3.1215 2.4712 2.0763 1.7519 1.5075 1.3142 沿程水头损失计算表 流速 管径
水泵管道压力损失计 算公式
精品资料 水泵的管道压力损失计算,水泵管道压力损失计算公式 点击次数：7953 发布时间：2011-10-28 管道压力损失,管道压力损失计算公式 为了方便广大用户在水泵选型时确定管道压力损失博禹公司技术工程师特意在此发布管道压力损失计算公式供大家选型参考。通过水泵性能曲线可以看出每台水泵在一定转速下，都有自己的性能曲线，性能曲线反映了水泵本身潜在的工作能力，这种潜在的工作能力，在泵站的实际运行中，就表现为在某一特定条件下的实际工作能力。水泵的工况点不仅取决于水泵本身所具有的性能，还取决于进、出水位与进、出水管道的管道系统性能。因此，工况点是由水泵和管路系统性能共同决定的。 水泵的管道系统，包括管路及其附件。由水力学知，管路水头损失包括管道沿程水头损失与局部损失。 Σh=Σhf+Σhj=Σλι/d v2/2g+Σζv2/2g （3-1） 式中Σh—管道水头损失，m； Σhf--管道沿程水头损失，m； Σhj--管道局部水头损失，m； λ--沿程阻力系数； ζ--局部水头损失系数； ι--管道长度，m； d--管道直径，m； v --管道中水流的平均流速，m/s。 对于圆管v=4Q/πd2,则式（3-1）可写成下列形式 Σh=（Σλι/12.1d5+Σζ/12.1d4）Q2=（ΣS沿+ΣS局）Q2=SQ2 （3-2） 式中 S沿--管道沿程阻力系数，S2/m5,当管材、管长和管径确定后，ΣS沿值为一常数； S局--管道局部阻力系数，S2/m5,当管径和局部水头损失类型确定后，ΣS局值为一常数；S--管路沿程和局部阻力系数之和，S2/m5。 由式（3-2）可以看出，管路的水头损失与流量的平方成正比，式（3-2）可用一条顶点在原点的二次抛物线表示，该曲线反映了管路水头损失与管路通过流量之间的规律，称为管路水头损失特性曲线。如图3-1所示。 在泵站设计和运行管理中，为了确定水泵装置的工况点，可利用管路水头损失特性曲线，并将它与水泵工作的外界条件联系起来。这样，单位重力液体通过管路系统时所需要的能量H需为 H需=H st+v2出-v2进/2g+Σh （3-3） 式中H需--水泵装置的需要扬程，m； 仅供学习与交流，如有侵权请联系网站删除谢谢2
管径和压力损失计算 一、管径计算 1、管径计算 蒸汽、热水、压缩空气、氮气、氧气、乙炔按下述三式计算： 按体积流量计算 按质量流量计算 按允许压降计算 式中—管道内径（mm）； —在工作状态下的体积流量（m3/h）； —在工作状态下的质量流量（t/h）； —在工作状态下的流速（m/s）； —在工作状态下的密度（kg/m3）； —摩擦阻力系数； —允许比压降（Pa/m）。 压缩空气、氮气、氧气、乙炔等气体工作状态下的体积流量可由标准状态（0℃，绝对压力0.1013MPa）下的体积流量换算而得 式中—标准状态下气体体积流量（m3/h）； —气体工作温度（℃）； —气体绝对工作压力（MPa）。 二、管道压力损失计算 管道中介质流动产生的总压差包括直管段的摩擦阻力压降和管道附件的局部阻力压降，以及管内介质的静压差。 管内介质的总静压差：； 直管的摩擦阻力压降：； 管道附件的局部阻力压降：； 管内介质的静压差：。 式中Δp—管内介质的总静压差（Pa）； Δpm—直管的摩擦阻力压降（Pa）； Δpd—管道附件的局部阻力压降（Pa）； Δpz—管内介质的静压差（Pa）； ∑ξ—管件局部阻力系数之和； ∑Ld—管道局部阻力当量长度之和（m）； H1—管段始点标高（m）； H2—管段终点标高（m）； 对液体，因其密度大，计算中应计入介质静压差。对蒸汽或气体，其静压差可以忽略不计。 三、允许比压降计算 对各种压力管路的计算公式为 式中—单位压力降（Pa/m）； 、—起点、终点压力（MPa）； —管道直管段总长度（m）；
—管道局部阻力当量长度（m）。 在做近似估算时，对厂区管路可取=（0.1-0.15）；对车间的蒸汽、压缩空气、热水管路，取=（0.3-0.5）；对车间氧气管路去=（0.15-0.20） 看见公式，写上自己知道的公式吧。 管径计算公式。 d=18.8乘以(Q/u)的开平方，其中Q=Qz（273+t）/(293*P),其中，Qz为标准状态下的压力，P为绝对压力。 对于u的确定，p=0.3~0.6MPa时，u=10~20s; p=0.6~1MPa时，u=10~15s; p=1~2MPa时，u=8~12s; p=2~3MPa时，u=3~6s; p>3MPa时，u=0~3s
空调水系统的水力计算 根据舒适性空调冷热媒参数，应对冷热源装置、末端设备、循环水泵功率等进行考虑，因此，空调冷水供回水温差应大于等于5℃。 一、沿程阻力（摩擦阻力） 流体流经一定管径的直管时，由于流体内摩擦力而产生的阻力，阻力的大小与路程长度成正比的叫做沿程阻力,即 (1-1) 若直管段长度l=1m时， 则 式中λ——摩擦阻力系数，m； ——管道直径，m； R——单位长度直管段的摩擦阻力（比摩阻），Pa/m； ——水的密度，kg/m3； ——水的流速，m/s。 对于紊流过渡区域的摩擦阻力系数λ，可由经验公式计算得到。当水温为20℃时，冷水管道的摩擦阻力计算表可以从《实用供热空调设计手册》中查询。根据管径、流速，查出管道动压、流量、比摩阻等参数。 计算管道沿程阻力时，室内冷、热负荷是计算管道管径大小的基本依据，对于PAU机组管道管径进行计算时，应考虑其提供的仅为新风负荷，室内负荷是由风机盘管承担。所以这种空调末端承担负荷应计算精确，以避免负荷叠加。同时应清楚了解水管系统的方式，如同程式，异程式。不同的接管方式对沿程阻力具有一定的影响。在计算工程中，比摩阻宜控制在100-300Pa/m，通常不应超过400Pa/m。 二、局部阻力 （一）局部阻力及其系数
在管内水的流动过程中，当遇到各种配件如阀门、弯头等时，由于涡流而导致能量损失，这部分损失习惯上称为局部阻力（）。
(2-1)式中——管道配件的局部阻力系数； ——水流速度，m/s。 常用管道的配件可以通过相应的表格进行查询。根据管道管径的不同以及管道上的阀门、弯头、过滤器、除污器、水泵入口等能出现局部阻力的类别进行查询，得到不同的局部阻力系数，再利用公式计算出局部阻力。 对于三通而言，不同的混合方向及方式，会出现不同的阻力系数，且数值相差比较大。因此，查询三通阻力系数时，应根据已有的混合方式进行查询，进而得到更准确的局部阻力系数。 在实际计算水管局部阻力时，应先确定管道上的管件种类、数目，尤其是水管接进机组、水泵、末端。可参见设备安装详图，其中会画出相应的管道配件。 （二）当量长度 利用相同管径直管段的长度表示局部阻力，这样称为局部阻力当量长度(m)： 式中——管道配件的局部阻力系数。 根据各种阀门、弯头、三通以及特殊配件（突扩、突缩、胀管、凸出管等）的工程直径，可以查出相应的当量长度。 三、设备压力损失 空调系统中含有很多制冷、制热设备，如冷凝器、蒸发器、冷却水塔、冷热盘管等等。这些设备自身都有一定的压力损失。在水系统的水力计算中，除了管道部分的阻力之外，还有设备的压力损失。将这两部分加起来，才是整个系统的水力损失。 但是因为设备的生产厂家、型号、运行条件及工况的不同，压力损失相差比较大，一般情况下，是由设备厂家提供该设备的压力损失。若缺乏该方面的资料，可以按照经验值进行估算。估算值见表3-1。
各种管道水头损失的简便计算公式 (879) 摘要：从计算水头损失的最根本公式出发，将各种管道的计算公式加以推导，得出了计算水头损失的简便公式，使得管道工程设计人员从繁琐的计算中解脱出来，提高了工作效率。 关键词：水头损失塑料管钢管铸铁管混凝土管钢筋混凝土管 在给水工程应用中经常要用到水头损失的计算公式，一般情况下计算水头损失都是从水力摩阻系数λ等基本参数出发，一步一步的代入计算。其实各个公式之间是有一定的联系的，有的参数在计算当中可以抵消。如果公式中只剩下流速、流量、管径这些基本参数，那么就会给计算者省去不少的麻烦。在此我们充分利用了各参数之间以及水头损失与水温的关系，将公式整理简化，供大家参考。 1、PVC-U、PE的水头损失计算 根据《埋地硬聚氯乙烯给水管道工程技术规程》规定，塑料管道沿程水头损失hf应按下式计算： （式1-1） 式中λ—水力摩阻系数； L—管段长度（m）； di—管道内径（m）；
v—平均流速（m/s）； g—重力加速度，9.81m/s2。 因考虑到在通常的流速条件下，常用热塑性塑料给水管PVC-U、PE管一般处于水力光滑区，管壁绝对当量粗糙度对结果的影响非常小或没有影响，故水力摩阻系数λ可按下式计算： （式1-2） 式中Re—雷诺数。 雷诺数Re应按下式计算： （式1-3） 式中γ—水的运动粘滞度（m3/s），在不同温度时可按表1采用。 表1水在不同温度时的γ值（×10-6） 05101520253040 水温℃ 1.78 1.52 1.31 1.14 1.000.890.80 0.66
γ（m3/s） 从前面的计算可知，若要计算水头损失，需将表1中的数据代入，并逐步计算，最少需要3个公式，计算较为繁琐。为将公式和计算简化，以减少工作量，特推导如下： 因具体工程水温的变化较大，水力计算中通常按照基准温度计算，然后根据具体情况，决定是否进行校正。冷水管的基准温度多选择10℃。 当水温为10℃时的γ=1.31×10-6 m3/s，代入式1-3 得（式1-4） 将式1-4代入式1-2 （式1-5） 再将式1-5代入式1-1 得（式1-6） 取L为单位长度时，hf即等同于单位长度的水头损失i，所以 （式1-7） 又因为（式1-8）
管路沿程水头损失实验 一、实验目的要求 1．加深了解圆管层流和紊流的沿程损失随平均流速变化的规律，绘制h曲线； l g V l g f 2．掌握管道沿程阻力系数的量测技术和应用水压差计及电测仪测量压差的 方法； 3．将测得的Re-f关系值与莫迪图对比，分析其合理性，并且与莫迪图比较，进一步提高实验成果分析能力。 二、实验装置 本实验的实验装置，如图１所示。 图１自循环沿程水头损失实验装置图 1．自循环高压恒定全自动供水器； 2．实验台； 3．回水管； 4．水压差计； 5．测压计； 6．实验管道 8．滑动测量尺； 9．测压点； 10．实验流量调节阀； 11．供水管与供水阀； 12．旁通管路与旁通阀； 13．稳压筒
实验装置配备如下： 1．测压装置：U形管水压差计和电子量测仪。 低压差用U形管水压差计量测，而高压差需要用电子量测仪来量测。电子量测仪（见图2）由压力传感器和主机两部分组成，经由连通管将其接入测点。压 差读数（以厘米水柱为单位）通过主机显示。 图2 电子量测仪 1．压力传感器； 2．排气旋钮； 3．连通管； 4．主机 2．自动水泵与稳压器： 自循环高压恒定全自动供水器由离心泵、自动压力开关、气--水压力罐式稳压器等组成。压力超高时能自动停机，过低能自动开机。为避免因水泵直接向实验管道供水而造成的压力波动等影响，离心泵的输水是先进入稳压器的压力罐， 经稳压后再送向实验管道。 3．旁通管与旁通阀： 由于本实验装置所采用水泵的特性，在供小流量时有可能时开时停，从而造成供水压力的较大波动。为避免这种情况出现，供水器设有与蓄水箱直通的旁通管，通过分流可使水泵持续稳定运行。旁通管中设有调节分流量至水箱的阀门， 即旁通阀。实验流量随旁通阀开度减小（分流量减小）而增大。设计上旁通阀又是本装置用以调节流量的阀门之一。所以调节流量有两种方法：一是调节实验流量调节阀（见图1）；二是调节旁通阀。 4．稳压筒： 为了简化排气，并防止实验中再进气，在传感器前连接稳压筒(2只充水不满顶的密封立筒)。
第四节管道内的局部阻力及损失计算 在实际的管路系统中，不但存在上一节所讲的在等截面直管中的沿程损失，而且也存在有各种各样的其它管件，如弯管、流道突然扩大或缩小、阀门、三通等，当流体流过这些管道的局部区域时，流速大小和方向被迫急剧地发生改变，因而出现流体质点的撞击，产生旋涡、 二次流以及流动的分离及再附壁现象。此时由于粘性的作用，流体质点间发生剧烈的摩擦和动量交换，从而阻碍着流体的运动。这种在局部 障碍物处产生的损失称为局部损失，其阻力称为局部阻力。因此一般的管路系统中，既有沿程损失，又有局部损失。 4.4.1 局部损失的产生的原因及计算 一、产生局部损失的原因 产生局部损失的原因多种多样，而且十分复杂，因此很难概括全面。这里结合几种常见的管道来说明。 （）（） 图4.9 局部损失的原因 对于突然扩张的管道，由于流体从小管道突然进入大管道如图 4.9 （）所示，而且由于流体惯性的作用，流体质点在突然扩张 处不可能马上贴附于壁面，而是在拐角的尖点处离开了壁面，出现了一系列的旋涡。进一步随着流体流动截面面积的不断的扩张，直到 2 截面处流体充满了整个管截面。在拐角处由于流体微团相互之间的摩擦作用，使得一部分机械能不可逆的转换成热能，在流动过程中，不断地 有微团被主流带走，同时也有微团补充到拐角区，这种流体微团的不断补充和带走，必然产生撞击、摩擦和质量交换，从而消耗一部分机械 能。另一方面，进入大管流体的流速必然重新分配，增加了流体的相对运动，并导致流体的进一步的摩擦和撞击。局部损失就发生在旋涡开 始到消失的一段距离上。 图4.9（）给出了弯曲管道的流动。由于管道弯曲，流线会发生弯曲，流体在受到向心力的作用下，管壁外侧的压力高于内侧的 压力。在管壁的外侧，压强先增加而后减小，同时内侧的压强先减小后增加，这样流体在管内形成螺旋状的交替流动。 综上所述，碰撞和旋涡是产生局部损失的主要原因。当然在 1-2之间也存在沿程损失，一般来说，局部损失比沿程损失要大得多。 在测量局部损失的实验中，实际上也包括了沿程损失。 二、局部损失的计算 如前所述，单位重量流体的局部能量损失以表示
压力损失的计算 管道1：据Q=4284m3/h ，v=14.80m/s ,查阅《工业通风》孙一坚附表，我们选定管段直径D=320mm 局部压力损失：集气罩1：ξ=0.16,90°弯头R d =1.5,ξ=0.17, ξ=0.27+0.17+0.17+0.21=0.82 ∴?p 1局部=ξ× ρ×v2 =0.82×169.24=138.78p a 沿程压力损失： l 垂直 =4?0.8?0.2?0.537?0.233=2.23m， ∴l 总 =2.23+1+7=10.23m 查表可知：R m=15.43P a·m?1 ∴?p 1沿程=R m×l 总 =157.85P a ∴?p 1总 =157.85+138.78=296.63P a 管道2：局部压力损失：集气罩1： ξ=0.27,90°弯头R d =1.5,ξ=0.17,45°合流三通，F2 F1 =0.5，F3 F1 =0.5，L3 L2 = 1，ξ=0.88 ξ=0.27+0.17+0.88=1.32 ∴?p 2局部=ξ× ρ×v2 =1.32×169.24=223.40p a 沿程压力损失： l 垂直 =4?0.8?0.2?0.537?0.233=2.23m， ∴l 总 =2.23+1.41=3.64m ∴?p 2沿程=R m×l 总 =56.17P a ∴?p 2总 =157.85+138.78=279.5P a 管道3：总流量q v=5927.04m3/h，v=16.16m/s 局部压力损失：90°弯头R d =1.5,ξ=0.17 ∴ξ=0.17×3=0.51，除尘器压力损失为1100Pa ∴?p 3局部=ξ× ρ×v2 +1100=0.51×169.24=1186.31p a 沿程压力损失： l 总 =1.9+4.4+3.5+0.975=10.775m
通风管道阻力计算 风管内空气流动的阻力有两种，一种是由于空气本身的粘滞性及其与管壁间的摩擦而产生的沿程能量损失，称为摩擦阻力或沿程阻力；另一种是空气流经风管中的管件及设备时，由于流速的大小和方向变化以及产生涡流造成比较集中的能量损失，称为局部阻力。 一、摩擦阻力根据流体力学原理，空气在横断面形状不变的管道内流动时的摩擦阻力按下式计算： ΔPm=λν2ρl/8Rs 对于圆形风管，摩擦阻力计算公式可改写为： ΔPm=λν2ρl/2D 圆形风管单位长度的摩擦阻力（比摩阻）为： Rs=λν2ρ/2D 以上各式中 λ————摩擦阻力系数 ν————风管内空气的平均流速，m/s; ρ————空气的密度，Kg/m3; l ————风管长度，m ; Rs————风管的水力半径，m; Rs=f/P f————管道中充满流体部分的横断面积，m2； P————湿周，在通风、空调系统中既为风管的周长，m； D————圆形风管直径，m。 矩形风管的摩擦阻力计算 我们日常用的风阻线图是根据圆形风管得出的，为利用该图进行矩形风管计算，需先把矩形风管断面尺寸折算成相当的圆形风管直径，即折算成当量直径。再由此求得矩形风管的单位长度摩擦阻力。当量直径有流速当量直径和流量当量直径两种； 流速当量直径：Dv=2ab/(a+b) 流量当量直径：DL=1.3（ab）0.625/(a+b)0.25 在利用风阻线图计算是，应注意其对应关系：采用流速当量直径时，必须用矩形中的空气流速去查出阻力；采用流量当量直径时，必须用矩形风管中的空气流量去查出阻力。 二、局部阻力当空气流动断面变化的管件（如各种变径管、风管进出口、阀门）、流向变化的管件（弯头）流量变化的管件（如三通、四通、风管的侧面送、排风口）都会产生局部阻力。
管道阻力损失计算式 一、雷若数Re 的计算 Re ＝d u ρ/μ ＝（m ）（m/s ）（kg/m 3）/（N.s/m 2）＝m 0kg 0s 0 式中：d 管径，u 流速，μ流体粘度，ρ流体密度。 流体粘度μ的计算式： μ=469 .0R (00158.0460.0s 11 ） φη-- = （mPa.s ） 式中：溶剂（水）密度η1（g/cm 3），纯溶质密度η2（g/cm 3 ）， R ＝η1/η2 ， 固体体积分率Φs 。 （备注：20℃时，水密度η1＝1g/cm 3 ，石灰密度η2＝0.64g/cm 3 ， 石灰浆液中质量浓度为5％，8％，10％，15％，20％的石灰浆液密度ρ（g/cm 3 ）和固体体积分率 Φs 分别为：1.031，1.055，1.061，1.093，1.126；0.05，0.08，0.1，0.15，0.2。） 二、湍流时的摩擦损失因数 λ （一）光滑管 1. 柏拉修斯式： λ＝0.316/Re 0.25 其适用范围为Re ＝5×103~105 2. 顾袖珍式： λ＝0.0056+0.5/ Re 0.32 其适用范围为Re ＝3×103～3×106 3. 尼库拉则与卡门式 1/λ 0.5 ＝2 logRe λ 0.5 －0.8 此式可用于更广的湍流范围，但由于式两边都含有待求的λ，计算较为不便。 （二）粗糙管 1. 顾袖珍式： λ＝0.01227+0.7543/ Re 0.38 上式适用范围为Re ＝3×103～3×106。此式所指的粗糙管为内径50～200mm 的新钢铁管。 2. 柯尔布鲁克式： 1/λ 0.5 ＝1.14－2 log[ e/d + 9.35/ (Re λ 0.5 ）] 其适用范围甚广（Re ＝4×103～108，e/d ＝5×10-2～10-6），但由于算式两边都含
流体力学二类考核 指导老师：冯亮花——小组成员：蒙伦智、周肖、王桐
供水管道水头损失产生原因及计算 摘要：水流在运动过程中克服水流阻力而消耗的能量称为水头损失，根据边界条件的不同把水头损失分为两类：对于平顺的边界，水头损失与沿程成正比的称为沿程水头损失，用hf 表示；由局部边界急剧改变导致水流结构改变、流速分布改变并产生旋涡区而引起的水头损失称为局部水头损失，用hj 表示，两者的计量单位都为米。 关键词：水头损失 原因 计算 真空有压流 1．在分析水头损失产生原因之前，首先应该明确两个概念。 1.1水流阻力 水流阻力是由于固体边界的影响和液体的粘滞性作用，使液体与固体之间、液体内有相对运动的各液层之间存在的摩擦阻力的合力，水流阻力必然与水流运动方向相反。 1.2水头损失 水流在运动过程中克服水流阻力而消耗的能量称为水头损失。其中边界对水流的阻力是产生水头损失的外因，液体的粘滞性是产生水头损失的内因，也是根本原因。根据边界条件的不同把水头损失分为两类：对于平顺的边界，水头损失与流程成正比的称为沿程水头损失，用hf 表示；由局部边界急剧改变导致水流结构改变、流速分布改变并产生旋涡区而列起的水头损失称为局部水头损失，用hj 表示，两者的计最单位都为米。 由水头损失所产生的能量消耗，将直接影响供水水泵的选型，管道材质与内径的确 定，增加机械能损耗，这一直是水利工作者在给水工程设计过程中想要尽量减小的设计 因子，要想将水头损失降低到最低限度，就要了解水头损失产生的真正原因。 2．水头损失产生的原因 2.1供水管道的糙率是产生沿程水头损失的外部原因，也是直接原因。 在理想的状态下，液体在管道内部流动是不受管道内壁影响的，但由于现在市场上 供应的各种管材，内壁绝对光滑的材质是不存在，现有的技术只是尽量减小管道材质的 糙率（即粗糙度，一般用n 表示）。如给水用的PVC 管，管道内壁糙率为一般取值0.009，球墨铸铁给水管道内壁糙率一般取值0.012-0.0 1 3，其它管材糙率国家都有相应的技术标 准。 由于管道糙率的存在，使的水流在行进过程液体与固体接触面产生摩擦阻力，水流 消耗动能，产生沿程水头损失。对沿程水头损失的计算可以参照如下经验公式。 经验公式： 3 16222**n *16*35.6h d L Q f π= — 哈森—威廉斯公式： 公式中：hf-沿程水头损失 d —管道内径