电场强度通量高斯定理

高斯定理与电场强度高斯定理是物理学中的一个重要定理，用于描述电场的性质和行为。

它与电场强度有着密切的关系，通过高斯定理我们可以更好地理解和分析电场的分布和性质。

1. 高斯定理的基本原理高斯定理是由德国数学家卡尔·弗里德里希·高斯于19世纪提出的。

它描述了电场通量与电场的源之间的关系。

根据高斯定理，一个确定闭合曲面上的电场通量（通过该曲面的电场线数量）等于该闭合曲面所包围的电荷量的代数和的1/ε0 倍（其中ε0 为真空介电常数）。

2. 电场强度与电场通量电场强度是描述电场在空间中的分布情况的物理量。

它是一个矢量量，在每个点上具有大小和方向。

根据高斯定理，通过一个闭合曲面的电场通量与该曲面所包围的电荷量有关。

当曲面与电荷分布有关时，电场通量的值不为零；而当曲面内没有电荷时，电场通量为零。

因此，通过对电场通量进行计算和观察，我们可以推断和了解电场强度在空间中的分布。

3. 高斯定理在电场分析中的应用高斯定理在电场分析中有着广泛的应用。

例如，在对均匀电荷分布产生的电场进行分析时，可以利用对称性和高斯定理来简化计算过程。

通过选择合适的闭合曲面，可以使被积函数的形式简化为常数或者与曲面法向量平行的形式，从而简化了积分运算。

这大大简化了电场强度的计算过程，提高了计算的效率。

4. 高斯定理的意义和应用范围高斯定理的意义不仅仅局限于电场分析，还能够应用于其他物理学领域中。

例如，它可以用于描述流体动力学中的流体流动和流量，用于量子力学中的波函数分布和球面波传播等。

高斯定理作为一个基础定理，为我们研究各种物理现象提供了重要的数学工具。

5. 实际应用举例高斯定理在现实生活和工程领域中有着广泛的应用。

例如，在电力输电线路的设计和分析中，可以利用高斯定理计算导线周围的电场分布，从而评估电线对周围环境的影响。

在电容器的设计中，可以通过高斯定理来分析电场强度分布，从而优化电容器的结构和性能。

另外，在雷达和天线设计中，高斯定理可以用来计算电磁波的辐射和接收效率，为信号处理和系统优化提供依据。

电通量、高斯定理1、均匀电场的场强E与半径为R 的半球面的轴线平行，则通过半球面的电场强度通量φ = πR 2E ，若在半球面的球心处再放置点电荷q ，q不改变E分布，则通过半球面的电场强度通量 φ =πR 2E ±q/2ε0。

2、真空中的高斯定理的数学表达式为∑⎰=⋅0/εq s d E i s ，其物理意义是静电场是有源场。

3、一点电荷q 位于一位立方体中心，立方体边长为a ，则通过立方体每个表面的E的通量是q/6ε0；若把这电荷移到立方体的一个顶角上，这时通过电荷所在顶角的三个面E的通量是 0 ，通过立方体另外三个面的E的通量是 q/8ε0。

4、两个无限大均匀带正电的平行平面，电荷面密度分别为σ1和σ2，且σ1＞σ2，则两平面间电场强度的大小是( C )(A)(B) (C)(D) 5、应用高斯定理求场强E时，要求E的分布具有对称性，对于没有对称性的电场分布，例如电偶极子产生的电场，高斯定理就不再成立，你认为这种说法：( B )(A)正确 (B)错误 (C)无法判断6、下述带电体系的场强分布可能用高斯定理来计算的是( D )(A)均匀带电圆板 (B)有限长均匀带电棒 (C)电偶极子 (D)带电介质球(电荷体密度是离球心距离r 的函数) 7、如果在静电场中所作的封闭曲面内没有净电荷，则( C )(A)封闭面上的电通量一定为零，场强也一定为零；()0212/εσσ+()021/εσσ+()0212/εσσ-()021/εσσ-(B)封闭面上的电通量不一定为零，场强则一定为零；(C)封闭面上的电通量一定为零；场强不一定为零；(D)封闭面上的电通量不一定为零；场强不一定为零。

8、无限长均匀带电圆柱体，电荷体密度为ρ，半径为R，求柱体内外的场强分布解：作一半径为r，高为h的同轴圆柱面为高斯面根据对称性分析，圆柱面侧面上任一点的场强大小相等，方向沿矢径方向⎰⎰⎰⎰⋅+⋅+⋅=⋅侧面下底上底s dEs dEs dEs dEs=⎰⋅侧面s dE=E⎰侧面ds=2rhEπ（1）r < R时, ∑=ρπhrqi2,2/2ερππhrrhE=,2ερrE=（2）r > R时, ∑=ρπhRqi2,2/2ερππhRrhE=,rRE22ερ=∴=E)(,2)(,22RrrRRrr><ερερ。

电场强度通量高斯定理思政电场强度通量高斯定理是电学中的重要定理之一，它描述了电场强度通过一个闭合曲面的总通量与该曲面内电荷的代数和之间的关系。

高斯定理在电学领域中具有广泛的应用，可以帮助我们理解电场的分布和性质，以及解决一些与电场有关的问题。

首先，让我们来理解什么是电场强度通量。

电场强度是描述电场对电荷施加的力的物理量，通常用矢量表示。

电场强度的大小和方向决定了电荷在电场中承受的力的大小和方向。

通量是描述矢量场通过一个曲面的“流量”量的物理量，用于衡量场的分布情况。

电场强度通量就是电场强度通过一个曲面的“流量”量。

然后，我们来看一下高斯定理的表达形式。

高斯定理告诉我们，闭合曲面内电场强度通量的总和等于该曲面内电荷的代数和的1/ε0倍，其中ε0是真空中的介电常数。

数学表达式为∮E·dA = Q/ε0，其中∮表示对整个曲面进行积分，E·dA表示电场强度和曲面微元面积向量的点乘，Q表示曲面内的电荷量。

高斯定理的应用非常广泛。

首先，我们可以通过高斯定理计算出一个闭合曲面内任意电荷分布所产生的电场强度。

根据高斯定理，只需知道闭合曲面内包围的总电荷量，就能计算出曲面上每个点的电场强度。

这在研究电场分布时非常有用。

此外，高斯定理还可以帮助我们在给定电场强度分布的情况下求解出电荷分布。

通过把高斯定理应用于不同的曲面，我们可以得到一组关于电场强度和电荷分布的方程。

通过求解这些方程，我们可以确定电荷分布的情况。

另外，高斯定理还能帮助我们判断给定电场分布的对称性。

根据高斯定理，如果一个曲面内没有电荷，那么曲面上任意一点的电场强度通量都为零。

通过观察电场强度通量变化的规律，我们可以推断出电场分布的对称性，从而更好地理解和描述电场的性质。

总之，电场强度通量高斯定理是电学中非常重要的定理，它可以帮助我们理解电场的分布和性质，解决与电场有关的问题。

通过应用高斯定理，我们能够计算出闭合曲面内任意电荷分布所产生的电场强度，求解电荷分布以及判断电场分布的对称性。

7-4 电场强度通量高斯定理为了更形象地描述电场，这一节将在介绍电场线的基础上，引进电场强度通量的概念；并导出静电场的重要定理——高斯定理一、电场线下图是几种带电系统的电场线。

在电场线上每一点处电场强度E的方向沿着该点的切线，并以电场线箭头的指向表示电场强度的方向。

电场线密度越大，该处的电场强度越大。

静电场的电场线有如下特点：（1）电场线总是始于正电荷，终止于负电荷，不形成闭合曲线；（2）任何两条电场线都不能相交，这是因为电场中每一点处的电场强度只能有一个确定的方向。

图7-12S E N d d =或E S N=d d （7-8）这就是说，通过电场中某点垂直于E 的单位面积的电场线数等于该点处电场强度E 的大小。

SNd d 也叫做电场线密度。

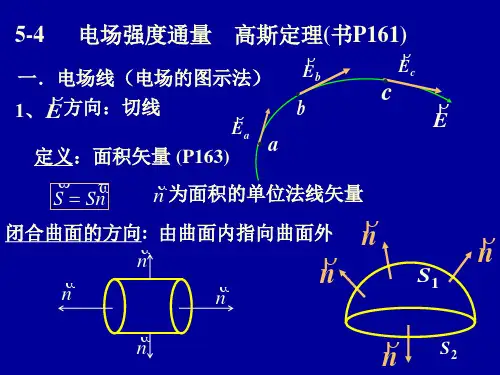
二、电场强度通量我们把通过电场中某一个面的电场线数叫做通过这个面的电场强度通量，用符号eΦ表示。

如下图(左)所示。

这是一个匀强电场，匀强电场的电场强度处处相等，所以电场线密度也应处处相等。

这样，通过面S 的电场强度通量为SE Φe =如果平面S 与匀强电场的E 不垂直，那么面S 在电场空间可取许多方位。

为了把面S 在电场中的大小和方位两者同时表示出来，我们引入面积矢量S ，规定其大小为S ，其方向用它的单位法线矢量e n 来表示，有S =S e n 在上图（中）中，面S 的单位法线矢量e n 与电场强度E 之间的夹角为θ。

因此，这时通过面S 的电场强度通量为θcos ES Φe =由矢量标积的定义可知，SΦn e E S E e ⋅=⋅=如果电场是非匀强电场，并且面S 不是平面，而是任意曲面[上图（右)]则可以把曲面分成无限多个面积元d S ，每个面积元d S 都可看成是一个小平面，而且在面积元d S 上，E 也可以看成处处相等。

仿照上面的办法，若e n 为面积元d S 的单位法线矢量，则e n d S =d S 。

如设面积元d S 的单位法线矢量e n 与该处的电场强度E 成θ角，于是，通过面积元d S 的电场强度通量为SE d cos d ⋅==θS E Φe d为了给出电场线密度与电场强度间的数量关系，我们对电场线的密度作如下规定：经过电场中任一点，想像地作一个面积元dS ，并使它与该点的E 垂 直（上图），由于dS 很小，所以dS 面上各点的E 可认为是相同的，则通过面积元dS 的电场线数dN 与该点E 的大小有如下关系：所以通过曲面S 的电场强度通量eΦ，就等于通过面S 上所有面积元dS 电场强度通量eΦd 的总和，即⎰⎰⎰⋅===SE d s s S E ΦΦd d e s e θcos （7-9）式中“⎰s ”表示整个曲面S 进行积分。