应用高斯定理求场强
- 格式:doc
- 大小:40.00 KB
- 文档页数:5

![浅谈用高斯定理求解电场问题[1]](https://uimg.taocdn.com/cde4c7efb8f67c1cfad6b812.webp)
浅谈用高斯定理求解电场问题摘要:本文主要介绍了电场强度,高斯定理,应用高斯定理求解电场问题以及步骤,注意事项。
利用高斯定理,可简洁地求得具有对称性的带电体场源(如球型、圆柱形、无限长和无限大平板型等)的空间场强分布。
计算的关键在于选取合适的闭合曲面——高斯面。
对应用高斯定理求解电场问题作了总结归纳。
高斯定理是电磁学的一条重要定理,这里对高斯定理作了比较详细的介绍,并提供了数学法、直接证明法等方法证明高斯定理,以及介绍高斯定理的应用和使用高斯定理应注意的问题,从中可以发现高斯定理在解决电场和磁场学中的方便之处。
关键词:电场强度;高斯定理;证明;方法;应用;步骤 正文:1.1.电场强度放入电场中某点的电荷所受的电场力F 跟它的电荷量q 的比值,叫做该点的电场强度,是描写电场强弱的物理量。
用E 来表示,定义式为:E=F /q ,单位(N/C)牛/库伦,付/米(V/m)。
1.2 电场强度的物理意义(1) 电场强度是从力的角度来反映电场本身性质的物理量。
(2) 定义式即电场内容某点的电场强度在数值上等于单位电荷在该点受到的电场力。
(3)电场强度E的大小,方向是由电场本身决定的,是客观存在的,与放不放检验电荷,以及放入检验电荷的正负,电量的多少均无关,既不能认为E 与成正比,也不能认为E与q 成反比。
检验电荷q 充当《测量工具》的作用。
电场强度的大小,关系到电工设备中各处绝缘材料的承受能力、导电材料中出现的电流密度、端钮上的电压,以及是否产生电晕、闪络现象等问题,是设计中需考虑的重要物理量之一。
电场中某点的场强方向规定为放在该点的正电荷受到的静电力方向。
1.3电场强度叠加原理电场强度遵从场强叠加原理,即空间总的场强等于各电场单独存在时场强的矢量和,即场强叠加原理是实验规律,它表明各个电场都在独立地起作用,并不因存在其他电场而有所影响。
以上叙述既适用于静电场也适用于有旋电场或由两者构成的普遍电场。
电场强度的叠加遵循矢量合成的平行四边形定则。


应用高斯定理求静电场的场强摘要:静电场的场强可以应用库仑定律及叠加原理、高斯定理、电势与场强间关系三种方法求得。
应用高斯定理求静电场场强具有简单易算的特点,但高斯定理只适用于求电荷对称分布的带电体静电场场强。
带电体电荷的对称性的正确分析和高斯面的恰当选取是应用高斯定理求静电场场强的关键。
其中带电体电荷分布的对称性一般可以分为轴对称、面对称和中心对称三类。
根据电荷分布的对称性通常选取可划分为几部分曲面的高斯面,且划分的曲面面矢量s d 的方向和场强E 的方向垂直或平行,可化矢量积分为标量积分以达到便于计算的目的。
关键词:场强;高斯定理;对称性;高斯面。
1引言已知静电场的高斯定理:静电场中任一闭合曲面的E 通量等于该曲面内电荷的代数和除以 ε,即ε内q S d E s =⋅⎰⎰ . (1)应用高斯定理可以计算闭合曲面的E 通量和求静电场的场强。
本文首先分析为什么高斯定理只适用于求电荷对称分布的带电体静电场场强,然后对应用高斯定理求静电场场强求解步骤中关于带电体电荷的对称性分析和高斯面选取两个问题加以分析和讨论。
3应用高斯定理求场强的适用范围高斯定理是关于闭合曲面E 通量的定理,反映的是闭合曲面E 通量与电荷的关系,而不是场强E 与电荷的关系。
只有带电体的电荷分布具有对称性,即静电场的分布具有对称性时,才可以通过选取合适的高斯面,化矢量积分为标量积分εθ内q dS E S d E s s =⋅⋅=⋅⎰⎰⎰⎰cos (2) 将场强的大小E 从积分号中提出。
所以高斯定理只适用于求电荷对称分布的带电体的静电场场强E 的大小,场强E 的方向需要根据对称性来判断。
4应用高斯定理求场强的求解步骤应用高斯定理求电场强度可以分为以下四个步骤。
第一,分析带电体电荷分布的对称性;第二,根据带电体电荷分布的对称性选取适当的高斯面;第三,计算高斯面内的E 通量和高斯面内电荷的代数和;第四,化矢量积分为标量积分,求出场强的大小,并根据对称性分析场强的方向。

第四章 电 场一、常见带电体的场强、电势分布2)均匀带电球面(球面半径 )的电场:3)无限长均匀带电直线(电荷线密度为): E = ,方向:垂直于带电直线。
2r( rR ) 4)无限长均匀带电圆柱面(电荷线密度为):E =2r (rR )5)无限大均匀带电平面(电荷面密度为)的电场: E =/20 ,方向:垂直于平面。
二、静电场定理 1、高斯定理:e = ÑE v dS v = q 静电场是有源场。
Sq 指高斯面内所包含电量的代数和;E 指高斯面上各处的电场强度,由高斯面内外的全 部电荷产生; Ñ E vdS v 指通过高斯面的电通量,由高斯面内的电荷决定。
2、环路定理: Ñ E v dl v =0 静电场是保守场、电场力是保守力,可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统: E v = E v i ;连续电荷系统: E v = dE v i =12、利用高斯定理求场强 四、求电势的两种方法n1、利用电势叠加原理求电势 分离电荷系统:U =U i ;连续电荷系统: U = dU i =1电势零点v v 2、利用电势的定义求电势 U =电势零点Edl五、应用vv b点电荷受力: F = qE电势差: U ab =U a -U b = b EdraE =1 qU =q4r 24r1)点电荷:E =0 (rR ) q2 (rR ) 4r 2U =q (r R ) 4r q (r R ) 4Ra 点电势能:W a = qU a由 a 到 b 电场力做功等于电势能增量的负值 A ab = -W = -(W b -W a )六、导体周围的电场1、静电平衡的充要条件: 1)、导体内的合场强为 0,导体是一个等势体。
2)、导体表面的场强处处垂直于导体表面。
E v ⊥表面。
导体表面是等势面。
2、静电平衡时导体上电荷分布: 1)实心导体: 净电荷都分布在导体外表面上。


电场中的高斯定理高斯定律(gauss' law),属物理定律。
在静电场中,穿过任一封闭曲面的电场强度通量只与封闭曲面内的电荷的代数和有关,且等于封闭曲面的电荷的代数和除以真空中的电容率。
该定律表明在闭合曲面内的电荷分布与产生的电场之间的关系。
静电场中通过任意闭合曲面(称高斯面)s 的电通量等于该闭合面内全部电荷的代数和除以真空中的电容率,与面外的电荷无关。
物理定律由于磁力线总是闭合曲线,因此任何一条进入一个闭合曲面的磁力线必定会从曲面内部出来,否则这条磁力线就不会闭合起来了。
如果对于一个闭合曲面,定义向外为正法线的指向,则进入曲面的磁通量为负,出来的磁通量为正,那么就可以得到通过一个闭合曲面的总磁通量为0。
这个规律类似于电场中的高斯定理,因此也称为高斯定理。
与静电场中的高斯定理相比较,两者有著本质上的区别。
在静电场中,由于自然界中存有着单一制的电荷,所以电场线存有起点和终点,只要闭合面内有净余的也已(或负)电荷,沿着闭合面的电通量就不等于零,即为静电场就是有源场;而在磁场中,由于自然界中没单独的磁极存有,n极和s极就是无法拆分的,磁感线都就是无头无尾的滑动线,所以通过任何闭合面的磁通量必等于零。
特别要强调两点: 1.关于电场线的方向的规定:电场线上每一点的切线方向就是该点电场的方向。
2.关于电场线的疏密的规定:电场线在某处的疏密要反映电场强度的大小,即在电场中通过某一点的电场线的数密度与该点电场强度的大小呈正相关,即: e=dn/ds,其中ds是在电场中的某一点取一个通过该点的且与电场线垂直的微分面,dn就是穿过该面ds的电场线的根数。
高斯定理来源于库仑定律,依赖场强共振原理,只有当电场线密度等同于场强悍小时场线通量就可以与场强通量等同于,并统一遵守高斯定理。
高斯面上的实际场强就是其内外所有电荷产生的场强共振而变成的合场强。
但利用高斯面所求出的场强则仅仅就是分析高斯面上场强原产时所牵涉的电荷在高斯面上产生的合场强,而不涵盖未牵涉的电荷所产生的场强。

静电场中的高斯定理:高斯定理是静电学中的一个重要定理, 它反映了静电场的一个基本性质, 即静电场是有源场, 其源即是电荷。
可表述为: 在静电场中, 通过任意闭合曲面的电通量, 等于该闭合曲面所包围的电荷的代数和的1/ε倍, 与闭合曲面外的电荷无关。
表达式为01()1/n i i S E ds q φε==∙=∑⎰⎰ (1)高斯定理是用来求场强E 分布, 定理中, S 是任意曲面, 由于数学水平的限制, 要由高斯定理计算出E,则对由场的分布有一定的要求, 即电荷分布具有严格的对称性( 若电荷分布不对称性即不是均匀的, 引起电场分布不对称, 不能从高斯定理求空间场强分布,高斯定理当然仍是成立的) , 由于电荷分布的对称性导致场强分布的对称性, 场强分布的对称性应包括大小和方向两个方面。
典型情况有三种:1) 球对称性, 如点电荷, 均匀带电球面或球体等;2) 轴对称性, 如无限长均匀带电直线, 无限长均匀带电圆柱或圆柱面, 无限长均匀带电同轴圆柱面3) 面对称性, 如均匀带电无限大平面或平板,或者若干均匀带电无限大平行平面。
根据高斯定理计算场强时, 必须先根据电荷分布的对称性, 分析场强分布的对称性; 再适当选取无厚度的几何面作为高斯面。
选取的原则是:○1 待求场强的场点必须在高斯面上;○2 使高斯面的各个部分或者与E 垂直, 或者E 平行;○3 与E 垂直的那部分高斯面上各点的场强应相等;○4 高斯面的形状应是最简单的几何面。
最后由高斯定理求出场强。
高斯定理说明的是通过闭合曲面的电通量与闭合曲面所包围的所有电荷的代数和之间的关系, 即闭合曲面的总场强E 的电通量只与曲面所包围的电荷有关, 但与曲面内电荷的分布无关。
但闭合曲面上的电场强度却是与曲面内外所有电荷相联系的,是共同激发的结果。
下面举一些例子来说静电场中高定理的应用:例1:一半径为R 的带电球体,其电荷体密度分布为()Ar r R ρ=≤,0()r R ρ=>,A 为大于零的常量。
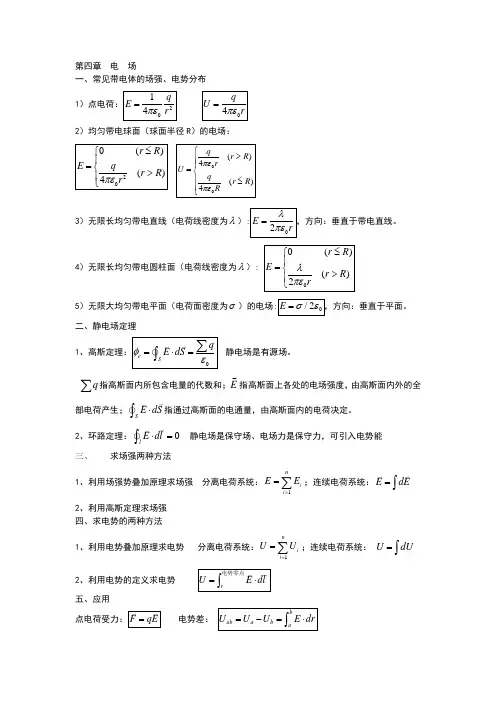
第四章 电 场一、常见带电体的场强、电势分布 1)点电荷:2014q E r πε=04q U rπε=2)均匀带电球面(球面半径R )的电场:200()()4r R E qr R r πε≤⎧⎪=⎨>⎪⎩00()4()4qr R r U q r R R πεπε⎧>⎪⎪=⎨⎪≤⎪⎩3)无限长均匀带电直线(电荷线密度为λ):02E rλπε=,方向:垂直于带电直线。
4)无限长均匀带电圆柱面(电荷线密度为λ): 00()()2r R E r R rλπε≤⎧⎪=⎨>⎪⎩5)无限大均匀带电平面(电荷面密度为σ)的电场:0/2E σε=,方向:垂直于平面。
二、静电场定理 1、高斯定理:0e Sq E dS φε=⋅=∑⎰静电场是有源场。
q ∑指高斯面内所包含电量的代数和;E指高斯面上各处的电场强度,由高斯面内外的全部电荷产生;SE dS ⋅⎰指通过高斯面的电通量,由高斯面内的电荷决定。
2、环路定理:0lE dl⋅=⎰ 静电场是保守场、电场力是保守力,可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统:1ni i E E ==∑;连续电荷系统:E dE =⎰2、利用高斯定理求场强 四、求电势的两种方法1、利用电势叠加原理求电势 分离电荷系统:1nii U U==∑;连续电荷系统: U dU =⎰2、利用电势的定义求电势 rU E dl =⋅⎰电势零点五、应用点电荷受力:F qE = 电势差: bab a b aU U U E dr =-=⋅⎰a由a 到b六、导体周围的电场1、静电平衡的充要条件: 1)、导体内的合场强为0,导体是一个等势体。
2)、导体表面的场强处处垂直于导体表面。
E ⊥表表面。
导体表面是等势面。
2、静电平衡时导体上电荷分布: 1)实心导体: 净电荷都分布在导体外表面上。
2)导体腔内无电荷: 电荷都分布在导体外表面,空腔内表面无电荷。
3)导体腔内有电荷+q ,导体电量为Q :静电平衡时,腔内表面有感应电荷-q ,外表面有电荷Q +q 。


收稿日期:2002-06-25.作者简介:雷桂林(1945-),男,山东平原人,甘肃联合大学理工学院副教授,从事理论物理和太阳能研究. 文章编号:1007-9912(2003)02-0055-04能用高斯定理求解场强问题的类型雷桂林1,路玉燕2,郑 卓1(1.甘肃联合大学理工学院,甘肃兰州730000;2.崇信一中,甘肃崇信744200)摘 要:通过典型例题,归纳出用高斯定理求解场强问题的四种类型.关键词:高斯定理;电场强度;问题类型中图分类号:O442 文献标识码:B高斯定理是静电场的两个基本定理之一,它从电场的角度反映了通过闭合曲面的E 或D 的通量与该曲面内总电荷的关系,揭示了电场是一个有源场的基本性质,同时为我们提供了一种较简便的计算场强的方法.当带电体系的电荷呈对称分布时,产生的电场也具有对称性,这时我们就可以利用高斯定理很简便地求出这些带电体系周围的场强分布.本文就运用高斯定理求解场强问题的常见类型进行归类.1 运用高斯定理求场强问题的步骤(1) 根据电荷分布的对称性,分析电场分布的对称性.这一步是解题的关键,也是解题的难点.(2) 根据电场分布的对称性,取合适的高斯面.要求高斯面上场强或者大小处处相等,方向处处与高斯面垂直或者方向与高斯面平行,以便在一部分面积分中能够将E (或D )提出积分号外,一部分面积分为零.(3) 根据高斯定理,列方程求解.2 运用高斯定理求解场强问题的四大类型2.1 电荷呈球对称分布的带电体系的场强该类问题高斯面都是取电荷分布对称中心为球心的球面,直接应用高斯定理,即可求得球内外的场强分布.2.1.1 点电荷激发的场强 可直接由库仑定律和场强定义得出,也可直接应用高斯定理得到,其场强为E =q r /4πε0r 3.2.1.2 均匀带电球面或球壳的场强[1~3] 设球壳带电荷电量为q ,其高斯面取以球壳球心为球心,分别在球壳内外作球面.直接用高斯定理可求得在距球心为r 处的电场强度E 为E =q 4πε0r3r , r >R (球壳外) 0. r <R (球壳内)第17卷第2期2003年4月甘肃教育学院学报(自然科学版)Journal of G ansu Educatio n College (N atural Sciences )Vol .17No .2Apr .2003DOI :10.13804/j .cn ki .2095-6991.2003.02.0152.1.3 均匀带电或电荷按r 分层分布的球体的场强 这类问题的场强分布也具有球对称性.通过下面例题说明这类问题的解法.例1 有一个内外半径分别为R 1和R 2的空心介质球,介质的电容率为ε,使介质内分布着电荷体密度ρ=kr ,式中的r 是径向距离,k 是常数,求空间各点的电场.图1 解 设ρ为电场中任一点,高斯面如图1中虚线所示,由高斯定理得r >R 2时,D ·d s =∫R 2R 1ρ4πr 2d r ,D 4πr 2=πk (R 42-R 41),D =k 4r 2(R 42-R 41),则E =D ε0=k (R 42-R 41)4ε0r 3r .R 1<r <R 2时,D ·d s =∫R 2R 1ρ4πr 2d r ,D 4πr 2=πk (r 4-R 41),D =k 4r (r 4-R 41),则E =D =k (r 4-R 41)4ε0r r .r <R 1时, D ·d s =0,E =0.2.2 电荷呈轴对称分布的带电体的场强该类问题高斯面取以对称轴为轴的圆柱体表面,直接用高斯定理可求得.2.2.1 均匀带电的无限长直线或细棒的场强[1~3] 设细棒上单位长度的电荷为λ,在距细棒为r 处的场强为E ,E =λr /2πε0r 2.图2 2.2.2 均匀带电的无限长直圆筒的场强例2 一对无限长的共轴直圆筒,半径分别R 1、R 2,筒面上都均匀带电,沿轴线单位长度的电量分别为λ1和λ2,求各区域内场强的分布.解 设p 为电场中任一点,高斯面如图2虚线所示的柱面,由高斯定理得r >R 2时,E ·d s =q ε0,2πrhE =h (λ1+λ2)ε0,2E =λ1+λ22πε0r 或E =λ1+λ22πε0r 2r .同理得R 1<r <R 2时,E =λ12πε0r 2r .r <R 1时,E =0.2.2.3 均匀带电的电荷按r 分层分布的无限长带电圆柱体的场强.2.3 电荷呈面对称分布的带电体的场强.2.3.1 无限大均匀带电平面[1~3] 设平面上的电荷面密度为σ,在距平面垂足连线上场强为E ,则E =σ2ε0e n .2.3.2 电荷按层分布的无限大带电平板.例3 如图3所示,一宽为b 的无限大非均匀带正电板电荷体密度为ρ=kx ,(0<x <b )试求:(1)平板两外侧任一点p 1、p 2处的电场强度.(2)平板内与其表面上O 点相距为x 的p 点处的场强.解 (1)在板内坐标为x 处取一厚度为d x 的薄层,这就是一个无限大均匀带电平面,其56 甘肃教育学院学报(自然科学版) 第17卷图3 电荷面密度为σ=ρd x =kx d x ,它在平板右侧的p 2点产生的场强是d E =σ2ε0=k x 2ε0d x .则点p 2的实际场强是E =∫d E =∫b 0k 2ε0x d x =k 4ε0b 2或E =k 4ε0b 2e n ,(匀强电场)e n 表示沿x 轴正方向的单位矢量.同理得E p 1=E =-k 4ε0b 2e n .(2)过板内p 点作一平面与x 轴垂直,这一平面将带电平面分成左右两部分,左部电荷在p 点产生的场强为E 1=∫x 0k 2ε0x d x =k 4ε0x 2.右部电荷在p 点产生的场强为E 2=∫b x k 2ε0x d x =k 4ε0(b 2-x 2).则E P =E 1-E 2=k 4ε0x 2-k 4ε0(b 2-x 2)=k 4ε0(2x 2-b 2)或E P =k 4ε0(2x 2-b 2)e n .对计算结果可进行讨论,这里不再讨论.2.4 以上几种情形的组合若干球电荷、若干柱电荷、若干板电荷的组合及它们之间的组合,如板夹球、柱夹球,面夹柱等.图4 例4 在半径为R ,体密度为ρ的均匀无限长带电柱体内部有一个半径为R 1,电荷体密度为ρ′的小球体,它的中心与圆柱体中心轴线的距离为a ,(a +R 1<R 2),求柱体外任一点的场强.解 如图4所示,柱体外或柱内任一点的场强,可以归结为一个半径为R ,体电荷密度为ρ的均匀带电的无限长柱体和一半径为R 1,体密度为ρ′-ρ的均匀带电球体所产生的场强的叠加.故任一点的场强是柱体和球体在该点所产生的场强的矢量和.则柱体在P 点产生的场强为E 1=ρR 2ε0r 3r ,球体在p 点产生的场强为E 2=(ρ′-ρ)R 313ε0r ′3r ′,其中r ′=r -a ,r ′=r 2+a 2-2ra cos α.则P 点的实际场强为E =E 1+E 2=ρR 2ε0r 3r +(ρ′-ρ)R 313ε0r ′3r ′.合场强的大小方向用立体几何运算可计算出.3 结束语由以上讨论可以看出,利用高斯定理可解决带电体电场分布的类型有三种:57第2期 雷桂林等:能用高斯定理求解场强问题的类型 (1)直接用高斯定理求解的问题有三类,即2.1、2.2、2.3等.(2)用高斯定理和场强叠加原理结合能求解以上三类问题的组合带电系的场强.(3)用高斯定理,场强叠加和电象法,可以求解点电荷带电小球等与导体平面、球面周围的电场问题.参考文献:[1]赵凯华,陈熙谋.电磁学(上册)[M ].北京:人民教育出版社,1978.28-51.[2]程守株,江之永.普通物理学(第2分册)[M ].北京:高等教育出版社,1998.38-43.[3]梁绍荣,刘昌年,盛正华.普通物理学(第3分册)[M ].北京:高等教育出版社,1988.38-56.[4]郭硕鸿.电动力学[M ].北京:高等教育出版社,1997.8-11.[5]周逊选,黄伯坚.新编普通物理习题解[M ].华中理工大学出版社,2000.242-255.Types Using Gauss Law to Solute Field StrengthLEI Gui -lin 1,LU Y u -yan 2,ZHENG Zhuo 1(1.T he Science and Engineering Colleg e of Gansu Association University ,Lanzhou G ansu 730000;2.Chong xin No .1M iddle School ,Chong xin Gansu 744200,China )A bstract :Do sum up four types using Gauss law to solute the Field streng th problem s by typical instances .Key words :Gauss law ;field strength ;problem type 58 甘肃教育学院学报(自然科学版) 第17卷。
第五章 静电场 思考题5-1 根据点电荷的场强公式2041rqE ⋅=πε,当所考察的点与点电荷的距离0→r 时,则场强∞→E ,这是没有物理意义的。
对这个问题该如何解释? 答:当时,对于所考察点来说,q 已经不是点电荷了,点电荷的场强公式不再适用.5-2 0FE q =与02014q E r r πε=⋅两公式有什么区别和联系? 答:前式为电场(静电场、运动电荷电场)电场强度的定义式,后式是静电点电荷产生的电场分布。
静电场中前式是后一式的矢量叠加,即空间一点的场强是所有点电荷在此产生的场强之和。
5-3 如果通过闭合面S 的电通量e Φ为零,是否能肯定面S 上每一点的场强都等于零?答:不能。
通过闭合面S 的电通量e Φ为零,即0=⋅⎰SS d E,只是说明穿入、穿出闭合面S的电力线条数一样多,不能讲闭合面各处没有电力线的穿入、穿出。
只要穿入、穿出,面上的场强就不为零,所以不能肯定面S 上每一点的场强都等于零。
5-4 如果在闭合面S 上,E 处处为零,能否肯定此闭合面一定没有包围净电荷? 答:能肯定。
由高斯定理∑⎰=⋅内qS d E S1ε,E 处处为零,能说明面内整个空间的电荷代数和0=∑内q,即此封闭面一定没有包围净电荷。
但不能保证面内各局部空间无净电荷。
例如,导体内有一带电体,平衡时导体壳内的闭合高斯面上E 处处为零0=∑内q,此封闭面包围的净电荷为零,而面内的带电体上有净电荷,导体内表面也有净电荷,只不过它们两者之和为零。
5-5 电场强度的环流lE dl ⋅⎰表示什么物理意义?0lE dl⋅=⎰表示静电场具有怎样的性质?答:电场强度的环流lE dl ⋅⎰说明静电力是保守力,静电场是保守力场。
0lE dl⋅=⎰表示静电场的电场线不能闭合。
如果其电场线是闭合曲线,我们就可以将其电场线作为积分回路,由于回路上各点沿环路切向,得⎰≠⋅Ll d E 0,这与静电场环路定理矛盾,说明静电场的电场线不可能闭合。
应用高斯定理求场强
1、均匀带电球壳的场强
设有一半径为的球壳均匀带电,其所带电量为,求球壳内外的电场强度。
解:(1)、球壳外的场强
通过点以为球心、为半径作一封闭球面为高斯面。
由于对称性,该面上场强的数值都相同,方向沿半径向外。
应用高斯定理,得
所以
(2)、球壳内的场强
通过点以为球心、为半径作一封闭球面为高斯面。
由于对称性,该面上场强的数值都相同,方向沿半径向外。
应用高斯定理,得
所以
2、均匀带电球体的场强
设有一半径为的均匀带电球体,其所带电荷的体密度为,求球体内外的电场强度。
解:(1)、球体外的场强
通过点以为球心、为半径作一封闭球面为高斯面。
由于对称性,该面上场强的数值都相同,方向沿半径向外。
应用高斯定理,得
所以
(2)、球体内的场强
通过点以为球心、为半径作一封闭球面为高斯面。
由于对称性,该面
上场强的数值都相同,方向沿半径向外。
应用高斯定理,得
所以
3、无限大均匀带电平面的场强
设有一无限大均匀带电平面,其所带电荷的面密度为,求带电平面的电场强度。
解:经过平面中部作一封闭圆柱面为高斯面,其轴线与平面正交,底面积为。
令为两底面上的场强,则通过的电通量为,由高斯定理,得
所以
若有两平行无限大均匀带电平面,其所带电荷的面密度为。
可以
证明,在两平行板中间,电场强度为
在两平行板外侧,电场强度为
4、无限长均匀带电直导线的场强
设有一无限长均匀带电直导线,其所带电荷的线密度为,求带电导线周围的电场强度。
解:过直导线作一高为、截面半径为r 的封闭圆柱面为高斯面。
根据电场轴的对称性,通过圆柱侧面的电通量为,通过圆柱底面的电通量为0。
由高斯定理,得
所以。