下载文档原格式
计算机科学中的信息论与编码信息论与编码是计算机科学中的重要理论，它们对于信息的传输、存储和处理起着至关重要的作用。
信息论主要研究信息的度量和传输的可靠性，而编码则是将信息以有效的方式表示和传递的技术手段。
本文将介绍信息论和编码在计算机科学中的应用，并探讨其对现代计算机技术的影响。
一、信息论的基本概念信息论是由香农在1948年提出的一门学科。
它通过熵和信息量的概念，量化了信息的度量和传输的质量。
熵是信息理论中的关键概念，用来表示一个随机变量的不确定性和信息量的平均值。
计算机系统中的信息可用二进制表示，因此信息的度量单位是比特（bit）。
二、信息论的应用1. 数据压缩信息论的一个重要应用是数据压缩。
利用信息论的原理，可以设计出高效的压缩算法，将大量的数据压缩成较小的文件。
常见的数据压缩算法有哈夫曼编码、LZ编码等。
这些算法通过统计字符或者字符组合出现的频率，将频率高的字符用较短的编码表示，从而实现数据的有损或无损压缩。
2. 信道编码信道编码是信息论的另一个重要应用领域。
在数据传输过程中，由于信道噪声等原因，数据容易出现误码。
为了提高传输的可靠性，可以使用信道编码技术。
常见的信道编码方案有纠错码和调制码，它们可以通过增加冗余信息或者改变信号的特性，提高传输系统的容错能力。
三、编码的基本原理编码是将信息转换成特定的符号或者编码字，以便能够有效地表示和传输。
在计算机科学中，常见的编码方式有ASCII码、Unicode和UTF-8等。
ASCII码是一种最早的字符编码方式，它将每个字符映射为一个7位的二进制数。
Unicode是一种全球通用的字符编码标准，它使用16位或32位的二进制数表示字符。
UTF-8则是Unicode的一种变体，它采用可变长度的编码方式，可以表示任意字符。
四、编码的应用1. 信息存储编码在信息存储中起着关键作用。
计算机系统中的文件和数据都需要以某种方式进行编码才能存储和读取。
不同的数据类型使用不同的编码方式，例如图片可以使用JPEG、PNG等图像编码格式，音频可以使用MP3、AAC等音频编码格式。
信息论部分基本概念和名词术语消息(或称为符号)：信息的数学表达层，它虽不是一个物理量，但是可以定量地加以描述，它是具体物理信号的进一步数学抽象，可将具体物理信号抽象为两大类型：自信息量：一个随机事件发生某一结果后所带来的信息量成为自信息量，定义为其发生概率对数的负值。
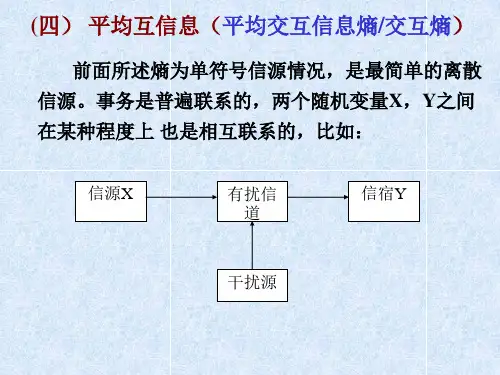
平均互信息：表达平均互信息量的熵I(X;Y), 是确定通过信道的信息量的多少，因此称它为信道传输率或传信率。
I(X;Y)就是接收到符号Y后平均每个符号获得的关于后平均每个符号获得的关于X的信息量——平均意义上每传送一个符号流经信道的平均信息量。
离散平稳无记忆信源：假定随机变量欲裂的长度是有限的，如果信源输出地信息序列中，符号之间的无相互依赖关系，则称这类信源为离散平稳无记忆信源。
信源冗余度：信源熵的相对率为信源实际的信息熵与同样符号数的最大熵的比值：η=H无穷/H0，定义信源的冗余度为1减去信源熵的相对率η，即ξ=1-η。
信道容量：信道在单位时间上能够传输的最大信息量。
平稳信源：概率分布函数与时间起点无关，平稳信源是有记忆的，记忆的长度有限。
香农信息：信息是事物运动状态或存在方式的不确定性的描述。
无记忆信道：在某一时刻信道的输出消息仅与当时的信道输入消息有关，而与前面时刻的信道输入或输出消息无关。
有记忆信道：在任意时刻信道的输出消息不仅与当时信道的输入消息有关，而且还与以前时刻的信道输入消息和（或）输出消息有关。
信道疑义度(含糊度) H(X|Y)：表示在输出端接收到Y后，发送端X尚存的平均不确定性。
这个对X尚存的不确定性是由于干扰引起的。
信道散布度H(Y|X)：表示在已知X后，对于输出Y尚存的平均不确定性；平均失真度：定义平均失真度为失真函数的数学期望，及d（xi,yi）在X和Y 得联合概率空间P(XY)中的统计平均值：D=E[D（xi,yi）] ，起是在平均的意义上，从总体上对整个系统失真情况的描述。
失真函数d(xi,yj)：是人为规定的，给出规定时应该考虑解决问题的需要以及失真可能引起的损失、风险和主观上感觉的差别等因素。
信息论与概率的联系信息论是一门研究信息传输和处理的学科，而概率论是一门研究随机现象的学科。
尽管两者看似不同，但实际上它们之间存在着密切的联系。
本文将探讨信息论与概率的联系，并阐述它们在现实生活中的应用。
一、信息论的基本概念信息论是由克劳德·香农于1948年提出的，它主要研究信息的度量和传输。
信息的度量通常使用信息熵来衡量，信息熵越大，信息的不确定性就越高。
信息熵的计算公式为：H(X) = -ΣP(x)log2P(x)其中，H(X)表示随机变量X的信息熵，P(x)表示随机变量X取值为x的概率。
二、概率论的基本概念概率论是研究随机现象的规律性的数学理论。
它通过概率的定义和性质，研究随机事件的发生规律和概率分布。
概率的计算通常使用频率概率和古典概率等方法。
三、信息论与概率的联系信息论与概率论之间存在着紧密的联系。
首先，信息熵可以看作是概率分布的度量，它反映了随机变量的不确定性。
信息熵越大，表示随机变量的不确定性越高，即信息量越大。
而概率分布越均匀，信息熵越大。
其次，信息论中的条件熵和互信息等概念与概率论中的条件概率和联合概率有着密切的关系。
条件熵表示在已知某一事件发生的条件下，另一事件的不确定性。
互信息表示两个事件之间的相关性，它可以通过条件熵和边际熵的差值来计算。
这些概念在概率论中有着重要的应用，可以用来描述随机事件之间的关联程度。
最后，信息论中的编码理论和信道容量等概念也与概率论有着密切的联系。
编码理论研究如何将信息进行编码和解码，以便在传输过程中减少误差和提高传输效率。
而信道容量则表示在给定信道条件下，能够传输的最大信息量。
这些概念都涉及到概率分布和概率计算，因此与概率论有着紧密的联系。
四、信息论与概率的应用信息论与概率论的联系在现实生活中有着广泛的应用。
首先，在通信领域中，信息论的概念和方法被广泛应用于数据压缩、信道编码和纠错编码等方面。
通过对信息的压缩和编码，可以提高数据传输的效率和可靠性。
《信息论》课程介绍摘要：一、课程背景二、课程目标三、课程内容1.信息论基本概念2.信息熵与信息量3.信道容量与信源编码4.信道编码与解码5.信息论在实际应用中的发展四、课程学习方法与要求正文：《信息论》课程是一门理论性较强的课程，主要研究信息传输、信息处理、信号检测等领域的基本理论。
通过本课程的学习，学生将掌握信息论的基本概念、基本原理和计算方法，了解信息论在实际应用中的发展，提高解决实际问题的能力。
一、课程背景信息论是20 世纪40 年代由香农（Claude Shannon）创立的，它是一门研究信息、通信、计算等领域的理论基础。
信息论不仅关注信息的量度，还关注信息传输的效率和可靠性等问题。
随着信息技术的迅速发展，信息论已成为现代通信技术、数据压缩、信号处理等领域的理论基石。
二、课程目标通过本课程的学习，学生将能够：1.理解信息论的基本概念、基本原理和计算方法；2.掌握信息熵、信息量、信道容量等基本概念，并会进行计算；3.了解信源编码、信道编码和解码的基本原理和方法；4.熟悉信息论在实际应用中的发展，提高解决实际问题的能力。
三、课程内容本课程主要包括以下内容：1.信息论基本概念：包括信息、熵、信息量、信道容量等基本概念，以及它们之间的关系。
2.信息熵与信息量：详细介绍信息熵的定义、性质和计算方法，以及信息量的概念和计算方法。
3.信道容量与信源编码：介绍信道容量的定义、性质和计算方法，以及信源编码的基本原理和方法。
4.信道编码与解码：介绍信道编码的基本原理和方法，以及解码的原理和过程。
5.信息论在实际应用中的发展：介绍信息论在通信技术、数据压缩、信号处理等领域的应用和发展。
四、课程学习方法与要求1.认真阅读教材，掌握课程的基本概念、基本原理和计算方法；2.积极参与课堂讨论，提高解决实际问题的能力；3.完成课后习题，巩固所学知识；4.结合实际应用，加深对课程内容的理解。
