练2.(1)如图1,已知△ABC,以AB,AC为边向△ABC外做等边 △ABD和等边△ACE,连接BE,CD,求证:BE=CD; (2)如图2,已知△ABC,以AB,AC为边向外作正方形ABFD和正 方形ACGE,连接BE,CD,BE与CD有什么关系?简单说明理由; (3)运用(1)、(2)解答中所积累的经验和知识,完成下题: 如图3,要测量池塘两岸相对的两点B,E的距离,已经测得 ∠ABC=45°,∠CAE=90°,AB=BC=60米,AC=AE,求BE的长.
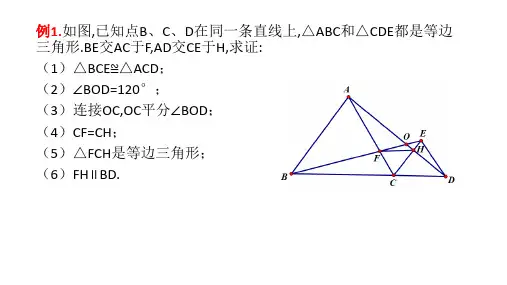
例1.如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边 三角形.BE交AC于F,AD交CE于H,求证: (1)△BCE≌△ACD; (2)∠BOD=120°; (3)连接OC,OC平分∠BOD; (4)CF=CH; (5)△FCH是等边三角形; (B上一点,分别以AC,BC为边在AB的同侧作 等边△ACM和△CBN,连接AN,BM.分别取BM,AN的中点E,F,连接 CE,CF,EF.观察并猜想△CEF的形状,并说明理由. (2)若将(1)中的“以AC,BC为边作等边△ACM和△CBN”改为“以 AC,BC为腰在AB的同侧作等腰△ACM和△CBN,”如图2,其他条件不 变,那么(1)中的结论还成立吗?若成立,加以证明;若不成立,请说明理 由.