反比例函数比例系数k的几何意义

《反比例函数K的几何意义》教学设计教学目标：1.了解反比例函数的定义及其特点。

2.掌握反比例函数的图像特征和变化规律。

3.理解反比例函数中k的几何意义。

教学重点：1.反比例函数的定义及其特点。

2.反比例函数中k的几何意义。

教学难点：理解反比例函数中k的几何意义。

教学准备：黑板、粉笔、绘图工具、反比例函数相关练习题。

教学过程：Step 1：导入新知1.引入：假设有一个正比例函数y=k/x，其中k为常数，x和y均为实数。

请回顾一下正比例函数的性质以及与直线的关系。

2.提问：那么，如果我们把正比例函数中的比例系数k变成k/x，会有什么不同的效果吗？3.要求学生独立思考并回答问题。

1.反比例函数的定义：反比例函数是指函数y=k/x，其中x≠0，k为常数，x和y均为实数。

2.特点：a.当x>0时，y随着x的增大而减小，与正比例函数相反。

b.当x<0时，y随着x的减小而减小，同样与正比例函数相反。

c.当x=0时，反比例函数无定义。

Step 3：反比例函数图像的绘制1.根据反比例函数的定义和特点，先选择几个不同的k的值，绘制出对应的反比例函数图像。

2.强调图像的特点：从x=1开始，k越大，图像越趋近于y轴；k越小，图像越平缓。

Step 4：反比例函数中k的几何意义1.提问：根据反比例函数的图像特点，我们发现k的大小对图像有何影响？2.学生回答：k的大小决定了反比例函数图像的陡峭程度。

3.引导思考：反比例函数中的k是什么意思？有什么几何意义？4.给出答案：在反比例函数图像上，k即为x轴上的一点的坐标。

5.教师解释：图像上在y轴上的其中一点的横坐标就是k，因此k表示了这个反比例函数相关的两个变量之间的比例关系。

1.教师出示几道反比例函数的相关练习题，要求学生独立完成并讨论。

2.部分学生上台解答题目，其他学生进行评价和讨论。

Step 6：归纳总结1.教师总结：反比例函数是由y=k/x的形式表示的函数，其中k是函数的比例系数，决定了函数图像的特点。

中考数学复习考点知识归类讲解 专题12 反比例函数比例系数k 的几何意义知识对接考点一、反比例函数比例系数k 的几何意义（1）意义：从反比例函数y ＝(k≠0)图象上任意一点向x 轴和y 轴作垂线，垂线与坐标轴所围成的矩形面积为|k|,以该点、一个垂足和原点为顶点的三角形的面积为1/2|k|. （2）常见的面积类型：失分点警示已知相关面积，求反比例函数的表达式，注意若函数图象在第二、四象限，则k ＜0. 例：已知反比例函数图象上任一点作坐标轴的垂线所围成矩形为3，则该反比例函数解析式为：3y x=或3y x =-专项训练 一、单选题1．如图，已知反比例函数2y x=-的图像上有一点P ，过点P 作PA x ⊥轴，垂足为点A ，则POA 的面积是（）A．2 B．1 C．1-D．122．如图，在平面直角坐标系中，A，B是反比例函数kyx=在第一象限的图象上的两点，且其横坐标分别为1，4，若AOB的面积为54，则k的值为（）A．23B．1C．2D．1543．若图中反比例函数的表达式均为4yx=，则阴影面积为4的有（）A．1个B．2个C．3个D．4个4．如图，点A是反比例函数4yx=-图象上的一个动点，过点A作AB⊥x轴，AC⊥y轴，垂足分别为B，C，则矩形ABOC的面积为（）A ．-4B ．2C ．4D ．85．如图，等腰ABC 中，5AB AC ==，8BC =，点B 在y 轴上，//BC x 轴，反比例函数k y x=（0k >，0x >）的图象经过点A ，交BC 于点D ．若AB BD =，则k 的值为（）A ．60B ．48C ．36D ．206．在平面直角从标系中，30°的直角三角尺直角顶点与坐标原点重合，双曲线11k y x=（x ＞0），经过点B ，双曲线22k y x=（x ＜0），经过点C ，则12k k ＝（ ）A．﹣3 B．3 C．D7．如图，A、B是双曲线y＝kx图象上的两点，过A点作AC⊥x轴于点C，交OB于点D，BD＝2OD，且ADO的面积为8，则DCO的面积为（）A．12B．1 C．32D．28．如图，平行于y轴的直线l分别与反比例函数kyx=（x＞0）和1yx=-（x＞0）的图象交于M、N两点，点P是y轴上一动点，若△PMN的面积为2，则k的值为（）A．2 B．3 C．4 D．59．如图，过x轴正半轴上的任意一点P，作y轴的平行线，分别与反比例函数y3=x（x＞0）和y6=x-（x＞0）的图象交于B、A两点．若点C是y轴上任意一点，则△ABC的面积为（）A ．3B ．6C ．9D ．9210．如图．在平面直角坐标系中，△AOB 的面积为278，BA 垂直x 轴于点A ，OB 与双曲线y ＝k x相交于点C ，且BC ∶OC ＝1∶2，则k 的值为（）A ．﹣3B ．﹣94C ．3D ．92二、填空题11．如图，平面直角坐标系中，O 是坐标原点，点A 是反比例函数()0k y k x=≠图象上的一点，过点A 分别作AM x ⊥轴于点M ，AN y ⊥轴于点N ．若四边形AMON 的面积为12，则k 的值是__________．12．如图，在反比例函数3yx=的图象上有一动点A，连接AO并延长交图象的另一支于点B，在第二象限内有一点C，满足AC=BC，当点A运动时，点C始终在函数kyx=的图象上运动，tan∠CAB=2，则k的值为_____13．如图，点P在反比例函数4yx=-的图像上，过点P作PA x⊥轴于点A，则POA的面积是_______．14．如图所示，反比例函数kyx=（0k≠，0x>）的图像经过矩形OABC的对角线AC的中点D ．若矩形OABC 的面积为8，则k 的值为________．15．如图，点A 与点B 分别在函数11(0)k y k x =>与220)k y k x=<（的图象上，线段AB 的中点M 在y 轴上．若△AOB 的面积为3，则12k k -的值是___．三、解答题16．如图，一次函数122y x =-的图象分别交x 轴、y 轴于A 、B ，P 为AB 上一点且PC 为AOB 的中位线，PC 的延长线交反比例函数ky x=（0k >）的图象于点Q ，32OQCS=．（1）求A 点和B 点的坐标； （2）求k 的值和Q 点的坐标．17．点O 为平面直角坐标系的原点，点A 、C 在反比例函数a y x=的图象上，点B 、D 在反比例函数b y x=的图象上，且0a b >>．（1）若点A 的坐标为()6,4，点B 恰好为OA 的中点，过点A 作AN x ⊥轴于点N ，交b y x=的图象于点P ． ①请求出a 、b 的值； ②试求OBP 的面积．（2）若////AB CD x 轴，32CD AB ==，AB 与CD 间的距离为6，试说明-a b 的值是否为某一固定值？如果是定值，试求出这个定值；若不是定值，请说明理由．18．如图，点C 在反比例函数y 1=x的图象上，CA ∥y 轴，交反比例函数y 3=x的图象于点A ，CB ∥x 轴，交反比例函数y 3=x的图象于点B ，连结AB 、OA 和OB ，已知CA ＝2，则△ABO 的面积为__．19．如图是反比例函数2yx=与反比例函数在第一象限中的图象，点P是4yx=图象上一动点，PA⊥X轴于点A，交函数2yx=图象于点C，PB⊥Y轴于点B，交函数2yx=图象于点D，点D的横坐标为a．（1）用字母a表示点P的坐标；（2）求四边形ODPC的面积；（3）连接DC交X轴于点E，连接DA、PE，求证：四边形DAEP是平行四边形．20．如图，点A（﹣2，y1）、B（﹣6，y2）在反比例函数y＝kx（k＜0）的图象上，AC⊥x轴，BD⊥y轴，垂足分别为C、D，AC与BD相交于点E．（1）根据图象直接写出y1、y2的大小关系，并通过计算加以验证；（2）结合以上信息，从①四边形OCED的面积为2，②BE＝2AE这两个条件中任选一个作为补充条件，求k 的值．你选择的条件是（只填序号）． 21．如图，一次函数()20y kx k k =-≠的图象与反比例函数1(10)m y m x-=-≠的图象交于点C ，与x 轴交于点A ，过点C 作CB y ⊥轴，垂足为B ，若3ABC S =△．（1）求点A 的坐标及m 的值；（2）若AB =22．如图，过C 点的直线y ＝﹣12x ﹣2与x 轴，y 轴分别交于点A ，B 两点，且BC ＝AB ，过点C 作CH ⊥x 轴，垂足为点H ，交反比例函数y ＝k x（x ＞0）的图象于点D ，连接OD ，△ODH 的面积为6（1）求k 值和点D 的坐标；（2）如图，连接BD ，OC ，点E 在直线y ＝﹣12x ﹣2上，且位于第二象限内，若△BDE 的面积是△OCD 面积的2倍，求点E 的坐标．11 / 11 23．如图，直线l 分别交x 轴，y 轴于A 、B 两点，交反比例函数(0)k y k x =≠的图象于P 、Q 两点．若2AB BP =，且AOB 的面积为4（1）求k 的值；（2）当点P 的横坐标为1-时，求POQ △的面积．。

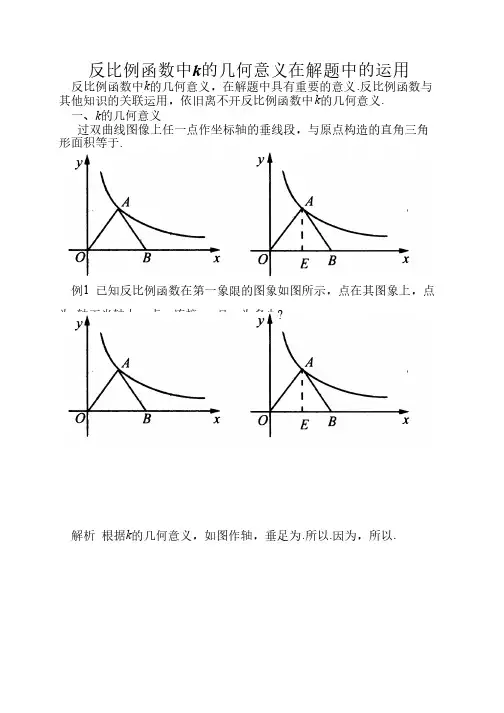
反比例函数中k的几何意义在解题中的运用反比例函数中k的几何意义，在解题中具有重要的意义.反比例函数与其他知识的关联运用，依旧离不开反比例函数中k的几何意义.一、k的几何意义过双曲线图像上任一点作坐标轴的垂线段，与原点构造的直角三角过双曲线图像上任一点作坐标轴的垂线段，与原点构造的直角三角形面积等于.已知反比例函数在第一象限的图象如图所示，点在其图象上，点例1 已知反比例函数在第一象限的图象如图所示，点在其图象上，点且，为多少?为x轴正半轴上一点，连接、,且，为多少根据k的几何意义，如图作轴，垂足为.所以.因为，所以.解析根据如图，在平面直角坐标系中，过点M(0,2)的直线l与x轴平行，且练习如图，在平面直角坐标系中，过点直线l分别与反比例函数和的图象交于点P、点Q(1)求点P的坐标;(2)若△POQ的面积为8，求k的值.因为点P在双曲线上，过M(0,2)的直线l与x轴平行，所以点P的纵解 因为点坐标为y=2，则横坐标x=3.所以点P的坐标为P(3,2)所以.因为，所以，所以或.因为图象在第二象限，所以.二、k的几何意义与线段比，面积比的知识关联如图，反比例函数的图象与矩形的两边相交于两点，若是的中例2 如图，反比例函数的图象与矩形的两边相交于两点，若是的中点，，求k的值.双曲线上存在点E与点F，根据k的几何意义，连接O E、OF，解析双曲线上存在点有.又因为点E是AB的中点，所以.可得;.所以点F是CB的中点.所以.可得.因为图象在第一象限，所以k=8.知识关联:此题用到k的几何意义、线段比与面积比的知识关联.三、k的几何意义与三角形相似知识的关联例3 如图，一次函数的图象与轴交于点如图，一次函数的图象与轴交于点A，与反比例函数的图象交于点B, BC垂直轴于点C.若△ABC的面积为1，求k的值.因为点B在反比例函数图象上，得由，得，得假设直线与y轴解析因为点交与点D，则点D(－1,0),OD=1.BC//OD得△ABC～△ADO，可得:.由OD=1得BC=2，把y=2代入得x=1.5.所以点B坐标为(1. 5,2).把x=1. 5,y=3代入中得k=8/3.知识关联:此题用到k的几何意义、三角形相似、线段比与面积比的知识关联.如图，若双曲线与边长为5的等边的边OA, AB分别相交于C, D两练习如图，若双曲线与边长为点，且OC=3BD,求k的值.解析过点作轴于点，过点作轴于点过点作轴于点，过点作轴于点.因为为等边三角形，，可得～，所以.又因为得.设,则.可得即.在中，可得..,所以图象在第一象限，所以作为九年级复习阶段，做好知识间的关联学习，对构成学生的知识系统具有很好的作用.。

反比例函数中K的几何意义
在反比例函数中，K表示比例系数或常数，也被称为反比例常数。

它
是用来确定两个变量之间反比关系的重要参数。

反比例函数的一般形式为：y=K/x，其中K表示比例系数。

K的几何意义可以通过分析反比例函数的图像得出。

反比例函数的图
像是一个双曲线，特点是曲线趋向于两个坐标轴。

下面将详细讨论K的几
何意义。

1.K的符号对于曲线的位置以及开口方向具有重要影响。

如果K为正数，那么曲线将位于第一和第三象限，并且开口方向为右上和左下。

如果
K为负数，那么曲线将位于第二和第四象限，并且开口方向为左上和右下。

2.K的绝对值越大，曲线就越“陡峭”。

当K增大时，曲线将更加接
近于坐标轴，并且在原点附近的斜率会越来越大。

反之，当K变小时，曲
线将更加平缓，斜率将减小。

3.K决定了特定坐标点的函数值。

例如，在函数y=K/x中，当x为K 时，y的值将为1、这是因为x与y成反比关系，而K是这种关系的常数。

4.K还决定了曲线相对于坐标轴的位置。

具体而言，当K增大时，曲
线将向坐标轴移动，而当K减小时，曲线将远离坐标轴。

总之，K代表了反比例函数中的比例系数或常数，它对于函数的位置、开口方向、陡峭程度以及特定坐标点的函数值都具有重要影响。

通过对K
的分析，我们可以更好地理解和解释反比例函数的几何特征。

?反比例函数中比例系数k 的几何意义?教学设计 本微课通过研究反比例函数()0≠=k xk y 中k 的几何意义，来解决反比例函数与面积类综合问题，能更好地考察学生灵活运用数学知识的能力及对数学思想方法掌握的情况，进一步让学生感悟数形结合分析数学问题的意识，培养学生把实际问题中的文字语言、符号语言、图形语言进展“互译〞并 “转换〞成有效的解题信息链，培养学生建立合理适宜的数学模型去解决实际问题的能力和方法。

教学目标：1、理解和掌握反比例函数()0≠=k xk y 中k 的几何意义 2、能灵活运用函数图象和性质解决一些较综合的问题学情分析：学生已有对一次函数和反比例函数关系式和图象认识的根底，再通过研究反比例函数()0≠=k xk y 中k 的几何意义，可以进一步唤醒学生数形结合分析数学问题的意识，培养学生把实际问题中的文字语言、符号语言、图形语言进展互译转换并形成有效的解题信息链，并通过建立合理适宜的数学模型，顺利解决问题的能力和方法。

教学重点、难点：1．重点：理解并掌握反比例函数 〔k ≠0〕中k 的几何意义；并能利用它们解决一些综合问题2．难点：通过反比例函数与矩形面积的对应关系渗透数形结合思想，感受理解反比例函数的比例系数 k 、函数解析式和函数图形之间的内在联系，并通过建立反比例函数模型解决实际几何问题。

教学过程：一、反比例函数中k 的几何意义xk y =y x B A P (m ,n )O 反比例函数()0≠=k xk y ，点),(n m P 是图像上的任意一点. (1)过点P 分别做x 轴和y 轴的垂线，垂足分别为点A ，B,那么 k n m nm OB OA S OAPB =⋅=⋅=⋅=矩形结论：任意一点横纵坐标的乘积是一个定值.〔2〕过点P 分别做x 轴和y 轴的垂线，垂足分别为点A ，B,连接OP,那么k n m n m AP OA S OAP 21212121=⋅=⋅=⋅=∆结论：k S S OBP OAP 21==∆∆通过构造学生熟悉的特殊多边形，并把k 值构造成特殊多边形的面积，从而可以发现过反比例函数()0≠=k xk y 的图象上任一点P 〔m,n 〕向x 轴、y 轴作垂线段，与x 轴、y 轴所围成的矩形面积k n m S OAPB =⋅=矩形，△OAP 和△OBP 面积k S S OBP OAP 21==∆∆让学生通过此题让学生感悟k 值与反比例函数图象的一一对应关系，核心感悟：k 值确定，图象确定，进而图形上从任意一点向坐标轴构造的特殊图象面积确定；图象确定或者图形上从任意一点向坐标轴构造的特殊图象面积确定， 那么k 值也随之确定。