5.4 三角函数的图象与性质(精讲)(原卷版附答案).docx

三角函数的图像和性质1、用五点法作正弦函数和余弦函数的简图（描点法）：正弦函数y=sinx ，x ∈[0，2π]的图象中，五个关键点是：(0,0) (2π,1) (π,0) (23π,-1) (2π,0) 余弦函数y=cosx x ∈[0,2π]的图像中，五个关键点是：(0,1) (2π,0) (π,-1) (23π,0) (2π,1) 2 sin y x = cos y x = tan y x =图象定义域 R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值 当22x k ππ=+时，max 1y =；当22x k ππ=- 时，min 1y =-．当2x k π=时，max 1y =；当2x k ππ=+时，min1y =-．既无最大值也无最小值周期性 2π 2ππ奇偶性奇函数 偶函数 奇函数单调性 在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦上是增函数； 在32,222k k ππππ⎡⎤++⎢⎥⎣⎦上是减函数． 在[]2,2k k πππ-上是增函数； 在[]2,2k k πππ+上是减函数．在,22k k ππππ⎛⎫-+⎪⎝⎭上是增函数．对称性 对称中心(),0k π 对称轴2x k ππ=+对称中心,02k ππ⎛⎫+ ⎪⎝⎭对称轴x k π=对称中心,02k π⎛⎫⎪⎝⎭无对称轴函数 性质例作下列函数的简图(1)y=|sinx|，x ∈[0，2π]， (2)y=-cosx ，x ∈[0，2π]例利用正弦函数和余弦函数的图象，求满足下列条件的x 的集合：21sin )1(≥x 21cos )2(≤x3、周期函数定义：对于函数()y f x =，如果存在一个非零常数T ，使得当x 取定义域内的每一个值时，都有：()()f x T f x +=，那么函数()y f x =就叫做周期函数，非零常数T 叫做这个函数的周期。

注意： 周期T 往往是多值的（如sin y x = 2π,4π,…,-2π,-4π,…都是周期）周期T 中最小的正数叫做()y f x =的最小正周期（有些周期函数没有最小正周期）sin y x =, cos y x =的最小正周期为2π （一般称为周期）正弦函数、余弦函数：ωπ=2T 。

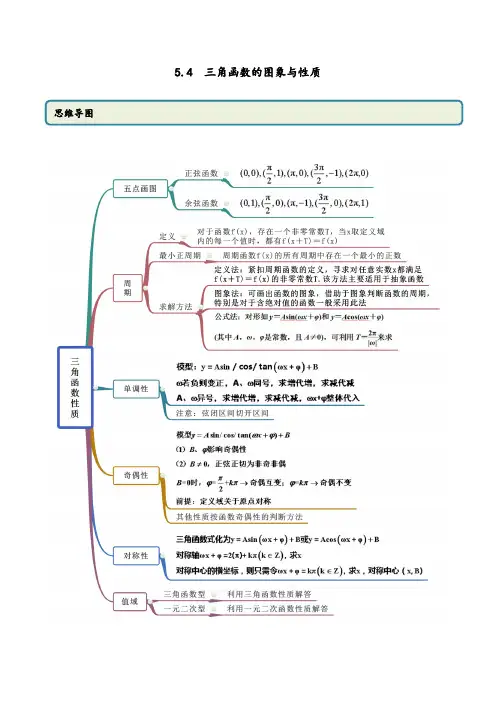
5.4 三角函数的图象与性质考点一 五点画图【例1】（1）（2020·全国高一课时练习）用五点法作出函数1cos (02)y x x π=-≤≤的简图.（2）（2020·全国高一课时练习）利用正弦或余弦函数图象作出3sin 2y x π⎛⎫=+⎪⎝⎭的图象．【一隅三反】1．（2020·全国高一课时练习）利用“五点法”作出函数y ＝1－sin x (0≤x ≤2π)的简图．2．（2020·全国高一课时练习）利用正弦曲线,求满足1sin 22x <≤的x 的集合．3．（2020·武功县普集高级中学高一月考）用五点法作出函数32cos y x =+在[]0,2π内的图像.考点二 周期【例2】（1）（2020·福建高二学业考试）函数cos y x =的最小正周期为（ ） A ．2πB ．πC ．32π D ．2π（2）（2020年广东潮州）下列函数中,不是周期函数的是( ) A.y ＝|cos x | B ．y ＝cos|x |C ．y ＝|sin x | D ．y ＝sin|x |【一隅三反】1．（2020·全国高一课时练习）下列函数中,最小正周期为π的是( ) A ．sin y x = B ．cos y x =C ．sin 2y x =D ．1cos2y x =2．（2019·云南高二期末）函数 ()2sin 36f x x π⎛⎫=-⎪⎝⎭的最小正周期为__________．考点三 对称性【例3】（2020·辽宁大连·高一期末）函数()cos 26f x x π⎛⎫=+⎪⎝⎭的图像的一条对称轴方程为（） A ．6x π=B ．512x π=C ．23x π=D ．23x π=-【一隅三反】1．（2020·永昌县第四中学高一期末）函数y ＝12sin 3x π⎛⎫- ⎪⎝⎭的图象的一条对称轴是（ ）A ．x ＝－2π B ．x ＝2π C ．x ＝－6π D ．x ＝6π2．（2020·山西省长治市第二中学校高一期末（理））下列函数中,最小正周期为π,且图象关于直线3x π=对称的函数是（ ）A ．2sin 23y x π⎛⎫=+⎪⎝⎭B ．2sin 26y x π⎛⎫=-⎪⎝⎭C ．2sin 23x y π⎛⎫=+⎪⎝⎭ D ．2sin 23y x π⎛⎫=-⎪⎝⎭3．（2020·河南平顶山·高一期末）如果函数()sin 2y x ϕ=+的图象关于直线πx =对称,那么ϕ取最小值时ϕ的值为（ ）A ．3π±B ．π3C ．π2-D ．2π±考点四 单调性【例4】（1）（2020·吉林扶余市第一中学高一期中）函数()1πsin 223f x x ⎛⎫=+ ⎪⎝⎭的单调递增区间为（ ） A ．5πππ,π1212k k ⎡⎤-+⎢⎥⎣⎦,k Z ∈ B ．π3ππ,π44k k ⎡⎤++⎢⎥⎣⎦,k Z ∈ C ．2πππ,π36k k ⎡⎤--⎢⎥⎣⎦,k Z ∈ D ．πππ,π44k k ⎡⎤++⎢⎥⎣⎦,k Z ∈ （2）（2020·吉林扶余市第一中学高一期中）已知函数()()sin 2f x x ϕ=+在π0,6⎡⎤⎢⎥⎣⎦上单调递减,则实数ϕ的一个值是（ ）． A ．3π2B ．π2-C ．πD ．2π【一隅三反】1．（2020·湖南益阳·高一期末）函数()cos 26f x x π⎛⎫=+⎪⎝⎭的单调递增区间为（ ）A ．()7,1212k k k Z ππππ⎡⎤--∈⎢⎥⎣⎦B ．()72,266k k k Z ππππ⎡⎤--∈⎢⎥⎣⎦C ．()5,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦D ．()52,266k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦2．（2020·全国高三其他（理））已知函数()()sin 06f x x πωω⎛⎫=+> ⎪⎝⎭,对任意x ∈R ,都有()3f x f π⎛⎫≤⎪⎝⎭,并且()f x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上不单调,则ω的最小值是（ ） A ．1 B ．3C ．5D ．73．（2020·全国高三其他（理））函数()()cos f x x θ=+在[]0,π上为增函数,则θ的值可以是（ ）A ．0B ．2πC ．πD ．32π考点五 奇偶性【例5】（2020·上海黄浦·高一期末）下列函数中,周期是π的偶函数为（ ）. A ．cos 2xy = B ．sin 2y x = C ．|sin |y x = D ．sin ||y x =【一隅三反】1．（2019·贵州高三月考（文））函数sin 2y x =是（ ）A ．最小正周期为2π的奇函数 B ．最小正周期为π的奇函数C ．最小正周期为2π的偶函数 D ．最小正周期为π的偶函数2．（2020·辽宁辽阳·高一期末）下列函数中,周期为π的奇函数是（ ） A ．cos2xy π+=B ．sin(23)y x π=+C ．cos(2)y x π=+D ．cos 2y x π⎛⎫=-⎪⎝⎭3．（2020·昆明市官渡区第一中学高一开学考试）已知函数()3()sin 42f x x x R π⎛⎫=-∈ ⎪⎝⎭,下面结论错误的是（ ）A ．函数()f x 的最小正周期为2π B ．函数()f x 在区间0,16π⎡⎤⎢⎥⎣⎦上是增函数 C ．函数()f x 的图象关于直线4x π=对称 D ．函数()f x 是偶函数考点六 定义域【例6】（1）（2020·宁县第二中学高一期中）函数y =的定义域是________.（2）（2020·宁县第二中学高一期中）函数y =__________.【一隅三反】1（2020·辽宁沈阳·高一期中）函数1tan 24y x π⎛⎫=+⎪⎝⎭的定义域是（ ）A ．4,2xx k k Z ππ⎧⎫≠-+∈⎨⎬⎩⎭∣ B ．2,2xx k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭∣ C ．32,2xx k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭∣ D ．,2xx k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭∣2．（2020·湖南高一月考）函数()=ln(sin f x x 的定义域为（ ） A ．2(,)()33k k k Z ππππ++∈ B ．5(,)()66k k k Z ππππ++∈ C ．2(2,2)()33k k k Z ππππ++∈ D ．5(2,2)()66k k k Z ππππ++∈3．（2020·吉林公主岭·高一期末（理））函数()f x =的定义域为（ ）A ．0,3π⎡⎤⎢⎥⎣⎦B ．,43ππ⎡⎤⎢⎥⎣⎦C ．(,]43ππD ．5,44ππ⎡⎤⎢⎥⎣⎦考点七 值域【例7】（1）（2019·福建高三学业考试）函数2sin y x =的最小值是 。

第三节三角函数的图象与性质1．用五点法作正弦函数和余弦函数的简图❶在正弦函数y ＝sin x ，x ∈[0,2π]的图象上，五个关键点是：(0,0)，⎝⎛⎭⎫π2，1，(π，0)，⎝⎛⎭⎫3π2，－1，(2π，0)．在余弦函数y ＝cos x ，x ∈[0,2π]的图象上，五个关键点是：(0,1)，⎝⎛⎭⎫π2，0，(π，－1)，⎝⎛⎭⎫3π2，0，(2π，1)．2．正弦、余弦、正切函数的图象与性质函数y ＝sin xy ＝cos xy ＝tan x五点法作图有三步：列表、描点、连线(注意光滑)．正切函数的图象是由直线x＝kπ＋π2(k∈Z)隔开的无穷多支曲线组成的．判断三角函数的奇偶性，应首先判断函数定义域是否关于原点对称．求函数y＝A sin(ωx＋φ)的单调区间时，应注意ω的符号，只有当ω＞0时，才能把ωx＋φ看作一个整体，代入y＝sin t的相应单调区间求解，否则将出现错误．写单调区间时，不要忘记k∈Z.(1)y＝tan x无单调递减区间；(2)y＝tan x在整个定义域内不单调.函数y＝A sin(ωx＋φ)和y＝A cos(ωx＋φ)的最小正周期都是2π|ω|，y＝A tan(ωx＋φ)的最小正周期是π|ω|.[熟记常用结论]1．对称与周期(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个周期，相邻的对称中心与对称轴之间的距离是14个周期．(2)正切曲线相邻两对称中心之间的距离是半个周期．2．奇偶性若f(x)＝A sin(ωx＋φ)(A≠0，ω≠0)，则：(1)f(x)为偶函数的充要条件是φ＝π2＋kπ(k∈Z)；(2)f (x )为奇函数的充要条件是φ＝k π(k ∈Z)．[小题查验基础]一、判断题(对的打“√”，错的打“×”) (1)y ＝sin x 在第一、第四象限是增函数．( ) (2)余弦函数y ＝cos x 的对称轴是y 轴．( ) (3)正切函数y ＝tan x 在定义域内是增函数．( ) (4)y ＝sin|x |是偶函数．( ) 答案：(1)× (2)× (3)× (4)√ 二、选填题1．函数y ＝tan 3x 的定义域为( ) A.⎩⎨⎧⎭⎬⎫x | x ≠3π2＋3k π，k ∈ZB.⎩⎨⎧⎭⎬⎫x |x ≠π6＋k π，k ∈ZC.⎩⎨⎧⎭⎬⎫x |x ≠－π6＋k π，k ∈Z D.⎩⎨⎧⎭⎬⎫x |x ≠π6＋k π3，k ∈Z解析：选D 由3x ≠π2＋k π(k ∈Z)，得x ≠π6＋k π3，k ∈Z.2．函数y ＝2－cos x3(x ∈R)的最大值和最小正周期分别是( )A ．2,3πB ．1,6πC ．3,6πD ．3,3π解析：选C 由y ＝2－cos x 3知，y max ＝2－(－1)＝3，最小正周期T ＝2π13＝6π.3．下列函数中最小正周期为π且图象关于直线x ＝π3对称的是( )A ．y ＝2sin ⎝⎛⎭⎫2x ＋π3B ．y ＝2sin ⎝⎛⎭⎫2x －π6 C ．y ＝2sin ⎝⎛⎭⎫x 2＋π3D ．y ＝2sin ⎝⎛⎭⎫2x －π3 解析：选B 函数y ＝2sin ⎝⎛⎭⎫2x －π6的最小正周期T ＝2π2＝π， ∵sin ⎝⎛⎭⎫2×π3－π6＝1， ∴函数y ＝2sin ⎝⎛⎭⎫2x －π6的图象关于直线x ＝π3对称． 4．函数y ＝sin ⎝⎛⎭⎫x －π4的图象的对称轴为______________，对称中心为________________． 解析：由x －π4＝π2＋k π，k ∈Z ，得x ＝3π4＋k π，k ∈Z ；由x －π4＝k π，k ∈Z ，得x ＝π4＋k π，k ∈Z ，故函数y ＝sin ⎝⎛⎭⎫x －π4的图象的对称轴为x ＝3π4＋k π，k ∈Z ，对称中心为⎝⎛⎭⎫π4＋k π，0，k ∈Z.答案：x ＝3π4＋k π，k ∈Z ⎝⎛⎭⎫π4＋k π，0，k ∈Z 5．函数f (x )＝32cos x －12sin x ()x ∈[0，π]的单调递增区间为________． 解析：f (x )＝32cos x －12sin x ＝cos ⎝⎛⎭⎫x ＋π6，由2k π－π≤x ＋π6≤2k π(k ∈Z)，得2k π－7π6≤x ≤2k π－π6(k ∈Z)．∵x ∈[0，π]，∴f (x )在⎣⎡⎦⎤5π6，π上单调递增． 答案：⎣⎡⎦⎤5π6，π6．函数f (x )＝sin ⎝⎛⎭⎫2x －π4在区间⎣⎡⎦⎤0，π2上的最小值为________． 解析：由x ∈⎣⎡⎦⎤0，π2，得2x －π4∈⎣⎡⎦⎤－π4，3π4， 所以sin ⎝⎛⎭⎫2x －π4∈⎣⎡⎦⎤－22，1，故函数f (x )＝sin ⎝⎛⎭⎫2x －π4在区间⎣⎡⎦⎤0，π2上的最小值为－22. 答案：－22考点一三角函数的定义域[基础自学过关][题组练透]1．函数f (x )＝－2tan ⎝⎛⎭⎫2x ＋π6的定义域是( ) A.⎩⎨⎧⎭⎬⎫x | x ≠π6B.⎩⎨⎧⎭⎬⎫x |x ≠－π12C.⎩⎨⎧⎭⎬⎫x |x ≠k π＋π6，k ∈ZD.⎩⎨⎧⎭⎬⎫x |x ≠k π2＋π6，k ∈Z解析：选D 由正切函数的定义域，得2x ＋π6≠k π＋π2(k ∈Z)，即x ≠k π2＋π6(k ∈Z)，故选D.2．函数y ＝sin x －cos x 的定义域为________．解析：法一：要使函数有意义，必须使sin x －cos x ≥0.利用图象，在同一坐标系中画出[0,2π]上函数y ＝sin x 和函数y ＝cos x 的图象，如图所示．在[0,2π]内，满足sin x ＝cos x 的x 为π4，5π4，再结合正弦、余弦函数的周期性，所以原函数的定义域为⎩⎨⎧⎭⎬⎫x | 2k π＋π4≤x ≤2k π＋5π4，k ∈Z .法二：利用三角函数线，画出满足条件的终边范围(如图阴影部分所示)．所以定义域为⎩⎨⎧⎭⎬⎫x |2k π＋π4≤x ≤2k π＋5π4，k ∈Z .答案：⎣⎡⎦⎤2k π＋π4，2k π＋5π4(k ∈Z) 3．函数y ＝lg(sin 2x )＋9－x 2的定义域为________．解析：由⎩⎪⎨⎪⎧sin 2x ＞0，9－x 2≥0，得⎩⎪⎨⎪⎧k π＜x ＜k π＋π2，k ∈Z ，－3≤x ≤3.∴－3≤x ＜－π2或0＜x ＜π2.∴函数y ＝lg(sin 2x )＋9－x 2的定义域为⎣⎡⎭⎫－3，－π2∪⎝⎛⎭⎫0，π2. 答案：⎣⎡⎭⎫－3，－π2∪⎝⎛⎭⎫0，π2 [名师微点]求三角函数定义域实际上是构造简单的三角不等式(组)，常借助三角函数线或三角函数图象来求解．考点二三角函数的值域(最值) [师生共研过关][典例精析](1)函数f (x )＝3sin ⎝⎛⎭⎫2x －π6在区间⎣⎡⎦⎤0，π2上的值域为________． (2)(2017·全国卷Ⅱ)函数f (x )＝sin 2x ＋3cos x －34⎝⎛⎭⎫x ∈⎣⎡⎦⎤0，π2的最大值是________． (3)函数y ＝sin x －cos x ＋sin x cos x 的值域为_________________________________． [解析] (1)当x ∈⎣⎡⎦⎤0，π2时，2x －π6∈⎣⎡⎦⎤－π6，5π6， ∴sin ⎝⎛⎭⎫2x －π6∈⎣⎡⎦⎤－12，1， 故3sin ⎝⎛⎭⎫2x －π6∈⎣⎡⎦⎤－32，3， ∴函数f (x )在区间⎣⎡⎦⎤0，π2上的值域为⎣⎡⎦⎤－32，3. (2)依题意，f (x )＝sin 2x ＋3cos x －34＝－cos 2x ＋3cos x ＋14＝－⎝⎛⎭⎫cos x －322＋1，因为x ∈⎣⎡⎦⎤0，π2，所以cos x ∈[0,1]， 因此当cos x ＝32时，f (x )max ＝1. (3)设t ＝sin x －cos x ，则－2≤t ≤2，t 2＝sin 2x ＋cos 2x －2sin x cos x ，则sin x cos x ＝1－t 22，∴y ＝－t 22＋t ＋12＝－12(t －1)2＋1.当t ＝1时，y max ＝1；当t ＝－2时，y min ＝－12－ 2.∴函数的值域为⎣⎡⎦⎤－12－2，1.[答案] (1)⎣⎡⎦⎤－32，3 (2)1 (3)⎣⎡⎦⎤－12－2，1 [解题技法]求三角函数的值域(最值)的3种类型及解法思路(1)形如y ＝a sin x ＋b cos x ＋c 的三角函数化为y ＝A sin(ωx ＋φ)＋k 的形式，再求值域(最值)；(2)形如y ＝a sin 2x ＋b sin x ＋c 的三角函数，可先设sin x ＝t ，化为关于t 的二次函数求值域(最值)；(3)形如y ＝a sin x cos x ＋b (sin x ±cos x )＋c 的三角函数，可先设t ＝sin x ±cos x ，化为关于t 的二次函数求值域(最值)．[过关训练]1．若函数f (x )＝(1＋3tan x )cos x ，－π3≤x ≤π6，则f (x )的最大值为( )A ．1B ．2 C. 3D.3＋1解析：选C f (x )＝(1＋3tan x )cos x ＝cos x ＋3sin x ＝2sin ⎝⎛⎭⎫x ＋π6.因为－π3≤x ≤π6，所以－π6≤x ＋π6≤π3，故当x ＝π6时，f (x )取最大值为3，故选C. 2．(2018·北京高考)已知函数f (x )＝sin 2x ＋3sin x cos x . (1)求f (x )的最小正周期；(2)若f (x )在区间⎣⎡⎦⎤－π3，m 上的最大值为32，求m 的最小值． 解：(1)因为f (x )＝sin 2x ＋3sin x cos x ＝12－12cos 2x ＋32sin 2x ＝sin ⎝⎛⎭⎫2x －π6＋12， 所以f (x )的最小正周期为T ＝2π2＝π. (2)由(1)知f (x )＝sin ⎝⎛⎭⎫2x －π6＋12. 由题意知－π3≤x ≤m ，所以－5π6≤2x －π6≤2m －π6. 要使f (x )在区间⎣⎡⎦⎤－π3，m 上的最大值为32，即sin ⎝⎛⎭⎫2x －π6在区间⎣⎡⎦⎤－π3，m 上的最大值为1. 所以2m －π6≥π2，即m ≥π3.所以m 的最小值为π3.考点三三角函数的单调性[全析考法过关][考法全析]考法(一) 求三角函数的单调区间[例1] (1)函数y ＝sin ⎝⎛⎭⎫π3－2x 的单调递减区间为________________． (2)函数y ＝|tan x |的单调递增区间为______________，单调递减区间为________________． [解析] (1)函数y ＝sin ⎝⎛⎭⎫π3－2x ＝－sin ⎝⎛⎭⎫2x －π3的单调递减区间是函数y ＝sin ⎝⎛⎭⎫2x －π3的单调递增区间．由2k π－π2≤2x －π3≤2k π＋π2，k ∈Z ，得k π－π12≤x ≤k π＋5π12，k ∈Z.故所给函数的单调递减区间为⎣⎡⎦⎤k π－π12，k π＋5π12，k ∈Z. (2)作出函数y ＝|tan x |的图象，如图．观察图象可知，函数y ＝|tan x |的单调递增区间为⎣⎡⎭⎫k π，k π＋π2，k ∈Z ；单调递减区间为⎝⎛⎦⎤k π－π2，k π，k ∈Z.[答案] (1)⎣⎡⎦⎤k π－π12，k π＋5π12，k ∈Z(2)⎣⎡⎭⎫k π，k π＋π2，k ∈Z ⎝⎛⎦⎤k π－π2，k π，k ∈Z 考法(二) 已知三角函数的单调性求参数[例2] (2018·全国卷Ⅱ)若f (x )＝cos x －sin x 在[－a ，a ]是减函数，则a 的最大值是( ) A.π4 B.π2 C.3π4D ．π[解析] f (x )＝cos x －sin x ＝－2sin ⎝⎛⎭⎫x －π4， 当x ∈⎣⎡⎦⎤－π4，3π4，即x －π4∈⎣⎡⎦⎤－π2，π2时， 函数y ＝sin ⎝⎛⎭⎫x －π4单调递增， 则函数f (x )＝－2sin ⎝⎛⎭⎫x －π4单调递减． ∵函数f (x )在[－a ，a ]是减函数， ∴[－a ，a ]⊆⎣⎡⎦⎤－π4，3π4，∴0＜a ≤π4， ∴a 的最大值为π4.[答案] A[规律探求]1．设函数f (x )＝sin ⎝⎛⎭⎫2x －π3，x ∈⎣⎡⎦⎤－π2，π，则以下结论正确的是( ) A ．函数f (x )在⎣⎡⎦⎤－π2，0上单调递减 B ．函数f (x )在⎣⎡⎦⎤0，π2上单调递增 C ．函数f (x )在⎣⎡⎦⎤π2，5π6上单调递减 D ．函数f (x )在⎣⎡⎦⎤5π6，π上单调递增解析：选C 由x ∈⎣⎡⎦⎤－π2，0，得2x －π3∈⎣⎡⎦⎤－4π3，－π3，所以函数f (x )先减后增；由x ∈⎣⎡⎦⎤0，π2，得2x －π3∈⎣⎡⎦⎤－π3，2π3，所以函数f (x )先增后减；由x ∈⎣⎡⎦⎤π2，5π6，得2x －π3∈⎣⎡⎦⎤2π3，4π3，所以函数f (x )单调递减；由x ∈⎣⎡⎦⎤5π6，π，得2x －π3∈⎣⎡⎦⎤4π3，5π3，所以函数f (x )先减后增．故选C.2．若函数f (x )＝sin ωx (ω＞0)在区间⎣⎡⎦⎤0，π3上单调递增，在区间⎣⎡⎦⎤π3，π2上单调递减，则ω＝________.解析：∵f (x )＝sin ωx (ω＞0)过原点，∴当0≤ωx ≤π2，即0≤x ≤π2ω时，y ＝sin ωx 是增函数；当π2≤ωx ≤3π2，即π2ω≤x ≤3π2ω时，y ＝sin ωx 是减函数． 由f (x )＝sin ωx (ω＞0)在⎣⎡⎦⎤0，π3上单调递增， 在⎣⎡⎦⎤π3，π2上单调递减，知π2ω＝π3，∴ω＝32. 答案：323．若函数y ＝12sin ωx 在区间⎣⎡⎦⎤－π8，π12上单调递减，则ω的取值范围是________． 解析：因为函数y ＝12sin ωx 在区间⎣⎡⎦⎤－π8，π12上单调递减，所以ω＜0且函数y ＝12sin(－ωx )在区间⎣⎡⎦⎤－π12，π8上单调递增，则⎩⎨⎧ω＜0，－ω·⎝⎛⎭⎫－π12≥2k π－π2，k ∈Z ，－ω·π8≤2k π＋π2，k ∈Z ，即⎩⎪⎨⎪⎧ω＜0，ω≥24k －6，k ∈Z ，ω≥－16k －4，k ∈Z ，解得－4≤ω＜0.答案：[－4,0)考点四三角函数的周期性、奇偶性、对称性[全析考法过关][考法全析]考法(一) 三角函数的周期性[例1] 在函数①y ＝cos|2x |，②y ＝|cos x |，③y ＝cos ⎝⎛⎭⎫2x ＋π6，④y ＝tan ⎝⎛⎭⎫2x －π4中，最小正周期为π的所有函数为( )A ．①②③B ．①③④C ．②④D ．①③[解析] ①y ＝cos|2x |＝cos 2x ，最小正周期为π； ②由图象知y ＝|cos x |的最小正周期为π； ③y ＝cos ⎝⎛⎭⎫2x ＋π6的最小正周期T ＝2π2＝π； ④y ＝tan ⎝⎛⎭⎫2x －π4的最小正周期T ＝π2，故选A. [答案] A考法(二) 三角函数的奇偶性[例2] (2019·抚顺调研)已知函数f (x )＝2sin ⎝⎛⎭⎫x ＋θ＋π3⎝⎛⎭⎫θ∈⎣⎡⎦⎤－π2，π2是偶函数，则θ的值为________．[解析] ∵函数f (x )为偶函数，∴θ＋π3＝k π＋π2(k ∈Z)．又θ∈⎣⎡⎦⎤－π2，π2，∴θ＋π3＝π2，解得θ＝π6，经检验符合题意．[答案]π6考法(三) 三角函数的对称性[例3] (1)已知函数f (x )＝2sin ⎝⎛⎭⎫ωx ＋π6(ω＞0)的最小正周期为4π，则该函数的图象( )A ．关于点⎝⎛⎭⎫π3，0对称 B ．关于点⎝⎛⎭⎫5π3，0对称 C ．关于直线x ＝π3对称D ．关于直线x ＝5π3对称 (2)(2018·江苏高考)已知函数y ＝sin(2x ＋φ)⎝⎛⎭⎫－π2＜φ＜π2的图象关于直线x ＝π3对称，则φ的值为________．[解析] (1)因为函数f (x )＝2sin ⎝⎛⎭⎫ωx ＋π6(ω＞0)的最小正周期为4π，而T ＝2πω＝4π，所以ω＝12，即f (x )＝2sin ⎝⎛⎭⎫x 2＋π6.令x 2＋π6＝π2＋k π(k ∈Z)，解得x ＝2π3＋2k π(k ∈Z)， 故f (x )的对称轴为x ＝2π3＋2k π(k ∈Z)．令x 2＋π6＝k π(k ∈Z)，解得x ＝－π3＋2k π(k ∈Z)， 故f (x )的对称中心为⎝⎛⎭⎫－π3＋2k π，0(k ∈Z)，对比选项可知B 正确． (2)由题意得f ⎝⎛⎭⎫π3＝sin ⎝⎛⎭⎫2π3＋φ＝±1， ∴2π3＋φ＝k π＋π2(k ∈Z)，∴φ＝k π－π6(k ∈Z)． ∵φ∈⎝⎛⎭⎫－π2，π2，∴φ＝－π6. [答案] (1)B (2)－π6[规律探求]只需令ωx ＋φ＝π2＋k π(k ∈Z)，求x 即可；如果求f (x )的对称中心的横坐标，只需令ωx ＋φ＝k π(k ∈Z)，求x 即可．(2)对于可化为f (x )＝A cos(ωx ＋φ)(ω＞0)形式的函数，如果求f (x )的对称轴，只需令ωx ＋φ＝k π(k ∈Z)，求x 即可；如果求f (x )的对称中心的横坐标，只需令ωx ＋φ＝π2＋k π(k ∈Z)，求x 即可找共性这类问题解题的关键是把原三角函数关系式统一角，统一名，即“一角一函数”，其解题思维流程是：[过关训练]1．若函数f (x )＝3sin(2x ＋θ)＋cos(2x ＋θ)(0＜θ＜π)的图象关于⎝⎛⎭⎫π2，0中心对称，则函数f (x )在⎣⎡⎦⎤－π4，π6上的最小值是________． 解析：f (x )＝2sin ⎝⎛⎭⎫2x ＋θ＋π6，又图象关于⎝⎛⎭⎫π2，0中心对称，所以2×π2＋θ＋π6＝k π(k ∈Z)， 所以θ＝k π－7π6(k ∈Z)，又0＜θ＜π，所以θ＝5π6，所以f (x )＝－2sin 2x ，因为x ∈⎣⎡⎦⎤－π4，π6， 所以2x ∈⎣⎡⎦⎤－π2，π3，f (x )∈[－3，2]， 所以f (x )的最小值是－ 3. 答案：－ 32．若x ＝π8是函数f (x )＝2sin ⎝⎛⎭⎫ωx －π4，x ∈R 的一个零点，且0＜ω＜10，则函数f (x )的最小正周期为________．解析：依题意知，f ⎝⎛⎭⎫π8＝2sin ⎝⎛⎭⎫ωπ8－π4＝0， 即ωπ8－π4＝k π，k ∈Z ，整理得ω＝8k ＋2，k ∈Z. 又因为0＜ω＜10，所以0＜8k ＋2＜10，得－14＜k ＜1，而k ∈Z ，所以k ＝0，ω＝2，所以f (x )＝2sin ⎝⎛⎭⎫2x －π4，f (x )的最小正周期为π. 答案：π。

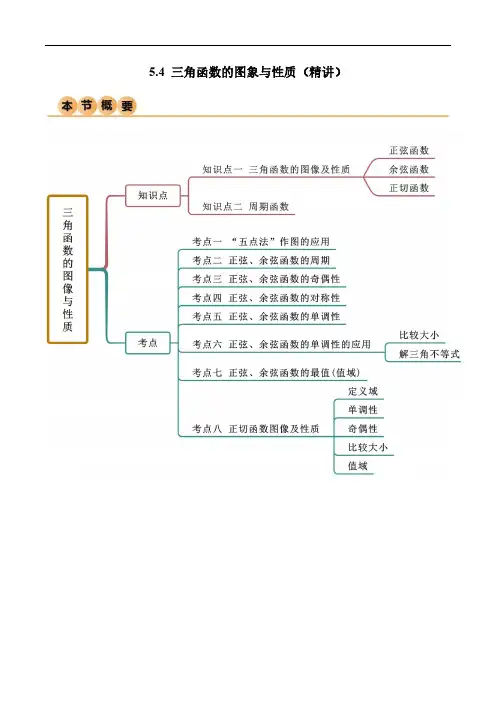
5.4三角函数的图象与性质（精讲）一．三角函数的图像及性质π1.周期函数概念①对于函数f(x)，存在一个非零常数T(T>0)条件②当x取定义域内的每一个值时，都有f(x＋T)＝f(x)结论函数f(x)叫做周期函数，非零常数T叫做这个函数的周期2.最小正周期条件如果周期函数f(x)的所有周期中存在一个最小的正数结论这个最小正数叫做f(x)的最小正周期一．用三角函数图象解三角不等式(1)作出相应正弦函数或余弦函数在[0，2π]上的图象；(2)写出适合不等式在区间[0，2π]上的解集；(3)根据公式一写出不等式的解集.二．求三角函数周期(1)定义法，即利用周期函数的定义求解.. (2)公式法，对形如y＝A sin(ωx＋φ)或y＝A cos(ωx＋φ)(A，ω，φ是常数，A≠0，ω≠0)的函数，T＝2π|ω|(3)观察法，即通过观察函数图象求其周期.三．判断函数奇偶性(1)看函数的定义域是否关于原点对称；(2)看f(－x)与f(x)的关系.对于三角函数奇偶性的判断，有时可根据诱导公式先将函数式化简后再判断.四．单调区间的求法求形如y＝A sin(ωx＋φ)或y＝A cos(ωx＋φ)的函数的单调区间，要先把ω化为正数．(1)当A>0时，把ωx＋φ整体代入y＝sin x或y＝cos x的单调递增区间内，求得的x的范围即为函数的单调递增区间．(2)当A<0时，把ωx＋φ整体代入y＝sin x或y＝cos x的单调递增区间内，求得的x的范围即为函数的单调递减区间；代入y＝sin x或y＝cos x的单调递减区间内，可求得函数的单调递增区间．五．比较三角函数值大小(1)异名函数化为同名函数．(2)利用诱导公式把已知角转化到同一单调区间上．(3)利用函数的单调性比较大小．六．求三角函数值域或最值（1）形如y＝sin(ωx＋φ)的三角函数，令t＝ωx＋φ，根据题中x的取值范围，求出t的取值范围，再利用三角函数的单调性、有界性求出y＝sin t的最值(值域).(2)形如y＝a sin2x＋b sin x＋c(a≠0)的三角函数，可先设t＝sin x，将函数y＝a sin2x＋b sin x＋c(a≠0)化为关于t 的二次函数y＝at2＋bt＋c(a≠0)，根据二次函数的单调性求值域(最值).(3)对于形如y＝a sin x(或y＝a cos x)的函数的最值还要注意对a的讨论.考点一“五点法”作图的应用【例1-1】（2022·全国·高一专题练习）作出下列函数在一个周期图象的简图：(1)3sin3x y =；(2)2sin 4y x π⎛⎫=+ ⎪⎝⎭；(3)2sin 214y x π⎛⎫=++ ⎪⎝⎭；(4)2cos 23x y π⎛⎫=+ ⎪⎝⎭．【答案】函数图象见解析【解析】（1）解：因为3sin 3xy =，取值列表：x 032π3π92π6π3x02ππ32π2πy33-0描点连线，可得函数图象如图示：（2）解：因为2sin 4y x π⎛⎫=+ ⎪⎝⎭，取值列表：x4π-4π34π54π74π4x π+02ππ32π2πy22-0描点连线，可得函数图象如图示：（3）解：因为2sin 214y x π⎛⎫=++ ⎪⎝⎭，取值列表：x 8π-8π38π58π78π24x π+02ππ32π2πy1311-1描点连线，可得函数图象如图示：（4）解：因为2cos 23x y π⎛⎫=+ ⎪⎝⎭，取值列表：x 23π-3π43π73π103π23x π+02ππ32π2πy22-02描点连线，可得函数图象如图示：【例1-2】（2023秋·高一课时练习）当[]2,2x ππ∈-时，作出下列函数的图象，把这些图象与sin y x =的图象进行比较，你能发现图象变换的什么规律？（1）sin y x =-；（2）sin y x =；（3）sin y x =.【答案】答案见解析【解析】（1）该图象与sin y x =的图象关于x 轴对称，故将sin y x =的图象作关于x 轴对称的图象即可得到sin y x =-的图象.（2）sin ,2,0,sin sin ,0,2,x x x y x x x x ππππππ-≤≤-≤≤⎧==⎨--≤≤≤≤⎩将sin y x =的图象在x 轴上方部分保持不变，下半部分作关于x 轴对称的图形，即可得到sin y x =的图象.（3）sin ,0,sin sin ,0,x x y x x x ≥⎧==⎨-<⎩将sin y x =的图象在y 轴右边部分保持不变，并将其作关于y 轴对称的图形，即可得到sin y x =的图象.【一隅三反】1．（2023秋·高一课时练习）用“五点法”作出下列函数的简图.(1)2sin y x =，[]0,2πx ∈；(2)πsin 3y x ⎛⎫=+ ⎪⎝⎭，π5π,33x ⎡⎤∈-⎢⎥⎣⎦.（3）1π3sin 23y x ⎛⎫=- ⎪⎝⎭在一个周期（4πT =）内的图像．(4)2sin y x =-,[]0,2πx ∈;(5)πcos 6y x ⎛⎫=+ ⎪⎝⎭,π11,π66x ⎡⎤∈-⎢⎥⎣⎦．（6）πcos 3y x ⎛⎫=+ ⎪⎝⎭，π5π,33x ⎡⎤∈-⎢⎥⎣⎦【答案】图象见解析图象见解析【解析】（1）列表：x 0π2π3π22π2sin x22-0描点、连线、绘图，如图所示.（2）列表：π3x +π2π3π22πx π3-π62π37π65π3πsin 3x ⎛⎫+ ⎪⎝⎭010－1描点连线如图.（3）列表:x 2π35π38π311π314π31π23x -0π2π3π22πy10-10图像如图所示：（4）解:由题知2sin y x =-,[]0,2x π∈,列表如下:xπ2π3π22πy21232根据表格画出图象如下:（5）解:由题知πcos 6y x ⎛⎫=+ ⎪⎝⎭,π11,π66x ⎡⎤∈-⎢⎥⎣⎦,列表如下:x π6-π35π64π311π6π6x +π2π3π22πy10-101根据表格画出图象如下:（6）[]π5ππ,0,2π333x x ⎡⎤∈-∴+∈⎢⎥⎣⎦根据五点法作图列表得：π3x +π2π3π22πxπ3-π62π37π65π3y11-01画图像得：考点二正弦、余弦函数的周期【例2-1】（2023湖南）下列函数中，最小正周期为π的函数是（）A ．y ＝sin xB ．y ＝cos xC ．y ＝sin 1π23x ⎛⎫+ ⎪⎝⎭D ．y ＝cos π23x ⎛⎫- ⎪⎝⎭【答案】D【解析】A.y ＝sin x 的最小正周期为2πT =，故错误；B.y ＝cos x 的最小正周期为2πT =，故错误；C.y ＝sin 1π23x ⎛⎫+ ⎪⎝⎭的最小正周期为2π4π12T ==，故错误；D.y ＝cos ππ2cos 233x x ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭2ππ2T ==，故正确；故选：D【例2-2】（2023秋·高一课时练习）下列函数，最小正周期为2π的是（）A ．sin 2x y =B ．sin2y x =C ．sin 2x y =D ．sin2y x=【答案】C【解析】函数sin 2x y =的最小正周期为2π4π12T ==，故A 不符合；函数sin2y x =，其最小正周期为2ππ2T ==，故B 不符合；因为函数sin2xy =的最小正周期为4πT =，所以函数sin 2x y =的最小正周期为2π，故C 符合；因为函数sin2y x =的最小正周期为2ππ2T ==，所以函数sin2y x =的最小正周期为π2，故D 不符合.故选：C.【一隅三反】1．（2023·全国·高一专题练习）函数()cos 26f x x π⎛⎫=-- ⎪⎝⎭的最小正周期是（）A ．2πB ．πC ．2πD ．4π【答案】B【解析】由函数()cos 26f x x π⎛⎫=-- ⎪⎝⎭，则其最小正周期22T ππ==-.故选：B.2．（2023北京）下列函数中，最小正周期为π的函数是（）A ．sin y x =B ．cos y x =C ．cos y x =D ．sin y x=【答案】B【解析】对于A ，函数sin y x =的最小正周期为2π，故A 不符合题意；对于B ，作出函数cos y x =的图象，由图可知，函数cos y x =的最小正周期为π，故B 符合题意；对于C ，函数cos y x =的最小正周期为2π，故C 不符合题意；对于D ，函数sin ,0sin sin ,0x x y x x x ≥⎧==⎨-<⎩，其图象如图，由图可知，函数sin y x =不是周期函数，故D 不符合题意.故选：B.3．（2023·全国·高一假期作业）（多选）下列函数中，是周期函数的是（）A ．cos y x =B ．cos y x =C ．sin y x =D ．sin y x=【答案】ABC【解析】对于A ，()cos πcos cos x x x +=-= ，cos y x ∴＝的最小正周期为π；对于B ，()cos cos cos x x x =-= ，cos y x ∴=的最小正周期为2π；对于C ，()sin πsin sin x x x +=-= ，sin y x ∴=的最小正周期为π；对于D ，∵sin ,0sin sin ,0x x y x x x ≥⎧==⎨-<⎩，∴函数图象关于y 轴对称，不具有奇偶性，故错误.故选：ABC4．（2023春·江西上饶·高一校联考期中）（多选）下列函数，最小正周期为π的有（）A ．sin y x =B ．sin y x =C ．πsin 23y x ⎛⎫=- ⎪⎝⎭D ．2cos 1y x =-【答案】BC【解析】对于A ，sin ||y x =为偶函数，图象关于y 轴对称，其图象如下，不是周期函数，故A 错误；对于B ，作出函数|sin |y x =的图象如下，观察可得其最小正周期为π，故B 正确；对于C ，由周期公式可得2π||T ω=，可得πsin 23y x ⎛⎫=- ⎪⎝⎭的最小正周期为π，故C 正确；对于D ，由周期公式可得2π||T ω=，可得2cos 1y x =-的最小正周期为2π，故D 错误.故选：BC考点三正弦、余弦函数的奇偶性【例3-1】7．（2023春·四川眉山·高一校考期中）下列函数中是奇函数，且最小正周期是π的函数是（）A ．cos 2y x =B ．sin y x=C ．πsin(2)2y x =+D ．3πcos(2)2y x =-【答案】D【解析】对于A ，∵cos 2()cos 2x x -=，∴函数cos 2y x =是偶函数，故A 错误；对于B ，∵sin()sin sin x x x -=-=，∴函数sin y x =是偶函数，故B 错误；对于C ，函数πsin(2)cos 22y x x =+=是偶函数，故C 错误；对于D ，函数3πcos(2)sin 22y x x =-=-是奇函数，最小正周期2ππ2T ==，故D 正确．故选：D.【例3-2】（2021春·陕西榆林·高一校考阶段练习）若函数()cos 203f x x πφφ⎛⎫=+-> ⎪⎝⎭（）是奇函数，则φ的最小值为（）A ．56πB ．43πC ．3πD ．512π【答案】A【解析】因为函数()cos 203f x x πφφ⎛⎫=+-> ⎝⎭（）是奇函数，所以,32k k Z ππφπ-=+∈，解得5,6k k Z πφπ=+∈，所以φ的最小值为56π，故选：A【例3-3】（2023秋·高一课时练习）判断下列函数的奇偶性．(1)1π()sin 22f x x ⎛⎫=-+ ⎪⎝⎭；(2)2π()cos 2f x x x ⎛⎫=+ ⎪⎝⎭；(3)21sin cos ()1sin x x f x x+-=+.【答案】(1)偶函数(2)奇函数(3)非奇非偶函数．【解析】（1）()f x 的定义域为R ，1π11()sin cos cos 2222f x x x x ⎛⎫⎛⎫=-+=-= ⎪ ⎪⎝⎭⎝⎭，因为11()cos cos ()22f x x x f x ⎛⎫-=-== ⎪⎝⎭，所以()f x 为偶函数，（2）()f x 的定义域为R ，22π()cos sin 2f x x x x x ⎛⎫=+=- ⎪⎝⎭，因为22()()sin()sin ()f x x x x x f x -=---==-，所以()f x 为奇函数，（3）由1sin 0x +≠，得sin 1x ≠-，解得π2π,Z 2x k k ≠-+∈，所以函数的定义域为πR 2π,Z 2x x k k ⎧⎫∈≠-+∈⎨⎬⎩⎭，因为定义域不关于原点对称，所以该函数是非奇非偶函数．【一隅三反】1．（2023秋·高一课时练习）函数()sin R f x x x x +∈=，（）A ．是奇函数，但不是偶函数B ．是偶函数，但不是奇函数C ．既是奇函数，又是偶函数D ．既不是奇函数，又不是偶函数【答案】A【解析】由()sin s ()(in )f x x x x x f x -=-+-=-=-可知()f x 是奇函数．故选:A2．（2023春·云南文山·高一校考阶段练习）下列函数中，最小正周期为π的偶函数是（）A ．cos y x =B ．2sin y x =C ．sin 2y x =D ．cos y x=【答案】A【解析】对于A ，()cos y f x x ==定义域为R ，因为()cos()cos ()f x x x f x -=-==，所以函数cos y x =为偶函数，因为cos y x =的图象是由cos y x =的图象在x 轴下方的关于x 轴对称后与x 轴上方的图象共同组成（如下图所示），又cos y x =的最小正周期为2π，所以cos y x =的最小正周期为π，故A 正确；对于B ：2sin y x =为最小正周期为2π的奇函数，故B 错误；对于C ：()sin 2y g x x ==定义域为R ，()()()sin 2sin 2g x x x g x -=-==，即sin 2y x =为偶函数，又()()ππsin 2sin 2πsin 2sin 222g x x x x x gx ⎛⎫⎛⎫+=+=+=-== ⎪ ⎪⎝⎭⎝⎭，所以π2为sin 2y x =的周期，故C 错误；对于D ：cos y x =为最小正周期为2π的偶函数，故D 错误；故选：A3．（2023秋·高一课时练习）（多选）已知函数()πsin()4f x x ϕ=++是奇函数，则ϕ的值可以是（）A ．0B ．π4-C ．π2D ．3π4【答案】BD【解析】由函数()πsin()4f x x ϕ=++为奇函数，可得ππ,Z 4k k ϕ+=∈，解得ππ,Z 4k k ϕ=-+∈，当0k =时，π4ϕ=-，所以B 满足题意；当1k =时，43πϕ=，所以D 满足题意；故选：BD.4．（2023秋·宁夏吴忠·高一青铜峡市高级中学校考期末）（多选）以下函数是偶函数的是（）A ．2sin y x =B ．cos2y x =C ．3sin y x x =D ．|sin |cos y x x=【答案】BCD【解析】四个选项中函数的定义域均为全体实数，满足关于原点对称，对于A :()2sin f x x =,()()()2sin 2sin f x x x f x -=-=-=-,所以2sin y x =为奇函数,故A 错误对于B :()cos2g x x =,()()()cos 2cos2g x x x g x -=-==所以()cos2g x x =为偶函数,故B 正确;对于C :()3sin h x x x =,()()()()()333sin sin sin h x x x x x x x h x -=--=--==,所以()3sin h x x x =为偶函数,故C 正确;对于D :()|sin |cos t x x x =,()()()()|sin |cos |sin |cos |sin |cos t x x x x x x x t x -=--=-==,所以()|sin |cos t x x x =为偶函数,故D 正确;故选:BCD考点四正弦、余弦函数的对称性【例4-1】（2023春·北京·高一北京市第一六一中学校考期中）函数πsin 26y x ⎛⎫=+ ⎪⎝⎭的图象（）A ．关于直线π3x =对称B ．关于直线π3x =-对称C ．关于点π,06⎛⎫⎪⎝⎭对称D ．关于点π,03⎛⎫⎪⎝⎭对称【答案】B【解析】A.πππ5πsin 2sin13366f ⎛⎫⎛⎫=⨯+=≠± ⎪ ⎪⎝⎭⎝⎭，所以函数不关于直线π3x =对称，故A 错误；B.ππππsin 2sin 13362f ⎡⎤⎛⎫⎛⎫⎛⎫-=⨯-+=-=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，所以函数关于直线π3x =对称，故B 正确；C.ππππsin 2sin 106662f ⎛⎫⎛⎫=⨯+==≠ ⎪ ⎪⎝⎭⎝⎭，所以函数不关于点π,06⎛⎫⎪⎝⎭对称，故C 错误；D.πππ5πsin 2sin03366f ⎛⎫⎛⎫=⨯+=≠ ⎪ ⎝⎭⎝⎭，所以函数不关于点π,06⎛⎫⎪⎝⎭对称，故D 错误；故选：B【例4-2】（2023春·上海杨浦·高一上海市控江中学校考期末）已知常数R ϕ∈，如果函数()cos 2y x ϕ=+的图像关于点4π,03⎛⎫⎪⎝⎭中心对称，那么ϕ的最小值为（）A ．π3B ．π4C ．π6D ．π2【答案】C【解析】因为函数()cos 2y x ϕ=+的图像关于点4π,03⎛⎫⎪⎝⎭中心对称，所以π24ππ32k ϕ⨯++=，Z k ∈，所以13ππ6k ϕ=-+，Z k ∈，所以当2k =时π6ϕ=-，当3k =时5π6ϕ=，1k =时7π6ϕ=-，所以ϕ的最小值为π6.故选：C 【一隅三反】1．（2023云南）函数π()2sin 213f x x ⎛⎫=++ ⎪⎝⎭图象的一个对称中心可以是（）A ．π,03⎛⎫⎪⎝⎭B ．π,112⎛⎫ ⎪⎝⎭C ．5π,012⎛⎫ ⎪⎝⎭D ．,16π⎛⎫- ⎪⎝⎭【答案】D【解析】对于A ，由π3x =，得π2π3x +=，1y =，则π,03⎛⎫⎪⎝⎭不是函数π()2sin 213f x x ⎛⎫=++ ⎪⎝⎭图象的一个对称中心，故A 错误；对于B ，由π12x =，得ππ232x +=，则π,112⎛⎫ ⎪⎝⎭不是函数π()2sin 213f x x ⎛⎫=++ ⎪⎝⎭图象的一个对称中心，故B 错误；对于C ，由5π12x =，得π7π236x +=，则5π,012⎛⎫⎪⎝⎭不是函数π()2sin 213f x x ⎛⎫=++ ⎪⎝⎭图象的一个对称中心，故C 错误；对于D ，π6x =-，得π203x +=，1y =，则,16π⎛⎫- ⎪⎝⎭是函数π()2sin 213f x x ⎛⎫=++ ⎪⎝⎭图象的一个对称中心，故D 正确.故选：D.2．（2023春·四川成都·高一校考期中）下列直线中，可以作为曲线πcos 22y x ⎛⎫=- ⎪⎝⎭的对称轴的是（）A ．π4x =B ．π3x =C ．π2x =D ．2π3x =【答案】A【解析】πcos(2)sin 22y x x =-=，对于A ，当π4x =时，πsin 12y ==，则π4x =是曲线πcos 22y x ⎛⎫=- ⎪⎝⎭的对称轴，A 是；对于B ，当π3x =时，2πsin 132y ==≠±，则π3x =不是曲线πcos 22y x ⎛⎫=- ⎪⎝⎭的对称轴，B 不是；对于C ，当π2x =时，sin π01y ==≠±，则π2x =不是曲线πcos 22y x ⎛⎫=- ⎪⎝⎭的对称轴，C 不是；对于D ，当2π3x =时，14π3sin 2y ==-≠±，则2π3x =不是曲线πcos 22y x ⎛⎫=- ⎪⎝⎭的对称轴，D 不是.故选：A3．（2023春·河南驻马店·高一统考阶段练习）（多选）已知函数()πcos π4f x x ⎛⎫=- ⎪⎝⎭，则（）A ．()f x 的图象关于直线12x =对称B ．()f x 的图象关于点1,04⎛⎫- ⎪⎝⎭对称C ．()f x 的图象关于点1,02⎛⎫- ⎪⎝⎭对称D ．()f x 的图象关于直线14x =对称【答案】BD【解析】因为()πcos π4f x x ⎛⎫=- ⎪⎝⎭，令πππ,Z 4x k k -=∈，则1,Z 4x k k =+∈，所以()f x 的对称轴方程为：1,Z 4x k k =+∈，令10,4k x ==，则D 正确，A 错误；令ππππ,Z 42x k k -=+∈，则3,Z 4x k k =+∈，所以()f x 的对称轴中心为：3,0,Z 4k k ⎛⎫+∈ ⎪⎝⎭，令1k =-，则()f x 的一个对称中心为1,04⎛⎫- ⎪⎝⎭，则B 正确，C 错误.故选：BD.考点五正弦、余弦函数的单调性【例5-1】（2023春·重庆江津·高一校考期中）（多选）函数πsin(2y x =-(R )x ∈在（）A ．区间ππ[,22-上是增函数B ．区间π[,π]2上是增函数C ．区间[π,0]-上是减函数D ．区间[,]-ππ上是减函数【答案】BC【解析】ππsin()sin cos 22y x x x ⎛⎫=-=--=- ⎪⎝⎭.A 选项，因cos y x =在π[,0]2-上单调递增，在π[0,]2上单调递减，则πsin()2y x =-在ππ[,]22-上无单调性，故A 错误；B 选项，因cos y x =在π[,π]2上单调递减，则πsin()cos 2y x x =-=-在π[,π]2上单调递增，故B 正确；C 选项，因cos y x =在[π,0]-上单调递增，则πsin()cos 2y x x =-=-在[π,0]-上单调递减，故C 正确；D 选项，因cos y x =在[π,0]-上单调递增，在[0,π]上单调递减，则πsin()2y x =-在[,]-ππ上无单调性，故D错误.故选：BC【例5-2】（2022春·上海浦东新·高一校考期末）函数π12cos 23y x ⎛⎫=+- ⎪⎝⎭的单调递增区间是.【答案】πππ,π,36k k k ⎡⎤-+∈⎢⎥⎣⎦Z 【解析】由π2ππ22π3k x k -≤-≤，解得ππππ36k x k -≤≤+，所以函数π12cos 23y x ⎛⎫=+- ⎪⎝⎭的单调递增区间是πππ,π,36k k k ⎡⎤-+∈⎢⎥⎣⎦Z .故答案为：πππ,π,36k k k ⎡⎤-+∈⎢⎥⎣⎦Z 【例5-3】（2023春·广西钦州·高一校考期中）（多选）下列函数在区间ππ,42⎡⎤⎢⎥⎣⎦上单调递增的是（）A ．()sin f x x =B ．()cos f x x =C ．()sin 2f x x =D ．()cos 2f x x=【答案】AD【解析】A 选项，ππ,42x ⎡⎤∈⎢⎥⎣⎦时，()sin sin f x x x ==，()f x 单调递增，故A 符合.B 选项，ππ,42x ⎡⎤∈⎢⎥⎣⎦时，()cos cos f x x x ==，()f x 单调递减，故B 不符合.C 选项，ππ,42x ⎡⎤∈⎢⎥⎣⎦时，π2,π2x ⎡⎤∈⎢⎥⎣⎦，()sin2sin 2f x x x ==，()f x 单调递减，故C 不符合.D 选项，ππ,42x ⎡⎤∈⎢⎥⎣⎦时，π2,π2x ⎡⎤∈⎢⎥⎣⎦，()cos2cos 2f x x x ==-，()f x 单调递增，故D 符合.故选：AD.【例5-4】（2023春·安徽马鞍山·高一安徽省当涂第一中学校考期中）已知函数π()cos (0)3f x x ωω⎛⎫=+> ⎪⎝⎭在区间π3,π44⎡⎤⎢⎥⎣⎦上单调递减，则实数ω的取值范围为.【答案】80,9⎛⎤⎥⎝⎦【解析】由题意有3ππππ4422T ω-=≤=,可得02ω<≤,又由πππ5π3436ω<+≤，cos y x =在[]0,π上为减函数，故必有3πππ43ω+≤,可得809ω<≤.故实数ω的取值范围为80,9⎛⎤ ⎝⎦.故答案为：80,9⎛⎤⎥⎝⎦【一隅三反】1．（2023春·宁夏吴忠·高一青铜峡市高级中学校考期中）函数cos y x =的一个单调减区间是（）A ．ππ,44⎡⎤-⎢⎥⎣⎦B ．π3π,44⎡⎤-⎢⎥⎣⎦C ．3ππ,2⎡⎤⎢⎥⎣⎦D ．3π,2π2⎡⎤⎢⎥⎣⎦【答案】C【解析】作出函数cos y x =的图象如图所示，由图象可知，A 、B 都不是单调区间，D 是单调增区间，C 是单调减区间．故选：C2．（2023·全国·高一专题练习）函数()πcos 26f x x ⎛⎫=- ⎪⎝⎭的一个单调递减区间为（）A ．5ππ,1212⎡⎤-⎢⎥⎣⎦B ．11π5π,1212⎡⎤--⎢⎥⎣⎦C ．ππ,63⎡⎤-⎢⎥⎣⎦D ．π5π,36⎡⎤⎢⎥⎣⎦【答案】B【解析】令()π2π2π2πZ 6k x k k ≤-≤+∈，解得()π7ππ+πZ 1212k x k k ≤≤+∈，即函数()f x 的单调递减区间为π7ππ+,π,Z 1212k k k ⎡⎤+∈⎢⎥⎣⎦，取1k =-可得，11π5π,1212⎡⎤--⎢⎥⎣⎦为函数()f x 的单调递减区间，B 正确；取0k =可得，π7π,1212⎡⎤⎢⎥⎣⎦为函数()f x 的单调递减区间，令()π2ππ22πZ 6k x k k -≤-≤∈，解得()5ππππZ 1212k x k k -≤≤+∈，即函数()f x 的单调递增区间为5πππ,π,Z 1212k k k ⎡⎤-+∈⎢⎥⎣⎦，取0k =可得，,12125ππ⎡⎤-⎢⎥⎣⎦为函数()f x 的单调递增区间，A 错误；因为()f x 在π12π,6⎡⎤-⎢⎥⎣⎦上单调递增，C 错误；取1k =可得，7π13π,1212⎡⎤⎢⎥⎣⎦为函数()f x 的单调递增区间，所以()f x 在7π5π,126⎡⎤⎢⎥⎣⎦上单调递增，D 错误故选：B.3．（2023秋·高一课时练习）函数π3sin 23y x ⎛⎫=- ⎪⎝⎭的单调递减区间为.【答案】5(Z)121,2k k k ππ⎡⎤-+ππ⎢⎥⎦∈+⎣【解析】因为3sin 23sin(2)33y x x ππ⎛⎫=-=-- ⎪⎝⎭，所以3sin 23y x π⎛⎫=- ⎪⎝⎭的单调递增区间就是3sin 23y x π⎛⎫=- ⎪⎝⎭的单调递减区间．令222(Z)232k x k k πππ-+π≤≤π∈-+，解得51212k x k ππππ-+≤≤+()k ∈Z .所以函数3sin 23y x π⎛⎫=- ⎪⎝⎭的单调递减区间为5,1212k k ππππ⎡⎤-++⎢⎥⎣⎦()k ∈Z .故答案为：5,1212k k ππππ⎡⎤-++⎢⎥⎣⎦()k ∈Z .4．（2023·全国·高一课堂例题）函数2πlog cos 3y x ⎡⎤⎛⎫=+ ⎪⎢⎥⎝⎭⎣⎦的单调递增区间为．【答案】5ππ2π,2π63k k ⎛⎤-+-+ ⎥⎝⎦，Zk ∈【解析】由题意，得πcos 03x ⎛⎫+> ⎪⎝⎭，所以πππ2π2π232k x k -+<+<+，Z k ∈，解得5ππ2π2π66k x k -+<<+，Z k ∈．令ππ2π2π3k x k -+≤+≤，Z k ∈，则4ππ2π2π33k x k -+≤≤-+，Z k ∈．所以πcos 3y x ⎛⎫=+ ⎪⎝⎭的单调递增区间为4ππ2π,2π33k k ⎡⎤-+-+⎢⎥⎣⎦，Z k ∈，所以函数2πlog cos 3y x ⎡⎤⎛⎫=+ ⎪⎢⎥⎝⎭⎣⎦的单调递增区间为5ππ2π,2π63k k ⎛⎤-+-+ ⎥⎝⎦，Z k ∈．故答案为：5ππ2π,2π63k k ⎛⎤-+-+ ⎥⎝⎦，Z k ∈5．（2023秋·江苏宿迁·高一江苏省泗阳中学校考期末）已知函数其中0ω>．若()π,4f x x ω⎛⎫=+ ⎪⎝⎭()f x 在区间π3π,24⎛⎫⎪⎝⎭上单调递增，则ω的取值范围是（）A ．(]0,4B ．0,13⎛⎤ ⎥⎝⎦C ．52,3⎡⎤⎢⎥⎣⎦D ．15,0332,⎛⎤⎡⎤⋃ ⎥⎢⎥⎝⎦⎣⎦【答案】D 【解析】由πππ2π2π,242k x k k ω-+≤+≤+∈Z 解得3π2ππ2π,44k k x k ωωωω-+≤≤+∈Z ，所以函数()f x 的单调递增区间为3π2ππ2π,,44k k k ωωωω⎡⎤-++∈⎢⎥⎣⎦Z ，因为()f x 在区间π3π,24⎛⎫⎪⎝⎭上单调递增，所以3πππ2422T ⎛⎫≥-= ⎪⎝⎭，所以04ω<≤.当0k =时，由()f x 在区间π3π,24⎛⎫⎪⎝⎭上单调递增可知3ππ42π3π44ωω⎧-≤⎪⎪⎨⎪≥⎪⎩，得103ω<≤；当1k =时，由5ππ429π3π44ωω⎧≤⎪⎪⎨⎪≥⎪⎩解得332ω≤≤；当2k =时，13ππ4217π3π44ωω⎧≤⎪⎪⎨⎪≥⎪⎩无实数解.易知，当1k ≤-或2k ≥时不满足题意.综上，ω的取值范围为15,0332,⎛⎤⎡⎤⋃ ⎥⎢⎥⎝⎦⎣⎦.故选：D6．（2023·全国·高一课堂例题）已知函数()πsin (0)4f x x ωω⎛⎫=-> ⎪⎝⎭在区间(1,2)上不单调，则ω的取值范围为（）A ．3π,8∞⎛⎫+ ⎪⎝⎭B ．3π3π7π,,848∞⎛⎫⎛⎫⋃+ ⎪ ⎪⎝⎭⎝⎭C ．3π7π7π,,888∞⎛⎫⎛⎫⋃+ ⎪ ⎪⎝⎭⎝⎭D ．3π,4∞⎛⎫+ ⎪⎝⎭【答案】B【解析】()πsin (0)4f x x ⎛⎫=-> ⎪⎝⎭ωω的图象的对称轴为直线3ππ4k x ω+=，k ∈Z ，因为()f x 在区间(1,2)上不单调，所以对称轴3ππ4k x ω+=，k ∈Z 在直线1x =与直线2x =之间，即3ππ412k ω+<<，k ∈Z ，化简得3ππ3ππ824k k ω+<<+，k ∈Z ，因为0ω>，所以令0k =，得3π3π84ω<<，又当1k ≥时，7π8ω>，综上3π3π7π,,848ω∞⎛⎫⎛⎫∈⋃+ ⎪ ⎪⎝⎭⎝⎭.故选：B ．考点六正弦、余弦函数的单调性的应用【例6-1】（2023春·福建泉州·高一校联考期中）下列结论正确的是（）A ．()sin 10sin50-︒>︒B ．tan70sin70︒<︒C ．()cos 40cos310-︒<︒D ．cos130cos200︒>︒【答案】D【解析】对于A ，因为()sin 10sin100-︒=-︒<，sin500︒>，所以()sin 10sin50-︒<︒，故A 错误；对于B ，因为0cos701<︒<，所以sin 70tan70sin70cos70︒︒=>︒︒，故B 错误；对于C ，因为()cos 40cos 40-︒=︒，()cos310cos 36050cos 50︒=︒-︒=︒，又cos 40cos50︒>︒，所以()cos 40cos310-︒>︒，故C 错误；对于D ，因为()cos130cos 9040sin 40︒=︒+︒=-︒，()cos 200cos 27070sin 70︒=-︒=-︒，又sin 40sin 70︒<︒，所以sin 40sin 70-︒>-︒，即cos130cos 200︒>︒，故D 正确.故选：D.【例6-2】（2023春·江苏苏州·高一统考期末）已知45a =，2sin 3b =，1cos 3c =，则a ，b ，c 的大小关系为（）A ．c b a <<B ．a b c<<C ．b a c<<D ．b<c<a【答案】C【解析】因为2π4πsinsin sin 34253<=<<=b a <，14cos cos 32π65c a =>==，所以c a >，所以b a c <<.故选：C.【一隅三反】1．（2023春·广西钦州·高一校考期中）sin1︒，sin1，sin π︒的大小顺序是（）A ．sin1sin1sin π︒<<︒B ．sin1sin πsin1︒<︒<C ．sin1sin1sin π︒=<︒D ．sin1sin1sin π<︒<︒【答案】B【解析】由正弦函数的单调性可知：sin y x =在π0,2⎛⎫⎪⎝⎭上单调递增，又易知π0<1<π°<1<2︒，所以sin1sin sin1π︒<︒<.故选：B2．（2023·全国·高一假期作业）下列选项中错误的是（）A ．ππsin sin 1810⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭B ．sin2sin1>C ．23π17πcos cos 54⎛⎫⎛⎫-<- ⎪ ⎪⎝⎭⎝⎭D ．sin508sin144︒︒>【答案】D 【解析】因为ππππ210182-<-<-<，sin y x =在ππ[,]22x ∈-上单调递增，所以ππsin sin 1810⎛⎫⎛⎫->- ⎪ ⎝⎭⎝⎭，故A 正确；因为21π1.522+=<，所以2比1距离正弦函数的对称轴π2x =近，所以sin2sin1>，故B 正确；因为23π23π3π17π17ππcos cos 4πcos ,cos cos4πcos 555444⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-=-=--=-=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，而3ππ05π4-<<-<-，函数cos y x =在(π,0)-上单调递增，所以23π17πcos cos 54⎛⎫⎛⎫-<- ⎪ ⎪⎝⎭⎝⎭，故C 正确；因为sin508sin148sin144︒︒=︒>，而90144148180︒<︒<︒<︒，由正弦函数的单调性可知sin508sin148sin144︒︒=︒<，故D 错误.故选：D3．（2023春·四川绵阳·高一四川省绵阳南山中学校考期中）设3sin20,cos80,4a b c =︒=︒=，则,,a b c 大小关系（）A ．b a c <<B ．a b c <<C ．c b a <<D ．a c b<<【答案】B【解析】因为2030︒<︒，且sin y x =在π0,2⎛⎫⎪⎝⎭上单调递增，则1sin 20sin 302︒<︒=，即12a <；又因为π80ππ41803<<，且cos y x =在π0,2⎛⎫⎪⎝⎭上单调递减，则1ππcos cos80cos 2342=<︒<=，即122b <<，且34c =>a b c <<.故选：B.考点七正弦、余弦函数的最值(值域)问题【例7-1】（2023春·四川眉山·高一校考期中）已知函数()ππ2sin 2,0,62f x x x ⎛⎫⎡⎤=-∈ ⎪⎢⎥⎝⎭⎣⎦，则()f x 的值域是（）A ．[]22-,B ．[]1,1-C ．[]1,2-D ．2⎡⎤⎣⎦【答案】C【解析】因为π0,2x ⎡⎤∈⎢⎣⎦，所以ππ5π2,666x ⎡⎤-∈-⎢⎥⎣⎦，所以π1sin 2,162x ⎛⎫⎡⎤-∈- ⎪⎢⎥⎝⎭⎣⎦，所以[]π2sin 21,26x ⎛⎫-∈- ⎪⎝⎭，所以()f x 的值域是[]1,2-.故选：C.【例7-2】（2023·全国·高一专题练习）函数22sin cos y x x =--的最小值是．【答案】34/0.75【解析】函数2213cos cos 1cos 24y x x x ⎛⎫=-+=-+ ⎪⎝⎭，1cos 1x -≤≤，当1cos 2x =时，函数取得最小值34.故答案为：34【例7-3】（2023春·河南周口·高一周口恒大中学校考阶段练习）函数sin cos ()1sin cos =++x xf x x x的值域为．【答案】11,122⎡⎫⎛⎤--⎪ ⎢⎪ ⎣⎭⎝⎦【解析】令sin cos 4t x x x π⎛⎫=+=+ ⎪⎝⎭，[1)(t ∈-- ，则212sin cos t x x =+，即21sin cos 2t x x -=，所以2112()12t t f t t --==+，又因为[1)(t ∈-- ，所以()11,11,22f t ⎡⎫⎛⎤-∈--⎪ ⎢⎥⎪ ⎣⎭⎝⎦，即函数sin cos ()1sin cos =++x xf x x x的值域为11,11,22⎡⎫⎛⎤---⎪ ⎢⎥⎪ ⎣⎭⎝⎦．故答案为：11,122⎡⎫⎛⎤--⎪ ⎢⎥⎪ ⎣⎭⎝⎦.【例7-4】（2023春·四川眉山·高一校联考期中）已知函数()πsin (0,[0,π])3f x x x ωω⎛⎫=->∈ ⎪⎝⎭的值域为[，则ω的取值范围是（）A ．15[,]33B ．5[,1]6C ．55[,63D ．513⎡⎤⎢⎥⎣⎦，【答案】C【解析】因为[0,π]x ∈，可得πππ[,π333x ωω-∈--，因为函数()πsin()3f x x ω=-的值域为[，所以ππ4π,323ωπ⎡⎤-∈⎢⎥⎣⎦，解得55[,]63ω∈.故选：C.【一隅三反】1（2022秋·江苏常州·高一常州高级中学校考期末）函数ππcos ,,032y x x ⎛⎫⎡⎤=+∈- ⎪⎢⎥⎝⎭⎣⎦的值域是（）A ．1,12⎡⎤⎢⎥⎣⎦B ．⎤⎥⎣⎦C ．12⎡⎢⎣⎦D ．,12⎡⎤⎢⎥⎣⎦【答案】A【解析】因为,02πx ⎡⎤∈-⎢⎥⎣⎦，所以πππ,363x ⎡⎤+∈-⎢⎥⎣⎦，因为函数cos t x =在π,06⎡⎤-⎢⎥⎣⎦上递增，π0,3⎡⎤⎢⎥⎣⎦上递减，又πcos 6⎛⎫-= ⎪⎝⎭cos 01=，π1cos 32=，所以π1cos ,132x ⎛⎫⎡⎤+∈ ⎪⎢⎥⎝⎭⎣⎦即1,12y ⎡⎤∈⎢⎥⎣⎦.故选：A ．2．（2023秋·陕西安康·高一校联考期末）函数2π2πsin 2cos 33y x x x ⎛⎫=+≤≤ ⎪⎝⎭的最小值是．【答案】14-/-0.25【解析】由()222sin 2cos 1cos 2cos cos 12y x x x x x =+=-+=--+，又π2π33x ≤≤，则11cos 22x -≤≤，所以()217cos 1244x -≤--+≤，所以函数2π2πsin 2cos 33y x x x ⎛⎫=+≤≤ ⎪⎝⎭的最小值是14-．故答案为：14-．3．（2023春·江西宜春·高一江西省丰城中学校考阶段练习）已知函数()cos 3f x x π⎛⎫=+ ⎪⎝⎭，若()f x 在[]0a ，上的值域是112⎡⎤-⎢⎥⎣⎦，，则实数a 的取值范围为（）A ．403π⎛⎤ ⎥⎝⎦，B ．2433ππ⎡⎤⎢⎥⎣⎦，C ．23π∞⎡⎫+⎪⎢⎣⎭，D ．2533ππ⎡⎤⎢⎥⎣⎦，【答案】B【解析】由题意可得()cos 3f x x π⎛⎫=+ ⎪⎝⎭，令3t x π=+则cos y t =,如图所示，∵()f x 的值域是112⎡⎤-⎢⎥⎣⎦，，0x a ，∴333x a πππ++，即：33ta ππ+∴由图可知533aπππ+，解得2433a ππ，所以实数a 的取值范围为2433ππ⎡⎤⎢⎥⎣⎦，.故选：B.4．（2023春·四川南充·高一四川省南充市白塔中学校考期中）函数2cos ()2cos xf x x-=+的值域为.【答案】1,33⎡⎤⎢⎥⎣⎦【解析】2cos 4()12cos 2cos x f x x x-==++，[]cos 1,1x ∈-，则[]cos 21,3x +∈，44,42cos 3x ⎡⎤∈⎢⎥+⎣⎦，故()1,33f x ∈⎡⎤⎢⎥⎣⎦.故答案为：1,33⎡⎤⎢⎥⎣⎦考点八正切函数图像及性质【例8】（2024秋·广东）（多选）已知函数()πtan 26f x x ⎛⎫=- ⎪⎝⎭，则下列说法正确的是（）A ．()f x 的最小正周期为π2B ．()f x 在ππ,63⎛⎫⎪⎝⎭上单调递减C ．π3π510f f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭D ．()f x 的定义域为ππ,Z 3x x k k ⎧⎫≠+∈⎨⎬⎩⎭【答案】AC【解析】因为()πtan 26f x x ⎛⎫=- ⎪⎝⎭，对于A ：()f x 的最小正周期为π2T =，故A 正确；对于B ：当ππ,63x ⎛⎫∈ ⎪⎝⎭时，πππ2,662x ⎛⎫-∈ ⎪⎝⎭，因为tan y z =在π0,2z ⎛⎫∈ ⎪⎝⎭上单调递增，故()f x 在ππ,63⎛⎫⎪⎝⎭上单调递增，故B 错误；对于C ：因为()f x 的最小正周期为π2T =，所以πππ3π55210f f f ⎛⎫⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，故C 正确；对于D ：令ππ2π62x k -≠+，Z k ∈，解得ππ32k x ≠+，Z k ∈，所以()f x 的定义域为ππ,Z 32k x x k ⎧⎫≠+∈⎨⎬⎩⎭，故D 错误．故选：AC ．【一隅三反】1．（2023春·辽宁大连·高一大连八中校考阶段练习）（多选）已知函数()tan 2f x x =，则下列说法正确的是（）A ．函数()f x 是奇函数B ．函数()f x 的最小正周期是πC ．函数()f x 在ππ(,44-上单调递增D ．函数()f x 图象的对称中心是π(,0)(Z)4k k ∈【答案】ACD【解析】对于A ，()tan 2f x x =的定义域为ππππ,(Z)4242k k k ⎛⎫-++∈ ⎪⎝⎭，定义域关于原点对称，因为()()tan(2)tan 2f x x x f x -=-=-=-，所以()f x 是奇函数，所以A 正确，对于B ，()f x 的最小正周期为π2T =，所以B 错误，对于C ，由ππ,44x ⎛⎫∈- ⎪⎝⎭，得ππ2,22x ⎛⎫∈- ⎪⎝⎭，因为tan y x =在ππ,22⎛⎫- ⎪⎝⎭上单调递增，所以()f x 在ππ(,)44-上单调递增，所以C 正确，对于D ，由π2,Z 2k x k =∈，得π,Z 4k x k =∈，所以()f x 图象的对称中心是π(,0)(Z)4k k ∈，所以D 正确，故选：ACD2．（2023春·广西钦州·高一校考阶段练习）（多选）已知函数()πtan 26f x x ⎛⎫=- ⎪⎝⎭，则下列说法错误的是（）A ．()f x 的最小正周期为π2B ．()f x 的定义域为ππ,3x x k k ⎧⎫≠+∈⎨⎬⎩⎭Z C ．ππ44f f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭D ．()f x 在ππ,32⎛⎫⎪⎝⎭上单调递减【答案】BD【解析】因为()πtan 26f x x ⎛⎫=- ⎪⎝⎭，对于A ：所以()f x 的最小正周期为π2T =，故A 正确；对于B ：令ππ2π,Z 62x k k -≠+∈，解得ππ,Z 32kx k ≠+∈，所以()f x 的定义域为ππ,32k x x k ⎧⎫≠+∈⎨⎬⎩⎭Z ，故B错误；对于C ：πππtan tan 4263πf ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭tan tan tan πππ242633π2ππf ⎛⎫⎛⎫⎛⎫⎛⎫-=--=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，故C 正确；对于D ：当ππ,32x ⎛⎫∈ ⎪⎝⎭时，ππ5π2,626x ⎛⎫-∈ ⎪⎝⎭，因为tan y z =在π5π,26z ⎛⎫∈ ⎪⎝⎭上单调递增，故()f x 在ππ,32⎛⎫⎪⎝⎭上单调递增，故D 错误.故选：BD3．（2023春·广东河源·高一校考阶段练习）（多选）已知函数()π7tan 23f x x ⎛⎫=+ ⎪⎝⎭，则（）A ．π6f ⎛⎫=- ⎪⎝⎭B ．π6f x ⎛⎫- ⎪⎝⎭为奇函数C ．()f x 图象的对称中心为()ππ,0Z 68k k ⎛⎫-+∈ ⎪⎝⎭D ．()f x 的定义域为ππ,Z 122k xx k ⎧⎫≠+∈⎨⎬⎩⎭∣【答案】ABD【解析】因为函数()π7tan 23f x x ⎛⎫=+ ⎪⎝⎭，所以πππ2π7tan 27tan76633f ⎛⎫⎛⎫=⨯+==- ⎪ ⎪⎝⎭⎝⎭A 正确；由()π7tan 23f x x ⎛⎫=+ ⎪⎝⎭得，π7tan 26f x x ⎛⎫-= ⎪⎝⎭，对于函数7tan 2y x =，令π2π,Z 2x k k ≠+∈，得ππ,Z 24k x k ≠+∈，可知定义域为ππ,Z 24k x x k ⎧⎫≠+∈⎨⎬⎩⎭关于原点对称，又()7tan 27tan 2x x -=-，所以函数7tan 2y x =为奇函数，即π6f x ⎛⎫- ⎪⎝⎭为奇函数，故B 正确；由ππ2(Z)32k x k +=∈，得到()ππZ 46k x k =-∈，所以()π7tan 23f x x ⎛⎫=+ ⎪⎝⎭的对称中心为()ππ,0Z 46k k ⎛⎫-∈ ⎪⎝⎭，故C 错误；令ππ2π,Z 32x k k +≠+∈，得ππ,Z 212k x k ≠+∈，所以()f x 的定义域为ππ,Z 122k xx k ⎧⎫≠+∈⎨⎬⎩⎭∣，故D 正确；故选：ABD。

数学三角函数的图象与性质试题答案及解析1.将函数的图象向右平移个单位长后与直线相交，记图象在轴右侧的第个交点的横坐标为，若数列为等差数列，则所有的可能值为（）A．B．C．或D．或【答案】C【解析】将函数的图象向右平移个单位长得，由题意知，与函数的图象的最高点或最低点相交时满足题意，此时或得即或，故选C.2.已知函数（，m是实数常数）的图像上的一个最高点，与该最高点最近的一个最低点是，(1)求函数的解析式及其单调增区间；(2)在锐角三角形△ABC中，角A、B、C所对的边分别为，且，角A的取值范围是区间M，当时，试求函数的取值范围.【答案】(1) (2)【解析】(1)∵，∴.∵和分别是函数图像上相邻的最高点和最低点，∴解得∴.由，解得.∴函数的单调递增区间是.(2)∵在中，，∴.∴，且，可解得：. ∴.当时，，考察正弦函数的图像，可知，.∴，即函数的取值范围是【考点】本题考查三角变换、三角函数的图象和性质、向量的数量积和解三角形等知识，意在考查学生的数形结合能力，整体思想的运用.3.（本题满分12分）已知，．（I）求函数的单调递增区间；（II）函数的图象可以由函数的图象经过怎样的变换得到？【答案】（I），（II）见解析【解析】（Ⅰ）由已知，4分当，，即，时，函数单调递增，所以函数的单调递增区间为，． 7分（II）函数图象向左平移个单位长度，得到函数的图象；然后使曲线上各点的横坐标缩为原来的倍得到函数的图象；再将曲线上各点的纵坐标伸长为原来的倍得到函数的图象． 12分另法：函数图象上各点的横坐标缩为原来的倍，得到函数的图象；然后使图象向左平移个单位长度，得到函数的图象；再将曲线上各点的纵坐标伸长为原来的倍得到函数的图象． 12分【考点】本题考查平面向量的坐标运算、三角恒等变换、三角函数图象得到变换等基础知识，意在考查考生的数学运算能力、作图视图的能力及应用数学知识解决问题的能力.4.函数的图象如图所示，则 .【答案】．【解析】由图象知，由的图象关于点以及直线对称知，，又，【考点】本题考查三角恒等变换、三角函数图象及其性质等知识，意在考查读图、识图、计算以及推理能力．5.如图所示，是函数图象的一部分．则的值为（）A．B．C．D．【答案】【解析】观察图象知，，即；将点代入得，结合，，即函数解析式为.所以，，故选.【考点】本题考查正弦型函数的图象和性质，三角函数的诱导公式等基础知识，意在考查计算能力及视图用图能力．6.将函数的图象沿轴向左平移个单位后，得到一个偶函数的图象，则的一个可能取值为A．B．C．D．【答案】B【解析】得到的偶函数解析式为，显然【考点】本题考查三角函数的图象和性质，要注意三角函数两种变换的区别，选择合适的值通过诱导公式把转化为余弦函数是考查的最终目的.7.已知函数。

5.4三角函数的图象与性质（精练）1．（2023春·北京昌平·高一统考期末）下列函数中，是偶函数且其图象关于点π(,0)4对称的是（）A ．()sin f x x =B ．()cos f x x =C ．()sin4f x x =D ．()cos2f x x=【答案】D【解析】对于A ，函数()sin f x x =是奇函数，A 不是；对于C ，函数()sin4f x x =是奇函数，C 不是；对于B ，函数()cos f x x =是偶函数，而ππ(cos 0442f ==≠，即()cos f x x =的图象不关于点π(,0)4对称，B 不是；对于D ，函数()cos2f x x =是偶函数，ππ(cos 042f ==，即()cos2f x x =的图象关于点π(,0)4对称，D 是.故选：D2．（2023·全国·高一假期作业）设函数()πcos ,(0)4f x x ωω⎛⎫=-> ⎪⎝⎭的最小正周期为π5，则它的一条对称轴方程为（）A ．π8x =B ．π8x =-C ．π12x =D ．π12x =-【答案】A【解析】因为的()f x 最小正周期为π5，所以2π10T ω==，所以()πcos 104f x x ⎛⎫=- ⎪⎝⎭，令104πx kπ-=，Z k ∈，解得()1040kππx k Z =+∈，所以()f x 的对称轴为直线()1040kππx k Z =+∈，当1k =时，π8x =，其它各项均不符合，所以π8x =是函数()f x 的对称轴，故选：A ．3．（2022·高一课时练习）已知函数()()2cos 3f x x ϕ=+，则“2πϕ=＋2kπ，k ∈Z ”是“()f x 为奇函数”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A【解析】当22k πϕπ=+，k ∈Z 时，()2cos(3)2sin 3f x x x ϕ=+=-，所以()f x 为奇函数．当()f x 为奇函数时，2k πϕπ=+，k ∈Z ．综上，“22k πϕπ=+，k ∈Z ”是“()f x 为奇函数”的充分不必要条件．故选：A.4．（2023春·江苏盐城·高一校联考期中）设函数π()sin()3f x x ω=+在区间(0,π)恰有三条对称轴､两个零点，则ω的取值范围是（）A ．513,36⎡⎤⎢⎣⎦B ．519,36⎡⎫⎪⎢⎣⎭C ．138(,63D ．1319(,66【答案】C【解析】由函数π()sin()3f x x ω=+，其中π()0,x ∈，可得πππ(,)333x ωωπ+∈+，因为函数()f x 在区间(0,π)恰有三条对称轴､两个零点，则满足5ππ3π23ωπ<+≤，解得13863ω<≤，所以ω的取值范围为138(,]63.故选：C.5．（2023春·辽宁抚顺·高一校联考期中）已知函数()πcos 26f x x ⎛⎫=- ⎪⎝⎭在[],m n 上单调递减，且()()2f m f n -=，则tan2m n+=（）A．BC．D【答案】D【解析】由函数()πcos 26f x x ⎛⎫=- ⎪⎝⎭在[],m n 上单调递减，且()()2f m f n -=，可得()π22π6Z π2π2π6m k k n k ⎧-=⎪⎪∈⎨⎪-=+⎪⎩，两式相加得π2()π4π,Z 3m n k k +-=+∈，即ππ,Z 23m n k k +=+∈，所以πtan tan 23m n +==故选：D.6．（2023春·四川绵阳·高一绵阳南山中学实验学校校考阶段练习）已知6πsin 7a =，4πsin 7b =，2πsin 7c =，则（）A ．a b c>>B ．c b a>>C ．c a b>>D ．b c a>>【答案】D【解析】由诱导公式知：ππsin πsin 77a ⎛⎫=-= ⎪⎝⎭，3π3πsin πsin 77b ⎛⎫=-= ⎪⎝⎭，sin y x = 在π0,2⎛⎫⎪⎝⎭上单调递增，3π2ππsin sin sin 777∴>>，即b c a >>.故选：D.7．（2023秋·高一单元测试）函数y =的定义域是（）A ．}{π|2π2π2,Z x k x k k ≤≤+∈B ．π|ππZ}{2,x k x k k ≤≤+∈C ．}{π|2ππZ 2,x k x k k ≤≤+∈D ．}{ππ|ππ,Z 33x k x k k -≤≤+∈【答案】D【解析】函数y 有意义，则2cos 210x +≥，即1cos 22x ≥-，因此2π2π2π22π,Z 33k x k k -≤≤+∈，解得ππππ,Z 33k x k k -≤≤+∈，所以函数y =的定义域是}{ππ|ππ,Z 33x k x k k -≤≤+∈.故选：D8．（2023春·河北衡水·高一校考阶段练习）不等式cos 20x ≥在[]π,π-上的解集为（）A ．2π2ππ,,π33⎡⎤⎡⎤--⎢⎥⎢⎥⎣⎦⎣⎦U B ．2π2π,33⎡⎤-⎢⎥⎣⎦C ．5π5ππ,,π66⎡⎤⎡⎤--⎢⎥⎢⎥⎣⎦⎣⎦U D ．5π5π,66⎡⎤-⎢⎥⎣⎦【答案】D【解析】∵cos 20x ≥，则cos 2x ≥-，注意到[]π,πx ∈-，结合余弦函数图象解得5π5π,66x ⎡⎤∈-⎢⎥⎣⎦.故选：D.9．（2023春·江西抚州·高一江西省抚州市第一中学校考阶段练习）已知函数()()lg 2cos 1f x x =-，则函数()f x的定义域为（）A ．ππ2π,2π,Z33k k k ⎛⎫-+∈ ⎪⎝⎭B ．ππ2π,2π,Z33k k k ⎡⎤-+∈⎢⎥⎣⎦C ．Zππ,ππ2,266k k k ⎛⎫-+∈ ⎪⎝⎭D ．Z ππ,ππ2,266k k k ⎡⎤-+∈⎢⎥⎣⎦【答案】A【解析】由题意得：2cos 10x ->，即1cos 2x >，则ππ2π,2π,Z 33x k k k ⎛⎫∈-+∈ ⎪⎝⎭.故选：A10．（2023春·四川眉山·高一校考阶段练习）已知()3sin2x f x =在区间π0,3⎡⎤⎢⎥⎣⎦上的最大值为（）A ．1B ．13C ．12D ．43【答案】A【解析】因为π0,,3x ⎡⎤∈⎢⎥⎣⎦所以,23π0,2x ⎡⎤∈⎢⎥⎣⎦结合三角函数的图像性质，函数()f x 在π0,3⎡⎤⎢⎥⎣⎦单调递增，所以()max π1,3f x f ⎛⎫== ⎪⎝⎭故选：A.11．（2023春·四川眉山·高一校考期中）函数23cos 4cos 1y x x =-+的最小值是（）A ．13-B ．154C ．0D ．14-【答案】A【解析】函数22213cos 4cos 13cos 33y x x x ⎛⎫=-+=--⎪⎝⎭又函数[]cos 1,1x ∈-，所以当2cos 3x =时，函数2213cos 33y x ⎛⎫=-- ⎪⎝⎭的最小值为13-.故选：A.12．（2023春·福建泉州·高一校考期中）（多选）若函数()π3sin 26f x x ϕ⎛⎫=-+ ⎪⎝⎭是偶函数，则ϕ的值不可能为（）A ．π6B ．π2C ．2π3D ．5π6【答案】ABD【分析】根据二次函数与余弦函数的性质求解最值即可.【详解】由函数()3sin 26f x x πϕ⎛⎫=-+ ⎪⎝⎭是偶函数，可得()03f =±，即πsin 16ϕ⎛⎫-+=± ⎪⎝⎭，则ππ,Z 62k k ϕπ-+=+∈，解得2ππ,Z 3k k ϕ=+∈，当0k =时，可得2π3ϕ=，无论k 取何值，ϕ都不可能等于π6或π2或5π6．故选：ABD ．13．（2023春·河南驻马店·高一校考阶段练习）（多选）下列大小关系中正确的是（）A ．cos11sin10cos168︒<︒<︒B ．cos168sin10cos11︒<︒<︒C ．sin11sin168cos10︒<︒<︒D ．sin168cos10sin11︒<︒<︒【答案】BC【分析】根据二次函数与余弦函数的性质求解最值即可.【详解】 cos11sin 79sin100︒=︒>︒>，又cos1680︒<，cos168sin10cos11∴︒<︒<︒；且sin11sin168sin12cos10cos80︒<︒=︒<︒=︒.故选：BC.14．（2023春·甘肃兰州·高一校考开学考试）（多选）下列不等式中成立的是（）A ．sin sin 810ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭B ．()cos400cos 50︒>-︒C ．sin 3sin 2>D ．87sincos 78ππ>【答案】BD【分析】根据二次函数与余弦函数的性质求解最值即可.【详解】对于A ，因为02810πππ-<-<-<，且函数sin y x =在,02π⎛⎫- ⎪⎝⎭上单调递增，则sin sin 810ππ⎛⎫⎛⎫-<- ⎪ ⎪⎝⎭⎝⎭，故A 错误；对于B ，因为()cos 400cos 36040cos 40︒=︒+︒=︒，()cos 50cos50-︒=︒，且函数cos y x =在π0,2⎛⎫⎪⎝⎭上单调递减，则cos 40cos50︒>︒，即()cos400cos 50︒>-︒，故B 正确；对于C ，因为32322ππ<<<，且函数sin y x =在3,22ππ⎛⎫⎪⎝⎭上单调递减，则sin3sin 2<，故C 错误；对于D ，因为7733cossin sin sin 82888πππππ⎛⎫⎛⎫=-=-=- ⎪ ⎪⎝⎭⎝⎭，8sin sin 77ππ⎛⎫=- ⎪⎝⎭，且30782πππ<<<，函数sin y x =在0,2π⎛⎫ ⎪⎝⎭上单调递增，则3sin sin 78ππ<，即87sin cos 78ππ>，故D 正确；故选：BD15．（2022春·辽宁大连·高一大连八中校考期中）（多选）下列坐标所表示的点中，是函数πtan(26x y =-图像的对称中心的是（）A ．5π(,0)3-B ．π(,0)3C ．2π(,0)3D ．4π(,0)3【答案】ABD【分析】根据二次函数与余弦函数的性质求解最值即可.【详解】令ππ,Z 262x k k -=∈，解得ππ,Z 3x k k =+∈，A 选项，当2k =-时，π5π2π33x =-+=-，故对称中心为5π(,0)3-，A 正确；B 选项，当0k =时，π3x =，故对称中心为π(,0)3，B 正确；C 选项，令π2ππ33k +=，解得13k =，不合要求，舍去，C 错误；D 选项，当1k =时，4π3x =，故对称中心为4π,03⎛⎫⎪⎝⎭，D 正确；故选：ABD16．（2023·上海）（多选）已知函数()πtan 2(0)6f x x ωω⎛⎫=-> ⎪⎝⎭的最小正周期是π2，则（）A ．2ω=B ．()()π2π125f f ->C ．()f x 的对称中心为()ππ,0412k k ⎛⎫+∈ ⎪⎝⎭Z D ．()f x 在区间ππ,123⎛⎫⎪⎝⎭上单调递增【答案】BCD【解析】因为函数()πtan 2(0)6f x x ωω⎛⎫=-> ⎪⎝⎭的最小正周期是π2，所以ππ22T ω==，又0ω>，得到1ω=，所以π()tan(26f x x =-，选项A ，因为1ω=，故选项A 错误；选项B ，因为()()πππ2π19π11πtan()tan ,tan()tan()123353030f f -=-=-==-，又π11ππ03302<<<，由tan y x =的性质知，π11πtan tan 330<，所以()()π2π125f f ->，故选项B 正确；选项C ，由ππ2(Z)62k x k -=∈，得到()ππ412k x k =+∈Z ，所以π()tan(2)6f x x =-的对称中心为()ππ,0412k k ⎛⎫+∈ ⎪⎝⎭Z ，故选项C 正确；选项D ，当ππ,123x ⎛⎫∈ ⎪⎝⎭时，ππ2(0,62x -∈，由tan y x =的性质知，()f x 在区间ππ,123⎛⎫⎪⎝⎭上单调递增，故选项D 正确.故选：BCD.17．（2023·全国·高一专题练习）（多选）下列关于函数πtan 23y x ⎛⎫=-+ ⎪⎝⎭的说法正确的是（）A ．在区间ππ,312⎛⎫-- ⎪⎝⎭上单调递减B ．最小正周期是πC ．图象关于点5π,012⎛⎫⎪⎝⎭成中心对称D ．图象关于直线π12x =-成轴对称【答案】AC【解析】对于A ，令ππππ2π232k x k -+<-<+，k ∈Z ，解得ππ5ππ122122k k x -+<<+，当1k =-时，7ππ1212x -<<-，所以πtan 23y x ⎛⎫=-+ ⎪⎝⎭在7ππ,1212⎛⎫-- ⎪⎝⎭上单调递减，又ππ7ππ,,3121212⎛⎫⎛⎫--⊆-- ⎪ ⎪⎝⎭⎝⎭，故函数πtan 23y x ⎛⎫=-+ ⎪⎝⎭在区间ππ,312⎛⎫-- ⎪⎝⎭上单调递减，正确；对于B ，πtan 23y x ⎛⎫=-+ ⎪⎝⎭最小正周期为ππ22T ==-，错误；对于C ，令ππ232k x -+=得，ππ,Z 64k x k =-∈，所以πtan 23y x ⎛⎫=-+ ⎪⎝⎭对称中心为ππ,0,Z 64k k ⎛⎫-∈ ⎪⎝⎭，当1k =-时，5π,012⎛⎫⎪⎝⎭是对称中心，正确；对于D ，函数πtan 23y x ⎛⎫=-+ ⎪⎝⎭不成轴对称，没有对称轴，错误.故选：AC.18．（2023·全国·高三专题练习）函数πtan 34y x ⎛⎫=-+ ⎪⎝⎭的单调递减区间为．【答案】ππππ,()12343k k k ⎛⎫-++∈ ⎪⎝⎭Z 【解析】ππtan 3tan 344y x x ⎛⎫⎛⎫=-+=-- ⎪ ⎪⎝⎭⎝⎭．由()()ππππ3πZ Z 242ππππ12343k k k k k x x k -+<-<+∈⇒+<<+∈-，故函数πtan 34y x ⎛⎫=-+ ⎪⎝⎭的单调递减区间为ππππ,()12343k k k ⎛⎫-++∈ ⎪⎝⎭Z 故答案为：ππππ,()12343k k k ⎛⎫-++∈ ⎪⎝⎭Z 19．（2023春·广东佛山·高一校考阶段练习）若()ππcos 232f x x ϕϕ⎛⎫⎛⎫=++< ⎪⎪⎝⎭⎝⎭是奇函数，则ϕ=.【答案】6π/16π【解析】由题设πππ32k ϕ+=+且Z k ∈，故ππ6k ϕ=+，Z k ∈，又π2ϕ<，故0k =有π6ϕ=.故答案为：π620．（2023春·高一课时练习）函数1πsin 226y x ⎛⎫=- ⎪⎝⎭与y 轴最近的对称轴方程是．【答案】π6x =-【解析】令ππ2π,62x k k -=+∈Z ，解得ππ,23k x k =+∈Z ，令1k =-，则π6x =-；令0k =，则π3x =；因为ππ63-<，所以与y 轴最近的对称轴方程是π6x =-.故答案为：π6x =-.21．（2023·全国·高一专题练习）已知函数()()()cos 2R ϕ=+∈f x x x 的图象关于点2π,03⎛⎫ ⎪⎝⎭中心对称，则ϕ的最小值为.【答案】π6【解析】因为函数()()()cos 2R ϕ=+∈f x x x 的图象关于点2π,03⎛⎫ ⎪⎝⎭中心对称，所以2ππ2π,Z 32k k ϕ⨯+=+∈，所以5ππ,Z 6k k ϕ=-+∈，则当1k =时，ϕ的最小值为π6.故答案为：π622．（2023春·高一单元测试）已知函数2π()log cos 26f x x ⎛⎫=- ⎪⎝⎭的单调增区间为．【答案】ππ(π,π+Z612k k k -∈【解析】令πcos 26t x ⎛⎫=- ⎪⎝⎭，由0t >，可得πcos 206x ⎛⎫-> ⎪⎝⎭，所以πππ2π22π+,Z 262k x k k -<-<∈，解得ππππ+,Z 63k x k k -<<∈，所以函数的定义域为ππ(π,π+Z 63k k k -∈，由余弦函数的性质可知：πcos 26t x ⎛⎫=- ⎪⎝⎭在ππ(π,π+Z 612k k k -∈上单调递增，在ππ(π+,π+),Z 123k k k ∈上单调递减，又因为2()log f x t =在定义域上为单调递增函数，由复合函数的单调性可知：函数2π()log cos 26f x x ⎛⎫=- ⎪⎝⎭的单调增区间为ππ(π,π+),Z 612k k k -∈.故答案为：ππ(π,π+),Z612k k k -∈23．（2023春·陕西渭南·高一白水县白水中学校考期中）若0πϕ<<，函数()cos(2)f x x ϕ=+在区间ππ,66⎡⎤-⎢⎥⎣⎦上单调递减，且在区间π0,6⎛⎫⎪⎝⎭上存在零点，则ϕ的取值范围是.【答案】ππ,32⎡⎫⎪⎢⎣⎭【解析】当ππ,66x ⎡⎤∈-⎢⎣⎦时，ππ2,33x ϕϕϕ⎡⎤+∈-++⎢⎥⎣⎦，因为0πϕ<<，函数()cos(2)f x x ϕ=+在区间ππ,66⎡⎤-⎢⎥⎣⎦上单调递减，所以[]ππ,0,π33ϕϕ⎡⎤-++⊆⎢⎥⎣⎦，所以π03ππ3ϕϕ⎧-+≥⎪⎪⎨⎪+≤⎪⎩，即π2π33ϕ≤≤，当π0,6x ⎛⎫∈ ⎪⎝⎭时，π2,3x ϕϕϕ⎛⎫+∈+ ⎪⎝⎭，因为0πϕ<<，()f x 在区间π0,6⎛⎫⎪⎝⎭上存在零点，所以ππ23ϕϕ<<+，解得ππ62ϕ<<，综上：ππ32ϕ≤<，故答案为：ππ,32⎡⎫⎪⎢⎣⎭24．（2023春·陕西西安·高一西北工业大学附属中学校考阶段练习）求函数()2ln cos 2f x x ⎛=- ⎝⎭的定义域为．【答案】ππ2π,2π,Z46k k k ⎛⎤-++∈ ⎥⎝⎦【解析】根据题意可得12sin 0x -≥，解得1sin 2x ≤，所以7ππ2π,2π,Z 66x k k k ⎡⎤∈-++∈⎢⎥⎣⎦；又2cos 02x -，即cos 22x >，解得ππ2π,2π,Z 44x k k k ⎛⎫∈-++∈ ⎪⎝⎭取交集部分可得，()f x 的定义域为ππ2π,2π,Z 46k k k ⎛⎤-++∈ ⎥⎝⎦.故答案为：ππ2π,2π,Z46k k k ⎛⎤-++∈ ⎥⎝⎦25．（2023·全国·高一专题练习）已知关于x 的不等式2cos 4cos 1x x a -+≥在π0,2⎡⎤⎢⎥⎣⎦内恒成立，则实数a 的取值范围是．【答案】[)4,∞+【解析】由2cos 4cos 1x x a -+≥得2cos 4cos 1a x x ≥-++，设cos t x =，因π0,2x ⎡⎤∈⎢⎥⎣⎦，所以[]cos 0,1t x =∈，则241a t t ≥-++在[]0,1t ∈上恒成立，设()241f t t t =-++，则二次函数()f t 的对称轴为2t =，因其开口向下，所以[]0,1t ∈时函数()f t 单调递增，所以()f t 的最大值()14f =，故4a ≥，故答案为：[)4,∞+26．（2023春·山东日照·高一统考期中）函数()π3cos 23f x x ω⎛⎫=+ ⎪⎝⎭()0ω>在π5π,36⎡⎤-⎢⎥⎣⎦上是减函数，且在[]0,2π上恰好取得一次最小值3-，则ω的取值范围是．【答案】12,65⎡⎤⎢⎥⎣⎦【解析】因为02x π≤≤，所以πππ24π333x ωω≤+≤+.因为()f x 在[]0,2π上恰好取得一次最小值3-，所以ππ4π3π3ω≤+<，所以1263ω≤<.因为π5π36x -≤≤，所以ππππ5ππ1322π9333339x ωωω-<-+≤+≤+<.因为，()f x 在π5π,36⎡⎤-⎢⎥⎣⎦上是减函数，根据余弦函数的单调性可知ππ20335πππ33ωω⎧-+≥⎪⎪⎨⎪+≤⎪⎩，解得205ω<≤.所以，1265ω≤≤.故答案为：12,65⎡⎤⎢⎥⎣⎦.27．（2022秋·黑龙江齐齐哈尔·高一统考期末）函数()πsin 14f x x ⎛⎫=++ ⎪⎝⎭的图象的对称轴方程为，对称中心为.【答案】()ππ4x k k =+∈Z ()ππ,04k k ⎛⎫-∈ ⎪⎝⎭Z 【解析】由πππ,42x k k +=+∈Z ，解得ππ,4x k k =+∈Z ，所以函数()f x 的对称轴方程为()ππ4x k k =+∈Z .令ππ,4x k k +=∈Z ，得ππ,4x k k =-+∈Z ，所以函数()f x 的对称中心为()ππ,04k k ⎛⎫-∈ ⎪⎝⎭Z .故答案为：()ππ4x k k =+∈Z ，()ππ,04k k ⎛⎫-∈ ⎪⎝⎭Z 28．（2023·全国·高一课堂例题）求函数π2sin 36y x ⎛⎫=-++ ⎪⎝⎭，[0,π]x ∈的最大值为，最小值为．【答案】41【解析】因为[0,π]x ∈，所以ππ7π,666x ⎡⎤+∈⎢⎥⎣⎦，所以1πsin 126x ⎛⎫-≤+≤ ⎪⎝⎭，所以π22sin 16x ⎛⎫-≤-+≤ ⎪⎝⎭，所以π12sin 346x ⎛⎫≤-++≤ ⎪⎝⎭，故函数π2sin 36y x ⎛⎫=-++ ⎪⎝⎭，[0,π]x ∈的最大值为4，最小值为1．故答案为：4，129．（2023秋·高一课时练习）（1）函数()π24f x x ⎛⎫=+ ⎪⎝⎭，π,02x ⎡⎤∈-⎢⎥⎣⎦的值域为；（2）函数()23πsin 0,42f x x x x ⎛⎫⎡⎤=-∈ ⎪⎢⎥⎣⎦⎝⎭的最大值是.【答案】⎡-⎣1【解析】（1）当π,02x ⎡⎤∈-⎢⎥⎣⎦时，π3ππ2,444x ⎡⎤+∈-⎢⎣⎦，πcos 242x ⎡⎤⎛⎫∴+∈⎢⎥ ⎪⎝⎭⎣⎦，()f x -∴∈⎡⎣，即()f x 的值域为⎡-⎣；（2）()222331sin 1cos cos 444f x x x x x x x =+-=-+-=-++，π0,2x ⎛⎫⎡⎤∈ ⎪⎢⎥⎣⎦⎝⎭；令cos x t =，则[]0,1t ∈，()221142g t t t ⎛⎫=-++=--+ ⎪ ⎪⎝⎭，则当2t =时，()max 1g t =，即()f x 的最大值为1.故答案为：⎡-⎣；1.30．（2023秋·高一课时练习）求下列函数的值域．(1)212cos 2sin y x x =-+；(2)2sin 2sin x y x-=+；(3)ππ()2sin 2,0,62f x x x ⎛⎫⎡⎤=+∈ ⎪⎢⎥⎝⎭⎣⎦.【答案】(1)332,⎡⎤-⎢⎥⎣⎦(2)13,3⎡⎤⎢⎥⎣⎦(3)[]1,2-【解析】（1）2221312cos 2sin 2sin 2sin 12sin .22y x x x x x ⎛⎫=-+=+-=+- ⎪⎝⎭当1sin 2x =-时，min 32y =-；当sin 1x =时，max 3y =.∴函数212cos 2sin y x x =-+的值域为3,32⎡⎤-⎢⎥⎣⎦.（2）()42sin 412sin 2sin x y x x-+==-++，∵1sin 1x -≤≤，∴12sin 3x ≤+≤，∴44432sin x≤≤+，141332sin x≤-≤+，即,133y ⎡⎤∈⎢⎥⎣⎦.∴函数2sin 2sin x y x -=+的值域为1,33⎡⎤⎢⎥⎣⎦.（3）πππ7π0,,2,2666x x ⎡⎤⎡⎤∈+∈⎢⎥⎢⎥⎣⎦⎣⎦，根据正弦函数的性质，可知π1sin 2,162x ⎛⎫⎡⎤+∈- ⎪⎢⎥⎝⎭⎣⎦故[]π2sin 21,26x ⎛⎫+∈- ⎪⎝⎭.即函数的值域为[]1,2-.2．（2023·全国·高一课堂例题）已知函数()π2sin (0)6f x x ωω⎛⎫=+> ⎪⎝⎭在区间ππ,43⎛⎫- ⎪⎝⎭上恰有一个最大值点和一个最小值点，则实数ω的取值范围为（）A ．8,73⎡⎫⎪⎢⎣⎭B ．8,43⎛⎫ ⎪⎝⎭C ．204,3⎡⎫⎪⎢⎣⎭D ．20,73⎛⎫ ⎪⎝⎭【答案】B【解析】因为()f x 在区间ππ,43⎛⎫- ⎪⎝⎭上恰有一个最大值点和一个最小值点，所以ππ342T ⎛⎫--> ⎪⎝⎭，所以127ω>．令π6t x ω=+，当ππ,43x ⎛⎫∈- ⎪⎝⎭时，ππππ,4636t ωω⎛⎫∈-++ ⎪⎝⎭，于是()π2sin 6f x x ω⎛⎫=+ ⎪⎝⎭在区间ππ,43⎛⎫- ⎪⎝⎭上的最值点个数等价于()2sin g t t =在ππππ,4636ωω⎛⎫-++ ⎪⎝⎭上的最值点个数．由127ω>知，ππ046ω-+<，ππ036ω+>，因为()g t 在ππππ,4636ωω⎛⎫-++ ⎪⎝⎭上恰有一个最大值点和一个最小值点，所以3ππππ,2462πππ3π,2362ωω⎧-<-+<-⎪⎪⎨⎪<+<⎪⎩解得843ω<<．答案：B.2．（2023春·河南新乡·高一新乡市第一中学校考阶段练习）已知2πππ()sin (0),363f x x f f ωω⎛⎫⎛⎫⎛⎫=+>= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，且()f x 在区间ππ,63⎛⎫ ⎪⎝⎭上有最大值，无最小值，则ω的值为（）A ．223B ．263C ．343D ．383【答案】A 【解析】因为2πππ()sin (0),363f x x f f ωω⎛⎫⎛⎫⎛⎫=+>= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以函数()f x 的图象关于πππ6324x +==对称，且()f x 在区间ππ,63⎛⎫ ⎪⎝⎭上有最大值，无最小值，所以ππ2πsin 1443f ω⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭，所以()π2ππ2π,Z 432k k ω+=+∈，所以()8282=8Z 33k k k ω=+--∈，当1k =时，223ω=，当2k =时，462π3πππ,46323363T ω===<-，此时在区间ππ,63⎛⎫ ⎪⎝⎭内已存在最小值;当2k >时，462π3πππ,46323363T ω><=<-，此时在区间ππ,63⎛⎫ ⎪⎝⎭内已存在最小值．故选：A ．3．（2023春·江西宜春·高一江西省宜丰中学校考阶段练习）已知函数()πcos (0)3f x x ωω⎛⎫=-> ⎪⎝⎭在ππ,64⎡⎤⎢⎣⎦上单调递增，且当ππ,43x ⎡⎤∈⎢⎥⎣⎦时，()0f x ≥恒成立，则ω的取值范围为（）A ．522170,,232⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦ B ．4170,8,32⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦ C ．4280,8,33⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦ D ．5220,,823⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦【答案】B【解析】由已知，函数()πcos (0)3f x x ωω⎛⎫=-> ⎪⎝⎭在ππ,64⎡⎤⎢⎥⎣⎦上单调递增，所以()111π2ππ2πZ 3k x k k ω-≤-≤∈，解得：()1112π2π2ππZ 33k k x k ωωωω-≤≤+∈，由于()111Z π,π,642π2π2ππ33k k k ωωωω⎡⎤⎡⎤⊆⎢⎥⎢⎣⎦⎣⎦-+∈，所以112ππ2π632πππ43k k ωωωω⎧≥-⎪⎪⎨⎪≤+⎪⎩，解得：()11141248Z 3k k k ω-≤≤+∈①又因为函数()πcos (0)3f x x ωω⎛⎫=-> ⎪⎝⎭在ππ,43x ⎡⎤∈⎢⎥⎣⎦上()0f x ≥恒成立，所以()222πππ2π2π+Z 232k x k k ω-≤-≤∈，解得：()2222π2ππ5πZ 66k k x k ωωωω-≤≤+∈，由于()2222π2ππ5π,Z 6π,46π3k k k ωωωω-+⎡⎤⎡⎤⊆⎢⎥⎢⎥⎣⎦⎣∈⎦，所以222πππ462ππ5π36k k ωωωω⎧≥-⎪⎪⎨⎪≤+⎪⎩，解得：()2222586Z 32k k k ω-≤≤+∈②又因为0ω>，当120k k ==时，由①②可知：04432532ωωω⎧⎪>⎪⎪-≤≤⎨⎪⎪-≤≤⎪⎩，解得403ω⎛⎤∈ ⎥⎝⎦，；当121k k ==时，由①②可知：028*******2ωωω⎧⎪>⎪⎪≤≤⎨⎪⎪≤≤⎪⎩，解得1782ω⎡⎤∈⎢⎥⎣⎦，.所以ω的取值范围为4170,8,32⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦.故选：B.4．（2023春·辽宁·高一辽宁实验中学校考阶段练习）若函数()()cos 03f x x πωω⎛⎫=-> ⎪⎝⎭在,63ππ⎛⎫ ⎪⎝⎭上不单调，则实数ω的取值范围是.【答案】()()1,24,⋃+∞【解析】由题意得()()cos cos 033f x x x ππωωω⎛⎫⎛⎫=-=-> ⎪ ⎪⎝⎭⎝⎭，若函数()()cos 03f x x πωω⎛⎫=-> ⎪⎝⎭在,63ππ⎛⎫ ⎪⎝⎭上单调递增，则π+2π2π,Z 3k x k k πω-≤-≤∈,解得：2+2π+2π33,Z k k x k ππωω-≤≤∈，所以2+2π36,Z +2π33k k k ππωππω⎧-⎪≤⎪⎪∈⎨⎪⎪≤⎪⎩，解得412,Z 16k k k ωω≥-+⎧∈⎨≤+⎩，即41216,Z k k k ω-+≤≤+∈，因为41216,k k k -+≤+∈Z ，所以56k ≤且0ω>，所以0k =，01ω<≤①若函数()()cos 03f x x πωω⎛⎫=-> ⎪⎝⎭在,63ππ⎛⎫ ⎪⎝⎭上单调递减，则2ππ+2π,Z 3k x k k πω≤-≤∈,解得4+2π+2π33,Z k k x k ππωω≤≤∈，所以+2π36,Z 4+2π33k k k ππωππω⎧⎪≤⎪⎪∈⎨⎪⎪≤⎪⎩，解得212,Z 46k k k ωω≥+⎧∈⎨≤+⎩，即21246,Z k k k ω+≤≤+∈，因为21246,Z k k k +≤+∈，所以13k ≤且0ω>，所以0k =，24ω≤≤②又因为函数()()cos 03f x x πωω⎛⎫=-> ⎪⎝⎭在,63ππ⎛⎫ ⎪⎝⎭上不单调，且0ω>，所以ω的取值为①②所表示的不等式的补集，即12ω<<或4ω>.故答案为：12ω<<或4ω>.。

专题01 三角函数的图象与性质【要点提炼】1.常用的三种函数的图象与性质(下表中k ∈Z ) 函数y ＝sin xy ＝cos xy ＝tan x图象递增 区间 ⎣⎢⎡⎦⎥⎤2k π－π2，2k π＋π2 [2k π－π，2k π]⎝ ⎛⎭⎪⎫k π－π2，k π＋π2 递减 区间 ⎣⎢⎡⎦⎥⎤2k π＋π2，2k π＋3π2 [2k π，2k π＋π]奇偶性 奇函数 偶函数 奇函数 对称 中心 (k π，0) ⎝ ⎛⎭⎪⎫k π＋π2，0 ⎝ ⎛⎭⎪⎫k π2，0 对称轴 x ＝k π＋π2 x ＝k π 周期性2π2ππ2.三角函数的常用结论(1)y ＝A sin(ωx ＋φ)，当φ＝k π(k ∈Z )时为奇函数；当φ＝k π＋π2(k ∈Z )时为偶函数；对称轴方程可由ωx ＋φ＝k π＋π2(k ∈Z )求得. (2)y ＝A cos(ωx ＋φ)，当φ＝k π＋π2(k ∈Z )时为奇函数；当φ＝k π(k ∈Z )时为偶函数；对称轴方程可由ωx ＋φ＝k π(k ∈Z )求得. (3)y ＝A tan(ωx ＋φ)，当φ＝k π(k ∈Z )时为奇函数. 3.三角函数的两种常见变换 (1)y ＝sin x ――——————————→向左(φ＞0)或向右(φ＜0)平移|φ|个单位y ＝sin(ωx ＋φ)――——————————→纵坐标变为原来的A 倍横坐标不变y ＝A sin(ωx ＋φ)(A ＞0，ω＞0).y ＝sin ωx ―————————————―→向左(φ＞0)或向右(φ＜0)平移|φω|个单位 y ＝sin(ωx ＋φ)————————————―→纵坐标变为原来的A 倍横坐标不变y ＝A sin(ωx ＋φ)(A ＞0，ω＞0).考点一 三角函数的图像与性质考向一 三角函数的定义与同角关系式【典例1】 (1)在平面直角坐标系中，AB ︵，CD ︵，EF ︵，GH ︵是圆x 2＋y 2＝1上的四段弧(如图)，点P 在其中一段上，角α以Ox 为始边，OP 为终边.若tan α<cos α<sin α，则P 所在的圆弧是( )A.AB ︵B.CD ︵C.EF ︵D.GH ︵(2)已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上有两点A (1，a )，B (2，b )，且cos 2α＝23，则|a －b |＝( ) A.15B.55C.255D.1解析 (1)设点P 的坐标为(x ，y )，且tan α＜cos α＜sin α，∴yx ＜x ＜y ，解之得－1＜x ＜0，且0＜y ＜1.故点P (x ，y )所在的圆弧是EF ︵.(2)由题意知cos α>0.因为cos 2α＝2cos 2α－1＝23，所以cos α＝306，sin α＝±66，得|tan α|＝55.由题意知|tan α|＝⎪⎪⎪⎪⎪⎪a －b 1－2，所以|a －b |＝55. 答案 (1)C (2)B探究提高 1.任意角的三角函数值仅与角α的终边位置有关，而与角α终边上点P 的位置无关.若角α已经给出，则无论点P 选择在α终边上的什么位置，角α的三角函数值都是确定的.2.应用诱导公式与同角关系开方运算时，一定要注意三角函数值的符号；利用同角三角函数的关系化简要遵循一定的原则，如切化弦、化异为同、化高为低、化繁为简等.【拓展练习1】 (1)(2020·唐山模拟)若cos θ－2sin θ＝1，则tan θ＝( ) A.43B.34C.0或43D.0或34(2)(2020·济南模拟)已知cos ⎝ ⎛⎭⎪⎫α＋π6－sin α＝435，则sin ⎝ ⎛⎭⎪⎫α＋11π6＝________.解析 (1)由题意可得⎩⎨⎧cos θ－2sin θ＝1，cos 2θ＋sin 2θ＝1，解得⎩⎨⎧sin θ＝0，cos θ＝1或⎩⎪⎨⎪⎧sin θ＝－45，cos θ＝－35，所以tan θ＝0，或tan θ＝43.故选C.(2)∵cos ⎝ ⎛⎭⎪⎫α＋π6－sin α＝32cos α－12sin α－sin α＝32cos α－32sin α＝3sin ⎝ ⎛⎭⎪⎫π6－α＝435，∴sin ⎝⎛⎭⎪⎫α－π6＝－45， ∴sin ⎝ ⎛⎭⎪⎫α＋11π6＝sin ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α－π6＋2π＝sin ⎝ ⎛⎭⎪⎫α－π6＝－45.答案 (1)C (2)－45考向二 三角函数的图象及图象变换【典例2】 (1)(多选题)(2020·新高考山东、海南卷)如图是函数y ＝sin(ωx ＋φ)的部分图象，则sin(ωx ＋φ)＝( )A.sin ⎝ ⎛⎭⎪⎫x ＋π3B.sin ⎝ ⎛⎭⎪⎫π3－2xC.cos ⎝ ⎛⎭⎪⎫2x ＋π6D.cos ⎝ ⎛⎭⎪⎫5π6－2x(2)(2019·天津卷)已知函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0，|φ|<π)是奇函数，将y ＝f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，所得图象对应的函数为g (x ).若g (x )的最小正周期为2π，且g ⎝ ⎛⎭⎪⎫π4＝2，则f ⎝ ⎛⎭⎪⎫3π8＝( )A.－2B.－ 2C. 2D.2解析 (1)由图象知T 2＝2π3－π6＝π2，得T ＝π，所以ω＝2πT ＝2.又图象过点⎝ ⎛⎭⎪⎫π6，0，由“五点法”，结合图象可得φ＋π3＝π，即φ＝2π3，所以sin(ωx ＋φ)＝sin ⎝ ⎛⎭⎪⎫2x ＋2π3，故A 错误；由sin ⎝ ⎛⎭⎪⎫2x ＋2π3＝sin ⎣⎢⎡⎦⎥⎤π－⎝ ⎛⎭⎪⎫π3－2x ＝sin ⎝ ⎛⎭⎪⎫π3－2x 知B 正确；由sin ⎝ ⎛⎭⎪⎫2x ＋2π3＝sin ⎝ ⎛⎭⎪⎫2x ＋π2＋π6＝cos ⎝ ⎛⎭⎪⎫2x ＋π6知C 正确；由sin ⎝ ⎛⎭⎪⎫2x ＋2π3＝cos ⎝ ⎛⎭⎪⎫2x ＋π6＝cos ⎣⎢⎡⎦⎥⎤π＋⎝ ⎛⎭⎪⎫2x －5π6＝－cos ⎝ ⎛⎭⎪⎫5π6－2x 知D 错误.综上可知，正确的选项为BC. (2)由f (x )是奇函数可得φ＝k π(k ∈Z )，又|φ|<π，所以φ＝0. 所以g (x )＝A sin ⎝ ⎛⎭⎪⎫12ωx ，且g (x )最小正周期为2π，可得2π12ω＝2π，故ω＝2，所以g (x )＝A sin x ，g ⎝ ⎛⎭⎪⎫π4＝A sin π4＝22A ＝2，所以A ＝2. 所以f (x )＝2sin 2x ，故f ⎝ ⎛⎭⎪⎫3π8＝2sin 3π4＝ 2.答案 (1)BC (2)C探究提高 1.在图象变换过程中务必分清是先相位变换，还是先周期变换.变换只是相对于其中的自变量x 而言的，如果x 的系数不是1，就要把这个系数提取后再确定变换的单位长度和方向.2.已知函数y ＝A sin(ωx ＋φ)(A >0，ω>0)的图象求解析式时，常采用待定系数法，由图中的最高点、最低点或特殊点求A ；由函数的周期确定ω；确定φ常根据“五点法”中的五个点求解，一般把第一个“零点”作为突破口，可以从图象的升降找准第一个“零点”的位置.【拓展练习2】 (1)(多选题)(2020·济南历城区模拟)将函数f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π6的图象向左平移π12个单位长度，再向上平移1个单位长度，得到函数g (x )的图象.若g (x 1)g (x 2)＝9，且x 1，x 2∈[－2π，2π]，则2x 1－x 2的可能取值为( ) A.－59π12B.－35π6C.25π6D.49π12(2)(2020·长沙质检)函数g (x )＝A sin(ωx ＋φ)(A ＞0，ω＞0，0＜φ＜2π)的部分图象如图所示，已知g (0)＝g ⎝ ⎛⎭⎪⎫5π6＝3，函数y ＝f (x )的图象可由y ＝g (x )图象向右平移π3个单位长度而得到，则函数f (x )的解析式为( )A.f (x )＝2sin 2xB.f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3C.f (x )＝－2sin 2xD.f (x )＝－2sin ⎝ ⎛⎭⎪⎫2x ＋π3 解析 (1)将函数f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π6的图象向左平移π12个单位长度，再向上平移1个单位长度，得到函数g (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3＋1的图象.由g (x 1)g (x 2)＝9，知g (x 1)＝3，g (x 2)＝3，所以2x ＋π3＝π2＋2k π，k ∈Z ，即x ＝π12＋k π，k ∈Z .由x 1，x 2∈[－2π，2π]，得x 1，x 2的取值集合为⎩⎨⎧⎭⎬⎫－23π12，－11π12，π12，13π12.当x 1＝－23π12，x 2＝13π12时，2x 1－x 2＝－59π12；当x 1＝13π12，x 2＝－23π12时，2x 1－x 2＝49π12.故选AD.(2)由函数g (x )的图象及g (0)＝g ⎝ ⎛⎭⎪⎫5π6＝3，知直线x ＝5π12为函数g (x )的图象的一条对称轴，所以T 4＝5π12－π6＝π4，则T ＝π，所以ω＝2πT ＝2，所以g (x )＝A sin(2x ＋φ)，由题图可知⎝ ⎛⎭⎪⎫π6，0为“五点法”作图中的第三点，则2×π6＋φ＝π，解得φ＝2π3，由g (0)＝3，得A sin 2π3＝3，又A ＞0，所以A ＝2，则g (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋2π3，所以g (x )的图象向右平移π3个单位长度后得到的图象对应的解析式为f (x )＝2sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x －π3＋2π3＝2sin 2x ，故选A. 答案 (1)AD (2)A 考向三 三角函数的性质【典例3】 (1)若f (x )＝cos x －sin x 在[－a ，a ]上是减函数，则a 的最大值是( ) A.π4B.π2C.3π4D.π(2)(2020·天一大联考)已知f (x )＝cos ⎝ ⎛⎭⎪⎫ωx －π6(ω＞0)，f ⎝ ⎛⎭⎪⎫π6＝f ⎝ ⎛⎭⎪⎫π3，且f (x )在区间⎝ ⎛⎭⎪⎫π6，π3内有最小值，无最大值，则ω＝( ) A.83 B.143 C.8 D.4 (3)已知函数f (x )＝sin ωx ＋cos ωx (ω＞0)，x ∈R .若函数f (x )在区间(－ω，ω)内单调递增，且函数y ＝f (x )的图象关于直线x ＝ω对称，则ω的值为________. 解析 (1)f (x )＝cos x －sin x ＝2cos ⎝ ⎛⎭⎪⎫x ＋π4，且函数y ＝cos x 在区间[0，π]上单调递减，则由0≤x ＋π4≤π，得－π4≤x ≤3π4.因为f (x )在[－a ，a ]上是减函数，所以⎩⎪⎨⎪⎧－a ≥－π4，a ≤3π4，解得a ≤π4.所以0<a ≤π4，所以a 的最大值是π4.(2)由于f ⎝ ⎛⎭⎪⎫π6＝f ⎝ ⎛⎭⎪⎫π3，且f (x )在区间⎝ ⎛⎭⎪⎫π6，π3内有最小值，∴f (x )在x ＝12⎝ ⎛⎭⎪⎫π6＋π3＝π4处取得最小值.因此π4ω－π6＝2k π＋π，即ω＝8k ＋143，k ∈Z .①又函数f (x )在区间⎝ ⎛⎭⎪⎫π6，π3无最大值，且ω＞0，∴T ＝2πω≥π3－π6＝π6，∴0＜ω≤12.②由①②知ω＝143.(3)f (x )＝sin ωx ＋cos ωx ＝2sin ⎝ ⎛⎭⎪⎫ωx ＋π4，因为f (x )在区间(－ω，ω)内单调递增，且函数图象关于直线x ＝ω对称，所以f (ω)必为一个周期上的最大值，所以有ω·ω＋π4＝2k π＋π2，k ∈Z ，所以ω2＝π4＋2k π，k ∈Z .又ω－(－ω)≤2πω2，即ω2≤π2，即ω2＝π4，所以ω＝π2. 答案 (1)A (2)B (3)π2探究提高 1.讨论三角函数的单调性，研究函数的周期性、奇偶性与对称性，都必须首先利用辅助角公式，将函数化成一个角的一种三角函数.2.求函数y ＝A sin(ωx ＋φ)(A >0，ω>0)的单调区间，是将ωx ＋φ作为一个整体代入正弦函数增区间(或减区间)，求出的区间即为y ＝A sin(ωx ＋φ)的增区间(或减区间).【拓展练习3】 (1)(多选题)(2020·济南质检)已知函数f (x )＝2sin(2x ＋φ)(0<φ<π)，若将函数f (x )的图象向右平移π6个单位长度后，得到图象关于y 轴对称，则下列结论中正确的是( ) A.φ＝5π6B.⎝ ⎛⎭⎪⎫π12，0是f (x )的图象的一个对称中心 C.f (φ)＝－2D.x ＝－π6是f (x )图象的一条对称轴(2)(多选题)关于函数f (x )＝|cos x |＋cos|2x |，则下列结论正确的是( ) A.f (x )是偶函数 B.π是f (x )的最小正周期C.f (x )在⎣⎢⎡⎦⎥⎤3π4，5π4上单调递增D.当x ∈⎣⎢⎡⎦⎥⎤34π，54π时，f (x )的最大值为2解析 (1)将函数f (x )的图象向右平移π6个单位长度后，得到y ＝2sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x －π6＋φ＝2sin ⎝ ⎛⎭⎪⎫2x ＋φ－π3的图象，∵其关于y 轴对称，∴φ－π3＝k π＋π2，k ∈Z ，∴φ＝k π＋5π6，k ∈Z .又0<φ<π，∴当k ＝0时，φ＝5π6，故A 正确；f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋5π6，f ⎝ ⎛⎭⎪⎫π12＝0，则⎝ ⎛⎭⎪⎫π12，0是f (x )的图象的一个对称中心，故B 正确；因为f (φ)＝f ⎝ ⎛⎭⎪⎫5π6＝2，故C错误；f ⎝ ⎛⎭⎪⎫－π6＝2，则x ＝－π6是f (x )图象的一条对称轴，故D 正确.故选ABD.(2)f (x )＝|cos x |＋cos|2x |＝|cos x |＋cos 2x ＝|cos x |＋2cos 2x －1＝2|cos x |2＋|cos x |－1，由f (－x )＝2|cos(－x )|2＋|cos(－x )|－1＝f (x )，且函数f (x )的定义域为R ，得f (x )为偶函数，故A 正确.由于y ＝|cos x |的最小正周期为π，可得f (x )的最小正周期为π，故B 正确. 令t ＝|cos x |，得函数f (x )可转化为g (t )＝2t 2＋t －1，t ∈[0，1]， 易知t ＝|cos x |在⎣⎢⎡⎦⎥⎤3π4，π上单调递增，在⎣⎢⎡⎦⎥⎤π，5π4上单调递减，由t ∈[0，1]，g (t )＝2⎝ ⎛⎭⎪⎫t ＋142－98，可得g (t)在[0，1]上单调递增，所以f (x )在⎣⎢⎡⎦⎥⎤3π4，π上单调递增，在⎣⎢⎡⎦⎥⎤π，5π4上单调递减，故C 错误.根据f (x )在⎣⎢⎡⎦⎥⎤34π，π上递增，在⎣⎢⎡⎦⎥⎤π，54π上递减，∴f (x )在x ＝π时取到最大值f (π)＝2，则D 正确. 答案 (1)ABD (2)ABD考向四 三角函数性质与图象的综合应用【典例4】 (2020·临沂一预)在①f (x )的图象关于直线x ＝5π6ω对称，②f (x )＝cos ωx －3sin ωx ，③f (x )≤f (0)恒成立这三个条件中任选一个，补充在下面横线处.若问题中的ω存在，求出ω的值；若ω不存在，请说明理由.设函数f (x )＝2cos(ωx ＋φ)⎝ ⎛⎭⎪⎫ω>0，0≤φ≤π2，_____________________________.是否存在正整数ω，使得函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上是单调的？(注：如果选择多个条件分别解答，按第一个解答计分)解 若选①，则存在满足条件的正整数ω.求解过程如下： 令ωx ＋φ＝k π，k ∈Z ，代入x ＝5π6ω， 解得φ＝k π－5π6，k ∈Z .因为0≤φ≤π2，所以φ＝π6，所以f (x )＝2cos ⎝ ⎛⎭⎪⎫ωx ＋π6.当x ∈⎣⎢⎡⎦⎥⎤0，π2时，ωx ＋π6∈⎣⎢⎡⎦⎥⎤π6，ωπ2＋π6.若函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上单调，则有ωπ2＋π6≤π，解得0<ω≤53.所以存在正整数ω＝1，使得函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上是单调的.若选②，则存在满足条件的正整数ω.求解过程如下： f (x )＝cos ωx －3sin ωx ＝2cos ⎝ ⎛⎭⎪⎫ωx ＋π3＝2cos(ωx ＋φ)，且0≤φ≤π2，所以φ＝π3.当x ∈⎣⎢⎡⎦⎥⎤0，π2时，ωx ＋π3∈⎣⎢⎡⎦⎥⎤π3，ωπ2＋π3. 若函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上单调，则有ωπ2＋π3≤π，解得0<ω≤43.所以存在正整数ω＝1，使得函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上是单调的.若选③，则存在满足条件的正整数ω.求解过程如下： 因为f (x )≤f (0)恒成立，即f (x )max ＝f (0)＝2cos φ＝2， 所以cos φ＝1.因为0≤φ≤π2，所以φ＝0，所以f (x )＝2cos ωx .当x ∈⎣⎢⎡⎦⎥⎤0，π2时，ωx ∈⎣⎢⎡⎦⎥⎤0，ωπ2. 若函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上单调，则有ωπ2≤π，解得0<ω≤2.所以存在正整数ω＝1或ω＝2，使得函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上是单调的.探究提高 1.研究三角函数的图象与性质，关键是将函数化为y ＝A sin(ωx ＋φ)＋B (或y ＝A cos(ωx ＋φ)＋B )的形式，利用正余弦函数与复合函数的性质求解. 2.函数y ＝A sin(ωx ＋φ)(或y ＝A cos(ωx ＋φ))的最小正周期T ＝2π|ω|.应特别注意y ＝|A sin(ωx ＋φ)|的最小正周期为T ＝π|ω|.【拓展练习4】 (2020·威海三校一联)已知函数f (x )＝2cos 2ω1x ＋sin ω2x . (1)求f (0)的值；(2)从①ω1＝1，ω2＝2，②ω1＝1，ω2＝1这两个条件中任选一个，作为题目的已知条件，求函数f (x )在⎣⎢⎡⎦⎥⎤－π2，π6上的最小值，并直接写出函数f (x )的一个周期.(注：如果选择多个条件分别解答，按第一个解答计分) 解 (1)f (0)＝2cos 20＋sin 0＝2. (2)选择条件①.f (x )的一个周期为π.当ω1＝1，ω2＝2时，f (x )＝2cos 2x ＋sin 2x ＝(cos 2x ＋1)＋sin 2x ＝2⎝ ⎛⎭⎪⎫22sin 2x ＋22cos 2x ＋1＝2sin ⎝ ⎛⎭⎪⎫2x ＋π4＋1.因为x ∈⎣⎢⎡⎦⎥⎤－π2，π6，所以2x ＋π4∈⎣⎢⎡⎦⎥⎤－3π4，7π12.所以－1≤sin ⎝ ⎛⎭⎪⎫2x ＋π4≤1，则1－2≤f (x )≤1＋ 2. 当2x ＋π4＝－π2，即x ＝－3π8时，f (x )在⎣⎢⎡⎦⎥⎤－π2，π6上取得最小值1－ 2.选择条件②.f (x )的一个周期为2π.当ω1＝1，ω2＝1时，f (x )＝2cos 2x ＋sin x ＝2(1－sin 2x )＋sin x ＝－2⎝ ⎛⎭⎪⎫sin x －142＋178.因为x ∈⎣⎢⎡⎦⎥⎤－π2，π6，所以sin x ∈⎣⎢⎡⎦⎥⎤－1，12.所以当sin x ＝－1，即x ＝－π2时，f (x )在⎣⎢⎡⎦⎥⎤－π2，π6上取得最小值－1.【专题拓展练习】一、选择题（1～10题为单项选择题，11～15题为多项选择题） 1．函数2()cos 3f x x π⎛⎫=+⎪⎝⎭的最小正周期为（ ） A ．4π B ．2πC ．2π D ．π2．把函数sin 2y x =的图象向左平移4π个单位长度，再把所得图象所有点的横坐标伸长到原来的2倍（纵坐标不变），所得函数图象的解析式为（ ） A ．sin y x =B ．cos y x =C ．sin()4y x π=+D ．sin y x =-3．若16x π=，256x π=是函数()sin()f x x ωϕ=+()0ω>两个相邻的极值点，则ω=（ ） A ．3B ．32C ．34D ．124．将函数()2sin 26f x x π⎛⎫=+⎪⎝⎭的图象向左平移12π个单位长度后得到函数()g x 的图象，则函数()g x 的单调递增区间是（ ） A ．(),36k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦B ．(),63k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦C ．()44k ,k k Z ππ⎡⎤-+π+π∈⎢⎥⎣⎦D ．()5,1212k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦5．函数()()2sin 06f x x πωω⎛⎫=+> ⎪⎝⎭的图像最近两对称轴之间的距离为2π，若该函数图像关于点()0m ,成中心对称，当0,2m π⎡⎤∈⎢⎥⎣⎦时m 的值为（ ）A ．6πB ．4π C ．3π D ．512π6．已知函数()22sin cos cos f x x x x x =+-，x ∈R ，则（ ） A ．()f x 的最大值为1 B ．()f x 的图象关于直线3x π=对称C ．()f x 的最小正周期为2π D ．()f x 在区间()0,π上只有1个零点7．已知函数()()()3cos 0g x x ωϕω=+>在7,6ππ⎛⎫ ⎪⎝⎭上具有单调性，且满足04g π⎛⎫=⎪⎝⎭，()3g π=，则ω的取值共有（ ）A ．6个B ．5个C ．4个D ．3个8．函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示，将函数()f x 的图象向左平移3π个单位长度后得到()y g x =的图象，则下列说法正确的是（ ）A ．函数()g x 为奇函数B ．函数()g x 的最小正周期为2πC ．函数()g x 的图象的对称轴为直线()6x k k ππ=+∈ZD ．函数()g x 的单调递增区间为5,()1212k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z9．设函数()sin 2cos 2f x a x b x =+，其中,,0a b R ab ∈≠，若()6f x f π⎛⎫≤⎪⎝⎭对一切x ∈R 恒成立，则以下结论：①函数()f x 的图象关于11,012π⎛⎫⎪⎝⎭对称；②函数()f x 的单调递增区间是2,()63k k k ππππ⎡⎤++∈⎢⎥⎣⎦Z ；③函数()f x 既不是奇函数也不是偶函数；④函数()f x 的图象关于()26k x k Z ππ=+∈对称．其中正确的说法是（ ） A ．①②③B ．②④C ．③④D ．①③④10．斐波那契螺线又叫黄金螺线，广泛应用于绘画、建筑等，这种螺线可以按下列方法画出：如图，在黄金矩形ABCD （51AB BC -=）中作正方形ABFE ，以F 为圆心，AB 长为半径作圆弧BE ；然后在矩形CDEF 中作正方形DEHG ，以H 为圆心，DE 长为半径作圆弧EG ；……；如此继续下去，这些圆弧就连成了斐波那契螺线.记圆弧BE ，EG ，GI 的长度分别为,,l m n ，对于以下四个命题：①l m n =+；②2m l n =⋅；③2m l n =+；④211m l n=+.其中正确的是（ ）A ．①②B ．①④C ．②③D ．③④11．已知函数()3sin sin3f x x x =+，则（ ） A ．()f x 是奇函数 B ．()f x 是周期函数且最小正周期为2π C ．()f x 的值域是[4,4]- D ．当(0,)x π∈时()0f x >12．设函数cos 2()2sin cos xf x x x=+，则（ ）A ．()()f x f x π=+B ．()f x 的最大值为12C ．()f x 在,04π⎛⎫-⎪⎝⎭单调递增 D ．()f x 在0,4π⎛⎫⎪⎝⎭单调递减 13．若将函数f (x )=cos(2x +12π)的图象向左平移8π个单位长度，得到函数g (x )的图象，则下列说法正确的是（ ） A ．g (x )的最小正周期为π B ．g (x )在区间[0，2π]上单调递减 C ．x =12π是函数g (x )的对称轴D ．g (x )在[﹣6π，6π]上的最小值为﹣1214．下列说法正确的是（ ） A ．函数()23sin 30,42f x x x x π⎛⎫⎡⎤=-∈ ⎪⎢⎥⎣⎦⎝⎭的最大值是1 B ．函数()cos sin tan 0,tan 2x f x x x x x π⎛⎫⎛⎫=⋅+∈ ⎪ ⎪⎝⎭⎝⎭的值域为(2 C ．函数()1sin 2cos 2f x x a x =+⋅在()0,π上单调递增，则a 的取值范围是(],1-∞-D ．函数()2222sin 42cos tx t x xf x x x π⎛⎫+++ ⎪⎝⎭=+的最大值为a ，最小值为b ，若2a b +=，则1t =15．如图是函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><的部分图象，则下列说法正确的是（ ）A ．2ω=B ．π,06⎛⎫-⎪⎝⎭是函数，()f x 的一个对称中心 C ．2π3ϕ= D ．函数()f x 在区间4ππ,5⎡⎤--⎢⎥⎣⎦上是减函数。

5.4 三角函数的图象和性质1. 用“五点法”作三角函数的图象；2. 利用图象变换作三角函数的图象；3. 利用正、余弦函数的图象解三角不等式；4. 利用正弦函数、余弦函数图象判断方程根的个数；5. 求三角函数的周期；6. 三角函数奇偶性的判断；7. 三角函数奇偶性与周期性的综合运用；8. 求三角函数的单调区间；9. 三角函数对称轴、对称中心；10. 与三角函数有关的函数的值域(或最值)的求解问题；11. 求定义域；12.三角函数的图像和性质的综合应用.一、单选题1．（浙北四校2021届高三12月模拟）若函数f (x )=2x ，x ∈R ，则f (x )是（ ）A ． 最小正周期为π为奇函数B ． 最小正周期为π为偶函数C ． 最小正周期为π2为奇函数 D ． 最小正周期为π2为偶函数【答案】A 【解析】∵+2x =-sin2x ，∴f（x ）=-sin2x ，可得f （x ）是奇函数，最小正周期T=2π2=π故选：A ．2．（2021·永州市第四中学高一月考）函数1sin y x =-，[]0,2x p Î的大致图像是（ ）A ．B ．C ．D ．【答案】B 【解析】当0x =时，1y =；当2x p=时，0y =；当πx =时，1y =；当3π2x =时，2y =；当2x p =时，1y =.结合正弦函数的图像可知B 正确.故选B.3．（2021·全国高三课时练习（理））已知函数，则()f x 在[]0,2p 上的零点的个数为（ ）A ．1B ．2C ．3D ．4【答案】C 【解析】由下图可得()f x 在[]0,2p 上的零点的个数为3，故选C.4．（2021·河南濮阳·高一期末（文））下列函数中，为偶函数的是（ ）A ．()21y x =+B ．2xy -=C ．sin y x =D ．()()lg 1lg 1y x x =++-【答案】C 【解析】对于A,函数关于1x =-对称，函数为非奇非偶函数，故A 错误；对于B,函数为减函数，不具备对称性，不是偶函数，故B 错误；对于C,()()()sin sin sin f x x x x f x -=-==-=，则函数()f x 是偶函数，满足条件，故C 正确；对于D,由1010x x +>ìí->î得11x x >-ìí>î得1x >，函数的定义为()1,+¥，定义域关于原点不对称，为非奇非偶函数，故D 错误.故选：C.5．（2021·河南信阳·°的大小属于区间（A ．1,02æö-ç÷èøB ．æççèC ．10,2æöç÷èøD ．【答案】B 【解析】cos 2020cos(5360220)cos 220cos(18040)cos 40°=´°+°=°=°+°=-°，因为cos y x =在(0,90)°上递减，且304045°<°<°，所以cos30cos 40cos 45°>°>°，cos 40>°>所以cos 40<-°<所以cos 2020<°<故选：B6．（2021·辽宁大连·高一期末）函数()cos 26f x x p æö=+ç÷èø的图像的一条对称轴方程为（）A ．6x p=B ．512x p =C ．23x p =D ．23x p =-【答案】B 【解析】函数()cos 26f x x p æö=+ç÷èø令()26x k k pp +=ÎZ ，则,212k x k p p=-ÎZ ，当1k =时，512x p =，故选B.7．（2021·海南枫叶国际学校高一期中）函数()f x =cos()x w j +的部分图像如图所示，则()f x 的单调递减区间为（ ）A ．13(,44k k k Z p p -+ÎB ．13(2,2),44k k k Z p p -+ÎC ．13(,),44k k k Z-+ÎD ．13(2,244k k k Z-+Î【答案】D 【解析】由五点作图知，1+42{53+42pw j p w j ==，解得=w p ，=4p j ，所以()cos()4f x x p p =+，令22,4k x k k Z pp p p p <+<+Î，解得124k -＜x ＜324k +，k Z Î，故单调减区间为（124k -，324k +），k Z Î，故选D.8．（2021·河南林州一中高一月考）函数()21sin 1xf x x eæö=-ç÷+èø的图象的大致形状是（ ）A ．B ．C ．D ．【答案】A【解析】()211sin sin 11x xxe f x x x ee æö-æö=-=ç÷ç÷++èøèø故()()f x f x -=则()f x 是偶函数，排除C 、D ，又当()0,0x f x ®> 故选：A.9．（2021·山东聊城·高一期末）用五点法作函数()sin 0,0,2y A x A p w j w j æö=+>><ç÷èø的图象时，得到如下表格：x6p 23p x w j+02pp32p 2py4-4则A ，w ，j 的值分别为（ ）A ．4，2，3p-B ．4，12，3p C ．4，2，6pD ．4，12，6p -【答案】A 【解析】由表中的最大值为4，最小值为4-，可得4A =，由21362T p p -=，则T p =，22p w p\==，4sin(2)y x j =+Q ，图象过(6p，0)，04sin(2)6p j \=´+，\226k pj p ´+=，()k ÎZ ，解得23k pj p =-，||2pj <Q ，\当0k =时，3pj =-．故选：A ．10．（2021·镇原中学高一期末）若点,26P p æö-ç÷èø是函数()()sin 0,2f x x m p w j w j æö=++><ç÷èø的图象的一个对称中心，且点P 到该图象的对称轴的距离的最小值为2p，则（ ）A ．()f x 的最小正周期是pB ．()f x 的值域为[]0,4C ．()f x 的初相3pj =D ．()f x 在4,23p p éùêúëû上单调递增【答案】D 【解析】由题意得()62k k Z m pw j p ì-+=Îïíï=î，且函数的最小正周期为422T p p =´=，故21T p w ==.代入()6k k Z p w j p -+=Î，得()6k k Z pj p =+Î，又2p j <，所以6π=j .所以()sin 26f x x p æö=++ç÷èø.故函数()f x 的值域为[]1,3，初相为6p.故A ，B ，C 不正确，当4[,2]3x p p Î时，313[,626x p p p +Î，而sin y x =在313[,26p p 上单调递增，所以()f x 在4,23p p éùêúëû上单调递增，故D 正确.故选：D.二、多选题11．（2021·陕西渭滨·高一期末）函数tan(2)6y x p=-的一个对称中心是（ ）A ．(,0)12pB ．2(,0)3pC ．(,0)6pD ．(,0)3p【答案】AD 【解析】因为tan()01266f p p p æö=-=ç÷èø；24tan()tan 3366f pp p p æö=-==ç÷èø；tan 66f p p æö==ç÷èø；当3x p =时， 2362p p p ´-=.所以(,0)12p 、(,0)3p 是函数tan(2)6y x p=-的对称中心.故选：AD12.（2021·浙江高三专题练习）下列函数中，是奇函数的是（ ）．A ．2sin y x x=B ．sin y x =，[0,2]x p ÎC ．sin y x =，[,]x p p Î-D ．cos y x x=【答案】ACD 【解析】对A ，由()2sin ==y f x x x ，定义域为R ，且()()()()22sin sin f x x x x x f x -=--=-=-，故函数2sin y x x =为奇函数，故A 正确对B ，由函数的定义域为[0,2]x p Î，故该函数为非奇非偶函数，故B 错对C ，()sin y gx x ==，定义域关于原点对称，且()()()sin sin -=-=-=-g x x x g x ，故C 正确对D ，()cos ==y m x x x 的定义域为R ，且()()()()cos cos -=--=-=-m x x x x x m x ，故该函数为奇函数，故D 正确故选：ACD13．（2021·湖南天心·长郡中学高三月考）下图是函数()sin()f x A x w j =+（其中0A >，0>w ，0||x j <<）的部分图象，下列结论正确的是（ ）A ．函数12y f x p æö=-ç÷èø的图象关于顶点对称B ．函数()f x 的图象关于点,012p æö-ç÷èø对称C ．函数()f x 在区间,34p p éù-êúëû上单调递增D ．方程()1f x =在区间23,1212p p éù-êúëû上的所有实根之和为83p 【答案】ABD 【解析】由已知，2A =，2543124T p p p=-=，因此T p =，∴22pw p==，所以()2sin(2)f x x j =+，过点2,23p æö-ç÷èø，因此43232k p pj p +=+，k ÎZ ，又0||j p <<，所以6π=j ，∴()2sin 26f x x p æö=+ç÷èø，对A ，2sin 212y f x x p æö=-=ç÷èø图象关于原点对称，故A 正确；对B ，当12x p=-时，012f p æö-=ç÷èø，故B 正确；对C ，由222262k x k pppp p -£+£+，有36k x k ppp p -££+，k ÎZ 故C 不正确；对D ，当231212x pp -££时，2[0,4]6x pp +Î，所以1y =与函数()y f x =有4个交点令横坐标为1x ，2x ，3x ，4x ，12317822663x x x x p p p+++=´+´=，故D 正确.故选：ABD.14．（2021·江苏海安高级中学高二期末）关于函数()sin cos f x x x =+()x R Î，如下结论中正确的是（ ）．A ．函数()f x 的周期是2pB ．函数()f x 的值域是éëC ．函数()f x 的图象关于直线x p =对称D ．函数()f x 在3,24p pæöç÷èø上递增【答案】ACD 【解析】A ．∵()sin cos f x x x =+，∴sin cos cos sin cos sin ()222f x x x x x x x f x p p p æöæöæö+=+++=+-=+=ç÷ç÷ç÷èøèøèø，∴()f x 是周期为2p的周期函数，A 正确，B ．当[0,]2x p Î时，()sin cos 4f x x x x p æö=+=+ç÷èø，此时3,444x p p p éù+Îêúëû，，∴()f x Î，又()f x 的周期是2p，∴x ÎR 时，()f x 值域是，B 错；C ．∵()()(2)sin 2cos 2sin cos sin cos ()f x x x x x x x f x p p p -=-+-=-+=+=，∴函数()f x 的图象关于直线x p =对称，C 正确；D ．由B 知[0,2x pÎ时，()4f x x p æö=+ç÷èø，当[0,]4x p Î时，[,]442x p p p +Î，()f x 单调递增，而()f x 是周期为2p的周期函数，因此()f x 在3,24p p æöç÷èø上的图象可以看作是在0,4p æöç÷èø上的图象向右平移2p 单位得到的，因此仍然递增．D 正确．故选：ACD ．三、填空题15．（2021·山东高一期末）函数tan 2xy =的定义域为_____．【答案】{}2,x x k k Z p p ¹+Î【解析】解不等式()22x k k Z pp ¹+Î，可得()2x k k Z p p ¹+Î，因此，函数tan2xy =的定义域为{}2,x x k k Z p p ¹+Î.故答案为：{}2,x x k k Z p p ¹+Î.16．（2021·河南林州一中高一月考）函数224sin 6cos 633y x x x pp æö=+--££ç÷èø的值域________．【答案】16,4éù-êúëû【解析】224sin 6cos 64(1cos )6cos 6y x x x x =+-=-+-22314cos 6cos 24(cos )44x x x =-+-=--+，233x p p -££Q ，1cos 12x \-££ ，故231164(cos )444x -£--+£，故答案为：16,4éù-êúëû17．（2021·全国高考题）关于函数f （x ）=1sin sin x x+有如下四个命题：①f（x ）的图像关于y 轴对称．②f（x ）的图像关于原点对称．③f（x ）的图像关于直线x=2p对称．④f（x ）的最小值为2．其中所有真命题的序号是__________．【答案】②③【解析】对于命题①，152622f p æö=+=ç÷èø，152622f p æö-=--=-ç÷èø，则66f f p p æöæö-¹ç÷ç÷èøèø，所以，函数()f x 的图象不关于y 轴对称，命题①错误；对于命题②，函数()f x 的定义域为{},x x k k Z p ¹Î，定义域关于原点对称，()()()()111sin sin sin sin sin sin f x x x x f x x x x æö-=-+=--=-+=-ç÷-èø，所以，函数()f x 的图象关于原点对称，命题②正确；对于命题③，11sin cos 22cos sin 2f x x x x x p p p æöæö-=-+=+ç÷ç÷æöèøèø-ç÷èøQ ，11sin cos 22cos sin 2f x x x x x p p p æöæö+=++=+ç÷ç÷æöèøèø+ç÷èø，则22f x f x p p æöæö-=+ç÷ç÷èøèø，所以，函数()f x 的图象关于直线2x p=对称，命题③正确；对于命题④，当0x p -<<时，sin 0x <，则()1sin 02sin f x x x=+<<，命题④错误.故答案为：②③.18．（2021·上海高一课时练习）函数42cos 133æö=+-ç÷èøx y p ，当x =_________时有最小值，最小值是___________.【答案】3,22k k Z pp +Î 3- 【解析】当4cos 133x p æö+=-ç÷èø时，即4233x k p p p +=+，可得3,22x k k Z pp =+Î，此时y 取得最小值；此时，最小值为3-；故答案为：3,22k k Z pp +Î； 3-.19．（2021·浙江高一课时练习）设函数()sin f x A B x =+，当0B <时，()f x 的最大值是32，最小值是12-，则A =_____，B =_____.【答案】121- 【解析】根据题意，得3212A B A B ì-=ïïíï+=-ïî，解得1,12A B ==-.故答案为：1,12-20．（2021·上海高一课时练习）函数sin 2sin =+xy x的最大值是________，最小值是________.【答案】131- 【解析】Q 21si 2sin 2sin n x y x x -==++，Q 221sin 11sin 232sin 23x x x -££Þ£+£Þ-£-£-+，\2111sin 23x -£-£+，\函数sin 2sin =+xy x 的最大值是13；最小值是1-.故答案为：13;1-.21．（2021·上海高一课时练习）若函数2()cos sin (0)=-+>f x x a x b a 的最大值为0，最小值为4-，则实数a =_________，b =________.【答案】2 2- 【解析】Q 2sin si )n (1x f a x b x =--++，令sin (11)t x t =-££，则21(11)y t at b t --++££=-，函数的对称轴为2a t =-，当12a-£-，即2a ³时，110,2,114,2,a b a a b b -+++==ììÞíí--++=-=-îî当102a -<-<，即02a <<时，2((1022a aa b ---×-++=且114a b --++=-，此时方程组无解；\2,2,a b =ìí=-î故答案为：2,2-.五、解答题22．（2021·全国高一课时练习）求下列函数的定义域.（1）y =（2）sin cos tan x xy x+=.【答案】（1）{|22,}x k x k k Z p p p ££+Î；（2）|,2k x x k Z p ìü¹Îíýîþ【解析】（1）要使函数有意义，必须使sin 0x ³.由正弦的定义知，sin 0x ³就是角x 的终边与单位圆的交点的纵坐标是非负数.∴角x 的终边应在x 轴或其上方区域，∴22,k x k k Z p p p ££+Î.∴函数y ={|22,}x k x k k Z p p p ££+Î.（2）要使函数有意义，必须使tan x 有意义，且tan 0x ¹.∴,()2x k k Z x k p p pì¹+ïÎíï¹î∴,2kx k Z p ¹Î.∴函数sin cos tan x x y x +=的定义域为|,2k x x k Z p ìü¹Îíýîþ.23.（2021·涡阳县第九中学高一月考）已知函数()()2sin (0,0)f x x w j w j p =+><<最小正周期为p，图象过点4p æçè.（1）求函数()f x 解析式（2）求函数()f x 的单调递增区间.【答案】（1）()2sin(2)4f x x p=+；（2）()3,88k k k Z p p p p éù-++Îêúëû.【解析】（1）由已知得2pp =w，解得2w =.将点4p æçè2sin 24p j æö=´+ç÷èø，可知cos j =，由0j p <<可知4pj =，于是()2sin 24f x x p æö=+ç÷èø.（2）令()222242k x k k Z pppp p -+£+£+Î解得()388k x k k Z p pp p -+££+Î， 于是函数()f x 的单调递增区间为()3,88k k k Z p pp p éù-++Îêúëû.24．（2021·全国高三（文））(1)利用“五点法”画出函数1()sin()26f x y x p==+在长度为一个周期的闭区间的简图.列表:126x p +x y 作图:(2)并说明该函数图象可由sin (R)y x x =Î的图象经过怎么变换得到的.(3)求函数()f x 图象的对称轴方程.【答案】(1)见解析(2) 见解析(3) 22,3x k k Z pp =+Î.【解析】（1）先列表,后描点并画图126x p +02pp32p 2px3p-23p 53π83p 113p y 01-1；（2）把sin y x =的图象上所有的点向左平移6p个单位, 再把所得图象的点的横坐标伸长到原来的2倍（纵坐标不变）,得到1sin(26y x p=+的图象，即1sin(26y x p=+的图象；（3）由12,2,2623x kx x k k Z p p pp +=+=+Î，所以函数的对称轴方程是22,3x k k Z pp =+Î.25．（2021·全国高一课时练习）求函数πtan(3)3y x =-的定义域、值域，并判断它的奇偶性和单调性.【答案】定义域为5|,,318k x x x k p p ìüι+ÎíýîþR Z 且，值域为R ，非奇非偶函数，递增区间为5,()183183k k k p p p pæö-++Îç÷èøZ 【解析】tan y t =的定义域为|,2t t k k Z p p ìü¹+Îíýîþ，单调增区间为,,22k k k Z pp p p æö-+Îç÷èø.又tan 33y x p æö=-ç÷èø看成tan ,33y t t x p==-的复合函数，由2t k pp ¹+得5,318k x k Z p p¹+Î，所以所求函数的定义域为5|,318k x x k Z p p ìü¹+Îíýîþ，值域为R ；函数tan 33y x p æö=-ç÷èø的定义域不关于原点对称，因此该函数是非奇非偶函数；令3232k x k pppp p -<-<+，解得5,318318k k x k Z p p p p -<<+Î，即函数tan 33y x p æö=-ç÷èø的单调递增区间为5,,318318k k k Z p p p p æö-+Îç÷èø.26．（2021·陕西省汉中中学（理））已知函数()2sin(1(0)6f x x pw w =-->的周期是p .（1）求()f x 的单调递增区间；（2）求()f x 在[0,2p上的最值及其对应的x 的值.【答案】（1）(),63k k k Z p p p p éù-++Îêúëû；（2）当0x =时，()min 2f x =-；当3x p =时，()max 1f x =.【解析】（1）解：∵2T pp w==,∴2w =,又∵0>w ,∴2w =,∴()2sin 216f x x p æö=--ç÷èø,∵222262k x k pppp p -+£-£+,k Z Î,∴222233k x k p pp p -+££+,k Z Î,∴63k x k ppp p -+££+,k Z Î,∴()f x 的单调递增区间为(),63k k k Z p p p p éù-++Îêúëû（2）解：∵02x p££,∴02x ££p ,∴52666x ppp-£-£,∴1sin 2126x p æö-£-£ç÷èø,∴12sin 226x p æö-£-£ç÷èø,∴22sin 2116x p æö-£--£ç÷èø,当0x =时,()min 2f x =-,当226x ππ-=,即3x p=时,()max 1f x =27．（2021·镇原中学高一期末）已知函数()()()sin 0,0,f x A x A w j w j p =+>><，在一周期内，当12x p=时，y 取得最大值3，当712x p=时，y 取得最小值3-，求（1）函数的解析式；（2）求出函数()f x 的单调递增区间、对称轴方程、对称中心坐标；（3）当,1212x p p éùÎ-êúëû时，求函数()f x 的值域.【答案】（1）()3sin 23f x x p æö=+ç÷èø；（2）增区间为()5,1212k k k Z p p p p éù-+Îêúëû，对称轴方程为212k x p p =+，k Z Î，对称中心为,062k p p æö-+ç÷èø（k Z Î）；（3）3,32éùêúëû.【解析】(1)由题设知，3A =，周期7212122T p p p =-=，T p =，由2T p w =得2w =.所以()()3sin 2f x x j =+.又因为12x p=时，y 取得最大值3，即3sin 36j p æö+=ç÷èø，262k p p j p \+=+，解得23k p j p =+，又j p <，所以3pj =，所以()3sin 23f x x p æö=+ç÷èø.(2)由222232k x k pppp p -£+£+，得51212k x k p p p p -££+.所以函数()f x 的单调递增区间为()5,1212k k k Z p p p p éù-+Îêúëû.由232x k ppp +=+，k Z Î，得212k x p p=+，k Z Î.对称轴方程为212k x p p=+，k Z Î..由23x k pp +=，得62πkπx =-+（k Z Î）.所以，该函数的对称中心为,062k p p æö-+ç÷èø（k Z Î）.(3)因为,1212x p p éùÎ-êúëû，所以2,362x p p p éù+Îêúëû，则1sin 2,132x p æöéù+Îç÷êúèøëû，所以33sin 2323x p æö£+£ç÷èø.所以值域为：3,32éùêúëû.所以函数()f x 的值域为3,32éùêúëû.。