中南大学高等数学下册试题全解

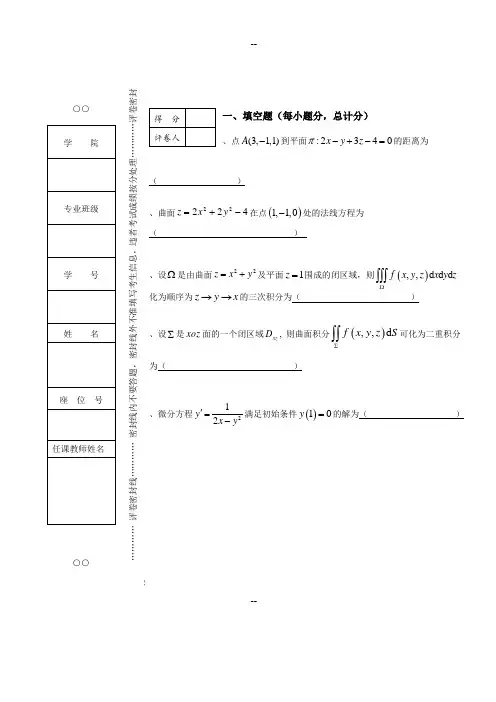
--○○○○………… 评卷密封线………… 密封线内不要答题，密封线外不准填写考生信息，违者考试成绩按分处理…………评卷密封线…………一、填空题（每小题分，总计分）、点(3,1,1)A -到平面:2340x y z π-+-=的距离为（ ）、曲面42222-+=y x z 在点()1,1,0-处的法线方程为（ ）、设Ω是由曲面22z x y =+及平面1z =围成的闭区域，则(),,d d d f x y z x y z Ω⎰⎰⎰化为顺序为z y x →→的三次积分为（ ）、设∑是xoz 面的一个闭区域xz D , 则曲面积分(),,d f x y z S ∑⎰⎰可化为二重积分为（ ）、微分方程212y x y'=-满足初始条件()10y =的解为（ ）--=1绕z 轴旋转而成的曲面为（ ）152=z ； （）154222=+-z y x ； 152=z ； （）()15422=+-z y x D 内具有二阶偏导数222222,,,f f f fx y x y y x∂∂∂∂∂∂∂∂∂∂，则（ ） 2fy x∂∂∂； （）则(,)f x y 在区域D 内必连续； D 内必可微； () 以上都不对 D 由2y x =及2y x =-所围成，则化为二次积分后的结果为I = ； （）⎰⎰-+2122y yxydx dy ；⎰⎰-+412xx xydy dx （）⎰⎰-+2122y yxydy dx2=介于点(0,2)到点(2,0)的一段，则=⎰( )（）; ; （）2. ()()()y p x y q x y f x '''++=的解， 则（）.（）12y y -也是方程的解（）122y y -也是方程的解三、（分）设平面∏:2450x y z---=,且直线0 :30x y blx ay z++=⎧⎨+--=⎩在平面∏上，求,a b的值.------…………评卷密封线………… 密封线内不要答题，密封线外不准填写考生信息，违者考试成绩按分处理…………评卷密封线…………四、（分）已知函数(,)f x y x y xy =++，曲线22:3C x y xy ++=，C 上的最大方向导数.----五、（分）计算由旋转抛物面226z x y =--及锥面z =所围成的立体的体积.六、求解下列各题（每题分，共分）{},1d d xy x y ，其中{}(,)02,02D x y x y =≤≤≤≤.sin )()y y dx x e dy +++，其中L 是从(1,0)A 沿y =到(1,0)B -的--七、（分）计算I xydydz yzdzdx xzdxdy ∑=++⎰⎰，其中∑是平面0,0,0,2x y z x y z ===++=所围空间区域整个边界曲面的外侧.--…………评卷密封线…………密封线内不要答题，密封线外不准填写考生信息，违者考试成绩按分处理…………评卷密封线…………具有二阶连续导数，(cos )xz f e y =满足2cos )x xy e ，若(0)0,(0)0f f '==， ()f u 的表达式．(),()3y x b z x a x b =-+=-+-，代入平面∏方5,2a b =-=-.--解法二：过直线l 的平面束方程设为3()0x ay z x y b λ+--+++= （或(3)0x y b x ay z λ++++--=），即(1)()30x a y z b λλλ+++--+= （或(1)(1)30x a y z b λλλλ+++-+-=）， 由题意知11241a λλ++-==--（或11241a λλλ++-==--）， 解得5,1a λ=-=，将5,1a λ=-=及平面∏上的点(1,2,5)-代入平面束方程，求得2b =-.四．解：最大方向导数即为梯度的模，(,)(1,1),(,)gradf x y y x gradf x y =++=令2222(,,)(1)(1)(3)F x y x y x y xy λλ=++++++-,由222(1)(2)02(1)(2)030x y F x x y F y y x x y xy λλ=+++=⎧⎪=+++=⎨⎪++-=⎩，解得1211,,,1112x x x x y y y y ===-=-⎧⎧⎧⎧⎨⎨⎨⎨==-=-=⎩⎩⎩⎩，比较：(1,1)gradf =(2,1)(1,2)3gradf gradf -=-=，(1,1)0gradf --=，所以(,)f x y 在曲线C 上的最大方向导数为.五．解法一： 26222032(6)3xyr rD V dv rdrd dz d r r rdr πθθπ-Ω===--=⎰⎰⎰⎰⎰⎰⎰⎰. 解法二：1226262120202832(6)833z zD D V V V dz dxdy dz dxdy z dz z dz πππππ=+=+=+-=+=⎰⎰⎰⎰⎰⎰⎰⎰.六．解： .123D D D I dxdy dxdy xydxdy =++⎰⎰⎰⎰⎰⎰--12221110221x xdx dy dx xydy =++⎰⎰⎰⎰19ln 24=+ .因为1P Q y x∂∂==∂∂，所以该曲线积分与路径无关， 选择积分路径从(1,0)A 沿x 轴到(1,0)B -，易得11(10)2I dx -=+=-⎰七．解法一：利用高斯公式，3222200()333 2.6xx yI xydydz yzdzdx xzdxdy y z x dvx zdv dx dy zdz dx ∑Ω---Ω=++=++-====⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰对称性（2）解法二：在平面0,0,0x y z ===上，积分值为，只需计算:2x y z '∑++=（取上侧）上的积分.因cos cos cos αβγ===(()dS I xydydz yzdzdx xzdxdy xy yz xz xy yz xz dxdy '''∑∑∑=++=++++⎰⎰⎰⎰⎰⎰[]22220(2)(2)()2xyxD xy y x y x x y dxdy dx x y xy x y dy -=+--+--=---++=⎰⎰⎰⎰.解法三：在平面0,0,0x y z ===上，积分值为，只需计算:2x y z '∑++=（取上侧）上的积分.2202(2)(2)3xyxD xzdxdy x x y dxdy xdx x y dy -'∑=--=--=⎰⎰⎰⎰⎰⎰.由被积函数和积分曲面关于积分变量的对称性，可得23xydydz yzdzdx xzdxdy '''∑∑∑===⎰⎰⎰⎰⎰⎰，所以，2323I =⋅=.--八．解：（）因为2222(cos )cos ,(cos )cos (cos )cos ,x x x x x x zzf e y e y f e y e y f e y e y x x∂∂''''==+∂∂ 2222(cos )sin ,(cos )sin (cos )cos ,x x x x x x zzf e y e y f e y e y f e y e y yy∂∂''''=-=-∂∂ 所以,已知条件22222(4cos )x x z zz e y e x y∂∂+=+∂∂化为22(cos )4(cos )cos x x x x xf e y e f e y e y e ''⎡⎤=+⎣⎦，所以函数()f u 满足方程()4()f u f u u ''=+.（）方程()4()f u f u u ''=+的特征方程为240r -=，得特征根1,22r =± 所以，其对应齐次方程的通解为2212()uu f u C eC e -=+，设非齐方程的特解为*y Au B =+，代入原方程，得1,04A B =-=得非齐方程的一个特解为*4uy =-，故方程的通解为 2212()u u f u C e C e -=+4u-，由(0)0,(0)0f f '==得1212012204C C C C +=⎧⎪⎨--=⎪⎩,得1211,1616C C ==-, 故221()(4)16u uf u e e u -=--．。

中南大学复习题及参考答案《高等数学》一、填空题1．函数1142-+-=x x y 的定义域是 . 解. ),2[]2,(∞+--∞Y 。

2．若函数52)1(2-+=+x x x f ，则=)(x f ．解. 62-x 3．________________sin lim =-∞→xxx x答案：1正确解法：101sin lim 1lim )sin 1(lim sin lim=-=-=-=-∞→∞→∞→∞→xxx x x x x x x x x4.已知22lim 222=--++→x x bax x x ，则=a _____, =b _____。

由所给极限存在知, 024=++b a , 得42--=a b , 又由23412lim 2lim 2222=+=+++=--++→→a x a x x x b ax x x x , 知8,2-==b a 5.已知∞=---→)1)((lim 0x a x b e x x ，则=a _____, =b _____。

∞=---→)1)((lim 0x a x b e x x Θ, 即01)1)((lim0=-=---→b abe x a x x x , 1,0≠=∴b a 6．函数⎪⎩⎪⎨⎧≥+<=0101sin)(x x x xx x f 的间断点是x = 。

解：由)(x f 是分段函数，0=x 是)(x f 的分段点，考虑函数在0=x 处的连续性。

因为 1)0(1)1(lim 01sinlim 00==+=+-→→f x xx x x所以函数)(x f 在0=x 处是间断的，又)(x f 在)0,(-∞和),0(+∞都是连续的，故函数)(x f 的间断点是0=x 。

7. 设()()()n x x x x y -⋅⋅--=Λ21, 则()=+1n y (1)!n + 8．2)(x x f =，则__________)1)((=+'x f f 。

1高等数学（下册）试题（含详细解答与点评）一、单项选择题（本大题共5小题，每小题3分，共15分） 1．在空间直角坐标系下，方程2x 2+3y 2=6表示的图形为（ ） A ．椭圆 B ．柱面 C ．旋转抛物面 D ．球面【答案】B【解析】考查了常见二次曲面的方程。

方程(,)0f x y =在空间表示母线平行于z 轴的柱面。

不难得到答案为B 。

注：一般来讲，关于x 、y 、z 的方程中不含哪一个字母，方程就表示母线平行于哪个轴的柱面。

2．极限021lim →→y x arcsin(x +y 2)=（ ）A ．6πB ．3π C ．2π D ．π【答案】A【解析】考查了二元函数极限的计算。

由于函数2arcsin()x y +在定义区域内是连续的，从而在点1,02⎛⎫⎪⎝⎭处是连续的，所以 221201limarcsin()arcsin(0)26x y x y π→→+=+=。

3．设积分区域22:y x Ω+≤R 2，0≤z ≤1，则三重积分⎰⎰⎰=+Ωdxdydz y x f )(22（ ）A ．⎰⎰⎰π200102)(Rdz r f drd θ B ．⎰⎰⎰π20012)(Rdz r f rdrd θC ．⎰⎰⎰+π20122)(Rrdz y x f drd θD ．⎰⎰⎰π12)(Rdz r f rdrd θ2【答案】B【解析】本题考查了在柱面坐标下二重积分的计算。

积分区域可表示为 :01,(,)z x y D Ω≤≤∈， 其中D 是上述区域在Oxy 平面上的投影，且 :0,02D r R θπ≤≤≤≤， 所以2122220()()()R ΩΩf xy dxdydz f r rdrd dz d rdr f r dz πθθ+==⎰⎰⎰⎰⎰⎰⎰⎰⎰。

4．以y =sin 3x 为特解的微分方程为（ ） A ．0=+''y y B ．0=-''y y C ．09=+''y y D ．09=-''y y【答案】C【解析】考查了微分方程的解与特解的概念。

2020年中南大学期末考试高 等 数 学 A （下）（满分：100分 考试时间：100分钟）一、选择题：1~5小题，每小题3分，共15分。

下列每题给出的四个选项中，只有一个选项是符合题目要求的。

请将答案填写在对应的括号内。

1．已知向量a 、b 的模分别为22a b ==，，且10a b +=，则a b ⨯=（ ） （A ）2（B ）（C （D ）12．设可微函数(),f x y 在()00,x y 处取得极小值，下列结论正确的是（ ） （A ）()00,0y f x y = （B ）()00,0y f x y < （C ）()00,0y f x y > （D ）()00,y f x y 不一定存在3．设(),f x y 在D 域()()22211x y ρ-+-≤上连续,则()21lim,Df x y d ρσπρ→⎰⎰=（ ）（A ）()0,0f （B ）()0,1f （C ）()1,1f （D ）0 4．设()f x 为连续函数。

()()1ttyF t dy f x dx =⎰⎰，则()'2F =（ ）（A ）2()2f （B ）()2f （C ）()2f - （D ）05．设非齐次线性微分方程()()'y R x y Q x +=有两个不同的解()()12y x y x 、，则该方程的通解为（ ）（A ）()()12C y x y x -⎡⎤⎣⎦ （B ）()()()212y x C y x y x ++⎡⎤⎣⎦ （C ）()()12C y x y x +⎡⎤⎣⎦ （D ）()()()112y x C y x y x +-⎡⎤⎣⎦ 二、填空题：6~10小题，每小题3分，共15分。

请将答案填写在对应的横线上。

6．已知直线L 的方程为1111x y z-==-，则将L 绕z 轴旋转一周得到的曲面∑的方 程_______________________________。

1.ห้องสมุดไป่ตู้.2习题二
题目：证明函数$f(x)=\begin{cases}x^2-1,\quad x<1\\3x+2,\quad x\geq1\end{cases}$在$x=1$处连续。
解析：要证明函数在$x=1$处连续，需要分别讨论左极限、右极限和函数值是否相等。首先计算左极限，即$$\lim_{x\to1^-}(x^2-1)=(1)^2-1=0$$。然后计算右极限，即$$\lim_{x\to1^+}(3x+2)=3(1)+2=5$$。最后计算$x=1$时的函数值，即$f(1)=3(1)+2=5$。由于左极限、右极限和函数值都相等，因此可以得出结论：函数$f(x)$在$x=1$处连续。
解析：要求函数的极值点，需要先求得函数的导数$f'(x)$。根据乘法法则和指数函数和三角函数求导法则，可以得到$f'(x)=2e^{2x}\sin x+e^{2x}\cos x$。然后，令$f'(x)=0$，解得$x=\frac{3\pi}{2}+k\pi$，其中$k$为整数。将这些解代入原函数$f(x)$，可以得到对应的极值点。
……
通过对高等数学下教材中习题的解析，我们可以更加深入地理解每个章节的内容和知识点。同时，这些答案的详细解析也有助于同学们发现自己在学习过程中的盲点和薄弱环节，从而进行有针对性的补充和提高。希望本文对同学们在学习高等数学下教材时有所帮助，让大家能够更好地掌握这门重要的学科。
总结
通过对高等数学下教材的答案进行详解，本文旨在提供同学们学习和理解教材内容的参考和指导。在学习过程中，同学们可以根据本文的解析，进一步掌握和巩固相关知识点，提升数学能力。当然，本文只是对部分习题进行了解析，同学们在学习过程中还需要充分理解教材中的其他内容，并进行适当的练习和实践。希望本文能够对同学们的学习有所帮助，让大家在高等数学下取得优秀的成绩！

高等数学2一．填空题(每小题3分，本大题满分30分)1．已知(1,2,3)a =，(3,2,1)b = ，则a b ⨯= (4,8,4)--.2．yOz 面上的抛物线21z y =-绕z 轴旋转一周所得曲面方程为221z x y =--.3．(,)(0,2)lim x y →=18. 4．对函数yz x =利用近似计算公式d z z ∆≈，则 2.02(1.04)≈ 1.08.5．曲线2211x ty t z t =⎧⎪=-⎨⎪=+⎩上点(2,3,5)处的切线方程为35244y z x ---==.6．将下列函数展开成(1)x -的幂级数：13x =-101(1)2n n n x ∞+=-∑，(13x -<<). 7．微分方程xy y e -'+=的通解为y =()x e x C -+.8．微分方程690y y y '''-+=的通解为y =312()xC C x e +.9．设2x f xy '=，2y f x '=，则(1,2)(0,0)f f -=2.10．已知L 为球面2222x y z R ++=被平面0x y z ++=所截得的圆周，则2d Ly s =⎰323R π.二．解答下列各题(每小题8分，本大题满分16分)1．已知(,)z f x y =是由方程2sin z z x y +=确定的隐函数，求z x ∂∂和22zx∂∂.解：令2(,,)sin F x y z z z x y =+-，则2x F xy =-，cos 1z F z =+， 2cos 1x z z F xyx F z ∂=-=∂+， 。

（5分）2222(cos 1)2(sin )(cos 1)x z y z xy z z x z ∂+-⋅-⋅=∂+ 22232(cos 1)4sin (cos 1)y z x y z z ++=+. 。

（8分） 2．求函数2(,)624ln f x y x y xy y =+--的极值.解：解方程组2204620x yf x y f x y '=-=⎧⎪⎨'=--=⎪⎩， 得驻点(1,1)，(2,2). 。

当 (0,0) 0时, f x (0,0) 0,
同理, f y (0,0) 0.
P74/2(2)
lim
f Ax By
0

x y ( x ) ( y )
2
lim
x y ( x , y )
0

lim
x 0 y 0
f l lim
( 0,0 )
f ( cos , sin ) f (0,0)
0

cos sin 2 2 lim sin[( cos ) ( sin ) ] 2 2 0 [( cos ) ( sin ) ]
cos sin 2 lim sin 0 2
cos 2 sin2
P80/7
(1) 0 xy x y
2 2
sin( x y )
2
2
xy 0 ( x 0, y 0)
lim
xy x2 y
x 0 y 0
2 2 sin( x y ) 0 f (0,0), 2
故f ( x , y )在(0,0)处连续.
P123/8 求u ln x ln y 3 ln z在球面x 2 y 2 z 2 5 R 2上的极大
值( x 0, y 0, z 0), 并证明当a 0, b 0, c 0时, 恒有
Solution.
abc 5 abc 27( ) 5
3
2 2 2 2
z dz u dz P ( y ) , y du y du 1
z z p( y ) p( x ) 0 x y

6、设 是一空间有界区域，其边界曲面
是由有限块分片光滑的曲面所组成，如果
函数 P( x, y, z) ， Q ( x, y, z) ， R(x, y, z) 在 上具有一阶连续偏导数， 则三重积分与
第二型曲面积分之间有关系式：
式称为
公式。
7、微分方程 y 6 y 9 y x2 6 x 9 的特解可设为 y*
dx dx
（ C） 方程 ( x 2 2xy 3) dx ( y2 3 x 2 y 2 ) dy 0 是全微分方程；
（ D） 方程 dy
1x
2y
是伯努利方程。
dx 2 x
7、已知曲线 y y(x) 经过原点， 且在原点处的切线与直线 2x y 6 0 平行，而 y(x)
满足微分方程 y 2 y 5 y 0 ，则曲线的方程为 y （
6
高等数学（下册）试卷（三）
一、填空题（每小题 3 分，共计 24 分）
1、设 u
yz et2 dt ， 则 u
。
xz
z
2、函数 f ( x, y) xy sin( x 2 y) 在点（ 0， 0）处沿 l (1,2) 的方向导数
f
l (0 ,0 ) =
。
3 、 设 为 曲 面 z 1 x2
y2 ,z
2a cos
r
4a 2
r 2 dr ；
0
（C） 8 2 d 0
2a cos
r
4a 2
r 2 dr ；
0
（D） 2 d
2
2 a cos
r
4a 2
0
r 2 dr 。
5、设有界闭区域 D 由分段光滑曲线 L 所围成， L 取正向，函数 P( x, y), Q ( x, y) 在 D

一. 单选题（共25题,共100分）1. 若在为（）. （4分）2. 设（4分）C.D.3. 的值为（）. （4分）4. 下列无穷积分中收敛的是()。

（4分）A.B.C.D.5. 下列函数中为偶函数的是（）（4分）A.B.C.D.6. 下列说法正确的是（）（4分）A.若可导B.若不连续C.若极限不存在D.若不可导7. 若内（）. （4分）A.B.C.D.8. （4分）D.9. 设函数（4分）B.C.D.E.11. 设函数（4分）A.B.C.D.12. 若（4分）A.B.C.D.13. 设（4分）A.B.C.D.14. 设则（）. （4分）A.B.C.D.15. 二重极限（4分）C.等于16. 函数在点处（）．（4分）17. 函数处（）（4分）18. （4分）19. 函数（4分）20. 若函数（4分）A.B.C.D.21. 下列函数中，（）不是基本初等函数．（4分）A.B.C.D.22. 函数的连续区间是（）（4分）A.B.C.D.8af41950-b1bc-single23. 设可导的（）（4分）4459256a-f13b-single24. 设记，则有（）. （4分）A.B.C.D.1fd6c4b4-ecd9-single25. 已知（4分）第二套一. 单选题（共25题,共100分）ab25448a-4896-single1. 设齐次线性方程组的系数矩阵记为A，若存在3阶非零矩阵B，使AB=0，则（）（4分）A.B.C.D.084201bf-ec80-single2. 设向量组不能由线性表示，则对于任意常数k必有（）（4分）A.线性无关B.线性相关C.线性无关D.线性相关557467a0-4af9-single3. 向量组线性相关的充分必要条件是() （4分）A.中含有零向量B.中有两个向量的对应分量成比例C.中每一个向量都可由其余个向量线性表示D.中至少有一个向量可由其余个向量线性表示fcd94325-e911-single4. 微分方程的通解为（）（4分）A.B.C.D.e063cd0e-b657-single5. A为3阶矩阵，（4分）A.B.2C.e8bc7257-565a-single6. 设线性方程组有唯一解，则相应的齐次方程组（）．（4分）d85d9502-509f-single7. 若的值为() （4分）7b5bb558-c1b2-single8. 设（4分）14f9b70c-b900-single9. 已知（4分）C.;D.-bdb4841d-7350-single10. M为n阶方阵，的一个特征值为(). （4分）设A、B均为n阶方阵，则必有（）. （4分）A.C.D.A是n阶正定矩阵的充分必要条件是（）. （4分）A.B.存在n阶矩阵C使094dae6c-371f-single13. 微分方程特解形式可设为（（4分）B.C.D.E.设A，B均为n阶矩阵，且AB=O，则必有（）（4分）A.B.C.D.26c1c271-3ae6-single15. 方程是（）（4分）A、B都是n阶方阵，且A与B有相同的特征值，则（）. （4分）A.D.f744a7dd-d0be-single17. ,则必有() （4分）A.B.C.D.0c63d9b9-2607-single18. 已知非齐次线性方程组是其导出组（4分）4a92f68a-ad91-single19. 二次型的矩阵表示为() （4分）A.B.C.D.5052f555-8f89-single20. 设级数（）. （4分）含s个向量的向量组线性无关的充要条件是() （4分）下列命题中正确的是（（4分）D.任何必然线性相关E.若只有才成立，且线性无关。

高等数学〔下册〕试卷〔一〕一、填空题〔每题3分，共计24分〕1、 z =)0()(log 22>+a y x a 的定义域为D=。

2、二重积分⎰⎰≤++1||||22)ln(y x dxdy y x 的符号为。

3、由曲线x y ln =及直线1+=+e y x ，1=y 所围图形的面积用二重积分表示为，其值为。

4、设曲线L 的参数方程表示为),()()(βαψϕ≤≤⎩⎨⎧==x t y t x 那么弧长元素=ds 。

5、设曲面∑为922=+y x 介于0=z 及3=z 间的局部的外侧，那么=++⎰⎰∑ds y x )122（ 。

6、微分方程xyx y dx dy tan +=的通解为。

7、方程04)4(=-y y 的通解为。

8、级数∑∞=+1)1(1n n n 的和为。

二、选择题〔每题2分，共计16分〕1、二元函数),(y x f z =在),(00y x 处可微的充分条件是〔 〕 〔A 〕),(y x f 在),(00y x 处连续；〔B 〕),(y x f x '，),(y x f y '在),(00y x 的某邻域存在；〔C 〕y y x f x y x f z y x ∆'-∆'-∆),(),(0000当0)()(22→∆+∆y x 时，是无穷小；〔D 〕0)()(),(),(lim2200000=∆+∆∆'-∆'-∆→∆→∆y x yy x f x y x f z y x y x 。

2、设),()(x y xf y x yf u +=其中f 具有二阶连续导数，那么2222yuy x u x ∂∂+∂∂等于〔 〕〔A 〕y x +；〔B 〕x ； (C)y ； (D)0 。

3、设Ω：,0,1222≥≤++z z y x 那么三重积分⎰⎰⎰Ω=zdV I 等于〔 〕〔A 〕4⎰⎰⎰202013cos sin ππϕϕϕθdr r d d ；〔B 〕⎰⎰⎰2012sin ππϕϕθdr r d d ；〔C 〕⎰⎰⎰ππϕϕϕθ202013cos sin dr r d d ；〔D 〕⎰⎰⎰ππϕϕϕθ2013cos sin dr r d d 。

n
.
1 3
1
23. 1
1 1 1
1 x 是关于 x 的一次多项式，则该多项式的一次项系数是 1
.
1
答案： 2;
3 1 x
24. f(x)= x
2 5是 x
次多项式，其一次项的系数是
。
1 4
解：由对角线法则知，f(x)为二次多项式，一次项系数为 4。 25. A、 B、 C 代表三事件， 事件 “A、 B、 C 至少有二个发生” 可表示为 AB+BC+AC 26. 事件 A、B 相互独立，且知 P A 0.2, P B 0.5 则 P A U B 解：∵A、B 相互独立， ∴P(AB)=P(A)P(B) ∴P(A∪B)=P(A)+P(B)–P(AB)=0.2+0.5–0.1=0.6 27. A，B 二个事件互不相容， P A 0.8, P B 0.1, 则 P A B . . .
故 2 x
当 x 2 时，幂级数成为数项级数 为 ( 2 , 2 ) .
1 1 1 1 19． y y 0 的满足初始条件 y1 , y 1 的特解为 y x . 12 4 12 2
2
3
20．微分方程 y 3 y 0 的通解为 y c1 c2 e 3 x . 21．微分方程 y 6 y 13 y 0 的通解为 y e 3 x c1 cos 2 x c2 sin 2 x . 22.设 n 阶方阵 A 满足|A|=3，则=| A A |= 答案： 1
2
）
2
2
B. x 2 ；
C. ( x 1) ； D. x 1 。
1 1 1 1 1 x 2 2 2 2 ( x ) 2 2 ，所以 f ( x ) ( x ) 2 2 2 x x x x x

中南大学高等数学答案[注意：以下内容仅为虚构，不是真实的答案]第一章：导数与微分1. 求下列函数的导数：(1) f(x) = 3x^2 - 2x + 1(2) g(x) = sin(2x) + cos(x)第二章：积分1. 求下列函数的不定积分：(1) F(x) = 2x + 3(2) G(x) = e^x / x^2第三章：微分方程1. 解下列微分方程：(1) dy / dx + y = 3e^x(2) d^2y / dx^2 + y = 0第四章：级数1. 判断下列级数的敛散性：(1) ∑(n=1 to ∞) (1 / n)(2) ∑(n=1 to ∞) (1 / n^2)第五章：空间解析几何1. 求下列平面和直线的交点：(1) 平面: 2x + y + z = 5直线: x = 1, y = 2 - t, z = t(2) 平面: x - y + z = 3直线: x = 2t, y = -t, z = 4t第六章：多元函数微分学1. 求下列函数的偏导数：(1) f(x, y) = x^2 + 2y^2 - 3xy(2) g(x, y, z) = sin(xy) + cos(yz) - e^z 第七章：多元函数积分学1. 求下列曲面的面积：(1) z = x^2 + y^2, 1 ≤ x ≤ 3, 0 ≤ y ≤ 2(2) z = e^(x^2 + y^2), x^2 + y^2 ≤ 1第八章：向量代数与空间解析几何1. 求下列向量的数量积与向量积：(1) a = (1, 2, 3), b = (4, 5, 6)(2) c = (2, 3, 4), d = (1, -2, 3)第九章：线性代数1. 求下列线性方程组的解：(1) 2x + y + z = 4x - y + 2z = 13x + 2y - z = 5(2) x + y - z = 02x - y + z = 63x + 4y + z = 2第十章：一元函数的级数展开1. 将下列函数展开成泰勒级数：(1) f(x) = sin(x), 在x = 0处展开(2) g(x) = e^x, 在x = 1处展开这是一个虚构的中南大学高等数学答案，仅供参考。

一、填空题1．设2)(xx a a x f -+=，则函数的图形关于 对称。

解：)(x f 的定义域为),(+∞-∞ ，且有)(222)()(x f a a a a a a x f xx x x x x =+=+=+=------即)(x f 是偶函数，故图形关于y 轴对称。

2．若⎩⎨⎧<≤+<<-=20102sin 2x x x x y ，则=)2(πy .解：412π+。

3． 极限 。

解：010sin lim 1sin lim )sin 1sin (lim sin 1sinlim00020=⨯=⋅==→→→→xx x x x x x x x x x x x x x 注意：01sin lim 0=→xx x （无穷小量乘以有界变量等于无穷小量）111sin lim 1sin 1lim sin lim000====→→→xx x x x x x x x ，其中xx x sin lim 0→=1是第一个重要极限。

4.已知22lim 222=--++→x x bax x x ，则=a _____, =b _____。

由所给极限存在知,024=++b a , 得42--=a b , 又由23412lim 2lim 2222=+=+++=--++→→a x a x x x b ax x x x , 知8,2-==b a 5.已知0→x 时，1)1(312-+ax 与1cos -x 是等价无穷小，则常数a =解. ()()().23,1321112lim 1cos 11lim3123222203120-=∴=-=⎥⎦⎤⎢⎣⎡++++-=--+→→a a ax ax x ax x ax x xlimsinsin x x x x→=0216.设)(22y z y z x ϕ=+，其中ϕ可微，则yz∂∂= 。

解2zz yy z ϕϕϕ'-∂='∂- 7.设2e yzu x =，其中),(y x z z =由0=+++xyz z y x 确定的隐函数，则=∂∂)1,0(xu 。

中南大学工程硕士“高等工程数学”考试试卷考试日期：20XX 年月日 时间110分钟注：解答全部写在答题纸上一、填空题(本题24分，每小题3分)（1）对方程32()2f x x x x =-+，写出其Newton 迭代公式【注意重根】，使得由迭代公式产生的序列{}n x 可以2阶收敛于方程的唯一正根*x ；（2）在[,]a b 上，设0)(=x f 与)(x x ϕ=等价，则当)(x ϕ满足，和时，由)(1k k x x ϕ=+（L ,2,1,0=k ）产生的序列{}k x 收敛于方程)(x x ϕ=的根；（3）用Doolittle 分解法求方程：123211413261225x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦则：L =，U =，解x =；（4）已知2114132,61225A x ⎡⎤⎡⎤⎢⎥⎢⎥=-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦， 则：A ∞=；1A =；1x =。

（5）已知)(x f y =在区间],[b a 上通过点(,),0,1,2,,i i x y i n =，则其三次样条插值函数)(x S 是满足，，；（6）设有线性回归模型1112122312322y y y βεββεββε=+⎧⎪=-+⎨⎪=++⎩，其中2~(0,)(1,2,3)i N i εσ=且相互独立，写出参数12,ββ的最小二乘估计。

（7）在多元线性回归建模过程中，需要考虑自变量的选择问题。

写出三种常用的自变量的选取方法。

（8）影响数学模型数值求解结果的误差有：，， 。

二、（本题8分）已知)(x f 的数据如表：试求三次Newton 插值多项式3()N x ，求(5)f 的近似值，并给出相应的误差估计式。

三、（本题10分）引入人工变量利用大M 法求解下面的线性规划（要求写出计算过程）：12121212max 34..240.510,Z x x s tx x x x x x =++≤-≥≥≥四、（本题8分）某厂生产甲、乙、丙三种产品，都分别经A,B 两道工序加工，A 工序在设备1A 或2A 上完成，B 工序在1B ，2B ，3B 三种设备上完成。

中南大学网络教育课程考试复习题及参考答案高等数学一、填空题：1.设2)(xxaa x f -+=，则函数的图形关于 对称。

2.若2sin x x y x x <<=+≤<⎧⎨⎩-20102，则=)2(πy .3.极限limsinsin x x x x→=021。

4.已知22lim222=--++→x x b ax x x ，则=a ,=b 。

5.已知0→x 时，1)1(312-+ax 与1cos -x 是等价无穷小，则常数a = 6.设)(22y z y z x ϕ=+，其中ϕ可微，则yz∂∂= 。

7.设2e yz u x =，其中),(y x z z =由0=+++xyz z y x 确定的隐函数，则=∂∂)1,0(xu 。

8.设ϕϕ,),()(1f y x y xy f xz ++=具有二阶连续导数，则=∂∂∂yx z 2。

9.函数y x xyxy y x f 22),(--=的可能极值点为 和 。

10.设||)1(sin ),(22xy x y x y x f -+=则'y f =(1,0) 。

11.=⎰xdx x 2sin 212.[0,]cos ,sin y x y x π==在区间上曲线之间所围图形的面积为 。

13.若21d e 0=⎰∞+-x kx，则k = 。

14.设Ｄ：221x y +≤ ，则由估值不等式得 ⎰⎰≤++≤Ddxdy y x )14(2215.设D 由22,,,y x y x y y ====212围成（0x ≥），则(),Df x y d σ⎰⎰在直角坐标系下的两种积分次序为 和 。

16.设D 为01,01y x x ≤≤-≤≤，则Dfdxdy ⎰⎰的极坐标形式的二次积分为 。

17.设级数∑∞=+121n pn收敛，则常数p 的最大取值范围是 。

18.=+-+-⎰1642)!3!2!11(dx xxxx 。

19.方程01122=-+-ydy xdx 的通解为 。

高等数学下册教材答案解析本文将对高等数学下册教材中一些重要且具有难度的题目进行答案解析，以帮助学生更好地掌握数学知识和解题技巧。

以下是几个题目的答案解析：1. 题目：求函数 f(x) = x^2 + 2x + 1 的最小值。

解析：首先，我们可以通过求导数的方法来求取函数的最小值。

对 f(x) 求一阶导数，得到 f'(x) = 2x + 2。

然后，令 f'(x) = 0，解得 x = -1。

将 x = -1 带入原函数 f(x)，得到f(-1) = 0。

因此，函数 f(x) 的最小值为 0，当 x = -1 时取得。

2. 题目：已知集合 A = {1, 2, 3, 4, 5}，集合 B = {3, 4, 5, 6, 7}，求 A 和 B 的交集和并集。

解析：集合的交集指的是两个集合中共有的元素，即A ∩ B。

根据给定的集合 A 和 B，可以得出A ∩ B = {3, 4, 5}。

集合的并集指的是两个集合中所有的元素，即 A ∪ B。

根据给定的集合 A 和 B，可以得出 A ∪ B = {1, 2, 3, 4, 5, 6, 7}。

3. 题目：已知函数 y = log(x)，求 y 的导函数和二阶导函数。

解析：函数 y = log(x) 的导函数可以通过对函数进行求导得到。

根据导数的定义，导函数为 y' = 1/x。

对导函数 y' = 1/x 再次求导，得到二阶导函数 y'' = -1/x^2。

4. 题目：已知二次曲线的一般方程为 y = ax^2 + bx + c，其中a ≠ 0。

求该二次曲线的顶点坐标。

解析：二次曲线的顶点坐标可以通过求导数的方法得到。

首先，对一般方程求导，得到 y' = 2ax + b。

将 y' = 0，解得 x = -b/(2a)。

将 x 带入一般方程，得到 y = a(-b/(2a))^2 + b(-b/(2a)) + c。

x一、填空题《高等数学(下册)》第八章练习题1.设z sin( x y)，则dz2.设z cos( x 2y), ，则(1, )23.函数z 6( x y) x 2y 2的极值点为4.设z e xy，则dz5.设x ln z ，则z y zx二、选择题1、、 f ( 、y) x 3y 3 3 x 2 3 y2、( )A. (2、2)B. (0、0)C. (2、0)D. (0 、2)2、f ( x, y) 在点(x,y)处偏导数f x( x0 , y0 )、的( ).f y( x0 , y0 ) 存在是f ( x, y) 在该点连续(a)充分条件，(b)必要条件，(c)充要条件，(d)既非充分条件又非必要条件。

3、设f ( x, y) ln( xy) ，则f2 x(1,1 、.（A） 1、3三、计算题y 2 x2（B） 1、3（C）5、6（D） 5 .6、、z x 3、( 、、1 、、2、设z z( x, y) 是由方程F ( x z, y z) 0 确定的隐函数，F 具有一阶连续偏导数，且F F 0, 其中u x z, v y z, 求z , z .u v x y3、求曲面x2y2xz z2 3 在点(1,2,1) 处的切平面及法线方程。

4、设u e x2y2z2,而z x2sin y,求u.x5、求曲线x e t, y e t, z t ,对应于t 0 点处的切线和法平面方程。

6、求函数z x 2y(4 x y) 在闭域x 0, y 0, x y 4 上的最大值及最小值。

xx z ，7、设z 2 cos 2 ( x1y ),求z 和z.2 x y8、设f ( x, y) e xy3 ，求f f x y9、求函数 f ( x, y) x 2xy y 2 3 x 的极大值或极小值10、设z11、设z f ( x, u, v), u 2 x y, v xy 求复合函数z 对x, y的全微分dz ycos( xy), 求z 和zx x y12、求曲面x 2yz 3 y 2 2 xz 28z 上点1,2,1)处的切平面和法线方程13 函数z z( x, y 由方程xz sin y求zyf ( x y, z y 所定，其中f 有连续的一阶偏导，四、综合应用题1.在平面xoy 上求一点M、、、，使它到三条直线x 、y 、x y 1 0 的距离平方和为最小，并求其最小值。