下载文档原格式
第八章 相关与回归分析一、填空题8.1.1 客观现象之间的数量联系可以归纳为两种不同的类型，一种是 ，另一种是 。
8.1.2 回归分析中对相互联系的两个或多个变量区分为 和 。
8.1.3 是指变量之间存在的严格确定的依存关系。
8.1.4 变量之间客观存在的非严格确定的依存关系，称为 。
8.1.5 按 的多少不同，相关关系可分为单相关、复相关和偏相关。
8.1.6 两个现象的相关，即一个变量对另一个变量的相关关系，称为 。
8.1.7 在某一现象与多个现象相关的场合，当假定其他变量不变时，其中两个变量的相关关系称为 。
8.1.8 按变量之间相关关系的 不同，可分为完全相关、不完全相关和不相关。
8.1.9 按相关关系的 不同可分为线性相关和非线性相关。
8.1.10 线性相关中按 可分为正相关和负相关。
8.1.11 研究一个变量与另一个变量或另一组变量之间相关方向和相关密切程度的统计分析方法，称为 。
8.1.12 当一个现象的数量由小变大，另一个现象的数量也相应由小变大，这种相关称为 。
8.1.13 当一个现象的数量由小变大，而另一个现象的数量相反地由大变小，这种相关称为 。
8.1.14 当两种现象之间的相关只是表面存在，实质上并没有内在的联系时，称之为 。
8.1.15根据相关关系的具体形态，选择一个合适的数学模型来近似地表达变量间平均变化关系的统计分析方法，称为 。
8.1.16 反映变量之间相关关系及关系密切程度的统计分析指标是 。
8.1.17 就是寻找参数01ββ和的估计值01ββ和，使因变量实际值与估计值的残差平方和达到最小。
8.1.18 正如标准差可以说明平均数代表性大小一样， 则可以说明回归线代表性的大小。
8.1.19 回归分析中的显著性检验包括两方面的内容，一是对 的显著性检验；二是对 的显著性检验。
8.1.20 对各回归系数的显著性检验，通常采用 ；对整个回归方程的显著性检验，通常采用 。
2015年《统计学》第八章相关与回归分析习题及满分答案一、单选题1.相关分析研究的是（ A ）A、变量间相互关系的密切程度B、变量之间因果关系C、变量之间严格的相依关系D、变量之间的线性关系2．若变量X的值增加时，变量Y的值也增加，那么变量X和变量Y之间存在着（A ）。
A、正相关关系B、负相关关系C、直线相关关系D、曲线相关关系3．若变量X的值增加时，变量Y的值随之下降，那么变量X和变量Y之间存在着（B）。
A、正相关关系B、负相关关系C、直线相关关系D、曲线相关关系4．相关系数等于零表明两变量（B）。
A.是严格的函数关系B.不存在相关关系C.不存在线性相关关系D.存在曲线线性相关关系5．相关关系的主要特征是（B）。
A、某一现象的标志与另外的标志之间的关系是不确定的B、某一现象的标志与另外的标志之间存在着一定的依存关系，但它们不是确定的关系C、某一现象的标志与另外的标志之间存在着严格的依存关系D、某一现象的标志与另外的标志之间存在着不确定的直线关系6．时间数列自身相关是指（ C ）。
A、两变量在不同时间上的依存关系B、两变量静态的依存关系C、一个变量随时间不同其前后期变量值之间的依存关系D、一个变量的数值与时间之间的依存关系7．如果变量X和变量Y之间的相关系数为负1，说明两个变量之间（D）。
A、不存在相关关系B、相关程度很低C、相关程度很高D、完全负相关8．若物价上涨，商品的需求量愈小，则物价与商品需求量之间（C）。
A、无相关B、存在正相关C、存在负相关D、无法判断是否相关9．相关分析对资料的要求是（A）。
A.两变量均为随机的B.两变量均不是随机的C、自变量是随机的，因变量不是随机的D、自变量不是随机的，因变量是随机的10．回归分析中简单回归是指（D）。
A.时间数列自身回归B.两个变量之间的回归C.变量之间的线性回归D.两个变量之间的线性回归11.已知某工厂甲产品产量和生产成本有直线关系，在这条直线上，当产量为10 00时，其生产成本为30000元，其中不随产量变化的成本为6000元，则成本总额对产量的回归方程为（ A ）A. y=6000+24xB. y=6+0.24xC. y=24000+6xD. y=24+6000x12.直线回归方程中，若回归系数为负，则（B） A.表明现象正相关B.表明现象负相关C.表明相关程度很弱D.不能说明相关方向和程度二、多项选择题1．下列属于相关关系的有（ABD ）。
第八章 相关与回归分析一、名词1、相关关系：是现象间确实存在的，但是不完全确定的，一种非严格的依存关系。
2、回归分析：是对具有相关关系的两个或两个以上变量之间数量变化的一般关系进行测定，确定一个相应的数学表达式，以便从一个已知量来推测另一个未知量，这种处理具有相关关系变量之间的统计方法。
3、相关系数：是测定变量之间相关密切程度和相关方向的代表性指标。
4、估计标准误差：就是回归分析的估计值与观测值（实际值）之间的平均误差大小的指标。
二、填空1.在自然界和社会现象中，现象之间的相互依存关系可以分为两种，一种是（函数关系），一种是（相关关系）。
2.相关关系按相关程度可分为（完全相关）、（不完全相关）和（不相关）；按相关性质可分为（正相关）和（负相关）；按相关形式可分为（直线相关）和（曲线相关）；按影响因素多少可分为（单相关）和（复相关）。
3.互为因果关系的两个变量x 和Y ，可编制两个回归方程，一个是（y 倚x 回归方程）回归方程；另一个是（x 倚y 回归方程）回归方程。
4.相关分析是（回归分析）的基础，回归分析是（相关分析）的继续。
5.在回归分析中，因变量是（随自变量而变化的量），自变量是（主动变化的量）。
6.建立一元直线回归方程的条件是：两个变量之间确实存在（相关关系），而且其（相关的密切程度）必须是显著的。
一元直线回归方程的基本形式为：（Yc ＝a+bx ）。
7.估计标准误可以说明回归方程的（代表性大小）；说明回归估计值的（准确程度）；说明两个变量x 和Y 之间关系的（密切程度）。
8.当相关系数(r)越大时，估计标准误差S Y 就（越小），这时相关密切程度就（越高），回归直线的代表性就（大）；当r 越小时，S Y 就（越大），这时相关密切程度就（越低），回归直线的代表性就（小）。
三、判断1.正相关是指两个变量之间的变化方向都是上升的趋势，而负相关是指两个变量之间的变化方向都是下降的趋势。
（×）2.负相关是指两个量之间的变化方向相反，即一个呈下降（上升）而另一个呈上升（下降）趋势。
第八章相关与回归分析一1. 进行相关分析，要求相关的两个变量（A. 都是随机的B.C. 一个是随机的，一个不是随机的D.2. 相关关系的主要特征是（A.B. 某一现象的标志与另一标志之间存在着一定的关系，但它们不是确定的关系C.D. 某一现象的标志与另一标志之间存在着函数关系3. 相关分析是研究（A. 变量之间的数量关系B.C.变量之间相互关系的密切程度D.4. 相关关系的取值范围是（A. r=0B. -1≤r≤0C. 0≤r≤1D. -1≤r≤15. 现象之间相互依存关系的程度越低，则相关系数（A. 越接近于0B. 越接近于-1C. 越接近于1D. 越接近于0.56. 当所有观察值都落在回归直线上，则x与y之间的相关系数（）。
A. r=0B. -1<r<1C. |r|=1D. 0<r<17. 在回归直线中，若b<0，则x与y之间的相关系数（A. r=0B. r=1C. 0<r<1D. -1<r<08. 在回归直线中，b表示（A. 当x增加一个单位，y增加a的数量B. 当y增加一个单位时，x增加bC. 当x增加一个单位时，y的平均增加量D. 当y增加一个单位时，x9. 当相关系数r=0时，表明（A. 现象之间完全无关B.C. 现象之间完全相关D.10. r值越接近于-1，表明两变量间（A. 没有相关关系B. 线性相关关系越弱C. 负相关关系越强D.11. 下列直线回归方程中，肯定错误的是（A. y=2+3x，r=0.88B. y=4+5x，r=0.55C. y=-10+5X，R=-0.90D. y=-100-0.9x，r=-0.8312. 正相关的特点是（A.B.C.D.13. 下列现象的相关密切程度高的是（A. 某商店的职工人数与商品销售额之间的相关系数为0.87B. 流通费用率与商业利润率之间的相关系数为-0.94C. 商品销售额与商业利润率之间的相关系数为0.51D. 商品销售额与流通费用率之间的相关系数为-0.8114. 计算估计标准误差的依据是（A. 因变量的数列B.C. 因变量的回归变差D.15. 两个变量间的相关关系称为（A. 单相关B. 复相关C. 无相关D.16. 从变量之间相关的方向看，可分为（A. 正相关与负相关B.C. 单相关与复相关D.17. 从变量之间相关的表现形式看，可分为（）。
第四章 统计描述【4.1】某企业生产铝合金钢，计划年产量40万吨，实际年产量45万吨；计划降低成本5%，实际降低成本8%；计划劳动生产率提高8%，实际提高10%。
试分别计算产量、成本、劳动生产率的计划完成程度。
【解】产量的计划完成程度=%5.112100%4045100%=⨯=⨯计划产量实际产量即产量超额完成12.5%。
成本的计划完成程=84%.96100%5%-18%-1100%-1-1≈⨯=⨯计划降低百分比实际降低百分比即成本超额完成3.16%。
劳动生产率计划完=85%.101100%8%110%1100%11≈⨯++=⨯++计划提高百分比实际提高百分比即劳动生产率超额完成1.85%。
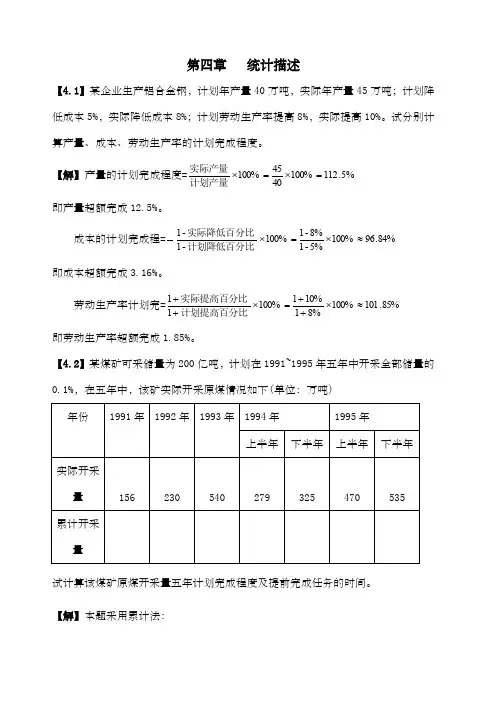
【4.2】某煤矿可采储量为200亿吨，计划在1991~1995年五年中开采全部储量的0.1%，在五年中，该矿实际开采原煤情况如下(单位：万吨)试计算该煤矿原煤开采量五年计划完成程度及提前完成任务的时间。
【解】本题采用累计法：（1）该煤矿原煤开采量五年计划完成=100%⨯数计划期间计划规定累计数计划期间实际完成累计 =75%.12610210253574=⨯⨯ 即：该煤矿原煤开采量的五年计划超额完成26.75%。
（2）将1991年的实际开采量一直加到1995年上半年的实际开采量，结果为2000万吨，此时恰好等于五年的计划开采量，所以可知，提前半年完成计划。
【4.3】我国1991年和1994年工业总产值资料如下表：要求：（1）计算我国1991年和1994年轻工业总产值占工业总产值的比重，填入表中； （2）1991年、1994年轻工业与重工业之间是什么比例（用系数表示）？ （3）假如工业总产值1994年计划比1991年增长45%，实际比计划多增长百分之几？ 【解】（1）（2）是比例相对数；1991年轻工业与重工业之间的比例=96.01.144479.13800≈；1994年轻工业与重工业之间的比例=73.04.296826.21670≈（3）%37.251%)451(2824851353≈-+即，94年实际比计划增长25.37%。
一．单项选择题1、用于测定两个变量之间密切程度的方法是〔 D 〕.A、定性判断B、相关表C、相关图D、相关系数2、产品产量与单位成本的相关系数是—0.95,单位成本与利润率的相关系数是0.90,产量与利润的相关系数是0.08,因此〔 C〕.A、产量与利润的相关程度最高B、单位成本与利润率的相关程度最高C、产量与单位成本的相关程度最高D、无法判断哪对变量的相关程度最高3、相关系数的取值X围是〔 D 〕.A、0≤r≤1B、-1≤r≤0C、r＞0D、-1≤r≤14、变量x与y之间的负相关是指〔C 〕.A、x值增大时y值也随之增大B、x值减少时y值也随之减少C、x值增大时y值随之减少,或x值减少时y值随之增大D、y的取值几乎不受x取值的影响5、两个变量之间的相关关系称为〔 B 〕.A、复相关B、单相关C、曲线相关D、直线相关6、、正方形的边长与周长的相关系数为〔 A 〕.A、1B、-1C、0D、无法计算7、在一元线性回归方程中,回归系数b的含义是< B >.A 、当x=0时,y 的平均值B 、当x 变动一个单位时,y 的平均变动数额C 、当x 变动一个单位时,y 增加的总数额D 、当y 变动一个单位时,x 的平均变动数额8、常用的求解一元线性回归方程的方法是< B >.A 、相关系数法B 、最小平方法C 、误差绝对值最小法D 、误差和最小法9、下列回归方程与相关系数的对应式中,错误的是〔 C 〕A 、89.0,5.2170ˆ-=-=r x yB 、94.0,8.35ˆ-=--=r x yC 、78.0,5.036ˆ-=+=r x yD 、98.0,9.25ˆ=+-=r x y 10、已知变量x 与y 线性相关,x 与y 的协方差为-60,x 的方差为64,y的方差为去100,则二者的相关系数的值为〔 B 〕.A 、0.75B 、-0.75C 、0.1D 、-0.111、已知变量x 与y 高度线性相关,x 与y 的协方差为-60,x 的方差为64,y 的方差为去100,则建立的y 依x 回归方程中的回归系数b的值为〔 B 〕.A 、0.94B 、-0.94C 、0.6D 、-0.612、若相关系数为正值,则回归系数的值〔 B 〕.A 、为负B 、为正C 、视a 的符号而定D 、不能确定13、回归估计标准误差是说明〔 C 〕的指标.A 、平均数代表性B 、现象之间相关程度C、回归直线代表性D、抽样误差平均程度14、已知变量x与y线性相关,x与y的协方差为-60,x的方差为100,y的方差为去64,建立了y依x的回归方程,则回归估计标准误差的值可能为〔 A 〕.A.-3.8B.0C.4.7D.8.915、进行回归分析,要求两个变量〔 C 〕.A、都是随机的B、都不是随机的C、一个是随机的,一个是给定的D、随机或不随机都可以二．多项选择题1.呈相关关系的各变量之间〔 A、B、D 〕A.一定存在严格的依存关系B.存在关系,但不确定C.存在着明显的因果关系D.存在着不固定的依存关系D.以上说法都不对2.直线积差相关系数可以表明两个变量之间的〔D、E 〕A.线性相关程度 B 因果关系 C.变异程度D.相关方向E.曲线相关密切程度3.可用来判断变量之间相关方向的指标有〔A、B〕A.相关系数B.回归系数C.回归方程参数D.估计标准误差E.x,y的平均数4.如果相关系数为0,则两变量〔 A、D 〕A.无直线相关B.呈负线性相关C.呈正线性相关D.可能存在曲线相关E.无线性相关,也无非线性相关5.回归系数和相关系数〔 A、C 〕A.一个为正值,另一个肯定也为正值B.一个为正值,另一个肯定为负值C.前者的取值X围为〔-∞,∞〕,后者的取值X围为〔-1,1〕D.前者的取值X围为〔-1,1〕,后者的取值X围为〔-∞,∞〕E.两者没有关系6.估计标准误差是反映〔 A、C、D 〕的指标.A.回归方程代表性B.自变量数列的离散程度C.因变量数列的离散程度D.因变量估计值的可靠程度E.因变量数列的集中程度7.相关系数的绝对值的大小〔 B、C〕A、和回归系数的绝对值呈反向关系B、和回归系数的绝对值呈正向关系C、和回归估计标准误差呈反向关系D、和回归估计标准误差呈正向关系E、和回归系数的绝对值没有关系8.若所有的观测点都落在回归直线上,则〔A、B、D〕A、相关系数可能为+1B、相关系数可能为-1C、两变量之间呈线性函数关系D、两变量之间呈完全相关关系E、相关系数可能为0.859.建立一元回归方程是为了〔 A 、B 〕A 、确定两个变量之间的数量关系B 、用自变量推算因变量C 、用于两个变量互相推算 D 、确定两个变量的相关程度E 、以上说法都对10.成本依产量回归方程bx a y+=ˆ中〔 A 、C 、D 〕 A 、x 代表产量 B 、y 代表产量 C 、b 叫作回归系数D 、b 代表x 增加一个单位时,y 平均增加b 个单位E 、b 代表y 增加一个单位时,x 平均增加b 个单位11.用最小平方法拟合的趋势线,必须满足〔 B 、D 〕A 、∑=-0)ˆ(yy B 、∑-)ˆ(y y 最小 C 、∑-)ˆ(y y 最大 D 、2)ˆ(∑-yy 最小 E 、2)ˆ(∑-y y 最大 三、判断题1.施肥量与收获率是正相关关系.〔 ×〕2.计算相关系数的两个变量都是随机变量.< × >3.当直线相关系数为0时,表明两个变量之间存在负相关关系.〔 ×〕4.若直线回归方程为ŷ=17+2.5X,则变量X 与Y 之间存在负相关关系.〔 ×〕5.计算相关系数是测定相关系数的唯一方法.〔×〕6.利用一个回归方程,两个变量可以互相推算.〔 ×〕7.回归估计标准误差指的就是实际值y 与估计值yˆ的平均误差程度.〔 √ 〕8.回归系数b 和相关系数r 都可以用来判断现象之间相关的密切程度.〔√〕9.在一元回归分析中,两个变量是对等的关系,不需要区分自变量和因变量.〔×〕10.回归估计标准误差的值越大,表明回归方程的代表性越低.〔√〕四、简答题1.相关关系与函数关系有何区别与联系？答：<1>区别：具有相关关系的变量之间的数量关系不确定,而具有函数关系的变量之间的数量关系是确定的.〔2〕__函数关系往往通过相关关系表现出来,相关关系也常常借助函数关系的方式进行研究.由于认识局限和测量误差等原因,确定性的函数关系在实际中往往表现为相关关系；反之,当人们对事物的内部规律了解得更深刻的时候,相关关系又可能转化为确定性的函数关系.2.简述相关关系的判别方法.答：〔1〕按现象相关的因素多少划分为单相关和负相关；〔2〕按现象之间的相关方向划分正相关与负相关；〔3〕按现象之间相关的形式划分为直线相关与曲线相关；〔4〕按现象之间相关的程度划分为不相关、完全相关和不完全相关.3.说明相关系数的取值X围与其判断标准.答：〔1〕相关系数的值在-1和+1之间,其绝对值越接近1,表示相关程度越高；〔2〕相关系数大于0,表示正相关；相关系数小于0,表示负相关. 〔3〕相关系数等于0,表示两个变量之间不存在直线相关,但并不表明两变量之间没有其他形式的相关关系.〔4〕|r| =1,表示存在完全直线相关；0<|r|<0.3,表示存在微弱直线相关；0.3≤|r|<0.5,表示存在低度直线相关；0.5≤|r|<0.8,表示存在显著直线相关；0.8≤|r|<1,表示存在高度直线相关.4.什么是估计标准误差？有什么作用？答：估计标准误差：是因变量的实际值与估计值得标准差,即以回归直线为中心反映各实际值与估计值之间的平均误差程度.作用：可以衡量回归方程的代表性大小.越小Sy,表明实际观测点与所拟合的回归线的离差越小,即回归线有较强的代表性；反之,其越大,表明实际观测点与所拟合的回归线的离差越大,即回归线的代表性较差.5．应用相关分析与回归分析应注意哪些问题？答：应用相关分析时,判断现象之间是否存在依存关系是相关分析的起始点.只有存在相互依存关系,才有必要和可能进行相关分析.应用回归分析时,回归分析是近似地表示变量间的平均变化关系.6.相关分析与回归分析有何区别？答：〔1〕相关分析不说明谁是自变量,谁是因变量；而回归分析必须首先要确定谁是自变量,谁是因变量,不能颠倒.〔2〕相关分析中每一个变量都是随机的；回归分析中的自变量是一般变量,因变量是随机变量.五、综合题1.在其他条件不变的情况下,某种商品的需求量〔y 〕与该商品的价格〔x 〕有关.现对给定时期内的价格与需求量进行观察,得到如下所示的一组数据：要求：（1） 计算价格与需求量之间的简单相关系数,并说明相关方向和程度；解：相关系数r==---∑∑∑∑∑∑∑2222)()(y y n x x n y x xy n 364816369680883692005677655640---=-0.854属于负相关;属于高度直线相关.（2） 拟合需求量对价格的回归直线,并解释回归系数的实际含义.解：设,bx a y +=^则,b=∑∑∑∑∑--22)(x x n yx xy n =883692005677655640--=121.3- a=---x b y=73.89=-∑∑n x b n y 则x y 121.373.89^-=该方程表明,该商品的价格每增加1元,商品的需求量就降3.121吨；该商品价格为0时,其固定的需求量为89.73吨.2.某地区家计调查资料显示,每户平均年收入为8800元,方差为4500元,每户平均年消费支出为6000元,均方差60元,支出对收入的回归系数为0.8.要求：（1） 计算相关系数；（2） 拟合支出对收入的回归方程.解：〔1〕设年收入为x,年消费支出为y,则,由题可知：设收入与消费支出之间的回归方程为： 则104088008.06000-=⨯-=-=x b y a所以,收入与消费支出之间的回归方程为： <2>回归系数b=0.8 =-x 8800,6000=-y .回归方程为 bx a y +=^ a=---x b y 可得a=1040即支出对收入的回归方程为x y 8.01040^+-= 3.下面是一个企业的广告费支出与销售额资料：单位：万元要求：〔1〕计算广告费支出与销售额间的相关系数；<2>若下月投资700万元的广告费,估计销售额的区间X 围是多少？设 用x y 分别表示广告费、销售额：由题意得;2500=∑x 25000=∑y由广告费与销售额可建立一元线性回归方程则 bx a y+=ˆ ∑∑∑∑∑--=x x n n b xy x y22)(2 =62500001450000525002500138000005-⨯⨯-⨯ =6.5 a=y - b x =5.652500525000⨯-=1750 y ˆ=1750+6.5x 当x=700时,yˆ=1750+6.5⨯700=6300〔万元〕 所以销售额的区间X 围是6300万元.4.检查五位学生"统计学原理〞的学习时间成绩如下所示：广告费 销售额 广告费 1 销售额 0.817265 1（1）计算学习时数与学习成绩之间的相关系数；解：学习时数和学习成绩之间的相关系数为：0.955779009 如图所示：（2）建立学习成绩〔y 〕与学习时间〔x 〕的直线回归方程；解：直线回归方程为：4.202.5ˆ+=x y 如图所示：（3）解释回归系数的含义； 660 750 1070 15 90解：回归系数是指X 每变化一个单位,y 的平均变化值本题是指学习成绩每增加一个小时,y 的平均变化值为5.2分.（4）计算回归估计标准误差.解：回归标准误差计算得： 6.53197264如图所示：5.根据某地区历年人均收入〔元〕与商品销售额〔万元〕资料计算的有关数据如下；〔x 代表人均收入,y 代表销售额〕n=9,546=∑x , 260=∑y , 343622=∑x ,16918=∑xy要求：建立以商品销售额为因变量的直线回归方程,并解释回归系数的含义.解：设=^y a+bx则,b=∑∑∑∑∑--22)(x x n y x xy n =2546343629260546169189-⨯⨯-⨯=1114210302=0.925 a=---x b y =nx b n y ∑∑- =228.279546925.09260-=⨯- 所以,=^y =-27.228+0.925x回归系数的含义：该方程表明人均收入每增加1元,商品销售额平均增加0.925万元.当人均收入为0时,商品销售额为-27.228万元.所有,翻版必究.。
