直线与椭圆位置关系学案及作业doc

第二课时 直线与椭圆的位置关系我们已经学习了直线与圆的位置关系的判断方法．[问题] 能否利用直线与圆的位置关系的判断方法(思想)，判断直线与椭圆的位置关系？知识点一 点与椭圆的位置关系点P (x 0，y 0)与椭圆x 2a 2＋y 2b2＝1(a >b >0)的位置关系：点P 在椭圆上⇔x 20a 2＋y 20b 2＝1；点P 在椭圆内部⇔x 20a 2＋y 20b 2<1；点P 在椭圆外部⇔x 20a 2＋y 20b2>1.知识点二 直线与椭圆的位置关系直线y ＝kx ＋m 与椭圆x 2a 2＋y 2b 2＝1(a >b >0)的位置关系，判断方法：联立⎩⎪⎨⎪⎧y ＝kx ＋m ，x 2a 2＋y 2b 2＝1，消y 得一元二次方程．当Δ>0时，方程有两解，直线与椭圆相交； 当Δ＝0时，方程有一解，直线与椭圆相切； 当Δ<0时，方程无解，直线与椭圆相离． 知识点三 直线与椭圆相交的弦长公式1．定义：连接椭圆上两个点的线段称为椭圆的弦． 2．求弦长的方法(1)交点法：将直线的方程与椭圆的方程联立，求出两交点的坐标，然后运用两点间的距离公式来求；(2)根与系数的关系法：如果直线的斜率为k ，被椭圆截得弦AB 两端点坐标分别为(x 1，y 1)，(x 2，y 2)，则弦长公式为：|AB |＝1＋k 2·（x 1＋x 2）2－4x 1x 2＝1＋1k2·（y 1＋y 2）2－4y 1y 2.1．已知点(2，3)在椭圆x 2m 2＋y 2n 2＝1上，则下列说法正确的是( )A ．点(－2，3)在椭圆外B ．点(3，2)在椭圆上C ．点(－2，－3)在椭圆内D ．点(2，－3)在椭圆上答案：D2．直线y ＝x ＋1被椭圆x 24＋y 22＝1所截得的弦的中点坐标是( )A.⎝⎛⎭⎫23，53B.⎝⎛⎭⎫43，73C.⎝⎛⎭⎫－23，13D.⎝⎛⎭⎫－132，172 答案：C3．设F 1，F 2分别是椭圆x 225＋y 216＝1的左、右焦点，P 为椭圆上一点，M 是F 1P 的中点，|OM |＝3，则点P 到椭圆左焦点的距离为________．答案：4直线与椭圆位置关系的判断 [例1] 已知直线l ：y ＝2x ＋m ，椭圆C ：x 24＋y 22＝1.试问当m 取何值时，直线l 与椭圆C ：(1)有两个不同的公共点？ (2)有且只有一个公共点？ (3)没有公共点？[解] 直线l 的方程与椭圆C 的方程联立，得方程组⎩⎪⎨⎪⎧y ＝2x ＋m ， ①x 24＋y 22＝1， ②将①代入②，整理得9x 2＋8mx ＋2m 2－4＝0，③关于x 的一元二次方程的判别式Δ＝(8m )2－4×9×(2m 2－4)＝－8m 2＋144. (1)由Δ>0，得－32<m <3 2.于是，当－32<m <32时，方程③有两个不同的实数根，可知原方程组有两组不同的实数解．这时直线l 与椭圆C 有两个不同的公共点．(2)由Δ＝0，得m ＝±3 2.也就是当m ＝±32时，方程③有两个相同的实数根，可知原方程组有两组相同的实数解．这时直线l 与椭圆C 有两个互相重合的公共点，即直线l 与椭圆C 有且只有一个公共点．(3)由Δ<0，得m <－32或m >3 2.从而当m <－32或m >32时，方程③没有实数根，可知原方程组没有实数解．这时直线l 与椭圆C 没有公共点．判断直线与椭圆的位置关系，通过解直线方程与椭圆方程组成的方程组，消去方程组中的一个变量，得到关于另一个变量的一元二次方程，通过Δ即可判断直线与椭圆的位置关系．[跟踪训练]在平面直角坐标系Oxy 中，经过点(0，2)且斜率为k 的直线l 与椭圆x 22＋y 2＝1有两个不同的交点P 和Q ，求k 的取值范围．解：由已知条件知直线l 的方程为y ＝kx ＋2， 代入椭圆方程得x 22＋(kx ＋2)2＝1，整理得⎝⎛⎭⎫12＋k 2x 2＋22kx ＋1＝0，直线l 与椭圆有两个不同的交点P 和Q 等价于Δ＝8k 2－4⎝⎛⎭⎫12＋k 2＝4k 2－2>0，解得k <－22或k >22， 所以k 的取值范围为⎛⎭⎫－∞，－22∪⎝⎛⎫22，＋∞.弦长及中点弦问题[例2] (链接教科书第114页练习2题)已知点P (4，2)是直线l 被椭圆x 236＋y 29＝1所截得的线段的中点，求直线l 的方程．[解] 法一(根与系数关系法)：由题意可设直线l 的方程为y －2＝k (x －4)， 而椭圆的方程可以化为x 2＋4y 2－36＝0. 将直线方程代入椭圆方程有(4k 2＋1)x 2－8k (4k －2)x ＋4(4k －2)2－36＝0. 所以x 1＋x 2＝8k （4k －2）4k 2＋1＝8，解得k ＝－12. 所以直线l 的方程为y －2＝－12(x －4)，即x ＋2y －8＝0.法二(点差法)：设直线l 与椭圆的交点为A (x 1，y 1)，B (x 2，y 2)，所以⎩⎪⎨⎪⎧x 21＋4y 21－36＝0，x 22＋4y 22－36＝0.两式相减，有(x 1＋x 2)(x 1－x 2)＋4(y 1＋y 2)·(y 1－y 2)＝0. 又x 1＋x 2＝8，y 1＋y 2＝4，所以y 1－y 2x 1－x 2＝－12，即k ＝－12.所以直线l 的方程为x ＋2y －8＝0.[母题探究](变设问)在本例条件下，求直线l 被椭圆截得的弦长．解：由题意可知直线l 的方程为x ＋2y －8＝0，与椭圆方程联立得x 2－8x ＋14＝0.法一：解方程得⎩⎪⎨⎪⎧x 1＝4＋2，y 1＝2－22， ⎩⎪⎨⎪⎧x 2＝4－2，y 2＝2＋22，所以直线l 被椭圆截得的弦长为 [（4＋2）－（4－2）]2＋⎣⎡⎦⎤⎝⎛⎭⎫2－22－⎝⎛⎭⎫2＋222＝10.法二：因为x 1＋x 2＝8，x 1x 2＝14. 所以直线l 被椭圆截得的弦长为 1＋⎝⎛⎭⎫－12282－4×14＝10.解决椭圆中点弦问题的两种方法(1)根与系数关系法：联立直线方程和椭圆方程构成方程组，消去一个未知数，利用一元二次方程根与系数的关系以及中点坐标公式解决；(2)点差法：利用交点在曲线上，坐标满足方程，将交点坐标分别代入椭圆方程，然后作差，构造出中点坐标和斜率的关系，具体如下：已知A (x 1，y 1)，B (x 2，y 2)是椭圆x 2a 2＋y 2b 2＝1(a >b >0)上的两个不同的点，M (x 0，y 0)是线段AB 的中点，则⎩⎨⎧x 21a 2＋y 21b2＝1， ①x 22a 2＋y22b 2＝1， ②由①－②，得1a 2(x 21－x 22)＋1b 2(y 21－y 22)＝0，变形得y 1－y 2x 1－x 2＝－b 2a 2·x 1＋x 2y 1＋y 2＝－b 2a 2·x 0y 0，即k AB ＝－b 2x 0a 2y 0. [跟踪训练]1．过点M (1，1)作斜率为－12的直线与椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)相交于A ，B 两点，若M 是线段AB 的中点，则椭圆C 的离心率等于________．解析：设A (x 1，y 1)，B (x 2，y 2)，则⎩⎨⎧x 21a 2＋y 21b2＝1，x 22a 2＋y 22b 2＝1，∴（x 1－x 2）（x 1＋x 2）a 2＋（y 1－y 2）（y 1＋y 2）b 2＝0，∴y 1－y 2x 1－x 2＝－b 2a 2·x 1＋x 2y 1＋y 2.∵y 1－y 2x 1－x 2＝－12，x 1＋x 2＝2，y 1＋y 2＝2，∴－b 2a 2＝－12，∴a 2＝2b 2.又∵b 2＝a 2－c 2，∴a 2＝2(a 2－c 2)， ∴a 2＝2c 2，∴c a ＝22.答案：222．椭圆x 2a 2＋y 2b 2＝1(a >b >0)的离心率为32，且椭圆与直线x ＋2y ＋8＝0相交于P ，Q ，且|PQ |＝10，求椭圆方程．解：∵e ＝32，∴b 2＝14a 2.∴椭圆方程为x 2＋4y 2＝a 2. 与x ＋2y ＋8＝0联立消去y ，得2x 2＋16x ＋64－a 2＝0，由Δ>0得a 2>32，由弦长公式得10＝54×[64－2(64－a 2)]．∴a 2＝36，b 2＝9.∴椭圆方程为x 236＋y 29＝1.椭圆的实际应用问题[例3] (链接教科书第113页例5)我国发射的第一颗人造地球卫星的运行轨道是以地心(地球的中心)F 2为一个焦点的椭圆．已知它的近地点A (离地面最近的点)距地面439 km ，远地点B (离地面最远的点)距地面2 384 km ，并且F 2，A ，B 在同一直线上，地球半径约为6 371 km ，求卫星运行的轨道方程(精确到1 km)．[解] 如图，建立平面直角坐标系，使点A ，B ，F 2在x 轴上，F 2为椭圆右焦点(记F 1为左焦点)，设椭圆的标准方程为x 2a 2＋y 2b 2＝1(a ＞b ＞0)，则a －c ＝|OA |－|OF 2|＝|F 2A |＝6 371＋439＝6 810， a ＋c ＝|OB |＋|OF 2|＝|F 2B |＝6 371＋2 384＝8 755， ∴a ＝7 782.5≈7 783， ∴b ＝a 2－c 2＝（a ＋c ）（a －c ）＝8 755×6 810≈7 721，∴卫星运行的轨道方程是x 27 7832＋y 27 7212＝1.解决椭圆的实际问题的基本步骤(1)认真审题，理顺题中的各种关系，如等量关系； (2)结合所给图形及题意建立适当的平面直角坐标系； (3)利用椭圆知识及其他相关知识求解．[跟踪训练]神舟五号飞船成功完成了第一次载人航天飞行，实现了中国人民的航天梦想．某段时间飞船在太空中运行的轨道是一个椭圆，地心为椭圆的一个焦点，如图所示．假设航天员到地球的最近距离为d 1，最远距离为d 2，地球的半径为R ，我们想象存在一个镜像地球，其中心在神舟飞船运行轨道的另外一个焦点上，上面住着一个神秘生物发射某种神秘信号，需要飞行中的航天员中转后地球人才能接收到，则传送神秘信号的最短距离为( )A ．d 1＋d 2＋RB ．d 2－d 1＋2RC ．d 2＋d 1－2RD ．d 1＋d 2解析：选D 设椭圆的方程为x 2a 2＋y 2b2＝1(a ＞b ＞0)，半焦距为c ，两焦点分别为F 1，F 2，飞行中的航天员为点P ，由已知可得⎩⎪⎨⎪⎧d 1＋R ＝a －c ，d 2＋R ＝a ＋c ，则2a ＝d 1＋d 2＋2R ，故传送神秘信号的最短距离为|PF 1|＋|PF 2|－2R ＝2a －2R ＝d 1＋d 2.1．已知直线l ：x ＋y －3＝0，椭圆x 24＋y 2＝1，则直线与椭圆的位置关系是( )A ．相离B ．相切C ．相交D ．相交或相切解析：选A 把x ＋y －3＝0代入x 24＋y 2＝1，得x 24＋(3－x )2＝1，即5x 2－24x ＋32＝0. ∵Δ＝(－24)2－4×5×32＝－64<0， ∴直线与椭圆相离．2．过椭圆x 2a 2＋y 2b 2＝1(a >b >0)的焦点F (c ，0)的弦中最短弦长是( )A.2b 2aB.2a 2bC.2c 2aD.2c 2b解析：选A 最短弦是过焦点F (c ，0)且与焦点所在坐标轴垂直的弦．将点(c ，y )的坐标代入椭圆x 2a 2＋y 2b 2＝1，得y ＝±b 2a ，故最短弦长是2b 2a.3．(多选)某颗人造地球卫星的运行轨道是以地球的中心F 为一个焦点的椭圆，如图所示，已知它的近地点A (离地面最近的点)距地面m 千米，远地点B (离地面最远的点)距地面n 千米，并且F ，A ，B 三点在同一直线上，地球半径约为R 千米，设该椭圆的长轴长、短轴长、焦距分别为2a ，2b ，2c ，则( )A ．a －c ＝m ＋RB ．a ＋c ＝n ＋RC ．2a ＝m ＋nD ．b ＝（m ＋R ）（n ＋R ）解析：选ABD ∵地球的中心是椭圆的一个焦点，并且根据图象可得⎩⎪⎨⎪⎧m ＝a －c －R ，n ＝a ＋c －R ，(*)∴a －c ＝m ＋R ，故A 正确； a ＋c ＝n ＋R ，故B 正确；(*)中两式相加m ＋n ＝2a －2R ，可得2a ＝m ＋n ＋2R ，故C 不正确；由(*)可得⎩⎪⎨⎪⎧m ＋R ＝a －c ，n ＋R ＝a ＋c ，两式相乘可得(m ＋R )(n ＋R )＝a 2－c 2.∵a 2－c 2＝b 2，∴b 2＝(m ＋R )(n ＋R )⇒b ＝（m ＋R ）（n ＋R ），故D 正确．4．已知F 是椭圆x 225＋y 29＝1的一个焦点，AB 为过椭圆中心的一条弦，则△ABF 面积的最大值为________．解析：S ＝12|OF |·|y 1－y 2|≤12|OF |·2b ＝12.答案：125．已知椭圆4x 2＋y 2＝1及直线y ＝x ＋m ，当直线与椭圆有公共点时，则实数m 的取值范围是________．解析：由⎩⎪⎨⎪⎧4x 2＋y 2＝1，y ＝x ＋m ，得5x 2＋2mx ＋m 2－1＝0，当直线与椭圆有公共点时，Δ＝4m 2－4×5(m 2－1)≥0， 即－4m 2＋5≥0，解得－52≤m ≤52. 答案：⎣⎡⎦⎤－52，52。

直线与椭圆的位置关系导学案一、引入本导学案旨在引导学生深入探究直线与椭圆的位置关系。

通过学习，学生将能够了解直线与椭圆之间的相交情况，并能够运用相关知识解决实际问题。

二、基础知识回顾在开始学习直线与椭圆的位置关系之前，我们先回顾一下相关的基础知识。

1. 直线的方程一条直线可以用方程y = mx + c来表示，其中m是直线的斜率，c是直线与y 轴交点的纵坐标。

2. 椭圆的方程一个标准椭圆的方程为((x - h) / a)^2 + ((y - k) / b)^2 = 1，其中(h, k)代表椭圆的中心坐标，a和b代表横轴和纵轴的半长轴。

三、直线与椭圆的位置关系当直线与椭圆相交时，可能存在以下几种情况：1. 直线与椭圆有两个交点当直线与椭圆有两个交点时，意味着直线与椭圆相交于两个不同的点。

这种情况下，直线穿过椭圆。

2. 直线与椭圆有一个交点当直线与椭圆有一个交点时，直线与椭圆相切。

此时，直线的斜率等于椭圆切线的斜率。

3. 直线与椭圆没有交点当直线与椭圆没有交点时，直线与椭圆相离。

四、求解直线与椭圆的位置关系1. 求解直线与椭圆的交点为了确定直线与椭圆的位置关系，我们需要求解直线与椭圆的交点坐标。

可以通过联立直线和椭圆的方程，解方程组来求解。

2. 判断直线与椭圆的位置关系通过求解方程组得到交点坐标后，可以根据交点的个数来判断直线与椭圆的位置关系。

若方程组有两个实数根，则直线与椭圆有两个交点，直线穿过椭圆。

若方程组有一个实数根，则直线与椭圆有一个交点，直线与椭圆相切。

若方程组无实数根，则直线与椭圆没有交点，直线与椭圆相离。

五、实例分析我们通过一个实例来进一步理解直线与椭圆的位置关系。

示例：求解直线y = 2x + 1和椭圆((x - 1) / 4)^2 + ((y - 2) / 3)^2 = 1的位置关系。

解：首先，我们将直线与椭圆的方程化为标准形式。

直线的方程已经是标准形式。

将椭圆的方程展开得到((x - 1) / 4)^2 + ((y - 2) / 3)^2 = 1，可以得出椭圆的中心坐标为(1, 2)，横轴的半长轴为4，纵轴的半长轴为3。

2。

2.2.2直线与椭圆的位置关系自主预习·探新知情景引入1．设椭圆的两焦点为点F1、F2，已知点P在椭圆上时,|PF1|＋｜PF2｜＝2a，那么点P在椭圆外时，设直线PF1交椭圆于Q，则|PF1｜＋|PF2|与｜QF1|＋|QF2｜的大小关系如何？2．直线与椭圆的位置关系，可否像讨论直线与圆的位置关系那样，将直线与椭圆的方程联立组成方程组，通过方程组的解的个数来讨论？新知导学1．点与椭圆的位置关系点P（x0,y0)与椭圆错误!＋错误!＝1(a〉b〉0)的位置关系：点P在椭圆上⇔__错误!＋错误!＝1__；点P在椭圆内部⇔__错误!＋错误!<1__；点P在椭圆外部⇔__错误!＋错误!>1__.2．直线与椭圆的位置关系直线y＝kx＋m与椭圆错误!＋错误!＝1（a>b>0）的位置关系判断方法:由错误!消去y(或x)得到一个一元二次方程。

位置关系解的个数Δ的取值相交两解Δ__>__0相切一解Δ__＝__0相离无解Δ__<__03．直线与椭圆相交弦长设直线斜率为k，直线与椭圆两交点为A(x1，y1）,B（x2,y2）,则|AB|＝错误!__｜x1－x2|__＝错误!__|y1－y2｜__，一般地，｜x1－x2｜＝错误!用根与系数关系求解.预习自测1．已知点（3,2）在椭圆错误!＋错误!＝1上，则（ C ）A．点（－3，－2）不在椭圆上B．点（3，－2）不在椭圆上C．点（－3，2）在椭圆上D．无法判断点（－3，－2），（3，－2），(－3,2）是否在椭圆上2．已知中心在原点的椭圆C的右焦点为F(错误!,0)，直线y＝x与椭圆的一个交点的横坐标为2，则椭圆方程为（ C ）A．x216＋y2＝1 B．x2＋y216＝1C．错误!＋错误!＝1 D．错误!＋错误!＝1［解析］由椭圆过点（2，2)，且焦点在x轴上,排除A、B、D，选C．3．直线l：x－2y＋2＝0过椭圆的左焦点F1和一个顶点B，则该椭圆的离心率为（ D )A．错误!B．错误!C．错误!D．错误!［解析] 令x＝0，得y＝1，令y＝0，得x＝－2，由题意知椭圆的半焦距c＝2，短半轴长b＝1，∴a＝错误!,∴离心率e＝错误!＝错误!。

直线与椭圆的位置关系学案直线与椭圆一、基础知识预备知识：直线、椭圆定义性质 预备技能：运算能力、转化能力1. 求解直线与圆锥曲线的位置关系的基本方法是解方程组，转化为利用判别式判断一元二次方程是否有解，应特别注意数形结合思想的应用.2. 注意根与系数的关系的应用. （1）弦长公式：斜率为k 的直线被圆锥曲线截得弦AB ，若A 、B 两点的坐标分别是()11,A x y ，()22,B x y则AB =12x =-==3. 有关中点弦问题.（1）已知直线与圆锥曲线方程，求弦的中点及与中点有关的问题，常用根与系数的关系. （2）有关弦的中点轨迹，中点弦所在直线方程，中点坐标问题，有时采用“点差法”可简化运算.4. 圆锥曲线中的有关最值问题，常用代数法和几何法解决.（1）若命题的条件和结论具有明显的几何意义，一般可用图形性质来解决.（2）若命题的条件和结论体现明确的函数关系式，则可建立目标函数（通常利用二次函数、三角函数、均值不等式等）求最值.二、重难点分析1．直线与椭圆位置关系的判断将直线的方程和椭圆的方程联立，通过讨论此方程组的实数解的组数来确定，即用消元后的关于x (或y )的一元二次方程的判断式Δ的符号来确定：当Δ>0时，直线和椭圆相交；当Δ＝0时，直线和椭圆相切；当Δ<0时，直线和椭圆相离．2．直线和椭圆相交的弦长公式 |AB |＝(1＋k 2)[(x 1＋x 2)2－4x 1x 2] 或|AB |＝⎝⎛⎭⎫1＋1k 2[(y 1＋y 2)2－4y 1y 2]. 3．直线与椭圆相交时的常见处理方法当直线与椭圆相交时：涉及弦长问题，常用“根与系数的关系”，设而不求计算弦长；涉及到求平行弦中点的轨迹、求过定点的弦中点的轨迹和求被定点平分的弦所在的直线方程问题，常用“点差法”设而不求，将动点的坐标、弦所在直线的斜率、弦的中点坐标联系起来，相互转化．三、考点突破考点1 点差法与中点弦例1 （1）椭圆221164x y +=的弦被点()2,1P 所平分，求此弦所在直线的方程.（2）已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)过点P (－1，－1)，c 为椭圆的半焦距，且c ＝2b .过点P 作两条互相垂直的直线l 1，l 2与椭圆C 分别交于另两点M ，N . (1)求椭圆C 的方程；(2)若直线l 1的斜率为－1，求△PMN 的面积； (3)若线段MN 的中点在x 轴上，求直线MN 的方程.考点2 直线与圆锥曲线的位置关系例2 在平面直角坐标系xOy 中，经过点(0且斜率为k 的直线l 与椭圆2212x y +=有两个不同的交点P 和Q ．求k 的取值范围.规律方法（1）解决直线与圆锥曲线的交点问题的方法：一是判别式法；二是几何法；（2）直线与圆锥曲线有唯一交点，不等价于直线与圆锥曲线相切，还有一种情况是平行于对称轴（抛物线）或平行于渐近线（双曲线）；（3）联立方程组、消元后得到一元二次方程，不但要对∆进行讨论，还要对二次项系数是否为0进行讨论.考点3 与弦长有关的问题例3 已知椭圆：1922=+y x ，过左焦点F 作倾斜角为π6的直线l 交椭圆于A 、B 两点，求弦AB 的长.例4 过点)0 ,3(-P 作直线l 与椭圆3x 2+4y 2=12相交于A 、B 两点，O 为坐标原点，求△OAB 面积的最大值及此时直线倾斜角的正切值.中，已知椭圆2222+by a x 率为22，且右焦点F 到左准线l 的距离为3. (1)求椭圆的标准方程；(2)过F 的直线与椭圆交于A ，B 两点，线段AB 的垂直平分线分别交直线l 和AB 于点P ，C ，若PC=2AB ，求直线AB 的方程.考点5 椭圆中的定点、定值问题例6 椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为32，过其右焦点F 与长轴垂直的弦长为1.(1)求椭圆C 的方程；(2)设椭圆C 的左、右顶点分别为A ，B ，点P 是直线x ＝1上的动点，直线P A 与椭圆的另一交点为M ，直线PB 与椭圆的另一交点为N .求证：直线MN 经过一定点.yxOABP例7.如图，在平面直角坐标系xOy 中，已知A ，B ，C 是椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)上不同的三点，A ⎝⎛⎭⎫32，322，B (－3，－3)，C 在第三象限，线段BC 的中点在直线OA 上.(1)求椭圆的标准方程； (2)求点C 的坐标；(3)设动点P 在椭圆上(异于点A ，B ，C )，且直线PB ，PC 分别交直线OA 于M ，N 两点，证明：OM →·ON →为定值，并求出该定值.探究提高 (1)求定值问题常见的方法有两种：①从特殊入手，求出定值，再证明这个值与变量无关.②直接推理、计算，并在计算推理的过程中消去变量，从而得到定值.(2)如果要解决的问题是一个定点问题，而题设条件又没有给出这个定点，那么，我们可以这样思考：由于这个定点对符合要求的一些特殊情况必然成立，那么我们根据特殊情况先找到这个定点，明确解决问题的目标，然后进行推理探究，这种先根据特殊情况确定定点，再进行一般性证明的方法就是由特殊到一般的方法.考点6 圆锥曲线中的最值、范围问题例8 已知圆为圆上一动点，点P 在AM 上，点N 在CM 上，且满足的轨迹为曲线E.（I ）求曲线E 的方程；（II ）若过定点F （0，2）的直线交曲线E 于不同的两点G 、H （点G 在点F 、H 之间），且满足，求的取值范围.M A y x C ),0,1(,8)1(:22定点=++N AM NP AP AM 点,0,2=⋅=FH FG λ=λ四、举一反三1.已知直线y =－x +1与椭圆22221(0)x y a b a b+=>>相交于A 、B 两点，且线段AB 的中点在直线l ：x －2y =0上，求此椭圆的离心率.2.已知椭圆C 的方程x y 22431+=，试确定m 的取值范围，使得对于直线4y x m =+，椭圆C 上有不同两点关于该直线对称.3.已知椭圆C ：)0(12222>>=+b a b y a x 的右焦点为F ，离心率22=e ，椭圆C 上的点到F的距离的最大值为12+，直线l 过点F 与椭圆C 交于不同的两点,.A B （1） 求椭圆C 的方程； （2） 若223||=AB ，求直线l 的方程.4.已知椭圆22221(0)x y a b a b+=>>，直线:l y kx m =+交椭圆于不同的两点A ，B .（Ⅰ）求椭圆的方程；（Ⅱ）若坐标原点O 到直线l 的距离为2，求AOB ∆面积的最大值.5.已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)过点P (－1，－1)，c 为椭圆的半焦距，且c ＝2b .过点P作两条互相垂直的直线l 1，l 2与椭圆C 分别交于另两点M ，N . (1)求椭圆C 的方程；(2)若直线l 1的斜率为－1，求△PMN 的面积； (3)若线段MN 的中点在x 轴上，求直线MN 的方程.6.已知椭圆C 的中心在坐标原点，焦点在x 轴上，椭圆C 上的点到焦点距离的最大值为3，最小值为1．（Ⅰ）求椭圆C 的标准方程；（Ⅱ）若直线:l y kx m =+与椭圆C 相交于A ，B 两点（A B ，不是左右顶点），且以AB 为直径的圆过椭圆C 的右顶点，求证：直线l 过定点，并求出该定点的坐标．7.已知，椭圆C 以过点A （1，），两个焦点为（－1，0）（1，0）. (1) 求椭圆C 的方程；(2) E ，F 是椭圆C 上的两个动点，如果直线AE 的斜率与AF 的斜率互为相反数，证明直线EF 的斜率为定值，并求出这个定值.课后作业321.椭圆221369x y +=的一条弦被()4,2A 平分，那么这条弦所在的直线方程是 .2.已知椭圆1222=+y x ，求过点⎪⎭⎫⎝⎛2121，P 且被P 平分的弦所在的直线方程．3.已知椭圆C 1：x 24＋y 2＝1，椭圆C 2以C 1的长轴为短轴，且与C 1有相同的离心率．(1)求椭圆C 2的方程；(2)设O 为坐标原点，点A ，B 分别在椭圆C 1和C 2上，OB ＝2OA ，求直线AB 的方程．4.如图，在平面直角坐标系xOy 中，椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的右焦点为F (1，0)，离心率为22.分别过O ，F 的两条弦AB ，CD 相交于点E (异于A ，C 两点)，且OE ＝EF . (1)求椭圆的方程；(2)求证：直线AC ，BD 的斜率之和为定值.能力提升5.已知,A B 是椭圆C :()222210x y a b a b+=>>的左，右顶点，B (2，0)，过椭圆C 的右焦点F 的直线交于其于点M ， N ， 交直线4x =于点P ，且直线PA ，PF ，PB 的斜率成等差数列． （Ⅰ）求椭圆C 的方程；（Ⅱ）若记,AMB ANB ∆∆的面积分别为12,S S 求12S S 的取值范围．6.已知椭圆的中点为坐标原点O ，椭圆短轴长为2，动点M (2，t )(t ＞0)在椭圆的准线上． (1)求椭圆的标准方程．(2)求以OM 为直径且被直线3x －4y －5＝0截得的弦长为2的圆的方程；(3)设点F 是椭圆的右焦点，过点F 作OM 的垂线FH ，且与以OM 为直径的圆交于点N ，求证：线段ON 的长为定值，并求出这个定值．x。

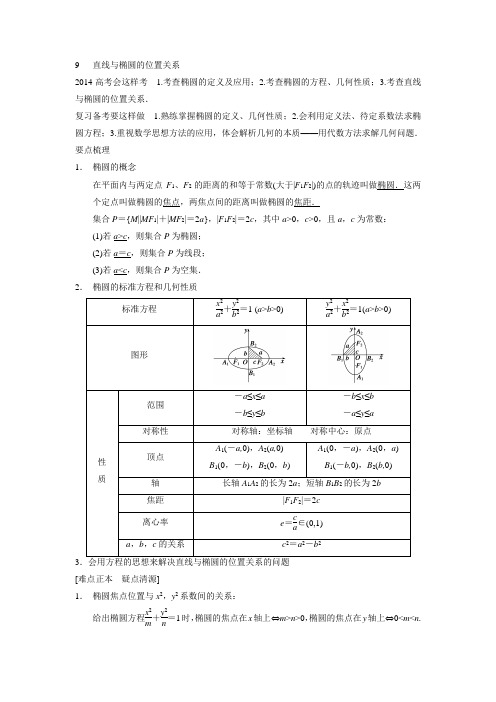
9 直线与椭圆的位置关系2014高考会这样考 1.考查椭圆的定义及应用；2.考查椭圆的方程、几何性质；3.考查直线与椭圆的位置关系．复习备考要这样做 1.熟练掌握椭圆的定义、几何性质；2.会利用定义法、待定系数法求椭圆方程；3.重视数学思想方法的应用，体会解析几何的本质——用代数方法求解几何问题． 要点梳理1． 椭圆的概念在平面内与两定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫做椭圆．这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距．集合P ＝{M ||MF 1|＋|MF 2|＝2a }，|F 1F 2|＝2c ，其中a >0，c >0，且a ，c 为常数：(1)若a >c ，则集合P 为椭圆；(2)若a ＝c ，则集合P 为线段；(3)若a <c ，则集合P 为空集．2． 椭圆的标准方程和几何性质3[难点正本 疑点清源]1． 椭圆焦点位置与x 2，y 2系数间的关系：给出椭圆方程x 2m ＋y 2n＝1时，椭圆的焦点在x 轴上⇔m >n >0，椭圆的焦点在y 轴上⇔0<m <n .2． 求椭圆离心率e 时，只要求出a ，b ，c 的一个齐次方程，再结合b 2＝a 2－c 2就可求得e(0<e <1)．3． 求椭圆方程时，常用待定系数法，但首先要判断是否为标准方程，判断的依据：①中心是否在原点；②对称轴是否为坐标轴．4．探究提高 (1)椭圆上一点与两焦点构成的三角形，称为椭圆的焦点三角形，与焦点三角形有关的计算或证明常利用正弦定理、余弦定理、|PF 1|＋|PF 2|＝2a ，得到a 、c 的关系．(2)对△F 1PF 2的处理方法⎩⎪⎨⎪⎧ 定义式的平方余弦定理面积公式⇔⎩⎪⎨⎪⎧PF 1|＋|PF 22＝a 24c 2＝|PF 1|2＋|PF 2|2－2|PF 1||PF 2|cos θS △＝12|PF 1||PF 2|sin θ.。

直线与椭圆的位置关系导学案The guiding plan of the position relation betw een straight line and ellipse直线与椭圆的位置关系导学案前言：小泰温馨提醒，数学是研究数量、结构、变化、空间以及信息等概念的一门学科，从某种角度看属于形式科学的一种，在人类历史发展和社会生活中，数学发挥着不可替代的作用，是学习和研究现代科学技术必不可少的基本工具。

本教案根据数学课程标准的要求和针对教学对象是高中生群体的特点，将教学诸要素有序安排，确定合适的教学方案的设想和计划、并以启迪发展学生智力为根本目的。

便于学习和使用，本文下载后内容可随意修改调整及打印。

（1）会判断直线与椭圆的位置关系,理解直线与椭圆相交所得的弦长公式;（2）通过求弦长具体实例，发现求弦长的一般规律，体验从特殊到一般的认识规律；（3）通过几何关系与代数运算的不断转化，感悟解析几何基本思想，培养学生逻辑推理能力和运算能力.教学重点：直线与椭圆的弦长公式探究教学难点：从特殊到一般规律的发现，“数”和“形”之间的相互转化.教学过程：教师：直线与圆有哪些位置关系？如何判断？学生：直线与圆的位置关系及其判定：几何方法：相离、相切、相交.代数方法：方程组无解相离、有唯一解相切、有两组解相交.教师：由于圆的特殊性，几何方法显得简单，而代数方法具有一般性.自然引出下面问题.类比直线和圆，直线与椭圆有哪些位置关系？（板书：：，e: ）学生：直线与椭圆有三种位置关系：相离、相切、相交.或直线与椭圆的公共点个数可能是零个、一个、两个.教师：当直线与椭圆没有公共点时，称直线与椭圆相离；当有一个公共点时，称直线与椭圆相切，这条直线叫椭圆的一条切线；当直线与椭圆有两个公共点时，称直线与椭圆相交.（板书：相离、相切、相交）板书课题：直线椭圆位置关系教师：请大家研究下面问题如何解决判断出直线与椭圆e：的位置关系是_______学生1：画图，直线与y的交点（0, 1）在椭圆内部，所以直线与椭圆相交.学生2：由（板书），得 ,，直线与椭圆相交.教师：（学生思考解答时，教师画出椭圆）学生1的方法简捷明了，使得我们对问题有了直观的认识，为什么多数同学没有这样解答呢？从“数形结合”是思考问题的首选。

直线和椭圆的位置关系一、知识点：1.直线和椭圆的位置关系（1）位置关系： _______、_______、________.（2）位置关系的判断（代数法）：已知直线:0l ax by c ++=，椭圆方程:(,)0M f x y =. 联立方程组0,(,)0,ax by c f x y ++=⎧⎨=⎩消元（消x 或y ），整理得20Ax Bx C ++=. ①当_________时，直线和椭圆M 相交，有两个不同的公共点；②当_________时，直线和椭圆M 相切，只有一个公共点；③当_________时，直线和椭圆M 相离，没有公共点.2.直线被椭圆所截弦长设直线l 与椭圆M 相交于11(,)A x y 、22(,)B x y ，则所得弦长AB =________ 二、例题与练习1.直线与椭圆的位置关系例.已知直线42:-=x y L 与椭圆112322=+y x 1)判断它们的位置关系；练习1：若直线m x y +=与椭圆1422=+y x相交，求m 的取值范围。

2．弦长问题例.已知直线42:-=x y L 与椭圆112322=+y x2)若相交于A 、B 两点，求弦AB 的长；练习2：已知斜率为1的直线过椭圆1422=+y x 的右焦点，交椭圆于A ，B 两点，求弦AB 的长．例.已知直线42:-=x y L 与椭圆112322=+y x3)若相交于A 、B 两点，O 为坐标原点，求ΔOAB 的面积。

三、课后巩固1．当m 为何值时，直线y=x+m 与椭圆1422=+y x 相交？相切？相离？2. 求直线x －y ＋1=0被椭圆141622=+y x 截得的弦长.3. 若直线y=x+m 被椭圆1422=+y x 所截得的线段长为258，求m 的值.4. 已知直线1:+=x y L 与椭圆12422=+y x 相交于P 、Q 两点，椭圆的右顶点为A ，求ΔAPQ 的面积.5.已知椭圆:C 22221(0)x y a b a b+=>>的离心率为21离心率,与过点A （0，1）且斜率为2的直线有且只有一个公共点，求椭圆方程.。

教学设计直线和椭圆的位置关系教学目标：1. 理解直线和椭圆的基本概念。

2. 掌握直线和椭圆的位置关系的判定方法。

3. 能够应用直线和椭圆的位置关系解决实际问题。

教学内容：第一章：直线和椭圆的基本概念1.1 直线的定义和性质1.2 椭圆的定义和性质第二章：直线和椭圆的位置关系的判定2.1 直线与椭圆相交的判定2.2 直线与椭圆相切的判定2.3 直线与椭圆相离的判定第三章：应用直线和椭圆的位置关系解决实际问题3.1 直线与椭圆的位置关系在几何中的应用3.2 直线与椭圆的位置关系在物理中的应用3.3 直线与椭圆的位置关系在计算机图形学中的应用第四章：直线和椭圆的位置关系的综合练习4.1 判断直线与椭圆的位置关系4.2 解决实际问题第五章：总结和复习5.1 直线和椭圆的位置关系的总结5.2 复习直线和椭圆的基本概念教学方法：1. 采用问题驱动的教学方法，引导学生通过探究和实践来理解和掌握直线和椭圆的位置关系。

2. 使用多媒体辅助教学，通过动画和图形来直观展示直线和椭圆的位置关系。

3. 提供丰富的练习题，让学生通过实践来巩固所学知识。

教学评估：1. 课堂参与度：观察学生在课堂上的积极参与程度和提问回答情况。

2. 练习题完成情况：检查学生完成练习题的正确性和解题思路。

3. 综合练习：评估学生在综合练习中的表现，包括判断直线与椭圆的位置关系和解决实际问题。

教学资源：1. 教学PPT：提供直线和椭圆的基本概念、位置关系判定和应用实例。

2. 练习题：提供丰富的练习题，包括判断题、选择题和解答题。

3. 综合练习：提供实际问题案例，让学生应用直线和椭圆的位置关系进行解决。

教学安排：1. 第一章：2课时2. 第二章：3课时3. 第三章：3课时4. 第四章：2课时5. 第五章：1课时六章：直线和椭圆的位置关系的深入探究6.1 直线与椭圆的交点个数的判定6.2 直线与椭圆的交点坐标的计算方法七章：直线和椭圆的位置关系的几何性质7.1 直线与椭圆的切线性质7.2 直线与椭圆的割线性质八章：直线和椭圆的位置关系在实际问题中的应用8.1 直线与椭圆的位置关系在工程中的应用8.2 直线与椭圆的位置关系在设计中的应用九章：直线和椭圆的位置关系的综合练习9.1 判断直线与椭圆的位置关系及交点个数9.2 解决实际问题十章：总结和复习10.1 直线和椭圆的位置关系的总结10.2 复习直线和椭圆的基本概念及位置关系的判定方法教学方法：1. 采用问题驱动的教学方法，引导学生通过探究和实践来理解和掌握直线和椭圆的位置关系。