二进制数的四则运算专题训练培训讲学

除1·0数＝…0…读…作…1“与10”01等) 于1 00 0 0 1 1 …………被除数
1 二与运进算也制叫乘逻辑法乘法、逻辑积。
二1进1 1制0 1减1 1法1
111
………………… 借位
1二0 进1 制 减 法
1 1 0 0 1 1 0 0 ………………… 被减数
— 0 0 1 0 0 1 0 1 ………………… 减数
❖ 1－0＝1 1·0＝1 0 读作1“与”0等于0
非例运：算 10又01称10逻10辑+0否0定11。1010=？，则加法过程如下：
01=011读作0的 “非”等于1
❖ 1－1＝0 逻二辑进变 制量乘之法间的的运运算算规称则为逻：辑运算。
1其0表1示方法是在逻辑变量上方加一横线。
❖ 0－1＝1有借位 然除后法把 是被乘除法数的的逆下运一算位。移到余数上。
❖ 1＋0＝1 读作1“或”0等于1
❖ 1＋1＝1 读作1“或”1等于1
例：
10101111
∨1 1 0 0 0 0 1 0
11101111
1.4 二进制数的运算
与运算
与运算也叫逻辑乘法、逻辑积。通常用符号
“·”、“∧”或“∩”表示。它的运算规则为：
❖ 0·0＝0 读作0“与”0等于0
❖ 0·1＝0 读作0“与”1等于0
1 0 1 0 0 1 1 1 …………………
1.4 二进制数的运算
二进制乘法
❖ 0×0＝0
❖ 0×1＝0
❖ 1×0＝0
❖ 1×1＝1
例：1101 × 1010=？，则乘法过程如下：
1 1 0 1 …………………被乘数
× 1 0 1 0 …………………乘数
0000

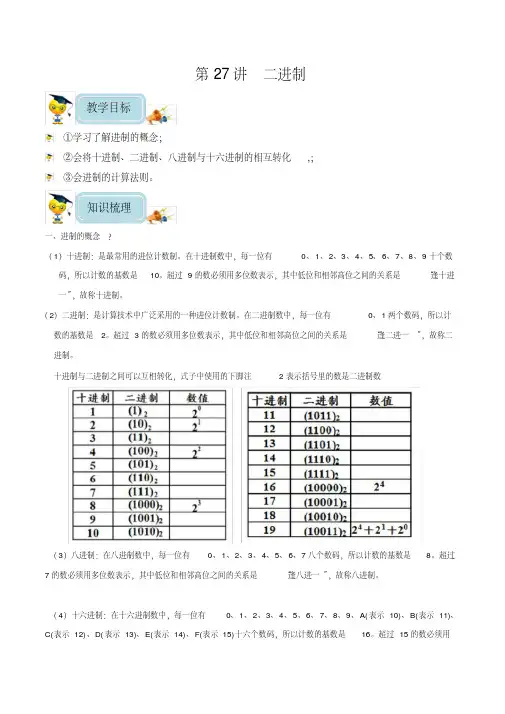
第27讲二进制教学目标①学习了解进制的概念；②会将十进制、二进制、八进制与十六进制的相互转化,；③会进制的计算法则。

知识梳理一、进制的概念？（1）十进制：是最常用的进位计数制。

在十进制数中，每一位有0、1、2、3、4、5、6、7、8、9十个数码，所以计数的基数是10。

超过9的数必须用多位数表示，其中低位和相邻高位之间的关系是“逢十进一”，故称十进制。

（2）二进制：是计算技术中广泛采用的一种进位计数制。

在二进制数中，每一位有0、1两个数码，所以计数的基数是2。

超过3的数必须用多位数表示，其中低位和相邻高位之间的关系是“逢二进一”，故称二进制。

十进制与二进制之间可以互相转化，式子中使用的下脚注2表示括号里的数是二进制数（3）八进制：在八进制数中，每一位有0、1、2、3、4、5、6、7八个数码，所以计数的基数是8。

超过7的数必须用多位数表示，其中低位和相邻高位之间的关系是“逢八进一”，故称八进制。

（4）十六进制：在十六进制数中，每一位有0、1、2、3、4、5、6、7、8、9、A(表示10)、B(表示11)、C(表示12)、D(表示13)、E(表示14)、F(表示15)十六个数码，所以计数的基数是16。

超过15的数必须用多位数表示，其中低位和相邻高位之间的关系是“逢十六进一”，故称十六进制。

二、十进制与n 进制的转化1、将十进制数转换为等值的n 进制数(n ≥2)时，整数部分采用“除n 倒取余数法”。

例如：整数10107转换成二进制采用“除2倒取余数法”，得10210711010112、将n 进制数(n ≥2)转换为等值的十进制数时，只要将n 进制数展开，然后将所有各项的数值按十进制数相加，就可以得到等值的十进制数了。

例如：21810101231828183，式子中使用的下脚注8表示括号里的数是八进制数。

21161010011160161512831B F，式子中使用的下脚注16表示括号里的数是十六进制数。

1.2.1 二进制数的运算方法电子计算机具有强大的运算能力，它可以进行两种运算：算术运算和逻辑运算。

1．二进制数的算术运算二进制数的算术运算包括：加、减、乘、除四则运算，下面分别予以介绍。

（1）二进制数的加法（2）根据“逢二进一”规则，二进制数加法的法则为：0＋0＝00＋1＝1＋0＝11＋1＝0 （进位为1）1＋1＋1＝1 （进位为1）例如：1110和1011相加过程如下：（2）二进制数的减法根据“借一有二”的规则，二进制数减法的法则为：0－0＝01－1＝01－0＝10－1＝1 （借位为1）例如：1101减去1011的过程如下：（3）二进制数的乘法二进制数乘法过程可仿照十进制数乘法进行。

但由于二进制数只有0或1两种可能的乘数位，导致二进制乘法更为简单。

二进制数乘法的法则为：0×0＝00×1＝1×0＝01×1＝1例如：1001和1010相乘的过程如下：由低位到高位，用乘数的每一位去乘被乘数，若乘数的某一位为1，则该次部分积为被乘数；若乘数的某一位为0，则该次部分积为0。

某次部分积的最低位必须和本位乘数对齐，所有部分积相加的结果则为相乘得到的乘积。

（4）二进制数的除法二进制数除法与十进制数除法很类似。

可先从被除数的最高位开始，将被除数（或中间余数）与除数相比较，若被除数（或中间余数）大于除数，则用被除数（或中间余数）减去除数，商为1，并得相减之后的中间余数，否则商为0。

再将被除数的下一位移下补充到中间余数的末位，重复以上过程，就可得到所要求的各位商数和最终的余数。

例如：100110÷110的过程如下：所以，100110÷110＝110余10。

2．二进制数的逻辑运算二进制数的逻辑运算包括逻辑加法（“或”运算）、逻辑乘法（“与”运算）、逻辑否定（“非”运算）和逻辑“异或”运算。

（1）逻辑“或”运算又称为逻辑加，可用符号“＋”或“∨”来表示。

逻辑“或”运算的规则如下：0＋0＝0或0∨0＝00＋1＝1或0∨1＝11＋0＝1或1∨0＝11＋1＝1或1∨1＝1可见，两个相“或”的逻辑变量中，只要有一个为1，“或”运算的结果就为1。

二进制数1001.01=1* 23 +0* 22 +0* 21 +1* 20 +0* 2-1 +1* 2-2
精选ppt课件2021
7
二、数制之间的相互转换
1．十进制数转换为二、八、十六进制
假设将十进制数转换为R进制数，整数部分 与小数部分须分别遵守不同的转换规则：
对整数部分：除以R取余数，即整数部分不断 除以R取余数，直到商为0为止，最先得到的余数
为最低位，最后得到的余数为最高位。
对小数部分：乘以R取整数，即小数部分不断 乘以R取整数，直到小数为0或达到有效精度为止， 最先得到的整数为最高位（最靠近小数点），最
后得到的整数为最低位。
精选ppt课件2021
8
2．二进制数转换为八、十六进制
8和16都是2的整数次幂，即8＝ 23 ,16＝ 24
因此3位二进制相当于1位八进制，4位二进制数 相当于1位十六进制数。
精选ppt课件2021
10
（2）字节：Byte（简写为B），八位为一个字节，一 个字节由八个二进制数位组成，是计算机中用来表示 存储空间大小的基本容量单位，除用字节为单位表示 存储容量外，还可以用千字节（KB），兆字节 （MB），以及十亿字节（GB）等表示存储容量，它 们之间的换算关系如下：
1B＝8bit 1KB＝1024B＝ 210 B 1MB＝1024KB＝ 220 B＝1024×1024B＝1048576B 1GB＝1024MB＝1073741824 B （3）字（Word）：在计算机中作为一个整体被存取、 传送、处理的二进制字符串叫做一个字或单位，每个 字中二进制位数的长度，称为字长。
转换规则为：将二进制数以小数点为中心分别向 两边分组，转换成八（十六）进制数每3（4）位为 一组，整数部分向左分组，不足位数左补0，小数部 分向右分组，不足部分右补0，然后将每组转换成八 （十六）进制即可。

添加标题
仔细核对运算步骤：在进行二进制数运算时，需要仔细核对运算步骤，确保每一步的运算都正确无误，避免因为运算步骤错误而导致结果不正确。
添加标题
避免溢出错误：在进行二进制数运算时，需要注意溢出问题，确保运算结果不会超出二进制数的表示范围，避免因为溢出错误而导致结果不正确。
添加标题
避免进位错误：在进行二进制数运算时，需要注意进位问题，确保每一位的运算结果都正确无误，避免因为进位错误而导致结果不正确。
二进制数的加法规则：0+0=0，0+1=1，1+1=0，进位为1
二进制数的减法规则：0-0=0，0-1=1（借位），1-1=0
二进制数的乘法规则：0*0=0，0*1=0，1*1=1
二进制数的除法规则：除法相当于连续减法，如10除以2等于5，等于5次2减去1的结果
二进制数运算在计算机科学中的重要性 * 计算机内部数据表示的基础 * 计算机程序运行的基本原理
二进制数的基数为2
二进制数的表示形式为0和1
二进制数的运算速度比十进制数更快
二进制数的运算规则为“逢二进一”
二进制数的基数是2
二进制数可以表示计算机中的所有信息
二进制数的运算规则是逢二进一
二进制数只有0和1两个数字
二进制数的运算规则
二进制数的加法规则
0+0=0, 1+0=1, 1+1=10
二进制数的进位规则
总结与回顾
二进制数的定义：二进制数是一种以0和1为基本符号的数制系统
二进制数的特点：二进制数的运算规则简单，易于实现，适合计算机内部运算
二进制数的应用：在计算机科学中，二进制数被广泛应用于计算机内部的数据表示和运算
二进制数与十进制数的转换：了解二进制数与十进制数的转换方法，方便我们在不同数制之间进行转换

括号前面是除号，打开括号要变号，除变乘，乘变除。 括号前面是乘号，打开括号不变号。
下面两个运算性质是否正确？ a÷(b＋c)=a÷b＋a÷c (a+b)÷c=a÷c＋b÷c
×
√
（ a b） c
（ a
b）
1 c
a
1 c
b
1 c
acbc
1、287+299 =287+300-1 =587-1 =586
括号前面是减号，打开括号要变号，加变减，减变加。 括号前面是加号，打开括号不变号。
64÷(16×2)=90÷30÷2 90÷(30÷2)=90÷30×2 15×(20÷10)=15×20÷10 25×(4×27)=25×4×27
a÷(b×c)=a÷b÷c a÷(b÷c)=a÷b×c a×(b÷c)=a×b÷c a×(b×c)=a×b×c
规律2：题目里有“和”、“差”、“积”、“商”的，要先算出来。
规律3：题目要求“求这个数”或“这个数是多少？”的文字题，一般要用方程解 答比较简便。
（8）一个数的4倍比0.4除15.6的商少7，求这个数。 解：设这个数为x。 15.6÷0.4 - 4x=7
（9）55.8与4.8的差除以0.51的商比162少多少？ 162 - 55.8（- 4.8 ÷ 0）.51
加
上 它 的3倍
等
于66的
1 2
，
求
这
个
数。
解：设这个数为x。
8
3
66
1 2
（6）一个数与8的和的2倍是36，这个数是多少？ 解：设这个数为x。 (x+8)×2=36
（7）一个数的4倍减去5个3.2的和，差是14，求这个数。 解：设这个数为x。 4x-3.2×5=14

二进制的四则运算二进制的四则运算二进制四则运算和十进制四则运算原理相同，所不同的是十进制有十个数码，“满十进一”，二进制只有两个数码0和1，“满二进一”。

二进制运算口诀则更为简单。

1．加法二进制加法，在同一数位上只有四种情况：0＋0＝0，0＋1＝1，1＋0＝1，1＋1＝10。

只要按从低位到高位依次运算，“满二进一”，就能很容易地完成加法运算。

例1 二进制加法（1）10110＋1101；（2）1110＋101011。

解加法算式和十进制加法一样，把右边第一位对齐，依次相应数位对齐，每个数位满二向上一位进一。

10110＋1101＝100011 1110＋101011＝111001通过计算不难验证，二进制加法也满足“交换律”，如101＋1101＝1101＋101＝10010。

多个数相加，先把前两个数相加，再把所得结果依次与下一个加数相加。

例2 二进制加法（1）101＋1101＋1110；（2）101＋（1101＋1110）。

解（1）101＋1101＋1110 （2）101＋（1101＋1110）＝10010＋1110 ＝101＋11011＝100000；＝100000从例2的计算结果可以看出二进制加法也满足“结合律”。

巩固练习二进制加法（1）1001＋11；（2）1001＋101101；（3）（1101＋110）＋110；（4）（10101＋110）＋1101。

2．减法二进制减法也和十进制减法类似，先把数位对齐，同一数位不够减时，从高一位借位，“借一当二”。

例3 二进制减法（1）11010－11110；（2）10001－1011。

解（1）110101－11110＝10111；（2）10001－1011＝110。

例4 二进制加减混合运算（1）110101＋1101－11111；（2）101101－11011＋11011。

解（1）110101＋1101－11111＝1000010－11111＝100011（2）101101－11011＋11011＝10011＋11011＝101101。

名人名言：少年读书，如隙中窥月;中年读书，如庭中望月;老年读书 ，如台上玩月。皆以阅历之深浅，为所得之深浅耳。
名人名言：少年读书，如隙中窥月;中年读书，如庭中望月;老年读书 ，如台上玩月。皆以阅历之深浅，为所得之深浅耳。
名人名言：少年读书，如隙中窥月;中年读书，如庭中望月;老年读书 ，如台上玩月。皆以阅历之深浅，为所得之深浅耳。
名人名言：少年读书，如隙中窥月;中年读书，如庭中望月;老年读书 ，如台上玩月。皆以阅历之深浅，为所得之深浅耳。
名人名言：少年读书，如隙中窥月;中年读书，如庭中望月;老年读书 ，如台上玩月。皆以阅历之深浅，为所得之深浅耳。
名人名言：少年读书，如隙中窥月;中年读书，如庭中望月;老年读书 ，如台上玩月。皆以阅历之深浅，为所得之深浅耳。
名人名言：少年读书，如隙中窥月;中年读书，如庭中望月;老年读书 ，如台上玩月。皆以阅历之深浅，为所得之深浅耳。
名人名言：少年读书，如隙中窥月;中年读书，如庭中望月;老年读书 ，如台上玩月。皆以阅历之深浅，为所得之深浅耳。
名人名言：少年读书，如隙中窥月;中年读书，如庭中望月;老年读书 ，如台上玩月。皆以阅历之深ห้องสมุดไป่ตู้，为所得之深浅耳。
名人名言：少年读书，如隙中窥月;中年读书，如庭中望月;老年读书 ，如台上玩月。皆以阅历之深浅，为所得之深浅耳。
名人名言：少年读书，如隙中窥月;中年读书，如庭中望月;老年读书 ，如台上玩月。皆以阅历之深浅，为所得之深浅耳。
名人名言：少年读书，如隙中窥月;中年读书，如庭中望月;老年读书 ，如台上玩月。皆以阅历之深浅，为所得之深浅耳。
名人名言：少年读书，如隙中窥月;中年读书，如庭中望月;老年读书 ，如台上玩月。皆以阅历之深浅，为所得之深浅耳。

乘法运算
总结词
小数乘法运算规则
详细描述
小数乘法运算时，应将小数点对齐，然后按照整数乘法规则进行计算，最后得出结果。 例如：0.5 × 0.3 = 0.15。
除法运算
总结词
小数除法运算规则
详细描述
小数除法运算时，应将小数点对齐，然后按 照整数除法规则进行计算，最后得出结果。
例如：0.8 ÷ 0.5 = 1.6。
01
小数四则运算
加法运算
总结词
小数加法运算规则
详细描述
小数加法运算时，应将小数点对 齐，然后按照整数加法规则进行 计算，最后得出结果。例如：0.5 + 0.3 = 0.8。
减法运算
总结词
小数减法运算规则
详细描述
小数减法运算时，应将小数点对齐， 然后按照整数减法规则进行计算，最 后得出结果。例如：0.8 - 0.5 = 0.3。
详细描述
括号在四则运算中具有优先级，学生在运算时可能会 忽略括号的存在，或者在括号内和括号外的运算处理 上出现混淆。例如，在算式“(2+3)×4”中，学生可 能会忽略括号，直接将“2+3”与“4”相乘，导致结 果错误。
运算顺序错误
总结词
运算顺序错误是指在运算过程中，对先进行哪一步运 算没有遵循正确的顺序，导致运算结果错误的情况。
总结词
乘除法混淆错误是指在进行四则运算时，将乘法误认为 是除法或除法误认为是乘法的情况。
详细描述
学生在进行乘除法运算时，可能会因为对概念理解不清 晰或注意力不集中而混淆乘除法的操作。例如，将 “×”误读为“÷”或将“÷”误读为“×”。
括号处理不当错误
总结词
括号处理不当错误是指在运算过程中，对括号内的内 容处理不当，导致运算结果错误的情况。

四则运算复习课件
本课件旨在复习四则运算知识，让您轻松理解并掌握这些数学概念，为您的 数学学习奠定坚实基础。
四则运算概述
四则运算是数学中最基本、最常见的运算方法，包括加法、减法、乘法和除法。它们是解决实际问题和 构建更复杂运算的基础。
加法
加法是将两个或多个数值相加以得到它们的总和。通过加法，我们可以计算 物体的数量、两个数值的和以及其他更复杂的运算。
混合运算
混合运算是指在一个数学表达式中同时使用加法、减法、乘法和除法。通过混合运算，我们可以解决更 复杂的计算问题。
问题练习
为了帮助您巩固所学的四则运算知识，请完成以下练习题，并在实践中提高您的计算能力。

总结和复习注意事项
通过这次复习，您已经复习了四则运算中的加法、减法、乘法和除法，并了 解了混合运算的概念。记住要掌握正确的运算顺序和运算符号使用，以确保 计算准确无误。
减法
减法是从一个数值中减去另一个数值以得到它们的差。减法可以用于计算物 体的剩余数量、两个数值之间的差异以及其他减法运算。
乘法
乘法是将两个数值相乘以得到它们的积。乘法可以用于计算物体的总数、速度和距离的关系等多种应用 场景。
除法
除法是将一个数值除以另一个数值以得到商和余数（如果有）。除法可以用于分配资源、计算平均值等 多种实际问题。

二进制数的四则运算专题训练知识梳理：二进制数的四则运算法则：加法法则：0+0=0 ；0+1=1；1+0=1；1+1=10；减法法则：0×0=0；0×1=0；1×0=0；1×1=1；例题精讲：1、加法运算：1+1=10，本位记0，向高位进 1.2、减法运算：被减数不够减，向高位借1。

1 当 2， 2-1=1 。

3、乘法运算：4、除法运算：计算后要养成验算的习惯，二进制数四则运算的验算方法与十进制数相同：加法验算时，用和减去其中的一个加数，它们的差应该等于另一个加数。

减法验算时，用差与减数相加，它们的和应该等于被减数。

乘法验算时，用积除以其中的一个因数，它们的商应该等于另一个因数。

除法验算时，用商乘以除数，乘积应该等于被除数；也可以用被除数除以商，看这时的商是否等于除数。

专题特训：1、计算下面二进制数的加减法。

①110+101② 11010+10111③1001001+101110④ 10011-1111⑤⑥2、计算下面二进制数的乘除法。

①110×101②1111×111③1110×1011④101101÷1001⑤100000÷100⑥1000110÷10103、计算下面二进制数的四则混合运算。

①（ 11011）2+（ 10110）2×（ 110）2÷（ 1011）2②（ 10111）2×（ 1110）2+（ 110110 ）2÷（ 1001 ）24、计算下面二进制加法，你能发现什么？（11）2+（ 11）2=（101）2+（ 101 ）2=（1110）2+（ 1110）2=（1111）2+（ 1111）2=5、计算下列二进制乘法，你发现了什么？（10）2×（ 101 ）2=（101）2×（ 1001）2=（1101）2×（ 10001 ）2=（11010）2×（ 100001）2=答案与解析1、①（ 1011）2②（ 110001）2③（ 1110111 ）2④（ 100）2⑤（ 111）2⑥（ 110011）22、①（ 11110） 2②（ 1101001 ）2③（） 2④（ 101）2⑤（ 1000）2⑥（ 111 ）23、二进制的四则混合运算与十进制相同，先算乘除再算加减，同一级运算从左向右依次计算。

二进制数的四则运算专题训练知识梳理：二进制数的四则运算法则：加法法则：0+0=0 ; 0+1=1 ;1+0=1 ；减法法则：0X0=0 ；0X1=0 ；1X0=0 ；例题精讲：1、加法运算：(111)* + (110)严(1101).111 +1101101_1 + 1=10，本位记0,向高位进1.2、减法运算：(1100),-(1010)»= (10)z1100- 1010被减数不够减，向高位借1。

1当2, 2-1=13、乘法运算：(111^x(110)^(101010),111X 1 10000111.1111010104、除法运算:1+1=10；1 X1=1；（liooj.-CioOz 二⑴人11100）1100 100100 100计算后要养成验算的习惯，二进制数四则运算的验算方法与十进制数相同： 加法验算时，用和减去其中的一个加数，它们的差应该等于另一个加数。

减法验算时，用差与减数相加，它们的和应该等于被减数。

乘法验算时，用积除以其中的一个因数，它们的商应该等于另一个因数。

除法验算时，用商乘以除数，乘积应该等于被除数；也可以用被除数除以商，看这时的商是 否等于除数。

专题特训：1、计算下面二进制数的加减法①110+101 ③1001001+101110 ⑤ 11000-10001 2、计算下面二进制数的乘除法① 110X 101 ③ 1110X 1011 ⑤ 100000-100 3、 计算下面二进制数的四则混合运算。

©( 11011) 2+ ( 10110) 2 X ( 110) 2-( 1011 ) 2购(10111) 2 X ( 1110) 2+ ( 110110) 2-( 1001 ) 24、 计算下面二进制加法，你能发现什么？(11) 2+ (11) 2=(101) 2+ (101) 2 =(1110) 2+ (1110) 2=(1111) 2+ ( 1111) 2=5、 计算下列二进制乘法，你发现了什么？(10) 2X ( 101 ) 2=(101) 2X(1001) 2=(1101 ) 2X ( 10001 ) 2= ②11010+10111④10011-1111⑥1001001-10110② 1111 X 111④ 101101-1001⑥1000110-1010(11010) 2X ( 100001 ) 2=答案与解析1、①(1011 ) 2 购(110001 ) 2 3( 1110111 ) 2100) 2 ⑤(111) 2 ©( 110011) 22、①(11110) 2 购(1101001 ) 2 3( 10011010) 2101) 2 ⑤(1000) 2 ©( 111 ) 23、二进制的四则混合运算与十进制相同，先算乘除再算加减，同一级运算从左向右依次计算。

第三讲二进制数的四则运算-----月----日姓名---------教学重点：二进制数计算法则教学难点：除法的计算知识要点二进制数计算法则：逢2进1,借1当2.1．加法法则：0＋0＝0 0＋1＝1 1＋0＝1 1＋1＝10 2．乘法法则：0×0＝0 0×1＝0 1×0＝0 1×1＝1典型例题例1 计算。

（1）1011（2）＋11（2）（2）101（2）＋110（2）（3）1011（2）－11（2）（2）1101（2）－101（2）例2 计算。

（1）1101（2）×11（2）（2）1001（2）×10（2）例3 计算。

（1）1111（2）÷101（2） （2）10010（2）÷11（2）随堂练习1．计算。

（1）101（2）＋10（2） （2）1110（2）＋11（2）（3）1011（2）＋1000（2）（4）101（2）－10（2）（5）1110（2）－11（2） （6）1001（2）－1000（2）2．计算。

（1）110（2）×10（2）（2）1011（2）×11（2）（3）1001（2）×11（2）（4）101（2）×11（2）（5）11011（2）×11（2）（6）11001（2）×11（2）3．计算。

（1）11100（2）÷100（2）（2）1111（2）÷11（2）（3）10101（2）÷11（2） （4）1100（2）÷11（2）（5）11011（2）÷11（2） （6）1000001（2）÷101（2）课后练习1．计算。

（1）1101（2）＋111（2） （2）101（2）－11（2）（3）11（2）×110（2）（4）1001（2）÷11（2）拓展练习计算（1）81（2）＋110（2）－110（2）（2）101101（2）×11011（2）－100100（2）（3）110（2）×1010（2）－7（10）（4）100010（2）×1101（2）－10001（2）小课堂口袋钱马戏团里有一个小丑，他身上有十个口袋。

二进制习题《信息技术基础》复习学案编制人：张东课时：1补充内容二：《二进制》一、进制的规则：逢N进1,如十进制逢10进1,二进制逢2进。

二、二进制计算机中采用二进制的原因：①二进制在物理上容易实现；②二进制运算规则简单1、二进制的运算加法：0+0=0, 0+1=1，1+1=10减法：0-0=0，1-0=1，0-1=1 .(借 1 当2).乘法：0X0=0, 0X1=0除法：0*1=0, 1*1=1, 1 ^0无意义，0P无意义(1)加法例：10111+1010=? 练习：① 11101+1101=? ②10110+11111=?解：10111+1010100001故10111+1010=100001B(2)减法(借1当2)例：11011-110仁？练习：① 1110-10仁?②11011-收集于网络，如有侵权请联系管理员删除解：11011 (借 1 当2)11011110(3)乘法例：1110X1 仁？练习：11011X101=?解：1110X11111011101010102、二进制与十进制的相互转化(1)十进制转化为二进制方法：除基数求余，逆序排列即得例：把十进制数130转化为二进制数解：2 |；| --- 0 计2 32 - —— 1 P2Id ----------- 0P1 I 兀---- u P收集于网络，如有侵权请联系管理员删除2 I 兀.... -0 P訂2 - ----------- 0 P订1“................ 0卩0 ----------- 1卩故：130D=10000010B（2）二进制数转化为十进制数方法：按权展开，相加即得例：101101B=?101101B=1X25+0X24+1 X23+1 X22+0X21+1 X2°=45D （D代表十进制）练习：1110011B=? D三、计算机中的数据表示1、比特（bit.）.是计算机中存储数据的最小单位。