人教A版新课标高中数学必修一练习 《诱导公式》第1课时同步测试

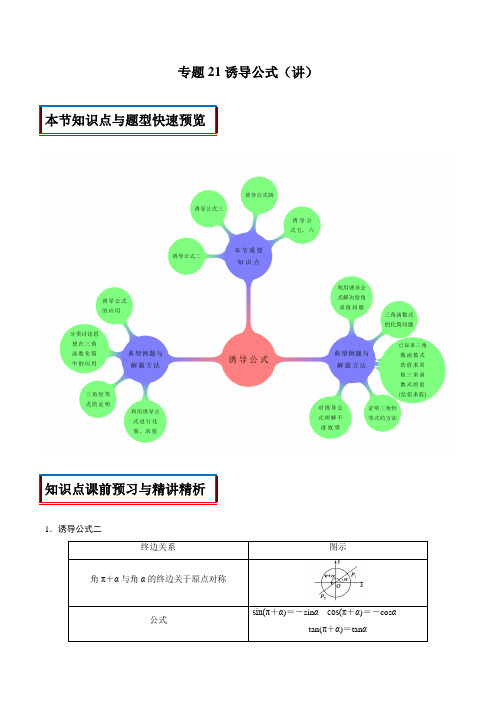
专题21诱导公式（讲）本节知识点与题型快速预览知识点课前预习与精讲精析1．诱导公式二终边关系图示角π＋α与角α的终边关于原点对称公式sin(π＋α)＝－sinαcos(π＋α)＝－cosαtan(π＋α)＝tanα2．诱导公式三终边关系图示角－α与角α的终边关于x 轴对称公式sin(－α)＝－sin α cos(－α)＝cos αtan(－α)＝－tan α3．诱导公式四终边关系图示角π－α与角α的终边关于y 轴对称公式sin(π－α)＝sin α cos(π－α)＝－cos α tan(π－α)＝－tan α特别提醒：1.公式一～四中的角α是任意角．2．公式一、二、三、四都叫做诱导公式，它们可概括如下：(1)记忆方法：2k π＋α(k ∈Z )，－α，π±α的三角函数值，等于α的同名函数值，前面加上一个把α看成锐角时原函数值的符号，可以简单地说成“函数名不变，符号看象限”．(2)解释：“函数名不变”是指等式两边的三角函数同名；“符号”是指等号右边是正号还是负号；“看象限”是指假设α是锐角，要看原三角函数值是取正值还是负值，如sin(π＋α)，若把α看成锐角，则π＋α是第三象限角，故sin(π＋α)＝－sin α． 3．诱导公式的作用(1)公式一的作用在于把绝对值大于2π的任一角的三角函数问题转化为绝对值小于2π的角的三角函数问题． (2)公式三的作用在于把负角的三角函数转化成正角的三角函数．(3)公式二、公式四的作用在于把钝角或大于180°的角的三角函数转化为0°～90°之间的角的三角函数． 4．诱导公式五、六如下表：公式五 sin(π2－α)＝cos α cos(π2－α)＝sin α公式六sin(π2＋α)＝cos α cos(π2＋α)＝－sin α公式五和公式六可以概括为：π2±α的正弦(余弦)函数值，分别等于α的余弦(正弦)函数值，前面加上一个把α看成锐角时原函数值的符号，公式一～六都叫做诱导公式[知识点拨]1.对诱导公式五、六的两点说明(1)诱导公式五、六反映的是角π2±α与α的三角函数值之间的关系．可借用口诀“函数名改变，符号看象限”来记忆．(2)诱导公式是三角变换的基本公式，其中角可以是是一个单角，也可以是一个复角，应用时要注意整体把握，灵活变通．2．对诱导公式一～六的两点说明(1)诱导公式一～六揭示了终边具有某种对称关系的两个角的三角函数之间的关系． (2)公式一～六的记忆口决和说明 ①口诀：奇变偶不变，符号看象限． ②说明：1．如果sin α，α为第三象限角，则sin （α）＝ ．【解析】解：∵sin α，α为第三象限角，∴cos α，则sin （α）＝﹣cos α．故答案为：．2．sin的值为．【解析】解：sin sin（2π）＝﹣sin．故答案为：3．计算sin330°＝．【解析】解：sin330°＝sin（360°﹣30°）＝﹣sin30°．故答案为：4．已知：，则．【解析】解：因为，∴sinθ．∵2（﹣tanθ）•（﹣cosθ）＝﹣sinθ+2sinθ＝sinθ．故答案为：．5．．【解析】解：sin（2π）cos（4π）＝sin cos．故答案为：．典型题型与解题方法重要考点一：利用诱导公式解决给角求值问题【典型例题】sin（）A．B．C．D．【解析】解：sin sin（673π）＝sin（π）＝﹣sin，故选：C．【题型强化】已知，则sin（270°﹣α）＝（）A．B．C．D．【解析】解：∵，∴sin（270°﹣α）＝﹣cosα．故选：B．【收官验收】若sin1000°＝a，则cos10°＝（）A．﹣a B．C．a D．【解析】解：因为sin1000°＝sin（360°×3﹣80°）＝sin（﹣80°）＝﹣sin80°＝﹣cos10°＝a，所以cos10°＝﹣a．故选：A．【名师点睛】利用诱导公式求任意角三角函数的步骤：(1)“负化正”——用公式一或三来转化；(2)“大化小”——用公式一将角化为0°到360°间的角；(3)“小化锐”——用公式二或四将大于90°的角转化为锐角；(4)“锐求值”——得到锐角的三角函数后求值．重要考点二：三角函数式的化简问题【典型例题】若α为第二象限角，sin（α），（1）求sinα的值；（2）若f（α），求f（α）的值．【解析】解：（1）∵α为第二象限角，sin（α）＝cosα，∴sinα；（2）∵f（α）sinα，∴f（α）．【题型强化】已知f（α）．（1）若α，求f（α）值；（2）若α为第三象限角，且，求f（α）的值．【解析】解：（1）由于，又，所以f（α）．（2）因为，又因为α为第三象限角，所以．【收官验收】已知α是锐角，且f（α）．（1）化简f（α）；（2）若cos（απ），求f（α）的值．【解析】解：（1）f（α）cosα．（2）∵cos（απ）＝﹣sinα，∴sinα，可得cosα，∴f（α）＝﹣cosα．【名师点睛】三角函数式的化简方法：(1)利用诱导公式将任意角的三角函数转化为锐角三角函数；(2)常用“切化弦”法，即通常将表达式中的切函数化为弦函数；(3)注意“1”的变形应用．重要考点三：已知某三角数函数式的值求其他三角函数式的值(给值求值)【典型例题】已知sinα，α∈（，π）．（1）求cosα，tanα；（2）求的值．【解析】解：（1）∴已知sinα，α∈（，π），∴cosα，∴tanα．（2）cos2α．【题型强化】若角α的终边上有一点P（m，﹣8），且cosα．（1）求m的值；（2）求的值．【解析】解：（1）点P到原点的距离为r＝|OP|，根据三角函数的概念可得cosα，解得m＝﹣6，或m＝6（舍去）．（2）sinα，由（1）可得r10，sinα，∴原式＝﹣sinα．【收官验收】已知，求下列各式的值：．（2）sin2α+2sinαcosα．【解析】解：，∴﹣sinα＝﹣2cosα，即sinα＝2cosα，则原式；（2）∵sinα＝2cosα，即tanα＝2，∴原式．【名师点睛】解决条件求值问题策略：解决条件求值问题，要仔细观察条件与所求式之间的角、函数名及有关运算之间的差异及联系，要么将已知式进行变形向所求式转化，要么将所求式进行变形向已知式转化．总之，设法消除已知式与所求式之间的种种差异是解决问题的关键．重要考点四：证明三角恒等式的方法【典型例题】证明下列三角恒等式：（1）1；（2）．【解析】证明：（1）左边1＝右边，得证．（2）左边，右边，可得左边＝右边，得证．【题型强化】（1）化简：sin2αtanα2sinαcosα；（2）若α为第二象限的角，证明：tanα．【解析】解：（1）sin2αtanα2sinαcosα2sinαcosα．（2）证明：∵α为第二象限的角，sinα＞0，cosα＜0，∴左边＝tanα＝右边，得证．【收官验收】求证：tanα．【解析】证：tanα【名师点睛】(1)三角恒等式的证明一般有三种方法：①一端化简等于另一端；②两端同时化简使之等于同一个式子；③作恒等式两端的差式使之为0．(2)证明条件恒等式，一般有两种方法：一是在从被证等式一边推向另一边的适当时候将条件代入，推出被证等式的另一边，这种方法称作代入法；二是直接将条件等式变形，变形为被证的等式，这种方法称作推出法，证明条件等式时，不论使用哪一种方法，都要依据要证的目标的特征进行变形．重要考点五：分类讨论思想在三角函数化简中的应用【典型例题】已知，f（α）．（1）化简f（α）；（2）若，求tanα．【解析】解：（1）f（α）sinα．（2）∵，∴sin（α），可得cosα，∴α是第二或第三象限角，当α是第二象限角时，sinα，tan，当α是第三象限角时，sinα，tan．【题型强化】化简计算：（1）已知tan x＝2，计算；（2）化简sin（α）cos（α﹣π）﹣cos（α﹣2π）cos（π+α）．【解析】解：（1）∵已知tan x＝2，∴．（2）sin（α）cos（α﹣π）﹣cos（α﹣2π）cos（π+α）＝cosα（﹣cosα）﹣cosα（﹣cosα）＝0．【收官验收】已知α是第四象限角，f（α）．（1）化简f（α）．（2）若cos，求f（α）的值．【解析】解：（1）f（α）．＝﹣cosα．（2）因为cos（）＝cos（）＝﹣sinα，所以sinα．因为α是第四象限角，所以cosα，所以f（α）＝﹣cosα．【名师点睛】1.本题型化简过程，突出体现了分类讨论的思想，当然除了运用分类讨论的思想将n分两类情况来讨论外，在解答过程中还处处体现了化归思想和整体思想．2．在转化过程中，缺乏整体意识，是出错的主要原因．。

第五章 5.3 第1课时A 组·素养自测一、选择题1．tan150°的值为( A ) A ．－33B ．33C ．－ 3D ． 3[解析] tan150°＝tan(180°－30°)＝－tan30°＝－33. 2．sin 2150°＋sin 2135°＋2sin210°＋cos 2225°的值是( A ) A ．14B ．34C ．114D ．94[解析] 原式＝sin 230°＋sin 245°－2sin30°＋cos 245°＝⎝⎛⎭⎫122＋⎝⎛⎭⎫222－2×12＋⎝⎛⎭⎫222＝14. 3．化简1＋2sin (π－2)·cos (π－2)的结果为( C ) A ．sin2＋cos2 B ．cos2－sin2 C ．sin2－cos2 D ．±(cos2－sin2)[解析] 1＋2sin (π－2)·cos (π－2)＝1－2sin2·cos2＝(sin2－cos2)2＝|sin2－cos2|.∵2弧度在第二象限， ∴sin2>0>cos2， ∴原式＝sin2－cos2.4．已知sin(π4＋α)＝32，则sin(3π4－α)的值为( C )A ．12B ．－12C ．32D ．－32[解析] ∵sin(π4＋α)＝32，∴sin(3π4－α)＝sin[π－(π4＋α)]＝sin(π4＋α)＝32.5．sin600°＋tan240°的值是( B ) A ．－32B ．32C ．－12＋ 3D ．12＋ 3[解析] sin600°＋tan240°＝sin(360°＋240°)＋tan(180°＋60°)＝sin240°＋tan60°＝sin(180°＋60°)＋tan60°＝－sin60°＋tan60°＝－32＋3＝32. 6．已知tan5°＝t ，则tan(－365°)＝( C ) A ．t B ．360°＋t C ．－tD ．与t 无关[解析] tan(－365°)＝－tan365°＝－tan(360°＋5°)＝－tan5°＝－t . 二、填空题 7．sin750°＝__12__.[解析] sin750°＝sin(2×360°＋30°)＝sin30°＝12.8．已知α∈(0，π2)，tan(π－α)＝－34，则sin α＝__35__.[解析] 由于tan(π－α)＝－tan α＝－34，则tan α＝34，解方程组⎩⎪⎨⎪⎧sin αcos α＝34，sin 2α＋cos 2α＝1，得sin α＝±35，又α∈(0，π2)，所以sin α>0.所以sin α＝35.9．设f (x )＝a sin(πx ＋α)＋b cos(πx ＋β)，其中a ，b ，α，β为非零常数，若f (2 018)＝－1，则f (2 019)＝__1__.[解析] f (2 019)＝a sin(2 019π＋α)＋b cos(2 019π＋β) ＝a sin(π＋2 018π＋α)＋b cos(π＋2 018π＋β) ＝－a sin(2 018π＋α)－b cos(2 018π＋β) ＝－[a sin(2 018π＋α)＋b cos(2 018π＋β)] ＝－f (2 018)＝1. 三、解答题10．已知角α的终边经过单位圆上的点P ⎝⎛⎭⎫45，－35.(1)求sin α的值； (2)求cos (2π－α)sin (π＋α)·tan (π＋α)cos (3π－α)的值．[解析] (1)∵点P 在单位圆上， ∴由正弦函数的定义得sin α＝－35.(2)原式＝cos α－sin α·tan α－cos α＝sin αsin α·cos α＝1cos α，由余弦函数的定义得cos α＝45，故原式＝54.11．已知cos (180°＋α)sin (α＋360°)sin (540°＋α)sin (－α－180°)cos (－180°－α)＝lg 1310，求cos (π＋α)cos α[cos (π－α)－1]＋cos (α－2π)cos αcos (π－α)＋cos (α－2π)的值．[解析] ∵cos (180°＋α)sin (α＋360°)sin (540°＋α)sin (－α－180°)cos (－180°－α)＝(－cos α)sin αsin (180°＋α)－sin (180°＋α)cos (180°＋α)＝(－cos α)sin α(－sin α)sin α(－cos α)＝－sin α＝lg 1310，∴sin α＝－lg 1310＝lg 310＝13.∴cos (π＋α)cos α[cos (π－α)－1]＋cos (α－2π)cos αcos (π－α)＋cos (α－2π) ＝－cos αcos α(－cos α－1)＋cos αcos α(－cos α)＋cos α＝1cos α＋1＋11－cos α＝(1－cos α)＋(1＋cos α)1－cos 2α＝2sin 2α＝18. B 组·素养提升一、选择题1．(多选题)下列各式正确的是( ACD ) A ．sin(α＋180°)＝－sin α B ．cos(－α＋β)＝－cos(α－β) C ．sin(－α－360°)＝－sin α D ．cos(－α－β)＝cos(α＋β)[解析] 对于B ，cos(－α＋β)＝cos[－(α－β)]＝cos(α－β)，B 错误，由诱导公式知A 、C 、D 都正确，故选ACD ．2．(多选题)下列化简正确的是( AB ) A ．tan(π＋1)＝tan1 B ．sin (－α)tan (360°－α)＝cos αC ．sin (π－α)cos (π＋α)＝tan αD ．cos (π－α)tan (－π－α)sin (2π－α)＝1[解析] A 正确；B 正确，sin (－α)tan (360°－α)＝－sin α－tan α＝cos α；C 错，sin (π－α)cos (π＋α)＝sin α－cos α＝－tan α；D 错，cos (π－α)tan (－π－α)sin (2π－α)＝(－cos α)(－tan α)－sin α＝－1.故选AB ．3．设tan(5π＋α)＝m (α≠k π＋π2，k ∈Z )，则sin (α－3π)＋cos (π－α)sin (－α)－cos (π＋α)的值为( A )A ．m ＋1m －1B ．m －1m ＋1C ．－1D ．1[解析] ∵tan(5π＋α)＝m ，∴tan α＝m ，原式＝－sin α－cos α－sin α＋cos α＝－tan α－1－tan α＋1＝－m －1－m ＋1＝m ＋1m －1，故选A ．4．若sin α＋cos αsin α－cos α＝2，则sin(α－5π)·cos(3π－α)等于( B )A ．34B ．310C ．±310D ．－310[解析] 由sin α＋cos αsin α－cos α＝2，得tan α＝3.则sin(α－5π)·cos(3π－α) ＝－sin(5π－α)·cos(2π＋π－α) ＝－sin(π－α)·cos(π－α) ＝－sin α·(－cos α) ＝sin α·cos α ＝sin αcos αsin 2α＋cos 2α＝tan αtan 2α＋1＝310.二、填空题5．cos1°＋cos2°＋cos3°＋…＋cos180°＝__－1__. [解析] ∵cos(π－θ)＝－cos θ， ∴cos θ＋cos(π－θ)＝0，即cos1°＋cos179°＝cos2°＋cos178°＝…＝cos90°＝0. ∴原式＝0＋0＋…＋0＋cos180°＝－1.6．若cos(π6＋θ)＝33，则cos(5π6－θ)＝__－3[解析] cos(5π6－θ)＝cos[π－(π6＋θ)]＝－cos(π6＋θ)＝－33.7．已知n 为整数，化简sin (n π＋α)cos (n π＋α)所得结果是__tan α__.[解析] 若n ＝2k (k ∈Z )，则sin (n π＋α)cos (n π＋α)＝sin (2k π＋α)cos (2k π＋α)＝sin αcos α＝tan α；若n ＝2k ＋1(k ∈Z )，则sin (n π＋α)cos (n π＋α)＝sin (2k π＋π＋α)cos (2k π＋π＋α)＝sin (π＋α)cos (π＋α)＝－sin α－cos α＝tan α.三、解答题8．已知f (α)＝sin (π－α)cos (2π－α)tan (－α＋π)－tan (－α－π)sin (－π－α).(1)化简f (α)；(2)若α是第三象限角，且sin(α＋π)＝15，求f (α)的值．[解析] (1)f (α)＝sin αcos α(－tan α)tan αsin α＝－cos α.(2)∵sin(α＋π)＝－sin α，∴sin α＝－15.又α是第三象限角， ∴cos α＝－265，∴f (α)＝265.9．在△ABC 中，若sin(2π－A )＝－2sin(π－B )，3cos A ＝－2cos(π－B )，求△ABC 的三个内角．[解析] 由已知得⎩⎪⎨⎪⎧sin A ＝2sin B ①，3cos A ＝2cos B ②，由①2＋②2，得2cos 2A ＝1，∴cos A ＝±22.当cos A ＝22时，cos B ＝32. 又A ，B 是三角形的内角，∴A ＝π4，B ＝π6.∴C ＝π－(A ＋B )＝712π.当cos A ＝－22时，cos B ＝－32. 又A ，B 是三角形的内角，∴A ＝34π，B ＝56π，A ＋B >π，不符合题意．综上可知，A ＝π4，B ＝π6，C ＝712π.。

第1课时 三角函数的诱导公式二~四课后·训练提升 基础巩固1.若sin(-110°)=a,则tan 70°等于( ) A.√1-a2 B.-a √1-a 2C.√1+a2D.√1+a 2sin(-110°)=-sin110°=-sin(180°-70°)=-sin70°=a,∴sin70°=-a.∴cos70°=√1-(-a )2=√1-a 2,∴tan70°=sin70°cos70°=-a √1-a 2.2.已知sin(θ+π)<0,cos(θ-π)>0,则θ是( ) A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角sin(θ+π)=-sinθ<0⇒sinθ>0,cos(θ-π)=-cosθ>0⇒cosθ<0,由{sinθ>0,cosθ<0,可知θ是第二象限角,故选B. 3.(多选题)下列化简正确的是( ) A.tan(π+1)=tan 1 B.sin (-)tan (360°-α)=cos αC.sin (π-α)cos (π+α)=tan αD.cos (π-α)tan (-π-α)sin (2π-α)=1tan(π+1)=tan1,故A 中化简正确;sin (-α)tan (360°-α)=-sinα-tanα=cosα,故B 中化简正确;sin (π-α)cos (π+α)=sinα-cosα=-tanα.故C 中化简不正确; cos (π-α)tan (-π-α)sin (2π-α)=-cosα(-tanα)-sinα=-1,故D 中化简不正确,故选AB. 4.已知sin (α-π4)=√32,则sin (5π4-α)的值为( )A.12B.-12C.√32D.-√32(5π4-α)=sin [π-(α-π4)]=sin(α-π4)=√32.5.cos 1°+cos 2°+cos 3°+…+cos 360°等于( ) A.0 B.2C.-2D.1-cosα,可得cos1°+cos2°+cos3°+…+cos360°=(cos1°+cos2°+cos3°+…+cos180°)+(cos181°+cos182°+cos183°+…+cos360°)=(cos1°+cos2°+cos3°+…+cos180°)-(cos1°+cos2°+cos3°+…+co s180°)=0.6.已知cos (π6+θ)=√33,则cos (5π6-θ)=( )A.√3B.-√3C.√33D.-√33解析cos (5π6-θ)=cos [π-(π6+θ)]=-cosπ6+θ=-√33.7.若tan(5π+α)=m,则sin (α-3π)+cos (π-α)sin (-α)-cos (π+α)= .tan(5π+α)=m,得tanα=m. 于是原式=-sinα-cosα-sinα+cosα=tanα+1tanα-1=m+1m -1.8.若点P(-4,3)是角α终边上的一点,则cos (α-3π)tan (α-2π)sin 2(π-α)的值为 . -53sinα=35,原式=(-cosα)tanαsin 2α=-sinαsin 2α=-1sinα=-53.9.cos (-585°)sin495°+sin (-570°)的值是 .√2-2 =cos (360°+225°)sin (360°+135°)-sin (210°+360°)=cos225°sin135°-sin210°=cos (180°+45°)sin (180°-45°)-sin (180°+30°)=-cos45°sin45°+sin30°=-√22√22+12=√2-2.10.计算下列各式的值: (1)sin (-19π3)cos 7π6;(2)sin(-960°)cos 1 470°-cos(-240°)sin(-210°). 原式=-sin (6π+π3)cos (π+π6)=sin π3cos π6=34.(2)原式=-sin(180°+60°+2×360°)cos(30°+4×360°)+cos(180°+60°)sin (180°+30°)=sin60°cos30°+cos60°sin30°=1. 11.已知sin(α+π)=45,且sin αcos α<0,求2sin (α-π)+3tan (3π-α)4cos (α-3π)的值.sin(α+π)=45,所以sinα=-45.又sinαcosα<0,所以cosα>0,cosα=√1-sin 2α=35,所以tanα=-43.所以原式=-2sinα-3tanα-4cosα=2sinα+3tanα4cosα=2×(-45)+3×(-43)4×35=-73.能力提升1.已知n 为整数,化简sin (nπ+α)cos (nπ+α)所得的结果是( )A.tan(nα)B.-tan(nα)C.tan αD.-tan αn 为偶数时,原式=sinαcosα=tanα;当n 为奇数时,原式=-sinα-cosα=tanα.故选C.2.(多选题)给出下列四个结论,其中正确的结论是( ) A.sin(π+α)=-sin α成立的条件是角α是锐角 B.若cos(nπ-α)=13(n ∈Z),则cos α=13C.若角α是三角形的一个内角,cos(π+α)=23,则tan(π-α)=√52D.若sin α+cos α=1,则sin n α+cos n α=1A,由诱导公式二,知α∈R 时,sin(π+α)=-sinα,所以A 中结论错误;对于B,当n=2k(k ∈Z)时,cos(nπ-α)=cos(-α)=cosα,此时cosα=13,当n=2k+1(k ∈Z)时,cos(nπ-α)=cos[(2k+1)π-α]=cos(π-α)=-cosα,此时cosα=-13,所以B 中结论错误;对于C,因为cos(π+α)=23,所以cosα=-23,又角α是三角形的一个内角,所以sinα=√53,所以tan(π-α)=-tanα=-sinαcosα=√52,所以C 中结论正确;对于D,将等式sinα+cosα=1两边平方,得sinαcosα=0,所以sinα=0或cosα=0,若sinα=0,则cosα=1,此时sin n α+cos n α=1,若cosα=0,则sinα=1,此时sin n α+cos n α=1,故sin n α+cos n α=1,所以D 中结论正确.故选CD.3.若sin(π-α)=log 814,且α∈(-π2,0),则cos(π+α)的值为( )A.√53B.-√53C.±√53D.以上都不对-α)=sinα=log 814=lo g 232-2=-23,α∈(-π2,0),∴cos(π+α)=-cosα=-√1-sin 2α=-√1-49=-√53.4.若cos(π+α)=-12,3π2<α<2π,则sin(α-2π)= .-√32cos(π+α)=-12,得cosα=12.又3π2<α<2π,故sin(α-2π)=sinα=-√1-cos 2α=-√1-(12)2=-√32. 5.已知a=tan (-7π6),b=cos23π4,c=sin (-33π4),则a,b,c 的大小关系是 .a=-tan 7π6=-tan π6=-√33,b=cos (6π-π4)=cos π4=√22, c=-sin33π4=-sin π4=-√22, 故b>a>c.6.已知f(x)={sinπx ,x <0,f (x -1)-1,x >0,则f (-116)+f (116)的值为 .解析因为f (-116)=sin (-11π6)=sin -2π+π6=sin π6=12,f (116)=f (56)-1=f (-16)-2=sin (-π6)-2=-12-2=-52,所以f (-116)+f (116)=-2.7.在△ABC 中,若sin(2π-A)=-√2sin(π-B),√3cos A=-√2cos(π-B),求△ABC 的三个内角.sinA=√2sinB,① √3cosA=√2cosB,②①2+②2,得2cos 2A=1,则cosA=±√22. 又A ∈(0,π),所以A=π4或3π4.当A=3π4时,cosB=-√32<0,所以B ∈(π2,π),此时A,B 均为钝角,不符合题意,舍去. 故A=π4,cosB=√32,所以B=π6,所以C=7π12.综上所述,A=π4,B=π6,C=7π12.8.已知f(α)=sin (π+α)cos (2π-α)tan (-α)tan (-π-α)sin (-π-α).(1)化简f(α);(2)若α是第三象限角,且sin(α-π)=15,求f(α)的值;(3)若α=-31π3,求f(α)的值.解(1)f(α)=-sinαcosα(-tanα)(-tanα)sinα=-cosα.(2)∵sin(α-π)=-sinα=15,∴sinα=-15.又α是第三象限角, ∴cosα=-2√65. ∴f(α)=2√65.(3)∵-31π3=-6×2π+5π3,∴f(-31π3)=-cos(-6×2π+5π3)=-cos 5π3=-cos π3=-12.。

5.3 诱导公式（精练）1 诱导公式应用1．(2023湖南）已知角 α 的终边过点(P - ，则 3sin()2πα-= （ ） A ．12-BC ．12D．-2．(2023·全国高一课时练习）化简：sin(5)cos()cos(8)23sin()sin(4)2πθπθπθπθθπ-------=（ ）A ．-sin θB ．sin θC ．cos θD ．-cos θ3．(2023·陕西）sin(600)tan 300-+︒︒的值是（ ） A． BC．12-+D．124(2023天津）（1）化简：3sin(3)cos(2)sin 2cos()sin()παπαπαπαπα⎛⎫-⋅-⋅- ⎪⎝⎭-⋅--（2）求值：()()sin 150cos210cos 420tan60-︒⋅︒⋅-︒⋅︒2 诱导公式与定义、同角三角函数综合1．(2023高一上·南充期末）设角α的顶点与坐标原点重合，始边与x 轴的非负半轴重合，它的终边上有一点(3)P m ，，且4α3tan =-. （1）求m 及ααsin cos ，的值；（2）求2(πα)α(πα)1(πα)sin cos cos tan -++++的值.2．(2023衡阳期末）已知α为第三象限角， ()()()()3sin cos +tan 22tan sin f ππααπαααπαπ⎛⎫⎛⎫-⋅⋅- ⎪ ⎪⎝⎭⎝⎭=--⋅-- ，. （1）化简f(α)； （2）若 31cos 25πα⎛⎫-= ⎪⎝⎭ ，求f(α)的值.3．(2023石家庄期末）已知cos(2)sin()tan()cos()()sin cos 22f πθθπθπθθππθθ--+-=⎛⎫⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭． （1）化简 ()f θ ；（2）若 θ 为第四象限角，且cos 3θ= ，求 ()f θ 的值．4．(2023菏泽期末）已知 ()()()()()sin 180cos 180tan 90sin 270f ααααα︒︒︒︒---=+ .（1）化简 ()f α ； （2）已知 22ππα-<<， ()45f α=，求 tan α .5．(2023铜仁月考）已知 ()()()()()sin sin tan 2tan 2sin f πααπααπαπα⎛⎫--- ⎪⎝⎭=-+ . （1）化简 ()f α .（2）若 α 为第三象限角，且 31cos 25πα⎛⎫-=⎪⎝⎭ ，求 ()f α 的值.6．(2023扬州月考）已知 ()()()()()()21sin cos cos 2tan cos f παααπαπαπα+----=-+ .（1）求 34f π⎛⎫⎪⎝⎭的值； （2）若 ()f α=，且 2παπ<< ，求 sin cos αα- 的值.7．(2023湖南）已知 3sin()cos cos 22()3sin()cos(2)sin tan()2f ππθπθθθππθπθθπθ⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭=⎛⎫---+-- ⎪⎝⎭.（1）化简 ()f θ ； （2）若 ()3f πθ-=- ，求3sin 2cos 5cos 2sin θθθθ-+ 的值；（3）解关于 θ 的不等式：2f πθ⎛⎫≥⎪⎝⎭.3 角的拼凑1．(2023湖南月考）已知α为锐角，若π4α35sin ⎛⎫+= ⎪⎝⎭，则5πα6sin ⎛⎫+= ⎪⎝⎭．2．(2023淄博期末）若 1sin 35πα⎛⎫-= ⎪⎝⎭ ，则 2sin 3πα⎛⎫+= ⎪⎝⎭ ， 5cos 6πα⎛⎫-= ⎪⎝⎭.3．(2023南充期末）若 12sin 313πα⎛⎫+= ⎪⎝⎭ ，则 cos 6πα⎛⎫-= ⎪⎝⎭ ．4．(2023·陕西省洛南中学高一月考）若1sin 63πα⎛⎫+= ⎪⎝⎭，则5sin 6πα⎛⎫-= ⎪⎝⎭__________．5(2023·建平县实验中学高一期末）（多选）已知π1sin 42α⎛⎫+= ⎪⎝⎭，下列结论正确的是（ ）A ．πcos 4α⎛⎫+= ⎪⎝⎭B ．π1cos 42α⎛⎫-= ⎪⎝⎭C ．5π1sin 42α⎛⎫+= ⎪⎝⎭D ．5π1cos 42α⎛⎫-=-⎪⎝⎭5.3 诱导公式（精练）1 诱导公式应用1．(2023湖南）已知角 α 的终边过点(P - ，则 3sin()2πα-= （ ） A ．12-B．2C ．12D．2-答案:C 解析：角 α 的终边过点(1P - ，2OP ∴== ，则1cos 2α=- ，∴31sin()cos 22παα-=-= .故答案为：C. 2．(2023·全国高一课时练习）化简：sin(5)cos()cos(8)23sin()sin(4)2πθπθπθπθθπ-------=（ ）A ．-sin θB ．sin θC ．cos θD ．-cos θ答案:A解析：原式=sin()cos()cos 2cos sin()πθπθθθθ-+-，=2(sin )cos cos (sin )θθθθ--，=-sin θ.故选：A 3．(2023·陕西）sin(600)tan 300-+︒︒的值是（ ） A．BC．12-D．12+答案:A解析：()sin(600)tan 300sin120tan 60sin 60tan 60-+︒=+-︒=︒︒-︒=︒故选：A.4(2023天津）（1）化简：3sin(3)cos(2)sin 2cos()sin()παπαπαπαπα⎛⎫-⋅-⋅- ⎪⎝⎭-⋅--（2）求值：()()sin 150cos210cos 420tan60-︒⋅︒⋅-︒⋅︒ 答案:（1）cos α；（2）38解析：（1）原式()sin cos cos cos cos sin αααααα⋅⋅-==-⋅；（2）原式()()()sin 18030cos 18030cos 36060tan60=-︒+︒⋅︒+︒⋅-︒-︒⋅︒()sin30cos30cos60tan60=-︒⋅-︒⋅︒⋅︒113228⎛=-⨯⨯= ⎝⎭. 2 诱导公式与定义、同角三角函数综合1．(2023高一上·南充期末）设角α的顶点与坐标原点重合，始边与x 轴的非负半轴重合，它的终边上有一点(3)P m ，，且4α3tan =-. （1）求m 及ααsin cos ，的值；（2）求2(πα)α(πα)1(πα)sin cos cos tan -++++的值.答案:见解析解析：（1）解：∵4α33y m tan x ===-，∴4m =-，即(34)P -，，||5OP ∴==4α||5y sin OP ∴==-，3α||5x cos OP ==. （2）解：原式2ααα1αsin cos cos tan +=+α(αα)αααcos sin cos cos sin cos +=+2αcos =925=. 2．(2023衡阳期末）已知α为第三象限角，()()()()3sin cos +tan 22tan sin f ππααπαααπαπ⎛⎫⎛⎫-⋅⋅- ⎪ ⎪⎝⎭⎝⎭=--⋅-- ，. （1）化简f(α)； （2）若 31cos 25πα⎛⎫-= ⎪⎝⎭ ，求f(α)的值. 答案:见解析解析：（1）解： ()()()()3sin cos +tan 22tan sin f ππααπαααπαπ⎛⎫⎛⎫-⋅⋅- ⎪ ⎪⎝⎭⎝⎭=--⋅--()cos sin tan tan sin ααααα-⋅⋅-=-⋅cos α=- ．（2）解：∵31cos 25πα⎛⎫-= ⎪⎝⎭，∴－sinα＝ 15 ，从而sinα＝－ 15 . 又∵α为第三象限角，∴cosα＝－=， ∴f(α)＝－cosα＝. 3．(2023石家庄期末）已知cos(2)sin()tan()cos()()sin cos 22f πθθπθπθθππθθ--+-=⎛⎫⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭． （1）化简 ()f θ ；（2）若 θ 为第四象限角，且cos 3θ=，求 ()f θ 的值． 答案:见解析解析：（1）解：由三角函数诱导公式可知：cos (sin )tan (cos )()cos (sin )f θθθθθθθ--=-tan cos θθ=-sin θ=-（2）解：由题意，sin 3θ==-， 可得()f θ=． 【知识点】同角三角函数间的基本关系；运用诱导公式化简求值 解析：（1）利用已知条件结合诱导公式，进而化简 ()f θ 。

5.3诱导公式课时1诱导公式二、三、四题组一诱导公式求三角函数值1.(6分)cos 585°的值为()A.-√22B.√22C.-√32D.√322.(6分)sin11π6的值是()A.12B.-12C.√32D.-√323.(6分)若cos(π+α)=-12，32π<α<2π，则sin(2π+α)等于()A.12B.±√32C.√32D.-√324.(6分)已知α∈(0，π)，cos(π+α)=35，则sin α= ()A.-45B.45C.-35D.355.(6分)已知α为锐角，且tan(π-α)+3=0，则sin α的值()A.13B.3√1010C.3√77D.3√556.(6分)若tan(5π+α)=m，则sin(α-3π)+cos(π-α)sin(-α)-cos(π+α)的值为( )A.m+1m -1B.m -1m+1C.-1D.17.(6分)已知sin(α-360°)-cos(180°-α)=m ，则sin(180°+α)·cos(180°-α)等于( )A.m 2-12 B.m 2+12 C.1-m 22 D.-m 2+128.(6分)已知sin(45°+α)=513，则sin(225°+α)= . 9.(6分)已知sin(3π+θ)=lg 103，则cos (π+θ)cosθ[cos (π-θ)-1]+cos (θ-2π)cosθ·cos (π-θ)+cos (θ-2π)= . 题组二 利用诱导公式对三角函数式化简与求值10.(11分)化简：tan (2π-θ)sin (-2π-θ)cos (6π-θ)cos (θ-π)sin (5π+θ).11.(11分)已知cos(π6-α)=√33，求cos(56π+α)-sin 2(α-π6)的值.12.(12分)若cos(α-π)=-23，求sin (α-2π)+sin (-α-3π)cos (α-3π)cos (π-α)-cos (-π-α)cos (α-4π)的值.13.(12分)已知tan α，1tanα是关于x 的方程3x 2-3kx+3k 2-13=0的两实根，且3π<α<7π2，求cos(2π-α)+sin(2π+α)的值.参考答案1.A 解析：本题考查利用诱导公式求余弦值.注意到585°=360°+180°+45°，因此cos 585°=cos(360°+180°+45°)=-cos 45°=-√22. 2.B 解析：本题考查利用诱导公式求正弦值.sin 11π6=sin(2π-π6)=sin(-π6)=-sin π6=-12. 3.D 解析：本题考查利用诱导公式求正弦值.已知cos(π+α)=-12，得cos α=12，∴sin(2π+α)=sin α=-√1-cos 2α=-√32(α为第四象限角). 4.B 解析：本题考查利用诱导公式求正弦值.依题意得-cos α=35，cos α=-35，sin α=√1-cos 2α=45. 5.B 解析：本题考查利用诱导公式与同角三角函数关系求值.由正切的诱导公式得 tan(π-α)=- tan α，故 tan(π-α)+3=0⇒ tan α=3，因为α为锐角，所以sin α>0，sin α=3√1010. 6.A 解析：本题考查利用诱导公式与同角三角函数关系化简求值.由题意 tan α=m ， 原式=sinα+cosαsinα-cosα=tanα+1tanα-1=m+1m -1. 7.A 解析：本题考查利用诱导公式与同角三角函数关系化简求值. sin(α-360°)-cos(180°-α)=sin α+cos α=m ，sin(180°+α)·cos(180°-α)=(-sin α)·(-cos α)=sin α·cos α=(sinα+cosα)2-12=m 2-12. 8.-513解析：本题考查诱导公式的简单应用. sin(225°+α)=sin[(45°+α)+180°]=-sin(45°+α)=-513. 9.18 解析：本题考查利用诱导公式与同角三角函数关系化简求值.由已知可得sin θ=13.原式=-cosθcosθ(-cosθ-1)+cosθcosθ(-cosθ)+cosθ=1cosθ+1+11-cosθ=21-cos 2θ=2sin 2θ=18.10.解析：本题考查利用诱导公式与同角三角函数关系化简求值.原式=tan (-θ)·sin (-θ)·cos (-θ)cos (π-θ)·sin (π+θ)= (-tanθ)·(-sinθ)·cosθ(-cosθ)·(-sinθ)=tanθsinθcosθcosθsinθ=tan θ. 11.解析：本题考查利用诱导公式与同角三角函数关系化简求值.cos(56π+α)-sin 2(α-π6)=cos[π-(π6-α)]-sin 2(π6-α)=-cos(π6-α)-[1-cos 2(π6-α)]=cos 2(π6-α)-cos(π6-α)-1=(√33)2-√33-1=-2+√33. 12.解析：本题考查利用诱导公式与同角三角函数关系化简求值. 原式=-sin (2π-α)-sin (3π+α)cos (3π-α)-cosα-(-cosα)cosα =sinα-sinαcosα-cosα+cos 2α=sinα(1-cosα)-cosα(1-cosα)=-tan α. ∵cos(α-π)=cos(π-α)=-cos α=-23，∴cos α=23.∴α为第一象限角或第四象限角.当α为第一象限角时，cos α=23，sin α=√1-cos 2α=√53，∴tan α=sinαcosα=√52，∴原式=-√52. 当α为第四象限角时，cos α=23，sin α=-√1-cos 2α=-√53，∴tan α=sinαcosα=-√52，∴原式=√52. 综上所得，原式=±√52. 13.解析：本题考查利用诱导公式与同角三角函数关系化简求值. 因为tan α，1tanα是关于x 的方程3x 2-3kx+3k 2-13=0的两实根， 所以tan α·1tanα=13·(3k 2-13)=1，可得k 2=163.因为3π<α<7π2，所以tan α>0，sin α<0，cos α<0，又因为tan α+1tanα=--3k 3=k ，所以k>0，故k=4√33， 所以tan α+1tanα=sinαcosα+cosαsinα=1sinαcosα=4√33，所以sin αcos α=√34， 所以(cos α+sin α)2=1+2sin αcos α=1+2·√34=2+√32. 因为cos α+sin α<0，所以cos α+sin α=-√3+12.所以cos(2π-α)+sin(2π+α)=cos α+sin α=-√3+12.。

滚动复习9一、选择题(每小题5分，共40分) 1．sin(－16π3)的值为( D ) A ．－32B ．－12C.12D.32解析：sin(－16π3)＝－sin 16π3＝－sin(5π＋π3)＝－(－sin π3)＝32，故选D.2．化简sin 2(π＋α)－cos(π＋α)·cos(－α)＋1的值为( D )A ．1B ．2sin 2αC ．0D ．2解析：原式＝(－sin α)2－(－cos α)·cos α＋1＝sin 2α＋cos 2α＋1＝2.3．已知cos α＝k ，k ∈R ，α∈(π2，π)，则sin(π＋α)＝( A )A ．－1－k 2B.1－k 2C ．±1－k 2D ．－k解析：∵cos α＝k ，α∈(π2，π)，∴sin α＝1－cos 2α＝1－k 2，∴sin(π＋α)＝－sin α＝－1－k 2，故选A.4．若角α的终边经过点P (sin780°，cos(－330°))，则sin α＝( C ) A.32B.12 C.22D ．1解析：因为sin780°＝sin(2×360°＋60°)＝sin60°＝32，cos(－330°)＝cos(－360°＋30°)＝cos30°＝32，所以P (32，32)，所以sin α＝22.5．化简sin(α＋π2)·cos(α－3π2)·tan(π2－α)的结果是( C )A ．1B ．sin 2αC ．－cos 2αD ．－1解析：因为sin(α＋π2)＝cos α，cos(α－3π2)＝cos[π＋(π2－α)]＝－sin α，tan(π2－α)＝sin (π2－α)cos (π2－α)＝cos αsin α，所以原式＝cos α·(－sin α)cos αsin α＝－cos 2α，选C.6．若|sin α|＝cos(π2＋α)，则角α的集合为( D )A ．{α|2k π≤α≤π＋2k π，k ∈Z }B ．{α|2k π≤α≤π2＋2k π，k ∈Z }C ．{α|2k π≤α≤3π2＋2k π，k ∈Z }D ．{α|π＋2k π≤α≤2π＋2k π，k ∈Z }解析：本题考查三角函数的诱导公式以及三角函数值符号的判定．∵|sin α|＝cos(π2＋α)＝－sin α，∴sin α≤0，∴角α的集合为{α|π＋2k π≤α≤2π＋2k π，k ∈Z }，故选D.7．已知cos29°＝m ，则sin241°tan151°的值是( B )A.1－m 2mB.1－m 2C.m 2－1m D ．－1－m 2解析：本题考查诱导公式以及平方关系式的应用．∵sin241°＝sin(180°＋61°)＝－sin61°＝－cos29°，tan151°＝tan(180°－29°)＝－tan29°，∴sin241°tan151°＝sin29°＝1－cos 229°＝1－m 2，故选B.8．k 为整数，化简sin[(k ＋1)π＋θ]·cos[(k ＋1)π－θ]sin (k π－θ)·cos (k π＋θ)的结果是( B )A ．±1B ．－1C ．1D ．tan θ解析：当k 为偶数时，设k ＝2n ，n ∈Z ，则原式＝sin[(2n ＋1)π＋θ]·cos[(2n ＋1)π－θ]sin (2n π－θ)·cos (2n π＋θ)＝sin (π＋θ)·cos (π－θ)－sin θ·cos θ＝－sin θ·(－cos θ)－sin θ·cos θ＝－1.当k 为奇数时，设k ＝2n ＋1，n ∈Z ，则原式＝sin[(2n ＋2)π＋θ]·cos[(2n ＋2)π－θ]sin[(2n ＋1)π－θ]·cos[(2n ＋1)π＋θ]＝sin[2(n ＋1)π＋θ]·cos[2(n ＋1)π－θ]sin (π－θ)·cos (π＋θ)＝sin θ·cos θsin θ·(－cos θ)＝－1. 综上，原式的值为－1.二、填空题(每小题5分，共15分)9．sin315°－cos135°＋2sin570°的值是－1.解析：本题考查三角函数的诱导公式的应用．原式＝sin(360°－45°)－cos(180°－45°)＋2sin(360°＋210°)＝－sin45°＋cos45°＋2sin210°＝－22＋22＋2sin(180°＋30°)＝－2sin30°＝－2×12＝－1.10．已知cos(π2＋φ)＝32，且|φ|<π2，则tan φ＝－ 3.解析：本题考查利用三角函数的诱导公式解决求值问题．由cos(π2＋φ)＝32，得sin φ＝－32，又|φ|<π2，∴φ＝－π3，∴tan φ＝－ 3. 11．给出下列四个结论，其中正确的结论序号是③④.①sin(π＋α)＝－sin α成立的条件是角α是锐角；②若cos(n π－α)＝13(n ∈Z )，则cos α＝13；③若α≠k π2(k ∈Z )，则tan(π2＋α)＝－1tan α；④若sin α＋cos α＝1，则sin n α＋cos n α＝1.解析：由诱导公式二，知α∈R 时，sin(π＋α)＝－sin α，所以①错误．当n ＝2k (k ∈Z )时，cos(n π－α)＝cos(2k π－α)＝cos(－α)＝cos α，此时cos α＝13，当n ＝2k ＋1(k ∈Z )时，cos(n π－α)＝cos[(2k ＋1)π－α]＝cos(π－α)＝－cos α，此时cos α＝－13，所以②错误．若α≠k π2(k ∈Z )，则tan(π2＋α)＝sin (π2＋α)cos (π2＋α)＝cos α－sin α＝－1tan α，所以③正确．将等式sin α＋cos α＝1两边平方，得sin αcos α＝0，所以sin α＝0或cos α＝0.若sin α＝0，则cos α＝1，此时sin n α＋cos n α＝1；若cos α＝0，则sin α＝1，此时sin n α＋cos n α＝1，故sin n α＋cos n α＝1.所以④正确．三、解答题(共45分)12．(15分)化简：cos (π－θ)cos θ[sin (3π2－θ)－1]＋cos (2π－θ)cos (π＋θ)sin (π2＋θ)－sin (3π2＋θ). 解：原式＝－cos θcos θ(－cos θ－1)＋cos θ－cos θcos θ＋cos θ＝11＋cos θ＋11－cos θ＝1－cos θ＋1＋cos θ(1＋cos θ)(1－cos θ)＝21－cos 2θ＝2sin 2θ.13．(15分)已知sin α是方程5x 2－7x －6＝0的根，且α是第三象限角，求sin (－α－3π2)cos (3π2－α)cos (π2－α)sin (π2＋α)·tan 2(π－α)的值． 解：原式＝－sin (π＋π2＋α)cos (π＋π2－α)sin αcos α·tan 2α ＝－sin (π2＋α)cos (π2－α)sin αcos α·tan 2α＝－cos αsin αsin αcos α·tan 2α＝－tan 2α. ∵方程5x 2－7x －6＝0的两根为x 1＝－35，x 2＝2. 又α是第三象限角，∴sin α＝－35，cos α＝－45.∴tan α＝34，故原式＝－tan 2α＝－916.14．(15分)已知A ，B ，C 为△ABC 的内角．(1)求证：cos 2A ＋B 2＋cos 2C 2＝1； (2)若cos(π2＋A )sin(3π2＋B )tan(C －π)<0，求证：△ABC 为钝角三角形．证明：(1)∵在△ABC 中，A ＋B ＝π－C ，∴A ＋B 2＝π2－C 2，∴cos A ＋B 2＝cos(π2－C 2)＝sin C 2.∴cos 2A ＋B 2＋cos 2C 2＝sin 2C 2＋cos 2C 2＝1. (2)∵cos(π2＋A )sin(3π2＋B )tan(C －π)<0，∴－sin A ·(－cos B )·tan C <0，即sin A cos B tan C <0. 又A ，B ，C ∈(0，π)，∴sin A >0，∴cos B tan C <0， 即cos B <0，tan C >0或tan C <0，cos B >0，∴B 为钝角或C 为钝角，∴△ABC 为钝角三角形．。