计量经济学第五章 异方差性

第五章 异方差二、简答题1．异方差的存在对下面各项有何影响？ （1）OLS 估计量及其方差； （2）置信区间；（3）显著性t 检验和F 检验的使用。

2．产生异方差的经济背景是什么？检验异方差的方法思路是什么？ 3．从直观上解释，当存在异方差时，加权最小二乘法（WLS ）优于OLS 法。

4．下列异方差检查方法的逻辑关系是什么？ （1）图示法 （2）Park 检验 （3）White 检验5．在一元线性回归函数中，假设误差方差有如下结构：()i i i x E 22σε=如何变换模型以达到同方差的目的？我们将如何估计变换后的模型？请列出估计步骤。

三、计算题1．考虑如下两个回归方程（根据1946—1975年美国数据）（括号中给出的是标准差）：t t t D GNP C 4398.0624.019.26-+= e s ：（2.73）（0.0060） （0.0736）R ²=0.999t t t GNP D GNP GNP C ⎥⎦⎤⎢⎣⎡-+=⎥⎦⎤⎢⎣⎡4315.06246.0192.25 e s ： （2.22） （0.0068）（0.0597）R ²=0.875式中，C 为总私人消费支出；GNP 为国民生产总值；D 为国防支出；t 为时间。

研究的目的是确定国防支出对经济中其他支出的影响。

（1）将第一个方程变换为第二个方程的原因是什么？（2）如果变换的目的是为了消除或者减弱异方差，那么我们对误差项要做哪些假设？ （3）如果存在异方差，是否已成功地消除异方差？请说明原因。

（4）变换后的回归方程是否一定要通过原点？为什么？（5）能否将两个回归方程中的R²加以比较？为什么？2．1964年，对9966名经济学家的调查数据如下：资料来源：“The Structure of Economists’Employment and Salaries”, Committee on the National Science Foundation Report on the Economics Profession, American Economics Review, vol.55, No.4, December 1965.（1）建立适当的模型解释平均工资与年龄间的关系。

第5章异 方 差习 题一、单项选择题1． 回归模型中具有异方差性时，仍用OLS 估计模型，则以下说法正确的是（ ）A. 参数估计值是无偏非有效的B. 参数估计量仍具有最小方差性C. 常用F 检验失效D. 参数估计量是有偏的 2．更容易产生异方差的数据为 ( )A. 时序数据B. 修匀数据C. 横截面数据D. 年度数据 3．在具体运用加权最小二乘法时, 如果变换的结果是则Var(u)是下列形式中的哪一种?( )A. B. C. D.4. 在异方差性情况下，常用的估计方法是（ ）A ．一阶差分法 B. 广义差分法 C ．工具变量法 D. 加权最小二乘法 5. 在异方差的情况下，参数估计值的方差不能正确估计的原因是（ ）A. B.C. D. 6. 设，则对原模型变换的正确形式为( )7. 下列说法不正确的是（ ）A.异方差是一种随机误差现象B.异方差产生的原因有设定误差C.检验异方差的方法有F 检验法D.修正异方差的方法有加权最小二乘法8. 如果回归模型违背了同方差假定，最小二乘估计是（ ）A ．无偏的，非有效的 B. 有偏的，非有效的011yx ux x x x ββ=++2x σ22xσσ2log x σ22()i E u σ≠()0()i j E u u i j ≠≠()0i i E x u ≠()0i E u ≠)()(,2221i i i i i i x f u Var u x y σσββ==++=01212222212...()()()().()()()()i i i i i i i i i i i i i i i i i A y x u B y x u C f x f x f x f x D y f x f x x f x u f x βββββββ=++=+=++=++C ．无偏的，有效的 D. 有偏的，有效的 9. 在检验异方差的方法中，不正确的是（ ）A. Goldfeld-Quandt 方法B. ARCH 检验法C. White 检验法D. DW 检验法10. 在异方差的情况下，参数估计值仍是无偏的，其原因是（ ）A.零均值假定成立B.序列无自相关假定成立C.无多重共线性假定成立D.解释变量与随机误差项不相关假定成立11. 在修正异方差的方法中，不正确的是（ ）A.加权最小二乘法B.对原模型变换的方法C.对模型的对数变换法D.两阶段最小二乘法 12. 下列说法正确的是（ ）A.异方差是样本现象B.异方差的变化与解释变量的变化有关C.异方差是总体现象D.时间序列更易产生异方差二、多项选择题1． 如果模型中存在异方差现象，则会引起如下后果（ ）A. 参数估计值有偏B. 参数估计值的方差不能正确确定C. 变量的显著性检验失效D. 预测精度降低E. 参数估计值仍是无偏的2． Goldfeld-Quandt 检验法的应用条件是（ ）A. 将观测值按解释变量的大小顺序排列B. 样本容量尽可能大C. 随机误差项服从正态分布D. 将排列在中间的约1/4的观测值删除掉 E ．除了异方差外，其它假定条件均满足三、计算题1．根据某城市1978——1998年人均储蓄(y)与人均收入(x)的数据资料建立了如下回归模型x y6843.1521.2187ˆ+-=se=（340.0103）（0.0622）下面取时间段1978——1985和1991——1998，分别建立两个模型（括号内为t 值）， 模型1：模型2：计算F 统计量，即，对给定的，查F 分布表，得临界值。

计量经济学第五章异⽅差性第五章异⽅差性本章教学要求：根据类型，异⽅差性是违背古典假定情况下线性回归模型建⽴的另⼀问题。

通过本章的学习应达到，掌握异⽅差的基本概念包括经济学解释，异⽅差的出现对模型的不良影响，诊断异⽅差的⽅法和修正异⽅差的若⼲⽅法。

经过学习能够处理模型中出现的异⽅差问题。

第⼀节异⽅差性的概念⼀、⼆个例⼦例1，研究我国制造业利润函数，选取销售收⼊作为解释变量，数据为1998年的⾷品年制造业、饮料制造业等28个截⾯数据（即n=28）。

数据如下表,其中y表⽰制造业利润函数，x表⽰销售收⼊（单位为亿元）。

Y对X的散点图为从散点图可以看出，在线性的基础上，有的点分散幅度较⼩，有的点分散幅度较⼤。

因此，这种分散幅度的⼤⼩不⼀致，可以认为是由于销售收⼊的影响，使得制造业利润偏离均值的程度发⽣变化，⽽偏离均值的程度⼤⼩的不同，就是所谓的随机误差的⽅差存在变异，即异⽅差。

如果⾮线性，则属于哪类⾮线性，从图形所反映的特征看，并不明显。

下⾯给出制造业利润对销售收⼊的回归估计。

模型的书写格式为212.03350.1044(0.6165)(12.3666)0.8547,..56.9046,152.9322213.4639,146.4905Y Y X R S E F Y s =+=====通过变量的散点图、参数估计、残差图，可以看到模型中（随机误差）很有可能存在异⽅差性。

例2，改⾰开放以来，各地区的医疗机构都有了较快发展，不仅政府建⽴了⼀批医疗机构，还建⽴了不少民营医疗机构。

各地医疗机构的发展状况，除了其他因素外主要决定于对医疗服务的需求量，⽽医疗服务需求与⼈⼝数量有关。

为了给制定医疗机构的规划提供依据，分析⽐较医疗机构与⼈⼝数量的关系，建⽴卫⽣医疗机构数与⼈⼝数的回归模型。

根据四川省2000年21个地市州医疗机构数与⼈⼝数资料对模型估计的结果如下：i iX Y 3735.50548.563?+-= （291.5778） (0.644284) t =(-1.931062) (8.340265)785456.02=R 774146.02=R 56003.69=F式中Y 表⽰卫⽣医疗机构数（个），X 表⽰⼈⼝数量（万⼈）。

第五章-异方差性-答案第五章 异方差性一、判断题1. 在异方差的情况下，通常预测失效。

（ T ）2. 当模型存在异方差时，普通最小二乘法是有偏的。

（ F ）3. 存在异方差时，可以用广义差分法进行补救。

（F ）4. 存在异方差时，普通最小二乘法会低估参数估计量的方差。

（F ）5. 如果回归模型遗漏一个重要变量，则OLS 残差必定表现出明显的趋势。

（ T ）二、单项选择题1.Goldfeld-Quandt 方法用于检验（ A ）A.异方差性B.自相关性C.随机解释变量D.多重共线性2.在异方差性情况下，常用的估计方法是（ D ）A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法3.White 检验方法主要用于检验（ A ）A.异方差性B.自相关性C.随机解释变量D.多重共线性4.下列哪种方法不是检验异方差的方法（ D ）A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数，从而提高估计精度，即（ B ）A.重视大误差的作用，轻视小误差的作用B.重视小误差的作用，轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用6.如果戈里瑟检验表明，普通最小二乘估计结果的残差与有显著的形式的相关关系（满足线性模型的全部经典假设），则用加权最小二乘法估计模型参数时，权数应为（ B ）A. B. C. D. 7.设回归模型为，其中()2i2i x u Var σ=，则b 的最有效估计量为（ D ）i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=A. B. C. D. ∑=i i x y n 1b ˆ 8.容易产生异方差的数据是（ C ）A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=，则使用加权最小二乘法估计模型时，应将模型变换为（ C ）。

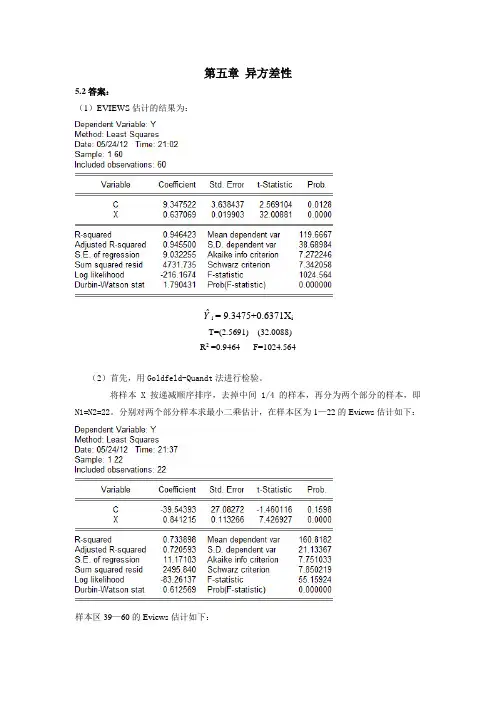
第五章异方差性5.2答案：（1）EVIEWS估计的结果为：Yˆi= 9.3475+0.6371X iT=(2.5691) (32.0088)R2 =0.9464 F=1024.564（2）首先，用Goldfeld-Quandt法进行检验。

将样本X按递减顺序排序，去掉中间1/4的样本，再分为两个部分的样本，即N1=N2=22。

分别对两个部分样本求最小二乘估计，在样本区为1—22的Eviews估计如下：样本区39—60的Eviews估计如下：得到两个部分各自的残差平方和，即∑e 12 =2495.840∑e 22 =603.0148求F 统计量为： F=∑∑e e 2221=2495.840/603.0148=4.1390给定α=0.05，查F 分布表，得临界值为F 0.05=(20,20)=2.12.比较临界值与F 统计量值，有F =4.1390>F 0.05=(20,20)=2.12，说明该模型的随机误差项存在异方差。

其次，用White 法进行检验结果如下：给定α=0.05，在自由度为2下查卡方分布表，得χ2=5.9915。

比较临界值与卡方统计量值，即nR2=10.8640>χ2=5.9915，同样说明模型中的随机误差项存在异方差。

（2）用权数W1=1/X，作加权最小二乘估计，得如下结果用White法进行检验得如下结果：F-statistic 3.138491 Probability 0.050925Obs*R-squared 5.951910 Probability 0.050999。

比较临界值与卡方统计量值，即nR2=5.9519<χ2=5.9915，说明加权后的模型中的随机误差项不存在异方差。

其估计的结果为：Yˆi= 10.3705+0.6309X iT=(3.9436) (34.0467)R2 =0.21144 F=1159.176 DW=0.95855.3答案：（1）EVIEWS估计结果：Yˆi= 179.1916+0.7195X iT=(0.808709) (15.74411)R2 =0.895260 F=247.8769 DW=1.461684 （2）利用White方法检验异方差，则White检验结果见下表：由上述结果可知，该模型存在异方差。

第五章 异方差性思考题5.1 简述什么是异方差？为什么异方差的出现总是与模型中某个解释变量的变化有关？答 ：设模型为),....,,(....n 21i X X Y i i 33i 221i =μ+β++β+β=，如果其他假定均不变，但模型中随机误差项的方差为),...,,()(n 21i Var 2i i =σ=μ，则称i μ具有异方差性。

由于异方差性指的是被解释变量观测值的分散程度是随解释变量的变化而变化的，所以异方差的出现总是与模型中某个解释变量的变化有关。

5.2 试归纳检验异方差方法的基本思想，并指出这些方法的异同。

答：各种异方差检验的共同思想是，基于不同的假定，分析随机误差项的方差与解释变量之间的相关性，以判断随机误差项的方差是否随解释变量变化而变化。

其中，戈德菲尔德-跨特检验、怀特检验、ARCH 检验和Glejser 检验都要求大样本，其中戈德菲尔德-跨特检验、怀特检验和Glejser 检验对时间序列和截面数据模型都可以检验，ARCH 检验只适用于时间序列数据模型中。

戈德菲尔德-跨特检验和ARCH 检验只能判断是否存在异方差，怀特检验在判断基础上还可以判断出是哪一个变量引起的异方差。

Glejser 检验不仅能对异方差的存在进行判断，而且还能对异方差随某个解释变量变化的函数形式进行诊断。

5.3 什么是加权最小二乘法？它的基本思想是什么？答：以一元线性回归模型为例：12i i i Y X u ββ=++经检验i μ存在异方差，公式可以表示为22var()()i i i u f X σσ==。

选取权数 i w ，当2i σ 越小 时，权数i w 越大。

当 2i σ越大时，权数i w 越小。

将权数与 残差平方相乘以后再求和，得到加权的残差平方和：2i 21i 2i i X Y w e w )(**β-β-=∑∑，求使加权残差平方和最小的参数估计值**ˆˆ21ββ和。

这种求解参数估计式的方法为加权最小二乘法。

第五章 异方差性一、判断题1. 在异方差的情况下，通常预测失效。

（ T ）2. 当模型存在异方差时，普通最小二乘法是有偏的。

（ F ）3. 存在异方差时，可以用广义差分法进行补救。

（F ）4. 存在异方差时，普通最小二乘法会低估参数估计量的方差。

（F ）5. 如果回归模型遗漏一个重要变量，则OLS 残差必定表现出明显的趋势。

（ T ） 二、单项选择题1.Goldfeld-Quandt 方法用于检验（ A ）A.异方差性B.自相关性C.随机解释变量D.多重共线性 2.在异方差性情况下，常用的估计方法是（ D ）A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法 3.White 检验方法主要用于检验（ A ）A.异方差性B.自相关性C.随机解释变量D.多重共线性 4.下列哪种方法不是检验异方差的方法（ D ）A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验 5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数，从而提高估计精度，即（ B ）A.重视大误差的作用，轻视小误差的作用B.重视小误差的作用，轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用 6.如果戈里瑟检验表明，普通最小二乘估计结果的残差与有显著的形式的相关关系（满足线性模型的全部经典假设），则用加权最小二乘法估计模型参数时，权数应为（ B ） A. B.C. D.7.设回归模型为，其中()2i2i x u Var σ=，则b 的最有效估计量为（ D ）A. B.C. D. ∑=ii x y n 1b ˆ8.容易产生异方差的数据是（ C ）A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=，则使用加权最小二乘法估计模i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=∑∑=2ˆxxy b 22)(ˆ∑∑∑∑∑--=x x n y x xy n b xyb=ˆ型时，应将模型变换为（ C ）。

计量经济学第五章异⽅差性参考答案讲解第五章异⽅差性课后题参考答案 5.1（1）因为22()i i f X X =，所以取221iiW X =，⽤2i W 乘给定模型两端，得 312322221i i ii i i i Y X u X X X X βββ=+++ 上述模型的随机误差项的⽅差为⼀固定常数，即22221()()i i i iu Var Var u X X σ==（2）根据加权最⼩⼆乘法，可得修正异⽅差后的参数估计式为***12233Y X X βββ=-- ()()()()()()()***2****22232322322*2*2**2223223?i i i i i i i i i i i i i i i i i iW y x W x W y x W x x W x W x W x x β-=-∑∑∑∑∑∑∑()()()()()()()***2****23222222332*2*2**2223223?ii ii i i iii i i ii i i i i iW y x W x W y x W x x Wx W x W x x β-=-∑∑∑∑∑∑∑其中22232***23222,,iii i i i iiiW XW X W Y X X Y WWW ===∑∑∑∑∑∑******222333i i i i i x X X x X X y Y Y=-=-=- 5.2 （1）2222211111 ln()ln()ln(1)1 u ln()1Y X Y X Yu u X X X u ββββββββββ--==+≈=-∴=+ [ln()]0 ()[ln()1][ln()]11E u E E u E u µ=∴=+=+=⼜（2）[ln()]ln ln 0 1 ()11i i iiP P i i i i P P i i E P E µµµµµµµ===?====∑∏∏∑∏∏不能推导出所以E 1µ（）=时，不⼀定有E 0µ（ln ）= (3)对⽅程进⾏差分得：1)i i βµµ--i i-12i i-1lnY -lnY =(lnX -X )+(ln ln则有：1)]0i i µµ--=E[(ln ln5.3（1）该模型样本回归估计式的书写形式为：Y = 11.44213599 + 0.6267829962*X (3.629253) (0.019872)t= 3.152752 31.5409720.944911R =20.943961R = S.E.=9.158900 DW=1.597946 F=994.8326（2）⾸先，⽤Goldfeld-Quandt 法进⾏检验。

第五章 异方差性一、判断题1. 在异方差的情况下，通常预测失效。

（ T ）2. 当模型存在异方差时，普通最小二乘法是有偏的。

（ F ）3. 存在异方差时，可以用广义差分法进行补救。

（F ）4. 存在异方差时，普通最小二乘法会低估参数估计量的方差。

（F ）5. 如果回归模型遗漏一个重要变量，则OLS 残差必定表现出明显的趋势。

（ T ） 二、单项选择题1.Goldfeld-Quandt 方法用于检验（ A ）A.异方差性B.自相关性C.随机解释变量D.多重共线性 2.在异方差性情况下，常用的估计方法是（ D ）A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法 3.White 检验方法主要用于检验（ A ）A.异方差性B.自相关性C.随机解释变量D.多重共线性 4.下列哪种方法不是检验异方差的方法（ D ）A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验 5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数，从而提高估计精度，即（ B ）A.重视大误差的作用，轻视小误差的作用B.重视小误差的作用，轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用 6.如果戈里瑟检验表明，普通最小二乘估计结果的残差与有显著的形式的相关关系（满足线性模型的全部经典假设），则用加权最小二乘法估计模型参数时，权数应为（ B ） A. B.C. D.7.设回归模型为，其中()2i2i x u Var σ=，则b 的最有效估计量为（ D ）A. B.C. D. ∑=ii x y n 1b ˆ8.容易产生异方差的数据是（ C ）A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=，则使用加权最小二乘法估计模i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=∑∑=2ˆxxy b 22)(ˆ∑∑∑∑∑--=x x n y x xy n b xyb=ˆ型时，应将模型变换为（ C ）。