7第五章 计量经济学检验

第五章 异方差二、简答题1．异方差的存在对下面各项有何影响？ （1）OLS 估计量及其方差； （2）置信区间；（3）显著性t 检验和F 检验的使用。

2．产生异方差的经济背景是什么？检验异方差的方法思路是什么？ 3．从直观上解释，当存在异方差时，加权最小二乘法（WLS ）优于OLS 法。

4．下列异方差检查方法的逻辑关系是什么？ （1）图示法 （2）Park 检验 （3）White 检验5．在一元线性回归函数中，假设误差方差有如下结构：()i i i x E 22σε=如何变换模型以达到同方差的目的？我们将如何估计变换后的模型？请列出估计步骤。

三、计算题1．考虑如下两个回归方程（根据1946—1975年美国数据）（括号中给出的是标准差）：t t t D GNP C 4398.0624.019.26-+= e s ：（2.73）（0.0060） （0.0736）R ²=0.999t t t GNP D GNP GNP C ⎥⎦⎤⎢⎣⎡-+=⎥⎦⎤⎢⎣⎡4315.06246.0192.25 e s ： （2.22） （0.0068）（0.0597）R ²=0.875式中，C 为总私人消费支出；GNP 为国民生产总值；D 为国防支出；t 为时间。

研究的目的是确定国防支出对经济中其他支出的影响。

（1）将第一个方程变换为第二个方程的原因是什么？（2）如果变换的目的是为了消除或者减弱异方差，那么我们对误差项要做哪些假设？ （3）如果存在异方差，是否已成功地消除异方差？请说明原因。

（4）变换后的回归方程是否一定要通过原点？为什么？（5）能否将两个回归方程中的R²加以比较？为什么？2．1964年，对9966名经济学家的调查数据如下：资料来源：“The Structure of Economists’Employment and Salaries”, Committee on the National Science Foundation Report on the Economics Profession, American Economics Review, vol.55, No.4, December 1965.（1）建立适当的模型解释平均工资与年龄间的关系。

第一章：绪论1.计量经济学的学科属性、计量经济学与经济学、数学、统计学的关系；2.计量经济研究的四个基本步骤（1）建立模型（依据经济理论建立模型,通过模型识别、格兰杰因果关系检验、协整关系检验建立模型）；（2）估计模型参数（满足基本假设采用最小二乘法，否则采用其他方法：加权最小二乘估计、模型变换、广义差分法等）；（3 ）模型检验:经济意义检验（普通模型、双对数模型、半对数模型中的经济意义解释，见例1、例2 ）,统计检验（T检验，拟合优度检验、F检验,联合检验等）；计量经济学检验（异方差、自相关、多重共线性、在时间序列模型中残差的白噪声检验等）；（4 ）模型应用。

例1:在模型中，y某类商品的消费支出，x收入，P商品价格，试对模型进行经济意义检验，并解释A"》的经济学含义。

In X = 0.213 +0.25 In 一0.31£其中参数卩'",都可以通过显著性检验。

经济意义检验可以通过（商品需求与收入正相关、与商品价格负相关\商品消费支出关于收入的弹性为0.25 （ 1心/畑）=0.251】心/仏））；价格增加一个单位，商品消费需求将减少31%。

例2 :硏究金融发展与贫富差距的关系，认为金融发展先使贫富差距加大（恶化）, 尔后会使贫富差距降＜氐（好转），成为倒U型。

贫富差距用GINI系数表示，金融发展用（贷款余额/存款总额）表示。

回归结果G/^VZ r =2.34 + 0.641；-1.29x；/模型参数都可以通过显著性检验。

在X的有意义的变化范围内,GINI系数的值总是大于1 ,细致分析后模型变的毫无意义；同样的模型还有：GINI系数的值总是为负= —13.34 + 7.12 兀一14.31#O3.计量经济学中的一些基本概念数据的三种类型：横截面数据、时间序列数据、面板数据；线性模型的概念；模型的解释变量与被解释变量，被解释变量为随机变量（如果—个变量为随机变量,并与随机扰动项相关，这个变量称为内生变量），被解释变量为内生变量,有些解释变量也为内生变量。

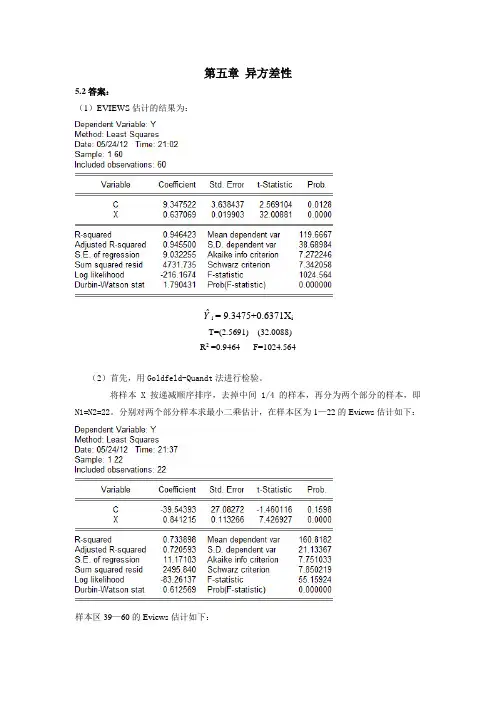
第五章异方差性5.2答案：（1）EVIEWS估计的结果为：Yˆi= 9.3475+0.6371X iT=(2.5691) (32.0088)R2 =0.9464 F=1024.564（2）首先，用Goldfeld-Quandt法进行检验。

将样本X按递减顺序排序，去掉中间1/4的样本，再分为两个部分的样本，即N1=N2=22。

分别对两个部分样本求最小二乘估计，在样本区为1—22的Eviews估计如下：样本区39—60的Eviews估计如下：得到两个部分各自的残差平方和，即∑e 12 =2495.840∑e 22 =603.0148求F 统计量为： F=∑∑e e 2221=2495.840/603.0148=4.1390给定α=0.05，查F 分布表，得临界值为F 0.05=(20,20)=2.12.比较临界值与F 统计量值，有F =4.1390>F 0.05=(20,20)=2.12，说明该模型的随机误差项存在异方差。

其次，用White 法进行检验结果如下：给定α=0.05，在自由度为2下查卡方分布表，得χ2=5.9915。

比较临界值与卡方统计量值，即nR2=10.8640>χ2=5.9915，同样说明模型中的随机误差项存在异方差。

（2）用权数W1=1/X，作加权最小二乘估计，得如下结果用White法进行检验得如下结果：F-statistic 3.138491 Probability 0.050925Obs*R-squared 5.951910 Probability 0.050999。

比较临界值与卡方统计量值，即nR2=5.9519<χ2=5.9915，说明加权后的模型中的随机误差项不存在异方差。

其估计的结果为：Yˆi= 10.3705+0.6309X iT=(3.9436) (34.0467)R2 =0.21144 F=1159.176 DW=0.95855.3答案：（1）EVIEWS估计结果：Yˆi= 179.1916+0.7195X iT=(0.808709) (15.74411)R2 =0.895260 F=247.8769 DW=1.461684 （2）利用White方法检验异方差，则White检验结果见下表：由上述结果可知，该模型存在异方差。

Chapter 5. Regression with a Single Regressor: Hypothesis Tests and Confidence Intervals5.1 Testing Hypotheses about One of the Regression Coefficients（对单一系数的假设检验）Suppose a skeptic suggests that reducing the number of students in a class has no effect on learning or, specifically, test scores. The skeptic thus asserts the hypothesis,1H0: β1 = 0We wish to test this hypothesis using data – reach a tentative conclusion whether it is correct or incorrect.Null hypothesis and two-sided alternative:H0: β1 = 0 vs. H1: β1≠ 0or, more generally,2H0: β1 = β1,0 vs. H1: β1≠β1,0where β1,0 is the hypothesized value under the null（β1,0是一个具体的数）.Null hypothesis and one-sided alternative:H0: β1 = β1,0 vs. H1: β1 < β1,0In economics, it is almost always possible to come up with stories in which an effect could “go either way,” so it is34standard to focus on two-sided alternatives.Recall hypothesis testing for population mean using Y :t=Y μ−then reject the null hypothesis if |t | >1.96.where the SE of the estimator is the square root of an estimator of the variance of the estimator.Applied to a hypothesis about β1:t = estimator - hypothesized value standard error of the estimator56sot = 11,01ˆˆ()SE βββ−where β1 is the value of β1,0 hypothesized under the null (for example, if the null value is zero, then β1,0 = 0.What is SE (1ˆβ)? SE (1ˆβ) = the square root of an estimator of the variance7of the sampling distribution of 1ˆβRecall the expression for the variance of 1ˆβ (large n ):var(1ˆβ) = 22var[()]()i X i X X u n μσ− = 24v Xn σσwhere v i = (X i –X )u i . Estimator of the variance of 1ˆβ:812ˆˆβσ = 2221estimator of (estimator of )v Xn σσ× = 2212211ˆ()121()ni i i n i i X X u n n X X n ==−−×⎡⎤−⎢⎥⎣⎦∑∑.OK, this is a bit nasty, but:• There is no reason to memorize this• It is computed automatically by regression software• SE (1ˆβis reported by regression software9• It is less complicated than it seems. The numerator estimates the var(v ), the denominator estimates var(X )2.Return to calculation of the t -statsitic:t = 11,01ˆˆ()SE βββ− =11,0ˆββ−• Reject at 5% significance level if |t| > 1.96•p-value is p = P(|t| > |t act|) = probability in tails of normal outside |t act|•Both the previous statements are based on large-n approximation; typically n = 50 is large enough for the approximation to be excellent.1011 Example: Test Scores and STR , California dataEstimated regression line: n TestScore = 698.9 – 2.28×STRRegression software reports the standard errors:SE (0ˆβ) = 10.4 SE (1ˆβ) = 0.52t -statistic testing “β1,0 = 0” = 11,01ˆˆ()SE βββ− = 2.2800.52−− = –4.38•The 1% 2-sided significance level is 2.58, so we reject the null at the 1% significance level.•Alternatively, we can compute the p-value. You can do this easily in Stata:. di normal(-4.38)*2. 00001187注：在Stata中，normal表示标准正态分布的cdf。

第五章 多元线性回归模型在第四章中，我们讨论只有一个解释变量影响被解释变量的情况，但在实际生活中，往往是多个解释变量同时影响着被解释变量。

需要我们建立多元线性回归模型。

一、多元线性模型及其假定 多元线性回归模型的一般形式是i iK K i i i x x x y εβββ++++= 2211令列向量x 是变量x k ，k =1，2，的n 个观测值，并用这些数据组成一个n ×K 数据矩阵X ，在多数情况下，X 的第一列假定为一列1，则β1就是模型中的常数项。

最后，令y 是n 个观测值y 1, y 2, …, y n 组成的列向量，现在可将模型写为：εββ++=K K x x y 11构成多元线性回归模型的一组基本假设为 假定1. εβ+=X y我们主要兴趣在于对参数向量β进行估计和推断。

假定2. ,0][][][][21=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n E E E E εεεε 假定3. n I E 2][σεε='假定4. 0]|[=X E ε我们假定X 中不包含ε的任何信息，由于)],|(,[],[X E X Cov X Cov εε= （1）所以假定4暗示着0],[=εX Cov 。

（1）式成立是因为，对于任何的双变量X ，Y ，有E(XY)=E(XE(Y|X))，而且])')|()([(])')((),(EY X Y E EX X E EY Y EX X E Y X Cov --=--=))|(,(X Y E X Cov =这也暗示 βX X y E =]|[假定5 X 是秩为K 的n ×K 随机矩阵 这意味着X 列满秩，X 的各列是线性无关的。

在需要作假设检验和统计推断时，我们总是假定： 假定6 ],0[~2I N σε 二、最小二乘回归 1、最小二乘向量系数采用最小二乘法寻找未知参数β的估计量βˆ，它要求β的估计βˆ满足下面的条件 22min ˆ)ˆ(ββββX y X y S -=-∆ （2）其中()()∑∑==-'-=⎪⎪⎭⎫ ⎝⎛-∆-nj Kj j ij i X y X y x y X y 1212ββββ，min 是对所有的m 维向量β取极小值。

第五章思考题5.2 各种异方差检验的基本思想是，基于不同的假定，分析随机误差项的方差与解释变量之间的相关性，以判断随机误差项的方差是否随解释变量变化而变化。

其中，戈德菲尔德-夸特检验、怀特检验、ARCH检验和Glejser检验都要求大样本，其中戈德菲尔德-夸特检验、怀特检验和Glejser检验对时间序列和截面数据模型都可以检验，ARCH检验只适用于时间序列数据模型中。

戈德菲尔德-夸特检验和ARCH检验只能判断是否存在异方差，怀特检验在判断基础上还可以判断出是哪一个变量引起的异方差。

Glejser检验不仅能对异方差的存在进行判断，而且还能对异方差随某个解释变量变化的函数形式进行诊断。

5.4 产生异方差的原因：①模型设定误差②测量误差的变化③截面数据中总体各单位的差异。

经济现象中的异方差性：研究低收入组的家庭消费情况与高收入组的家庭消费情况时，由于高收入组家庭有更多的可支配收入，因而消费的分散程度较大，造成不同组别收入的家庭消费偏离均值程度的差异，反映在随机误差项偏离均值的程度时出现异方差。

5.5 异方差对模型的影响：①当模型中的误差项存在异方差时，参数估计仍然是无偏的但方差不再是最小的；②在异方差存在的情况下，参数估计量的方差会比真实估计量的方差大，会严重破坏t检验和F检验的有效性；③Y预测值的精确度降低。

异方差的存在会对回归模型的正确建立和统计推断带来严重后果，不能进行应用分析。

练习题5.1 （1）设f(X i)=X2i 2，则Var(u i)=σ2X2i 2，得：Y i X2i =β11X 2i+β2+β3X3iX2i+u iX2i则Var(u iX2i )=1X 2iVar(u i)=σ25.2 （1）Y=-50.01991+0.X+52.37082Tt = (-1.011) (2.944) (10.067)由上面散点图可知，残差平方随解释变量的增大而增大，可见，模型存在异方差。

（2）模型存在异方差，可通过变换模型、进行对数变换和加权最小二乘法来估计参数。