激波问题经典数值算例
- 格式:docx
- 大小:17.56 KB
- 文档页数:3

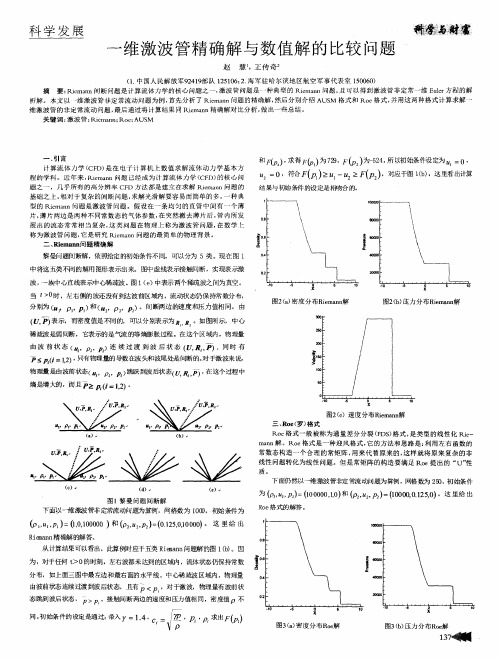



第十章膨胀波和激波第十章膨胀波和激波折角与波后气流的马赫数的关系。
称为Prandtl-Mayer函数,或Prandtl-Mayer角。
它表示对于来流马赫数为1时,经过膨胀后气流速度达到M时,所能偏转的角度。
这个式子已经制成表格,在知道M数或后,从这个表格中可以查到另一个值。
(三)对于来流马赫数为M1而最后速度为M2,气流总偏转角为:㈣如果壁面转折是朝上的,膨胀波将沿逆时针方向,此时普郎特-梅耶角取正数。
否则为负数。
(也可以理解为取绝对值。
)㈤当最终马赫数为∞,达到普郎特-梅耶角的最大可能值但这只是一个理论值,因为早在达到这个速度前,气流就会冷凝了。
[例1]马赫数1.4的空气,绕一外钝角偏转了20o。
已知来流的初始静压和静温分别是p1=101325N/m2,T1=288K,求膨胀后气流的马赫数、静压和静温。
[解]由来流马赫数M1,可以查表或者根据Prandtl-Mayer角求得v1=8.987 ,这个角度表示音速的来流经过膨胀后气流马赫数为M1后的偏转角。
这样,从音速的来流膨胀到M2的总偏转角为v2=8.987+20=28.987再查表或计算得到M2=2.096。
因为气流经过膨胀波是绝能等熵的,所以总温总压不变,借此可以计算出波后静压和静温。
㈥在连续转折或凸曲面处的膨胀波。
不论多道转折,还是曲面转折,在已知来流马赫数后,只要知道气流膨胀之后的马赫数、或者总的折转角,便可求得另一个。
[例2]拉瓦尔喷管的出口处,Me=1.2 ,气流出口处的总压为3个大气压,问:①出口处气流是膨胀还是压缩?②膨胀或者压缩的气流偏转角多大?绝热指数取1.4。
[解] ①根据拉瓦尔喷管的出口总压和马赫数,可求得出口气流的静压为:p=1.237因为这个压力比环境压力高,所以气流必须继续膨胀减压②为了求得气流膨胀后的转角,必须求得气流膨胀后的马赫数M2。
根据膨胀波是绝能等熵的过程,而膨胀后气流压力必须达到环境压力,因此可以求出气流膨胀后的马赫数为:[说明]拉瓦尔喷管的作用是依靠气流加速产生推力的,当出口处产生膨胀时,表明气流在喷管内膨胀不足,因此这个工作状态下,喷管是损失掉能量了。

经典数值算例一维数值算例算例1(Lax激波管问题)算例特点:为左稀疏波,右激波类型,能够检验数值算法捕捉间断的能力;求解区域:;初始条件:边界条件:左右两边采用紧支边界条件;计算时间:t=0.13.算例2(Sod激波管问题)求解区域:;初始条件:边界条件:左右两边采用紧支边界条件;计算时间:t=0.25.算例3(Shu-Osher问题)‘算例特点:具有高震荡的性质,用来检验高阶数值格式比低阶数值格式对该类型的解具有更好的逼近效果;求解区域:;初始条件:边界条件:左边界采用紧支边界条件,右边界采用流入边界条件;计算时间:t=0.18.算例4(Woodward-Colella激波相互碰撞问题)算例特点:双激波的碰撞,其物理量过程更为复杂,检验数值算法捕捉间断的能力及稳定性;求解区域:;初始条件:边界条件:左右两边采用反射边界条件;计算时间:t=0.038.二维数值算例算例1(二维Riemann问题)求解区域:初始条件:边界条件:x,y方向均采用紧支边界条件;计算时间:t=0.8.算例2(激波通过气泡的问题)求解区域:初始条件:边界条件:左边界采用紧支边界条件,右边界采用流入边界条件,上下边界均采用反射边界条件;计算时间:t=2.0.算例3(Rayleigh-Taylor不稳定性问题)计算区域:初始条件:其中为声速,绝热指数;边界条件:左右边界均采用反射边界条件,上下边界均采用Dirichelet边界条件,其中下边界满足,上边界满足;计算时间:t=1.95.算例4(Double Mach Reflect problem不稳定性问题)问题描述:马赫数为10的强激波,入射与x轴成60度,计算区域:初始条件:在马赫数为10的激波;边界条件:左边界采用流入边界条件,右边界采用流出边界条件,上边界采用马赫数为10的激波真解,下边界采用exact post-shock条件();计算时间:t=0.2.算例5(内爆问题)求解区域:初始条件:边界条件:左右边界和下边界均采用反射边界条件,上边界采用流出边界条件;计算时间:t=0.8.边界处理周期边界条件:密度,速度,压力按周期T取值;反射边界条件:密度,压力取边界对称值,压力取边界对称值的相反数;流入(流出)边界条件:即延拓边界条件;固壁边界条件:速度取0,密度,压力全取边界上的值;紧支边界条件:密度,速度,压力全等于边界上的值;Dirichelet边界条件:密度,速度,压力取常值。
激波前后总压变化计算
【原创版】
目录
1.激波概述
2.激波前后总压变化的计算方法
3.激波前后总压变化的应用实例
4.总结
正文
一、激波概述
激波,又称冲击波,是一种高压激化的压缩波。
当流体中某一区域的压力突然升高时,高压激化的压缩波将以极快的速度向前传播,这种压力波就是激波。
激波在流体力学、航空航天、爆炸力学等领域具有广泛的应用。
二、激波前后总压变化的计算方法
在激波前后,流体中的总压会发生变化。
为了计算这种变化,需要先了解激波前后的静压和动压。
1.静压:流体在静止状态下所产生的压力称为静压。
2.动压:流体在运动状态下所产生的压力称为动压。
3.总压:静压与动压之和称为总压。
激波前后总压变化的计算公式为:
ΔP = Δρ * a
其中,ΔP 表示总压变化,Δρ表示密度变化,a 表示激波传播速度。
三、激波前后总压变化的应用实例
激波前后总压变化在航空航天、爆炸力学等领域具有广泛的应用。
例如,在火箭发动机的喷管设计中,需要考虑激波前后总压变化对喷管性能的影响;在爆炸波的传播过程中,激波前后总压变化对于爆炸威力的评估具有重要意义。
四、总结
激波前后总压变化是流体力学中的一个重要概念。
了解激波前后总压变化的计算方法,有助于我们更好地分析和解决实际问题。
流体动力学中激波的数值计算分析流体动力学(fluid dynamics)是研究流体运动规律和流体力学基本原理的学科。
在流体动力学中,激波是一个重要而常见的现象。
它主要是由于在介质中传播的涡旋状扰动引起流体的瞬间压缩和加速所产生的。
激波的产生和传播过程具有复杂的动力学特征和现象,因此对其数值计算分析很具有研究价值,也对日常工程实践和科学研究具有非常重要的参考意义。
基本理论流体动力学中的激波通常采用守恒律方程组表示,主要包括质量、动量、能量等方程。
对于一维定常流动而言,常用的守恒律方程组包括Euler方程和Navier-Stokes方程等。
Euler方程是在假设流体为完全无黏的情况下得到的:$\frac{\partial \rho}{\partial t}+\frac{\partial (\rho u)}{\partial x}=0$$\frac{\partial (\rho u)}{\partial t}+\frac{\partial (\rho u^{2}+p)}{\partial x}=0$$\frac{\partial (\rho E)}{\partial t}+\frac{\partial (\rho uE+p u)}{\partial x}=0$其中,$\rho$是流体的密度,$u$是流体的速度,$p$是流体的压力,$E$是总能量(包括动能和内能),$x$是坐标。
数值计算分析为了研究和分析激波的产生和传播,需要对激波进行数值计算模拟。
数值计算分析的一般方法是将流动区域离散化成网格,并在每个网格上求解守恒律方程组。
常用的数值方法包括有限差分法,有限元法和有限体积法等。
有限差分法是一种将连续的微分方程转化为差分方程的数值计算方法。
在离散化过程中,需要将流动区域分成若干个网格,每个网格的参数通过有限差分来求取。
这种方法的优点主要有计算简单、过程易懂。
但是其精度受到网格大小和步长限制,精度难以提高。
经典数值算例
一维数值算例
算例1(Lax激波管问题)
算例特点:为左稀疏波,右激波类型,能够检验数值算法捕捉间断的能力;求解区域:x∈0,1;
初始条件:
ρ,v,p=0.445,0.698,3.528当0≤x≤0.5, 0.5,0,0.571当0.5≤x≤0.571,
边界条件:左右两边采用紧支边界条件;计算时间:t=0.13.
算例2(Sod激波管问题)
求解区域:x∈0,1;
初始条件:
ρ,v,p=
1,0,1当x≤0.5, 0.125,0,0.1当x>0.5,
边界条件:左右两边采用紧支边界条件;
计算时间:t=0.25.
算例3(Shu-Osher问题)‘
算例特点:具有高震荡的性质,用来检验高阶数值格式比低阶数值格式对该类型的解具有更好的逼近效果;
求解区域:x∈0,1;
初始条件:
ρ,v,p=3.85714,2.629369, 10.333333当0≤x≤0.1, 1.0+0.2sin50x−25, 0, 1当0.1≤x≤1,
边界条件:左边界采用紧支边界条件,右边界采用流入边界条件;
计算时间:t=0.18.
算例4(Woodward-Colella激波相互碰撞问题)
算例特点:双激波的碰撞,其物理量过程更为复杂,检验数值算法捕捉间断的能力及稳定性;求解区域:x∈0,1;
初始条件:
ρ,v,p=1,0,1000当0≤x≤0.1, 1,0,0.01当0.1<x≤0.9 1,0,100当0.9<x≤1,
边界条件:左右两边采用反射边界条件;计算时间:t=0.038.
二维数值算例
算例1(二维Riemann问题)
求解区域:x,y∈0,1×0,1;初始条件:
ρu v p T
=
1.5,0,0,1.5当x∈0.8,1,y∈0.8,1,
0.5323,1.206,0,0.3当x∈[0,0.8],y∈0.8,1,
0.138,1.206,1.206,0.029当x∈0,0.8,y∈0,0.8,
0.5323,0,1.206,0.3当x∈0.8,1,y∈0,0.8,
边界条件:x,y方向均采用紧支边界条件;
计算时间:t=0.8.
算例2(激波通过气泡的问题)
求解区域:x,y:0≤x≤325,−44.5≤y≤44.5;初始条件:
ρ
u v p =
1.3764,0.394,0,1.5698, 当x≥225.0,
0.138,0,0,1, 当(x−175)2+y2≤225.0,
1,0,0,1, 其他
边界条件:左边界采用紧支边界条件,右边界采用流入边界条件,上下边界均采用反射边界条件;
计算时间:t=2.0.
算例3(Rayleigh-Taylor不稳定性问题)
计算区域:x,y∈0,1
4
×0,1;
初始条件:
ρ
u v p =
2,0,−0.025c∙cos8πx,2y−1, 当x,y∈0,
1
×0,
1
, 1,0,−0.025c∙cos8πx,y+
3
2
, 当x,y∈0,
1
4
×
1
2
,1,
其中c=γp/ρ为声速,绝热指数γ=5
3
;
边界条件:左右边界均采用反射边界条件,上下边界均采用Dirichelet边界条件,其中下边界满足ρ,u,v,p=(2,0,0,1),上边界满足ρ,u,v,p=(1,0,0,2.5);
计算时间:t=1.95.
算例4(Double Mach Reflect problem不稳定性问题)
问题描述:马赫数为10的强激波,入射与x轴成60度,
计算区域:x,y∈0,4×0,1;
初始条件:在x=1
6
,y=0马赫数为10的激波;
边界条件:左边界采用流入边界条件,右边界采用流出边界条件,上边界采用马赫数为10
的激波真解,下边界采用exact post-shock条件(0≤x≤1
6
); 计算时间:t=0.2.
算例5(内爆问题)
求解区域:x,y:−0.3≤x≤0.3, 0.3≤y≤0.3;
初始条件:
ρ
u v p =
1,0,0,1, 当x−0.15≤y≤−x+0.15,
0.125,0,0,0.14, 其他,
边界条件:左右边界和下边界均采用反射边界条件,上边界采用流出边界条件;计算时间:t=0.8.
边界处理
周期边界条件:密度,速度,压力按周期T取值;
反射边界条件:密度,压力取边界对称值,压力取边界对称值的相反数;
流入(流出)边界条件:即延拓边界条件;
固壁边界条件:速度取0,密度,压力全取边界上的值;
紧支边界条件:密度,速度,压力全等于边界上的值;
Dirichelet边界条件:密度,速度,压力取常值。