exp6数学实验之数据拟合
- 格式:ppt
- 大小:17.01 MB
- 文档页数:54

北理工_数据分析_实验5_数据拟合实验5:数据拟合1. 实验目的本实验旨在通过数据拟合方法,掌握数据分析中的拟合技巧,以及分析和解释拟合结果的能力。
2. 实验原理数据拟合是一种通过数学模型来描述和预测实验数据的方法。
常见的拟合方法包括线性拟合、多项式拟合、非线性拟合等。
在拟合过程中,通过选择合适的模型和拟合参数,使得拟合曲线与实验数据之间的误差最小。
3. 实验步骤步骤一:收集实验数据在本次实验中,我们收集了一组与某个物理现象相关的实验数据。
数据包括自变量和因变量,其中自变量为时间,因变量为物理量的测量值。
步骤二:选择拟合模型根据实验数据的特点和研究目的,选择适合的拟合模型。
在本实验中,我们选择了一种非线性拟合模型,用来描述实验数据的曲线关系。
步骤三:拟合数据利用数据分析软件(如Python、MATLAB等),进行数据拟合。
通过调整拟合参数,使得拟合曲线与实验数据的误差最小。
步骤四:分析拟合结果根据拟合结果,评估拟合曲线与实验数据的拟合程度。
常用的评估指标包括拟合优度、均方根误差等。
通过分析拟合结果,我们可以得出对实验数据的解释和预测。
4. 实验数据与结果在本次实验中,我们采集了一组与温度变化相关的实验数据。
数据如下:时间(min)温度(℃)0 255 2710 3015 3420 3825 4230 47根据实验数据,我们选择了一个非线性拟合模型,并进行了数据拟合。
拟合结果如下:拟合模型:温度 = a * exp(b * 时间) + c拟合参数:a = 23.5b = 0.1c = 1.2拟合优度:0.98均方根误差:1.5通过对拟合结果的分析,我们可以得出以下结论:- 温度随着时间的增加而增加,且增加的速率逐渐减小。
- 拟合模型对实验数据的拟合优度较高,说明拟合曲线与实验数据的拟合程度较好。
- 均方根误差较小,说明拟合曲线与实验数据的误差较小。
5. 结论与讨论通过本次实验,我们成功地利用数据拟合方法对实验数据进行了分析和解释。

数据拟合原理
数据拟合原理(准线拟合法)是一种通过已有的离散数据点来建立一个数学模型,以便预测或推断未知数据点的方法。
在数据拟合中,寻找一条数学函数曲线,使其能够穿过尽可能多的数据点。
这样的曲线被称为拟合曲线,其对应的函数称为拟合函数。
拟合函数的选择通常基于数据的特性和需求。
常用的拟合函数包括线性、多项式、指数、对数和三角函数等。
具体的选择需要根据数据的特征和分析目的来确定。
拟合的基本原理是最小化拟合函数与实际数据点的误差。
常用的误差度量方法有最小二乘法、最小平均绝对误差法等。
最小二乘法是最常用的拟合方法之一。
它通过最小化实际数据点到拟合曲线的垂直距离的平方和,来确定拟合函数的参数。
最小平均绝对误差法则是最小化实际数据点到拟合曲线的绝对误差的平均值。
拟合过程中,还要考虑拟合函数的复杂度和拟合优度。
复杂度指的是拟合函数所包含的参数个数或阶数。
拟合优度则描述了拟合函数对实际数据的拟合程度,常用的指标有决定系数R²
和调整决定系数R²_adj等。
需要注意的是,数据拟合仅仅是对已知数据进行预测或插值,并不能准确地预测未来的数据点。
因此,在进行数据拟合时需要注意模型的局限性和适用范围。
综上所述,数据拟合原理通过最小化拟合函数与实际数据点之间的误差,建立一个数学模型,以预测或推断未知数据点。
该方法依赖于选择合适的拟合函数和合适的拟合方法,同时要考虑拟合函数的复杂度和拟合优度。
’.第二讲 数据拟合方法在实验中,实验和戡测常常会产生大量的数据。
为了解释这些数据或者根据这些数据做出预测、判断,给决策者提供重要的依据。
需要对测量数据进行拟合,寻找一个反映数据变化规律的函数。
数据拟合方法与数据插值方法不同,它所处理的数据量大而且不能保证每一个数据没有误差,所以要求一个函数严格通过每一个数据点是不合理的。
数据拟合方法求拟合函数,插值方法求插值函数。
这两类函数最大的不同之处是,对拟合函数不要求它通过所给的数据点,而插值函数则必须通过每一个数据点。
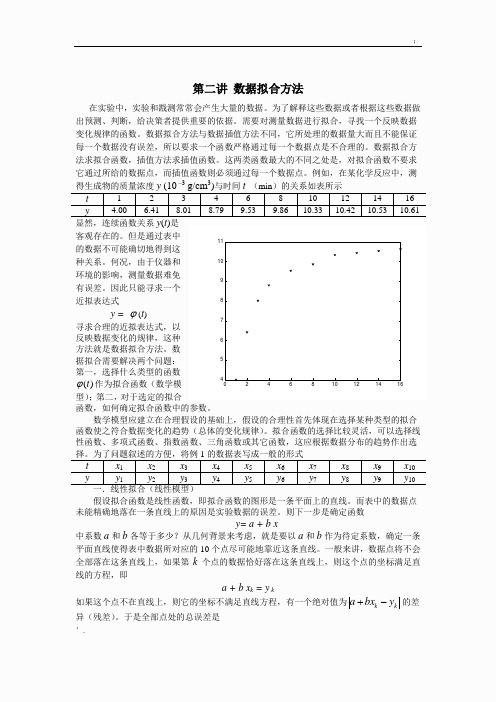
例如,在某化学反应中,测得生成物的质量浓度y (10 –3 g/cm 3)与时间t (min )的关系如表所示t1 2 3 4 6 8 10 12 14 16 y4.00 6.41 8.01 8.79 9.53 9.86 10.33 10.42 10.53 10.61 显然,连续函数关系y (t )是客观存在的。
但是通过表中的数据不可能确切地得到这种关系。
何况,由于仪器和环境的影响,测量数据难免有误差。
因此只能寻求一个近拟表达式y = ϕ(t )寻求合理的近拟表达式,以反映数据变化的规律,这种方法就是数据拟合方法。
数据拟合需要解决两个问题:第一,选择什么类型的函数)(t ϕ作为拟合函数(数学模型);第二,对于选定的拟合函数,如何确定拟合函数中的参数。
数学模型应建立在合理假设的基础上,假设的合理性首先体现在选择某种类型的拟合函数使之符合数据变化的趋势(总体的变化规律)。
拟合函数的选择比较灵活,可以选择线性函数、多项式函数、指数函数、三角函数或其它函数,这应根据数据分布的趋势作出选择。
为了问题叙述的方便,将例1的数据表写成一般的形式 t x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 y y 1 y 2 y 3 y 4 y 5 y 6 y 7 y 8 y 9 y 10 一.线性拟合(线性模型)假设拟合函数是线性函数,即拟合函数的图形是一条平面上的直线。


拟合实验原理的应用介绍拟合实验是一种常用的数据分析方法,通过拟合数据点来找到数据背后的规律和模型。
这个方法在各个领域都有广泛的应用,包括物理学、化学、生物学等等。
本文将介绍拟合实验的原理以及它在各个领域中的应用。
拟合实验的原理拟合实验的原理是通过选择一个拟合函数来拟合实验数据点。
拟合函数可以是简单的线性函数,也可以是复杂的非线性函数。
拟合函数的选择取决于实验数据的性质和拟合的目的。
然后,通过最小化实际数据和拟合函数之间的误差,来确定拟合函数的参数。
拟合实验的步骤拟合实验一般包括以下几个步骤:1.数据收集:收集实验数据点,并记录实验数据的相关信息。
2.拟合函数的选择:根据实验数据的性质和拟合目的,选择合适的拟合函数。
3.参数估计:使用拟合函数对数据进行拟合,估计拟合函数的参数。
4.误差分析:分析拟合结果的误差,并评估拟合函数的拟合程度。
5.拟合结果的应用:根据拟合结果的应用需求,对拟合函数进行进一步处理和分析。
拟合实验的应用举例物理学领域的应用在物理学中,拟合实验常常用于确定物理量之间的关系。
例如,在测量运动物体的速度-时间关系时,可以采集多个时间点的数据,并使用拟合方法来确定速度-时间关系的数学表达式。
这样,就可以利用拟合结果来预测未来的速度值。
生物学领域的应用在生物学研究中,拟合实验常用于分析生物过程中的动力学关系。
例如,在酶反应的研究中,可以通过测量不同底物浓度下的反应速率来获得实验数据。
然后,可以使用拟合方法来确定酶反应速率和底物浓度之间的关系,从而了解反应速率的变化规律。
经济学领域的应用在经济学中,拟合实验常用于分析经济数据的趋势和周期性。
例如,可以使用拟合方法来确定商品价格的走势,从而帮助预测未来的价格变化趋势。
此外,还可以使用拟合方法来分析经济周期的周期性和规律,从而为经济政策的制定提供参考。
化学领域的应用在化学研究中,拟合实验常用于分析化学反应动力学和化学平衡。
例如,在测量化学反应速率时,可以通过收集一系列实验数据点,并使用拟合方法来确定反应速率与反应物浓度之间的关系式。

数据拟合方法研究数据拟合是数据分析中非常重要的工作,其主要目的是找到最佳的函数形式来描述数据之间的关系。
在实际应用中,数据拟合通常用于模型建立、预测分析、实验设计等领域。
本文将介绍数据拟合的基本概念、常用方法以及其在实际应用中的应用。
一、数据拟合基本概念数据拟合是指通过已有数据的样本值,寻找一个函数形式使其最佳地描述这些数据所表现出的规律。
在拟合过程中,常常涉及到拟合函数的选择、参数的求解以及拟合程度的评价等问题。
拟合函数的选择通常依赖于研究问题的不同以及观测数据的特点。
二、常用的数据拟合方法1.最小二乘法拟合在最小二乘法拟合中,我们试图找到一个函数形式使其预测值与观测值之间的误差平方和最小。
这种方法在拟合过程中,通常需要确定待拟合函数的形式、参数估计以及拟合程度的评价指标等问题。
最小二乘法拟合常用于线性回归、非线性回归以及多项式拟合等问题。
2.最大似然估计拟合最大似然估计拟合是一种常用的参数估计方法,其主要思想是选择使得已观测数据样本概率最大化的参数值。
最大似然估计拟合常用于分布拟合、生存分析、统计模型等领域。
通过最大似然估计拟合,可以推测出数据背后的概率分布模型,从而进行预测和推断分析。
3.核函数拟合核函数拟合是一种非参数拟合方法,其主要思想是通过一系列核函数的线性组合来逼近数据分布。
核函数拟合具有较强的灵活性和拟合能力,适用于各种类型的数据分布,并且能够处理多维数据。
在核函数拟合中,需要选择合适的核函数以及核函数的参数,并通过交叉验证等方法选择最佳模型。
4.贝叶斯拟合贝叶斯拟合是一种基于贝叶斯理论的数据拟合方法,其主要思想是通过先验分布和观测数据来更新参数的后验分布,从而得到参数的估计值。
贝叶斯拟合能够处理参数不确定性、模型不确定性以及过拟合等问题,具有较好的鲁棒性和泛化能力。
三、数据拟合的应用数据拟合在实际应用中有着广泛的应用。
以下是几个典型的应用案例:1.经济学中的数据拟合:在经济学中,数据拟合常常用于建立经济模型以及预测分析。
实验报告一·实验指导书解读本次实验是通过两个变量的多组记录数据利用最小二乘法寻求两个变量之间的函数关系!两个变量之间的函数关系要紧有两种:一是线性关系(一次函数);二是非线性关系(非一次的其它一元函数)。
因此本实验做两件事:一是线性拟合(练习1);二是非线性拟合(练习2、3、4)。
练习2是用多项式函数拟合,练习3是用指数函数、对数函数、双曲函数、三角函数、分式有理多项式函数等初等函数拟合,练习4是用分段函数(非初等函数)拟合。
二、实验打算1.用线性函数拟合程序线性拟合曲线ft1可由如下mathematica程序求出:lianxi1biao= { {100,45} , {110,51} , { 120,54} , {130,61} , {140,66} , {150,70} , {160,74} , {170,78} , {180,85} , {190,89} }ft1=Fit[lianxi1biao,{1,x},x]gp = Plot [ ft1 , {x,100,190} , PlotStyle -> { RGBColor[1,0,0]} ]fp = ListPlot [ lianxi1biao,PlotStyle->{PointSize[],RGBColor[0,0,1]} ]Show[fp,gp]a= ;b= ;f[x_]=a*x+b;dareta=Sum[(lianxi1biao[[i,2]]-f[lianxi1biao[[i,1]]])^2,{i,1,10}]修改、补充程序:要说明拟合成效,要紧从形(大多数散点是不是在拟合曲线上或周围)与量(残差是不是小)!计算残差的程序:假设对两个变量的多组记录数据已有程序biao={{x1,y1},{x2,y2},…,{xn,yn}}而且通过Fit取得线性拟合函数y=ax+b咱们能够先概念函数(程序)f[x_]:=a*x+b再给出计算残差的程序dareta=Sum[(biao[[i ,2]]-f[biao[[i ,1]]])^2,{i ,1, n}]程序说明:biao[[i]]是提取表biao的第i行,即{xi,yi}biao[[i ,1]] 是提取表biao的第i行的第一个数, 即xibiao[[i ,2]] 是提取表biao的第i行的第一个数, 即yibiao[[i ,2]]-f[biao[[i ,1]]] 即yi-(a*xi+b)实验思路1、先对练习1的十组数据线性拟合,并从形与量看拟合成效;2、对练习1的十组数据中的九组数据线性拟合,并从形与量看拟合成效;3、对练习1的十组数据中的八组数据线性拟合,并从形与量看拟合成效;4、对练习1的十组数据中的七组数据线性拟合,并从形与量看拟合成效;5、对练习1的十组数据中的六组数据线性拟合,并从形与量看拟合成效。
计算实验技术数据拟合技巧分享在科学研究和工程技术领域中,拟合实验数据是非常常见的一项技术。
通过拟合实验数据,我们可以找到合适的函数模型来描述实验现象,并做出相应的预测和分析。
在本文中,我将分享一些计算实验技术数据拟合的技巧和经验。
首先,拟合实验数据的第一步是选择合适的函数模型。
通常情况下,我们可以根据实验数据的特点和物理规律来选择一个适合的函数模型。
例如,如果实验数据呈现出指数增长或衰减的趋势,我们可以选择指数函数作为拟合模型。
如果实验数据呈现出周期性的变化,我们可以选择三角函数或周期函数作为拟合模型。
除了选择函数模型外,我们还需要确定函数中的参数。
这可以通过使用拟合算法来完成。
常见的拟合算法有最小二乘法、非线性最小二乘法和曲线拟合法等。
在实际拟合过程中,我们需要根据实验数据的特点和要求选择合适的拟合算法。
在选择拟合算法时,我们还需要考虑数据的误差情况。
实验数据通常会受到各种因素的干扰,从而引入误差。
为了准确地拟合实验数据,我们需要将误差考虑在内。
在拟合过程中,我们可以使用加权最小二乘法来处理带有误差的数据。
通过赋予不同数据点不同的权重,我们可以更好地拟合实验数据并降低误差对拟合结果的影响。
除了选择合适的函数模型和拟合算法外,数据预处理也是拟合实验数据的重要环节。
通过数据预处理,我们可以去除实验数据中的噪声和异常值,从而提高拟合结果的准确性。
常用的数据预处理方法包括平滑法、滤波法和去噪法等。
通过对数据进行适当的处理,我们可以消除一些不必要的干扰,使得拟合结果更加可靠。
在进行实验数据拟合时,我们还需要进行结果的评估和验证。
一种常见的评估方法是计算拟合误差。
拟合误差是拟合数据和实验数据之间的差异,通过计算拟合误差,我们可以评估拟合结果的准确性和可信度。
此外,我们还可以使用图形比较、统计检验或交叉验证等方法对拟合结果进行验证。
最后,拟合实验数据的过程也是一个不断优化的过程。
在实际拟合过程中,我们可能会遇到各种问题和挑战。
适用范围:在解决实际问题的生产(或工程)实践和科学实验过程中,通常需要通过研究某些变量之间的函数关系来帮助我们认识事物的内在规律和本质属性,而这些变量之间的未知函数关系又常常隐含在从试验、观测得到的一组数据之中。
因此,能否根据一组试验观测数据找到变量之间相对准确的函数关系就成为解决实际问题的关键。
在科学计算中经常要建立实验数据的数学模型。
给定函数的实验数据,需要用比较简单和合适的函数来逼近(或拟合)实验数据。
这种逼近的特点是:(a) 适度的精度是需要的;(b) 实验数据有小的误差;(c) 对于某些问题,可能有某些特殊的信息能够用来选择实验数据的数学模型。
逼近离散数据的基本方法就是曲线拟合,常采用最小二乘拟合。
拟合以及插值还有逼近是数值分析的三大基础工具,通俗意义上它们的区别在于:拟合是已知点列,从整体上靠近它们,插值是已知点列并且完全经过点列;逼近是已知曲线,或者点列,通过逼近使得构造的函数无限靠近它们。
[原理:拟合是指已知某函数的若干离散函数值{f1,f2,…,fn},通过调整该函数中若干待定系数f(λ1, λ2,…,λn),使得该函数与已知点集的差别(最小二乘意义)最小。
如果待定函数是线性,就叫线性拟合或者线性回归(主要在统计中),否则叫作非线性拟合或者非线性回归。
表达式也可以是分段函数,这种情况下叫作样条拟合。
拟合:已知有限个数据点,求近似函数,不要求过已知数据点,只要求在某种意义下它在这些点上的总偏差最小形象的说,拟合就是把平面上一系列的点,用一条光滑的曲线连接起来。
因为这条曲线有无数种可能,从而有各种拟合方法。
拟合的曲线一般可以用函数表示。
在MATLAB中可以用polyfit来拟合多项式。
方法及步骤:Matlab曲线拟合最小二乘法 polyfit曲线拟合已知离散点上的数据集,即已知在点集上的函数值,构造一个解析函数(其图形为一曲线)使在原离散点上尽可能接近给定的值,这一过程称为曲线拟合。