总长为 L = Na , N为原胞总数。
质量为M的原子编号为:··· n-1,1、 n,1、n+1,1、···
质量为m的原子编号为:··· n-1,2、 n,2、n+1,2、···
设
u
n
、
,1
un
,
2是相应于原子M、m在沿链方向对其平衡位置的偏离
.
方程和解
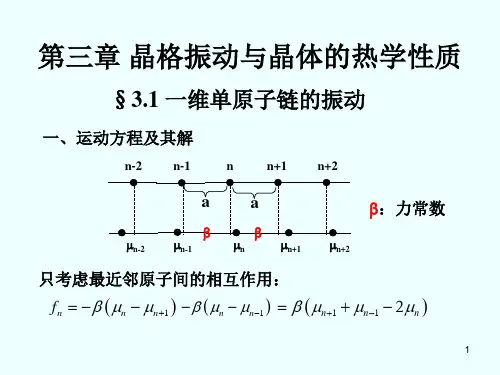
和单原子链类似,若只考虑最近邻原子的相互作用,则有:
.
当δ很小时,作二级近似
恢复力 ------简谐近似
----胡克定律 ( 为倔强系数)
研究一维单原子链的振动
模型:设一维单原子链中,原子间距(晶格常量)为a, 总长为 L = Na , N为原子总数(晶胞数 ) ,原子质量为m。
.
第n个粒子的受力情况:
运动方程:
假设晶格足够长,可忽略边界。以行波作试探解,即
举例说明 un Aei(qn at)
第一布里渊区
(1) (2)
对格点振动有贡献的是原 子,两原子之间的振动在 物理上没有意义。
.
/aq/a 第一布里渊区(倒格子空间)
倒格子空间-波矢空间
.
(3)周期性边界条件、第一布里渊区中的模数
a
波恩-卡门边界条件 a
(周期性边界条件)
q的取值采用波恩-卡门边界条件(周期性边界条件)来定:
u1 uN1
N为晶格中的原子个数(晶胞数 )
即: A i(q e a t) A i[q (N e 1 )a t]
un Aei(qn at)
.
u1 uN1 A i(q e a t) A i[q (N e 1 )a t]
eiqNa1
得: qN a2l l =0,±1,±2……等整数