设计IIR滤波器的双线性变换法

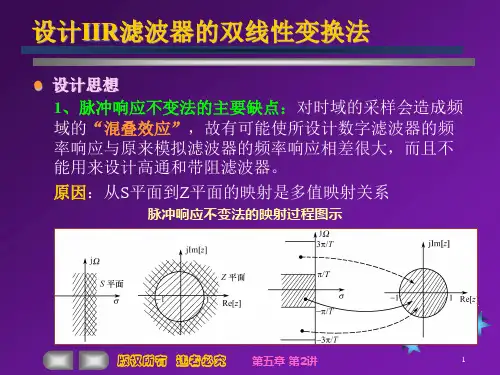
%IIR数字滤波器的设计；%采用脉冲响应不变法和双线性变换法；clear;close all;clc;wp1=0.3*pi;wp2=0.4*pi; %初始化指标参数ws1=0.1*pi;ws2=0.6*pi;Rp=1;As=40;Fs=2000;T=1/Fs;ripple=10^(-Rp/20);attn=10^(-As/20);Omgp1=wp1*Fs;Omgp2=wp2*Fs;Omgp=[Omgp1 Omgp2];Omgs1=ws1*Fs;Omgs2=ws2*Fs;Omgs=[Omgs1 Omgs2];B=Omgp2-Omgp1;w0=sqrt(Omgp1*Omgp2);[n wc]=cheb1ord(Omgp,Omgs,Rp,As,'s'); %设计切比雪夫1型滤波器[z0 p0 k0]=cheb1ap(n,Rp);ba1=k0*real(poly(z0));aa1=real(poly(p0));[ba aa]=lp2bp(ba1,aa1,w0,B);ww=Omgs1:Omgs2;hh=freqs(ba,aa,ww);dBHH=20*log10((abs(hh)+eps)/max(abs(hh)));%[ba aa]=butter(n,wc,'s');[bd ad]=impinvar(ba,aa,Fs);[H w]=freqz(bd,ad);dBH=20*log10((abs(H)+eps)/max(abs(H)));%画图；subplot(1,2,1);plot(ww/2/pi,abs(hh));xlabel('频率:Hz');ylabel('H(e^{j\omega})');title('幅频响应');set(gca,'XTickMode','manual','XTick',[ws1*Fs/2/pi wp1*Fs/2/pi wp2*Fs/2/pi ws2*Fs/2/pi]);set(gca,'YTickMode','manual','YTick',[attn 1/sqrt(2) ripple]);grid; subplot(1,2,2);plot(ww/2/pi,dBHH);xlabel('频率:Hz');ylabel('dB');title('幅频响应');grid;set(gca,'XTickMode','manual','XTick',[ws1*Fs/2/pi wp1*Fs/2/pi wp2*Fs/2/pi ws2*Fs/2/pi]);set(gca,'YTickMode','manual','YTick',[-As -3 -Rp 0]);figure;subplot(2,2,1);plot(w/pi,abs(H));xlabel('频率:\pi');ylabel('H(e^{j\omega})');title('幅频响应');axis([0 1 0 1.1]);set(gca,'XTickMode','manual','XTick',[0 ws1/pi wp1/pi wp2/pi ws2/pi 1]);set(gca,'YTickMode','manual','YTick',[0 attn 1/sqrt(2) ripple 1]);grid;subplot(2,2,2);plot(w/pi,angle(H));xlabel('相频响应');ylabel('相位');title('相频响应');axis([0 11.1*min(angle(H)) 1.1*max(angle(H))]);set(gca,'XTickMode','manual','XTick',[0 ws1/pi wp1/pi wp2/pi ws2/pi 1]);set(gca,'YTickMode','manual','YTick',[-1 0 1]);grid;subplot(2,2,3);plot(w/pi,dBH);xlabel('频率:\pi');ylabel('dB');title('幅度响应');axis([0 1 -80 10]); set(gca,'XTickMode','manual','XTick',[0 ws1/pi wp1/pi wp2/pi ws2/pi 1]);set(gca,'YTickMode','manual','YTick',[-As -3 -Rp 0]);grid;subplot(2,2,4);zplane(bd,ad);%采用双线性变换法；omgp1=(2/T)*tan(wp1/2);omgp2=(2/T)*tan(wp2/2);omgp=[omgp1 omgp2]; omgs1=(2/T)*tan(ws1/2);omgs2=(2/T)*tan(ws2/2);omgs=[omgs1 omgs2]; Bw=omgp2-omgp1;omgw0=sqrt(omgp1*omgp2);[n0 wc0]=cheb1ord(omgp,omgs,Rp,As,'s'); %设计切比雪夫1型滤波器[z0 p0 k0]=cheb1ap(n0,Rp);a1=k0*real(poly(z0));b1=real(poly(p0));[bc1 ac1]=lp2bp(a1,b1,omgw0,Bw);[be ae]=bilinear(bc1,ac1,Fs);[HH w1]=freqz(be,ae);dbHH=20*log10((abs(HH)+eps)/max(abs(HH)));%画图figure;subplot(2,2,1);plot(w1/pi,abs(HH));xlabel('频率:\pi');ylabel('H(e^{j\omega})');title('幅频响应');axis([0 1 0 1.1]);set(gca,'XTickMode','manual','XTick',[0 ws1/pi wp1/pi wp2/pi ws2/pi 1]);set(gca,'YTickMode','manual','YTick',[0 attn 1/sqrt(2) ripple 1]);grid;subplot(2,2,2);plot(w1/pi,angle(HH));xlabel('相频响应');ylabel('相位');title('相频响应');axis([0 1 1.1*min(angle(HH)) 1.1*max(angle(HH))]);set(gca,'XTickMode','manual','XTick',[0 ws1/pi wp1/pi wp2/pi ws2/pi 1]);set(gca,'YTickMode','manual','YTick',[-1 0 1]);grid;subplot(2,2,3);plot(w1/pi,dbHH);xlabel('频率:\pi');ylabel('dB');title('幅度响应');axis([0 1 -80 10]); set(gca,'XTickMode','manual','XTick',[0 ws1/pi wp1/pi wp2/pi ws2/pi 1]);set(gca,'YTickMode','manual','YTick',[-As -3 -Rp 0]);grid;subplot(2,2,4);zplane(be,ae);%生成信号，并进行滤波；f1=100;f2=200;phi1=0;phi2=0;fs=1000;T=1;t=0:1/fs:T;A=1;y0=A*sin(2*pi*f1*t)+A*sin(2*pi*f2*t);N=length(t);noise=0.5*randn(1,N);f=y0+noise; %信号+噪声y=filter(bd,ad,f);%y=filter(be,ae,f);xx=-fs/2:1/T:fs/2;ff=abs(1/fs*fftshift(fft(f)));yy=abs(1/fs*fftshift(fft(y)));%画图figure;subplot(1,2,1);plot(t,f);axis([0,1,-3.5,3.5]); xlabel('t/s');ylabel('f');title('信号+噪声时域波形'); subplot(1,2,2);plot(t,y);xlabel('t/s');ylabel('y');title('滤波后时域波形'); figure;subplot(1,2,1);plot(xx,ff);xlabel('f/Hz');ylabel('ff');title('信号+噪声频谱图'); subplot(1,2,2);plot(xx,yy);xlabel('f/Hz');ylabel('yy');title('滤波后频谱图');Ps=A^2;Pn1=sum(noise.^2)/N;SNR1=10*log10(Ps/Pn1);disp('输入信噪比如下：');SNR1yy=filter(bd,ad,noise);Pn2=sum(yy.^2)/N;SNR2=10*log10(Ps/Pn2);disp('输出信噪比如下：');SNR2disp('信噪比增益如下：');SNR2-SNR1。

用双线性变换法设计IIR数字滤波器[实验目的]熟悉模拟巴特沃茨滤波器设计和用双线性变换法设计IIR数字滤波器的方法。

[实验原理]利用双线性变换设计IIR数字滤波器，首先要设计出满足指标要求的模拟滤波器的传递函数Ha(S),然后由Ha(S)通过双线性可得所要设计的IIR数字滤波器的系统函数H(Z)。

[实验内容及要求]用双线性变换法设计IIR滤波器是IIR滤波器设计的经典方法，首先根据模拟滤波器的指标设计出来相应的模拟滤波器，然后将设计好的模拟滤波器转换为满足给定技术指标的数字滤波器。

在MATLAB的数字信号处理工具箱中提供了相应的设计函数，常用的有：1、butterworth数字和模拟2、零极点增益模型到传递函数模型的转换函数3、低通到低通模拟滤波器的转换函数4、双线性变换函数5、Butterworth数字和模拟滤波器设计函数6、计算butterworth低通原型模拟滤波器的极点和增益函数7、计算离散时间系统的频率响应函数用双线性变换法设计BUTTERWORTH低通IIR数字滤波器，要求使用buttord，butter，biliner。

滤波器技术指标：取样频率1HZ，通带内临界频率0.2HZ，通带内衰减小于1db，阻带临界频率0.3HZ，阻带内衰减大于25DB。

解：wp=0.2*2*pi;ws=0.3*2*pi;rp=1;rs=25;fs=1;ts=1/fs;wp2=2*fs*tan(wp/2*ts);ws2=2*fs*tan(ws/2*ts);[n,wn]=buttord(wp2,ws2,rp,rs,'s')[z,p,k]=buttap(n)[bap,aap]=zp2tf(z,p,k)[b,a]=lp2lp(bap,aap,wn)[bz,az]=bilinear(b,a,fs);[h,w]=freqz(bz,az);subplot(2,1,1);plot(w/pi,abs(h));grid onxlabel('频率');ylabel('幅度');subplot(2,1,2);plot(w/pi,20*log10(abs(h)));grid onxlabel('频率');ylabel('幅度');n = 6wn = 1.7043z =[]p =-0.2588 + 0.9659i-0.2588 - 0.9659i-0.7071 + 0.7071i-0.7071 - 0.7071i-0.9659 + 0.2588i-0.9659 - 0.2588ik =1bap =0 0 0 0 0 0 1 aap =1.0000 3.8637 7.4641 9.1416 7.4641 3.8637 1.0000 b =24.5076a =1.0000 6.5850 21.6809 45.2558 62.976555.5591 24.5076频率幅度频率幅度。

双线性变换法设计IIR数字滤波器一：实验目的1）熟悉用双线性变换法设计IIR数字滤波器的原理和方法。

2）掌握数字滤波器设计的计算机仿真方法。

3）观察对心电图信号的实际滤波作用，获得数字滤波器的感性认识。

二：实验原理在滤波器的设计过程中，毕竟那是一个重要环节，所谓逼进就是根据性能指标的要求，对理想特性进行逼进，以求得一个因果、稳定且客户实现的传递函数。

目前模拟滤波器的频域设计理论已经发展的相当成熟，它不仅具有简单而严格的设计公式，而且设计参数已经表格化了。

借助模拟滤波器的逼进方法，用模拟与大树自语的某种变换，完成数字滤波器的逼进，这是一类简单而又行之有效的方法。

双线性变换法采用非线性频率压缩方法，将整个频域轴上的频率范围压缩到-π/T~π/T之间，再用z=e sT转换到z平面上。

也就是说，第一步现将整个S平面压缩映射到S1平面的-π/T~π/T一条横带里；第二步再通过标准变换关系1e S T将此横带变换到整个z平面上去。

这样就使S平面与Z平面建立了一一对应的胆汁关系，消除了多只变换性，也就消除了频谱混跌现象，映射关系如图所示。

为了将S 平面的整个虚轴j Ω压缩到1S 平面轴上的-π/T 到π/T 段上，可以通过以上的正切的变换实现Ω=2/Ttan(1ΩT/2)（1-1）式中，T 仍是采样间隔。

当1Ω由-π/T 经过0变化到π/T 时，Ω由-∞经过0变化到+∞，也即映射了整个j Ω轴。

将上式（1-1）写成111122222T Tj j T T j j e e j T e e ΩΩΩΩ--Ω=•+ （1-2）将此关系解析延拓到整个S 平面和1S 平面，令j Ω=s, 1j Ω=S 1,则得111221tan()21e s Ts TS T e T T --==•+(1-3)再将S 1平面通过以下标准变换关系映射到Z 平面：z=S1T e （1-4）从而得到S 平面和Z 平面的单值映射关系为;11211ZS T Z ---=+(1-5) 122122T T S S Z T TS S ++==--(1-6)式（1-5）和式（1-6）是S 平面与Z 平面之间的单值映射关系，这种变换都是两个线性函数之比，因此成为双线性变换。

目录一、摘要 (3)二、设计思想 (3)2.1 IIR数字滤波器设计思路 (3)2.2设计IIR数字滤波器的两种方法 (4)2.3双线性变换法的基本原理 (5)2.4用双线性变换法设计IIR数字滤波器的步骤 (6)三、程序源代码和运行结果 (6)3.1低通滤波器 (6)3.2高通滤波器 (9)3.3带通滤波器 (12)3.4带阻滤波器 (14)四、网络结构图 (17)五、心得体会 (19)参考文献 (19)一、摘要数字滤波器是具有一定传输选择特性的数字信号处理装置,其输入、输出均为数字信号,实质上是一个由有限精度算法实现的线性时不变离散系统。

它的基本工作原理是利用离散系统特性对系统输入信号进行加工和变换,改变输入序列的频谱或信号波形,让有用频率的信号分量通过,抑制无用的信号分量输出。

数字滤波器和模拟滤波器有着相同的滤波概念,根据其频率响应特性可分为低通、高通、带通、带阻等类型,与模拟滤波器相比,数字滤波器除了具有数字信号处理的固有优点外,还有滤波精度高(与系统字长有关)、稳定性好(仅运行在0与l两个电平状态)、灵活性强等优点。

数字滤波器按单位脉冲响应的性质可分为无限长单位脉冲响应滤波器IIR和有限长单位脉冲响应滤波器(FIR)两种。

本文介绍IIR数字滤波器的设计。

二、设计思想2.1 IIR数字滤波器设计思路IIR 数字滤波器可用一个n阶差分方程表示y(n)=Σb r x(n-r)+Σa k y(n-k)或用它的Z域系统函数:对照模拟滤波器的传递函数:不难看出,数字滤波器与模拟滤波器的设计思路相仿,其设计实质也是寻找一组系数{b,a},去逼近所要求的频率响应,使其在性能上满足预定的技术要求;不同的是模拟滤波器的设计是在S平面上用数学逼近法去寻找近似的所需特性H(S),而数字滤波器则是在Z平面寻找合适的H(z)。

IIR数字滤波器的单位响应是无限长的,而模拟滤波器一般都具有无限长的单位脉冲响应,因此与模拟滤波器相匹配。

实验六用双线性变换法设计IIR数字滤波器一、实验目的学会运用MATLAB设计数字低通、带通、高通、带阻滤波器的设计方法。

二、实验涉及的matlab子函数bilinear功能：双线性变换——将s域映射到z域。

调用格式：[numd,dend]= bilinear (num,den,Fs)，将模拟域系统函数转换为数字域的系统函数，Fs为采样频率。

三、实验原理下面举例说明用双线性变换法设计各种数字滤波器的过程。

例1、采用双线性变换法设计一个巴特沃斯数字低通滤波器，要求：wp=0.25*pi，rp=1db，ws=0.4*pi，as=15db，滤波器采样频率Fs=100hz。

MATLAB源程序为：%数字滤波器指标wpd=0.25*pi; %滤波器的通带截止频率wsd=0.4*pi; %滤波器的阻带截止频率Rp=1;As=15; %输入滤波器的通阻带衰减指标%转换为模拟原型滤波器指标Fs=100;T=1/Fs;wp=(2/T)*tan(wpd/2);ws=(2/T)*tan(wsd/2);%模拟原型滤波器计算[n,wc]=buttord(wp,ws,Rp,As,'s') %计算阶数n和截止频率[z0,p0,k0]=buttap(n); %归一化切比雪夫1型原型设计ba=k0*poly(z0); %求原型滤波器系数baa=poly(p0); %求原型滤波器系数a[ba1,aa1]=lp2lp(ba,aa,wc);%变换为模拟低通滤波器%用双线性变换法计算数字滤波器系数[bd,ad]=bilinear(ba1,aa1,Fs) %双线性变换%求数字系统的频率特性[H,w]=freqz(bd,ad);dbH=20*log10(abs(H)/max(abs(H))); %化为分贝值subplot(2,2,1),plot(w,abs(H));ylabel('|H|');title('幅度响应');axis([0,pi,0,1.1]);grid subplot(2,2,2),plot(w,angle(H));ylabel('\phi');title('相位响应');axis([0,pi,-4,4]);grid subplot(2,2,3),plot(w,dbH);title('幅度响应(dB)'); ylabel('dB');xlabel('频率');axis([0,pi,-40,5]);grid subplot(2,2,4),zplane(bd,ad); axis([-1.1,1.1,-1.1,1.1]);title('零极图');运行结果为： n = 5wc = 103.2016bd = 0.0072 0.0362 0.0725 0.0725 0.0362 0.0072 ad = 1.0000 -1.9434 1.9680 -1.0702 0.3166 -0.0392 则所求滤波器的系统函数为54321-5432-10.0392z 166z 3.01.0702z z 68.911.9434z 1z 072.00z 362.00z 725.00z 725.000.0362z 0.0072H(z)---------+-+-+++++=|H |幅度响应φ相位响应幅度响应(dB)d B频率-1-0.500.51Real PartI m a g i n a r y P a r t零极图例2、采用双线性变换法设计一个椭圆数字高通滤波器，要求通带250hz ，1db ，阻带150hz ，20db ，滤波器采样频率为Fs=1000hz 。

用双线性变换法设计IIR滤波器
O 引言滤波器从广义上来说对特定的频点或频点以外的频率进行有效滤波的电路，这种电路保留输入信号中的有用信息，滤除不需要的信息，从而达到信号的检测、提取、识别等不同的目的。

如果处理的信号是时域离散信号，那么相应的处理系统就称为数字滤波器，由于在实际工作中被处理的信号都是幅度量化的数字信号，因此，数字滤波器实际上是用有限精度的算法实现一个线性时不变的时域离散系统。

目前，数字滤波器的应用越来越广泛，它已深入到很多领域，如图象处理、医学生物信息处理、地质信号处理和模式识别处理等。

数字滤波器的种类很多，分类方法也不同，可以从功能上分类，也可以从实现方法上及设计方法上来分类等等。

滤波器在功能上总的可分为四类，即低通(LP)、高通(HP)、带通(BP)、带阻(BS)滤波器等，从实现方法上，由有限
长冲激响应的数字滤波器被称为FIR滤波器，具有无限长冲激响应的数字滤波器称作IIR滤波器。

1 IIR滤波器的设计1．1 双线性变换法的基本原理本文中用的是双线性变换法，因此这里简单介绍一下。

双线性变换法的S域与Z域间的变换关系为：
 由式(1)可以看出，z和s之间可以直接代换，由于这是一非线性变换，需
考察一下是否能把jΩ映射成单位圆，以及是否能将s域左半平面映射到单位圆内部。

对于5平面上的虚轴jΩ，用s=jΩ代入式(1)得：
 可见：上式表明S平面与Z平面一一单值对应，S平面的虚轴(整个jΩ)经映射后确已成为z平面上的单位圆，但Ω与为非线性关系，因此，通过双线性变换后两个滤波器的频率特性形状不能保持相同，双线性变换不存在混迭效应。

对于s域的左半平面，用s=σ+jΩ入式(1)，得到：。

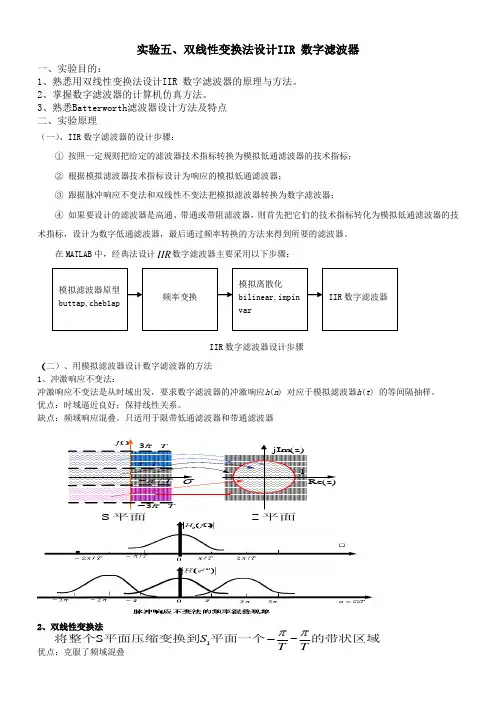
实验五、双线性变换法设计IIR 数字滤波器一、实验目的：1、熟悉用双线性变换法设计IIR 数字滤波器的原理与方法。

2、掌握数字滤波器的计算机仿真方法。

3、熟悉Batterworth 滤波器设计方法及特点 二、实验原理（一）、IIR 数字滤波器的设计步骤：① 按照一定规则把给定的滤波器技术指标转换为模拟低通滤波器的技术指标； ② 根据模拟滤波器技术指标设计为响应的模拟低通滤波器；③ 跟据脉冲响应不变法和双线性不变法把模拟滤波器转换为数字滤波器；④ 如果要设计的滤波器是高通、带通或带阻滤波器，则首先把它们的技术指标转化为模拟低通滤波器的技术指标，设计为数字低通滤波器，最后通过频率转换的方法来得到所要的滤波器。

在MATLAB 中，经典法设计IIR 数字滤波器主要采用以下步骤：IIR 数字滤波器设计步骤（二）、用模拟滤波器设计数字滤波器的方法 1、冲激响应不变法：冲激响应不变法是从时域出发，要求数字滤波器的冲激响应h (n ) 对应于模拟滤波器h (t ) 的等间隔抽样。

优点：时域逼近良好；保持线性关系。

缺点：频域响应混叠。

只适用于限带低通滤波器和带通滤波器2、双线性变换法优点：克服了频域混叠模拟滤波器原型 buttap,cheb1ap频率变换 模拟离散化 bilinear,impin varIIR 数字滤波器/Tπ/T π-3/Tπ3/Tπ-j ΩσjIm (z)Re(z)1S 平面Z 平面1S ~S T Tππ-将整个平面压缩变换到平面一个的带状区域缺点：高频时会引起畸变1）冲激响应不变法impinvar格式：[BZ,AZ]= impinvar （B,A,Fs ）功能：把具有[B,A]模拟滤波器传递函数模型转换为采样频率为Fs 的数字滤波器的传递函数模型[BZ,AZ]，Fs 默认值为1。

例：一个4阶的Butterworth 模拟低通滤波器的系统函数如下：12251)(234++++=s s s s s H a试用冲激响应不变法求出Butterworth 模拟低通数字滤波器的系统函数。

基于双线性变换法的IIR数字高通滤波器设计摘要随着信息时代和数字世界的到来，数字信号处理已成为当今一门极其重要的学科和技术领域。

在数字信号处理中起着重要的作用并已获得广泛应用的是数字滤波器（DF，Digital Filter）。

数字滤波器是一种用来过滤时间离散信号的数字系统，通过对抽样数据进行数学处理来达到频域滤波的目的。

实现IIR滤波器的阶次较低，所用的存储单元较少，效率高，精度高，而且能够保留一些模拟滤波器的优良特性，因此应用很广。

Matlab软件以矩阵运算为基础，把计算、可视化及程序设计有机融合到交互式工作环境中，并且为数字滤波的研究和应用提供了一个直观、高效、便捷的利器。

尤其是Matlab中的信号处理工具箱使各个领域的研究人员可以直观方便地进行科学研究与工程应用。

本次主要利用matlab的信号处理工具箱设计一个数字高通IIR滤波器，并用此滤波器处理一段音频信号。

此报告重点介绍了用双线性不变法设计IIR数字滤波器的基本流程，比较了各种设计方法的优缺点，总结了模拟滤波器的性能特征。

最后以双线性不变法设计了一个高通巴特沃斯IIR数字滤波器，介绍了设计步骤，然后在Matlab环境下进行了仿真与调试，实现了设计目标。

关键字 IIR数字滤波器巴特沃斯高通双线性变换 MATLABAbstractWith the information era and the advent of the digital world, digitalsignal processing has become one of the important fields of science and technology. In the digital signal processing plays an important role and has been widely applied in the digital filter. Digital filter is a discrete time signal is used to filter the digital system,through the mathematical processing of sampling data to reach the goal of frequency domain filterin. Implementation of IIR filter order is low, less storage unit, with high efficiency, high precision, and can keep some simulation characteristics of filter, so a very wide application. Matlab software based on matrix computation, the calculation,visualization and program design of organic integration to interactive environment, and provides an intuitive, efficient, convenient tool for the research and application of digital filter..The main use of signal processing toolbox of MATLAB to design a digital high-pass IIR filter, and an audio signal with the filter. This report focuses on the basic process of using the bilinearinvariant IIR digital filter design, compares the advantages and disadvantages of various design methods, summarizes thecharacteristics of the analog filter. Finally, by bilinear invariant to design a high Butterworth IIR digitalfilter, introduces the design steps, and then in the Matlab environment for the simulation and debugging, achieves the design goal.Keywords IIR Butterworth high-pass bilinear transform MATLABdigital filter目录摘要 (I)Abstract (II)1．数字滤波器 (1)1.1 数字滤波器介绍 (1)1.2 IIR数字滤波器设计原理 (2)1.2.2双线性变换法 (3)2．数字滤波器设计实现 (6)2.1 典型模拟滤波器比较 (6)2.2 设计步骤 (6)2.3 程序流程图 (7)2.4音频信号部分程序 (8)2.5仿真结果 (8)2.5.1滤波器性能仿真 (9)2.5.2滤波器除噪性能 (10)3．总结 (10)致谢 (11)参考文献 (12)附录 (13)1． 数字滤波器1.1 数字滤波器介绍数字滤波器是具有一定传输选择特性的数字信号处理装置,其输入、输出均为数字信号,实质上是一个由有限精度算法实现的线性时不变离散系统。

实验三 用双线性变换法设计I ＩＲ滤波器一、实验目的１、了解两种工程上最常用的变换方法：脉冲响应不变法和双线性变换法。

2、掌握双线性变换法设计IIR 滤波器的原理及具体设计方法，熟悉双线性法设计低通、带通和高通II Ｒ滤波器的计算机程序。

3、观察用双线性变换法设计的滤波器的品与特性，并与脉冲响应不变法相比较,了解双线性变换法的特点。

4、熟悉用双线性变换法涉及数字Butterworth 和Chebyshev 滤波器的全过程。

5、了解多项式呈几何多项式乘方运算的计算机变成方法。

二、实验原理与方法从模拟滤波器设计IIR 数字滤波器具有四种方法:微分—差分变换法、脉冲响应不变法、双线性变换法、匹配Z 变换法：在工程上常用的是其中两种：脉冲响应不变法、双线性变换法。

脉冲响应不变法需要经历如下步骤：由已知系统传输函数)(s H 计算系统冲激响应)(t h :对)(t h 进行等间隔取样得到)()(nT h t h =，由)(t h 获得数字滤波器的系统响应)(z H 。

这种方法非常直观,其算法宗旨是保证所设计的IIR 滤波器的脉冲响应和响应模拟滤波器的冲激响应在采样个点上完全一致。

而双线性变换法的设计准则是使数字滤波器的频率响应与参考模拟滤波器的频率响应相似。

脉冲响应不变法一个重要的特点是频率坐标的变换式现行的，其缺点是有频谱的周期延拓效应,存在频谱混淆的现象。

为了克服脉冲响应不变法可能产生的频谱混淆，提出了双线性变换法，它依靠双线性变换式：ss z z z s -+=+-=--11,1111 其中,jw re z j s =Ω+=,σ 建立起s 平面和z 平面的单值映射关系，数字频域和模拟频域之间的关系：Ω==Ωarctg w w tg 2),2( (3—1）由上面的关系式可知,当∞>-Ω时,w 中止在折叠频率π=w 处，整个Ωj 周单值的对应于单位圆的一周。

因此双线性变换法不同于脉冲响应不变法，不存在频谱混淆的问题。

双线性变换法在IIR滤波器设计中的应用张登奇;彭鑫;陈海兰【摘要】数字滤波器的设计是数字信号处理课程的重要教学内容，而双线性变换法是间接设计IIR数字滤波器的重要方法。

本文介绍了双线性变换法的设计原理，并以巴特沃斯数字低通滤波器为例，归纳了双线性变换法的设计步骤，对设计过程中较难理解的过渡滤波器和频率预畸变进行了分析，对变换常数和采样周期的取值问题进行了讨论，并以实例给出了MATLAB实现的程序。

%Digital filter design is the most important component in teaching of digital signal processing. Bilinear Transformation Method is an important method in the indirect design of IIR filter. We deduce the procedure of IIR filter design based on the fundamentals of Bilinear Transformation. And taking Butterworth low pass filter for instance, we introduce the design steps of filter. Furthermore, we deeply analyze that the unintelligible steps in the design procedure including transitional filters and frequency prewarping. And then, the value of transform constant and sampling period is discussed. Finally, the MATLAB source code of the filter design is given.【期刊名称】《湖南理工学院学报（自然科学版）》【年(卷),期】2016(029)003【总页数】5页(P21-25)【关键词】数字滤波器;双线性变换法;预畸变;MATLAB【作者】张登奇;彭鑫;陈海兰【作者单位】湖南理工学院信息与通信工程学院，湖南岳阳 414006;湖南理工学院信息与通信工程学院，湖南岳阳 414006;湖南理工学院信息与通信工程学院，湖南岳阳 414006【正文语种】中文【中图分类】TN713.7间接设计IIR数字滤波器的常用方法有脉冲响应不变法和双线性变换法. 文［1］对脉冲响应不变法进行了介绍和分析，但由于存在频谱混叠失真，故不适合设计高通和带阻滤波器. 双线性变换法通过频率的非线性变换，解决了频谱混叠问题，得到了广泛应用. 但一般教材对其原理论述简单，对某些参数介绍不详，导致学习理解困难. 本文从脉冲响应不变法的频谱混叠入手，先分析双线性变换法的原理思想，再以巴特沃斯数字低通滤波器的设计为例，归纳双线性变换法的设计步骤，并对设计过程中较难理解的过渡滤波器和频率预畸变进行深入分析，最后以实例给出MATLAB的实现程序.1.1 设计原理脉冲响应不变法的主要问题是频谱混叠失真［1］，产生的原因是过渡模拟滤波器在时系统函数Ha（s）≠0. 如果能将Ha（s）的复自变量沿虚轴方向压缩到的横带内，变换成一个新的中间模拟滤波器H1（ s1），再按变换成H（ z），就不会出现频谱混叠，整个变换过程如图1所示. 为了保证整个s平面能沿虚轴方向压缩到s1平面的横带内，可先考虑将整个jΩ轴压缩到jΩ1轴的段［2］. 利用（1）式可实现这个压缩要求：其中C是一个正实常数，也称变换常数. 由于将（2）式描述的虚轴压缩关系延拓到整个复平面，即则s平面和s1平面的映射关系可写成再将s1平面通过映射到z平面，得（4）式描述了从s平面直接到z平面的映射关系，由于分子和分母都是变量的线性函数，故称双线性变换.可以证明，双线性变换映射关系，将s左半平面映射到了z平面的单位圆内，将s右半平面映射到了z平面的单位圆外，将s平面的虚轴映射到了z平面的单位圆上［3］. 这种映射关系克服了频谱混叠失真，但付出了频率变换非线性的代价. 后面的分析可知，变换常数C不参与设计，取1C=是最简映射，计算也最简单，但为了减小低频段频率的非线性失真，常取所以，教材中一般将双线性变换关系直接写成1.2 设计步骤双线性变换法可由（5）式直接将）（sHa变换成）（zH，但设计）（sHa 的技术指标并不好理解.下面以巴特沃斯低通滤波器的设计为例，结合图2所示设计指标及幅频特性的变化过程，介绍双线性变换法的设计步骤，并对设计指标进行分析说明.实例对输入的模拟信号进行采样得离散时间信号，设采样频率Fs=20kHz，要求保留3000Hz以下的频率成分，幅度失真小于2dB；滤除5000Hz以上的频率成分，衰减大于10dB. 试用双线性变换法设计数字滤波器实现上述要求.（1）确定采用巴特沃斯数字低通滤波器.数字指标为ωp=0.3π rad ，ap=2dB （即0.7943倍），ωs=0.5π rad，as=10dB （即0.3162倍）. 在用双线性变换法设计数字滤波器的公式中，幅度指标要以分贝为单位代入数据，但用分贝为单位图示的幅频曲线感觉衰减不明显. 故在图2（a）点状图所示的幅频指标中，幅度指标数据的单位改用倍数.（2）将数字低通滤波器的技术指标转换成虚构的过渡模拟滤波器技术指标. （5）式描述了s平面与z平面的映射关系，令s=jΩ，z=ejω，代入（5）式可得过渡模拟角频率与数字频率之间的非线线关系设采样周期T=2s（采样周期T不参与设计，取2s计算最简），转化后的过渡模拟滤波器技术指标为Ωp=0.5095rad/s， Ap=2dB（即0.7943倍），Ωs=1rad/s， As=10dB （即0.3162倍）. 过渡模拟滤波器的技术指标参见图2（c）中的点状图.（3）按照虚构的过渡模拟滤波器技术指标设计过渡模拟滤波器系统函数［5］.过滤模拟滤波器的最低阶次及3dB频率计算公式为：其中，［x］表示不超过实数x的最大整数. 代入过渡模拟指标数据，算得N=3，Ωcp=0.5572 rad/s ，Ωcs= 0.6934 rad/s. 根据最小阶次N直接得到归一化原型系统函数再用代入（7）式得过渡模拟滤波器系统函数这里取Ωc=Ωcp，代入（8）式算得过渡模拟低通滤波器的幅频曲线如图2（c）所示. 因取Ωc=Ωcp，所以设计的过渡模拟滤波器通带边界指标精确满足，而阻带边界指标留有余量.（4）用双线性变换法将设计的过渡模拟滤波器系统函数转变成数字滤波器系统函数. 取T=2s，将（5）式代入（9）式并化简得用双线性变换法设计的数字低通滤波器幅频曲线如图2（a）所示，与图2（c）对比可知幅频曲线的形状差别较大，这是由于双线性变换法中频率的非线性关系引起的.2.1 过渡模拟滤波器间接设计IIR数字滤波器，要先设计一个过渡模拟滤波器，过渡模拟滤波器可根据数字指标自定义一个采样周期T进行虚构. 后面的分析可知采样周期T不参与设计， T值不同，算得的过渡模拟指标会不同，由此设计的过渡模拟滤波器也肯定不同，但按同一T值进行转换得到的数字滤波器是一样的. 如果数字滤波器的技术指标是以数字指标形式给出，则无需再给出采样周期或采样频率；若是以模拟指标形式给出，则一定要注意设计指标中用于离散连续信号的采样周期sT和用于设计过渡模拟滤波器的采样周期T不是同一个概念，前者用于计算数字指标，后者用于虚构模拟指标. 一些教材中混用了这两个符号，有的还直接用T=Ts设计过渡模拟滤波器，理论上虽然可行，但学生可能会认为过渡模拟滤波器必须这样设计，既误导了学生，也增加了计算难度，甚至还会引起较大误差，设计中应尽量避免.2.2 频率预畸变校正（4）式实现了Ha（s）到H（ z）的变换，具体到s平面的虚轴到z平面的单位圆，则是把Ha（jΩ）按非线性变换成H（ejω）. 也就是说，从模拟频响特性到数字频响特性本质上是横坐标的非线性压缩. 如果边界频率按进行非线性变换，则设计的Ha（s）按（4）式变换得到的H（z）一定满足边界频率要求. 图2（c）给出了通带指标精确满足的模拟滤波器幅频特性曲线，图2（a）给出了变换后数字滤波器的幅频特性曲线，其通带指标也精确满足. 假如用Ωp=ωpT ，Ωs=ωsT 作为过渡模拟滤波器的边界频率，则设计的Ha（s）按（4）式变换得到的H（z）就不会满足边界频率要求. （11）式中的Ω与ω的非线性关系，称为频率预畸变校正.2.3 变换常数C对设计的影响双线性变换法中的频率预畸变校正和模数滤波器变换都涉及到变换常数C. 只要保证过渡模拟滤波器的边界频率按（11）式进行预畸变校正，那么按（4）式变换得到的数字滤波器一定满足边界频率要求，变换常数C只要在频率预畸变和滤波器变换中取值不变就可以了，取值大小不影响设计. 这可从图2所示的波形变化中进行理解. 图2所示的幅频特性曲线变化是横坐标的非线性伸缩引起的，变换常数C虽会按（11）式影响Ωp和Ωs的位置，但只要设计的模拟滤波器满足Ωp和Ωs所确定的边界指标，那么经（4）式变换得到的数字滤波器也一定满足边界指标要求. 所以， C的取值不影响设计，但为了减小低频段频率的非线性失真，常取.2.4 采样周期T对设计的影响在双线性变换法的设计过程中有一个参数T，其实设计过程中的参数T只影响变换常数C，而C的取值不影响设计，所以参数T也不影响设计. 当然，采样周期T不影响设计还应从图2所示的坐标变换中进行理解. 对任一给定的变换常数C，采样周期T对从ω到Ω1的影响和从Ω1到Ω的影响可以相互抵消. 也就是说，C一定时，采样周期T会影响图2（a）到图2（b）的坐标变换，也会影响图2（b）到图2（c）的坐标变换，这两种影响正好使图2（a）到图2（c）的坐标变换与T无关. 理论上，采样周期T对设计结果没有影响，但由于在设计过程中T参与了计算，考虑到计算机的有限字长效应和计算简单，一般取T=2s.用双线性变换法设计实例中所要求的滤波器程序如下：%技术指标： Fs=20kHz，fp=3kHz，fs=5kHz，Ap=2dB，As=10db，clc； close all； clear； format compact；wp=0.3*pi， ws=0.5*pi， ap=2， as=10， Ts=1/20000；%输入数字技术指标T=2，%改变T值不影响设计结果Wp=（2/T）*tan（wp/2）， Ws=（2/T）*tan（ws/2）， Ap=ap， As=as， %双线性变换法指标转换Mn=log10（（10^（0.1*Ap）-1）/（10^（0.1*As）-1）），Md=（2*log10（Wp/Ws）），%先算分子分母N=ceil（Mn/Md），%计算过渡模拟滤波器最小阶次Wcpd=（10^（0.1*Ap）-1）^（1/（2*N）），Wcsd=（10^（0.1*As）-1）^（1/（2*N））， %先算分母Wcp=Wp/Wcpd； Wcs=Ws/Wcsd； %计算截止频率Wc=Wcp，%通带精确满足，取Wc=Wcs时阻带精确满足［bp1，ap1］ = butter（N，1，'s'）； %%计算归一化低通原型模拟滤波器的系统函数Ga（p）tf（bp1，ap1， 'variable'， 'p'）， %%显示归一化低通原型模拟滤波器的系统函数［bs，as］ = lp2lp（bp1，ap1，Wc）； %%计算过渡模拟低通滤波器的系统函数Ha（s）tf（bs，as）， %%显示过渡模拟滤波器的系统函数［bz，az］ = bilinear （bs，as，1/T），%将过渡模拟滤波器转换为数字滤波器tf（bz，az，Ts，'variable'，'z^-1'），%显示设计的数字滤波器系统函数freqz（bz，az，200），%绘图并验证设计技术指标该程序的运行结果在MATLAB的命令窗或图形窗中直接显示. 从图形窗中显示的幅频曲线可以直接测出ω=0.3π时衰减为2dB，ω=0.5π时衰减为15.37dB，通带指标精确满足，阻带指标富有余量. 如果改用Ωc=Ωcs重新设计，测出ω=0.3π时衰减0.6352dB，ω=0.5π时衰减10dB，通带指标富有余量，阻带指标精确满足.改变采样周期T，设计结果相同.双线性变换法是一种简单的代数变换方法，它以频率的非线性变换为代价，解决了频谱的混叠失真问题，故广泛应用于片段常数特性的滤波器设计. 设计过渡模拟滤波器，采样周期T可任意设置，取T=Ts理论上可行但不是必须. 设计过渡模拟滤波器的边界频率需进行预畸变处理. 变换常数C虽不影响设计，但为了减小低频段频率的非线性失真，常取. 采样周期T本不参与设计，但由于变换常数C 的取值与之关联，故在设计过程中参与了计算，但为了避免计算机有效字长效应并使计算简单，一般取T=2s. 文中介绍的频率变换思想，对从低通到高通、带通和带阻滤波器的转换有一定的引导作用，列举的巴特沃斯滤波器设计实例，对其它各型滤波器的设计也有一定的参考价值.【相关文献】［1］张登奇，彭鑫. 脉冲响应不变法在IIR滤波器设计中的应用［J］. 湖南理工学院学报（自然科学版）. 2015（04）： 23～26［2］吴镇扬. 数字信号处理的原理与实现［M］. 南京：东南大学出版社， 2001： 77［3］李芬华. 双线性变换中的映射［J］. 河北大学学报（自然科学版）. 1991（02）： 65～71 ［4］吴湘淇. 信号、系统与信号处理（下）［M］. 北京：电子工业出版社，1996： 60～67 ［5］刘顺兰，吴杰. 数字信号处理［M］. 西安：西安电子科技大学出版社， 2003： 158 ［6］高西全，丁玉美. 数字信号处理［M］. 第3版. 西安：西安电子科技大学出版社， 2008：184～189。

IIR 数字滤波器设计原理利用双线性变换设计IIR 滤波器（只介绍巴特沃斯数字低通滤波器的设计），首先要设计出满足指标要求的模拟滤波器的传递函数)(s H a ，然后由)(s H a 通过双线性变换可得所要设计的IIR 滤波器的系统函数)(z H 。

如果给定的指标为数字滤波器的指标，则首先要转换成模拟滤波器的技术指标，这里主要是边界频率s p w w 和的转换，对s p αα和指标不作变化。

边界频率的转换关系为)21tan(2w T =Ω。

接着，按照模拟低通滤波器的技术指标根据相应设计公式求出滤波器的阶数N 和dB 3截止频率c Ω；根据阶数N 查巴特沃斯归一化低通滤波器参数表，得到归一化传输函数)(p H a ；最后，将c sp Ω=代入)(p H a 去归一，得到实际的模拟滤波器传输函数)(s H a 。

之后，通过双线性变换法转换公式11112--+-=z z T s ，得到所要设计的IIR 滤波器的系统函数)(z H 。

步骤及内容1) 用双线性变换法设计一个巴特沃斯IIR 低通数字滤波器。

设计指标参数为：在通带内频率低于π2.0时，最大衰减小于dB 1；在阻带内[]ππ,3.0频率区间上，最小衰减大于dB 15。

2) 以π02.0为采样间隔，绘制出数字滤波器在频率区间[]2/,0π上的幅频响应特性曲线。

3) 程序及图形程序及实验结果如下：%%%%%%%%%%%%%%%%%%%iir_1.m%lskyp%%%%%%%%%%%%%%%%%%rp=1;rs=15;wp=.2*pi;ws=.3*pi;wap=tan(wp/2);was=tan(ws/2);[n,wn]=buttord(wap,was,rp,rs,'s');[z,p,k]=buttap(n);[bp,ap]=zp2tf(z,p,k);[bs,as]=lp2lp(bp,ap,wap);[bz,az]=bilinear(bs,as,.5);[h,f]=freqz(bz,az,256,1);plot(f,abs(h));title('双线性z 变换法获得数字低通滤波器，归一化频率轴'); xlabel('\omega/2\pi');ylabel('低通滤波器的幅频相应');grid;figure;[h,f]=freqz(bz,az,256,100);ff=2*pi*f/100;absh=abs(h);plot(ff(1:128),absh(1:128));title('双线性z 变换法获得数字低通滤波器,频率轴取[0,\pi/2]'); xlabel('\omega');ylabel('低通滤波器的幅频相应');grid on;运行结果：00.050.10.150.20.250.30.350.40.450.500.10.20.30.40.50.60.70.80.91双线性z 变换法获得数字低通滤波器，归一化频率轴ω/2π低通滤波器的幅频相应00.20.40.60.81 1.2 1.4 1.600.10.20.30.40.50.60.70.80.91双线性z 变换法获得数字低通滤波器,频率轴取[0,π/2]ω低通滤波器的幅频相应。

双线性变换法IIR数字滤波器设计一、实验目的1、掌握用双线性变换法设计低通IIR数字滤波器的基本原理和算法。

2、掌握用双线性变换法设计髙通和带通IIR数字滤波器的基本原理和算法。

3、进一步了解数字滤波器和模拟滤波器的频率响应特性。

二、实验原理与计算方法1、双线性变换法设计IIR低通数字滤波器的基本原理和算法双线性变换法设汁数字滤波器，采用了二次映射的方法，就是先将整个£平而压缩到平而的一个-岭~吟的横形条带范用内，然后再将这个条带映射到Z平而上，就能建立S平面到Z平面的一一对应关系。

对于低通数字滤波器，映射关系为5 = --!—— = —(1) T 1 + z"1T 1 + z其中T为抽样周期。

用双线性变换法设讣低通IIR数字滤波器的基本步骤，首先根据设讣要求确泄相应的模拟滤波器的传递函数再应用(1)式得数字滤波器的传递函数H⑵H(z) = Hg I 2-z (2) 通常可以给左的参数为：低通数字滤波器通带边界频率G\p=27Tfp、阻带边界频率◎ =2龙儿和对应的通带衰减函数勺、阻带衰减函数匕。

si平而中的模拟角频率口与数字角频率s的关系为线性关系® = ，在计算模拟滤波器的阶数N、极点/和传递函数H a(s)之前，应作预畸变处理p = l t an^- = -tan^^- (3)T 2 T 2模拟滤波器的阶数N、极点$和传递函数耳⑴的讣算方法与冲激响应不变法相同，可以采用Butterworth逼近或Chebyshev逼近a2.双线性变换法设计IIR髙通、带通、带阻数字滤波器的基本原理和算法由于双线性变换法获得的数字滤波器频率响应特性中不会出现混叠现象，因此可以适用于髙通、带通和带阻滤波器的设ih HR数字滤波器的设计通常要借助于模拟低通滤波器的设计，由原型低通滤波器到其他形式(高通、带通、带阻)IIR数字滤波器的频带变换有模拟频带变换法和数字频带变换法。

(1)模拟频带变换法首先将给左的对数字滤波骼(DF)的技术要求转换为一个低通模拟滤波器(AF)的技术要求，根据这种要求用某种逼近设计出原型的低通模拟滤波器(LPAF),讣算出模拟滤波器的阶数N、极点曲和传递函数77.(5),再按照双线性变换的变换关系，将模拟滤波器的传递函数(s)转换为数字滤波器的传递函数H⑵。