电磁场中的基本物理量
- 格式:ppt
- 大小:1.04 MB
- 文档页数:30

第二章 电磁场中的基本物理量和基本实验定律2.1电磁场的源量——电荷和电流一、电荷与电荷密度 C e 1910602.1-⨯+=1、 自然界中最小的带电粒子包括电子和质子——电子电荷量191.60210C e -=-⨯←基本电荷量 一般带电体的电荷量 ,3,2,1±==n neq2、电荷的几种分布方式从微观上看,电荷是以离散的方式出现在空间中,从宏观电磁学的观点上看,大量带电粒子密集出现在某空间范围内时,可假设电荷是以连续的形式分布在这个范围内中。
空间中——体电荷 面上——面电荷 线上——线电荷体电荷:电荷连续分布在一定体积内形成的电荷体。
体电荷密度)(r 'ρ定义:在电荷空间V 内,任取体积元V ∆,其中电荷量为q ∆,则⎰'=⇒=∆∆='→∆v v dv r q dvdq v q linr )()(0ρρ 3/m c面电荷:当电荷存在于一个薄层上时,称其为面电荷。
面电荷密度)(r s 'ρ的定义:在面电荷上,任取面积元s ∆,其中电荷量为q ∆,则ds r q dsdq s q linr s s s s ⎰'=⇒=∆∆='→∆)()(0ρρ 2/m c线电荷:当电荷只分布于一条细线上时,称其为线电荷。
线电荷密度)(r l 'ρ的定义:在线电荷上,任取线元l ∆,其中电荷量为q ∆,则dl r q dldq l q linr s l l l ⎰'=⇒=∆∆='→∆)()(0 ρρ 点电荷:当电荷体积非常小,q 无限集中在一个几何点上可忽略时,称为点电荷。
点电荷的)(rδ函数表示:∞→∆=→∆vq linv 0ρ,保持总电荷不变,⎩⎨⎧'=∞'≠='-r r r r r r0)(δ 筛选特性:⎰='-vr f dv r r r f )()()(δ)()(r r q r '-=δρ当点电荷q 位于坐标原点时,)()(,0r q r rδρ=='电荷量 ⎰⎰⎩⎨⎧'='≠='-==vv r r qr r dv r r q dv r q0)()(δρ 二、电流与电流密度1、 电流强度 I定向流动的电荷形成电流,通常用单位时间通过某一截面的电荷 即电流强度表示,定义为:dtdqt q lin t i t =∆∆=→∆0)( 电流强度的大小:单位时间内S 的电荷量。

电磁场数值分析方法及其应用电磁场是无处不在的,它在我们的日常生活中也发挥着极其重要的作用,比如说电视、手机、电脑和家用电器等等。
由于电磁现象的特殊性质,使得电磁场的理论计算非常困难,因此需要引入数值计算方法,对电磁场进行模拟分析,这就是电磁场数值分析方法的基本概念。
一、电磁场数值分析方法简介1. 经典电磁场理论在介绍电磁场数值分析方法之前,我们需要先了解一下经典电磁场理论,也即麦克斯韦方程组。
麦克斯韦方程组描述了电磁场的本质规律,包括电场E、磁场B、电荷密度ρ和电流密度J等四个基本物理量。
这些物理量之间的关系是非常复杂的,因此对于麦克斯韦方程组的求解,需要引入数值计算方法。
2. 电磁场数值计算方法电磁场数值计算方法是指采用离散化方法,将复杂的连续介质分割成有限的、简单的小单元,通过在每个小单元内求解基本电磁场变量的数值解,再通过数值方法进行拼合,最终得到求解区域内的电磁场分布特征。
3. 数值计算方法分类目前常用的电磁场数值计算方法主要包括有限元法、时域有限差分法、频域有限差分法、矩量法等等。
这些方法各有特点,适用于不同的电磁问题求解。
二、电磁场数值分析方法应用1. 微波器件设计微波器件中电磁场的分布特征是十分重要的,它决定了微波器件的性能。
采用电磁场数值分析方法可以清晰地描述微波场的分布特征,从而进行优化和改进设计,提高微波器件的性能。
2. 汽车电磁兼容性分析汽车中各类电子设备的数量越来越多,它们之间的干扰和互相影响也越来越严重。
采用电磁场数值分析方法可以对汽车中的电磁问题进行深入分析,确定干扰成因,从而提出解决方案。
3. 太阳能电池板设计太阳能电池板在光电转化过程中,需要考虑光的反射、折射和吸收等问题。
而这些问题都涉及到电磁场的分布特征。
因此,采用电磁场数值分析方法可以对太阳能电池板的设计进行优化,并提高其能量转换效率。
三、结论电磁场数值分析方法是一种强大的工具,它可以帮助我们深入了解电磁场的本质规律,并对各类电磁问题进行分析和优化设计。


电磁场与电磁波摘要:电磁场与电磁波课程与电气专业息息相关,是我们电气专业学生必须学习的,这学期我们进行了电磁场与电磁波的学习。
主要讲解了矢量分析,电磁场的基本定律,时变电磁场,简述了静态电磁场极其边值问题的解。
第一章:矢量分析是研究电磁场在空间分布和变化规律的基本数学工具之一。
第二章以大学物理(电磁学)为基础,介绍电磁场的基本物理量和基本规律,第三章分别介绍了静电场、恒定电场和恒定磁场的分析方法。
第四章主要讨论时变电磁场的普遍规律。
一、矢量分析电磁场是是分布在三维空间的矢量场,矢量分析是研究电磁场在空间的分布和变化规律的基本教学工具之一。
1:标量和矢量(1) 标量:一个只用大小描述的物理量。
矢量:一个既有大小又有方向特性的物理量,常用黑体字母或带箭头的字母表示。
矢量一旦被赋予“物理单位”,则成为一个具有物理意义的矢量,如:电场强度矢量E 、磁场强度矢量H 、作用力矢量F 、速度矢量v 等。
(2) 两个矢量A 与B 相加,其和是另一个矢量D 。
矢量D=A+B 可按平行四边形法则得到:从同一点画出矢量A 与B ,构成一个平行四边形,其对角线矢量即为矢量D 。
两个矢量A 与B 的点积是一个标量,定义为矢量A 与B 的与它们之间较小的夹角的余弦之积。
(3) 两个矢量A 与B 的叉积是一个矢量,它垂直于包含矢量A 和B 的平面,大小定义为矢量A 与B 的与它们之间较小的夹角的正弦之积,方向为当右手四个手指从矢量A 到B 旋转时大拇指的方向。
2:标量场的梯度(1)等值面: 标量场取得同一数值的点在空间形成的曲面,形象直观地描述了物理量在空间的分布状态。
对任意给定的常数C ,方程C z y x u ),,(就是等值方程。
(2)梯度的概念:标量场u 在点M 处的梯度是一个矢量,它的方向沿场量u 变化率最大的方向,大小等于其最大变化率,并记作grad u,即 grad u= e l |max直角坐标系中梯度的表达式为grad u=,标量场u 的梯度可用哈密顿算符表示为grad u=().u =(3)标量场的梯度具有以下特性:①标量场u 的梯度是一个矢量场,通常称▽u为标量场u 所产生的梯度场;②标量场u (M )中,再给定点沿任意方向l 的方向导数等于梯度在该方向上的投影;③标量场u (M )中每一点M 处的梯度,垂直于过该点的等值面,且指向u (M )增加的方向。

描述磁场强弱和方向的物理量磁场是对电磁现象的一种抽象概念,它以某种方式影响着物体的运动。
它的特性可以以物理量的方式来描述,包括磁场强度、磁场方向和磁场梯度等等。
本文将对这些物理量进行描述和分析,以便更加清楚地理解磁场。
磁场强度是磁场的最基本物理量,它使得相邻的磁体之间存在着相互吸引或排斥的作用,从而影响到物体的运动轨迹。
磁场强度可以用物理量B来表示,单位为特斯拉(T)。
磁场强度的大小反映了磁力的强弱,当磁力很弱时,磁场强度B也就很小。
磁场的方向决定着磁力的作用的方向,它与磁力线的方向相同。
它可以用极坐标形式来表示,以相对地球的经纬度来表示。
在空间中,磁场的方向可以用磁极的位置呈现出来,磁场强度B也是这样。
为了更加全面地理解和描述磁场,科学家还提出了更加复杂的物理量磁场梯度。
磁场梯度指磁场强度随空间位置的变化而变化的程度。
它可以用物理量F来表示,单位为特斯拉每米(T/m)。
磁场梯度的变化决定了磁力的变化,从而影响物体的运动轨迹。
通过上文,我们可以明白描述磁场强弱和方向的物理量包括磁场强度B、磁场方向和磁场梯度F,它们分别使用特斯拉(T)、极坐标和特斯拉每米(T/m)来表示。
它们的变化会对相应的磁力幅度和方向产生影响,从而影响物体的运动轨迹。
要更加全面地理解磁场,还需要进行方程的建立,以研究一般磁场的特性,以及具体物体对磁场的反应。
有关磁力的方程需要引入电磁场的概念,以及由电流的改变产生的磁力的关系。
这些方程可以为研究磁场的特性和对物体的影响提供实际的依据。
总之,磁场的强弱和方向可以以物理量的形式描述,其中包括磁场强度B、磁场方向和磁场梯度F。
磁力是由静态磁场和电磁场共同产生,它们的变化可以影响到物体的运动轨迹。
要更加全面地理解磁场,还需要进行相应的方程建立。
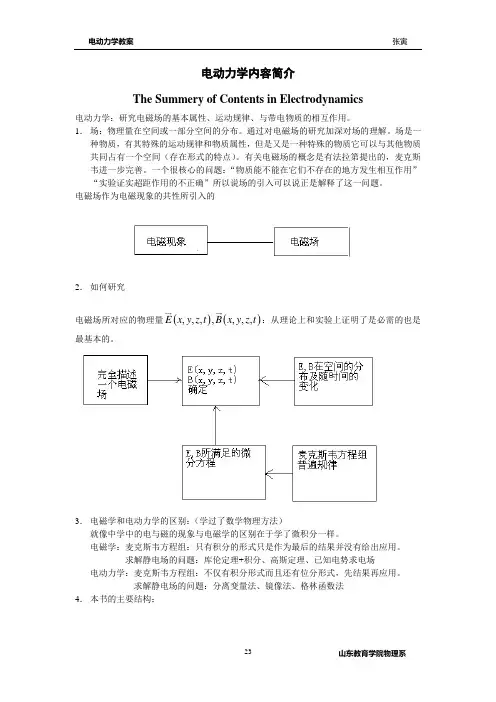
电动力学内容简介The Summery of Contents in Electrodynamics电动力学:研究电磁场的基本属性、运动规律、与带电物质的相互作用。
1. 场:物理量在空间或一部分空间的分布。
通过对电磁场的研究加深对场的理解。
场是一种物质,有其特殊的运动规律和物质属性,但是又是一种特殊的物质它可以与其他物质共同占有一个空间(存在形式的特点)。
有关电磁场的概念是有法拉第提出的,麦克斯韦进一步完善。
一个很核心的问题:“物质能不能在它们不存在的地方发生相互作用” “实验证实超距作用的不正确”所以说场的引入可以说正是解释了这一问题。
电磁场作为电磁现象的共性所引入的2. 如何研究电磁场所对应的物理量()(),,,,,,,E x y z t B x y z t :从理论上和实验上证明了是必需的也是最基本的。
3. 电磁学和电动力学的区别:(学过了数学物理方法)就像中学中的电与磁的现象与电磁学的区别在于学了微积分一样。
电磁学:麦克斯韦方程组:只有积分的形式只是作为最后的结果并没有给出应用。
求解静电场的问题:库伦定理+积分、高斯定理、已知电势求电场电动力学:麦克斯韦方程组:不仅有积分形式而且还有位分形式,先结果再应用。
求解静电场的问题:分离变量法、镜像法、格林函数法4. 本书的主要结构:⎧⎧→⎨⎪⎪⎩→⎨⎧⎪→⎨⎪⎩⎩第二章静电场静第三章静磁场第一章电磁现象的普遍规律第四章电磁场的的传播动第五章电磁场的发射第六章相对论第一章 电磁现象的普遍规律Universal Law of Electromagnetic Phenomenon本章将从基本的电磁实验定律出发建立真空中的Maxwell’s equations 。
并从微观角度论证了存在介质时的Maxwell’s equations 的形式及其电磁性质的本构关系。
继而给出Maxwell’s equat ions 在边界上的形式,及其电磁场的能量和能流,最后讨论Maxwell’s equations 的自洽性和完备性。
![电磁场导论 第三章]](https://uimg.taocdn.com/531f55c7240c844769eaee8a.webp)



大学物理电磁学基础知识点汇总一、电场1、库仑定律库仑定律描述了真空中两个静止点电荷之间的相互作用力与它们电荷量的乘积成正比,与它们之间距离的平方成反比,作用力的方向沿着它们的连线。
其表达式为:$F = k\frac{q_1q_2}{r^2}$,其中$k$为库仑常量,$q_1$和$q_2$为两个点电荷的电荷量,$r$为它们之间的距离。
2、电场强度电场强度是描述电场力的性质的物理量,定义为单位正电荷在电场中所受到的力。
其表达式为:$E =\frac{F}{q}$。
对于点电荷产生的电场,其电场强度的表达式为:$E = k\frac{q}{r^2}$,方向沿径向向外(正电荷)或向内(负电荷)。
3、电场线电场线是用来形象地描述电场的一种工具。
电场线的疏密表示电场强度的大小,电场线的切线方向表示电场强度的方向。
静电场的电场线不闭合,始于正电荷或无穷远,终于负电荷或无穷远。
4、电通量电通量是通过某一面积的电场线条数。
对于匀强电场,通过平面的电通量为:$\Phi = ES\cos\theta$,其中$E$为电场强度,$S$为平面面积,$\theta$为电场强度与平面法线的夹角。
5、高斯定理高斯定理表明,通过闭合曲面的电通量等于该闭合曲面所包围的电荷量的代数和除以$\epsilon_0$。
即:$\oint_S E\cdot dS =\frac{1}{\epsilon_0}\sum q$。
高斯定理是求解具有对称性电场分布的重要工具。
二、电势1、电势电势是描述电场能的性质的物理量,定义为把单位正电荷从电场中某点移动到参考点(通常取无穷远处)时电场力所做的功。
某点的电势等于该点到参考点的电势差。
点电荷产生的电场中某点的电势为:$V = k\frac{q}{r}$。
2、等势面等势面是电势相等的点构成的面。
等势面与电场线垂直,沿电场线方向电势降低。
3、电势差电场中两点之间的电势之差称为电势差,也称为电压。
其表达式为:$U_{AB} = V_A V_B$。

常见磁学量单位简介磁学量单位是描述物体与电磁场相互作用的基本量度单位,也是物理学研究中最重要的量度单位之一。
它们用来衡量电磁场的大小、质量、力矩和动能,描述电磁学的基本概念。
除此之外,磁学量单位还可以用来测量电磁辐射的强度、量子效应的能量以及量子力学现象。
常见的磁学量单位有吉拉伯伏(Gillber volts,V)、安培(Amperes,A)、碟特(Dynes,D)、波特(Watts,W)、相位(Phase,P)、强度(Intensity,I)、波瓣(Bands,B)、电荷(Charge,Q)、磁力矩(Torque,T)以及磁能(Magnetic Energy,E)。
吉拉伯伏(V)是一个物理量,表示电势差的大小,简称“伏”。
物理系统中,电势差的大小取决于两个电荷之间的距离。
它的定义就是一个电荷,移动一个吉拉伯伏的距离,耗费的电能等于1伏特所需要的能量。
安培(A)是一个物理量,表示电流的大小,简称“安”。
安培是指一定时间内,从一个电极经过的电子的多少,或电流通过的正负离子的数量。
它的定义就是,一定的安培表示,每秒经过的电子数量都是一定的,并且可以计算出电流的强度。
碟特(D)是一个物理量,表示电磁力的大小,简称“特”。
它的定义就是单位正电荷受到的单位正电荷的力的大小,它也可以用来衡量静电场、磁场和电磁辐射的强度等。
波特(W)是一个物理量,表示功率的大小,简称“瓦”。
它的定义就是电功率,单位时间内消耗的能量,以特定强度的电流或电压为基准。
它主要用于测量供电系统的功率,以及量化动力系统的和电磁辐射的强度。
相位(P)是一个物理量,表示振荡信号的定向。
在电磁场方面,它表示电流与电压之间的相对阶段,这种阶段表示波形信号的方向。
强度(I)是一个物理量,表示能量的强度。
在电磁场方面,它是用来衡量电流或电压的强度,以及描述电磁辐射的强弱程度。
波瓣(B)是一个物理量,用来衡量圆锥或圆柱形电流线圈的磁场线圈的数量,它也可以表示电磁辐射的强度。
第一章 电磁场和电磁波基础1 电磁学基本物理量 2 电磁场定律 3 边界条件 4 本构关系 5 波动方程 6 场和方程的复数形式 7 波数和波阻抗 8 均匀平面波 9 平面波的反射和折射 10 坡印亭定理1 电磁学基本物理量在电磁场基本方程中,所涉及到的基本物理量有:E :称为电场强度(伏/米)H :称为磁场强度(安/米)D :称为电通密度(库/米 2) B :称为磁通密度(韦/米 2)电位移矢量 磁感应强度⎯真空→ ε 0 E ⎯ ⎯ ⎯真空→ μ 0 H ⎯ ⎯J :电流密度(安/米 2)ρ :电荷密度(库/米 )3⎧ ⎪基本物理量:E , B ⎨ ⎪导出物理量:D, H ⎩瞬时值或时域表示 一般情况下,各场量和源量既是空间坐标的函数,又是时 间的函数,即2 电磁学场定律电磁学场定律描述场和源的关系,包括积分形式场定 律和微分形式场定律。
微分场定律形式把某点的场与就在该点的源及该点 的其它场量联系起来,适用于场、源量都是连续函数并有 S 连续的导数的良态域。
•⎧ E = E ( r , t ) = E ( x, y , z , t ) ⎪ ⎪ D = D ( r , t ) = D ( x, y , z , t ) ⎪ B = B ( r , t ) = B ( x, y , z , t ) ⎪ ⎨ ⎪ H = H ( r , t ) = H ( x, y , z , t ) ⎪ ρ = ρ (r , t ) = ρ ( x, y, z , t ) ⎪ ⎪ J = J (r , t ) = J ( x, y, z , t ) ⎩对应不同时刻,这些场量和源量的方向和数值会发生变 化,对应着一般时变场,称为场量的时域表示,或者瞬时 值。
P⎧ ⎪场:E , B ⎨ ⎪源:ρ,J ⎩2.1 自由空间场定律 2.2 物质中场定律V2.1 自由空间场定律∇× E = −B∂B (1a) ∂t∂ε 0 E (1b) ∂tVS自由空间指真空或同真空基本上具有同样特性的任 何其它媒质 (如空气) 自由空间场定律描述纯粹的源 ρ 、 。
《电磁场与电磁波》教学大纲一、课程基本信息课程名称:电磁场与电磁波课程编码:58083004课程类别:专业教育必修适用专业:通信工程开课学期:3—3课程学时:总学时: 64学时;其中理论 48 学时,实验 16 学时。
课程学分:4先修课程:大学物理、模拟电子线路、数字逻辑电路并修课程:课程简介:《电磁场与电磁波》课程是高等学校通信工程等电子科学与技术类各专业本科生必修的一门技术基础课.电磁场与电磁波是通信技术的理论基础,是通信工程专业本科学生的知识结构中重要组成部分。
本课程包括电磁场与电磁波两大部分。
电磁场部分是在《电磁学》课程的基础上,运用矢量分析的方法,描述静电场和恒定磁场的基本物理概念,在总结基本实验定律的基础上给出电磁场的基本规律,研究静态场的解题方法.电磁波部分主要是介绍有关电磁波在各种介质中的传播规律及天线的基本理论.二、课程教育目标本课程使学生掌握电磁场的有关定理、定律、麦克斯韦方程等的物理意义及数学表达式。
使学生熟悉一些重要的电磁场问题的数学模型(如波动方程、拉氏方程等)的建立过程以及分析方法。
培养学生正确的思维方法和分析问题的能力,使学生学会用"场"的观点去观察、分析和计算一些简单、典型的场的问题。
其教育目标主要表在以下三方面:1、内容方面,应使学生牢固掌握矢量运算,梯度、散度和旋度概念,高斯公式和斯托克司公式;掌握恒定和时变电磁场的麦克斯韦方程组、泊松方程、电磁波的波动方程等;掌握分离变量法、镜像法、有有界空间中电磁波的求解方法等;理解电磁场的矢势¦和标势、规范变换、规范不变性、库仑规范、洛仑兹规范、时谐平面电磁波、推迟势、电磁辐射、截止频率和谐振频率等概念。
2、能力方面,应使学生学会和掌握如何通过数学方法求解一些基本和实际问题,对结果给予物理解释的科学研究方法;使学生在运算能力和抽象思维能力方面受到初步而又严格的训练;培养学生解决和研究问题的能力,培养学生严谨的科学学风.3、方法方面,着重物理概念、基本规律和基本问题的解释和阐述,注意本课程与大学物理电磁学的衔接,以及与后继课程联系,注重解决常见基本问题和实际问题。