下载文档原格式
电压源与电流源的等效变换
电压源与电流源的等效变换依据是对外部电路等效，即相同的负载接入后性状相同。
当电流源变为电压源时，电压源的电流（实际也就是负载的电流）可以变的，是和原来的电流源的电流不相等。
电压源与电流源的等效变换，求解复杂电路的步骤如下：
（1）将电压源等效变换成电流源或将电流源等效变换成电压源。
（2）将几个并联的电流源（或串联的电压源）合并成一个电流源（或电压源）。
（3）应用分流公式（或分压公式）求出未知数。
电压源电流源等效变换一、引言电压源和电流源是电路中常见的两种基本元件，它们在电路分析和设计中起着重要的作用。
在电路分析中，有时需要将电压源转化为电流源，或者将电流源转化为电压源，以便于更好地理解和分析电路的特性。
这种转化称为电压源电流源等效变换。
二、电压源电流源的基本概念2.1 电压源电压源是一个能够提供稳定电压输出的元件，它的输出电压保持不变，不受电路负载的影响。
电压源的符号为一个短杠和一个长杠，表示正极和负极。
2.2 电流源电流源是一个能够提供稳定电流输出的元件，它的输出电流保持不变，不受电路负载的影响。
电流源的符号为一个圆圈和一个箭头，表示电流的流向。
三、电压源电流源的等效变换3.1 电压源到电流源的转换将电压源转换为电流源的方法是将一个电阻与电压源串联，使得电阻的电流与电压源的电压成正比。
这样，可以通过改变电阻的阻值来改变电流源的输出电流。
3.2 电流源到电压源的转换将电流源转换为电压源的方法是将一个电阻与电流源并联，使得电阻两端的电压与电流源的电流成正比。
这样，可以通过改变电阻的阻值来改变电压源的输出电压。
四、电压源电流源等效变换的应用4.1 电路分析在电路分析中，有时需要将复杂的电路转化为简化的等效电路，以便于更好地理解和分析电路的特性。
电压源电流源等效变换提供了一种将电路中的电压源和电流源进行转化的方法，能够简化电路分析的过程。
4.2 电路设计在电路设计中，有时需要根据特定的要求选择合适的电压源或电流源。
电压源电流源等效变换可以帮助设计师将电路中的电压源和电流源进行转化，从而满足设计要求。
五、总结电压源电流源等效变换是电路分析和设计中常用的方法之一，它可以将电路中的电压源和电流源进行转化，以便于更好地理解和分析电路的特性。
通过电压源电流源等效变换，可以简化电路分析的过程，满足电路设计的要求。
在实际应用中，需要根据具体情况选择合适的等效变换方法，并注意电路参数的变化。
1．5电压源和电流源的等效变换实际使用的电源，按其外特性，可分为电压源和电流源。
当一个电压源和一个电流源能够为同一个负载提供相同的电压、电流和功率时，这两个电源对该负载来说是等效的，可以互相置换，这种置换称为等效变换。
下面来讨论电压源和电流源的等效变换。
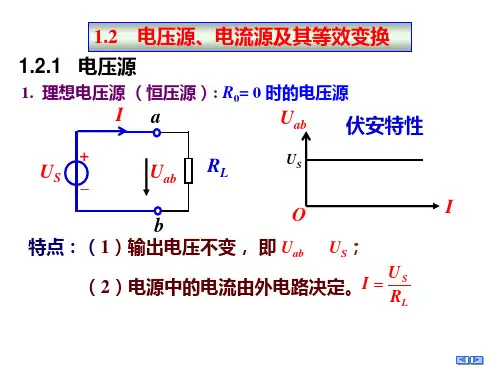
1．5．1 电压源在电路分析课程中，将能够向外电路提供电压的器件称为电压源。
如，电池，发电机等均是电压源。
在物理学中，电池表示成电动势E和内阻R相串联的电路模型，电池是一个典型的电压源，所以，电压源也可表示成电动势和内阻相串联的电路模型。
为了利用KVL的方便，对电压源特性进行标定时，通常不使用电动势E，而改用电压源所能输出的恒压值US，如图1-30（a）所示虚线框内部的电路。
图中电压源旁的箭头为US的参考方向。
注意： US 和E是不同性质的两个物理量，US是描述电压源所能输出的恒值电压，该值的大小与E相等，设定的参考方向与E相反。
当电压源与负载电阻RL相连时，根据KVL可得描述电压源外特性的函数式。
描述理想化电压源外特性的函数式是（1-57）由式1-57可见，理想化电压源的外特性曲线是直线，如图1-30（b）所示，图1-30（b）又称为电压源伏（U）-安（A）特性曲线。
图1-30（b）纵轴上的点，为电压源输出电流等于0的情况，相当于电压源处在开路的状态下。
当电压源开路时，电压源的输出电压U就等于US ，所以，US的值等于电压源的开路电压。
图1=30（b）横轴上的点，为电压源输出电压等于0的情况，相当于电压源处在短路的状态下（实际上这是不允许的），电压源输出电流为IS ，所以，IS称为短路电流。
计算短路电流的表达式为（1-58）U=f（I）曲线的斜率为R0，R越小，斜率越小，直线越平坦。
当R=0时，电源外特性曲线是一条平行与I轴的直线。
具有这种外特性曲线的电压源输出电压保持恒定值US，这种电压源称为理想电压源，简称恒压源。
将图1-30（a）虚线框内部电路的电阻R去掉，剩下的电路就是恒压源电路的模型。
电压源与电流源是电路中常见的两种基本元件，它们分别以恒定的电压和恒定的电流来驱动电路。
在电路分析和设计中，经常需要将电压源转换为等效的电流源，或将电流源转换为等效的电压源，以便更方便地进行电路分析和计算。
下面将分别介绍电压源与电流源的等效变换方法。
一、将电压源转换为等效的电流源1. 理论基础电压源的等效电流源转换是基于欧姆定律进行的。
根据欧姆定律，电流等于电压除以电阻，即I=V/R。
我们可以将电压源转换为等效的电流源，通过在电压源的正负端并联一个等效电阻，使得该电阻上的电流等于电压源的电压除以电阻值。
2. 转换公式电压源转换为等效电流源的公式为：I=V/R，其中I为等效电流源的输出电流，V为电压源的电压，R为等效电流源的电阻。
3. 举例说明假设有一个5V的电压源，需要将其转换为等效的电流源。
如果我们希望等效电流源的输出电流为1A，那么根据公式I=V/R，可得等效电阻R=V/I=5Ω。
我们可以在电压源的正负端并联一个5Ω的电阻，即可将电压源转换为等效的电流源。
二、将电流源转换为等效的电压源1. 理论基础电流源的等效电压源转换同样是基于欧姆定律进行的。
根据欧姆定律，电压等于电流乘以电阻，即V=IR。
我们可以将电流源转换为等效的电压源，通过在电流源的两端串联一个等效电压源，使得该电压等于电流源的电流乘以电阻值。
2. 转换公式电流源转换为等效电压源的公式为：V=IR，其中V为等效电压源的输出电压，I为电流源的电流，R为等效电压源的电阻。
3. 举例说明假设有一个2A的电流源，需要将其转换为等效的电压源。
如果我们希望等效电压源的输出电压为10V，那么根据公式V=IR，可得等效电阻R=V/I=5Ω。
我们可以在电流源的两端串联一个10V的电压源，并在其正负端串联一个5Ω的电阻，即可将电流源转换为等效的电压源。
电压源与电流源的等效变换方法可以在电路分析和设计中起到重要的作用。
通过合理应用这些方法，可以使得电路分析更加简便和直观，为电路设计提供重要的参考依据。
XXX 实验室学生实验报告课程名称电路分析基础实验学院XXX专业XXX班级XXX学号XXX姓名XXX辅导教师XXX实验时间：X 年X 月X 日预 习 实 验 报 告1、 实验名称电压源、电流源及其电源等效变换2、实验目的1．掌握建立电源模型的方法。
2．掌握电源外特性的测试方法。
3．加深对电压源和电流源特性的理解。
4．研究电源模型等效变换的条件。
3、实验内容1．电压源和电流源电压源具有端电压保持恒定不变，而输出电流的大小由负载决定的特性。
其外特性，即端电压U 与输出电流I 的关系U ＝ f (I ) 是一条平行于Ｉ轴的直线。
实验中使用的恒压源在规定的电流范围内，具有很小的内阻，可以将它视为一个电压源。
电流源具有输出电流保持恒定不变，而端电压的大小由负载决定的特性。
其外特性，即输出电流I 与端电压U 的关系I ＝ f (U ) 是一条平行于U 轴的直线。
实验中使用的恒流源在规定的电流范围内，具有极大的内阻，可以将它视为一个电流源。
2．实际电压源和实际电流源实际上任何电源内部都存在电阻，通常称为内阻。
因而，实际电压源可以用一个内阻R S 和电压源U S 串联表示，其端电压U 随输出电流I 增大而降低。
在实验中，可以用一个小阻值的电阻与恒压源相串联来模拟一个实际电压源。
实际电流源是用一个内阻R S 和电流源I S 并联表示，其输出电流I 随端电压U 增大而减小。
在实验中，可以用一个大阻值的电阻与恒流源相并联来模拟一个实际电流源。
3．实际电压源和实际电流源的等效互换一个实际的电源，就其外部特性而言，既可以看成是一个电压源，又可以看成是一个电流源。
若视为电压源，则可用一个电压源U s 与一个电阻R S 相串联表示；若视为电流源，则可用一个电流源I S 与一个电阻R S 相并联来表示。
若它们向同样大小的负载供出同样大小的电流和端电压，则称这两个电源是等效的，即具有相同的外特性。
实际电压源与实际电流源等效变换的条件为： （1）取实际电压源与实际电流源的内阻均为R S ；（2）已知实际电压源的参数为U s 和R S ，则实际电流源的参数为SS S R UI =和R S ，若已知实际电流源的参数为I s 和R S ，则实际电压源的参数为S S S R I U =和R S 。
一、电压源与电流源及其等效变换理想的电压源就是串联内阻为零的恒压源，理想的电流源就是并联内阻为∞的恒流源。
理想的情况在实践中并不存在，因此用电压源或电流源表示都是可以的。
在什么场合使用电压源或电流源，视需要和方便而定，并没有固定地说必须用哪一种。
3、电压源与电流源的等效变换变换的原则：不论是使用电压源模型还是电流源模型，在负载上电压、电流都应该完全相同。
电压源与电流源之间作等效变换时，传统的推导过程如下：Ua=E －Ia*Ra ，Ub=(Is-Ib)*Rb由于Ia=Ib ，Ua=Ub ，所以，E －Ia*Ra=(Is-Ib)*Rb ，展开与替换后即：E －Ia*Ra=Is*Rb －Ia*Rb推导至此，传统方法就认为上面等式左右两边的分项各自相等，即E= Is*Rb ，Ia*Ra= Ia*Rb ，进而Ra=Rb 。
这应该很牵强，怎么能说A —B=C —D ，就一定会有A=B ，C=D ？我使用一种更直观、更好理解的方式推导如下：负载上电压、电流完全相同，实际上就是两种模型下的电流-电压曲线完全相同（重叠）。
电压源与电流源模型下的电流-电压曲线如下图所示：由于Ua=Ub ，Ia=Ib ，所以①、E= Is*Rb ；②、Is=E/Ra （亦即E=Is*Ra ）。
综合①和②，由电源源转换为电流源时：Rb=Ra ，Is= E/Ra由电流源转换为电压源时：Ra=Rb ，E= Is*Rb负载 RL + _ 负载 RL + _ 0 电流 电压 电压源模型的电流-电压曲线： Ua=E －I*Ra Ia=0，Ua=E Ia=E/Ra ，Ua=0 0 电流 电压 电流源模型的电流-电压曲线： Ub=(Is-Ib)*Rb Ib=0，Ub=Is*RbIb=Is ，Ub=0。
