电压源与电流源及其等效变换

电压源电流源等效变换电压源和电流源是电路中常用的两种基本电子元件，它们在电路中起到不同的作用。

在某些情况下，可以将电压源和电流源等效变换，使得电路分析更加简化。

本文将从电压源和电流源的定义、特性以及等效变换的方法等方面进行探讨。

一、电压源和电流源的定义与特性电压源是指能够提供稳定电压的电子元件，它的输出特性可以看作是一个恒定的电压源。

电压源的电压不受外部电路负载的影响，始终保持恒定。

电压源通常用符号“E”表示，单位为伏特（V）。

电流源是指能够提供稳定电流的电子元件，它的输出特性可以看作是一个恒定的电流源。

电流源的电流不受外部电路负载的影响，始终保持恒定。

电流源通常用符号“I”表示，单位为安培（A）。

二、电压源和电流源的等效变换方法1. 电压源到电流源的等效变换将一个电压源等效为一个电流源，可以使用电流分配定律来实现。

根据电流分配定律，一个电阻电路中的电流分配与电阻值的比例成正比。

因此，可以通过串联一个大电阻来实现电压源到电流源的等效变换。

假设有一个电压源E和一个大电阻R，将它们串联连接，接在一个负载电阻上。

根据欧姆定律，电压等于电流乘以电阻值。

由于电压源的电压恒定，当电压源等效为电流源时，电流也应恒定。

因此，通过调整电阻R的值，可以使得电流恒定，从而实现电压源到电流源的等效变换。

2. 电流源到电压源的等效变换将一个电流源等效为一个电压源，可以使用电压分配定律来实现。

根据电压分配定律，一个电阻电路中的电压分配与电阻值的比例成正比。

因此，可以通过并联一个大电阻来实现电流源到电压源的等效变换。

假设有一个电流源I和一个大电阻R，将它们并联连接，接在一个负载电阻上。

根据欧姆定律，电压等于电流乘以电阻值。

由于电流源的电流恒定，当电流源等效为电压源时，电压也应恒定。

因此，通过调整电阻R的值，可以使得电压恒定，从而实现电流源到电压源的等效变换。

三、电压源和电流源的应用举例1. 电压源的应用电压源常用于提供稳定的电压给电子设备，例如电池、直流电源、稳压器等。

电压源与电流源及其等效变换————————————————————————————————作者：————————————————————————————————日期：2课题3-5电压源与电流源及其等效变换课型新授授课日期授课时数总课时数教具使用教学目标掌握电源的两种模型（电压源和电流源）教学重点和难点电源的两种模型的特点及等效变换方法。

学情分析学生对电动势和内阻串联的模型比较熟悉，对电流源模型不是很清楚，尚需详细讲解板书设计两种电源模型的等效变换二、电流源通常所说的电流源一般是指理想电流源，其基本特性是所发出的电流固定不变(I s)或是一定的时间函数i s(t)，但电流源的两端电压却与外电路有关。

实际电流源是含有一定内阻r S的电流源图3-19 电流源模型教学后记第1页教学过程：一、导入新课1 、什么叫电压源？什么叫电流源？2、穷举生活中电压源和电流源的实例。

二、讲授新课两种实际电源模型之间的等效变换实际电源可用一个理想电压源E和一个电阻r0串联的电路模型表示，其输出电压U与输出电流I之间关系为U = E-r0I实际电源也可用一个理想电流源I S和一个电阻r S并联的电路模型表示，其输出电压U与输出电流I之间关系为U = r S I S -r S I对外电路来说，实际电压源和实际电流源是相互等效的，等效变换条件是r0 = r S ， E = r S I S 或I S = E/r0【例】如图3-18所示的电路，已知电源电动势E=6 V，内阻r0 = 0.2 Ω，当接上R= 5.8 Ω负载时，分别用电压源模型和电流源模型计算负载消耗的功率和内阻消耗的功率。

第 2 页解：(1) 用电压源模型计算： A 10=+=Rr E I ，负载消耗的功率P L = I 2R= 5.8 W ，内阻的功率P r = I 2r 0 = 0.2 W(2) 用电流源模型计算：电流源的电流I S = E /r 0 = 30 A ，内阻r S = r 0 = 0.2 Ω 负载中的电流 A 1S S S =+=I Rr r I ，负载消耗的功率 P L = I 2R = 5.8 W ，内阻中的电流 A 29S S =+=I Rr R I r ，内阻的功率 P r = I r 2r 0 = 168.2 W两种计算方法对负载是等效的，对电源内部是不等效的。

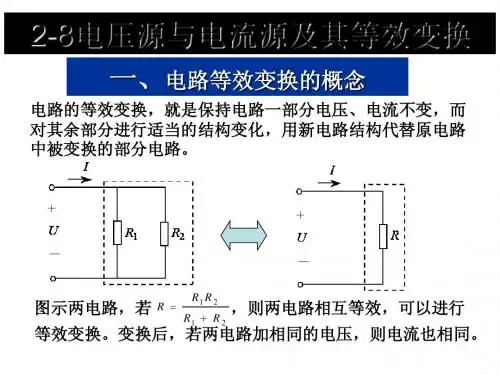
1．5电压源和电流源的等效变换实际使用的电源，按其外特性，可分为电压源和电流源。

当一个电压源和一个电流源能够为同一个负载提供相同的电压、电流和功率时，这两个电源对该负载来说是等效的，可以互相置换，这种置换称为等效变换。

下面来讨论电压源和电流源的等效变换。

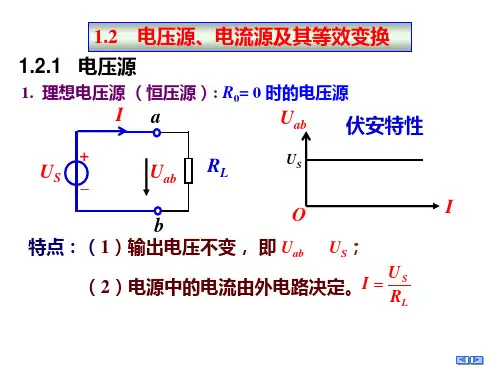
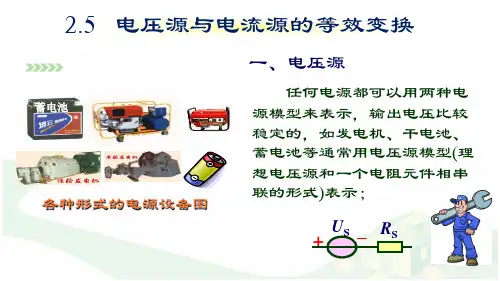
1．5．1 电压源在电路分析课程中，将能够向外电路提供电压的器件称为电压源。

如，电池，发电机等均是电压源。

在物理学中，电池表示成电动势E和内阻R相串联的电路模型，电池是一个典型的电压源，所以，电压源也可表示成电动势和内阻相串联的电路模型。

为了利用KVL的方便，对电压源特性进行标定时，通常不使用电动势E，而改用电压源所能输出的恒压值US，如图1-30（a）所示虚线框内部的电路。

图中电压源旁的箭头为US的参考方向。

注意： US 和E是不同性质的两个物理量，US是描述电压源所能输出的恒值电压，该值的大小与E相等，设定的参考方向与E相反。

当电压源与负载电阻RL相连时，根据KVL可得描述电压源外特性的函数式。

描述理想化电压源外特性的函数式是（1-57）由式1-57可见，理想化电压源的外特性曲线是直线，如图1-30（b）所示，图1-30（b）又称为电压源伏（U）-安（A）特性曲线。

图1-30（b）纵轴上的点，为电压源输出电流等于0的情况，相当于电压源处在开路的状态下。

当电压源开路时，电压源的输出电压U就等于US ，所以，US的值等于电压源的开路电压。

图1=30（b）横轴上的点，为电压源输出电压等于0的情况，相当于电压源处在短路的状态下（实际上这是不允许的），电压源输出电流为IS ，所以，IS称为短路电流。

计算短路电流的表达式为（1-58）U=f（I）曲线的斜率为R0，R越小，斜率越小，直线越平坦。

当R=0时，电源外特性曲线是一条平行与I轴的直线。

具有这种外特性曲线的电压源输出电压保持恒定值US，这种电压源称为理想电压源，简称恒压源。

将图1-30（a）虚线框内部电路的电阻R去掉，剩下的电路就是恒压源电路的模型。

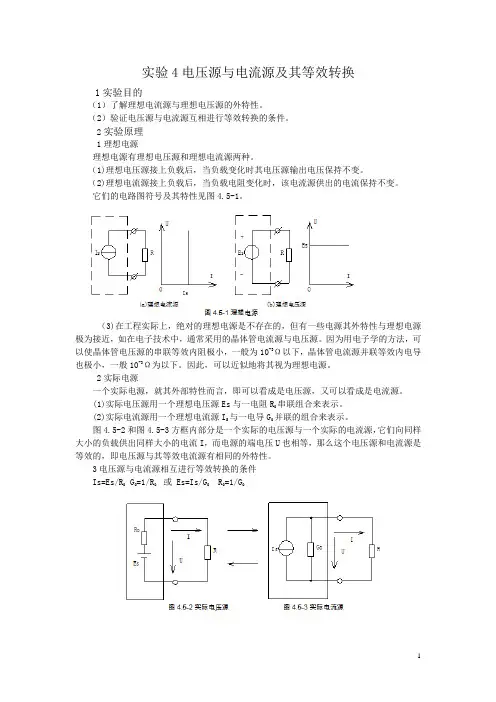
实验4电压源与电流源及其等效转换1实验目的（1）了解理想电流源与理想电压源的外特性。

（2）验证电压源与电流源互相进行等效转换的条件。

2实验原理1理想电源理想电源有理想电压源和理想电流源两种。

（1)理想电压源接上负载后，当负载变化时其电压源输出电压保持不变。

（2)理想电流源接上负载后，当负载电阻变化时，该电流源供出的电流保持不变。

它们的电路图符号及其特性见图4.5-1。

（3)在工程实际上，绝对的理想电源是不存在的，但有一些电源其外特性与理想电源极为接近，如在电子技术中，通常采用的晶体管电流源与电压源。

因为用电子学的方法，可以使晶体管电压源的串联等效内阻极小，一般为10-3Ω以下，晶体管电流源并联等效内电导也极小，一般10-3Ω为以下。

因此，可以近似地将其视为理想电源。

2实际电源一个实际电源，就其外部特性而言，即可以看成是电压源，又可以看成是电流源。

(1)实际电压源用一个理想电压源Es与一电阻R0串联组合来表示。

(2)实际电流源用一个理想电流源I S与一电导G0并联的组合来表示。

图4.5-2和图4.5-3方框内部分是一个实际的电压源与一个实际的电流源，它们向同样大小的负载供出同样大小的电流I，而电源的端电压U也相等，那么这个电压源和电流源是等效的，即电压源与其等效电流源有相同的外特性。

3电压源与电流源相互进行等效转换的条件Is=Es/R0 G0=1/R0 或 Es=Is/G0 R0=1/G04实验内容及步骤1）测量理想电流源的外特性当负载电阻在一定的范围内变化时（注意必须使电流源两端的电压不超出额定值），电流基本不变，即可将其视为理想电流源。

(1)将一可变电阻R接至稳流源的输出端上，串联接入直流电流表，并联接入直流电压表，即接成图4.5-4的实验电路。

(2)首先置可变电阻R=0，调节直流电流源，使其输出电流I=50mA，测出此时电流源的端电压U和输出电流I记入表4.5-1。

(3)改变电阻电阻R，每改变R值记下U和I，但应使Rmax*I≤20V，此时数据记入表4.5-1，即可得至理想电流源的外特性。

电压源与电流源是电路中常见的两种基本元件，它们分别以恒定的电压和恒定的电流来驱动电路。

在电路分析和设计中，经常需要将电压源转换为等效的电流源，或将电流源转换为等效的电压源，以便更方便地进行电路分析和计算。

下面将分别介绍电压源与电流源的等效变换方法。

一、将电压源转换为等效的电流源1. 理论基础电压源的等效电流源转换是基于欧姆定律进行的。

根据欧姆定律，电流等于电压除以电阻，即I=V/R。

我们可以将电压源转换为等效的电流源，通过在电压源的正负端并联一个等效电阻，使得该电阻上的电流等于电压源的电压除以电阻值。

2. 转换公式电压源转换为等效电流源的公式为：I=V/R，其中I为等效电流源的输出电流，V为电压源的电压，R为等效电流源的电阻。

3. 举例说明假设有一个5V的电压源，需要将其转换为等效的电流源。

如果我们希望等效电流源的输出电流为1A，那么根据公式I=V/R，可得等效电阻R=V/I=5Ω。

我们可以在电压源的正负端并联一个5Ω的电阻，即可将电压源转换为等效的电流源。

二、将电流源转换为等效的电压源1. 理论基础电流源的等效电压源转换同样是基于欧姆定律进行的。

根据欧姆定律，电压等于电流乘以电阻，即V=IR。

我们可以将电流源转换为等效的电压源，通过在电流源的两端串联一个等效电压源，使得该电压等于电流源的电流乘以电阻值。

2. 转换公式电流源转换为等效电压源的公式为：V=IR，其中V为等效电压源的输出电压，I为电流源的电流，R为等效电压源的电阻。

3. 举例说明假设有一个2A的电流源，需要将其转换为等效的电压源。

如果我们希望等效电压源的输出电压为10V，那么根据公式V=IR，可得等效电阻R=V/I=5Ω。

我们可以在电流源的两端串联一个10V的电压源，并在其正负端串联一个5Ω的电阻，即可将电流源转换为等效的电压源。

电压源与电流源的等效变换方法可以在电路分析和设计中起到重要的作用。

通过合理应用这些方法，可以使得电路分析更加简便和直观，为电路设计提供重要的参考依据。

一、电压源与电流源及其等效变换理想的电压源就是串联内阻为零的恒压源，理想的电流源就是并联内阻为∞的恒流源。

理想的情况在实践中并不存在，因此用电压源或电流源表示都是可以的。

在什么场合使用电压源或电流源，视需要和方便而定，并没有固定地说必须用哪一种。

3、电压源与电流源的等效变换变换的原则：不论是使用电压源模型还是电流源模型，在负载上电压、电流都应该完全相同。

电压源与电流源之间作等效变换时，传统的推导过程如下：Ua=E －Ia*Ra ，Ub=(Is-Ib)*Rb由于Ia=Ib ，Ua=Ub ，所以，E －Ia*Ra=(Is-Ib)*Rb ，展开与替换后即：E －Ia*Ra=Is*Rb －Ia*Rb推导至此，传统方法就认为上面等式左右两边的分项各自相等，即E= Is*Rb ，Ia*Ra= Ia*Rb ，进而Ra=Rb 。

这应该很牵强，怎么能说A —B=C —D ，就一定会有A=B ，C=D ？我使用一种更直观、更好理解的方式推导如下：负载上电压、电流完全相同，实际上就是两种模型下的电流-电压曲线完全相同（重叠）。

电压源与电流源模型下的电流-电压曲线如下图所示：由于Ua=Ub ，Ia=Ib ，所以①、E= Is*Rb ；②、Is=E/Ra （亦即E=Is*Ra ）。

综合①和②，由电源源转换为电流源时：Rb=Ra ，Is= E/Ra由电流源转换为电压源时：Ra=Rb ，E= Is*Rb负载 RL + _ 负载 RL + _ 0 电流 电压 电压源模型的电流-电压曲线： Ua=E －I*Ra Ia=0，Ua=E Ia=E/Ra ，Ua=0 0 电流 电压 电流源模型的电流-电压曲线： Ub=(Is-Ib)*Rb Ib=0，Ub=Is*RbIb=Is ，Ub=0。

电压源与电流源等效变换的依据是对外部电路等效，即相同的负载接入后性状相同。

一个电压源与一个电流源对同一个负载如果能提供等值的电压，电流和功率，则这两个电源对此负载是等效的，换言之，即如果两个电源的外特性相同，则对任何外电路它们都是等效的。

电压源变换成电流源时，其电流的大小等于电压除于与其串联的电阻。

然后该电阻直接与电流源并联就是了。

电流源变换成电压源时，其电压的大小等于电流源电流乘于与其并联的电阻。

然后该电阻直接与电流源串联就是了。

扩展资料：
电流是电荷的定向移动形成的。

但是电荷本身无法直接看见，不象水流、车流那么直观。

由于导体有电流通过时会产生一定的效应（化学效应、热效应、磁效应），因此，教材通过小灯泡发光来判断电流的存在与否。

电阻发生变化时，在电压一定的条件下，会导致电路中的电流发生变化，引起小灯泡的亮度变化。

通过亮度的比较来比较电阻的大小。

将不可见的电阻转换为直观的亮度来反映。