第_9_讲_电压源与电流源及其等效变换

电压源与电流源的等效变换方向电压源和电流源是电路中常见的两种电源，它们在电路中起到重要的作用。

在电路的分析和设计中，我们时常需要将电路中的电压源转化成等效的电流源，或将电路中的电流源转化成等效的电压源，这便是电压源与电流源的等效变换方向。

首先，我们来看一下如何将电压源转化成等效的电流源。

在许多电路分析问题中，我们往往需要将电压源转换为电流源。

这是因为在一些电路中，电压源会因为电路中的负载变化而发生变化，而电流源不会受到负载的影响。

因此将电压源转换为电流源可以使得电路分析更加简单。

要将电压源转化成等效的电流源，我们需要先确定电压源的内阻。

我们将电压源的内阻与电压源串联，得到一个等效的电压源电路。

然后，我们需要计算出通过电压源的电流，这是由欧姆定律可以得到的。

最后，我们将电流源与电压源串联在一起，即可完成电压源到电流源的等效变换。

这样，通过等效变换，我们可以将电路简化，从而更方便地进行分析和设计。

接下来，我们来探讨一下如何将电流源转换为等效的电压源。

与将电压源转化成等效的电流源相比，将电流源转化成等效的电压源相对来说要复杂一些。

因为电流源的输出电压不是确定的，而是随着负载的变化而变化的。

因此，在将电流源转换为等效的电压源时，我们需要考虑电流源的内部电阻和负载电阻之间的关系，以及电流源的输出电压变化规律等。

要将电流源转化成等效的电压源，我们需要通过瑞利商来计算电流源的内阻。

接着，我们需要将内阻与负载电阻并联，来得到一个等效的电压源电路。

为了确定输出电压，我们需要确定负载电阻时电流源的电压，这可以用欧姆定律来计算。

最后，我们串联电压源与电流源，这样就可以得到等效的电压源电路。

通过这一变换，我们可以更方便地进行电路分析和设计。

总而言之，电压源与电流源可以通过等效变换相互转换。

在实际问题中，当我们需要对电压源或电流源进行分析或设计时，可以选择将其转化为等效的电流源或电压源。

这样可以使得电路分析更简便，同时也能更好地了解电源的特性和影响因素。

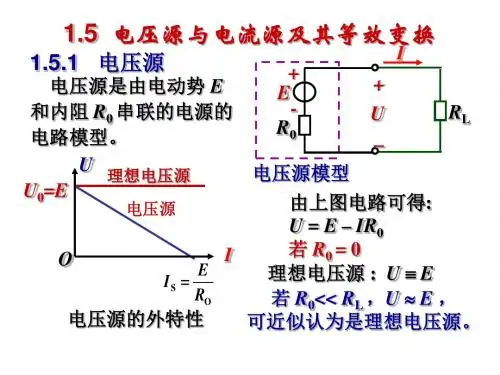
1．5电压源和电流源的等效变换实际使用的电源，按其外特性，可分为电压源和电流源。

当一个电压源和一个电流源能够为同一个负载提供相同的电压、电流和功率时，这两个电源对该负载来说是等效的，可以互相置换，这种置换称为等效变换。

下面来讨论电压源和电流源的等效变换。

1．5．1 电压源在电路分析课程中，将能够向外电路提供电压的器件称为电压源。

如，电池，发电机等均是电压源。

在物理学中，电池表示成电动势E和内阻R相串联的电路模型，电池是一个典型的电压源，所以，电压源也可表示成电动势和内阻相串联的电路模型。

为了利用KVL的方便，对电压源特性进行标定时，通常不使用电动势E，而改用电压源所能输出的恒压值US，如图1-30（a）所示虚线框内部的电路。

图中电压源旁的箭头为US的参考方向。

注意： US 和E是不同性质的两个物理量，US是描述电压源所能输出的恒值电压，该值的大小与E相等，设定的参考方向与E相反。

当电压源与负载电阻RL相连时，根据KVL可得描述电压源外特性的函数式。

描述理想化电压源外特性的函数式是（1-57）由式1-57可见，理想化电压源的外特性曲线是直线，如图1-30（b）所示，图1-30（b）又称为电压源伏（U）-安（A）特性曲线。

图1-30（b）纵轴上的点，为电压源输出电流等于0的情况，相当于电压源处在开路的状态下。

当电压源开路时，电压源的输出电压U就等于US ，所以，US的值等于电压源的开路电压。

图1=30（b）横轴上的点，为电压源输出电压等于0的情况，相当于电压源处在短路的状态下（实际上这是不允许的），电压源输出电流为IS ，所以，IS称为短路电流。

计算短路电流的表达式为（1-58）U=f（I）曲线的斜率为R0，R越小，斜率越小，直线越平坦。

当R=0时，电源外特性曲线是一条平行与I轴的直线。

具有这种外特性曲线的电压源输出电压保持恒定值US，这种电压源称为理想电压源，简称恒压源。

将图1-30（a）虚线框内部电路的电阻R去掉，剩下的电路就是恒压源电路的模型。

电流源与电压源等效变换
电源是电路中的核心部件，提供电能以驱动电路中的各种元器件正常工作。

根据其特性，电源可以分为电压源和电流源两种。

在不同的电路应用中，电压源和电流源的等效变换具有不同的意义。

电流源与电压源之间的等效变换是指将一个电路中的电流源转换为等效的电压源，或将电压源转换为等效的电流源。

这种变换的目的在于简化电路分析和设计。

在一些电路分析和设计中，需要将电流源变换为等效的电压源。

这时候就需要求出电流源的内电阻和电压源的电动势。

根据欧姆定律和基尔霍夫电压定律，我们可以得到等效电压源的公式：
U=I×Ri
其中，U表示等效电压源的电动势，I表示电路中的电流源，Ri表示电流源的内电阻。

同样地，在一些电路分析和设计中，需要将电压源变换为等效的电流源。

这时候就需要求出电压源的内电阻和电压源的电动势。

根据欧姆定律和基尔霍夫电流定律，我们可以得到等效电流源的公式：
I=U/Rv
其中，I表示等效电流源的电流，U表示电路中的电压源，Rv表示电压源的内电阻。

需要注意的是，在进行电流源和电压源的等效变换时，要根据电源的具体特性进行判断。

例如，在电流源的内电阻趋近于无穷大时，电流源可以看做是理想的电流源，这时候电流源和电压源的等效变换会出现不同的情况。

总之，电流源和电压源的等效变换是电路分析和设计中的重要内容，可以帮助我们更加方便地分析电路中的各种问题，并加快电路的设计过程。

电压源与电流源等效变换的条件当我们讨论电路中的电压源和电流源等效变换时，咱们就像是在搞一个有趣的魔术表演。

你瞧，电压源和电流源在电路里各自扮演着不同的角色，就像是舞台上的两位演员，各自用不同的方式为电路这个大戏增光添彩。

那么，它们要怎么变换成对方呢？这里有一些条件是必不可少的，就像魔术师需要精准的技巧和条件才能变出兔子一样。

1. 电压源与电流源的等效变换基础首先，我们得搞清楚什么是电压源和电流源。

电压源就像是你家里的电池，无论电路里发生什么变化，它总是坚持给你一个固定的电压。

电流源呢，则像是水龙头，不管你怎么拧，流出来的水量总是那么多，也就是固定的电流。

电压源和电流源就像是两个各有千秋的角色，他们在电路里发挥着不同的作用。

不过，它们之间的“变脸”其实也有门道。

1.1 电压源与电流源的等效变换条件要把电压源换成电流源，或者把电流源换成电压源，有几个条件得满足。

第一个条件是，它们之间的等效变换必须在相同的电阻负载下进行。

想象一下，你不能在游泳池和干旱沙漠中用相同的水量来测试水龙头的流量对吧？同样的道理，电压源和电流源的等效变换也需要在相同的“环境”下进行。

第二个条件是，它们之间的变换需要保持电路的整体行为不变。

就是说，无论你怎么换，它们在电路里的效果要保持一致。

这就像换了一身新衣服，虽然风格不同，但穿上去的效果得保持不变，不然人家就会觉得奇怪了。

1.2 电压源变换成电流源具体来说，要把一个电压源变换成电流源，你需要确定电压源的电压值和它的内阻。

比如，你有一个5伏的电压源，内阻是2欧姆。

按照等效变换的原则，你可以把它换成一个电流源，其电流值是5伏除以2欧姆，也就是2.5安培。

这样，即使电流源的表现方式和电压源不同，但它在电路中的作用却没变，仍然能够提供相同的效果。

1.3 电流源变换成电压源同样的，如果你想把一个电流源变换成电压源，你也得确定这个电流源的电流值和它的内阻。

例如，你有一个3安培的电流源，内阻是4欧姆。

电压源与电流源是电路中常见的两种基本元件，它们分别以恒定的电压和恒定的电流来驱动电路。

在电路分析和设计中，经常需要将电压源转换为等效的电流源，或将电流源转换为等效的电压源，以便更方便地进行电路分析和计算。

下面将分别介绍电压源与电流源的等效变换方法。

一、将电压源转换为等效的电流源1. 理论基础电压源的等效电流源转换是基于欧姆定律进行的。

根据欧姆定律，电流等于电压除以电阻，即I=V/R。

我们可以将电压源转换为等效的电流源，通过在电压源的正负端并联一个等效电阻，使得该电阻上的电流等于电压源的电压除以电阻值。

2. 转换公式电压源转换为等效电流源的公式为：I=V/R，其中I为等效电流源的输出电流，V为电压源的电压，R为等效电流源的电阻。

3. 举例说明假设有一个5V的电压源，需要将其转换为等效的电流源。

如果我们希望等效电流源的输出电流为1A，那么根据公式I=V/R，可得等效电阻R=V/I=5Ω。

我们可以在电压源的正负端并联一个5Ω的电阻，即可将电压源转换为等效的电流源。

二、将电流源转换为等效的电压源1. 理论基础电流源的等效电压源转换同样是基于欧姆定律进行的。

根据欧姆定律，电压等于电流乘以电阻，即V=IR。

我们可以将电流源转换为等效的电压源，通过在电流源的两端串联一个等效电压源，使得该电压等于电流源的电流乘以电阻值。

2. 转换公式电流源转换为等效电压源的公式为：V=IR，其中V为等效电压源的输出电压，I为电流源的电流，R为等效电压源的电阻。

3. 举例说明假设有一个2A的电流源，需要将其转换为等效的电压源。

如果我们希望等效电压源的输出电压为10V，那么根据公式V=IR，可得等效电阻R=V/I=5Ω。

我们可以在电流源的两端串联一个10V的电压源，并在其正负端串联一个5Ω的电阻，即可将电流源转换为等效的电压源。

电压源与电流源的等效变换方法可以在电路分析和设计中起到重要的作用。

通过合理应用这些方法，可以使得电路分析更加简便和直观，为电路设计提供重要的参考依据。

电流源与电压源的等效变换1. 前言：电流与电压的“朋友圈”嘿，大家好！今天我们来聊聊电流源和电压源，这两个小家伙在电路中可是常常“交朋友”，相互转换。

可能有小伙伴会觉得，这些东西听起来有点晦涩，但其实就像你们的朋友一样，有时候一杯咖啡就能把事情说清楚。

电流源和电压源就像是电路中的两种好伙伴，它们各有各的特点，有的亮点就像春天的花儿，绽放得不可思议。

首先，什么是电流源呢？简单来说，电流源就像一个永远在发电的“工作狂”，不管外面的电路条件怎样变化，它总是坚持提供稳定的电流。

说白了，它就是个“稳重”的家伙。

而电压源呢，哎，这就像是个自由自在的“艺术家”，它提供一个固定的电压，但电流却可以根据负载的不同而变化，听起来是不是很有个性？所以，当我们说到它们的等效变换时，其实就是在探讨这两个角色如何互相转变和影响彼此。

2. 电流源与电压源的基本概念2.1 电流源电流源，这家伙可真是个厉害角色！它会保持电流恒定，简单点说，就是不管你拉多少电流，它都照样给你固定的输出。

比如说，想象一下，你在吃自助餐，电流源就像是那个一直在给你补菜的服务员，无论你吃得多快，它都能保证你有足够的食物。

这种特性在一些特殊的电路设计中非常重要，尤其是那些对电流要求严格的场合。

2.2 电压源而电压源呢，它就像是一个随心所欲的“创作家”，提供的电压是固定的，但电流却是根据负载的变化而变化的。

就好比你在喝饮料，如果杯子小，饮料流得快；如果杯子大，那流得就慢了。

这个特性在一些设备中，比如手机充电器，特别好用。

因为它们需要根据不同的设备调整电流，这样才能确保充电的效果最佳。

3. 等效变换的奥秘3.1 从电流源到电压源那么，电流源和电压源怎么变来变去呢？其实，转换的过程就像是在跳舞，电流源转变成电压源时，首先你需要知道电流源的输出电流是恒定的，然后通过负载电阻的关系，可以找到电压源的输出电压。

简单来说，就是通过欧姆定律 ( V = I times R ) 来计算。

电压源与电流源的等效变换的条件
电压源与电流源之间的等效变换是电子学中一个基本的概念，它指的是当给出一种电源及其连接线路时，可以将这种电源替换为完全等效的一种另外电源来模拟它。

一般来说，电压源与电流源之间的等效变换具有三个基本条件：一是輸入阻抗值需要相等；二是模拟线路中輸入阻抗要大於0；三是输出电流和电压之间的比值可以作为转换的依据。

首先，輸入阻抗值必须要求相等，将电流源替换成电压源时，輸入电路的总阻抗不变。

根据阻抗定律，电流源的输出电流与电受到的阻抗有关，所以如果把电流源替换成电压源，輸入阻抗的值必须要求相等。

其次，模拟线路中輸入阻抗要大於0，也就是说，当电压源与电流源之间进行等效变换时，输入电路中的参考阻抗不能小于0。

这是因为当输入阻抗小于0时，电流源和电压源的输出电流和输出电压之间的比值会变成虚数，这是不可能的。

最后，两者之间的比值也可用作变换的依据，即：电流源与电压源之间存在一个确定的比率，即输出电流与输出电压之间的比值，这一比率也可以用作电压源与电流源之间等效变换的基础。

电压源与电流源之间的等效变换具有重要的意义，它为工程师设计复杂系统提供了方便，并且能够有效地控制电子电路。

但是，这种等效变换需要满足三个基本条件：首先，输入阻抗要求是相同的；其次，输入阻抗也必须大於0；最后，电流源与电压源之间的比值也可以作为变换的依据。

只有满足这三个条件，才能进行有效的等效变换。

电压源电流源等效变换
内容:
电压源和电流源是两种基本的电源形式。

在电路分析中,有时需要将一种电源形式变换为另一种形式,这称为电压源电流源的等效变换。

电压源到电流源的等效变换方法是:
1. 确定电压源的电压U和内阻R
2. 用电流源替代电压源,电流源电流值为I=U/R
3. 并联一个与原电压源内阻R相同的电阻
电流源到电压源的等效变换方法是:
1. 确定电流源的电流I
2. 用电压源替代电流源,电压源电压值为U=I*R
3. 串联一个电阻R
通过电压源电流源的等效变换,可以将含有电压源的电路变换为仅含电流源的电路,或者将含有电流源的电路变换为仅含电压源的电路,从而简化电路分析。

掌握电压源电流源等效变换的方法,是进行电路分析的重要工具。

电压源和电流源的等效变换江苏师范大学电路分析实验报告姓名：______学号：______班级：______院系：______电压源和电流源的等效变换一、实验目的(1)掌握电源外特性的测试方法。

(2)验证电压源和电流源等效变换的条件。

二、实验原理(1) 直流稳压电源在一定的电流范围内具有很小的内阻，故在实用中，常将它视为一个理想的电压源，即其输出电压不随负载电流而变，其外特性曲线即其伏安特性曲线U=f(1)是一条平行于1轴的直线。

实际使用中的恒流源在一定的电压范围内可视为一个理想的电流源，即其输出电流不随负载电压而变，其外特性曲线即其伏安特性曲线1=g(u)是一条平行于U轴的直线。

(2)实际使用的电压源(或电流源)其端电压(或输出电流)不可能不随负载而变，因它具有一定的内阻值，故在实验中用一个小阻值的电阻器(或大阻值的电阻器)与稳压源(或恒流源)相串联(或并联)来模拟一个实际的电压源(或电流源)，实际的电压源(或电流源)的外特性是一条下倾的直线。

(3)一个实际使用的电源，就其外部特性而言，既可以看成是一个电压源，又可以看成是一个电流源。

若视为电压源，则可用一个理想的电压源Us与一个电阻Ro相串联的组合来表示；若视为电流源，则可用一个理想电流源Is与一电导go相并联的组合来表尔。

如果这两种电源能向同样大小的负载提供同样大小的电流和端电压，则称这两个电源是等效的，即具有相同的外特性。

一个电压源与一个电流源等效变换条件为Is?或Es1gO= RoRoEs?如下图6-1所示：Is1 RO=g0g0江苏师范大学电路分析实验报告三、实验设备直流稳压电源、直流恒流源、直流数字电压表、直流数字毫安表、万用表、电阻器、可调电阻箱、实验线路四、实验内容(1) 测定直流稳压电源的外特性按图（a）接线，US为+12V直流稳压电源。

调节R2，令其值由大至小变化，记录电压表、电流表的读数，数据记入表1中。

(2) 测定直流实际电压源的外特性按图（b）接线，虚线框可模拟为一个实际的电压源，调节R2，令其值由大至小变化，记录电压表、电流表的读数，数据记入表2中。