河北省廊坊市省级示范高中联合体2017-2018学年高二下学期第二次联考数学(理)试卷 扫描版含答案

河北省廊坊市省级示范高中联合体2017-2018学年高一下学期第二次联考试题一、选择题1．关于物体的运动，以下说法正确的是（ ） A ．物体做匀速圆周运动时，加速度不改变B ．物体做匀速圆周运动时，加速度大小不变，方向不变且始终指向圆心C ．物体做曲线运动时，加速度一定改变D ．物体做曲线运动时，加速度可能不变2，从倾角为θ足够长的斜面上的M 点，以初速度0v 水平抛出一小球，不计空气阻力，落到斜面上的N 点，此时速度方向与水平方向的夹角为α，经历时间为t 。

下列各图中，能正确反映t 及tan α与0v 关系的图象是（ ）3．如图所示，同一物体沿倾角不同的光滑斜面AB 和AC 的项端A 点分别由静止开始下滑到底端，斜面固定，则下列说法中不正确的是（ ）A ．两次运动中重力对物体做功相同B ．滑到底端时，两次重力的瞬时功率不同C ．滑到底端时，两次物体的速度相同D ．滑到底端时，两次物体的动能相同4.人造地球卫绕地球做匀速圆周运动，其轨道半径为R ，线速度为v ，周期为T ，若使卫星周期变为2T ，可能的方法有（ ） A.R 不变，使线速度变为2vB.v 不变，使轨道半径变为2RC.D.以上方法均不可以5．如图所示，人在岸上拉船，已知船的质量为m ，水的阻力恒为f ，当轻绳与水平面的夹角为θ时，船的速度为v,此时人的拉力大小为F ，则( )A ．人拉绳行走的速度为sin v θB ．人拉绳行走的速度为v cos θD ．船的加速度为Fcos fm θ-C ．船的加速度为F fm- 6．一同学用120N 的力将质量为05kg ．静止在水平地面上的足球以10/m s 的初速度沿水平方向踢出25m 远，则该同学对足球做的功至少为（ ） A.25JB.250JC.1200JD.3000J7．“黑洞”是近代引力理论所预言的宇宙中的一种特殊天体，研究认为，黑洞可能是由于超中子星发生塌缩而形成的。

欧洲航天局由卫星观测发现银河系中心存在一个超大型黑洞并将它命名为：MCG6-30-15r ，假设银河系中心仅此一个照洞。

2017-2018学年河北省卓越联盟高二（下）第二次月考数学试卷（文科）一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．若复数z=（其中a∈R，i是虚数单位）的实部与虚部相等，则a=（）A．3 B．6 C．9 D．122．用反证法证明“三角形中最多只有一个内角是钝角”时，结论的否定是（）A．没有一个内角是钝角B．有两个内角是钝角C．有三个内角是钝角 D．至少有两个内角是钝角3．在极坐标系中，圆ρ=﹣2sinθ的圆心的极坐标系是（）A．B．C．（1，0）D．（1，π）4．若点P为曲线（θ为参数）上一点，则点P与坐标原点的最短距离为（）A．B．C．D．25．化极坐标方程ρ2cosθ﹣ρ=0为直角坐标方程为（）A．x2+y2=0或y=1 B．x=1 C．x2+y2=0或x=1 D．y=16．在△ABC中，E，F分别为AB，AC的中点，则有EF∥BC．这个的大前提为（）A．三角形的中位线平行于第三边B．三角形的中位线等于第三边的一半C．EF为中位线D．EF∥CB7．下面几种推理过程是演绎推理的是（）A．两条直线平行，同旁内角互补，如果∠A和∠B是两条平行直线的同旁内角，则∠A+∠B=180°B．由平面三角形的性质，推测空间四面体的性质C．某校高三共有10个班，1班有51人，2班有53人，三班有52人，由此推测各班都超过50人D．在数列{a n}中，a1=1，a n=（a n+）（n≥2），计算a2、a3，a4，由此猜测通项a n﹣18．在极坐标系中，设曲线C1：ρ=2sinθ与C2：ρ=2cosθ的交点分别为A，B，则线段AB的垂直平分线的极坐标方程为（）A．ρ=B．ρ=C．θ=（ρ∈R）D．θ=（ρ∈R）9．设P（x，y）是曲线C：为参数，0≤θ＜2π）上任意一点，则的取值范围是（）A．B． C．D．10．下面给出了关于复数的三种类比推理：其中类比错误的是（）①复数的乘法运算法则可以类比多项式的乘法运算法则；②由向量的性质||2=2可以类比复数的性质|z|2=z2；③由向量加法的几何意义可以类比得到复数加法的几何意义．A．②B．①②C．①③D．③11．给出计算的值的一个程序框图如图，其中判断框内应填入的条件是（）A．i＞10 B．i＜10 C．i＞20 D．i＜2012．以下四个中：①从匀速传递的产品流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；②两个随机变量的线性相关性越强，相关系数的绝对值越接近于1；③若数据x1，x2，x3，…，x n的方差为1，则2x1，2x2，2x3，…，2x n的方差为2；④对分类变量X与Y的随机变量k2的观测值k来说，k越小，判断“X与Y有关系”的把握程度越大．其中真的个数为（）A．1 B．2 C．3 D．4二、填空题：本大题共4小题，每小题5分.13．如表为一组等式，某学生根据表猜想S2n=（2n﹣1）（an2+bn+c），老师回答正确，则﹣1a﹣b+c=．S1=1，S2=2+3=5，S3=4+5+6=15，S4=7+8+9+10=34，S5=11+12+13+14+15=65，…则y与x的线性回归方程=bx+a必过点．15．在以O为极点的极坐标系中，圆ρ=4sinθ和直线ρsinθ=a相交于A、B两点，若△AOB 是等边三角形，则a的值为．16．观察下面关于循环小数化成分数的等式：（注意：头上加点的数字）0.==，1.==，0.=，0.000=×=，据此推测循环小数0.2可化成分数．三、解答题：解答应写出文字说明、证明过程或演算步骤.17．已知．（1）是z的共轭复数，求的值；（2）类比数列的有关知识，求的值．18．已知△ABC的三条边分别为a，b，c求证：．19．在直角坐标系中，曲线C的参数方程为，（ϕ为参数），直线l的参数方程为（t为参数）．以原点为极点，x轴的正半轴为极轴建立极坐标系，点P的极坐标为．（Ⅰ）求点P的直角坐标，并求曲线C的普通方程；（Ⅱ）设直线l与曲线C的两个交点为A，B，求|PA|+|PB|的值．20．对任意函数f（x），x∈D，可按如图构造一个数列发生器，数列发生器产生数列{x n}．（1）若定义函数f（x）=，且输入x0=，请写出数列{x n}的所有项；（2）若定义函数f（x）=2x+3，且输入x0=﹣1，求数列{x n}的通项公式．21．某校有1400名考生参加市模拟考试，现采用分层抽样的方法从文、理考生中分别抽取2．在平面直角坐标系中，以为极点，轴的正半轴为极轴建立的极坐标系中，直线l 的极坐标方程为θ=（ρ∈R ），曲线C 的参数方程为（θ为参数）．（1）写出直线l 及曲线C 的直角坐标方程（2）过点M 平行于直线l 的直线与曲线C 交于A ，B 两点，若|MA |•|MB |=，求点M 轨迹的直角坐标方程，并说明轨迹是什么图形．2015-2016学年河北省卓越联盟高二（下）第二次月考数学试卷（文科）参考答案与试题解析一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．若复数z=（其中a∈R，i是虚数单位）的实部与虚部相等，则a=（）A．3 B．6 C．9 D．12【考点】复数代数形式的乘除运算．【分析】化简复数为a+bi的形式，利用复数的实部与虚部相等，求解a即可．【解答】解：复数z===．由条件复数z=（其中a∈R，i是虚数单位）的实部与虚部相等，得，18﹣a=3a+6，解得a=3．故选：A．2．用反证法证明“三角形中最多只有一个内角是钝角”时，结论的否定是（）A．没有一个内角是钝角B．有两个内角是钝角C．有三个内角是钝角 D．至少有两个内角是钝角【考点】的否定．【分析】写出“三角形中最多只有一个内角是钝角”的结论的否定即可【解答】解：“三角形中最多只有一个内角是钝角”的结论的否定是“至少有两个内角是钝角”故选D．3．在极坐标系中，圆ρ=﹣2sinθ的圆心的极坐标系是（）A．B．C．（1，0）D．（1，π）【考点】简单曲线的极坐标方程．【分析】先在极坐标方程ρ=﹣2sinθ的两边同乘以ρ，再利用直角坐标与极坐标间的关系，即利用ρcosθ=x，ρsinθ=y，ρ2=x2+y2，进行代换即得直角坐标系，再利用直角坐标方程求解即可．【解答】解：将方程ρ=﹣2sinθ两边都乘以p得：ρ2=﹣2ρsinθ，化成直角坐标方程为x2+y2+2y=0．圆心的坐标（0，﹣1）．∴圆心的极坐标故选B．4．若点P为曲线（θ为参数）上一点，则点P与坐标原点的最短距离为（）A．B．C．D．2【考点】参数方程化成普通方程．【分析】将曲线方程化为普通方程，根据几何意义得出最短距离．【解答】解：曲线的普通方程为（x﹣1）2+（y﹣1）2=1，∴曲线表示以（1，1）为圆心，以1为半径的圆．∴曲线的圆心到原点得距离为，∴点P与坐标原点的最短距离为．故选：A．5．化极坐标方程ρ2cosθ﹣ρ=0为直角坐标方程为（）A．x2+y2=0或y=1 B．x=1 C．x2+y2=0或x=1 D．y=1【考点】点的极坐标和直角坐标的互化．【分析】利用直角坐标与极坐标间的关系，即利用ρcosθ=x，ρsinθ=y，ρ2=x2+y2，进行代换即得．【解答】解：∵ρ2cosθ﹣ρ=0，∴ρcosθ﹣1=0或ρ=0，∵，∴x2+y2=0或x=1，故选C．6．在△ABC中，E，F分别为AB，AC的中点，则有EF∥BC．这个的大前提为（）A．三角形的中位线平行于第三边B．三角形的中位线等于第三边的一半C．EF为中位线D．EF∥CB【考点】演绎推理的基本方法．【分析】三段论是由两个含有一个共同项的性质判断作前提得出一个新的性质判断为结论的演绎推理．在三段论中，含有大项的前提叫大前提，如本例中的“三角形的中位线平行于第三边”．【解答】解：本题的推理过程形式是三段论，其大前提是一个一般的结论，即三角形中位线定理，故选：A．7．下面几种推理过程是演绎推理的是（）A．两条直线平行，同旁内角互补，如果∠A和∠B是两条平行直线的同旁内角，则∠A+∠B=180°B．由平面三角形的性质，推测空间四面体的性质C．某校高三共有10个班，1班有51人，2班有53人，三班有52人，由此推测各班都超过50人D．在数列{a n}中，a1=1，a n=（a n+）（n≥2），计算a2、a3，a4，由此猜测通项a n﹣1【考点】演绎推理的基本方法．【分析】由推理的基本形式，逐个选项验证可得．【解答】解：选项A为三段论的形式，属于演绎推理；选项B为类比推理；选项C不符合推理的形式；选项D为归纳推理．故选：A8．在极坐标系中，设曲线C1：ρ=2sinθ与C2：ρ=2cosθ的交点分别为A，B，则线段AB的垂直平分线的极坐标方程为（）A．ρ=B．ρ=C．θ=（ρ∈R）D．θ=（ρ∈R）【考点】简单曲线的极坐标方程．【分析】分别求出曲线C1和C2的直角坐标方程，联立方程组求出A、B的坐标，先求出线段AB的垂直平分线的普通方程，由此能求出线段AB的垂直平分线极坐标方程．【解答】解：∵曲线C1：ρ=2sinθ，∴ρ2=2ρsinθ，∴曲线C1的直角坐标方程为x2+y2=2y，∵C2：ρ=2cosθ，∴ρ2=2ρcosθ，∴C2的直角坐标方程为x2+y2=2x，联立，得，或，∴线段AB的垂直平分线的斜率k=﹣1，AB的中点为（，），∴线段AB的垂直平分线的方程为：y﹣=﹣（x﹣），即x+y﹣1=0．∴线段AB的垂直平分线极坐标方程为ρsinθ+ρcosθ=1，即．故选：A．9．设P（x，y）是曲线C：为参数，0≤θ＜2π）上任意一点，则的取值范围是（）A．B． C．D．【考点】直线与圆的位置关系；直线的斜率；圆的参数方程．【分析】求出圆的普通方程，利用的几何意义，圆上的点与坐标原点连线的斜率，求出斜率的范围即可．【解答】解：曲线C：为参数，0≤θ＜2π）的普通方程为：（x+2）2+y2=1，P（x，y）是曲线C：（x+2）2+y2=1上任意一点，则的几何意义就是圆上的点与坐标原点连线的斜率，如图：．故选C．10．下面给出了关于复数的三种类比推理：其中类比错误的是（）①复数的乘法运算法则可以类比多项式的乘法运算法则；②由向量的性质||2=2可以类比复数的性质|z|2=z2；③由向量加法的几何意义可以类比得到复数加法的几何意义．A．②B．①②C．①③D．③【考点】类比推理．【分析】利用复数的加减法运算法则判断出①对；利用复数加法的几何意义判断出③对；通过举反例判断出②错．【解答】解：对于复数的加减法运算法则判断出①对；对于②向量a的性质||2=2，但|z|2是实数，但z2不一定是实数，如z=i，就不成立，故错；对于③复数加法的几何意义判断出③对，故选：A．11．给出计算的值的一个程序框图如图，其中判断框内应填入的条件是（）A．i＞10 B．i＜10 C．i＞20 D．i＜20【考点】循环结构．【分析】结合框图得到i表示的实际意义，要求出所需要的和，只要循环10次即可，得到输出结果时“i”的值，得到判断框中的条件．【解答】解：根据框图，i﹣1表示加的项数当加到时，总共经过了10次运算，则不能超过10次，i﹣1=10执行“是”所以判断框中的条件是“i＞10”故选A12．以下四个中：①从匀速传递的产品流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；②两个随机变量的线性相关性越强，相关系数的绝对值越接近于1；③若数据x1，x2，x3，…，x n的方差为1，则2x1，2x2，2x3，…，2x n的方差为2；④对分类变量X与Y的随机变量k2的观测值k来说，k越小，判断“X与Y有关系”的把握程度越大．其中真的个数为（）A．1 B．2 C．3 D．4【考点】独立性检验的基本思想；的真假判断与应用；两个变量的线性相关．【分析】对于①，从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样系统抽样；对于②，根据相关系数与相关性的关系可知正确；对于③根据数据扩大n倍，方差扩大n2倍，可得2x1，2x2，2x3，…，2x n的方差为4，对于④对分类变量X与Y的随机变量k2的观测值k来说，k越小，判断“X与Y有关系”的把握程度越小．【解答】解：从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样系统抽样，故①错误；两个随机变量的线性相关性越强，相关系数的绝对值越接近于1，线性相关性越弱，相关系数的绝对值越接近于0，故②正确；若数据x1，x2，x3，…，x n的方差为1，则2x1，2x2，2x3，…，2x n的方差为4，故③错误；对分类变量X与Y的随机变量k2的观测值k来说，k越小，判断“X与Y有关系”的把握程度越小，故④错误；故真有1个，故选：A二、填空题：本大题共4小题，每小题5分.13．如表为一组等式，某学生根据表猜想S2n=（2n﹣1）（an2+bn+c），老师回答正确，则﹣1a﹣b+c=5．S1=1，S2=2+3=5，S3=4+5+6=15，S4=7+8+9+10=34，S5=11+12+13+14+15=65，…【考点】归纳推理．=（2n﹣1）（an2+bn+c），进行赋值，即可得到结论．【分析】利用所给等式，对猜测S2n﹣1【解答】解：由题意，，∴a=2，b=﹣2，c=1，∴a﹣b+c=5．故答案为：5则y与x的线性回归方程=bx+a必过点（1.5，4）．【考点】线性回归方程．【分析】要求y与x的线性回归方程为y=bx+a必过的点，需要先求出这组数据的样本中心点，根据所给的表格中的数据，求出横标和纵标的平均值，得到样本中心点，得到结果．【解答】解：∵，=4，∴本组数据的样本中心点是（1.5，4），∴y与x的线性回归方程为y=bx+a必过点（1.5，4）故答案为：（1.5，4）15．在以O为极点的极坐标系中，圆ρ=4sinθ和直线ρsinθ=a相交于A、B两点，若△AOB 是等边三角形，则a的值为3．【考点】简单曲线的极坐标方程．【分析】把极坐标方程化为直角坐标方程，求出B的坐标的值，代入x2+（y﹣2）2=4，可得a的值．【解答】解：直线ρsinθ=a即y=a，（a＞0），曲线ρ=4sinθ，即ρ2=4ρsinθ，即x2+（y﹣2）2=4，表示以C（0，2）为圆心，以2为半径的圆，∵△AOB 是等边三角形，∴B （a ，a ），代入x 2+（y ﹣2）2=4，可得（a ）2+（a ﹣2）2=4，∵a ＞0，∴a=3． 故答案为：3．16．观察下面关于循环小数化成分数的等式：（注意：头上加点的数字）0. = =，1.==，0. =，0.000=×=，据此推测循环小数0.2可化成分数．【考点】归纳推理．【分析】由已知中循环小数化分数的等式0. = =，1. = =，0. =，0.000=×=，分析出分母分子与循环节，及循环节位数的关系，可得答案．【解答】解：∵0. = =，1. = =，0. =，0.000=×=，…∴0.2=0.2+0.1×0. = =，故答案为．三、解答题：解答应写出文字说明、证明过程或演算步骤.17．已知．（1）是z 的共轭复数，求的值；（2）类比数列的有关知识，求的值．【考点】数列的求和；虚数单位i及其性质；复数的基本概念．【分析】（1）利用复数的乘法与加减运算法则化简求解即可．（2）利用数列的求和，直接求解化简即可．【解答】解：（1），（2），∵，∴1﹣z2016=1﹣（z3）672=1﹣1=0，∴．18．已知△ABC的三条边分别为a，b，c求证：．【考点】不等式的证明；不等式的基本性质．【分析】设，利用函数单调性的定义可得其单调递增，利用其单调性即可证明．【解答】证明：设，设x1，x2是（0，+∞）上的任意两个实数，且x2＞x1≥0，则，∵x2＞x1≥0，∴f（x1）＜f（x2）．∴在（0，+∞）上是增函数．由a+b＞c＞0可得f（a+b）＞f（c）．即．19．在直角坐标系中，曲线C的参数方程为，（ϕ为参数），直线l的参数方程为（t为参数）．以原点为极点，x轴的正半轴为极轴建立极坐标系，点P的极坐标为．（Ⅰ）求点P的直角坐标，并求曲线C的普通方程；（Ⅱ）设直线l与曲线C的两个交点为A，B，求|PA|+|PB|的值．【考点】参数方程化成普通方程；简单曲线的极坐标方程．【分析】（I）消参数即可得到普通方程，根据极坐标的几何意义即可得出P的直角坐标；（II）将l的参数方程代入曲线C的普通方程得出A，B对应的参数，利用参数得几何意义得出|PA|+|PB|．【解答】解：（Ⅰ），y=sin=，∴P的直角坐标为；由得cosφ=，sinφ=．∴曲线C的普通方程为．（Ⅱ）将代入得t2+2t﹣8=0，设A，B对应的参数分别为t1，t2，则t1+t2=﹣2，t1t2=﹣8，∵P点在直线l上，∴|PA|+|PB|=|t1|+|t2|=|t1﹣t2|==6．20．对任意函数f（x），x∈D，可按如图构造一个数列发生器，数列发生器产生数列{x n}．（1）若定义函数f（x）=，且输入x0=，请写出数列{x n}的所有项；（2）若定义函数f（x）=2x+3，且输入x0=﹣1，求数列{x n}的通项公式．【考点】程序框图．【分析】（1）函数f（x）=的定义域D=（﹣∞，﹣1）∪（﹣1，+∞），由此能推导出数列{x n}只有三项x1=，x2=，x3=﹣1．（2）f （x ）=2x +3的定义域为R ，若x 0=﹣1，则x 1=1，则x n +1+3=2（x n +3），从而得到数列{x n +3}是首项为4，公比为2的等比数列，由此能求出数列{x n }的通项公式． 【解答】解：（1）函数f （x ）=的定义域D=（﹣∞，﹣1）∪（﹣1，+∞），… 把x 0=代入可得x1=，把x1=代入可得x2=，把x2=代入可得x 3=﹣1，因为x 3=﹣1∉D ，所以数列{x n }只有三项：x1=，x2=，x3=﹣1．…（2）f （x ）=2x +3的定义域为R ，… 若x 0=﹣1，则x 1=1， 则x n +1=f （x n ）=2x n +3， 所以x n +1+3=2（x n +3），…所以数列{x n +3}是首项为4，公比为2的等比数列， 所以xn +3=4•2n ﹣1=2n +1， 所以xn=2n +1﹣3，即数列{x n }的通项公式xn=2n +1﹣3． …21．某校有1400名考生参加市模拟考试，现采用分层抽样的方法从文、理考生中分别抽取2【分析】（1）根据平均数公式，即可求解文科数学平均分，再根据表中数据可求解理科考生的及格人数．（2）利用独立性检验的公式，求解K 2=1.4＜2.706，可判断没有90%的把握认为概念失分与文、理考生的不同有关．【解答】解：（1）估计文科数学平均分为：=76.5．∵1400×=1000，1000×，∴理科考生的及格人数为560人．（2）K2==1.4＜2.706，∴没有90%的把握认为概念失分与文、理考生的不同有关．22．在平面直角坐标系xoy中，以O为极点，x轴的正半轴为极轴建立的极坐标系中，直线l的极坐标方程为θ=（ρ∈R），曲线C的参数方程为（θ为参数）．（1）写出直线l及曲线C的直角坐标方程（2）过点M平行于直线l的直线与曲线C交于A，B两点，若|MA|•|MB|=，求点M轨迹的直角坐标方程，并说明轨迹是什么图形．【考点】参数方程化成普通方程．【分析】（1）利用极坐标与直角坐标方程的互化，直接写出直线l的普通方程，消去参数可得曲线C的直角坐标方程；（2）设点M（x0，y0）以及平行于直线l的直线参数方程，直线l与曲线C联立方程组，通过|MA|•|MB|=，即可求点M轨迹的直角坐标方程．通过两个交点推出轨迹方程的范围．【解答】解：（1）∵直线l的极坐标方程为θ=（ρ∈R），∴直线l的倾斜角为，且经过原点，故直线的直角坐标方程为y=x，∵曲线C的参数方程为（θ为参数），∴曲线C的直角坐标方程为．（2）设点M（x0，y0）及过点M的直线为l1：，由直线l1与曲线C相交可得： +，∵|MA|•|MB|=，∴||=，即：，∴点M轨迹的直角坐标方程x2+2y2=6，表示一椭圆．取y=x+m代入得：3x2+4mx+2m2﹣2=0由△≥0得﹣故点M的轨迹是椭圆x2+2y2=6夹在平行直线y=x之间的两段弧．2016年11月7日。

2017—2018学年度第二学期期末教学质量检测高二理科数学第Ⅰ卷（选择题共60分）一、选择题（共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1. 已知复数满足，则（）A. B. C. D.【答案】C【解析】分析：根据复数的除法法则求解可得结果．详解：∵，∴．故选C．点睛：本题考查复数的除法运算，考查学生的运算能力，解题时根据法则求解即可，属于容易题．2. 有一段“三段论”推理是这样的：对于可导函数，如果，那么是函数的极值点，因为函数在处的导数值，所以，是函数的极值点.以上推理中（）A. 大前提错误B. 小前提错误C. 推理形式错误D. 结论正确【答案】A【解析】试题分析：导数为0的点不一定是极值点，而极值点的导数一定为0．所以本题是大前提错误。

考点：1．演绎推理；2．利用导数求函数的极值。

3. 在回归分析中，的值越大，说明残差平方和（）A. 越小B. 越大C. 可能大也可能小D. 以上都不对【答案】A【解析】分析：根据的公式和性质，并结合残差平方和的意义可得结论．详解：用相关指数的值判断模型的拟合效果时，当的值越大时，模型的拟合效果越好，此时说明残差平方和越小；当的值越小时，模型的拟合效果越差，此时说明残差平方和越大．故选A．点睛：主要考查对回归分析的基本思想及其初步应用等知识的理解，解题的关键是熟知有关的概念和性质，并结合条件得到答案．4. 用火柴棒摆“金鱼”，如图所示，按照上面的规律，第个“金鱼”图需要火柴棒的根数为（）A. B. C. D.【答案】C【解析】由题意得，第1个“金鱼”需要火柴棒的根数为；第2个“金鱼”需要火柴棒的根数为；第3个“金鱼”需要火柴棒的根数为，构成首项为，公差为的等差数列，所以第个“金鱼”需要火柴棒的根数为，故选C.5. 如果函数的图象如图所示，那么导函数的图象可能是（）A. B. C. D.【答案】A【解析】分析：根据图象得到函数的单调性，进而得到导函数的符号，再结合所给选项可得答案．详解：由函数的图象可得，函数在定义域上先增、再减、再增、再减，因此导函数的符号为先正、再负、再正、再负．结合选项可得A符合条件．故选A．点睛：本题考查函数的单调性和导函数的符号间的关系，即函数单调增时导函数值大于等于零，函数单调减时导函数小于等于零，解题的关键是根据图象得到函数的单调性，再结合所给选项求解．6. 某产品的广告费用万元与销售额万元的统计数据如下表：根据以上数据可得回归直线方程，其中，据此模型预报广告费用为6万元时，销售额为65.5万元，则，的值为（）A. ，B. ，C. ，D. ，【答案】C【解析】分析：根据回归直线过样本中心和条件中给出的预测值得到关于，的方程组，解方程组可得所求．详解：由题意得，又回归方程为，由题意得，解得．故选C．点睛：线性回归方程过样本中心是一个重要的结论，利用此结论可求回归方程中的参数，也可求样本数据中的参数．根据回归方程进行预测时，得到的数值只是一个估计值，解题时要注意这一点．7. 利用数学归纳法证明不等式的过程，由到时，左边增加了（）A. 1项B. 项C. 项D. 项【答案】D【解析】分析：式子中最后一项的分母表示的是式子的项数，由时的项数减去时的项数即为增加的项数，所以用两个式子的最后一项的分母相减即可得结果.详解：由题意，时，最后一项是，当时，最后一项是，所以由变到时，左边增加了项，故选D.点睛：本题是一道关于数学归纳法应用的题目，解答本题的关键是熟悉数学归纳法的证明思路及指数幂的运算性质，化简还是比较关键的.8. 如图，用，，三类不同的元件连接成一个系统.当正常工作且，至少有一个正常工作时，系统正常工作.已知，，正常工作的概率依次为0.9，0.8，0.8，则系统正常工作的概率为（）A. 0.960B. 0.864C. 0.720D. 0.576【答案】B【解析】试题分析：系统正常工作当①正常工作，不能正常工作，②正常工作，不能正常工作,③正常工作，因此概率.考点：独立事件的概率.9. 设复数，若，则的概率为（）A. B. C. D.【答案】D【解析】若则，则的概率为：作出如图，则概率为直线上方与圆的公共部分的面积除以整个圆的面积，即：..............................10. 设函数的定义域为，若对于给定的正数，定义函数，则当函数，时，定积分的值为（）A. B. C. D.【答案】D【解析】分析：根据的定义求出的表达式，然后根据定积分的运算法则可得结论．详解：由题意可得，当时，，即．所以．故选D．点睛：解答本题时注意两点：一是根据题意得到函数的解析式是解题的关键；二是求定积分时要合理的运用定积分的运算性质，可使得计算简单易行．11. 已知等差数列的第8项是二项式展开式的常数项，则（）A. B. 2 C. 4 D. 6【答案】C【解析】试题分析：二项式展开中常数项肯定不含，所以为，所以原二项式展开中的常数项应该为，即，则，故本题的正确选项为C.考点：二项式定理.12. 已知函数的定义域为，为的导函数，且，若，则函数的取值范围为（）A. B. C. D.【答案】B【解析】分析：根据题意求得函数的解析式，进而得到的解析式，然后根据函数的特征求得最值．详解：由，得，∴，设（为常数），∵，∴，∴，∴，∴，∴当x=0时，；当时，，故当时，，当时等号成立，此时；当时，，当时等号成立，此时．综上可得，即函数的取值范围为．故选B．点睛：解答本题时注意从所给出的条件出发，并结合导数的运算法则利用构造法求出函数的解析式；求最值时要结合函数解析式的特征，选择基本不等式求解，求解时注意应用不等式的条件，确保等号能成立．第Ⅱ卷（非选择题共90分）二、填空题（本大题共4小题，每小题5分，共20分）13. 已知随机变量服从正态分布，若，则等于__________．【答案】0.36【解析】.14. 从6男2女共8名学生中选出队长1人，副队长1人，普通队员2人，组成4人服务队，要求服务队中至少有1名女生，共有__________种不同的选法．（用数字作答）【答案】660【解析】分析：由题意分两类选女男或选女男，再利用加法原理、乘法原理以及排列组合知识求解即可.详解：第一类，先选女男，有种，这人选人作为队长和副队长有种，故有种；第二类，先选女男，有种，这人选人作为队长和副队长有种，故有种，根据分类计数原理共有，故答案为.点睛：本题主要考查分类计数原理与分步计数原理及排列组合的应用，属于难题.有关排列组合的综合问题，往往是两个原理及排列组合问题交叉应用才能解决问题，解答这类问题理解题意很关键，一定多读题才能挖掘出隐含条件.解题过程中要首先分清“是分类还是分步”、“是排列还是组合”，在应用分类计数加法原理讨论时，既不能重复交叉讨论又不能遗漏，这样才能提高准确率.15. 的展开式中的系数是__________．【答案】243【解析】分析：先得到二项式的展开式的通项，然后根据组合的方式可得到所求项的系数．详解：二项式展开式的通项为，∴展开式中的系数为.点睛：对于非二项式的问题，解题时可转化为二项式的问题处理，对于无法转化为二项式的问题，可根据组合的方式“凑”出所求的项或其系数，此时要注意考虑问题的全面性，防止漏掉部分情况．16. 已知是奇函数，当时，，（），当时，的最小值为1，则的值等于__________．【答案】1【解析】试题分析：由于当时，的最小值为，且函数是奇函数，所以当时，有最大值为-1，从而由，所以有；故答案为：1．考点：1．函数的奇偶性；2．函数的导数与最值．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 复数，，若是实数，求实数的值.【答案】【解析】分析：由题意求得，进而得到的代数形式，然后根据是实数可求得实数的值．详解：.∵是实数，∴，解得或，∵，∴，∴．点睛：本题考查复数的有关概念，解题的关键是求出的代数形式，然后根据该复数的实部不为零虚部为零得到关于实数的方程可得所求，解题时不要忽视分母不为零的限制条件．18. 某险种的基本保费为（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：设该险种一续保人一年内出险次数与相应概率如下：（1）求一续保人本年度的保费高于基本保费的概率；（2）已知一续保人本年度的保费高于基本保费，求其保费比基本保费高出的概率.【答案】（1）0.55（2）【解析】分析：（1）将保费高于基本保费转化为一年内的出险次数，再根据表中的概率求解即可．（2）根据条件概率并结合表中的数据求解可得结论．详解：（1）设表示事件：“一续保人本年度的保费高于基本保费”，则事件发生当且仅当一年内出险次数大于1，故．（2）设表示事件：“一续保人本年度的保费比基本保费高出”，则事件发生当且仅当一年内出险次数大于3，故．又，故，因此其保费比基本保费高出的概率为．点睛：求概率时，对于条件中含有“在……的条件下，求……发生的概率”的问题，一般为条件概率，求解时可根据条件概率的定义或利用古典概型概率求解．19. 在数列，中，，，且，，成等差数列，，，成等比数列（）. （1）求，，及，，；（2）根据计算结果，猜想，的通项公式，并用数学归纳法证明.【答案】(1) ，，，，， (2) 猜想，，证明见解析【解析】分析：（1）根据条件中，，成等差数列，，，成等比数列及所给数据求解即可．（2）用数学归纳法证明．详解：（1）由已知条件得，，由此算出，，，，，.（2）由（1）的计算可以猜想，，下面用数学归纳法证明：①当时，由已知，可得结论成立.②假设当（且）时猜想成立，即，.则当时，，，因此当时，结论也成立.由①②知，对一切都有，成立．点睛：用数学归纳法证明问题时要严格按照数学归纳法的步骤书写，特别是对初始值的验证不可省略，有时可能要取两个(或两个以上)初始值进行验证，初始值的验证是归纳假设的基础；第二步的证明是递推的依据，证明时必须要用到归纳假设，否则就不是数学归纳法．20. 学校为了对教师教学水平和教师管理水平进行评价，从该校学生中选出300人进行统计.其中对教师教学水平给出好评的学生人数为总数的，对教师管理水平给出好评的学生人数为总数的，其中对教师教学水平和教师管理水平都给出好评的有120人.（1）填写教师教学水平和教师管理水平评价的列联表：请问是否可以在犯错误概率不超过0.001的前提下，认为教师教学水平好评与教师管理水平好评有关？（2）若将频率视为概率，有4人参与了此次评价，设对教师教学水平和教师管理水平全好评的人数为随机变量.①求对教师教学水平和教师管理水平全好评的人数的分布列（概率用组合数算式表示）；②求的数学期望和方差.（，其中）【答案】(1) 可以在犯错误概率不超过0.001的前提下，认为教师教学水平好评与教师管理水平好评有关.(2) ①见解析②，【解析】分析：（1）由题意得到列联表，根据列联表求得的值后，再根据临界值表可得结论．（2）①由条件得到的所有可能取值，再求出每个取值对应的概率，由此可得分布列．②由于，结合公式可得期望和方差．详解：（1）由题意可得关于教师教学水平和教师管理水平评价的列联表：由表中数据可得，所以可以在犯错误概率不超过0.001的前提下，认为教师教学水平好评与教师管理水平好评有关.（2）①对教师教学水平和教师管理水平全好评的概率为，且的取值可以是0，1，2，3，4，其中；；；；，所以的分布列为：②由于，则，.点睛：求离散型随机变量的均值与方差关键是确定随机变量的所有可能值，写出随机变量的分布列，正确运用均值、方差公式进行计算，对于二项分布的均值和方差可根据公式直接计算即可．21. 已知函数，（为自然对数的底数，）.（1）判断曲线在点处的切线与曲线的公共点个数；（2）当时，若函数有两个零点，求的取值范围.【答案】(1)见解析(2)【解析】分析：（1）根据导数的几何意义可得切线方程，然后根据切线方程与联立得到的方程组的解的个数可得结论．（2）由题意求得的解析式，然后通过分离参数，并结合函数的图象可得所求的范围．详解：（1）∵，∴，∴.又，∴曲线在点处的切线方程为．由得.故，所以当，即或时，切线与曲线有两个公共点；当，即或时，切线与曲线有一个公共点；当，即时，切线与曲线没有公共点.（2）由题意得，由，得，设，则.又，所以当时，单调递减；当时，单调递增．所以.又，，结合函数图象可得，当时，方程有两个不同的实数根，故当时，函数有两个零点．点睛：函数零点个数（方程根的个数、两函数图象公共点的个数）的判断方法：（1）结合零点存在性定理，利用函数的性质确定函数零点个数；（2）构造合适的函数，判断出函数的单调性，利用函数图象公共点的个数判断方程根的个数或函数零点个数．请考生在22～23两题中任选一题作答，如果多做，则按所做的第一题记分.22. 在平面直角坐标系中，以坐标原点为极点，轴的正半轴为极轴建立极坐标系.已知点的直角坐标为，曲线的极坐标方程为，直线过点且与曲线相交于，两点.（1）求曲线的直角坐标方程；（2）若，求直线的直角坐标方程.【答案】(1) (2) 直线的直角坐标方程为或【解析】分析：（1）根据极坐标和直角坐标间的转化公式可得所求．（2）根据题意设出直线的参数方程，代入圆的方程后得到关于参数的二次方程，根据根与系数的关系和弦长公式可求得倾斜角的三角函数值，进而可得直线的直角坐标方程．详解：（1）由，可得，得，∴曲线的直角坐标方程为.（2）由题意设直线的参数方程为（为参数），将参数方程①代入圆的方程，得，∵直线与圆交于，两点，∴．设，两点对应的参数分别为，，则，∴，化简有，解得或，∴直线的直角坐标方程为或.点睛：利用直线参数方程中参数的几何意义解题时，要注意使用的前提条件，只有当参数的系数的平方和为1时，参数的绝对值才表示直线上的动点到定点的距离．同时解题时要注意根据系数关系的运用，合理运用整体代换可使得运算简单．23. 已知函数的定义域为.（1）若，解不等式；（2）若，求证：.【答案】(1) (2)见解析【解析】分析：（1）由可得，然后将不等式中的绝对值去掉后解不等式可得所求．（2）结合题意运用绝对值的三角不等式证明即可．详解：（1），即，则，∴，∴不等式化为．①当时，不等式化为，解得；②当时，不等式化为，解得.综上可得．∴原不等式的解集为.（2）证明：∵，∴.又，∴.点睛：含绝对值不等式的常用解法（1）基本性质法：当a>0时，|x|＜a⇔－a＜x＜a，|x|＞a⇔x＜－a或x＞a．（2）零点分区间法：含有两个或两个以上绝对值符号的不等式，可用零点分区间法去掉绝对值符号，将其转化为与之等价的不含绝对值符号的不等式(组)求解．（3）几何法：利用绝对值的几何意义，画出数轴，将绝对值转化为数轴上两点的距离求解．（4）数形结合法：在直角坐标系中作出不等式两边所对应的两个函数的图象，利用函数图象求解．。

廊坊市重点名校2017-2018学年高二下学期期末检测数学试题一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。

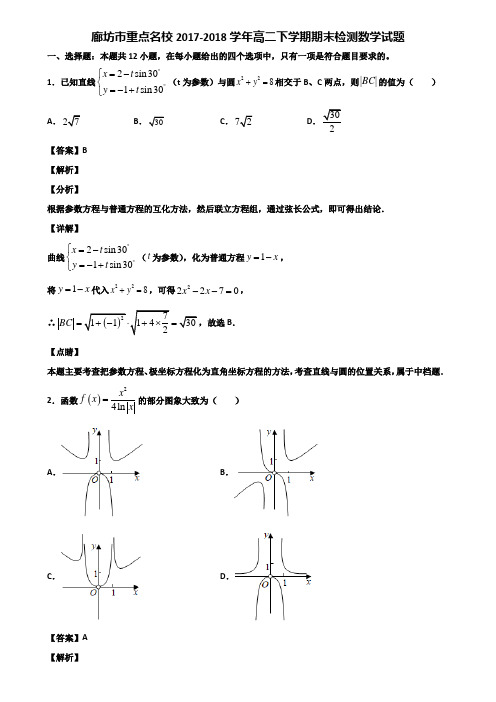
1．已知直线2sin 301sin 30x t y t ︒︒⎧=-⎨=-+⎩（t 为参数）与圆228x y +=相交于B 、C 两点，则||BC 的值为（ ） A ．27 B ．30C ．72D ．30 【答案】B 【解析】 【分析】根据参数方程与普通方程的互化方法，然后联立方程组，通过弦长公式，即可得出结论． 【详解】曲线2sin 301sin 30x t y t ︒︒⎧=-⎨=-+⎩（t 为参数），化为普通方程1y x =-， 将1y x =-代入228x y +=，可得22270x x --=，∴()271114302BC =+-⋅+⨯=，故选B ． 【点睛】本题主要考查把参数方程、极坐标方程化为直角坐标方程的方法，考查直线与圆的位置关系，属于中档题．2．函数()24ln x f x x=的部分图象大致为（ ）A ．B ．C ．D ．【答案】A【分析】判断函数的奇偶性，排除B ，确定01x <<时函数值的正负，排除C ，再由x →+∞时函数值的变化趋势排除D ．从而得正确结论． 【详解】因为()24ln x f x x =是偶函数，排除B ，当01x <<时，ln 0x <，()204ln x f x x=<，排除C ， 当x e =时()214ef e =>，排除D .故选：A. 【点睛】本题考查由解析式选图象，可能通过研究函数的性质，如奇偶性、单调性、对称性等排除一些选项，通过特殊的函数值、特殊点如与坐标轴的交点，函数值的正负等排除一些，再可通过函数值的变化趋势又排除一些，最多排除三次，剩下的最后一个选项就是正确选项．3．若实数,x y 满足不等式组422010y x y x y ≤⎧⎪-+≤⎨⎪+-≥⎩，则2z x y =+的最大值为（ ）A ．8B ．10C ．7D ．9【答案】D 【解析】 【分析】根据约束条件，作出可行域，将目标函数2z x y =+化为122zy x =-+，结合图像，即可得出结果. 【详解】由题意，作出不等式组表示的平面区域如下图所示， 目标函数2z x y =+可化为122zy x =-+， 结合图像可得，当目标函数2z x y =+过点C 时取得最大值， 由4220y x y =⎧⎨-+=⎩解得(1,4)C .此时max 189=+=z . 选D 。

一、选择题1．纵波不可能产生的现象是（）A．偏振现象B．折射现象C．干涉现象D．衍射现象2．关于速度和加速度的关系，以下说法中正确的是（）A．加速度大的物体，速度越来越大B．物体的加速度不断减小，速度一定越来越小C．速度不为零时，加速度一定不为零D．加速度不断增加，而速度可能越来越小3．如图所示是A、B两质点从同一地点运动的x t－图象，则下列说法错误的是的（）A．A质点以20m／s的速度匀速运动B．B质点先沿正方向做直线运动，后沿负方向做直线运动C．B质点最初4s做加速运动，后4s做减速运动D．A、B两质点在4s末相遇4．在水中同一深度并排放着红、蓝、紫三种颜色的球，若在水面正上方俯视这三个球，感觉最浅的是（）A．紫色球B，蓝色球C．红色球D．三个球同样深5．一个质点做简谐运动，它的振动图象如图，则（）A ．图中的曲线部分是质点的运动轨迹B ．有向线段OA 是质点在1t 时间内的位移C ．有向线段OA 在x 轴的投影是质点在1t 时间内的位移D ．有向线段段OA 的斜率是质点在1t 时刻的瞬时速率6．两种单色光由玻璃射向空气时发生了全反射，临界角分别为1θ、2θ且1θ>2θ，1n 、2n 分别表示玻璃对这两种单色光的折射率，1v 、2v 分别表示这两种单色光在玻璃中的传播速度，则（ ） A.12n n <，12v v < B.12n n <，12v v > C.12n n >，12v v < D.12n n >，12v v >7．如图所示是一个单摆做受迫振动时的共振曲线，表示振幅A 与驱动力的颜率f 的关系，下列说法正确的是（ ）A.此单摆的固有周期的为0.5sB.此单摆的摆长约为1mC.若增大摆长，单摆的固有频率增大D.若增大摆长，共振曲线的“峰”将向右移动8．两列简谐横波的振幅都是20cm ，传播速度大小相同。

实线波的频率为2Hz ，沿x 轴正方向传播；虚线波沿x 轴负方向传播。

河北省廊坊市省级示范高中联合体2017-2018学年高二下学期第二次联考化学试题可能用到的相对原子质量: H-1 C-12 N-14 O-16 Si-28 P-31 S-32 C1-35.5 Ar-20 Br-80 Na-23 Mg-24 Al-27 Ca-40 Fe-56 Cu-64 Zn-65 Ag-108 Ba-137 Mn- 55第Ⅰ卷(共50分)选择题，每小题只有一个正确答案，共25小题，每小题2分。

1. 把一小块金属钠放入下列溶液中，说法正确的是A. 放入饱和NaOH溶液中:有氢气放出，恢复至原温度后溶液的pH增大B. 放入稀CuSO4溶液中:有氢气放出，有紫红色铜析出C. 放入MgCl2溶液中:有氢气放出，有白色沉淀生成D. 放入NH4NO3溶液中:有无色无味气体放出【答案】C【解析】分析：钠与水或酸碱盐的溶液反应，均可以看出钠与溶液中的氢离子反应，生成的氢氧化钠再与溶液中的其他离子反应。

详解：A．钠和水反应生成氢氧化钠和氢气，消耗水，饱和的氢氧化钠溶液中有NaOH晶体析出，温度不变，氢氧化钠的溶解度不变，溶液仍然是饱和溶液，浓度不变，所以pH值不变，故A错误；B．钠和硫酸铜溶液反应生成氢气和氢氧化铜沉淀，为蓝色沉淀，故B错误；C．钠和氯化镁溶液反应生成氢气和白色氢氧化镁沉淀，故C正确；D. 放入NH4NO3溶液中，反应生成氢气和氨气，氨气具有刺激性气味，故D错误；故选C。

点睛：本题考查了钠与水反应的本质。

本题的易错点为B，要注意钠与硫酸铜溶液反应时，钠首先与水反应，生成的氢氧化钠再与硫酸铜反应。

2. 在给定条件下，下列选项所示的物质间转化均能实现的是A. Fe FeCl2Fe(OH)2B. S SO3H2SO4C. CaCO3CaO CaSiO3D. NH3NO HNO3【答案】C【解析】A．铁与氯气反应只能生成氯化铁，A错误；B．硫在空气或氧气中燃烧只能生成二氧化硫，B错误；C．两步均能实现，C正确；D．NO不与H2O反应，D错误。

一、选择题1．【四川省三台中学2017-2018学年高二上学期开】直线的倾斜角为（ ）A . 30°B . 45°C 。

60°D 。

90°【答案】B【解析】试题分析：由直线方程可知斜率考点：直线倾斜角和斜率2．【湖北省长阳县第一高级中学2017-2018学年高二9月月考】设点A （2，－3），B (－3，－2)，直线过点P （1，1）且与线段AB 相交,则的斜率k 的取值范围是（ )A 。

k ≥或k ≤－4B 。

－4≤k ≤C 。

－≤k ≤4D 。

以上都不对 【答案】A考点：直线的斜率运用.3．【湖北省荆州中学2017-2018学年高二上学期第一次月考】直线22sin cos 055x y ππ-=的倾斜角α是（ ）A .25π-B 。

25πC 。

35π D 。

75π 【答案】B【解析】直线22sin cos 055x y ππ-=的斜率为2sin25k tan25cos 5πππ==，∴25πα=.故选：B4．【河北省廊坊市省级示范高中联合体2016-2017学年高一下学期期末】直线102n mx y +-=在y 轴上的截距是—1，且它的倾斜角是直线3330x y --=的倾斜角的2倍，则( ）A .3,2m n == B .3,2m n =-=- C .3,2m n ==- D 。

3,2m n =-=【答案】B 【解析】设直线3330x y --=的倾斜角是α ,则直线:102n l mx y +-=的倾斜角为2α ∵tan 3α=，∴直线102n mx y +-=m 的斜率222323113tan k tan tan ααα====---∴直线l 的斜截式方程为： 31y x =--， 3,m ∴=- 2n =- ，故选：B .5．【襄阳市第四中学2017-2018学年高二上学期第一次月考】直线sin cos 77x y ππ+的倾斜角α是（ ）A .7π-B 。

理科数学答案2018年5月一、选择题（每题5分，共60分）1．A 2．C 3．B 4．B 5．A 6．A 7．D 8．B 9．D 10．A 11．B 12．D11.【解析】设椭圆和双曲线的半焦距为，由于是以为底边的等腰三角形，若，即有，由椭圆的定义可得，由双曲线的定义可得，即有，再由三角形的两边之和大于第三边，可得，则，即有，由离心率公式可得，由于，则由，则，所以的取值范围是.12.【解析】∵函数满足：当时，恒成立，∴函数为上的偶函数，且在上为单调递增函数，且有，∴，恒成立恒成立，只要使得定义域内，由，得，即函数的周期，∵时，，求导得，该函数过点，如图，且函数在处取得极大值，在处取得极小值，即函数在上的最大值为2，∵，函数的周期是，∴当时，函数的最大值为2，由，即，则，解得或.二、填空题（每题5分，共20分）13．（2）P>Q 14.(1)(2) 15．16．6815.【解析】分析：分三种情况讨论，分别求出甲乙都入选、甲不入选，乙入选、甲乙都不入选,，相应的情况不同的组队形式的种数，然后求和即可得出结论. 详解：若甲乙都入选，则从其余人中选出人，有种，男生甲不适合担任一辩手，女生乙不适合担任四辩手，则有种，故共有种；若甲不入选，乙入选，则从其余人中选出人，有种，女生乙不适合担任四辩手，则有种，故共有种；若甲乙都不入选，则从其余6人中选出人，有种，再全排，有种，故共有种，综上所述，共有，故答案为.16.【解析】2113是第1057个奇数，宝塔形数表第i 行i 有个数， ∴前i 行共有()1123 (2)i i i +++++=个数，454610352⨯=， 2017∴在宝塔形数表的第46行中， 2017∴为第46行从右向左数第22个数，即46,222017a =， 462268i j ∴+=+=，故答案为68. 三、解答题（共70分） 17．（本小题满分12分）解：p ： 3x a -<等价于： 33x a -<-<即33a x a -<<+；…………2分q ()lg 6x -有意义等价于： 10{60x x +≥->，即16x -≤<…………4分（1）1a =时， p 即为24x -<<若“p q ∧”为真命题，则24{16x x -<<-≤<，得： 14x -≤<故1a =时，使“p q ∧”为真命题的实数x 的取值范围是[1-， 4)…………8分 （2）记集合{|33}A x a x a =-<<+， {|16}B x x =-≤< 若p 是q 成立的充分不必要条件，则A B ⊂， 因此： 31{36a a -≥-+≤， ∴ 23a ≤≤，故实数a 的取值范围是[]2,3。

河北高二2017~2018学年度第二学期期末联考试题高二数学(理科)本试卷共4页，全卷满分150分，考试时间120分钟。

一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1. 已知集合，集合，则A. B. C. D.2. 已知命题；命题，则下列命题中为真命题的是A. B. C. D.3. 设随机变量x服从正态分布N（2，9），若，则m=A. B. C. D. 24. 设复数，若，则的概率为A. B. C. D.5. 某几何体的三视图如图所示，则该几何体的体积为A. B. C. D.6. 若双曲线的一条渐近线与圆至多有一个交点，则双曲线的离心率为...A. B. C. D.7. 设x，y满足约束条件则的最大值是A. B. C. D.8. 若抛物线上一点到焦点和抛物线对称轴的距离分别为10和6，则抛物线方程为A. B.C. 或D. 或9. 用数字0，1，2，3，4，5组成没有重复数字的五位数，其中比40000大的偶数共有A. 144个B. 120个C. 96个D. 72个10. 公元前300年欧几里得提出一种算法，该算法程序框图如图所示。

若输入m=98，n=63，则输出的m=A. 7B. 28C. 17D. 3511. 在三棱锥中，，为等边三角形，，是的中点，则异面直线和所成角的余弦值为A. B. C. D.12. 定义：如果函数在上存在，满足，，则称函数是上的“双中值函数”，已知函数是上的“双中值函数”，则实数a的取值范围是A. B. C. D.二、填空题（本大题共4小题，每小题5分，共20分．把答案填在答题卡上对应题号后的横线上）13. 如图，点A的坐标为（1，0），点C的坐标为（2，4），函数．若在矩形ABCD内随机取一点，则此点取自阴影部分的概率等于______．14. 的展开式中，的系数是______．（用数字填写答案）15. 设圆的切线l与x轴的正半轴、y轴的正半轴分别交于点A，B，当|AB|取最小值时，切线l的方程为______．16. 设表示不超过x的最大整数，如：．给出下列命题：①对任意实数x，都有；②若，则；③；...④若函数，则的值域为．其中所有真命题的序号是______．三、解答题（本大题共6个小题，共70分．解答应写出文字说明，证明过程或演算步骤）17. 已知各项均不相等的等差数列的前四项和，且成等比数列．（Ⅰ）求数列的通项公式；（Ⅱ）设为数列的前n项和，若对恒成立，求实数的最小值．18. 某城市一汽车出租公司为了调查A，B两种车型的出租情况，现随机抽取了这两种车型各100辆，分别统计了每辆车某个星期内的出租天数，统计数据如下表：A车型B车型...（Ⅰ）从出租天数为3天的汽车（仅限A，B两种车型）中随机抽取一辆，估计这辆汽车恰好是A型车的概率；（Ⅱ）根据这个星期的统计数据，估计该公司一辆A型车，一辆B型车一周内合计出租天数恰好为4天的概率；（Ⅲ）（ⅰ）试写出A，B两种车型的出租天数的分布列及数学期望；（ⅱ）如果两种车辆每辆车每天出租获得的利润相同，该公司需要从A，B两种车型中购买一辆（注：两种车型的采购价格相当），请你根据所学的统计知识，建议应该购买哪一种车型，并说明你的理由．19. 如图所示的平面图形中，ABCD是边长为2的正方形，△HDA和△GDC都是以D为直角顶点的等腰直角三角形，点E是线段GC的中点．现将△HDA和△GDC分别沿着DA，DC翻折，直到点H和G重合为点P．连接PB，得如图的四棱锥．（Ⅰ）求证：PA//平面EBD；（Ⅱ）求二面角大小．20. 已知椭圆，抛物线的焦点均在x轴上，的中心和的顶点均为原点O，从每条曲线上各取两个点，其坐标分别是，，，．（Ⅰ）求，的标准方程；（Ⅱ）是否存在直线l满足条件：①过的焦点F；②与交于不同的两点M，N且满足？若存在，求出直线方程；若不存在，请说明理由．21. 已知函数（Ⅰ）当时，求函数的单调区间；（Ⅱ）设函数的图象在点两处的切线分别为l，l2．若，且，求实数c的最小值．1请考生在22，23两题中任选一题作答。

数 学 答 案2018年5月1.【答案】D 【解析】由题意得},21|{}012|{B }32|{}065|{A 2>=>-=≥≤=≥+-=x x x x x x x x x x ，或∴}3221|{A ≥≤<=x x x B 或 ．选D ． 2．【答案】C 【解析】由正弦定理，22135sin 30sin 2sin sin =⇒=⇒=c c C c A a 3.【答案】D 【解析】由于数列为等差数列,依题意得1139{ 4624a d a d +=+=.解得2d =,所以7439615a a d =+=+=.4. 【答案】 C【解析】 直观图中等腰直角三角形直角边长为1，因此面积为12，又直观图与原平面图形面积比为2∶4，所以原图形的面积为2，故选C.5.【答案】D【解析】由题意知三棱锥11P A B A -的侧视图即为三棱锥在侧面11CDD C 上的正投影，点P的投影为其本身，点1B 的投影为1C ,点1A 的投影为1D，点A 的投影为D ，故侧视图为上宽下窄的梯形，且左下到右上的对角线为实线，左上到右下的对角线为虚线，故D 选项满足。

选D 。

6. 【答案】D3a 与23b 的等比中项，∴2223333a b a b +⨯===，∴21a b +=， ∴()212142448b a a b a b a b a b ⎛⎫+=++=++≥+= ⎪⎝⎭，当且仅当4b a a b =且21a b +=，即11,24a b ==时等号成立．选D ． 7.【答案】 C 【解析】 设球的半径为R ，则32＋42＝R 2，故R ＝5.所以球的体积为V ＝43πR 3＝43π×125＝500π3(cm 3)． 8．【答案】D【解析】∵()()1159131721143n n S n -=-+-+-++--， ∴()()()()1515913495357475729S =-+-++-+=-⨯+=，()()()()22159131721818541144S =-+-+-++-=-⨯=-， ()()()()3115913172111311712141512161S =-+-+-++-+=-⨯+=， ∴15223129446176S S S +-=--=-．本题选择D 选项.9.【答案】C.【解析】∵等比数列{}n a ，∴3618a a a a =，又∵18,a a 是关于x的方程22sin 0x x -αα=的两根，∴182sin a a α+=，18a a α=，∴221836()264sin 6a a a a +=+⇒α=-α+，即sin 2α=或sin α=（舍去），又∵锐角α，∴3πα=. 10.【答案】A【解析】在ACM ∆ 中，00000012060180,451560=-=∠=-=∠AMC MCA ，由正弦定理得AMC AC MCA AM ∠=∠sin sin ，即23221200AC =，解得6600=AC ．在ACD ∆ 中，∵33tan ==∠AC DC DAC ，∴2600336600tan =⨯=∠⋅=DAC AC DC ．、故选A ． 11.【答案】B【解析】设圆锥的底面半径是r ，母线长为l ，∵圆锥的侧面积是其底面积的2倍， 22rl r ππ∴= ，解得2l r =，则圆锥的轴截面是正三角形，设圆锥的外接球的半径为,R，2,3R ∴= ∴该圆锥的表面积2213,S rl r r πππ=+=外接球的表面积为22221644,33S R r πππ⎛⎫=== ⎪ ⎪⎝⎭ 212239.16163S r S r ππ∴== 故选B ．12.【答案】A【解析】a 1=9，a 2为整数，可知：等差数列{a n }的公差d 为整数，由S n ≤S 5，∴a 5≥0，a 6≤0，则9+4d ≥0，9+5d ≤0，解得99d 45-≤≤-，d 为整数，d=﹣2．∴a n =9﹣2（n ﹣1）=11﹣2n ．()()111111112n 92n 292n 112n n n a a +⎛⎫==- ⎪⋅--⎝⎭﹣﹣， ∴数列11n n a a +⎧⎫⎨⎬⋅⎩⎭前n 项和为11111111112795792n 112n 292n 9⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-+-++-=- ⎪ ⎪ ⎪ ⎪⎢⎥--⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦﹣ 令b n =192n -，由于函数f （x ）=192x-的图象关于点（4.5，0）对称及其单调性，可知：0＜b 1＜b 2＜b 3＜b 4，b 5＜b 6＜b 7＜…＜0，∴b n ≤b 4=1．∴最大值为=49． 故选：A13.【答案】{|10}x x -≤<【解析】111220010x x x x x x x--+≥⇔-≥⇔≤⇔-≤<,所以不等式的解集为{|10}x x-≤<.14.【答案】5【解析】由已知可将刍甍切割成一个三棱柱和一个四棱锥，三棱柱的体积为3，四棱锥的体积为2，则刍甍的体积为5.15.【答案】)2【解析】,,a b c 分别为ABC ∆的三个内角,,A B C 的对边，当(),a bsinA b ∈时，满足条件的三角形有两个所以060xsin x 2x <<.答案为： )2. 16.【解析】当2n =时，得22212a a +=+，即21a =，由()122n n S a n =+≥可知： 1112n n S a ++=+，两式相减可得1122n n n a a a ++=-，即12n n a a +=，故数列{}n a 是从第二项起以2为公比的等比数列，则()19192011222112S -=+=+-.17.【解析】（1）在ABC ∆中，由正弦定理得，)())((c a a c b c b -=+-， … …（2分）即ac c a b -+=222， 由余弦定理，得212cos 22=-+=ac ac c a B ， … … … …… … …（4分） ∵3),0(ππ=∴∈B B ； … … … …… … …（5分）（2）由（1）知ac c a ac c a 3)(9222-+=-+= 于是22)2(39)(c a ac c a +≤=-+ ， … … … …… … …（8分） 解得 6≤+c a ，当且仅当3==c a 时，取等号. … … … …… … …（9分）所以c a +的最大值为6. … … … …… … …（10分）18.【解析】（1）∵22n n n a a a ++=，∴数列{}n a 是等差数列 … … …（2分）由148,2a a ==知2d =-∴()821210n a n n =--=-+ … … … …… …… …… …（4分）（2）由（1）可得数列{}n a 的前n 项和为()2n 821092n n T n n -+==-+。