一元一次方程-经典难题复习巩固

《一元一次方程》全章复习与巩固用一元一次方程解决实际问题的常见类型1.行程问题：路程＝速度×时间2.和差倍分问题：增长量＝原有量×增长率3.利润问题：商品利润＝商品售价－商品进价4.工程问题：工作量＝工作效率×工作时间，各部分劳动量之和＝总量5.银行存贷款问题：本息和＝本金+利息，利息＝本金×利率6.数字问题：多位数的表示方法：例如：32101010abcd a b c d =⨯+⨯+⨯+.【典型例题】类型一、一元一次方程的相关概念1．已知方程(3m -4)x 2-(5-3m )x -4m ＝-2m 是关于x 的一元一次方程，求m 和x 的值．举一反三： 【变式】下面方程变形中，错在哪里：(1)方程2x=2y 两边都减去x+y ，得2x-(x+y)=2y-(x+y), 即x-y=-(x-y).方程 x-y=-(x-y)两边都除以x-y, 得1=-1.（2）3721223x x x -+=+，去分母，得3(3-7x)=2(2x+1)+2x ，去括号得：9-21x=4x+2+2x.2. 如果5(x+2)＝2a+3与(31)(53)35a xa x +-=的解相同，那么a 的值是________．举一反三： 【变式】已知|x+1|+(y+2x )2＝0，则y x =________．类型二、一元一次方程的解法3．解方程：4621132xx -+-=． 4．解方程3{2x -1-[3(2x -1)+3]}＝5．举一反三：【变式1】解方程 【变式2】解方程：26752254436z z z zz +---++=- 0.10.050.20.05500.20.54x x +--+=.类型三、特殊的一元一次方程的解法1．解含字母系数的方程 2．解含绝对值的方程5.解关于x 的方程：11()(2)34m x n x m -=+ 6. 解方程|x -2|＝3．举一反三：【变式1】若关于x 的方程230x m -+=无解，340x n -+=只有一个解，450x k -+=有两个解， 则,,m n k 的大小关系为： ( )A . m n k >> B.n k m >> C.k m n >> D.m k n >>【变式2】若9x =是方程123x m -=的解，则__m =；又若当1n =时，则方程123x n -=的解是 ． 类型四、一元一次方程的应用7．李伟从家里骑摩托车到火车站，如果每小时行30千米，那么比火车开车时间早到15分钟；若每小时行18千米，则比火车开车时间迟到15分钟，现在李伟打算在火车开车前10分钟到达火车站，求李伟此时骑摩托车的速度应是多少?8. 黄冈某地“杜鹃节”期间，某公司70名职工组团前往参观欣赏，旅游景点规定：①门票每人60元，无优惠；②上山游玩可坐景点观光车，观光车有四座和十一座车，四座车每辆60元，十一座车每人10元．公司职工正好坐满每辆车且总费用刚好为4920元时，问公司租用的四座车和十一座车各多少辆?【答案与解析】举一反三：【变式】某商品进价2000元，标价4000元，商店要求以利润率不低于20%的售价打折出售，售货员最低可以打几折出售此商品？。

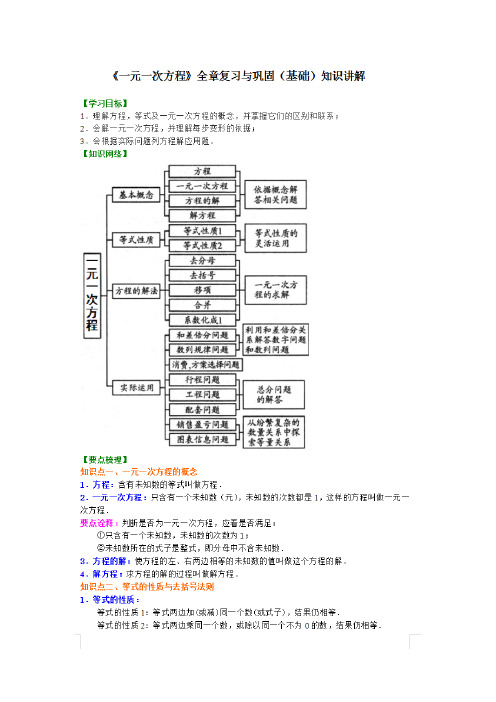
第三章《一元一次方程》复习巩固类型一 灵活解一元一次方程 1.方程解的意义； 2.解一元一次方程.经典例题1 解方程：13[x －12(x －1)]＝23(x －12).类型二 方程的解的应用 方程的解与绝对值等有理数知识的综合求值.经典例题2 若|a －3|＋(b ＋1)2＝0，代数式2b －a ＋3m 的值比b －a ＋m 多1，求m 的值.类型三 一元一次方程的应用经典例题3 某养殖专业户计划购买甲、乙两种牲畜，已知乙种牲畜的单价是甲种牲畜单价的2倍多200元，买3头甲种牲畜和1头乙种牲畜共需5700元.(1)甲、乙两种牲畜的单价各是多少元？(2)若购买以上两种牲畜50头，共需资金9.4万元，求甲、乙两种牲畜各购买多少头？综 合 检 测一、选择题1. 下列方程：①x ＝3；①x ＋2y ＝1；①1x ＋2＝0；①x 2－1＝x ；①x 2－4＝3x .其中是一元一次方程的有( ) A. 2个 B. 3个 C. 4个 D. 5个2. 关于x 的方程2x －m 3＝1的解为2，则m 的值是( )A. 2.5 B. 1 C. －1 D. 3 3. 下列方程的变形中，正确的是( )A. 方程3x －2＝2x ＋1，移项，得3x －2x ＝－1＋2B. 方程3－x ＝2－5(x －1)，去括号，得3－x ＝2－5x －1C. 方程23x ＝32，未知数系数化为1，得x ＝1D. 方程x －12－x 5＝1化成5(x －1)－2x ＝10 4. 对于实数a ，b ，规定a ※b ＝a －2b ，若4※(x －3)＝2，则x 的值为( )A.－2 B. －12 C. 52D. 4 5. 一家商店一月份把某种商品按进货价提高60%出售，到三月份再声称以8折大拍卖，那么该商品三月份的价格比进货价( )A. 高12.8% B. 低12.8% C. 高28% D. 高40%6. 已知方程2－x －13＝1－x 2＋3－x 与方程4－kx ＋23＝3k －1－x 2的解相同，则k 的值为( ) A. 0 B. 2 C. 1 D. －17. 制一张桌子要用一个桌面和4条桌腿，1立方米木材可制作20个桌面，或者制作400条桌腿.现有12立方米木材，应安排多少立方米木材制作桌面才能使桌子配套( )A. 2 B. 6 C. 8 D. 108. “国际购物中心”在国庆节期间举行优惠活动，规定一次购物不超过500元的不优惠；超过500元的，全部按8折优惠.小丽买了一件服装，付款480元，这件服装的标价是( )A. 480元B. 500元C. 600元D. 480元或600元9. 某电信公司的一种计费标准是：通话时间不超过3分钟，收话费0.2元，以后每分钟收话费0.1元，若小张的话费仅有2.4元，则他能持续通话的最长时间为( )分钟。

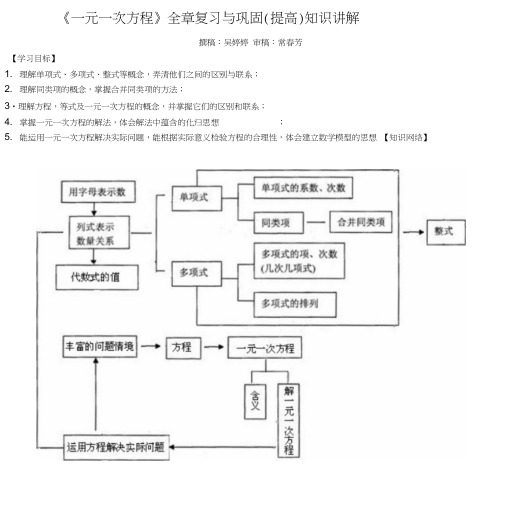
《一元一次方程》全章复习与巩固(提高)知识讲解撰稿：吴婷婷审稿：常春芳【学习目标】1. 理解单项式、多项式、整式等概念，弄清他们之间的区别与联系；2. 理解同类项的概念，掌握合并同类项的方法；3•理解方程，等式及一元一次方程的概念，并掌握它们的区别和联系；4. 掌握一元一次方程的解法，体会解法中蕴含的化归思想；5. 能运用一元一次方程解决实际问题，能根据实际意义检验方程的合理性，体会建立数学模型的思想【知识网络】【要点梳理】要点一、整式的相关概念1•代数式的定义：诸如：5.6n , 3.5x , m+n , 34,, 2一1v n 等式子，它们都是用运算符号把数和字母连接而成的，像这样的式子叫做代数式，单独的一个数或一个字母也是代数式.要点诠释：带等号或不等号的式子不是代数式，如3x=3, 3x>3, 3x^3等都不是代数式.2. 列代数式：在解决实际问题时，常常先把问题中涉及的数量关系用代数式来表示，这就是列出代数式•用数值代替代数式里的字母，按照代数式原有的运算关系计算得出的结果，叫做代数式的值.要点诠释：代数式的书写规范：(1)字母与数字或字母与字母相乘时，通常把乘号写成“•”或省略不写；(2)除法运算一般以分数的形式表示；(3)字母与数字相乘时，通常把数字写在字母的前面；(4)字母前面的数字是分数的，如果既能写成带分数又能写成假分数，一般写成假分数的形式；(5)如果字母前面的数字是1,通常省略不写.3. 单项式：由数字或字母的积组成的代数式叫做单项式，单独的一个数或一个字母也是单项式. 要点诠释：3)单项式的系数是指单项式中的数字因数.(2)单项式的次数是指单项式中所有字母的指数和.4. 多项式：几个单项式的和叫做多项式.在多项式中，每个单项式叫做多项式的项. 要点诠释：(1)在多项式中，不含字母的项叫做常数项.(2) 多项式中次数最高的项的次数，就是这个多项式的次数.(3) 多项式的次数是n次，有m个单项式，我们就把这个多项式称为n次m项式.5. 多项式的降幕与升幕排列：把一个多项式按某一个字母的指数从大到小的顺序排列起来，叫做把这个多项式按这个字母降幕排列.另外，把一个多项式按某一个字母的指数从小到大的顺序排列起来，叫做把这个多项式按这个字母升幕排列•要点诠释：(1)利用加法交换律重新排列时，各项应带着它的符号一起移动位置；(2)含有多个字母时，只按给定的字母进行降幕或升幕排列.6•整式：单项式和多项式统称为整式.要点二、同类项与合并同类项1. 同类项：所含字母相同，并且相同字母的指数也相同的项叫做同类项.所有的常数项都是同类项. 要点诠释：辨别同类项要把准“两相同，两无关” ：(1)“两相同”是指：①所含字母相同；②相同字母的指数相同；(2)“两无关”是指：①与系数无关；②与字母的排列顺序无关.2. 合并同类项：把多项式中的同类项合并成一项，叫做合并同类项.要点诠释：合并同类项时，只是系数相加减，所得结果作为系数，字母及字母的指数保持不变. 要点三、等式和一元一次方程的概念1. 等式的概念：用符号“三’来表示相等关系的式子叫做等式•2. 等式的性质：等式的性质1：等式两边加(或减)同一个数(或式子)，结果仍相等.等式的性质2：等式两边乘同一个数，或除以同一个不为0的数，结果仍相等.3. 方程：含有未知数的等式叫做方程.4. 一元一次方程：只含有一个未知数(元)，未知数的次数都是1,这样的方程叫做一元一次方程. 要点诠释：(1) 一元一次方程变形后总可以化为ax+b=O(a工0)的形式，它是一元一次方程的标准形式.(2) 判断是否为一元一次方程，应看是否满足：①只含有一个未知数，未知数的次数为1；②未知数所在的式子是整式，即分母中不含未知数；5. 方程的解：使方程的左、右两边相等的未知数的值叫做这个方程的解. 6•解方程：求方程的解的过程叫做解方程.要点四、一元一次方程的解法解一元一次方程的一般步骤(1) 去分母：在方程两边同乘以各分母的最小公倍数.(2) 去括号：依据乘法分配律和去括号法则，先去小括号，再去中括号，最后去大括号.(3) 移项：把含有未知数的项移到方程一边，常数项移到方程另一边.(4) 合并：逆用乘法分配律，分别合并含有未知数的项及常数项，把方程化为ax=b(0H0)的形式.(5) 系数化为1：方程两边同除以未知数的系数得到方程的解=-(a^0).x a(6) 检验：把方程的解代入原方程，若方程左右两边的值相等，则是方程的解；若方程左右两边的值不相第2页共仃页等，则不是方程的解. 要点五、用一元一次方程解决实际问题的常见类型 1 •行程问题：路程=速度X 时间 2•和差倍分问题：增长量=原有量x 增长率 3•利润问题：商品利润=商品售价一商品进价4•工程问题：工作量=工作效率X 工作时间，各部分劳动量之和=总量 5•银行存贷款问题： 本息和=本金+利息，利息=本金x 利率3+bx 103+cx 10+d6 •数字问题：多位数的表示方法： abcd= ax 10【典型例题】、整式的相关概念1.指出下列各式中的整式、单项式和多项式，是单项式的请指出系数和次数，是多项式的请说出是 几次几项式.2 (1) b a a3 (2) 5 (3)【答案与解析】解:整式:(1)> (2)、(4)、(5)、(6)、(7)、(8)、(9)x x m - - 1y (% (8) (a (4)2( 5)1+a %2b)3xy 5( 9) h (6)71— + -单项式：(2)、(5)、(6),其中：5的系数是5,次数是0； 3xy 的系数是3,次数是2；的系数是次数是1.多项式：(1)> (4)、(7)、X(8)、(9),其中：a 3是一次二项式；y 是一次二项式;2—+— — +次二项式；1+a%是一次二项式;1(a b)*~h 是二次二项 2式。

2．合并法则：合并时，把系数相加(减)作为结果的系数，字母和字母的指数保持不变．3．去括号法则：（1）括号外的因数是正数，去括号后各项的符号与原括号内相应各项的符号相同．（2）括号外的因数是负数，去括号后各项的符号与原括号内相应各项的符号相反． 知识点三、一元一次方程的解法解一元一次方程的一般步骤：(1)去分母：在方程两边同乘以各分母的最小公倍数．(2)去括号：依据乘法分配律和去括号法则，先去小括号，再去中括号，最后去大括号．(3)移项：把含有未知数的项移到方程一边，常数项移到方程另一边．(4)合并：逆用乘法分配律，分别合并含有未知数的项及常数项，把方程化为ax ＝b (a ≠0)的形式．(5)系数化为1：方程两边同除以未知数的系数得到方程的解b x a =(a ≠0)． (6)检验：把方程的解代入原方程，若方程左右两边的值相等，则是方程的解；若方程左右两边的值不相等，则不是方程的解．知识点四、用一元一次方程解决实际问题的常见类型1.行程问题：路程＝速度×时间2.和差倍分问题：增长量＝原有量×增长率3.利润问题：商品利润＝商品售价－商品进价4.工程问题：工作量＝工作效率×工作时间，各部分劳动量之和＝总量5.银行存贷款问题：本息和＝本金+利息，利息＝本金×利率×期数6.数字问题：多位数的表示方法：例如：32101010abcd a b c d =⨯+⨯+⨯+.【典型例题】类型一、一元一次方程的概念1．下列方程中，哪些是一元一次方程? 哪些不是? (1)2x+y ＝5； (2)x 2-5x+6＝0； (3)23x x -=； (4)1123y y -+=． 【思路点拨】若一个整式方程经过化简变形后，只含有一个未知数，并且未知数的次数都是1，系数不为0，则这个方程是一元一次方程．【答案与解析】 (4)是一元一次方程．因为它们或等价变形后是只含有一个未知数、并且未知数的次数是1的方程；(1)、(2)、(3)都不是一元一次方程，因为(1)中含有两个未知数；(2)中未知数的最高次数是2；(3)中分母含有未知数，它不是整式方程．【总结升华】凡是分母中含有未知数的方程一定不是一元一次方程．举一反三：【变式】下列说法中正确的是( ).A ．2a-a=a 不是等式B ．x 2-2x-3是方程C ．方程是等式D ．等式是方程【答案】C2. 若方程3(x -1)+8＝2x+3与方程253x k x +-=的解相同，求k 的值．【答案与解析】解：解方程3(x-1)+8＝2x+3，得x＝-2．将x＝-2代入方程253x k x+-=中，得22253k-++=．解这个关于k的方程，得263k=．所以，k的值是263k=．【总结升华】由于两个方程的解相同，所以可以将其中一个方程的解代入另一个方程中，从而求得问题的答案．举一反三：【变式】（2015春•泉州期中）当x=时，代数式2x+1与5x﹣8的值相等．【答案】3．解：根据题意得：2x+1=5x﹣8，∴2x﹣5x=﹣8﹣1，∴﹣3x=﹣9，∴x=3.类型二、一元一次方程的解法3．解方程2351 46y y+--=【思路点拨】通过方程的同解原理(去分母，去括号，合并同类项，系数化为1)，一步一步将一个复杂的方程转化成与它同解的最简的方程，从而达到求解的目的．【答案与解析】解：去分母，得3(y+2)-2(3-5y)＝12去括号，得3y+6-6+10y＝12合并同类项，得13y＝12未知数的系数化为1，得1213 y=【总结升华】转化思想是初中数学中一种常见的思想方法，它能将复杂的问题转化为简单的问题，将生疏的问题转化为熟悉的问题，将未知转化为已知．事实上解一元一次方程就是利用方程的同解原理，将复杂的方程转化为简单的方程直至求出它的解．4．解方程：113(1)(1)2(1)(1)22x x x x+--=--+【思路点拨】本题按常规方法求解，比较繁锁，如能根据题目的特点，巧用“整体思维”，就能算得又快又对，起到事半功倍的效果．【答案与解析】解：113(1)(1)2(1)(1)22x x x x+++=-+-75(1)(1)22x x +=- 7(1)5(1)x x +=-7755x x +=-212x =-x ＝-6【总结升华】直接去括号太繁琐，若将(x+1)及(x -1)看作一个整体，并移项合并同类项，解答十分巧妙，可免去去分母的步骤及简化去括号的过程．举一反三：【变式】解方程：278(x -4)-463(8-2x )-888(7x -28)＝0【答案】解：原方程可化为278(x -4)+463×2(x -4)-888×7(x -4)＝0(x -4)(278+463×2-888×7)＝0x -4＝0x ＝4类型三、一元一次方程的应用5． (南京)甲车从A 地出发以60 km ／h 的速度沿公路匀速行驶，0.5 h 后，乙车也从A 地出发，以80 km ／h 的速度沿该公路与甲车同向匀速行驶，求乙车出发后几小时追上甲车．【答案与解析】解：设乙车出发后x 小时追上甲车，依题意得60×0.5+60x ＝80x ，解得x ＝1.5． 答：乙车出发后1.5小时追上甲车．【总结升华】此题的等量关系为：甲前0.5 h 的行程+甲后来的行程＝乙的行程．6. （2015•东城区一模）列方程或方程组解应用题：2015年“植树节”前夕，某小区为绿化环境，购进200棵柏树苗和120棵枣树苗，且两种树苗所需费用相同．每棵枣树苗的进价比每棵柏树苗的进价的2倍少5元，每棵柏树苗的进价是多少元？【答案与解析】解：设每棵柏树苗的进价是x 元，则每棵枣树苗的进价是（2x ﹣5）元，根据题意，列方程得：200x=120（2x ﹣5），解得：x=15．答：每棵柏树苗的进价是15元．【总结升华】此题考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．举一反三：【变式】某文具店为促销X 型计算器，优惠条件是一次购买不超过10个，每个38元，超过10个，超过部分每个让利2元(即每个36元)，问李老师用812元共买了多少个？【答案】解：设李老师用812元共买了x 个，依题意可得：381036(10)812x ⨯+⨯-=解得：22x =答：李老师用812元共买了22个．【巩固练习】一、选择题1．下列方程中，是一元一次方程的是( )．A ．250x +=B ．42x y +=-C ．162x= D ．x ＝0 2. 下列变形错误的是( )A.由x + 7= 5得x+7－7 = 5－7 ;B.由3x －2 =2x + 1得x= 3C.由4－3x = 4x －3得4+3 = 4x+3xD.由－2x= 3得x= －32 3. 某书中一道方程题：213x x ++=，□处在印刷时被墨盖住了，查书后面的答案，得知这个方程的解是 2.5x =-，那么□处应该是数字( )．A ．-2.5B ．2.5C ．5D ．74. 将(3x ＋2)－2(2x －1)去括号正确的是( )A 3x ＋2－2x ＋1B 3x ＋2－4x ＋1C 3x ＋2－4x －2D 3x ＋2－4x ＋25. 当x=2时，代数式ax －2x 的值为4，当x=－2时，这个代数式的值为（ ）A.－8B.－4C.－2D.86．解方程121153x x +-=-时，去分母正确的是( )． A ．3(x+1)＝1-5(2x -1) B ．3x+3＝15-10x -5C ．3(x+1)＝15-5(2x -1)D ．3x+1＝15-10x+57．某球队参加比赛，开局11场保持不败，积23分，按比赛规则，胜一场得3分，平一场得1分，则该队获胜的场数为( )．A ．4B ．5C ．6D ．78.（2015•河北模拟）某单位元旦期间组织员工到正定出游，原计划租用28座客车若干辆，但有4人没有座位，若租用同样数量的33座客车，只有一辆空余了11个座位，其余客车都已坐满，则该单位组织出游的员工有（ ）A ．80人B ． 84人C ． 88人D ．92人二、填空题9．在0，－1，3中， 是方程3x －9=0的解.10．如果3x 52a -＝－6是关于x 的一元一次方程，那么a ＝ ，方程的解=x .11.（2015•苏州一模）若关于x 的方程2x+a=5的解为x=﹣1，则a= 7 ．12．由3x ＝2x ＋1变为3x －2x ＝1，是方程两边同时加上 .13．“代数式9－x 的值比代数式x 32－1的值小6”用方程表示为 . 14．当x ＝ 时，代数式223x -与32x -互为相反数. 15．有两桶水，甲桶水装有180升，乙桶装有150升，要使两桶水的重量相同，则甲桶应向乙桶倒水升.16．某商场把彩电按标价的8折出售，仍可获利20%，若该彩电的进价为2000元，则标价是 .三、解答题17．（1）310.10.3542x x -=+； （2）122(1)(3)23x x x --=+． 18．已知代数式11213y y ---+的值为0，求代数式312143y y ---的值． 19.（2015•泰州）某校七年级社会实践小组去商场调查商品销售情况，了解到该商场以每件80元的价格购进了某品牌衬衫500件，并以每件120元的价格销售了400件，商场准备采取促销措施，将剩下的衬衫降价销售．请你帮商场计算一下，每件衬衫降价多少元时，销售完这批衬衫正好达到盈利45%的预期目标？20．学校校办工厂需制作一块广告牌，请来师徒二人，已知师傅单独完成需4天，徒弟单独完成需6天，现由徒弟先做一天，再两人合作，完成后共得到报酬450元，如果按各人完成的工作量计算报酬，那么该如何分配?【答案与解析】一、选择题1.【答案】D2.【答案】D【解析】由23x -=，得32x =- 3.【答案】C【解析】把x ＝-2.5代入方程，再把□当作未知数解方程即可．4.【答案】D【解析】(32)2(21)32222(1)3242x x x x x x +--=+-⋅-⋅-=+-+5．【答案】B【解析】将2x =代入得：244a -=，得28a =；将2x =-代入得：24844a -+=-+=-6．【答案】C【解析】去分母时避免漏乘常数项，当分子是多项式时，去分母后给分子加上括号．7．【答案】C【解析】设该队获胜x 场，则平的场数为(11-x)，则3x+(11-x)＝23．解得x ＝6．故选C ．8.【答案】C.【解析】设租用28座客车x 辆．则28x+4=33x ﹣11，解得 x=3，则28x+4=28×3+4=88（人）， 即该单位组织出游的员工有88人．二、填空题9. 【答案】3；【解析】代入验证即可．10. 【答案】35，-2； 【解析】35215a a -=⇒=，362x x =-⇒=- 11.【答案】7.【解析】把x=﹣1代入方程2x+a=5，得：﹣2+a=5，解得：a=7．12. 【答案】-2x ；13. 【答案】29)613x x -+=-（； 14. 【答案】138； 【解析】322023x x --+=，解得：138x = 15. 【答案】15；【解析】设倒x 升，得：180150x x -=+，解得：15x = 16. 【答案】3000.【解析】设标价为x 元，则0.82000(120%)x =+,解得：3000x =三、解答题17．【解析】解：(1)去分母，得3x -0.4＝2x+1.4．移项，得3x -2x ＝1.4+0.4．合并同类项，得x ＝1.8．(2)去分母，得12x -3(x -1)＝4(x+3)．去括号，得12x -3x+3＝4x+12．移项，得12x -3x -4x ＝12-3．合并同类项．得5x ＝9．系数化为1，得95x =． 18．【解析】 解：由题意，得112103y y ---+=．去分母，得61130y y --++=． 移项合并同类项，得714y -=-．系数化为1，得y ＝2．当y ＝2时，3121321221143434y y --⨯-⨯--=-=，即若代数式11213y y ---+的值为0，则代数式312143y y ---的值为14． 19.【解析】解：设每件衬衫降价x 元，依题意有120×400+（120﹣x ）×100=80×500×（1+45%），解得x=20．答：每件衬衫降价20元时，销售完这批衬衫正好达到盈利45%的预期目标．20．【解析】解：设两人一起做x 天，据题意，得：11(1)164x x ++=，解得x ＝2． 师傅应得报酬为14×2×450＝225(元)． 徒弟应得报酬为450-225＝225(元)．答：师傅应得报酬为225元，徒弟应得报酬为225元．。

1.某校女生占全体学生数的52%，比男生多80人，这个学校有多少学生？2.用买10大水杯的钱，可以买15个小水杯，大水杯比小水杯的单价多5元，两种水杯的单价各是多少元？3.王芳和李丽同时采摘樱桃，王芳平均每小时采摘8kg，李丽平均每小时采摘7kg，采摘结束后王芳从她采摘的樱桃中取出0.25kg给了李丽，这时两人的樱桃一样多，她们采摘用了多少时间？4.小新出生时父亲28岁，现在父亲的年龄是小新年龄的3倍，求现在小新的年龄？5.在风速为24km/h的条件下，一架非议顺风从A机场飞到B机场要用2.8小时，它逆风飞行同样的航线要用3h。

求:(1)无风时这架飞机在这一航线的平均航速；（2）两机场之间的航程。

6.一列火车匀速行驶，经过一条长300m的隧道需要20s的时间。

隧道的顶上有一盏灯，垂直向下发光，灯光照在火车上的时间是10s。

求这列车的长度。

7.有一些相同的房间需要粉刷墙面。

一天3名一级技工去粉刷8个房间，结果其中有50㎡墙面未来得及粉刷；同样时间内5名二级技工粉刷了10个房间之外，还多粉刷了另外的40㎡墙面。

每名一级技工比二级技工一天多粉刷10㎡墙面，求每个房间需要粉刷的墙面面积。

8.小刚和小强从A，B两地同时出发，小刚骑自行车，小强步行，沿同一条路线相向匀速而行，出发后2h两人相遇，相遇时小刚比小强多行进24km，相遇后0.5h小刚到达B地。

两人的行进速度分别是多少？相遇后经过多少时间小强到达A地？9.父亲和女儿的年龄之和诗91，当父亲的年龄是女儿现在年龄的2倍的时候，女儿的年龄是父亲现在年龄的1/3，求女儿现在的年龄？。

1一元一次方程提高巩固练习一、解下列方程（一）常规方程（1）135467221--=---x x x 562233102xx -=-- （2）16110312=+-+x x 03433221=-+++++x x x（3）103.02.017.07.0=--x x4.06.0-x +x = 3.011.0+x（4） 0533321212121=-⎭⎬⎫⎩⎨⎧-⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-x 526513121=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛---x x x x（5）2362132432⎪⎭⎫ ⎝⎛+--=+--x x x x x 143)1(2111=-+-x（6）200920102009433221=⨯++⨯+⨯+⨯x x x x（二）字母已知数方程（x 为未知数）⑴ x ax +=1 ⑵ ()()m x n x m+=+413⑶ ()132-=-x x k ⑷ ()()111-=+-k x k k二、解答题1、8=x 是方程a x x 2433+=- 的解，又是方程 ()[]b x b x x x +=⎥⎦⎤⎢⎣⎡---913131的解，求 b2、小张在解方程1523=-x a （x 为未知数）时，误将 - 2x 看成 2x 得到的解为3=x ， 请你求出原来方程的解3、已知关于x 的方程 ()1233+=-x a x 无解，求 a4、已知关于x 的方程()x x k 2124=-+ 无解，求 k25、已知关于x 的方程()0232=+++b ax x b a 有唯一的解，求这个方程的解6、已知关于x 的方程()()b x a x a 3512+-=- 无穷多解，求 a 、b7、已知关于x 的方程 ()()x n x m 121232+=-+无穷多解，求m 、n8、关于x 的方程 ()x x k 5165-=+-的解为整数，求正整数k三、应用题1、小张和小王，分别从甲乙两地出发步行，1小时30分后，小张走了甲乙两地距离的一半多1.5千米，此时与小王相遇。

专题09 一元一次方程章末重难点题型（12个题型）一、经典基础题题型1 方程与一元一次方程的辨别题型2 利用一元一次方程的定义和方程的解求值题型3等式的性质及应用题型4 一元一次方程中的同解问题题型5 方程的特殊解问题（求参数的值）题型6 解方程题型7 含参数的一元一次方程题型8 一元一次方程中的错解和遮挡问题题型9 一元一次方程中的新定义问题题型11 一元一次方程中的整体换元题型12 一元一次方程中的实际应用二、优选提升题题型1 方程与一元一次方程的辨别例1．（2022·吉林·大安市七年级期末）下列各式中，是一元一次方程的是（）A．x+2y=5B．x2+x-1=0C．1xD．3x+1= 10【点睛】本题主要考查了一元一次方程的定义，熟记一元一次方程的定义是解题的关键．变式1．（2022·河南三门峡·七年级期末）在①21x +；②171581+=-+；③1112x x -=-；④23x y +=中，方程共有（ ）A ．1个B ．3个C ．2个D ．4个变式2．（2022·广东湛江·七年级期末）下列各式中，不是方程的是（ ）A ．2a a a+=B ．23x +C ．215x +=D ．()2122x x +=+【答案】B【分析】根据方程的定义（含有未知数的等式称为方程）依次进行判断即可．【详解】解：根据方程的定义可得：A 、C 、D 选项均为方程，选项B 不是等式，所以不是方程，故选：B ．【点睛】题目主要考查方程的定义，深刻理解方程的定义是解题关键．题型2 利用一元一次方程的定义和方程的解求值【解题技巧】依据一元一次方程的定义，x 的次数为1，系数不为0方程的解：解方程就是求出使方程中等号左右两边相等的未知数的值，这个值叫方程的解．例1．（2022·河南郑州·七年级期末）若使方程(2)1m x +=是关于x 的一元一次方程，则m 的值是（ ）A ．2m ¹-B ．0m ¹C ．2m ¹D ．2m >-【答案】A【分析】根据一元一次方程的定义：只含有一个未知数，未知数的次数都是1，等号两边都是整式的方程叫做一元一次方程进行求解即可．【详解】解：∵方程()21m x +=是关于x 的一元一次方程，∴20m +¹即2m ¹-．故选：A ．【点睛】本题主要考查了一元一次方程的定义，解题的关键在于能够熟练掌握一元一次方程的定义．变式1．（2022·福建泉州·七年级期末）若3x =是关于x 的方程5ax b -=的解，则622a b --的值为（ ）A ．2B ．8C ．－3D ．－8【答案】B 【分析】将x =3代入ax -b =5中得3a -b =5，将该整体代入6a -2b -2中即可得出答案．【详解】解：将x =3代入ax -b =5中得：3a -b =5，所以6a -2b -2=2（3a -b ）-2=2×5-2=8．故选：B ．【点睛】本题考查了一元一次方程的解，求代数式的值，熟练掌握整体法是解题的关键．变式2．（2022·河南南阳·七年级期末）若()110m x -+=是关于x 的一元一次方程，则m 的值可以是______(写出一个即可)【答案】2（答案不唯一）【分析】只含有一个未知数，并且未知数的次数是一次的整式方程叫一元一次方程，利用一元一次方程的定义得出10m -¹，即可得出答案．【详解】解：()110m x -+=Q 是关于x 的一元一次方程，10m \-¹，解得1m ¹，m \的值可以是2．故答案为：2(答案不唯一)．【点睛】此题主要考查了一元一次方程的定义，正确掌握一元一次方程定义是解题关键．题型3 等式的性质及应用【解题技巧】等式的性质1：等式两边加同一个数（或式子）结果仍得等式；等式的性质2：等式两边乘同一个数或除以一个不为零的数，结果仍得等式．例1．（2022·海南·七年级期末）已知a b =，根据等式的性质，可以推导出的是（ ）A ．21a b +=+B ．33a b -=-C ．232a b -=D ．a b c c=例1．（2022·四川成都·八年级期末）某小组设计了一组数学实验，给全班同学展示以下三个图，其中（a ）（b ）中天平保持左右平衡，现要使（c ）中的天平也平衡，需要在天平右盘中放入砝码的克数为（ ）A ．25克B ．30克C ．40克D ．50克【答案】C 【分析】由图（a ）和图（b ）可得5个黑三角和5个黑圆共重150克，从而1个黑三角和1个黑圆共重30克，由此可计算出1个黑三角重20克，1个黑圆重10克，可计算出此题结果．【详解】设一个黑三角重a 克，一个黑圆重b 克，由题意，得5（a +b ）=150，解得a +b =30，由图（a ）得，a +2（a +b ）=80，即a +2×30=80，解得a =20，∴b =30-20=10，∴a +2b =20+10×2=20+20=40，故选：C ．【点睛】此题考查了利用等式的性质和方程解决实际问题的能力，关键是能根据题意列出关系式，利用等式的性质进行计算．例2．（2022·江苏泰州·七年级期末）已知方程x -2y =5，请用含x 的代数式表示y ，则y =_______．题型4 一元一次方程中的同解问题解题技巧：通过前一个方程求得x 的值并代入后一个方程，转化为含另一未知数的方程、例1．（2022·黑龙江大庆·期末）关于x 的方程4231x m x -=-的解是23x x m =-的解的2倍，则m 的值为（ ）A ．12B ．14C ．14-D ．12-【答案】C变式1．（2022·辽宁大连·七年级期末）如果方程24=x 与方程的解相同，则k 的值为（ ）A ．2B ．C ．4D ．【答案】C【分析】解方程2x =4，求出x ，根据同解方程的定义计算即可．【详解】解：∵2x =4，∴x =2，∵方程2x =4与方程3x +k =-2的解相同，∴3×2+k =10解得，k =4，故选：C ．【点睛】本题考查的是同解方程，掌握一元一次方程的解法是解题的关键．变式2．（2022·山东烟台·期末）若关于x 的方程()3212x k x -=+的解与关于x 的方程()821k x -=+的解互为相反数，则k =______．310x k +=2-4-题型5 方程的特殊解问题（求参数的值）解题技巧：求含参数一元一次方程的逆过程例1．（2022·河南安阳·七年级期末）关于x 的方程的解是正整数，则整数k 可以取的值是__________．【答案】3【分析】把含x 的项合并，化系数为1求x ，再根据x 为正整数求整数k 的值．【详解】解：移项、合并，得，解得：，∵x 为正整数，k 为整数，∴解得k=3．故答案为：3．【点睛】本题考查一元一次方程的解．关键是按照字母系数解方程，再根据正整数解的要求求整数k 的值．变式1．（2022·上海金山·八年级期末）如果关于x 的方程ax ＝b 无解，那么a 、b 满足的条件（）A ．a ＝0，b ＝0B ．a ≠0，b ≠0C ．a ≠0，b ＝0D ．a ＝0，b ≠0【答案】D【分析】根据方程无解，可知含x 的系数为0，常数不为0，据此求解．【详解】解：∵关于x 的方程ax =b 无解，∴a =0，b ≠0，故选：D ．【点睛】本题考查一元一次方程的解，理解方程无解时含x 的系数为0，常数项不为0是解题关键．变式2．（2022·湖南）关于x 的方程（a +1）x ＝a ﹣1有解，则a 的值为（ ）A ．a ≠0B ．a ≠1C ．a ≠﹣1D ．a ≠±1【答案】C【分析】根据一元一次方程有解，可得一元一次方程的系数不能为零，可得答案．【详解】根据一元一次方程有解，可得一元一次方程的系数不能为零，可得答案．21x kx +=21x kx -=-12x k=--2=-1k -解：由关于x 的方程（a +1）x ＝a ﹣1有解，得a +1≠0，解得a ≠﹣1．故选：C ．【点睛】本题考查了一元一次方程有解的条件，利用了一元一次方程的系数不能为零．变式3．（2022·黑龙江大庆·期末）关于x 的方程()()2153a x a x b -=-+有无穷多个解，则a b -=______．题型6 解方程【解题技巧】解含有括号的一元一次方程：一般方法是由内到外逐层去括号，但有时这样做不一定能简化运算。

⼀元⼀次⽅程的解法（基础）知识讲解及巩固练习1．（2015?⼴州）解⽅程：5x=3（x ﹣4）【答案与解析】解：⽅程去括号得：5x=3x ﹣12，移项合并得：2x=﹣12，解得：x=﹣6．【总结升华】⽅法规律：解较简单的⼀元⼀次⽅程的⼀般步骤：(1)移项：即通过移项把含有未知数的项放在等式的左边，把不含未知数的项(常数项)放在等式的右边．(2)合并：即通过合并将⽅程化为ax ＝b (a ≠0)的形式．(3)系数化为1：即根据等式性质2：⽅程两边都除以未知数系数a ，即得⽅程的解b x a =．举⼀反三：【变式】下列⽅程变形正确的是( )．A ．由2x -3＝-x -4，得2x+x ＝-4-3B ．由x+3＝2-4x ，得5x ＝5C ．由2332x -=，得x ＝-1 D ．由3＝x -2，得-x ＝-2-3【答案】D类型⼆、去括号解⼀元⼀次⽅程2．解⽅程：【思路点拨】⽅程中含有括号，应先去括号再移项、合并、系数化为1，从⽽解出⽅程．【答案与解析】（1）去括号得：42107x x +=+移项合并得：65x -=解得：56x =- （2）去括号得：32226x x --=-移项合并得：47x -=-解得：74x = 【总结升华】去括号时，要注意括号前⾯的符号，括号前⾯是“+”号，不变号；括号前⾯是“-”，各项均变号．举⼀反三：【变式】解⽅程： 5(x -5)+2x ＝-4．【答案】解：去括号得：5x -25+2x ＝-4．移项合并得： 7x ＝21．解得： x ＝3．类型三、解含分母的⼀元⼀次⽅程()()1221107x x +=+()()()232123x x -+=-3．解⽅程：4343431 623x x x+++++=．【答案与解析】解法1：去分母，得(4x+3)+3(4x+3)+2(4x+3)＝6．去括号，得4x+3+12x+9+8x+6＝6．移项合并，得24x＝-12，系数化为1，得12x=-．解法2：将“4x+3”看作整体，直接合并，得6(4x+3)＝6，即4x+3＝1，移项，得4x＝-2，系数化为1，得12x=-．【总结升华】对于解法l：(1)去分母时，“1”不要漏乘分母的最⼩公倍数“6”；(2)注意适时添括号3(4x+3)防⽌出现3×4x+3．对于解法2：先将“4x+3”看作⼀个整体来解，最后求x．举⼀反三：【变式】（2015?岳池县模拟）解⽅程：x+=﹣．【答案】解：去分母得：12x+30=24x﹣8﹣3x+24，移项合并得：﹣9x=﹣14，解得：x=．类型四、解较复杂的⼀元⼀次⽅程4．解⽅程：0.170.21 0.70.03x x--=【思路点拨】先将⽅程中的⼩数化成整数，再去分母，这样可避免⼩数运算带来的失误．【答案与解析】原⽅程可以化成：1017201 73x x-去分母，得：30x-7(17-20x)＝21．去括号、移项、合并同类项，得：170x＝140．系数化成1，得：1417x=．【总结升华】解此题的第⼀步是利⽤分数基本性质把分母、分⼦同时扩⼤相同的倍数，以使分母化整，与去分母⽅程两边都乘以分母的最⼩公倍数要区分开．5. 解⽅程：112 [(1)](1) 223x x x--=-【答案与解析】解法1：先去⼩括号得：11122 ()22233 x x x-+=-再去中括号得：11122 24433 x x x-+=-移项，合并得：511 1212x-=-系数化为1，得：115 x=解法2：两边均乘以2，去中括号得：14(1)(1)23x x x--=-去⼩括号，并移项合并得：51166x-=-，解得：解法3：原⽅程可化为：112 [(1)1(1)](1) 223x x x-+--=-去中括号，得1112 (1)(1)(1) 2243x x x-+--=-移项、合并，得51(1)122x--=-解得115 x=【总结升华】解含有括号的⼀元⼀次⽅程时，⼀般⽅法是由⾥到外或由外到内逐层去括号，但有时根据⽅程的结构特点，灵活恰当地去括号，以使计算简便．例如本题的⽅法3：⽅程左、右两边都含(x-1)，因此将⽅程左边括号内的⼀项x变为(x-1)后，把(x-1)视为⼀个整体运算．举⼀反三：【变式】32[(1)2]2 234xx---=【答案】解：去中括号得：3(1)22 42xx--?-=去⼩括号，移项合并得：3-=，解得x＝-8类型五、解含绝对值的⽅程6．解⽅程|x|-2＝0【答案与解析】解：原⽅程可化为：2x=当x≥0时，得x=2，当x＜0时，得-x=2，即，x＝-2．所以原⽅程的解是x＝2或x＝-2．【总结升华】此类问题⼀般先把⽅程化为ax b=的形式，再根据ax的正负分类讨论，注意不要漏解．【巩固练习】⼀、选择题1．（2014春?唐河县期末）⽅程|2x ﹣1|=2的解是（） A. x= B. x=﹣ C. x=或x=﹣ D. x=﹣2．下列解⽅程的过程中，移项错误的是( )．A ．⽅程2x+6＝-3变形为2x ＝-3+6B ．⽅程2x -6＝-3变形为2x ＝-3+6C ．⽅程3x ＝4-x 变形为3x+x ＝4D ．⽅程4-x ＝3x 变形为x+3x ＝4 3. ⽅程1143x =的解是（）． A ．12x = B ．112x = C ．43x = D ．34x = 4．对⽅程2(2x -1)-(x -3)＝1，去括号正确的是( )．A ．4x -1-x -3＝1B ．4x -1-x+3＝1C ．4x -2-x -3＝1D ．4x -2-x+3＝15．⽅程1302x --=可变形为( )． A ．3-x -1＝0 B ．6-x -1＝0 C ．6-x+1＝0 D ．6-x+1＝2 6．3x -12的值与13-互为倒数，则x 的值为( )．A ．3B ．-3C ．5D ．-57．解⽅程21101136x x ++-=时，去分母，去括号后，正确结果是( )． A ．4x+1-10x+1＝1 B ．4x+2-10x -1＝1 C ．4x+2-10x -1＝6D ．4x+2-10x+1＝68. （2011⼭东⽇照）某道路⼀侧原有路灯106盏，相邻两盏灯的距离为36⽶，现计划全部更换为新型的节能灯，且相邻两盏灯的距离变为70⽶，则需更换的新型节能灯有（）．A ．54盏B ．55盏C ．56盏D ．57盏⼆、填空题9．(1)⽅程2x+3＝3x -2，利⽤________可变形为2x -3x ＝-2-3，这种变形叫________．(2)⽅程-3x ＝5，利⽤________，把⽅程两边都_______，把x 的系数化为1，得x ＝________．10．⽅程2x -kx+1＝5x -2的解是x ＝-1，k 的值是_______．11．（2014秋?铜陵期末）如果|a+3|=1，那么a= ．12．将⽅程1111124396x x x x +++=去分母后得到⽅程________． 13．(黔东南州)在有理数范围内定义⼀种运算“※”，其规则为a ※b ＝a -b ．根据这个规则，求⽅程(x -2)※1＝0的解为________．14．⼀列长为150m 的⽕车，以15m/s 的速度通过600m 的隧道，则这列⽕车完全通过此隧道所需时间是________s ．三、解答题15．解下列⽅程：(1)4(2x -1)-3(5x+2)＝3(2-x )；(2)12323x x x ---=-； (3)0.10.2130.020.5x x -+-= ． 16.（2015春?宜阳县期中）当k 取何值时，关于x 的⽅程2（2x ﹣3）=1﹣2x 和8﹣k=2（x+）的解相同？17．⼩明的练习册上有⼀道⽅程题，其中⼀个数字被墨汁污染了，成为31155x x ++?=-，他翻看了书后的答案，知道了这个⽅程的解是14，于是他把被污染了的数字求出来了，请你把⼩明的计算过程写出来．【答案与解析】⼀、选择题1.【答案】C.【解析】由题意，2x ﹣1=2，或2x ﹣1=﹣2，解这两个⽅程得：x=，或x=﹣2. 【答案】A【解析】A 中移项未改变符号．3. 【答案】C【解析】系数化为1，两边同乘以4即可．4. 【答案】D【解析】A 中，去掉第1个括号时第⼆项漏乘，去掉第2个括号时，-3没变号；B 中，去掉第1个括号时第⼆项漏乘；C 中，去掉第2个括号时，-3没变号．5．【答案】C【解析】A 中，去分母时3没有乘以2，-1没变号；B 中，去分母时-1没变号；D 中，等号右边0乘以2应是0，⽽不应是2．6．【答案】A【解析】-3x-12与13-互为倒数，所以3x -12＝-3，x ＝3． 7. 【答案】C【解析】两边同乘以6得：2(21)(101)6x x +-+=，再去括号得：421016x x +--=．8. 【答案】B【解析】设有x 盏，则有(1)x -个灯距，由题意可得：36(1061)70(1)x -=-，解得：55x =．⼆、填空题9．【答案】(1)等式性质1，移项； (2)等式性质2，除以-3， 53-10．【答案】k ＝-6【解析】将1x =-代⼊得：2152k -++=--，解得：6k =-．11.【答案】﹣2或﹣4．【解析】∵|a+3|=1，∴a+3=1或a+3=﹣1，∴a=﹣2或﹣4．12．【答案】43x ＝6【解析】将⽅程两边乘以36，得18x+9x+12x+4x ＝6．13．【答案】x ＝3【解析】根据规则得：x -2-1＝0，x ＝3．14．【答案】50 【解析】6001505015+=(秒) ．三、解答题15．【解析】解：(1)8x -4-15x -6＝6-3x8x -15x+3x ＝6+4+6-4x ＝16x ＝-4(2)12323x x x ---=- 6x -3(1-x )＝18-2(x -2)11x ＝252511x = (3)原⽅程可化为：10201010325x x -+-=，约分得：5x -10-(2x+2)＝3，去括号得5x -10-2x -2＝3，移项及合并，得3x ＝15，系数化为1，得x ＝5．16.【解析】解2（2x ﹣3）=1﹣2x ，得x=，把x=代⼊8﹣k=2（x+），得8﹣k=2（+），解得k=4，当k=4时，关于x 的⽅程2（2x ﹣3）=1﹣2x 和8﹣k=2（x+）的解相同．17．【解析】解：将14x =代⼊，得： 113144155++=-．解得：3?=．所以被污染的数字为3．。

一元一次方程巩固练习一、选择题1.方程1x a +=与方程2213+=-x x 的解相同，则a 的值为（ ）A. 3 B . －3 C. －2 D. 22.关于x 的方程143+=+x ax 的解为正整数，如a 也为正整数，则a 的值为 ( )A 、2B 、3C 、1或2D 、2或33.下列方程中是一元一次方程的是( )A ．23x y =B ．()7561x x +=-C ．()21112x x +-=D ．12x x-= 4.方程532=+x ，则106+x 等于（ ） A.15 B.16 C.17 D.345.要使多项式221231002x kxy y xy x --+--中不含xy 的项，则k 应取（ ） A.1 B.1- C.14- D.146.方程｜3x ｜= 18 的解的情况是（ ）A.6B. ±6C.无解D.有无数个解7.若2a 和1-a 互为相反数，则a 的值是A.1B. ±1C.-1D.28.海信牌电视机原价a 元，今年降价x% ，则今年的价格是（ ）A. ax%B. a - x%C.a(1-x)D. a(1-x%)9.下列等式变形正确的是（ ）A. 如果12s ab =，那么 2s b a =B. 如果162x =，那么 3x = C. 如果x-3 = y-3，那么 x-y = 0 D. 如果mx = my ，那么x = y10.电视机售价连续两次降价10％，降价后每台电视机的售价为a 元，则该电视机的原价为（ ）A. 0.81a 元B. 1.21a 元C. 21.1a 元 D. 81.0a 元11.某商店卖出两件衣服，每件60元，其中一件赚25%，另一件亏25%，那么这两件衣服卖出后，商店是( )A .不赚不亏B .赚8元C .亏8元D . 赚8元12.已知等式523+=b a ，则下列等式中不一定．．．成立的是（ ） A .;253b a =- B .;6213+=+b a C .;523+=bc ac D ..3532+=b a 13.儿子今年12岁，父亲今年39岁，（ ）父亲的年龄是儿子的年龄的4倍.A .3年后；B .3年前；C .9年后；D .不可能.14.足球是由32块黑白相间的牛皮缝制而成的，其中黑皮可看作正五边形，白皮可看作正六边形，黑、白皮块的数目比为3:5，要求出黑皮、白皮的块数，若设黑皮的块数为x ，则列出的方程正确的是（ ）A .;323x x -=B .();3253x x -=C .();3235x x -=D ..326x x -=15.珊瑚中学修建综合楼后，剩有一块长比宽多5m 、周长为50m 的长方形空地. 为了美化环境，学校决定将它种植成草皮，已知每平方米草皮的种植成本最低是a 元，那么种植草皮至少需用（ ）A .a 25元；B .a 50元；C .a 150元；D .）a 250元.二、填空题1．若m 使得代数式21(36)m --取得最大值，则关于x 的方程54321m x -=+的解是_____2．小李在解方程135=-x a （x 为未知数）时，误将x -看作x +，解得方程的解2-=x ，则原方程的解为______．3．已知等式0352=++m x 是关于x 的一元一次方程，则m =_______．4．已知方程()7421=+--m x m 是关于x 的一元一次方程，则m=______ ． 5．已知等式2(2)10a x ax -++=是关于x 的一元一次方程，则这个方程的解为____6．已知｜m ＋4－n ｜＋（n －2）2 ＝0，则m ＝_____ ，n ＝______7．方程（m ＋2）2＋｜n －1｜＝0，则3m －5n ＝_____．8．若x=1时，代数式ax 3＋bx ＋1的值为5，则x=－1时，代数式ax 3＋bx ＋1的值等于_____9．已知关于x 的方程3x －2m = 4的解是x = m ，则m 的值是___10．已知三个连续的偶数的和是60，则这三个数是_____________11．若｜a ｜= 3，且2a+b=0 则b 的值是_____________12．若4a-9与3a-5互为相反数，则 a 2-2a+1的值为____________13．某数的3倍比它的一半大2，若设某数为y ，则列方程为___________14．国庆期间，“新世纪百货”搞换季打折. 简爽同学以8折的优惠价购买了一件运动服节省16元，那么他购买这件衣服实际用了___________元.三、探究题1、先阅读下列解题过程，然后解答问题（1）、（2）解方程：｜x+3｜=2解：当x+3≥0时，原方程可化为：x+3=2，解得x=-1当x+3＜0时，原方程可化为：x+3=-2，解得x=-5所以原方程的解是x=-1，x=-5（1）解方程：｜3x-2｜-4=0（2）探究：当b 为何值时，方程｜x-2｜=b+1 ① 无解；②只有一个解；③ 有两个解.一元一次方程巩固练习参考答案一、选择题1.C.2.D3.B4.B5.D6.B7.C8.D9.C 10.D 11.C 12.C 13. B 14.C 15.C二、填空题x 3．m= -1 4．m = 0 5．x = 1/2 6．m＝-2，n＝2 7．-111．x = -5 2．28．－3 9．m的值是4（把x = m代入）10．18、20、2211．±612．1 13．3y - 1/2y = 2 14．64。

初一数学一元一次方程知识梳理与练习巩固第二讲 一元一次方程✍知识网络1.定义：在一个方程中,如果只含有一个未知数，且未知数的最高次数是1的整式方程叫做一元一次方程。

（linear equation in one ）一般形式：ax+b=0（a 、b 为常数，a ≠0）。

一元一次方程只有一个解。

一元一次方程的最终结果(方程的解)是x=a 的形式2.性质：一元一次方程的“等式的性质1”和“等式的性质2” 1）.等式两边同时加或减一个相同数，等式两边相等。

（如果a=b ，那么a ±c=b ±c 。

）2）.等式两边同时乘或除以一个相同数（0除外），或一个整式,等式两边相等。

（如果a=b ，那么ac=bc 。

如果a=b ，c ≠0，那么a/c=b/c 。

）解法是通过移项将未知数移到一边，再把常数移到一边(等式基本性质1，注意符号!)，然后两边同时除以未知数系数(化系数为1,等式基本性质2)，即可得到未知数的值。

3.一般解法：1）去分母 方程两边同时乘各分母的最小公倍数。

2）去括号 一般先去小括号，在去中括号，最后去大括号。

但顺序有时可依据情况而定使计算简便。

可根据乘法分配律。

3）移项 把方程中含有未知数的项移到方程的另一边，其余各项移到方程的另一边移项时别忘记了要变号。

4）合并同类项 将原方程化为ax=b(a ≠0)的形式。

5）系数化1 方程两边同时除以未知数的系数，得出方程的解。

✍例题精选例1.3 1.50.2x --0.20.10.03x -=2.5例2．解方程：312-x -12110+x =412+x -1例3.已知关于x 的方程3a-x=2x +3的解是4，则（-a ）2-2a ＝ 例4.当m= 时，方程5x+4=4x-3和方程2(x+1)-m=-2(m-2)的解相同；当n= 时，代数式4n+8与3n-10的值互为相反数。

例5.已知关于x 的方程2a(x-1)=(5-a)x+3b 有无数多解，试求a 、b 的值。