受力分析--力的计算
- 格式:dps
- 大小:1.20 MB
- 文档页数:44

有限元受力分析–结构梁-力-计算1. 前言受力分析是工程设计中至关重要的一环,能够帮助工程师完善设计并避免安全事故的发生。
在此,我们将介绍有限元受力分析在结构梁设计中的应用。
本文将重点讲解有限元受力分析的相关理论和计算方法。
2. 有限元受力分析有限元分析是数值计算的一种方法,可用于解决工程中的受力分析问题。
它把结构离散为有限个单元,然后对每个单元进行分析。
有限元分析可分为线性有限元分析和非线性有限元分析两种类型。
本文我们只讨论线性有限元分析。
在有限元分析中,结构被分解为离散的单元,每个单元都是基于解析解的一部分。
有限元的形状、尺寸和材料属性可以通过计算机程序进行定义。
使用数学模型和有限元方法,可以计算单元的应力、变形和应变,从而进行结构的受力分析。
3. 结构梁结构梁相信大家应该都知道,它是工程中最为常用的结构之一。
它具有一定的强度和刚度,可以支撑和传递载荷。
一般来说,结构梁通常由简单的杆件单元组成。
在进行结构梁受力分析时,我们需要考虑弯曲、剪切和挤压等不同形式的载荷,以及结构在工作条件下的应变和应力分布情况。
有限元受力分析对于这些问题的研究提供了很好的解决方案。
4.力的分析在受力分析中,载荷是非常关键的参数。
载荷可以是点载荷、均布载荷、集中荷载等。
在本文中,我们将分别介绍这些载荷类型的有限元分析方法。
4.1 点载荷分析点载荷通常是一个单点受到的载荷。
对于点载荷的有限元分析,我们可以通过构建一个网格模型,然后将点载荷作用在网格的节点上。
此外,还需要设定材料的弹性模量和截面的截面面积,以计算结构的应力和变形。
需要注意的是,点载荷分析过程中的网格划分应当尽量精细,以达到更为优秀的数值精度。
4.2 均布载荷分析均布载荷是沿着梁的长度方向均匀分布的载荷,例如一根梁的自重、荷载等。
在进行均布载荷的有限元分析时,我们可以在网格的中央位置放置均布载荷,然后将梁的边缘节点设置为固定的约束条件。
同样,需要设定材料的弹性模量和截面的截面面积以计算结构的应力和变形。

受力分析方法受力分析是工程力学中的重要内容,它是研究物体受到外部力作用时的力学性质和运动规律的一门学科。
受力分析方法是为了解决物体受力情况而进行的一系列分析和计算过程,它可以帮助工程师和设计师更好地理解和预测物体的受力情况,从而指导工程设计和实际施工。
在工程实践中,受力分析方法具有非常重要的意义,下面将介绍几种常用的受力分析方法。
首先,静力学方法是最基本的受力分析方法之一。
静力学是研究物体在静止状态下受力平衡的学科,它通过平衡方程和力的平衡条件来分析物体受力情况。
静力学方法适用于解决物体受力平衡的问题,例如梁、柱、桁架等结构的受力分析。
在实际工程中,静力学方法可以帮助工程师计算物体受力的大小、方向和作用点位置,为工程设计提供重要参考。
其次,有限元分析方法是一种现代化的受力分析方法。
有限元分析是利用计算机对物体进行离散建模,通过数值计算方法求解物体受力情况的一种技术。
有限元分析方法适用于复杂结构和大变形情况下的受力分析,它可以模拟物体受到外部力作用后的变形和应力分布情况,为工程设计和结构优化提供科学依据。
另外,试验分析方法是一种重要的受力分析手段。
试验分析是通过对物体进行实验测试,获取物体受力情况的一种方法。
试验分析方法可以直接观测和测量物体在受力状态下的变形和应力情况,为工程师提供真实可靠的受力数据。
试验分析方法在工程实践中具有重要的应用,例如对材料的拉伸试验、结构的载荷试验等。
最后,有限差分法和有限体积法是一种数值分析方法,它们适用于求解物体受力情况的偏微分方程。
有限差分法和有限体积法通过离散化偏微分方程,将连续的受力问题转化为离散的代数方程,然后利用数值计算方法求解物体的受力情况。
这两种方法在流体力学、固体力学等领域有着广泛的应用,可以帮助工程师分析复杂的受力情况。
总之,受力分析方法是工程力学中的重要内容,它对工程设计和实际施工具有重要的指导作用。
不同的受力分析方法适用于不同的受力情况,工程师需要根据实际问题选择合适的受力分析方法,进行科学准确的受力分析。

结构内力计算分析案例以下是一个关于结构内力计算分析的案例,以帮助读者更好地理解该过程。
案例:栋多层住宅楼的楼板结构受力分析和计算。
1.结构描述:该楼为一栋钢筋混凝土框架结构的多层住宅楼,楼高5层,每层高度为3米。
楼板采用承重梁和板的形式,梁间距为6米,梁宽为0.3米。
2.受力分析:根据力学原理,梁和板在受力作用下会产生内力。
梁的受力情况分为竖向和横向两个方向:-竖向受力:竖向受力主要包括自重、活载和楼层间的等分荷载。
自重一般按照材料密度计算,活载是指居住者的活动荷载,楼层间的等分荷载指的是各个楼层产生的附加荷载。
-横向受力:横向受力主要包括风荷载和地震荷载。
这些荷载会通过墙体和梁传递到结构内部。
3.内力计算:根据受力分析结果,可以进行结构内力的计算。
具体计算方法有两种:静力分析和弹性力学方法。
-静力分析:这是一种通过平衡受力和力矩的方法进行计算的方法。
根据平衡条件,可以得到各个构件的内力。
-弹性力学方法:这是一种通过应力和应变的关系进行计算的方法。
根据材料力学性质和结构的几何形状,可以计算出各个构件的内力。
4.结果分析和验证:计算得到的结构内力结果需要进行分析和验证。
主要包括两个方面:构件强度和位移。
-构件强度:计算得到的内力和构件的截面尺寸一起,可以判断构件是否满足强度要求。
如果内力超过了构件材料的承载力,需要进行加固。
-位移:根据结构内力和材料的弹性模量,可以计算出结构的位移。
结构的位移应该满足设计的要求,如果超过了预定的限值,需要进行刚度调整。
总结:结构内力计算分析是工程的关键环节,其目的是保证结构的安全性和可靠性。
通过对不同构件的受力分析和力学计算,可以得到结构的内力结果,并进行分析和验证。
这样可以确保结构的设计和施工符合规范,并达到预期的使用寿命和性能要求。

杆件的受力分析与计算杆件是广泛应用于各种工程领域的构件,承载着复杂的受力和力学挑战。
在设计和计算杆件时,准确的受力分析是至关重要的。
本文将介绍杆件的受力分析与计算方法,以及一些常见的杆件受力计算案例。
一、杆件受力分析方法1. 自由体图法自由体图法是一种基本的受力分析方法,通过将杆件从主体结构中分离出来,将外力和内力表示在图上,利用平衡条件进行力的计算。
首先,需要选择合适的自由体图方案,通常选择具有对称性或受力简单的自由体图。
然后,根据平衡条件,在自由体图上标示出支持反力和外载荷。
最后,根据力的平衡条件,确定杆件内部的受力分布。
2. 叠加法叠加法是一种常用的受力分析方法,将外力拆解为多个简单的力,并分别计算各个力对杆件的影响。
叠加法适用于受力复杂、存在多个外力作用的杆件。
首先,将外力按照需要的方向和大小进行分解,得到各个简单力。
然后,通过计算各个简单力对杆件产生的受力和力偶,求解最终受力分布。
3. 假设法假设法是在力学分析中常用的方法之一,通过假设杆件中某些部分受力的方式,并进行受力计算。
假设法适用于复杂的受力情况,通过合理的假设可以简化问题的复杂性。
在假设法中,需要合理选择假设的受力方式,并根据受力平衡条件进行计算。
二、杆件受力计算案例1. 杆件的拉伸和压缩对于受到拉伸或压缩的杆件,可以根据杨氏模量和截面面积计算受力。
首先,根据受力方向和大小选择合适的杆件横截面积。
然后,根据应变-应力关系确定杆件的应力。
最后,通过应力和截面积的乘积计算出杆件所受的力。
2. 杆件的弯曲对于受到弯曲的杆件,计算受力需要考虑弯矩和截面惯性矩。
首先,利用受力分析方法确定弯矩的大小和分布。
然后,计算出截面的惯性矩。
最后,根据杆件的材料性质和几何特征,计算弯曲应力和弯曲力。
3. 杆件的剪切对于受到剪切力的杆件,计算受力需要考虑剪切应力和截面剪切面积。
首先,根据剪切力的大小和方向确定剪切应力的分布。
然后,计算出截面的剪切面积。


杆件受力分析杆件的内力计算和受力平衡杆件受力分析是工程力学中一个重要的内容,能够帮助我们了解和计算杆件内力以及保证杆件的受力平衡。
本文将介绍杆件受力分析的基本概念和计算方法,并根据实际例子进行说明和分析。
一、杆件受力分析概述杆件,指的是工程结构中的长条形构件,常用于支撑和传递力量。
在实际应用中,杆件往往会受到多方向的力的作用,因此需要进行受力分析,计算出杆件内部的力,以保证其受力平衡。
在进行杆件受力分析时,我们需要明确以下几个概念:1. 受力点:指的是外力作用到杆件上的点,也是进行受力分析的起点。
2. 内力:指的是杆件内部存在的力,可以是拉力或压力。
3. 受力平衡:指的是杆件上所有受力的合力和合力矩为零的状态,保证了杆件受力的平衡。
二、杆件内力计算方法1. 自由体图法:自由体图法是杆件受力分析的基本方法,通过将杆件与外界切割开来,分析切割面上的受力情况,进而计算出杆件内力。
过程:选择合适的切割面,画出自由体图,分析受力平衡条件,解方程计算内力。
2. 杆件法:杆件法是将整个杆件视为一个整体,通过利用杆件的几何关系和受力条件进行计算。
过程:根据杆件的几何形状和受力情况,建立方程组求解。
三、杆件受力分析实例为了更好地理解和应用杆件受力分析的方法,下面以一个实际例子进行说明:假设有一根长度为L的杆件,一端固定在墙上,另一端悬挂一个质量为m的物体。
我们需要计算杆件的内力以及保证受力平衡。
首先,我们选择杆件的中点作为切割面,并画出自由体图。
根据受力平衡条件,我们可以得出以下方程:∑Fx = 0: T - F = 0 (水平方向受力平衡)∑Fy = 0: N - mg = 0 (竖直方向受力平衡)其中,T代表杆件的张力,F代表杆件所受悬挂物体的重力,N代表杆件与墙壁接触点的支撑力,g代表重力加速度。
通过解以上方程组,我们可以计算出T和N的数值,进而得到杆件内部的力。
根据实际情况,可以通过杆件截面积和材料的力学性质,计算出杆件的应力和变形情况。

如何计算物体在重力作用下的受力分析?
计算物体在重力作用下的受力分析是一个基础但重要的物理问题。
首先,我们需要明确物体所受的重力。
重力是由于地球的吸引而使物体受到的力,单位是牛顿(N),也可以用地球的质量和物体的质量来计算。
其次,我们需要考虑物体的质量。
物体的质量是物体所含物质的量,单位是千克(kg)。
在地球上,物体的质量可以通过使用精密的测量仪器来测量,也可以通过物体的重量和重力加速度来计算。
接下来,我们需要计算物体所受的重力。
物体所受的重力可以用以下的数学公式表示:F = G * m1 * m2 / r^2,其中F是物体所受的重力,G是地球的质量,m1是地球的质量,m2是物体的质量,r是地球和物体之间的距离。
这个公式也说明了重力与物体质量的平方成正比,与地球和物体之间的距离的平方成反比。
最后,我们需要考虑物体的加速度。
在地球上,物体的加速度总是向下的,大小约为9.8m/s^2。
如果物体在静止状态下释放,那么它将以9.8m/s^2的加速度向下加速。
如果物体在空中自由落体时受到空气阻力的影响,那么它的加速度将会减小。
综上所述,计算物体在重力作用下的受力分析需要考虑物体的质量、地球的质量、物体和地球之间的距离以及物体的加速度等因素。
通过这些因素的计算和分析,我们可以更好地理解物体在重力作用下的运动规律和受力情况。

物体的受力分析与力矩的计算在物理学中,物体的受力分析与力矩的计算是解决力学问题的基础。
通过分析物体所受的力和力矩,我们可以了解物体的运动状态和力的作用方式。
下面将重点讨论物体的受力分析和力矩的计算方法。
一、物体的受力分析物体在运动或静止状态下受到的力可以分为几种类型,包括重力、摩擦力、弹力等。
为了描述物体所受力的性质和情况,我们需要进行受力分析。
首先,重力是物体受到的基本力之一。
在地球表面上,物体的重力可以用公式F = mg进行计算,其中F为物体所受的重力,m为物体的质量,g为重力加速度。
重力的方向垂直于地面向下。
其次,摩擦力是在物体与其他物体接触时产生的力。
摩擦力分为静摩擦力和动摩擦力两种类型。
静摩擦力是物体在静止状态下受到的力,动摩擦力是物体在运动状态下受到的力。
摩擦力的大小取决于物体之间的接触面积和表面的粗糙程度。
再次,弹力是物体被压缩或拉伸时产生的力。
当物体发生形变时,弹性力会使物体进行恢复。
弹力的大小与物体的形变量成正比。
除了上述力之外,物体还可能受到其他外力的作用,如空气阻力、浮力等。
根据具体情况,我们可以将这些力纳入受力分析中。
二、力矩的计算力矩是描述力对物体产生转动效果的物理量。
当一个力作用在物体上时,它会产生一个力矩,力矩的大小与力的大小、力的作用点到旋转轴的距离以及力与旋转轴之间的夹角有关。
力矩可以通过以下公式进行计算:τ = F × d × sinθ,其中τ为力矩,F为力的大小,d为力作用点到旋转轴的距离,θ为力与旋转轴之间的夹角。
当力矩为正值时,表示力会引起物体逆时针方向的转动;当力矩为负值时,表示力会引起物体顺时针方向的转动。
在静力学中,力矩的平衡条件是力矩的合为零。
当物体处于平衡状态时,所受的力矩总和为零,即∑(τ) = 0。
根据这个条件,我们可以解决平衡物体上力的大小、方向和作用点等问题。
总结物体的受力分析与力矩的计算是力学中的重要内容。
通过对物体所受力的分析,可以了解物体的运动状态和力的作用方式,而力矩的计算则可以帮助我们解决平衡问题。

静力学平衡状态下物体受力的分析与计算在静力学中,平衡是指一个物体处于静止状态或者匀速直线运动状态下,其受力合力为零的状态。
而静力学平衡状态下,物体的受力情况可以通过受力分析和计算来确定。
本文将就静力学平衡状态下物体受力的分析与计算进行探讨。
一、问题引入在物体处于静力学平衡状态下时,其受力情况可以通过作用在物体上的外力以及物体本身的重力来描述。
为了方便分析与计算,我们通常将外力分为水平方向的力和垂直方向的力。
二、受力分析在进行受力分析时,我们首先需要明确物体所受到的所有外力和重力的大小、方向以及作用点位置。
接下来,我们可以将这些受力以矢量的形式表示出来,并进行合力分解。
1. 合力分解对于物体所受到的多个力,我们可以将其分解为水平力和垂直力。
通过合力分解,我们可以得到水平方向上的合力以及垂直方向上的合力。
2. 力的平衡条件在静力学平衡状态下,物体所受的水平力和垂直力的合力都必须为零。
即所有水平方向上的力合力为零,所有垂直方向上的力合力为零。
根据这个原理,我们可以得到静力学平衡的两个基本条件:(1)∑F_horizo ntal = 0:物体受到的所有水平方向的力合力为零。
(2)∑F_vertical = 0:物体受到的所有垂直方向的力合力为零。
三、受力计算一旦我们完成了受力分析,我们就可以进行受力计算,并求解静力学平衡状态下物体所受到的各个力的大小。
1. 力的计算对于物体所受到的各个力,我们可以通过力的计算公式或者力的分解来求解其大小。
2. 力的方向在求解力的大小之后,我们还需要确定力的方向。
根据受力分析的结果,我们可以发现物体所受到的力的方向往往与物体所受到的支撑或者施力对象有关。
3. 力的作用点除了力的大小和方向外,力的作用点也是非常重要的。
力的作用点决定了力矩的大小,是静力学计算的关键。
四、力矩的计算对于物体所受到的力,除了进行合力分解和力的计算外,我们还可以通过力矩的计算来获得更多的受力信息。

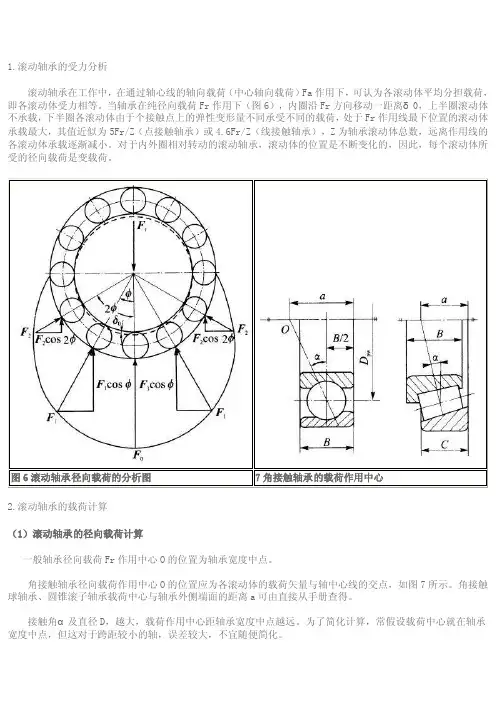
1.滚动轴承的受力分析滚动轴承在工作中,在通过轴心线的轴向载荷(中心轴向载荷)Fa作用下,可认为各滚动体平均分担载荷,即各滚动体受力相等。
当轴承在纯径向载荷Fr作用下(图6),内圈沿Fr方向移动一距离δ0,上半圈滚动体不承载,下半圈各滚动体由于个接触点上的弹性变形量不同承受不同的载荷,处于Fr作用线最下位置的滚动体承载最大,其值近似为5Fr/Z(点接触轴承)或4.6Fr/Z(线接触轴承),Z为轴承滚动体总数,远离作用线的各滚动体承载逐渐减小。
对于内外圈相对转动的滚动轴承,滚动体的位置是不断变化的,因此,每个滚动体所受的径向载荷是变载荷。
2.滚动轴承的载荷计算(1)滚动轴承的径向载荷计算一般轴承径向载荷Fr作用中心O的位置为轴承宽度中点。
角接触轴承径向载荷作用中心O的位置应为各滚动体的载荷矢量与轴中心线的交点,如图7所示。
角接触球轴承、圆锥滚子轴承载荷中心与轴承外侧端面的距离a可由直接从手册查得。
接触角α及直径D,越大,载荷作用中心距轴承宽度中点越远。
为了简化计算,常假设载荷中心就在轴承宽度中点,但这对于跨距较小的轴,误差较大,不宜随便简化。
图8角接触轴承受径向载荷产生附加轴向力1)滚动轴承的轴向载荷计算当作用于轴系上的轴向工作合力为FA,则轴系中受FA作用的轴承的轴向载荷Fa=FA,不受FA作用的轴承的轴向载荷Fa=0。
但角接触轴承的轴向载荷不能这样计算。
角接触轴承受径向载荷Fr时,会产生附加轴向力FS。
图8所示轴承下半圈第i个球受径向力Fri。
由于轴承外圈接触点法线与轴承中心平面有接触角α,通过接触点法线对轴承内圈和轴的法向反力Fi将产生径向分力Fri;和轴向分力FSi。
各球的轴向分力之和即为轴承的附加轴向力FS。
按一半滚动体受力进行分析,有FS ≈ 1.25 Frtan α(1)计算各种角接触轴承附加轴向力的公式可查表5。
表中Fr为轴承的径向载荷;e为判断系数,查表6;Y 为圆锥滚子轴承的轴向动载荷系数,查表7。
受力分析步骤【受力分析】受力情况决定运动情况,要研究物体的运动,必须首先搞清物体的受力情况。
正确分析物体的受力情况,是研究力学问题的关键,是必须掌握的基本功。
1.分析方法:进行受力分析的基本方法是隔离体法,即将所选定的研究对象(一般是一个物体,也可以是几个物体构成的整体)从它所处的环境中隔离出来,然后依次分析环境中的物体对所选定的研究对象施加的力。
分析的依据,一是力的性质和各种力的产生条件;二是物体的运动状态即从共点力的平衡条件和牛顿第二定律入手分析。
下边是受力分析常用的一些辅助方法。
(1)整体法:即选择几个物体构成的整体作为研究对象,既可用于研究整体的受力,也可作为分析某个物体受力情况的辅助方法。
如(例一)。
(2)假设法:即在某个力的有无或方向不容易判断时,可先假设这个力不存在,看物体的运动会受什么样的影响,从而得出结论。
如分析弹力可用假设拿开法,分析静摩擦力可用假设光滑法等。
(3)利用牛顿第三定律分析。
(4)画出物体的受力示意图,这样会使问题形象直观。
在不涉及转动问题时,一般要将力的作用点平移到物体的重心上来,示意图不但要表示力的方向,还要定性表示力的大小。
图画的越准确,越便于分析解决问题。
2.一般步骤:(1)选定研究对象;(2)依次分析重力、已知力(外界施加的拉力、推力等)、场力;(3)利用隔离体法依次分析和研究与对象相接触的物体对它是否施加弹力或摩擦力。
之所以这样安排分析顺序,主要考虑到“2”中的力是主动力,而弹力和摩擦力是被动力。
注意事项:(1)合力和分力不能重复的列为物体所受的力。
分析物体的受力情况一般只分析实际力,在分析具体问题列方程时,合力和分力作为一种等效替代的手段不能重复考虑。
(2)要把握好研究对象,不要将研究对象对其它物体的力纳入,即只研究它的受力情况。
(4)然后要做一番检查,看每个力是否存在施力物体,受力情况是否和物体的运动状态相矛盾。
【例题精析】思考拓宽:解法二,取A、B整体为研究对象,因为整体在水平方向不受其它力,所以它也不受地面的摩擦力。
考点05 受力分析(三)——力的大小的计算1.掌握力的计算公式2.掌握求解平衡问题中力的大小的两种方法(矢量三角形、正交分解法)3.掌握求解非平衡问题中力的大小方法4.能利用牛顿第三定律求解力的大小力大小的计算主要有三种方法:公式法、力学方程、牛顿第三定律,这三种计算力的大小方法中,采用运动状态寻找力学关系,列方程式求解这一类型(第二类)的题目较多,本专题也是重在强化这一类型的训练。
具体情况如下:(一)公式法(二)结合运动状态,采用力学方程计算1.平衡状态(1)平衡状态的类型:①匀速运动;②静止;(2)平衡状态下物体的受力特点:F合=0(3)处理方法①矢量三角形:若物体受到三个力F 1、F 2、F 3处于平衡状态,一般采用矢量三角形中的三角函数来表示各个力的关系②正交分解法:若物体受到多个力F 1、F 2、F 3…F n 处于平衡状态,一般采用正交分解法,可列出的力学方程为: 在x 轴,ΣF X =0;在y 轴,ΣFX =02.非平衡状态非平衡状态求力的大小的解决方法多数情况下采用正交分解法,物体在非平衡状态对应的坐标轴上的力学方程为:F 合=ma(三)利用牛顿第三定律计算计算力的大小时可以采用作用力与反作用力的规律,通过转换受力对象来求解力的大小例1.(2019·原创经典)如图所示,光滑半球形容器固定在水平面上,O 为球心.一质量为 m 的小滑块,在水平力 F 的作用下静止于P 点,OP与水平方向的夹角为θ.则( )A.推力F 大小为mg/tanθB.推力F 大小为mgtanθC.若推着物体向上匀速滑动,F N 增大D.若推着物体向上匀速滑动,F N 将减小【答案】 AC【解析】本题考查应用矢量三角形、动态三角形解决平衡问题由题意可知,小滑块处于平衡状态,且它受力个数为3个,可采用矢量三角形来表示三个力间的力学关系。
滑块的受力示意图如图1,将三个力平移后构成下图2虚线所示的矢量三角形,则推力F 与重力的力学关系为:tanθ=mg/F ,所以F=mg/tanθ,A 对,B 错;若推着物体向上滑动,矢量三角形的最右端的顶点将沿水平虚线向右移动,FN 、F 对应的边在增大,所以FN 、F 两个力均增大,C 对,D 错。
梁的受力分析与计算梁是一种常见的结构,在建筑工程和机械设计中被广泛应用。
对于梁的受力分析与计算,可以通过数学方法和力学原理进行有效求解。
本文将从基本原理、受力分析、应力求解和变形计算等方面,对梁的受力分析与计算进行详细介绍。
一、基本原理在进行梁的受力分析与计算前,我们首先需要了解一些基本原理。
梁的力学性质由两个主要方面组成:受力分析和变形计算。
受力分析是指对梁的内力分布进行分析,包括弯矩、剪力和轴力等。
变形计算是指对梁的纵向与横向变形进行计算,包括挠度和切变变形等。
二、受力分析1. 弯矩分析梁在受到外力作用时,会产生弯曲变形,形成弯矩。
根据梁的几何形状和外力情况,可以通过弯矩图和弯矩计算公式来进行弯矩分析。
弯矩的大小和分布对梁的受力性能和承载能力有重要影响。
2. 剪力分析剪力是指梁受到垂直于轴线方向的内力作用所引起的剪切应力。
剪力分析可以通过剪力图和剪力计算公式进行求解。
剪力的大小和分布对梁的稳定性和强度具有重要影响。
3. 轴力分析轴力是指梁受到沿轴线方向的内力作用所引起的轴向应力。
轴力分析可以通过轴力图和轴力计算公式进行求解。
轴力的大小和分布对梁的承载能力和变形性能具有重要影响。
三、应力求解在进行梁的受力分析时,除了要对弯矩、剪力和轴力进行计算外,还需要对梁的应力进行求解。
应力是指梁内外部形成的力与横截面积的比值,反映了梁内部的受力状态。
当梁受到外力作用时,会在横截面产生不同的应力分布,包括正应力、剪应力和轴向应力等。
四、变形计算在进行梁的受力分析与计算时,除了要考虑梁的内力分布和应力情况外,还需要对梁的变形进行计算。
梁在受到外力作用时,会产生不同形式的变形,包括弯曲变形、挠度和切变变形等。
这些变形对梁的受力性能和使用寿命有一定影响,需要进行相应的计算和分析。
五、实例分析以下是一个简单的梁实例,通过对这个实例进行受力分析和计算,可以更好地理解梁的受力性能。
假设梁的长度为L,宽度为b,高度为h,材料的弹性模量为E,弯矩M作用在梁的中心位置。
螺栓组受力分析与计算之迟辟智美创作一.螺栓组联接的设计设计步伐:1.螺栓组结构设计2.螺栓受力分析3.确定螺栓直径4.校核螺栓组联接接合面的工作能力5.校核螺栓所需的预紧力是否合适确定螺栓的公称直径后,螺栓的类型,长度,精度以及相应的螺母,垫圈等结构尺寸,可根据底板的厚度,螺栓在立柱上的固定方法及防松装置等全面考虑后定出.1. 螺栓组联接的结构设计螺栓组联接结构设计的主要目的,在于合理地确定联接接合面的几何形状和螺栓的安插形式,力求各螺栓和联接接合面间受力均匀,便于加工和装配.为此,设计时应综合考虑以下几方面的问题:1)联接接合面的几何形状通常都设计成轴对称的简单几何形状,如圆形,环形,矩形,框形,三角形等.这样不单便于加工制造,而且便于对称安插螺栓,使螺栓组的对称中心和联接接合面的形心重合,从而保证接合面受力比力均匀.2)螺栓的安插应使各螺栓的受力合理.对铰制孔用螺栓联接,不要在平行于工作载荷的方向上成排地安插八个以上的螺栓,以免载荷分布过于不均.当螺栓联接接受弯矩或转矩时,应使螺栓的位置适当靠近联接接合面的边缘,以减小螺栓的受力(下图).如果同时接受轴向载荷和较年夜的横向载荷时,应采纳销,套筒,键等抗剪零件来接受横向载荷,以减小螺栓的预紧力及其结构尺寸.接合面受弯矩或转矩时螺栓的安插3)螺栓排列应有合理的间距,边距.安插螺栓时,各螺栓轴线间以及螺栓轴线和机体壁间的最小距离,应根据扳手所需活动空间的年夜小来决定.扳手空间的尺寸(下图)可查阅有关标准.对压力容器等紧密性要求较高的重要联接,螺栓的间距t0不得年夜于下表所推荐的数值.扳手空间尺寸螺栓间距t0注:表中d为螺纹公称直径.4)分布在同一圆周上的螺栓数目,应取成4,6,8等偶数,以便在圆周上钻孔时的分度和画线.同一螺栓组中螺栓的资料,直径和长度均应相同.5)防止螺栓接受附加的弯曲载荷.除要在结构上设法保证载荷不偏心外,还应在工艺上保证被联接件,螺母和螺栓头部的支承面平整,并与螺栓轴线相垂直.对在铸,锻件等的粗拙概况上应装置螺栓时,应制成凸台或沉头座(下图1).当支承面为倾斜概况时,应采纳斜面垫圈(下图2)等.图1 凸台与沉头座的应用图2 斜面垫圈的应用2. 螺栓组联接的受力分析1).受横向载荷的螺栓组联接2).受转矩的螺栓组联接3).受轴向载荷的螺栓组联接4).受倾覆力矩的螺栓组联接进行螺栓组联接受力分析的目的是,根据联接的结构和受载情况,求出受力最年夜的螺栓及其所受的力,以便进行螺栓联接的强度计算.为了简化计算,在分析螺栓组联接的受力时,假设所有螺栓的资料,直径,长度和预紧力均相同;螺栓组的对称中心与联接接合面的形心重合;受载后联接接合面仍坚持为平面.下面针对几种典范的受载情况,分别加以讨论.1).受横向载荷的螺栓组联接图所示为一由四个螺栓组成的受横向载荷的螺栓组联接.横向载荷的作用线与螺栓轴线垂直,并通过螺栓组的对称中心.当采纳螺栓杆与孔壁间留有间隙的普通螺栓联接时(图a).靠联接预紧后在接合面间发生的摩擦力来抵当横向载荷;当采纳铰制孔用螺栓联接时(图b),靠螺栓杆受剪切和挤压来抵当横向载荷.虽然两者的传力方式分歧,但计算时可近似地认为,在横向总载荷F∑的作用下,各螺栓所承当的工作载荷是均等的.因此,对铰制孔用螺栓联接,每个螺栓所受的横向工作剪力为(5-23)式中z为螺栓联接数目.对普通螺栓联接,应保证联接预紧后,接合面间所发生的最年夜摩擦力必需年夜于或即是横向载荷.假设各螺栓所需要的预紧力均为Qp,螺栓数目为z,则其平衡条件为或(5-24)图:受横向载荷的螺栓组联接式中:f——接合面间的摩擦系数,见下表;i——接合面数(图中,i=2);Ks——防滑系数,K.由式(5-24)求得预紧力Qp,然后按式(5-14)校核螺栓的强度.联接接合面间的摩擦系数被联接件接合面的概况状态摩擦系数f钢或铸铁零件干燥的加工概况0.有油的加工概况0.06-0.10钢结构轧制概况,钢丝刷清理浮锈0.30-0.35 涂富锌漆0.35-0.40喷砂处置0.45-0.55钢铁对砖料,混凝土或木材干燥概况0.40-0.45 2).受转矩的螺栓组联接如下图所示,转矩T作用在联接接合面内,在转拒T的作用下,底板将绕通过螺栓组对称中心O并与接合面相垂直的轴线转动.为了防止底板转动,可以采纳普通螺栓联接,也可以采纳铰制孔用螺栓联接.其传力方式和受横向载荷的螺栓组联接相同.图:受转矩的螺栓组联接采纳普通螺栓时,靠联接领紧后在接合面间发生的摩擦力矩来抵当转矩T.假设各螺栓的预紧水平相同,即各螺栓的预紧力均为Qp,则各螺栓联接处发生的摩擦力均相等,并假设此摩擦力集中作用在螺栓中心处.为阻止接合面发生相对转动,各摩擦力应与各该螺栓的轴线到由上式可得各螺栓所需的预紧力为【5-25】式中:f——接合面的摩擦系数,见表;ri——第i个螺栓的轴线到螺栓组对称中心O的距离;z——螺栓数目;Ks ——防滑系数,同前.由上式求得预紧力Qp,然后按式(5-14)校核螺栓的强度.采纳铰制孔用螺栓时,在转矩T的作用下,各螺栓受到剪切和挤压作用,各螺栓所受的横向工作剪力和各该螺栓轴线到螺栓组对称中心O的连线(即力臂r.)相垂直(图b).为了求得各螺栓的工作剪力的年夜小,计算时假定底板为刚体,受载后接合面仍坚持为平面.则各螺栓的剪切变形量与各该螺栓轴线到螺栓组对称中心O的距离成正比.即距螺栓组对称中心O越远,螺栓的剪切变形量越年夜.如果各螺栓的剪切刚度相同,则螺栓的剪切变形量越年夜时,其所受的工作剪力也越年夜.如图b所示,用ri、rmax分别暗示第i个螺栓和受力最年夜螺栓的轴线到螺栓组对称中心O的距离;Fi、Fmax.分别暗示第i 个螺栓和受力最年夜螺栓的工作剪力,则得【5-26】根据作用在底板上的力矩平衡的条件得即. 【5-27】联解式(5-26)及(5-27),可求得受力最年夜的螺栓的工作剪力为【5-28】图所示的凸缘联轴器,是接受转矩的螺栓组联接的典范部件.各螺栓的受力根据r1=r2=…=rz的关系以及螺栓联接的类型,分别代人式(5-25)或(5-28)即可求得.3).受轴向载荷的螺栓组联接下图为一受轴向总载荷F的汽缸盖螺栓组联接.F的作用线与螺栓轴线平行,并通过螺栓组的对称中心O.计算时,认为各螺栓平均受载,则每个螺栓所受的轴向工作载荷为图:受轴向载荷的螺栓组联接4).受倾覆力矩的螺栓组联接下图a为一受倾覆力矩的底板螺栓组联接.倾覆力矩M作用在通过x-x轴并垂直于联接接合面的对称平面内.底板接受倾覆力矩前,由于螺栓已拧紧,螺栓受预紧力Qp,有均匀的伸长;地基在各螺栓的Qp作用下.有均匀的压缩,如图b所示.当底板受到倾覆力矩作用后,它绕轴线O—O倾转一个角度,假定仍坚持为平面.此时,在轴线O-O左侧,地基被放松,螺栓被进一步拉伸,在右侧,螺栓被放松,地基被进一步压缩.底板的受力情况如图c所示.图:受倾覆力矩的螺栓组联接联接接合面资料的许用挤压应力[σ]p,可查下表.表:联接接合面资料的许用挤压应力[σ]p注:l)σs为资料屈服权限,MPa; σB为资料强度极限,MPa.2)当联接接合面的资料分歧时,应按强度较弱者选取.3)联接接受载荷时,[σ]p应取表中较年夜值;接受变载荷时,则应取较小值计算受倾覆力矩的螺栓组的强度时,首先由预紧力Qp、最年夜工作载荷Fmax确定受力最年夜的螺栓的总拉力Q,由式(5-18)得【5-38】然后接式(5-19)进行强度计算.确定螺栓直径首先选择螺栓资料,确定其性能品级,查出其资料的屈服极限,并查出平安系数,计算出螺栓资料的许用应力[σ]= σs/S.根据以下公式计算螺纹小径d1:最后按螺纹标准,选用螺纹公称直径.螺纹联接件的资料适合制造螺纹联接件的资料品种很多,经常使用资料有低碳钢Q215、10号钢和中碳钢Q235、35、45号钢.对接受冲击、振动或变载荷的螺纹联接件,可采纳低合金钢、合金钢,如15Cr、40Cr、30CrMnsi等.对特殊用途(如防锈蚀、防磁、导电或耐高温等)的螺纹联接件,可采纳特种钢或铜合金、铝合金等.表:螺栓的性能品级(摘自 GB 3098.1-82)注:规定性能品级的螺栓、螺母在图纸中只标出性能品级,不应标出资料牌号.表:螺母的性能品级(摘自GB 3098.2-82),是根据实际情况,对螺栓进行强度校核..采纳公式为:碳素钢螺栓合金钢螺栓式中:s——螺栓资料的屈服极限;A1——螺栓危险截面的面积.式(5-14)松螺纹联接强度计算拉伸强度条件为:【5-14】式中:F--螺栓工作载荷,N;d1--螺栓危险截面的直径,mm;[σ]--螺栓资料的许用拉应力,MPa.紧螺栓联接强度计算1.仅接受预紧力的紧螺栓联接拉伸强度条件为:式中:Qp—螺栓所受预紧力,N .其余符号意义同前.2. 接受预紧力和工作拉力的紧螺栓联接①拉伸强度条件为:式中:Q—螺栓总拉力,N .其余符号意义同前.螺栓总拉力的计算:Q=Qp+[Cb/(Cb+Cm)]·F式中:Cb/(Cb+Cm)称为螺栓的相对刚度,一般设计时,可按下表推荐的数据选取.螺栓的相对刚度Cb/(Cb+Cm)被联接钢板间所用垫片类别Cb/(Cb+Cm)金属垫片(或无垫片)0.2~0.3皮革垫片0.7铜皮石棉垫片0.8橡胶垫片0.9②疲劳强度计算对受轴向变载荷的重要联接,应对螺栓的疲劳强度作精确校核,计算其最年夜应力计算平安系数:式中:-1tc ——螺栓资料的对称循环拉压疲劳极限,MPa ,-1tc 值见表——试件的资料特性,即循环应力中平均应力的折算系数,对碳素钢,=0.1—0.2,对合金钢,=0.2—0.3;——拉压疲劳强度综合影响系数,如忽略加工方法的影响,则Kσ=kσ/εσ,Kσ此处为有效应力集中系数,见表εσ为尺寸系数,见附表;S ——平安系数.螺纹联接件经常使用资料的疲劳极限(摘自GB38-76)资料疲劳极限(MPa)σ-1σ-1tc10 Q215 35 45 40C r 160~220170~220220~300250~340320~440120~150120~160170~220190~250240~340螺纹联接的平安系数 S受载类型静载荷变载荷松螺栓联接~1.7紧螺栓联接受轴向及横向载荷的普通螺栓联接不考虑预紧力的简化计算M6~M16 M16~M30 M30~M60 M6~M16 M16~M30 M30~M60 碳钢5~4 4~~2 碳钢~~合金钢~5 5~~3 合金钢10~~10考虑预力的计~~(S a~4)紧算铰制孔用螺栓联接钢:S r铸铁:S~钢:S r~5,S铸铁:S~3.接受工作剪力的紧螺栓联接螺栓杆与孔壁的挤压强度条件为螺栓杆的剪切强度条件为式中:F ——螺栓所受的工作剪力,N;d0——螺栓剪切面的直径(可取为螺栓孔的直径),mm;L min——螺栓杆与孔壁挤压面的最小高度,mm,设计时应使L min d0;[σ]p——螺栓或孔壁资料的许用挤压应力,MPa ;[τ] ——螺栓资料的许用切应力,MPa .接受工作剪力的紧螺栓联接有效应力集中系数资料的400 600 800 1000尺寸系数回顶部直径1620242832404856647280 d(mm)1联接接合面资料的许用挤压应力材料钢铸铁混凝土砖(水泥浆缝)木材螺栓的性能品级(摘自GB 3098.1--82)性能品级(标识表记标帜)抗拉强度极限330 400 420 500 520 600 800 900 1040 1220 屈服极限190 240 340 300 420 480 640 720 940 1100硬度90 109 113 134 140 181 232 269 312 365推荐资料低碳钢低碳钢或中碳钢中碳钢,淬火并回火中碳钢,低、中碳合金钢,淬火并回火,合金钢合金钢。
第四章力的计算
力的计算在物理学中是一个重要的概念。
在力学中,力是一种
使物体产生运动或发生变形的物理量。
力的计算可以帮助我们理解
物体之间的相互作用和力的大小。
力的计算通常可以通过使用牛顿第二定律来实现。
牛顿第二定
律表明,当一个物体受到外力作用时,它的加速度与作用在它上面
的力成正比,与物体的质量成反比。
因此,可以使用以下公式计算力:
力 = 质量 ×加速度
在使用这个公式时,需要注意将质量和加速度的单位统一,例
如将质量单位转换为千克,加速度单位转换为米每秒的平方。
当物体受到多个力的作用时,可以使用向量的方法来计算合力。
合力是所有作用在物体上的力的矢量和,可以通过将每个力的矢量
相加来计算。
这可以表示为以下公式:
合力 = F1 + F2 + F3 + ...
其中,F1、F2、F3等表示每个力的矢量。
除了使用牛顿第二定律和向量的方法,力的计算还可以通过其他物理原理和公式来实现。
例如,弹簧的弹性力可以根据胡克定律进行计算,电场力可以根据库仑定律进行计算,重力可以根据万有引力定律进行计算。
力的计算在许多领域中都有应用,包括工程学、物理学、力学等。
它可以帮助我们理解物体的运动状态、相互作用和力的大小,从而推导出更深入的物理现象和规律。
总结而言,力的计算是物理学中一个重要的概念。
通过使用牛顿第二定律、向量的方法和其他物理原理,我们可以计算力的大小和方向,进而理解物体之间的相互作用和力的作用。
力的计算在多个领域中都有应用,是物理学研究和应用的基础之一。
1.静力学研究物体的受力分析、力系的等效替换(或简化)、建立各种力系的平衡条件的科学.1、物体的受力分析:分析物体(包括物体系)受哪些力,每个力的作用位置和方向,并画出物体的受力图.2、力系的等效替换(或简化):用一个简单力系等效代替一个复杂力系.3、建立各种力系的平衡条件:建立各种力系的平衡方程,并应用这些条件解决静力学实际问题.几个基本概念:力:力是使得物体运动的原因.力是一个物体对另一个物体的作用.物体间相互的机械作用,作用效果使物体的机械运动状态发生改变.力的作用效果:使物体运动状态发生变化使物体形状发生变化对力的认识还处于发展中.(导致科学的发展和社会的变革)力的三要素:大小、方向、作用点.力是矢量力的表示方法:黑体F 加矢量符号F F F 大小用模表示F力的单位:牛(N)千牛(kN)F A FA力系:一群力.可分为:平面汇交(共点)力系,平面平行力系,平面力偶系,平面任意力系;空间汇交(共点)力系,空间平行力系,空间力偶系,空间任意力系.平衡:物体相对惯性参考系(如地面)静止或作匀速直线运动.刚体:在力的作用下,其内部任意两点间的距离始终保持不变的物体.永远不变形的物体.2.静力学公理公理1 二力平衡公理作用在刚体上的两个力,使刚体保持平衡的必要和充分条件是:这两个力的大小相等,方向相反,且作用在同一直线上。
21F F -=等值, 反向, 共线二力使刚体平衡二力使刚体平衡等值, 反向, 共线对变形体是必要而非充分条件.公理2加减平衡力系公理在已知力系上加上或减去任意的平衡力系,并不改变原力系对刚体的作用。
平衡力系对刚体的总效应为零,它不会改变刚体的运动状态.F3F4推论1 力的可传性原理作用在刚体上的力是滑动矢量,力的三要素为大小、方向和作用线(作用点).作用于刚体上某点的力,可以沿着它的作用线移到刚体内任意一点,并不改变该力对刚体的作用。
A FB A B F F 1F 2AB F 2==证明公理3 力的平行四边形法则作用在物体上同一点的两个力,可以合成为一个合力。
合力的作用点也在该点,合力的大小和方向,由这两个力邻为边构成的平行四边形的对角线确定。
21F F F R +=A 它是力系简化的基础。
F 1F R F 2推论2三力平衡汇交定理平衡时必与共线则三力必汇交O 点,且共面.3F 12F 刚体受三个不平行的力作用而保持平衡,则此三力必在同一平面内,且作用线相交于一点。
证明F 2F 1B AC F 3O公理4作用和反作用定律在画物体受力图时要注意此公理的应用.注意与平衡力的区别思考:天花板上通过绳子悬挂一重物,其中哪些力为平衡力,哪些力为作用力与反作用力?作用力和反作用力总是同时存在,同时消失,等值、反向、共线,作用在相互作用的两个物体上.F F约束:对非自由体的位移起限制作用的物体.约束力:约束对非自由体的作用(约束力,约束反力,反力).约束力⎩⎨⎧大小——待定方向——与该约束所能阻碍的位移方向相反作用点——接触处3.受力图铁轨对于火车, 地面对于桌子等体现为力.工程常见的约束1、具有光滑接触面(线、点)的约束(光滑接触面约束)特点:只限制物体沿接触面法线向内部的位移,不能限制沿切向的位移.常见的有不考虑摩擦的支持面、齿轮的啮合面等.表示通常用N F NF2、由柔软的绳索、胶带或链条等构成的约束(绳索约束)特点:柔索只能受拉力。
柔索对物体的约束力沿着柔索背向被约束物体.T F 用表示.胶带对轮的约束力沿轮缘的切线方向,为拉力.3、光滑铰链约束(径向轴承、圆柱铰链、固定铰链支座等)约束特点:(1)径向轴承(向心轴承)轴轴承轴在轴承孔内,只能一点接触.光滑接触面约束当不计摩擦时,轴与孔在接触为光滑接触约束为法向约束力.约束力作用在接触处,沿径向指向轴心.当外界载荷不同时,接触点会变,则约束力的大小与方向均有改变.可用二个正交的分力表示.y x F F ,By F BxF(2)光滑圆柱铰链约束特点:由两个各穿孔的构件及圆柱销钉组成,如剪刀.其中有作用反作用关系cy cy cxcx F F F F '-='-= ,一般不必分析销钉受力,当要分析时,必须把销钉单独取出.光滑圆柱铰链:亦为孔与轴的配合问题,与轴承一样,可用两个正交分力表示.(3)固定铰链支座由构件,销钉与地面或固定支座连接而成.约束力:与圆柱铰链相同以上三种约束(经向轴承、光滑圆柱铰链、固定铰链支座)其约束特性相同,均为轴与孔的配合问题,都可称作光滑圆柱铰链.CxF CyF 简图4、其它类型约束(1)滚动铰链支座(滑移铰链支座)在固定铰支座与光滑固定平面之间装有光滑辊轴而成.约束力:构件受到垂直于光滑面的约束力.yF xF yF(2) 球铰链约束特点:通过球与球壳将构件连接,构件可以绕球心任意转动,但构件与球心不能有任何移动.约束力:当忽略摩擦时,球与球座亦是光滑约束问题.约束力通过接触点,并指向球心,是一个不能预先确定的空间力.可用三个正交分力表示.(3)止推轴承约束特点:止推轴承比径向轴承多一个轴向的位移限制.约束力:比径向轴承多一个轴向的约束反力,亦有三个正交分力.Az Ay Ax F F F ,,(2)柔索约束——拉力TF(5)滑移铰链支座——⊥光滑面y F(3)光滑铰链——一对正交分力y x F F(1)光滑面约束——法向约束力NF(4)固定铰链支座——一对正交分力y x F F画受力图步骤:1、取所要研究物体为研究对象(隔离体)画出其简图.2、画出所有主动力(重力,风力,拉力等),一般为已知力.3、按约束性质画出所有被动力(约束反力).注意:1.在受力图上应画出所有力,主动力和约束反力(被动力)2.只画外力,不画内力.3.研究对象要一个一个取.例1解:隔离研究对象画出简图画出主动力画出约束力碾子重为,拉力为,、处光滑接触,画出碾子的受力图.FA B P FPBABAPFF AF B例2解:取屋架画出主动力画出约束力q 屋架受均布风力(N/m ),屋架重为,画出屋架的受力图.PAxF AyF ByF Pq例3不计三铰拱桥的自重与摩擦,画出左、右拱的受力图与系统整体受力图.解:隔离右拱CyFCxFByFBxF AyFAxFFCyF'CxF'隔离左拱注意作用力与反作用力的方向要相反整体受力图By F Bx F AyF Ax F F思考:此时C 处的约束力需要画么?另一种画法:用定理画公理1 二力平衡公理作用在刚体上的两个力,使刚体保持平衡的必要和充分条件是这两个力等值, 反向, 共线解:右拱BC 满足这个条件象BC拱这样的刚体,不论形状如何,如果只在两个力作用下平衡(只在两点受力),则称之为二力杆或二力构件.它所受的两个力一定等值,反向,共线.推论2三力平衡汇交定理作用于刚体上三个相互平衡的力,若其中两个力的作用线汇交于一点,则此三力必在同一平面内,且第三个力的作用线通过汇交点。
左拱呢?考虑到左拱在三个力作用下平衡,可按三力平衡汇交定理画出左拱的受力图.FBCF OAF整体受力图思考:若左、右两拱都考虑自重,如何画出各受力图?此时上述定理画法不再适用例4 取CD 杆,其为二力构件(二力杆),画它的受力图水平均质梁重为,电动机重为,不计杆CD 的自重,画出杆CD 和梁AB 的受力图.2P AB 1P 解:(有二力杆么?)取AB 梁,其受力图如图若这样画,梁AB 的受力图又如何改动?思考: CD 杆的受力图能否画为下图所示?F 2F 1A B C D F 1B CF Bx F By F CA F CDF 2F 1A B C F CDF Ax F Ay F 2F 1AB CD F Ax F Ay F D F AD 例5练习:考虑球的自重,绘制每个球的受力图.ABAP AF CF DB DF P BF EF NABPABEDCGF练习:不考虑各杆件自重(重物不计),绘制每根杆件的受力图.F BBCF CF GA BD GF AxF AyF DyF DxBF 'DC FC F 'DxF 'DyF 'FyF FxF Fx F 'FyF 'F F EPPABEDCGF小结:正确的绘制受力图是进行力学分析的基础,需注意一下几点:1.取出恰当的研究对象进行隔离,可以取单个物体,也可以取整体,还可以取部分物体组成的系统.取一次研究对象画一个受力图.2.准确的确定力的数目.既不能凭空“创造”一个力,也不能漏掉一个力.一般来说,凡是研究对象与外界接触的地方都有约束力的存在.不同的约束方式力的数目不同.3.注意作用力与反作用力.若确定其中一个力的方向,则其反作用力一定要与之相反.4.内力不画,只画外力.5.注意先找二力杆;销钉不画.6.力是矢量;要有名称.。