第四章 双原子分子的结构.
- 格式:doc
- 大小:780.04 KB
- 文档页数:23



1、填空题1、双原子分子刚性转子模型主要内容:原子核体积是可以忽略不计的质点;分子的核间距不变;分子不受外力作用。
2、谐振子模型下,双原子分子转动光谱选律为:极性分子,3、谐振子模型下,双原子分子振动光谱选律为:极性分子,谱线波数为:。
4、刚性转子模型下,转动能级公式为。
5、谐振子模型下的双原子分子能量公式为,其中特征频率为6、分子H2,N2,HCl,CH4,CH3Cl,NH3中不显示纯转动光谱的有:H2,N2,不显示红外吸收光谱的分子有: H2,N2,CH4。
二、选择题1、已知一个双原子分子的转动常数B(波数单位),纯转动光谱中第二条谱线的波长为( D )?(A)B/4(B)B/2(C)1/6B(D)1/4B解:2、HCl分子的正则振动方式共有( B )种?线性3N-5 非线性3N-6(A)0(B)1(C)2(D)3CO2分子的正则振动方式共有( D )种?(A)1(B)2(C)3(D)4HCN分子的正则振动方式共有( D )种?(A)1(B)2(C)3(D)4对H2O而言,其平动、转动、振动自由度分别为( A )(A)3,3,3(B)3,2,4(C)3,2,3(D)1,2,33、已知一双原子分子转动光谱的第四条谱线在80cm-1,则第九条谱线位置为( D )?(A)120cm-1(B)140cm-1(C)160cm-1(D)180cm-14、运用刚性转子模型处理异核双原子分子纯转动光谱,一般需知几条谱线位置(J),可计算其核间距( B )(A)5 (B)2 (C)3 (D)45、红外光谱(IR)由分子内部何种能量跃迁引起( D )(A)转动(B)电子-振动(C)振动(D)振动-转动6、H2和D2的零点能比值为:( B )(A)1 (B)(C)(D)不确定四、计算题1、已知HCl的纯转动光谱每二谱线间的间隔为20.8cm-1,试求其键长。
解:2、已知1H79Br在远红外区给出了间隔为16.94cm-1的一系列谱带,计算HBr的平衡核间距。


双原子分子光谱分子的能量状态与原子的能量状态一样存在能级,而且分子能级发生跃迁时发射或吸收辐射。
然而分子同原子相比,由于它的结构和运动状态的复杂性,分子光谱比原子光谱复杂得多。
双原子分子光谱是较简单的分子光谱。
分子光谱随分子能级跃迁间隔的不同,可以出现在从紫外到微波的不同光谱区。
本实验的目的是通过拍摄双原子分子的电子一振动光谱,来了解分子光谱的特点,测量各顺序谱带组的带头波长,计算分子的振动频率ω、非筒谐性常数ωx 和分子振动力常数k 等。
【预习提要】双原子分子是结构较为简单的分子。
因而反映分子结构特征和举动状态的双原子分子光谱也是较简单的分子光谱。
用色散率不大的摄谱仪伯摄的双原子分子光谱呈现带状,实际上,它们是由大量的、密集的、分布有规律的谱线所组成的。
不同波段的谱线反映分子不同运动状态的能级跃迁。
1.双原子分子有哪些不同形式的能量,怎样利用“不确定性关系”说明不同形式的能级间隔之间的数量关系?2.用莫尔斯函数表示双原子分子的势阱时,分子振动能级间隔有什么特点?3.什么叫顺序带组,试说明相邻顺序谱组带头的波数差出现“突变”的能级结构的内在原因。
4.试判断(0,0),(1,0)和(0,1)顺序带组列出b a ,或b a '',的测定方程和相应的正则方程。
5.利用近似的谐振子频率公式,求出分子振动力常数值。
【实验原理】一、双原子分子的结构与运动状态双原子分子是由两个原子核和电子相互结合而成的微观系统。
当两个原子相结合而构成一个双原子分子时,在每个原子内部构成完整壳层的电子仍然分别属于各自的原子核,而外层的价电子向对方原子核提供库仑引力,当两核过于靠近时产生斥力,从而使两个原子核相距一定地联系在一起构成稳定的结构。
分子具有三种基本运动:①外层价电子在两个原子核共同产生的电场中绕核间轴的运动,这种运动如同价电子在孤立的原子中运动一样形成各种不同的电子能量状态。
②双原子分子的原子核由于交替地受到来自对方价电子的引力和核的斥力,在平衡位置附近,带着其周围的电子沿核间轴方向振动,伸缩核间轴长短。

2组长:070601314组员:070601313070601315070601344070601345070601352第四章 双原子分子结构与性质1.简述 LCAO-MO 的三个基本原则,其依据是什么?由此可推出共价键应具有什么样的特征?答:1.(1)对称性一致(匹配)原则: φa = φs 而φb = φ pz 时, φs 和φ pz 在σˆ yz 的操作下对称性一致。
故 σˆ yz ⎰φs H ˆφ pz d τ = β s , pz ,所以, β s , pz ≠ 0 ,可以组合成分子轨道(2)最大重叠原则:在 α a 和α b 确定的条件下,要求 β 值越大越好,即要求 S ab 应尽可能的大(3)能量相近原则: 当α a = α b 时,可得 h = β ,c 1a = c 1b , c 1a =- c 1b ,能有效组合成分子轨道;2.共价键具有方向性。
2、以 H 2+为例,讨论共价键的本质。
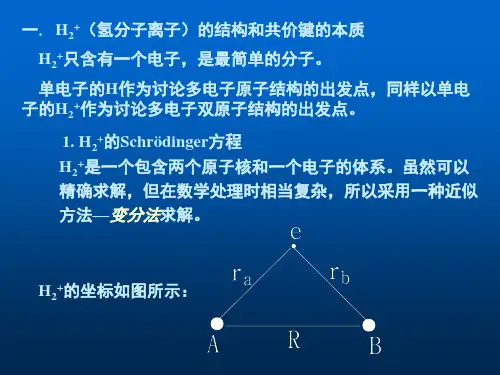
答:下图给出了原子轨道等值线图。
在二核之间有较大几率振幅,没有节面,而在核间值则较小且存在节面。
从该图还可以看出,分子轨道不是原子轨道电子云的简单的加和,而是发生了波的叠加和强烈的干涉作用。
图 4.1 H + 的 ψ 1(a)和 ψ 2(b)的等值线图研究表明,采用 LCAO-MO 法处理 H 2+是成功的,反映了原子间形成共价键 的本质。
但由计算的得到的 Re=132pm ,De=170.8kJ/mol ,与实验测定值Re=106pm、De=269.0 kJ/mol 还有较大差别,要求精确解,还需改进。
所以上处理方法被称为简单分子轨道法。
当更精确的进行线性变分法处理,得到的最佳结果为Re=105.8pm、De=268.8 kJ/mol,十分接近H2+的实际状态。
成键后电子云向核和核间集中,被形象的称为电子桥。
通过以上讨论,我们看到,当二个原子相互接近时,由于原子轨道间的叠加,产生强烈的干涉作用,使核间电子密度增大。


双原子分子的结构双原子分子是由两个原子组成的分子。
这些分子可以是同一种类型的原子,也可以是两种不同种类的原子。
在化学和物理学中,研究双原子分子的结构和性质是非常重要的。
双原子分子的结构可以使用带电的球体模型来描述。
一个带电的球体代表原子的正电荷核心和周围的负电子云。
在一对双原子分子中,两个原子之间通过共享电子而相互吸引。
由于双原子分子中只有两个原子,因此它们的结构比较简单。
主要有两种类型的双原子分子结构:线性和非线性。
线性类型的双原子分子是指两个原子组成的分子在平衡位置时处于一条直线上。
这些分子的最简单例子是氧气(O2)和氮气(N2)。
比较而言,非线性双原子分子是指由两个原子组成的分子不在一条直线上。
其中最常见的非线性分子是水(H2O)和二氧化碳(CO2)。
线性双原子分子的结构非常简单。
在这些分子中,两个原子之间的距离是相等的。
这种分子的结构描述通常包括键长(L)和键角(θ)。
键长是指原子核之间的距离,它测量的是两个原子之间的距离。
键角是指两个相邻键的方向之间的夹角,它描述了分子的几何构型。
对于线性分子,键角为180度。
非线性双原子分子的结构要复杂一些。
对于这些分子,键长和键角的测量方法也是不同的。
对于非线性双原子分子,键长是平均距离,因为原子核之间的距离在分子中会变化。
而键角的测量则需要考虑到分子的几何构型。
水分子的结构是一个典型的非线性双原子分子。
当两个氢原子与氧原子结合时,分子的几何构型呈V字形。
分子中存在的氢键使得分子在水相中具有许多独特的性质。
这些性质包括高的表面张力和卓越的溶解性。
二氧化碳(CO2)也是一个非线性双原子分子。
但与水不同的是,二氧化碳是一种线性三角形分子。
根据量子力学的计算,氧原子和碳原子之间的键长约为1.1625埃,而氧原子和中央的C-O键角约为180度。
总之,双原子分子的结构和性质对于化学和物理学的研究非常重要。
无论是线性还是非线性,双原子分子都具有自身独特的结构和性质,这些结构和性质使我们更好地理解分子之间相互作用的原理。

2组长:070601314 组员:070601313070601315 070601344 070601345070601352第四章 双原子分子结构与性质1.简述 LCAO-MO 的三个基本原则,其依据是什么?由此可推出共价键应具有什么样的特征?答:1.(1)对称性一致(匹配)原则: φa = φs 而φb = φ pz 时, φs 和φ pz 在σˆ yz 的操作下对称性一致。
故 σˆ yz ⎰φs H ˆφ pz d τ = β s , pz ,所以, β s , pz ≠ 0 ,可以组合成分子轨道(2)最大重叠原则:在 α a 和α b 确定的条件下,要求 β 值越大越好,即要求 S ab 应尽可能的大(3)能量相近原则: 当α a = α b 时,可得 h = β ,c 1a = c 1b , c 1a =- c 1b ,能有效组合成分子轨道;2.共价键具有方向性。
2、以 H 2+为例,讨论共价键的本质。
答:下图给出了原子轨道等值线图。
在二核之间有较大几率振幅,没有节面,而在核间值则较小且存在节面。
从该图还可以看出,分子轨道不是原子轨道电 子云的简单的加和,而是发生了波的叠加和强烈的干涉作用。
图 4.1 H +的 ψ 1(a)和 ψ 2(b)的等值线图研究表明,采用 LCAO-MO 法处理 H 2+是成功的,反映了原子间形成共价键的本质。
但由计算的得到的Re=132pm,De=170.8kJ/mol,与实验测定值Re=106pm、De=269.0 kJ/mol 还有较大差别,要求精确解,还需改进。
所以上处理方法被称为简单分子轨道法。
当更精确的进行线性变分法处理,得到的最佳结果为Re=105.8pm、De=268.8 kJ/mol,十分接近H2+的实际状态。
成键后电子云向核和核间集中,被形象的称为电子桥。
通过以上讨论,我们看到,当二个原子相互接近时,由于原子轨道间的叠加,产生强烈的干涉作用,使核间电子密度增大。
第四章双原子分子的结构Chapter 4. Diatomic molecules前言:两个原子相互靠近,它们之间存在什么样的作用力,怎样才能形成稳定的分子结构?这是化学键理论讨论的主要问题。
两个原子相距较长距离时,它们倾向于相互吸引,而在短距离内它们会互相排斥。
某一对原子间相互吸引力很弱,而另一对原子间吸引力强到足以形成稳定分子。
为什么有这么大的差别? 这正是本章要讨论的内容。
§4.1化学键理论简介(Brief introduction to chemical bond theory)一、原子间相互作用力原子是由带电粒子组成的,我们预计原子间相互作用力大多是静电相互作用,主要取决于两个方面,一是原子的带电状态(中性原子或离子),二是原子的电子结构,按原子最外价电子层全满状态(闭壳层)或未满状态(开壳层)来分类。
闭壳层包括中性原子,如稀有气体He、Ne、Kr……,及具有稀有气体闭壳层结构的离子如Li+、Na+、Mg2+、F-、Cl-等。
开壳层则包括大多数中性原子,如H、Na、Mg、C、F等。
显然,闭壳层原子(或离子)与开壳层原子之间相互作用很不相同。
原子间相互作用大致可分为以下几类:(1)两个闭壳层的中性原子,例如 He-He,它们之间是van der Waals(范德华)引力作用。
(2)两个开壳层的中性原子,例如H-H,它们之间靠共用电子对结合称为“共价键”。
(3)一个闭壳层的正离子与一个闭壳层的负离子,例如Na+-Cl-,它们之间是静电相互作用,称之为“离子键”。
(4)一个开壳层离子(一般是正离子)与多个闭壳层离子(或分子),例如过渡金属配合物M n+(X-)m,它们之间形成配位键(属共价键范围)。
(5)许多金属原子聚集在一起,最外层价电子脱离核的束缚,在整个金属固体内运动——金属键。
讨论这些成键原理的理论称化学键理论。
二、化学键理论从二十世纪初发展至今,化学键理论已形成三大流派:分子轨道理论(Molecular Orbital)、价键理论(Valence Bond)和密度泛函理论(Density Functional Theory)。
1.分子轨道理论:从20世纪30年代初,由Hund,Mulliken,Lennard-Jones开创,Slater,Hückel,Pople 发展至今。
该方法的分子轨道具有较普通的数学形式,较易程序化。
六十年代以来,随着计算机的发展,该方法得到了很大的发展。
如Pople等研制的Gaussian从头算程序, 已成为当今研究化学键理论的主流方法,以后我们将主要介绍该方法。
分子轨道理论(MO)要点:(1)分子轨道采用原子轨道线性组合(LCAO),例如CH4分子,C原子有1s,2s,2p等5个轨道,加上4个H原子1s轨道,共有9个原子轨道,可组合成9个分子轨道。
( 其中为分子轨道,为原子轨道)(2)分子中每个电子看作是在核与其它电子组成的平均势场中运动,每个电子在整个分子中运动——称为单电子近似。
(3)分子轨道按能级高低排列,电子从低至高两两自旋反平行填入分子轨道。
2.价键理论(VB):三十年代由Heitler-London、Pauling、Slater等创立的化学键理论,VB很重视化学图像。
价键波函数采用可能形成化学键的大量共价结构和少量离子结构形成键函数,通过变分计算得到状态波函数和能量。
例如苯分子的π电子可形成以下多种共振结构图4-1 苯分子的多种共振结构图这是描述电子空间轨道运动的键函数,还有描述电子自旋运动的键函数。
由这些结构的键函数通过各种近似计算,可得到体系的分子轨道与能级.键函数形式因不同分子而异,很难用一个统一的公式表示,因此给价键理论的程序化带来很大的困难。
在二十世纪三十年代,化学家都倾向于用价键理论来解释分子结构,但到了五十年代,价键理论发展缓慢;到了八十年代,又有人对价键理论方法进行改进,我校张乾二院士带领的课题组也在价键方法程序化方面取得了突破性的进展。
3.密度泛函理论(DFT)DFT是1964年由Kohn等提出,Ellis 、Lee-Yang-Parr 等发展、九十年代流行的一种化学键理论,在DFT中,用电荷密度函数代替单电子波函数描述体系的状态,在解Schrödinger方程时,用统计方法代替交换积分计算,因而取得了计算时间短、精度高的效果,特别适用重原子,多原子体系。
§4.2变分法与H2+的结构+的结构和共价键的本质一、H2原子通过化学键结合成分子,分子是物质中独立地、相对稳定地存在并保持该化合物特性的最小颗粒,是参与化学反应的基本单元。
原子相互吸引、相互排斥,以一定的次序和方式结合成分子。
物质的化学性质主要决定于分子的性质,而分子的性质主要由分子的结构决定。
因此探索分子内部的结构,了解结构和性能的关系,就成了结构化学的重要组成部分。
化学键是指分子中将原子结合在一起的相互作用力,广义而论还包括分子间的相互作用。
两个或多个原子(或离子)之间依靠化学键将原子结合成相对稳定的分子或晶体。
典型的化学键有三种:共价键、离子键和金属键。
气态分子中的化学键主要是共价键。
离子键和金属键分别存在于离子化合物与块状金属中。
分子间和分子内部有时还形成氢键,其强弱介于共价键和范德华力之间。
现代化学键理论是建立在量子力学基础上的。
由于分子的Schrödinger方程比较复杂,严格求解经常遇到困难,常采用某些近似的假定以简化计算。
随着量子力学的发展,为处理分子结构问题提出了三个基本理论:分子轨道理论、价键理论和配位场理论。
这三个理论互有联系。
最早发展起来的是价键理论,1927年Heitler和London成功地解了H2分子的Schrödinger方程,这是最早的价键理论的成果,也是价键理论的基础。
以后Pauling引进杂化轨道概念,使价键理论获得发展。
分子轨道理论是后来发展起来的,从50年代以来,用它处理有机共轭分子结构,取得了很大成功,获得迅猛发展,成为当代化学键理论的主流。
配位场理论则是根据配位化合物的结构特征发展起来的。
这些化学键理论都将陆续在后面详细地介绍。
H2+的结构和共价键的本质H2+的分子,在化学上虽不稳定,很容易从周围获得一个电子变为氢分子,但已通过实验证明它的存在,并已测定出它的键长为106pm,键离解能为255.4KJ·mol-1。
正像单电子的氢原子作为讨论多电子原子结构的出发点一样,单电子的H 2+可为讨论多电子的双原子分子结构提供许多有用的概念。
H2+的Schrödinger方程H2+是一个包含两个原子核和一个电子的体系。
其坐标如图所示。
图中和代表电子与两个核的距离,代表两个核的距离。
图4-2 H2+的座标的方程以原子单位表示为式中和E分别为 H2+的波函数和能量。
左边方括号中第一项代表电子动能算符,第二项和第三项代表电子受核的吸引能,第四项代表两个原子核的静电排斥能。
由于电子质量比原子核质量小很多,电子运动速度比核快得多,电子绕核运动时,核可以看作不动。
式中不含核的动能运动项,电子处在固定的核势场中运动,此即Born-Oppenheimer(波恩-奥本哈默)近似。
因而解得的波函数只反映电子的运动状态。
这样,把核看作不动,固定核间距R解方程,得到分子的电子波函数和能级,改变R值可得一系列波函数和相应的能级。
与电子能量最低值相对应的R就是平衡核间距Re。
二、变分法解Schrödinger方程变分法是解方程的一种近似方法,它基于下面的原理:对任一个品优函数,用体系的算符求得的能量平均值,将大于或接近于体系基态的能量(E0),即据此原理,利用求极值的方法调节参数,找出能量最低时对应的波函数,即为和体系相近似的波函数。
上式可证明如下:设…组成一正交、归一完全的函数组,其能量依次增加,E0≤E1≤E2…,由此可得将上式中的按照体系的本征函数展开利用的正交归一性,可得平均能量因恒为正值,(据1.2假设IV),0< ≤1,故得所以<E>≥E0常用的线性变分法是选择一品优的线性变分函数求出E值最低时对应的c1值。
因为电子运动到核A附近区域时,分子轨道很像原子轨道;同样,当电子运动到核B附近区域时,分子轨道近似于。
根据态叠加原理,分子轨道可用原子轨道的线性组合表示作为H 2+的变分函数,式中c a和c b为待定参数,而将代入中,得由于H 2+的两面个核是等同的,而和又都是归一化函数,展开上式并令得对c a和c b偏微商求极值,得消去Z,因为得,将Y,Z值代入,并化简,可得久期方程(4-2-2-1式)为了使c a和c b有不完全为零的解,可得久期行列式解此行列式,得E的两个解将E1值代回(4-2-2-1式)的E,得c a=c b,相应的波函数将E2值代回(4-2-2-1式)的E,得c a=-c b,相应的波函数通过波函数归一化条件,可求得+的结构三、积分意义和H2通常把和称为库仑积分。
根据算符表达式,可得E H代表基态氢原子的能量表示电子处在轨道时受到核b作用的平均吸引能,由于为球形对称,这的平均值近似等于电子在a核处受到的b核吸引能,其绝对值与二核排斥能1/R相近,因符号相反,几乎可以抵消。
据计算,在H2+平衡距离时,J值只是E H的5.5%,所以和叫交换积分,或积分。
积分与和的重叠程度有关,因而是与核间距R有关的函数。
K为负值,为正值, =-13.6eV,就使为负值。
所以当两个原子接近成键时,体系能量降低,起到重大的作用。
S ab称重叠积分或简称S积分。
它与核间距R有关:当R=0时,S ab=1;当R=∞时,S ab→0;R为其他值时,S ab的数值可通过具体计算得到。
将上述关系代入(3.7)式,可得§4.3分子轨道理论和双原子结构( Molecular orbital(MO) theory and diatomic molecules )一、分子轨道理论1.分子中每个电子是在原子核与其它电子组成的平均势场中运动,运动状态可用波函数来描述。
体系总波函数电子函数的乘积体系总Hamilton算符可写为单电子算符之和通过变数分离,可得到单电子函数满足的方程这就是MO采用的独立电子物理模型。
2.分子轨道可用原子轨道线性组合得到(Linear Combination of Atomic Orbitals), 简写为(LCAO)。
由n个原合可得到n个分子轨道,线性组合系数可用变分法或其它方法确定。
两个原子轨道形成的分子轨道,能级低于的称为成键轨道,能级高于原子轨道的称为反键轨道,能级接近原子轨道的一般为非键轨道。
3.两个原子轨道要有效地组合成分子轨道,必须满足对称性匹配,能级相近和轨道最大重叠三个条件。