费马
- 格式:doc
- 大小:82.50 KB
- 文档页数:11

费马定理证明过程全文共四篇示例,供读者参考第一篇示例:费马定理是数论中的一个重要定理,由著名数学家费马在17世纪时提出并据一直引起数学界的广泛关注和研究。
费马定理又称费马大定理,其表述为:对于大于2的正整数n,不存在三个正整数a、b、c,使得满足a^n + b^n = c^n。
费马定理证明的过程是一个漫长而又复杂的数学推理过程,而直到1995年,英国数学家安德鲁·怀尔斯才最终给出了费马定理的证明。
费马定理的证明历经了数百年间许多数学家的探索和努力,费马本人曾在他的笔记本上写下了:“我找到了这个证明,但是这个空间太小,无法容纳这个证明。
”这句话也在一定程度上激发了后世数学家对这个问题的研究和探索。
费马定理的证明过程可以大致被分为三个阶段,分别是费马猜想的提出、证明的辅助工具的建立、以及最终的证明。
费马猜想的提出发生在17世纪,费马在一个边注中提出了这个猜想,称其为“我无法证明的定理”,这也给后世数学家提供了一个极大的挑战。
费马猜想的提出激发了许多数学家的研究热情,这个定理的证明一度被认为是不可能的。
随后的数百年间,许多数学家纷纷投入到费马定理的研究之中,他们提出了许多有关费马定理的猜想和假设。
于是,证明费马定理的难度立即从退化为一个普通的数学难题而变得异常复杂。
在费马定理的证明中,数学家们创立了许多重要的数学概念和工具,例如椭圆曲线、调和模形式等,这一系列的辅助工具为费马定理的证明提供了坚实的数学基础。
这些独立的数学概念在费马定理的证明过程中发挥了至关重要的作用。
最终,英国数学家安德鲁·怀尔斯于1995年成功地证明了费马定理,这也为整个数学界带来了一场轰动。
怀尔斯的证明过程异常复杂,包含了许多高深的数学知识和技巧,这也是费马定理证明过程中最为汗牵动人心的部分。
通过费马定理的证明过程,我们可以看到数学家们在对一个数学难题进行探索和研究的过程中所需付出的辛勤努力和不懈追求。
费马定理的证明,实际上也反映了数学研究的艰辛和复杂性。

费马定理极值必要条件1.引言1.1 概述费马定理是数学中的一个重要定理,它关于极值问题给出了一个必要条件。
极值问题是数学中研究函数在一定区间上取得最大值或最小值的问题,它在经济学、物理学、工程学等领域中都有着广泛的应用。
费马定理通过对函数的导数进行分析,给出了一个在极值点附近的特殊性质。
本文将首先介绍费马定理的背景和相关概念,然后从数学推导的角度解释极值必要条件,并最终利用费马定理推导出极值必要条件的表达式。
通过本文的阐述,读者将能够更加深入地理解极值问题以及费马定理的作用。
1.2 文章结构本文主要分为引言、正文和结论三个部分。
引言部分包括概述、文章结构和目的三个小节。
概述部分将简要介绍费马定理的极值问题及其重要性。
文章结构部分将详细说明本文按照怎样的顺序和方式来讨论费马定理的极值必要条件。
目的部分将阐明本文的写作目的,即通过对费马定理的极值必要条件的推导和讨论,帮助读者更好地理解和运用该定理。
正文部分主要分为费马定理的介绍与极值问题的背景两个小节。
费马定理的介绍将回顾费马定理的基本定义和主要内容,介绍其在求解极值问题中的重要作用。
极值问题的背景将探讨极值问题的起源和应用领域,并举例说明极值问题在实际生活和科学研究中的重要性。
结论部分主要包括极值必要条件的推导和费马定理的极值必要条件两个小节。
极值必要条件的推导将详细推导出费马定理的极值必要条件,通过对导数的分析和运用,解释为什么该定理能够有效地帮助我们找到极值点。
费马定理的极值必要条件将阐述该定理在实际问题中的应用,并列举一些实例进行说明。
综上所述,本文将通过分析费马定理的极值必要条件,帮助读者更好地理解和运用该定理,并展示该定理在求解极值问题中的重要性和应用价值。
1.3 目的本文旨在探讨费马定理在极值问题中的应用,并推导出极值条件的必要性。
通过深入研究费马定理的原理和极值问题的背景,我们将阐述费马定理的极值必要条件,帮助读者更好地理解极值问题的求解过程。

光学费马定理概述光学费马定理是光学中非常重要的一条定理,它描述了光线在传播过程中的轨迹。
费马定理由法国科学家皮埃尔·德·费马于17世纪提出,它是光学的基石之一,为光的传播提供了重要的理论基础。
在本文中,我们将全面、详细、完整地探讨光学费马定理及其应用。
光学费马定理的表述光学费马定理可以用如下方式表述:光线在传播过程中,只有沿着光程时间最小的路径传播,也就是说,光线在两个点之间传播时,它所经过的路径是使得传播时间取极值的路径。
费马定理的表述可以采用最小时间原理或最小路径原理,这两种表述等价。
最小时间原理指出光线传播的路径所需的传播时间是一个极值,而最小路径原理则强调光线传播的路径是一条光程量取极值的路径。
光学费马定理的证明费马定理最早是凭经验提出的,后来由很多科学家进行了证明。
以下是一种较为简单的证明方法:1.假设我们有一个点光源S和两个点A、B。
我们需要证明:光线从S到A再到B的路径光程最短。
2.设光线SA的入射角为α,光线AB的折射角为β。
根据光线在介质中传播的规律,我们知道光线在两个介质界面上的入射角和折射角之间满足折射定律,即n₁sinα = n₂sinβ,其中n₁和n₂分别是介质1和介质2的折射率。
3.根据几何光学,光线的路径符合直线传播原则,因此光线的路径可以用直线段SA和AB来表示。
4.假设有另一条路径SCB,使得光线的光程更短。
则根据费马定理,光线在传播过程中只选取使得光程取极值的路径,所以原路径更接近使得光程取极值的路径。
5.假设光线从点A射出射向CB,令入射角为α’,折射角为β’。
根据折射定律,我们有n₂sinβ’ = n₂sinβ。
6.观察三角形SAB和SCB,我们可以得出两个结论:一是三角形SAB和SCB的入射角相等,即α = α’;二是三角形SAB和SCB的外接圆相同,即它们的半径相等。
7.由于三角形SAB和SCB有共边AB和SB,并且它们的两个角相等,这意味着这两个三角形全等。

费玛(Pierre de Fermat)费马(Pierre de Fermat)(1601-1665)是十七世纪最伟大的数学家之一,1601年8月20日生於法国南部土鲁士(Toulous)附近的一个小镇,父亲是一个皮革商,1665年1月12日逝世。
费马在大学时专攻法律,学成後成为专业的律师,也曾经当过土鲁士议会议员。
费马是一位博览群书见广多闻的谆谆学者,精通数国语言,对於数学及物理也有浓厚的兴趣,是一位多采多艺的人。
虽然他在近三十岁才开始认真专研数学,但是他对数学的贡献使他赢得业余王子(the prince of amateurs)之美称。
这个头衔正足以表彰他在数学领域的一级成就,他在笛卡儿(Descartes)之前引进解析几何,而且在微积分的发展上有重大的贡献,尤其为人称道的是费马和巴斯卡(Pascal)被公认是机率论的先驱。
然而人们所津津乐道的则是他在数论上的一些杰作,例如费马定理(又称费马小定理,以别於费马最後定理):apoa(modp),对任意整数a及质数p均成立。
这个定理第一次出现於1640年的一封信中,此定理的证明後来由欧拉(Euler)发表。
费马为人非常谦虚、不尚名利,生前很少发表论文,他大部分的作品都见诸於与友人之间的信件和私人的札记,但通常都未附证明。
最有名的就是俗称的费马最後定理,费马天生的直觉实在是异常敏锐,他所断言的其他定理,後来都陆续被人证出来。
有先见之明的费马实在是数学史上的一大奇葩。
费玛(Pierre de Fermat)是一个17世纪的法国律师,也是一位业余数学家。
之所以称费玛「业余」,是由于他具有律师的全职工作。
著名的数学史学家贝尔(E. T. Bell)在20世纪初所撰写的著作中,称费玛为「业余数学家之王」。
贝尔深信,费玛比他同时代的大多数专业数学家更有成就。
17世纪是杰出数学家活跃的世纪,而贝尔认为费玛是17世纪数学家中最多产的明星。
费玛的父亲多米尼克·费玛(Dominique Fermat)是一位皮货商,同时也是波蒙特-洛门地区的第二执政官。
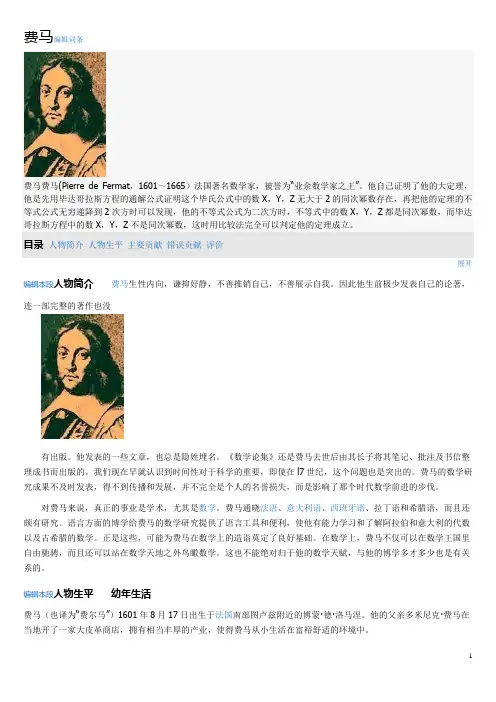
![费马是谁_费马[1]](https://uimg.taocdn.com/6548c593cfc789eb162dc807.webp)
费马是谁_费马[1]皮耶·德·费玛1601年(辛丑年)8月17日出生于法国,于1665年(乙巳年)1月12日逝世,他是律师和业余数学家。
他在数学上的成就不比职业数学家差,他似乎对数论最有兴趣,亦对现代微积分的建立有所贡献。
被誉为“业余数学家之王”。
费马,是当今常见译法,80年代的书籍文章也多见译为“费尔玛”的情况,但“费玛”则少见。
个人成就对解析几何的贡献费马独立于勒奈·笛卡儿发现了解析几何的基本原理。
1629年以前,费马便着手重写公元前三世纪古希腊几何学家阿波罗尼奥斯失传的《平面轨迹》一书。
他用代数方法对阿波罗尼奥斯关于轨迹的一些失传的证明作了补充,对古希腊几何学,尤其是阿波罗尼奥斯圆锥曲线论进行了总结和整理,对曲线作了一般研究。
并于1630年用拉丁文撰写了仅有八页的论文《平面与立体轨迹引论》。
费马于1636年与当时的大数学家梅森、罗贝瓦尔开始通信,对自己的数学工作略有言及。
但是《平面与立体轨迹引论》的出版是在费马去世14年以后的事,因而1679年以前,很少有人了解到费马的工作,而现在看来,费马的工作却是开创性的。
《平面与立体轨迹引论》中道出了费马的发现。
他指出:“两个未知量决定的—个方程式,对应着一条轨迹,可以描绘出一条直线或曲线。
”费马的发现比勒奈·笛卡儿发现解析几何的基本原理还早七年。
费马在书中还对一般直线和圆的方程、以及关于双曲线、椭圆、抛物线进行了讨论。
平面几何有名的费马点。
“费马点”是指位于三角形内且到三角形三个顶点距离之和最短的点。
若给定一个三角形△ABC的话,从这个三角形的费马点P到三角形的三个顶点A、B、C的距离之和比从其它点算起的都要小。
这个特殊点对于每个给定的三角形都只有一个。
对微积分的贡献16、17世纪,微积分是继解析几何之后的最璀璨的明珠。
人所共知,牛顿和莱布尼茨是微积分的缔造者,并且在其之前,至少有数十位科学家为微积分的发明做了奠基性的工作。
费马编辑词条费马费马(Pierre de Fermat,1601~1665)法国著名数学家,被誉为“业余数学家之王”。
他自己证明了他的大定理,他是先用毕达哥拉斯方程的通解公式证明这个毕氏公式中的数X,Y,Z无大于2的同次幂数存在,再把他的定理的不等式公式无穷递降到2次方时可以发现,他的不等式公式为二次方时,不等式中的数X,Y,Z都是同次幂数,而毕达哥拉斯方程中的数X,Y,Z不是同次幂数,这时用比较法完全可以判定他的定理成立。
目录人物简介人物生平主要贡献错误贡献评价展开编辑本段人物简介费马生性内向,谦抑好静,不善推销自己,不善展示自我。
因此他生前极少发表自己的论著,连一部完整的著作也没有出版。
他发表的一些文章,也总是隐姓埋名。
《数学论集》还是费马去世后由其长子将其笔记、批注及书信整理成书而出版的。
我们现在早就认识到时间性对于科学的重要,即使在l7世纪,这个问题也是突出的。
费马的数学研究成果不及时发表,得不到传播和发展,并不完全是个人的名誉损失,而是影响了那个时代数学前进的步伐。
对费马来说,真正的事业是学术,尤其是数学。
费马通晓法语、意大利语、西班牙语、拉丁语和希腊语,而且还颇有研究。
语言方面的博学给费马的数学研究提供了语言工具和便利,使他有能力学习和了解阿拉伯和意大利的代数以及古希腊的数学。
正是这些,可能为费马在数学上的造诣莫定了良好基础。
在数学上,费马不仅可以在数学王国里自由驰骋,而且还可以站在数学天地之外鸟瞰数学。
这也不能绝对归于他的数学天赋,与他的博学多才多少也是有关系的。
编辑本段人物生平幼年生活费马(也译为“费尔马”)1601年8月17日出生于法国南部图卢兹附近的博蒙·德·洛马涅。
他的父亲多米尼克·费马在当地开了一家大皮革商店,拥有相当丰厚的产业,使得费马从小生活在富裕舒适的环境中。
费马的父亲由于富有和经营有道,颇受人们尊敬,并因此获得了地方事务顾问的头衔,但费马小的时候并没有因为家境的富裕而产生多少优越感。

费马大定理费马大定理在数论领域,费马的名字因“费马大定理”而特别响亮。
费马大定理亦称“费马猜想”,最先由费马在阅读巴歇(CBachet)校订的丢番图《算术》时作为卷2命题8的一条页边批注而提出。
1670年费马之子萨缪尔(Samue1)连同其父的批注一起出版了巴歇的书的第二版,此后三个多世纪,费马大定理成为世界上最著名的数学问题,吸引历代数学家为它的证明付出了巨大的努力,有力地推动了数论乃至整个数学的进步;1994年,这一旷世难题被英国数学家威尔斯(A。
Wi1es)解决以下就是费马的页边批注,原文为法文,把一个数的立方分成另两个数的立方和,把一个数的四次方分成另两个数四次方的和,或一般地,把一个数的高于2的任何次方分成两个数的同次方的和是不可能的。
我确信已找到了一个极佳的证明,但书的空白大窄,写不下。
费马小定理费马经常把他的一些研究结果写信告诉其他数学家。
在1640年10月18日致德·贝西(RRdeBessy)的一封信中包含了后以" 费马小定理”著称的如下结果:如果p 是素数,a与p 互素,则被p 整除。
费马曾对欧凡里得《几何原本的定理》,36很感兴趣,该定理是说:如果2”一1是素数,则形如2~’(2”一1)的数是完全数,即它等于其所有因子的和。
这种像2一‘的数费马叫做完全数的根。
在1640年6月写给梅森神父(M。
Mersenne的信中费马有如下结论:如果n 非素,贝2”一 1非素;如果”是素数,则2”一2可被门整除;如果”是素数,贝:J 2、一:只能被形士口2kn+i的素数整除。
同年8月在给贝西的信中,费马讨论了2、+1型的数(当”一2’时, 22t+1型数后被称为“费马数”。
)费马在10月18日写给贝西的信中首先回顾了上述诸信的结果,然后转向“费马小定理”。
以下摘录该信有关部分,转译自趴J.Struik:A、 Source BOok in Math. pp。
28~29。


费马定理高数费马定理,又称为费马小定理,是数论中的一条重要定理,由法国数学家费马在17世纪提出并证明。
这个定理在数论和密码学等领域有着广泛的应用,是一种非常强大的工具。
费马定理的表述非常简洁明了:如果p是一个素数,a是任意一个整数,那么a的p次方减去a一定能被p整除。
换句话说,对于任意一个整数a,当p是一个素数时,a的p次方与a模p同余。
这个定理的证明并不难,可以通过数学归纳法来进行。
首先,当a=1时,定理显然成立。
然后,我们假设当a=k时,定理成立,即k的p次方与k模p同余。
那么我们来看a=k+1的情况,根据二项式定理,(k+1)^p的展开式中,除了首尾两项外,其他所有的项都能被p整除。
而根据归纳假设,k的p次方与k模p同余,所以k^p与k模p同余。
因此,(k+1)^p ≡ k^p + 1 ≡ k + 1 (mod p),即(k+1)^p与k+1模p同余。
由此可见,当a=k+1时,定理也成立。
综上所述,根据数学归纳法,费马定理得证。
费马定理虽然简单,但却有着广泛的应用。
其中一个重要的应用是在密码学中的素数测试。
素数的选取在密码学中至关重要,而费马定理提供了一种快速判断一个数是否为素数的方法。
通过随机选取一些整数a,然后利用费马定理进行检验,如果a的p次方减去a 不能被p整除,那么p一定不是素数。
这种方法称为费马检验,被广泛应用于素数的筛选和生成。
费马定理还有其他的一些应用。
例如,在计算机科学中,费马定理可以用来加速大数取模运算,从而提高计算效率。
在代数数论中,费马定理可以用于研究数的整除性质。
在密码学中,费马定理也被用于构建一些重要的加密算法,如RSA算法。
费马定理的发现和证明,不仅体现了费马的数学才华,也展示了数学的魅力和力量。
费马定理虽然简短,但它以其广泛的应用领域和重要的理论意义,成为了数学中的一颗明星。
通过深入研究和理解费马定理,我们可以更好地应用它解决实际问题,也能更好地欣赏数学的美妙之处。


费马大定理及其应用费马大定理,也被称为费马最后定理,是数学中一个著名的问题。
该定理内容为:对于大于2的正整数n,方程x^n + y^n = z^n 没有整数解。
这个定理的历史可以追溯到17世纪,由法国数学家费马提出,但其证明一直是未解决的难题。
经历了多个数学家的努力,直至20世纪才由英国数学家迪尔金在长达109页的论文中给出了完整的证明。
这又使得费马大定理能够被普及和应用。
费马大定理的应用可以涉及到多个领域。
以下是几个应用实例:1. 密码学密码学是安全通信领域的一个重要分支。
费马大定理可以被用于一种叫做RSA加密的安全协议中。
该协议基于数字分解问题,是一种公钥加密方法。
其原理是将两个大质数p和q相乘得到一个更大的数字N,将其作为公共密钥。
而私密密钥则是p和q的乘积的欧拉函数,并且保证私密密钥是一个大的、难以分解的数字。
RSA的安全性基于质因数分解问题的困难程度,即在没有获得私密密钥的情况下,不能从公共密钥N推断出p和q的值。
而由于费马大定理的存在,可以得出一个结论,即若N可以分解为多个质数的乘积,则证明了费马大定理是假的,因此RSA加密无法进行。
2. 保密信息的随机性随机数是密码学中的一个关键概念。
由于计算机是有规律的,因此需要一种随机方式来寻求保密。
费马大定理可以对随机数的生成产生影响。
当使用某一种算法生成随机数时,如果该算法蕴含着费马大定理,则生成数字的随机性更高。
因此,很多随机数生成器都会利用费马大定理来改进其随机性。
3. 分形几何学分形几何学是一种将自相似性作为几何形态的理论,其灵感来源于自然中的普遍现象。
而费马大定理可以用于特定类型的分形类型,比如类似克莱因瓶等。
在处理这种问题时,费马大定理的求解能力非常关键。
总之,费马大定理虽然看起来并不直接应用,但其背后的数学思想为多个领域的应用和研究提供了坚实的基础。
在安全通信、随机性生成、分形几何学等方面,费马大定理都具有着重要的作用。
它告诉我们,高深的数学理论千回百转,最终,往往都可以为我们所用。
费马定理
费马定理,也称为费马大定理或费马最后定理,是法国数学家皮埃尔·德·费马在17世纪提出的一个数论问题。
该定理的原始陈述是:对于任何大于2的整数n,不可能找到三个正整数a、b、c使得a^n + b^n = c^n成立。
费马在其手稿中提出了这个猜想,并表示自己有证明,但未给出具体证明。
这个猜想在数学界引起了长期的关注和研究,成为数论中的一个重要问题。
直到1994年,英国数学家安德鲁·怀尔斯证明了费马定理的一个特例,即当n大于2时,方程a^n + b^n = c^n没有正整数解。
这一证明被广泛认可并获得了费尔马奖。
然而,怀尔斯的证明并不能推广到一般情况,即对于所有大于2的整数n。
至今,费马定理在一般情况下仍然是一个未解决的问题。
数学家们一直在寻找一个通用的证明方法,但目前还没有找到。
费马定律解释费马定律是光学中重要的基本定律之一,它描述了光在传播过程中的行为。
以下是费马定律的详细解释和各个方面:1. 光的传播定律光的传播定律是指光在传播过程中所遵循的规律。
根据这个定律,光在传播过程中总是沿着最短的路径前进,除非遇到障碍物或介质不均匀。
这意味着光总是遵循最快的路径到达目的地。
2. 最小作用量原理最小作用量原理是费马定律的核心思想。
这个原理认为,在给定的时间内,光沿着所需时间最短的路径传播,以使总作用量最小。
这个作用量是由光在介质中传播时的能量和时间决定的。
3. 干涉现象和衍射现象干涉现象是指两个或多个波源的波的叠加,当波的相位相同或相反时,会出现明暗相间的条纹。
衍射现象是指波绕过障碍物传播的现象,这使得波的传播路径更加复杂。
费马定律解释了这些现象背后的原理,即光总是沿着最短的路径传播,但在遇到障碍物或介质不均匀时,会绕过它们继续传播。
4. 光的本性和光速不变原理光的本性是电磁波,它以光速在真空中传播。
光速不变原理是指光在真空中的速度恒定不变,与观察者的参考系无关。
这个原理是相对论的基础之一,也是费马定律的重要基础。
5. 相对论和量子力学对费马定律的诠释相对论和量子力学是现代物理学的两大支柱。
相对论对时间的概念进行了重新定义,认为时间不再是绝对的,而是与参考系的选择有关。
量子力学则描述了微观粒子在空间和时间上的行为。
在相对论和量子力学的框架下,费马定律仍然成立,但需要考虑到时空的弯曲和量子效应的影响。
6. 费马定律与几何光学基本定律的关系几何光学是光学的一个分支,主要研究光线在物体表面的反射和折射现象。
费马定律与几何光学基本定律之间存在密切的联系。
几何光学的基本定律可以看作是费马定律在不同情况下的具体应用。
例如,反射定律和折射定律可以解释为光在遇到不同介质表面时的行为,而像差和色差等效应也可以用费马定律来解释。
7. 费马定律与薛定谔方程的关系薛定谔方程是描述量子力学中粒子行为的偏微分方程。
数学皮埃尔·费马名言
皮埃尔·费马(Pierre de Fermat)是一位法国数学家,他在数论、代数和几何等领域做出了重要贡献。
以下是一些他的名言:
1. “数学是自然科学的皇后。
”
2. “数学是一种语言,它可以用来表达任何科学或自然现象。
”
3. “数学是一种艺术,它可以用来创造美丽的图案和结构。
”
4. “数学是一种工具,它可以用来解决许多实际问题。
”
5. “数学是一种哲学,它可以用来理解宇宙的本质。
”
这些名言反映了费马对数学的深刻理解和热爱,他认为数学是一种强大的工具,可以用来解决许多实际问题,同时也是一种美丽的艺术和哲学,可以帮助我们更好地理解自然和宇宙的本质。
费马定理的意义
费马定理是17世纪著名数学家莱布尼茨·费马提出的定理,它指出了在整数范围内满足一定条件的数的存在性。
这个定理的重要性不言而喻,它在后来的数学发展中发挥了重要作用。
费马定理的具体内容是:如果n是一个大于2的正整数,那么对于任意正整数a,存在另外一个正整数b,使得a^n +
b^n = c^n成立,其中c也是一个正整数,这个定理也称为费
马大定理,简称费马定理。
费马定理的发现对数学的发展产生了重大影响。
它的发现使得数论的发展有了重大进展,使得数论的研究得以深入探讨,也为数论领域的进一步发展提供了参考。
费马定理的发现也对其他领域的发展产生了重大影响,例如编码理论、计算机科学等。
编码理论是一门探讨数据和息处理的学科,它可以利用费马定理来解决息传输中的安全性问题。
计算机科学也可以利用费马定理来解决复杂的计算问题,从而更有效地研究数据的运算处理。
总之,费马定理提出以后,对后来数学及其他领域的发展都产生了重要影响,它给数论、编码理论和计算机科学研究带来了新的发展思路,使各个领域的研究能够朝着更高的境界发展。
费马定理的重要性不言而喻,它是17世纪数学史上一个
重要的里程碑,也是数学史上一项伟大的成就。
费马大定理:当整数n > 2时,关于x, y, z的不定方程x^n + y^n = z^n.((x , y) = (x , z) = (y , z) = 1[n是一个奇素数]x>0,y>0,z>0)无整数解。
这个定理,本来又称费马最后定理,由17世纪法国数学家费马提出,而当时人们称之为“定理”,并不是真的相信费马已经证明了它。
虽然费马宣称他已找到一个绝妙证明,但经过三个半世纪的努力,这个世纪数论难题才由普林斯顿大学英国数学家安德鲁·怀尔斯和他的学生理查·泰勒于1995年成功证明。
证明利用了很多新的数学,包括代数几何中的椭圆曲线和模形式,以及伽罗华理论和Hecke代数等,令人怀疑费马是否真的找到了正确证明。
而安德鲁·怀尔斯(AndrewWiles)由于成功证明此定理,获得了1998年的菲尔兹奖特别奖以及2005年度邵逸夫奖的数学奖。
1637年,费马在阅读丢番图《算术》拉丁文译本时,曾在第11卷第8命题旁写道:“将一个立方数分成两个立方数之和,或一个四次幂分成两个四次幂之和,或者一般地将一个高于二次的幂分成两个同次幂之和,这是不可能的。
关于此,我确信已发现了一种美妙的证法,可惜这里空白的地方太小,写不下。
”(拉丁文原文: "Cuius rei demonstrationem mirabilem sane detexi. Hancmarginis exiguitas noncaperet.")毕竟费马没有写下证明,而他的其它猜想对数学贡献良多,由此激发了许多数学家对这一猜想的兴趣。
数学家们的有关工作丰富了数论的内容,推动了数论的发展。
对很多不同的n,费马定理早被证明了。
但数学家对一般情况在首二百年内仍一筹莫展。
1908年,德国佛尔夫斯克宣布以10万马克作为奖金奖给在他逝世后一百年内,第一个证明该定理的人,吸引了不少人尝试并递交他们的“证明”。
在一战之后,马克大幅贬值,该定理的魅力也大大地下降。
1983年,en:Gerd Faltings证明了Mordell猜测,从而得出当n > 2时(n为整数),只存在有限组互质的a,b,c使得a^n + b^n= c*n。
1986年,Gerhard Frey 提出了“ε-猜想”:若存在a,b,c使得a^n + b^n = c^n,即如果费马大定理是错的,则椭圆曲线y^2 =x(x - a^n)(x + b^n) 会是谷山-志村猜想的一个反例。
Frey的猜想随即被KennethRibet证实。
此猜想显示了费马大定理与椭圆曲线及模形式的密切关系。
1995年,怀尔斯和泰勒在一特例范围内证明了谷山-志村猜想,Frey的椭圆曲线刚好在这一特例范围内,从而证明了费马大定理。
怀尔斯证明费马大定理的过程亦甚具戏剧性。
他用了七年时间,在不为人知的情况下,得出了证明的大部分;然后于1993年6月在一个学术会议上宣布了他的证明,并瞬即成为世界头条。
但在审批证明的过程中,专家发现了一个极严重的错误。
怀尔斯和泰勒然后用了近一年时间尝试补救,终在1994年9月以一个之前怀尔斯抛弃过的方法得到成功,这部份的证明与岩泽理论有关。
他们的证明刊在1995年的数学年刊(en:Annalsof Mathematics)之上。
1:欧拉证明了n=3的情形,用的是唯一因子分解定理。
2:费马自己证明了n=4的情形。
3:1825年,狄利克雷和勒让德证明了n=5的情形,用的是欧拉所用方法的延伸,但避开了唯一因子分解定理。
4:1839年,法国数学家拉梅证明了n=7的情形,他的证明使用了跟7本身结合的很紧密的巧秒工具,只是难以推广到n=11的情形;于是,他又在1847年提出了“分圆整数”法来证明,但没有成功。
5:库默尔在1844年提出了“理想数”概念,他证明了:对于所有小于100的素指数n,费马大定理成立,此一研究告一阶段。
6:勒贝格提交了一个证明,但因有漏洞,被否决。
7:希尔伯特也研究过,但没进展。
8:1983年,德国数学家法尔廷斯证明了一条重要的猜想——莫代尔猜想x的平方+y 的平方=1这样的方程至多有有限个有理数解,他由于这一贡献,获得了菲尔兹奖。
9:1955年,日本数学家谷山丰首先猜测椭圆曲线于另一类数学家们了解更多的曲线——模曲线之间存在着某种联系;谷山的猜测后经韦依和志村五郎进一步精确化而形成了所谓“谷山——志村猜想”,这个猜想说明了:有理数域上的椭圆曲线都是模曲线。
这个很抽象的猜想使一些学者搞不明白,但它又使“费马大定理”的证明向前迈进了一步。
10:1985年,德国数学家弗雷指出了“谷山——志村猜想”和“费马大定理”之间的关系;他提出了一个命题:假定“费马大定理”不成立,即存在一组非零整数A,B,C,使得A的n次方+B的n次方=C 的n次方(n>2),那么用这组数构造出的形如y的平方=x(x+A的n次方)乘以(x-B的n次方)的椭圆曲线,不可能是模曲线。
尽管他努力了,但他的命题和“谷山——志村猜想”矛盾,如果能同时证明这两个命题,根据反证法就可以知道“费马大定理”不成立,这一假定是错误的,从而就证明了“费马大定理”。
但当时他没有严格证明他的命题。
11:1986年,美国数学家里贝特证明了弗雷命题,于是希望便集中于“谷山——志村猜想”。
12:1993年6月,英国数学家维尔斯证明了:对有理数域上的一大类椭圆曲线,“谷山——志村猜想”成立。
由于他在报告中表明了弗雷曲线恰好属于他所说的这一大类椭圆曲线,也就表明了他最终证明了“费马大定理”;但专家对他的证明审察发现有漏洞,于是,维尔斯又经过了一年多的拼搏,于1994年9月彻底圆满证明了“费马大定理”。
13:至1991年对费马大定理指数n<1,000,000费马大定理已被证明, 但对指数n>1,000,000没有被证明. 已成为世界数学难题。
1676年数学家根据费马的少量提示用无穷递降法证明n=4。
1678年和1738年德国数学家莱布尼兹和瑞士数学家欧拉也各自证明n=4。
1770年欧拉证明n=3。
1823年和1825年法国数学家勒让德和德国数学家狄利克雷先后证明n=5。
1832年狄利克雷试图证明n=7,却只证明了n=14。
1839年法国数学家拉梅证明了n =7,随后得到法国数学家勒贝格的简化……19世纪贡献最大的是德国数学家库麦尔,他从1844年起花费20多年时间,创立了理想数理论,为代数数论奠下基础;库麦尔证明当n<100时除37、59、67三数外费马大定理均成立。
为推进费马大定理的证明,布鲁塞尔和巴黎科学院数次设奖。
1908年德国数学家佛尔夫斯克尔临终在哥廷根皇家科学会悬赏10万马克,并充分考虑到证明的艰巨性,将期限定为100年。
数学迷们对此趋之若鹜,纷纷把“证明”寄给数学家,期望凭短短几页初等变换夺取桂冠。
德国数学家兰道印制了一批明信片由学生填写:“亲爱的先生或女士:您对费马大定理的证明已经收到,现予退回,第一个错误出现在第_页第_行。
”在解决问题的过程中,数学家们不但利用了广博精深的数学知识,还创造了许多新理论新方法,对数学发展的贡献难以估量。
1900年,希尔伯特提出尚未解决的23个问题时虽未将费马大定理列入,却把它作为一个在解决中不断产生新理论新方法的典型例证。
据说希尔伯特还宣称自己能够证明,但他认为问题一旦解决,有益的副产品将不再产生。
“我应更加注意,不要杀掉这只经常为我们生出金蛋的母鸡。
”数学家就是这样缓慢而执着地向前迈进,直至1955年证明n<4002。
大型计算机的出现推进了证明速度,1976年德国数学家瓦格斯塔夫证明n<125000,1985年美国数学家罗瑟证明n<41000000。
但数学是严谨的科学,n值再大依然有限,从有限到无穷的距离漫长而遥远。
1983年,年仅29岁的德国数学家法尔廷斯证明了代数几何中的莫德尔猜想,为此在第20届国际数学家大会上荣获菲尔茨奖;此奖相当于数学界的诺贝尔奖,只授予40岁以下的青年数学家。
莫德尔猜想有一个直接推论:对于形如x^n+y^n=z^n(n≥4)的方程至多只有有限多组整数解。
这对费马大定理的证明是一个有益的突破。
从“有限多组”到“一组没有”还有很大差距,但从无限到有限已前进了一大步。
1955年日本数学家谷山丰提出过一个属于代数几何范畴的谷山猜想,德国数学家弗雷在1985年指出:如果费马大定理不成立,谷山猜想也不成立。
随后德国数学家佩尔提出佩尔猜想,补足了弗雷观点的缺陷。
至此,如果谷山猜想和佩尔猜想都被证明,费马大定理不证自明。
事隔一载,美国加利福尼亚大学伯克利分校数学家里比特证明了佩尔猜想。
1993年6月,英国数学家、美国普林斯顿大学教授安德鲁·怀尔斯在剑桥大学牛顿数学研究所举行了一系列代数几何学术讲演。
在6月23日最后一次讲演《椭圆曲线、模型式和伽罗瓦表示》中,怀尔斯部分证明了谷山猜想。
所谓部分证明,是指怀尔斯证明了谷山猜想对于半稳定的椭圆曲线成立——谢天谢地,与费马大定理相关的那条椭圆曲线恰好是半稳定的!这时在座60多位知名数学家意识到,困扰数学界三个半世纪的费马大定理被证明了!这一消息在讲演后不胫而走,许多大学都举行了游行和狂欢,在芝加哥甚至出动了警察上街维持秩序。
但专家对他的证明审察发现有漏洞,于是,怀尔斯又经过了一年多的拼搏,于1994年9月20日上午11时彻底圆满证明了“费马大定理”五十年代日本数学家谷山丰首先提出一个有关椭圆曲线的猜想,后来由另一位数学家志村五郎加以发扬光大,当时没有人认为这个猜想与费马定理有任何关联。
在八十年代德国数学家佛列将谷山丰的猜想与费马定理联系在一起,而安德鲁·怀尔斯所做的正是根据这个关联论证出一种形式的谷山丰猜想是正确的,进而推出费马最后定理也是正确的。
这个结论由威利斯在1993年的6月21日於美国剑桥大学牛顿数学研究所的研讨会正式发表,这个报告马上震惊整个数学界,就是数学门墙外的社会大众也寄以无限的关注。
不过怀尔斯的证明马上被检验出有少许的瑕疵,于是怀尔斯与他的学生又花了十四个月的时间再加以修正。
1994年9月19日他们终于交出完整无瑕的解答,数学界的梦魇终於结束。
1997年6月,怀尔斯在德国哥庭根大学领取了佛尔夫斯克尔奖。
当年的十万马克约为两百万美金,不过怀尔斯领到时,只值五万美金左右,但安德鲁·怀尔斯已经名列青史,永垂不朽了。
用不定方程来表示,费马大定理即:当n > 2时,不定方程x^n + y^n = z^n 没有xyz≠0的整数解。
为了证明这个结果,只需证明方程x^4 +y^4 = z^4 ,(x , y) = 1和方程x^p + y^p = z^p ,(x , y) = (x , z) = (y , z) =1[p是一个奇素数]均无xyz≠0的整数解。