差分方程建立离散系统的状态空间表达式

−T −T −T
−T −T
−T
)
−T
z 2 − (1 + e −T ) z + e −T
)
0 x( k + 1) = −T -e
0 x ( k ) + u( k ) −T 1+ e 1 1
y( k ) = 1 − e −T − Te − T
T − 1 + e −T x( k )
x(k+1) = [I +TA]x(k) + TBu(k) G = I +TA H =TB
17
0 1 0 & 的近似离散化方程。 例2-13 求 x = x + 1 u 的近似离散化方程。 0 −2
解： G = I + TA = 1 0 + 0 − T = 1 − T 0 1 0 − 2T 0 1 − 2T
x( k + 1) = G ( k ) x( k ) + H ( k )u( k ) y( k ) = C ( k ) x ( k ) + D( k )u( k )
2
2.结构图 2.结构图
3
3.差分方程和脉冲传递函数与离散状态空间表 3.差分方程和脉冲传递函数与离散状态空间表 达式之间的转换 在单变量离散系统中， 在单变量离散系统中，数学模型分为差分方程 和脉冲传递函数两类， 和脉冲传递函数两类，它们与离散状态空间表达式 之间的变换，和连续系统分析相类似。 之间的变换，和连续系统分析相类似。 离散 差分方程 连续 D.E
x1 ( k ) y ( k ) = [1 −4 ] + u( k ) x2 ( k )

2326.4 离散系统的数学模型为研究离散系统的性能，需要建立离散系统的数学模型。

线性离散系统的数学模型有差分方程、脉冲传递函数和离散状态空间表达式三种。

本节主要介绍差分方程及其解法，脉冲传递函数的定义，以及求开环脉冲传递函数和闭环脉冲传递函数的方法。

有关离散状态空表达式及其求解，将在第8章介绍。

6.4.1 线性常系数差分方程及其解法对于线性定常离散系统，k 时刻的输出)(k c ，不但与k 时刻的输入)(k r 有关，而且与k 时刻以前的输入 ),2(),1(--k r k r 有关，同时还与k 时刻以前的输出 ),2(),1(--k c k c 有关。

这种关系一般可以用n 阶后向差分方程来描述，即∑∑==-+--=mj jni i j k r bi k c a k c 01)()()( (6-34)式中，i a ，i =1，2，…，n 和j b ，j ＝0，1，…，m 为常系数，n m ≤。

式(6-34)称为n 阶线性常系数差分方程。

线性定常离散系统也可以用n 阶前向差分方程来描述,即∑∑==-++-+-=+mj jni i j m k r bi n k c a n k c 01)()()( (6-35)工程上求解常系数差分方程通常采用迭代法和z 变换法。

1. 迭代法若已知差分方程式(6-34)或式(6-35)，并且给定输出序列的初值，则可以利用递推关系，在计算机上通过迭代一步一步地算出输出序列。

例6-10 已知二阶差分方程)2(6)1(5)()(---+=k c k c k r k c输入序列1)(=k r ，初始条件为1)1(,0)0(==c c ，试用迭代法求输出序列)(k c ， ,5,4,3,2,1,0=k 。

解 根据初始条件及递推关系，得0)0(=c 1)1(=c6)0(6)1(5)2()2(=-+=c c r c 25)1(6)2(5)3()3(=-+=c c r c 90)2(6)3(5)4()4(=-+=c c r c301)3(6)4(5)5()5(=-+=c c r c2. z 变换法233设差分方程如式(6-34)所示，对差分方程两端取z 变换，并利用z 变换的实数位移定理，得到以z 为变量的代数方程，然后对代数方程的解)(z C 取z 反变换，可求得输出序列)(k c 。

（28） 状态空间方程实现非唯一，书p28, 图1.16b求得其对应的传递函数为： （29）
为求得 令式（29）与式（26）相等，通过对 多项式系数的比较得： 故得： （30）
也可将式(30)写成式(31)的形式，以便记忆。 （31）
将上图a的每个积分器输出选作状念变最，如图所示，得这种结构下的 状态空间表达式：
解：
→
→
u
y
－
＋
例： 解： 比例积分环节： → → u y ＋
例：
解：
综合惯性环节、积分环节模拟结构图得：
u
y
－
＋
u
y
解：选积分器的输出为状态变量得：
u
y
状态方程：
输出方程：
状态空间表达式
1.3.2 从系统的机理出发建立状态空间表达式
一般常见的控制系统，按其能量属性，可分为电气、机械、机电、气动 液压、热力等系统。根据其物理规律，如基尔霍夫定律、牛顿定律、能量守 恒定律等，即可建立系统的状态方程。当指定系统的输出时，很容易写出系 统的输出方程。
同一系统，经非奇异变换后，得：
其特征方程为：
（44）
1.5.2 系统特征值的不变性及系统的不变量
1.系统特征值
式(43)与式(44)形式虽然不同，但实际是相等的，即系统的非奇异变换，其特征值是不变的。可以证明如下：
将特征方程写成多项式形式 由于特征 值全由特征多项式的系数 唯一确定，而特征值 经非奇异变换是不变的，那么这些系统 也是不变 的量。所以称特征多项式的系数为系统的不变量。
(3)有共轭复根时，以四阶系统其中有一对共轭复根为例，即 此时
1.6 从状态空间表达式求传递函数阵
1.6.1 传递函数(阵)

06
CATALOGUE
离散系统的发展趋势与展望
离散系统的新理论与方法
离散系统的新理论
随着科技的不断发展，离散系统的新理论也在不断涌现。例如，离散概率论、离散控制论、离散信息论等，这些 新理论为离散系统的发展提供了重要的理论支持。
离散系统的新方法
在实践中，人们不断探索新的方法来处理离散系统的问题。例如，离散数学、离散优化算法、离散模拟技术等， 这些新方法为离散系统的研究提供了更有效的工具。
状态转移图的绘制方法
根据状态方程，通过计算或模拟得到状态变量的时间序列解，并绘 制成图形。
状态转移图的应用
通过观察状态转移图，可以直观地了解系统动态行为和变化趋势。
04
CATALOGUE
离散系统的稳定性分析
线性离散系统的稳定性分析
定义
线性离散系统是指系统 的数学模型可以表示为 离散时间的线性方程组 ，如差分方程或离散时 间状态方程。
状态方程
1
状态方程是描述离散时间动态系统状态变化的基 本方程，通常表示为离散时间序列的递推关系。
2
状态方程通常由当前状态和输入量来预测下一个 状态，是离散系统分析的重要基础。
3
状态方程的解法包括递归法和矩阵法等，其中递 归法较为直观，而矩阵法适用于大规模系统。
转移矩阵
转移矩阵是描述离散系统状态转移关系的矩阵，其元素表示状态之间的转 移概率。
社会科学领域
在社会学、经济学、管理学等领域中，离散系统也有着广泛的应用。例如，在经济学中，离散模型被用 于描述经济活动中的离散事件；在社会学中，离散模型被用于描述社会结构和社会动态。
离散系统未来的研究方向
要点一
复杂离散系统的研究
随着科技的不断发展，复杂离散系统 的研究已经成为一个重要的研究方向 。例如，复杂网络、离散事件动态系 统等，都是复杂离散系统的研究重点 。

y( k ) x1 ( k ) h0u( k )
2019/1/5
13
写成矩阵形式，得到状态空间描述为：
1 x1 ( k 1) 0 x ( k 1) 0 0 2 x ( k 1 ) 0 n 1 0 xn ( k 1) a0 a1 0 1 0 0 x1 ( k ) h1 x2 ( k ) h2 0 u( k ) 1 xn1 ( k ) hn1 an1 xn ( k ) hn
y( k ) x1 ( k )
2019/1/5 10
写成矩阵形式，得到离散系统的状态空间表达式：
x1 ( k 1) 0 x ( k 1) 0 2 xn1 ( k 1) 0 xn ( k 1) a0 1 0 0 0 1 0 0 x1 ( k ) 0 x2 ( k ) 0 0 u( k ) 1 x n 1 ( k ) 0 an1 xn ( k ) b0
2019/1/5
8
4、将差分方程化为状态空间描述：或转换为Z传递函数，再求 离散系统差分方程描述形式：
y( k n) an1 y( k n 1) a1 y( k 1) a0 y( k ) bnu( k n) bn1u( k n 1) b0u( k ) ( k 0,1,2)
当初始状态 x(0) 0 时，对以下状态空间描述做Z变换：
x ( k 1) Gx( k ) Hu( k ) y( k ) Cx ( k ) Du( k )

T{ax [n]}= a2x2[n] 除了a=0,1情况，T{ax [n]} aT{x [n]}。故系统不满 足线性系统的的定义，所以系统是非线性系统。
2. 时不变系统
如果 T[x(n)]=y(n)， 则 T[x(n-n0)]=y(n-n0) （ n0为任意整数） 即系统的特性不随时间而变化。
线性时不变系统简称为：LTI
1 az1 z M 1 (z a)
如果a为正实数，H（z）的零点为
2
zk
jk
ae M ,k
0,1,, M
1
这些零点分布在|z|=a的圆周上，对圆周进行M等分，它的第一个零点k=0，
恰好与分母上的极点（z-a）抵消，因此，整个函数H（z）共有
2
改写成 y（n-1）=2[ y（n）-1.5x（n）] 此时 y（0）=2[ y（1）-1.5x(1) ]=0
y(1) 2y(0) 1.5x(0) 1.5 1 1
2
y(2) 2y(1) 1.5x(1) 1.5 1 2
2
依此类推，得到
y(n) h(n) 1.5 1 n u(n 1) 2
例：若系统输入输出关系为： y(n)=nx(n)
试判断系统是否为时不变系统？
3. 线性时不变系统
线性时不变系统——既满足迭加原理又具有时不变性的系统。线性时不 变系统可以用单位脉冲响应来表示。
我们知道，任一序列都可表示成各延时单位脉冲序列的加权和
x(n) x(m) (n m) m
如令h（n）为系统对单位脉冲序列的响应， h（n）=T[δ（n）]
因此 y(n) x(m)h(n m) x(n) * h(n) m 该式表明：对任何线性时不变系统，可完全通过其单位脉冲响应h（n）来
表示。这个公式和模拟系统的卷积是类似的，称为离散卷积，或线性卷积。 卷积过程： ① 对 h（ m）绕纵轴折叠，得h（-m）； ② 对 h（-m）移位得 h（n-m）； ③ 将 x(m)和 h(n-m)所有对应项相乘之后相加，得离散卷积结果 y（n）。

即 Y (sC 1 s 1 1)3(sC 1 s 2 1)2sC 13 s1sC 2 s2sC 3 s3 U ( • s )
选取
X 11
(s
1 s1
)
3
U
X 13
s
1
U s1
X12
(s
1 s1
)2
U
X
2
s
1 s2
U
X3
s
1 s3
U
x•11 s1 x 1 1 x 1 2 x12 s1x12 x13
x2
s 1
xY
s 1 3
8
（ 1 ） 、 确 定 状 态 变 量 ， 若 选 择
若将传递函数进行一般实现，并取积分 器的输出为状态变量。
（ 2 ） 、 列 写 状 态 方 程
•
x1 8x3 15u
•
x2 x114x38u
•
x3 x2 7x3u
（ 3 ） 、 写 成 矩 阵 形 式
7 14
0 0 8 15
G (s)G 1(s)G 2(s) [ 3 ] 、 系 统 一 和 二 反 并 联 时 ( 负 反 馈 )
u
（A1,B1,C1） y
（A2,B2,C2）
G (s ) [I G 1 (s )G 2 (s )] 1 G 1 (s )
参见 p.461
作业：p.536;9-13,
电气工程学院
➢关于输入输出解耦控制问题 解耦问题是一个比较复杂的问题，对线性定常系统就有几套理论：
于是有； (1)、 选 状 态 变 量
X1(s)
s
1 U(s), 1
X2(s)
s
1
U(s), 2
X3(s)

例7-16 已知系统差分方程、初始状态和r(k)如下
n
c(k ) 5c(k 1) 6c(k 2) r (k )； r (k ) 1(k )； c(0) 0, c(1) 1。
试用递推法计算输出序列c(k)，k = 0,1,2,…,10。
解 采用递推关系 c(k+2) = 1+5c(k+1) - 6c(k)； 得 c(0) 0；c(1) 1；
7-4 离散系统的数学模型
1. 离散系统的数学定义
2. 线性常系数差分方程及其解法
3. 脉冲传递函数 4. 组合环节的等效脉冲传递函数 5. 闭环系统的脉冲传递函数计算
6. Z变换的局限性及修正Z变换
离散系统的数学模型 与连续系统类似，单输入单输出线性时不变 离散系统数学模型有三大类：差分方程 ( 时域 ) 、 脉冲传递函数 ( 复数域 ) 和状态空间模型。本节重 点讨论差分方程及其解法、脉冲传递函数的基本 概念、开环和闭环脉冲传递函数的建立方法。 1. 离散系统的数学定义
k 1
2
z c(kT ) ( z 2)( z 3)
z k 1 ( z 1)( z 2) z 3
z 1
z ( z 1)( z 3)
k 1
z 2
0.5 2
k 1
0.5 3 ，k 0；
k 1
c(2) 6； c(3) 25； c(10) 86526；
┇
k
c(0) 1； c(1) 1 0.5 1.5；
lim c(k ) 1.0；
这两个示例表明，用递推法求解差分方程， 计算过于烦琐，不易得到c(k)的通项表达式。
(2) Z变换法(例7-17 )

现代控制理论知识结构（研究的顺序符合控制理论的一般步骤：系统建模、模型求解、提出性能指标、系统设计校正。

）一、系统的状态空间建模1、从2个角度4种方法建立状态空间表达式。

2、状态空间表达式的线性变换3、由状态空间表达式反推传递函数4、建立离散系统的状态空间表达式5、需要注意的地方6、公式集锦二、状态空间表达式的求解1、无输入的情况下状态变量求解（齐次方程求解）2、对于有输入的系统的状态变量求解（非齐次方程）3、、状态转移矩阵的性质及判别4、对于系统的状态转移矩阵的唯一性研究5、几点注意6、公式集锦三、提出性能指标：能控性和能观性。

及其判断方法1、提出能控性和能观性的原因。

2、判断能控性和能观性的方法：直观分析和四大判据3、得到能观能控标准型的两种方法4、几点注意5、系统的结构分解6、公式集锦四、系统设计校正：状态反馈1、状态反馈改变系统性能的原理2、状态反馈的特点3、两种计算K阵的方法4、公式集锦一、系统的状态空间建模1、从2个角度4种方法建立状态空间表达式。

已知一个物理系统，我们给它建立了一个微分方程模型，我们想用经典理论和现代理论对其进行研究，即建立传递函数模型和状态空间表达式。

经典的传递函数模型太好建了呀，直接变换，一比就出来了。

可是状态空间模型呢，我们有两个角度①我们当然可以根据模型的定义，利用系统的性能进行建模，这也是建立状态空间表达式的第一种方法。

②从经典控制模型的角度，首先1、运用将传递函数或结构图降阶，化成状态空间特有的结构图（不同于传递函数结构图，它只有积分器、加法器、减法器、系数器）这是第二种方法。

2、从经典控制理论的微分方程来建立。

（分成了单入单出、单入单出输入有导数项、多路多出）微分方程就是一串积分器，再加系数反馈就好了。

这是第三种方法3、传递函数（有三种方法、直接程序法、串联程序法、并联程序法）。

这是第四种方法这样说来，其实状态空间表达式所对应的结构图是从经典控制理论角度（三种方法）建立其模型的中介。

第一章1.1 计算机控制系统是怎么样分类的？按功能和控制规律可各分几类？答：计算机控制系统可按功能分类，按控制规律分类和按控制方式分类。

按功能计算机控制系统的分类：（1）数据处理系统。

（2）直接数字控制（简记为DDC）。

（3）监督控制（简记为SCC）。

（4）分级控制。

（5）集散控制。

（6）计算机控制网络。

按照控制规律计算机控制系统的分类：（1）程序和顺序控制。

（2）比例积分微分控制（简称PID控制）。

（3）有限拍控制。

（4）复杂规律控制。

（5）智能控制。

1.2 计算机控制系统由哪些部分组成？并画出方框图。

答：计算机控制系统由控制对象、执行器、测量环节、数字调节器及输入输出通道等组成。

方框图：P115 图1.21 输出反馈计算机控制系统1.9 简述采样定理及其含义。

答：采样定理：如果采样角频率ωω=2π/T大于2ωmax，即ωω≥2ωmax，则采样的离散信号ω∗(t)能够不失真地恢复原来的连续信号y(t)。

式中ωmax是连续信号y(t)的频谱特性中的最高角频率。

含义：要使采样信号ω∗(t)能够不失真地恢复原来的连续信号y(t)，必须正确选择采样角频率，使ωω≥2ωmax1.10 多路巡回检测时，采样时间τ，采样周期T和通道数N之间的关系。

答：采样时间是足够短的时间，y(kT)≈y(kT+?t),0<?t<ωω。

应满足 T≥Nωω。

1.12 设有模拟信号(0～5)V 和(2.5～5)V ，分别用8位、10位和12位A/D 转换器，试计算并列出各自的量化单位和量化误差。

答：量化单位q=ωωωω∗−ωωωω∗2ω−1≈ωωωω∗−ωωωω∗2ω,量化误差ε=q /2根据以上公式可求得(0~5)V ：(2.5~5)V ：1.14 试述数模转换器的作用？如何选择转换器的位数？答：数模转换器把数字量u(kT)转换成离散的模拟量ω∗(t)。

转换的精度取决模-数转换器的位数n ，当位数足够多时，转换可以达到足够高的精度。

3-1 判断下列系统的状态能控性和能观测性。系统中 a,b,c,d 的取值对能控性和能观性是否 有关，若有关，其取值条件如何？ （1）系统如图 3.16 所示：
解：由图可得：
状态空间表达式为：
由于 、 、 与 无关，因而状态不能完全能控，为不能控系统。由于 只与 有关， 因而系统为不完全能观的，为不能观系统。 （3）系统如下式：
《现代控制理论》课后习题全部答
解：如状态方程与输出方程所示，A 为约旦标准形。要使系统能控，控制矩阵 b 中相对于
约旦块的最后一行元素不能为 0，故有
。
要使系统能观，则 C 中对应于约旦块的第一列元素不全为 0，故有
。
3-2 时不变系统
试用两种方法判别其能控性和能观性。 解：方法一：
方法二：将系统化为约旦标准形。
解：将此图化成模拟结构图
图 2.2 系统结构图
列出状态方程
《现代控制理论》课后习题全部答
则离散时间状态空间表达式为
由
和
得：
当 T=1 时 当 T=0.1 时
《现代控制理论》课后习题全部答
《现代控制理论》课后习题全部答
《现代控制理论》课后习题全部答
《现代控制理论》课后习题全部答
第三章习题答案
《现代控制理论》课后习题全部答
，
中有全为零的行，系统不可控。 中没有全为 0 的列，系统可观。 3-3 确定使下列系统为状态完全能控和状态完全能观的待定常数
解：构造能控阵：
要使系统完全能控，则 构造能观阵：
，即
要使系统完全能观，则 3-4 设系统的传递函数是
，即
（1）当 a 取何值时，系统将是不完全能控或不完全能观的？
《现代控制理论》课后习题全部答

向量－矩阵形式为
x1 (k + 1) 0 1 0 0 x1 (k) 0
x2 (k
+ 1)
0
0
1
0
x2 (k)
0
= 0 0 0 0 + u(k)
xn−1
(k
+
1)
0
0
0
1
x
n−1
(k
)
0
xn (k + 1) − a0 − a1 − a2 − an−1 xn (k) 1
量和输入量：ai ,bi (i = 0,1,2,, n且an = 1) 为表征系统特性的常系
数。考虑初始条件为零时的z变换关系有
[ y(k)] = Y (z), [ y(k + i)] = ziY (z)
对式(9—87)两端取z变换并加以整理可得
G(z)
=
Y (z) U (z)
=
bn z n + bn−1 z n−1 + + b1 z + b0 z n + an−1 z n−1 + + a1 z + a0
（9－95）
三、线性定常离散动态方程的解
求解离散动态方程的方法友递推法和z变换法，这里只介绍常
用的递推法，对z变换法感兴趣的读者可参阅有关书籍。下面以解
离散化状态方程为例来说明如何使用递推法求解。令式（9－93）
中的k = 0,1,, k −1可得到 T,2T,, kT 时刻的状态，即
k = 0 : x(1) = (T )x(0) + G(T )u(0)
=
bn
+
z n−1 n−1
+

现代控制理论理论教案绪论【教学目的】了解现代控制理论的基本原理及方法，以便进行系统分析与设计，同时为进一步学习现代控制理论打下较扎实的基础。

【教学重点】了解控制理论发展的三个阶段并掌握各阶段的主要任务。

【教学方法及手段】课堂教学【课外作业】阅读教材【学时分配】2学时【教学内容】本教材绪论部分主要讲述了以下几个问题：一、控制理论发展简况1）古典控制理论：研究对象以单输入、单输出线性定常系统为主，以传递函数为系统的基本描述，以频率法和根轨迹法为主要分析与设计手段。

2）现代控制理论以状态状态空间模型为基础，可研究多输入、多输出、时变、非线性等各种对象；研究系统内部结构的关系提出了能控性、能观测性等重要概念，提出了不少设计方法。

3）大系统与智能控制阶段。

二、现代控制理论的基本内容(1)线性多变量系统理论。

这是现代控制理论中最基础、最成熟的部分。

它揭示系统的内在想律，从能控性、能观测性两个基本概念出发，研究系统的极点配置、状态观测器设计和抗干扰问题的一般理论。

(2)最优控制理论。

在被控对象数学模型已知的情况下，寻求一个最优控制规律(或最优控制函数)，使系统从某一个初始状态到达最终状态并使控制系统的性能在某种意义下是最优的。

(3)最优估计理论。

在对象数学模型已知的情况下，最优估计理论研究的问题是如何从被噪声污染的观测数据中，确定系统的状态，并使这种估计在某种意义下是最优的。

由于噪声是随机的，而且是非乎稳随机过程(随机序列)，这种憎况下的状态估计是卡尔曼提出和解决的，故又称卡尔曼滤波。

这种滤波方法是保证状态估计为线性无偏最小估计误差方差的估计。

(4)系统辨识与参数估计。

这是基于对象的输入、输出数据、在希望的估计准则下，建立与对象等价的动态系统(即建立对象的数学模型)，由于效学模型一船地说，是由阶致和参数决定的。

因此，要决定系统的阶数和参数(即参数估计)。

三、本课程的基本任务该课程是工业自动化专业的一门重要的专业基础课程。

计算机控制系统是怎样分类的按功能和控制规律可分为几类答：可以按照系统的功能、控制规律、控制方式进行分类。

按功能可分为：a.数据处理系统b.直接数字控制（DDC）c.监督控制（SCC）d.分级控制e.集散型控制（DCS）f.计算机控制网络按照控制规律可分为：a.程序和顺序控制控制c.有限拍控制d.复杂规律的控制e.智能控制计算机控制系统由哪些部分组成并画出方框图。

答：由数字控制器、D/A转换器、保持器、执行器、被控对象、测量元件、变送单元、A/D转换器组成。

数字控制器D/A保持器执行器被控对象A/D变送单元测量元件+-给定值被控参数设有模拟信号（0-5）V和（）V，分别用8位、10位和12位A/D转换器，使计算并列出各自的量化单位和量化误差。

计算机控制系统由哪些主要的性能指标如何衡量答：计算机控制系统的性能跟连续系统类似，可以用稳定性、能控性、能观测性、稳定特性、动态特性来表征，相应地用稳定裕量（相角裕量和幅值裕量）、稳态指标（稳态误差）、动态指标（超调量、调节时间、峰值时间、振荡次数）和综合指标（积分型指标、末值型指标、复合型指标）来衡量一个系统的好坏或优劣。

计算机控制将向哪些方向发展答：a.最优控制b.自适应控制c.系统辨识d.分级控制e.集散型控制已知拉氏变换式，试求离散化后的Z变换式：s解:1/s的拉氏反变换是1，故Z变换式是z/z-1。

试求下列函数的Z反变换;已知系统的方框图，G(s)=K/s(s+a)，试求系统（见习题）的闭环Z传递函数Gc （z）。

(1-e-Ts)/sR(s)T TY(z)G(s)T=1s_+所有牵扯到求闭环传递函数的题目，将a,T代入上式即可。

T=1s,G(s)=1/s（s+），试分析系统在典型输入作用下的输出响应和稳态误差。

1.单位阶跃响应2.单位速度输入3.单位加速度输入解：带入a= T=1s K=1得闭环传递函数（单位阶跃响应）已知系统反方框图如中，G(s)=K/s(s+1)，试求系统的临界放大倍数。

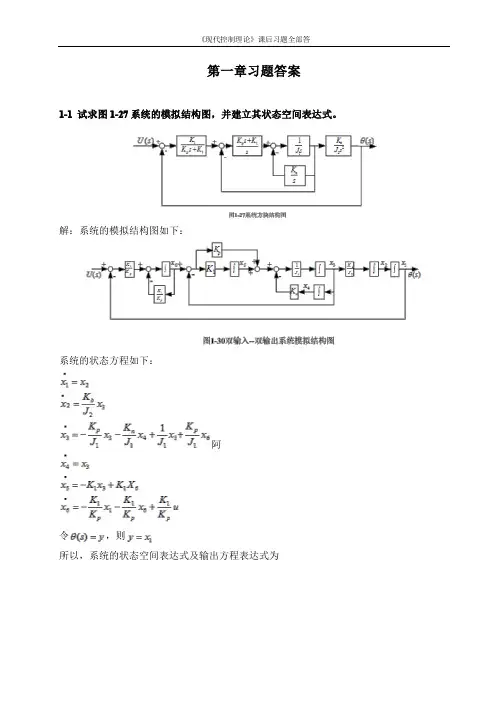
第一章习题答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解：系统的模拟结构图如下：)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙阿令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CC L L R L L R x x x 。

V(x)对所有x都具有连续的一阶偏导 V(x)正定，即当x=0，V(x)=0; x0，V(x) >0; V(x)沿状态轨迹方向计算的时间导数V’(x)满足条件： V’(x)半负定(0)：xe李亚普诺夫意义下稳定； V’(x)负定，或V’(x)半负定(0)但除x=0外V’(x)不恒为零：
xe渐近稳定。 渐近稳定时，若||x||时， V(x) ： xe大范围渐近
M满秩，M=？注意矩阵维数
能观
特殊情况判别：对角线，特征值互异；约当阵，特征值 有重复
N满秩，N=？注意矩阵维数
离散时间系统的能控能观性判别M, N->G, H。
第三章复习要点
3、标准型及转化 (单输入单输出，系统能控)
标准型：
能控标准I型 A (I在右上角)，B=(0, … 0, 1)T，C 能控标准II型 A (I在左下角), B=(1, 0, … 0)T ，C 能观标准I型 A (I在右上角) ，B，C=(1, 0, …, 0) 能观标准II型 A(I在左下角)，B，C= (0, …, 0 1) 直接写出传递函数： 能控I，能观II
原理：状态反馈增益矩阵K… 结构图？ 特点：改变闭环系统的特征值，可配置极点
2、输出反馈
原理：输出反馈增益矩阵H… 结构图？ 特点：
3、闭环系统的能控性、能观性
状态反馈不改变系统的能控性，但不保证能观性不变 输出反馈不改变系统的能控性和能观性
第五章复习要点
4、极点配置
状态反馈：前提：系统完全能控
第二章 系统解的表达式
要求内容：
包括线性定常系统状态方程齐次解，矩阵指数函数和 状态转移矩阵的概念及其计算方法，线性定常系统状 态方程的非齐次解，离散系统状态方程解，连续时间 系统状态方程离散化

第一章计算机控制系统概述1、计算机控制系统的概念是什么计算机控制系统是以计算机技术、控制理论及自动化技术相结合并应用于工业生产过程的结果，是以自动控制理论为基础，以计算机为手段的控制系统。

2、计算机系统由哪些部分组成并画出方框图。

计算机控制系统由计算机、外部设备、操作台、输入通道、输出通道、检测装置、执行机构、被控对象以及相应的软件组成。

3、计算机控制系统的主要性能指标有哪些稳定性/动态指标/稳态指标/能控性与能观性4、计算机控制系统的主要特点有哪些各项连续控制系统计算机控制系统信号形式都是模拟信号模拟信号、数字信号皆有控制规律实现由模拟电路实现由计算机通过程序实现控制形式整个过程始终连续控制整个过程始终离散控制控制器作用一个控制器控制一个回路一个控制器分时控制多个回路功能强度简单控制具有丰富的指令系统和很强的逻辑判断功能自动化程度自动化程度低便于实现控制与管理的一体化5、计算机控制系统是怎样分类的按功能和控制规律可分为几类一、按控制系统的功能及结构特点分类①操作指导控制系统②直接数字控制系统DDC③监督控制系统SCC④计算机分级控制⑤集散控制系统DCS⑥现场总线控制系统FCS二、按控制规律分类 ①程序和顺序控制 ② PID 控制 ③最少拍控制 ④复杂规律的控制 ⑤智能控制第二章 离散控制系统及Z 变换分析法1、计算机控制系统的信号形式有哪些连续模拟信号:时间与幅值上均连续，如 r(t)、y(t)、u(t) 离散模拟信号:时间是离散的，幅值上连续，如y*(t)、u*(t) 离散数字信号:时间离散的，幅值为数字量，如y(kT)、u(kT)2、香农(Shannon)采样定理是如何描述的一个连续时间信号f(t)，设其频带宽度是有限的，其最高频率为ωmax(或fmax)，如果在等间隔点上对该信号f(t)进行连续采样，为了使采样后的离散信号f *(t)能包含原信号f(t)的全部信息量。

则采样角频率只有满足下面的关系： ωs ≥2ωmax采样后的离散信号f *(t)才能够无失真地复现f(t)。